Abstract
The application of fractional calculus to interval analysis is vital for the precise derivation of integral inequalities on set-valued mappings. The objective of this article is to reformulated the well-known Hermite–Hadamard inequality into various new variants via fractional integral operator (Riemann–Liouville) and generalize the various previously published results on set-valued mappings via center and radius order relations using harmonical h-convex functions. First, using these notions, we developed the Hermite–Hadamard () inequality, and then constructed some product form of these inequalities for harmonically convex functions. Moreover, to demonstrate the correctness of these results, we constructed some interesting non-trivial examples.
MSC:
26A48; 26A51; 33B10; 39A12; 39B62
1. Introduction
Fractional calculus focuses on fractional order integrals and derivatives, as well as their applications, over real and complex domains. To generate more realistic results with fractional analysis, classical analysis arithmetic is essential. There are a wide variety of mathematical models that can be solved using fractional differential equations and integral equations. Mathematical models with fractional order have more broad and accurate conclusions than classical mathematical models because they are special instances of fractional order mathematical models. As opposed to integer orders, fractional theory permits handling of any number of orders, real or integer, so it is a more appropriate method. Almost no field of nonlinear disciplines or research in contemporary times is uninfluenced by methods and instruments. Many fields of engineering have numerous and fruitful applications, including electrical engineering, control theory, mechanical engineering, viscoelasticity, rheology, optics, and physics, see Refs. [1,2].
A mathematical technique called interval analysis limits errors caused by rounding and measurement in mathematical computations. The Japanese scientist Teruo Sunag has published the most leading paper on interval analysis, see Ref. [3]. There is not only a systematic investigation of the rules which govern basic operations with intervals in this publication, but also a mathematical analysis of the rules that govern them. Using only the terminal points of rational functions over intervals, the range of rational functions can be determined. The corresponding operations are also discussed for interval vectors as multidimensional intervals. Using interval arithmetic tools, a pointwise enclosure for the solution of an initial value problem is computed by enclosing the remainder term and bounding the value of a definite integral. During the last three decades, a compact interval has become an independent object in numerical analysis for verifying or enclosing solutions to a variety of mathematical problems or proving that such problems cannot be solved in a given domain. Further, here are some practical applications of interval analysis in various linear and nonlinear disciplines, see Refs. [4,5]. As we know, Hermite–Hadamard inequality is the first geometric interpretation of a convex function and it is widely used in several disciplines that involve convex optimization. We also know that in order to check the accuracy of various mathematical models based on real life, inequalities must be included to verify their existence, uniqueness, and stability. To visualize better accuracy of results, authors often use mathematical models based on nature as fractional forms, so to handle uncertainty and check the stability of differential models, authors have developed fractional forms of inequalities.
However, generalized convexity mapping is able to deal with a wide variety of problems in both applied and pure analysis. A number of well-known inequalities have been constructed using related classes of convexity, including Simpson, Ostrowski, Opial, Hardy, and the famous Hermite–Hadamard, which has been extended to interval-valued functions. To construct these inequalities, various authors employ different notions of convex classes and integral operators, including the standard Riemann integral, Caputo Fabrizo, Riemann–Liouville, and k-fractional operators. Wang et al. [6] investigated several identities for a differentiable functions involving Hadamard fractions and Riemann–Liouville fractions, and proved some inequalities based on s-convex, r-convex, m-convex, -convex, etc. In addition, Işcan [7] utilized the notion of preinvexity to obtain various new forms of Hermite–Hadamard via fractional operators. Pachpette established the refined form of Hermite–Hadamard inequalities for the product of two convex mappings using fractional integral in [8]. Based on Riemann–Liouville fractional integrals, Chan established various Hermite–Hadamard inequalities for products of convex functions, see Ref. [9]. Using the Riemann–Liouville fractional integral operator, Khan et al. [10] developed () inequalities in an expanded form for harmonically convex mappings in the context of fuzzy interval-valued setting. Shi et al. [11] began by developing Hermite–Hadamard inequality results using h-convex and harmonically h-convex functions, and extended their own work to coordinated convex interval-valued functions through fractional integrals. With the idea of h-convexity, Dragomir developed Hermite–Hadamard inequalities using Riemann–Liouville fractional integrals, see Ref. [12]. Khan and his colleagues created Hermite–Hadamard inequalities using left-right set-valued functions via Riemann–Liouville integral operators, see Ref. [13]. Recently, Afzal et al. [14] employed the notions of Riemann integral operator via center-radius order relations to develop a more generalized form of double inequality for harmonically - convex mappings. Sharma et al. [15] developed Hermite–Hadamard inequalities based on general h-harmonic preinvex functions for real-valued stochastic processes. Based on exponentially -preinvexity, Chen et al. [16] developed various variants of Hermite–Hadamard inequality based on Riemann–Liouville fractional integrals. Awan et al. [17] established several new Hermite–Hadamard type inequalities by using n-polynomial mappings of harmonically convex functions. Viloria et al. [18] developed Hermite–Hadamard-type inequalities for harmonically convex functions based on n-coordinates. Kunt et al. [19] developed new fractional integral inequalities of Hermite–Hadamard–Fejer type for harmonically convex functions. Moshin et al. [20] developed different variants of Hermite–Hadamard inequalities with bounds through q-calculus. For some recent developments regarding developed inequalities, see Refs. [21,22,23,24,25,26].
Bhunia examined the optimality of multi-objective optimization problems using various interval metrics in 2014. He also introduced the concept of center-radius order using radius and interval midpoints, see Ref. [27]. A recent work by the following authors uses Bhunia’s notion to construct various types of inequalities more precisely based on different integral operators, see Refs. [28,29,30,31]. According to our literature review, most of these inequalities are caused by partial order relations. In the case of harmonically h-convex functions, the main advantage of center-radius order relations is that the inequality term can be predicted more accurately. This argument can be proved by valuable examples of proposed theorems. As a result, it is important to understand how total order relations can be used to analyze a variety of convex mapping classes.
This study is significant and original because it investigates the center-radius order relationship in relation to the harmonic convexity and fractional integral for the first time. It suggests a novel approach to inequalities research that includes set-valued functions. This order relation’s main benefit is that it has full order, which allows us to compare intervals while several other interval order relations have significant flaws that prevent us from doing so in set-valued mappings. Unlike the various partial order relations, this one can be calculated very differently, e.g.,: and , are center and interval order representation of interval, respectively, where interval =.
We are inspired by quality literature and particular articles for our research, see Refs. [13,14,28,29,30]. We developed some variants of Hermite–Hadamard inequalities on set-valued mappings via harmonically h-convex functions in conjunction with fractional integrals. Additionally, we created some examples to demonstrate their accuracy. To conclude, the article follows the following format. There is a brief background provided in Section 2. The main findings are discussed in Section 3. A brief conclusion is provided in Section 4.
2. Preliminaries
There are a few terms used in the paper without being defined, see Ref. [28]. You will find it very helpful throughout the paper to be familiar with a few basic arithmetic principles related to interval analysis. As a result, all the intervals and positive intervals can be represented as and of set of real . The following are the definitions for scalar multiplication and interval addition:
where .
Let , then and are the representation of center- radius form of interval , respectively. The representation of interval can be defined as:
Definition 1
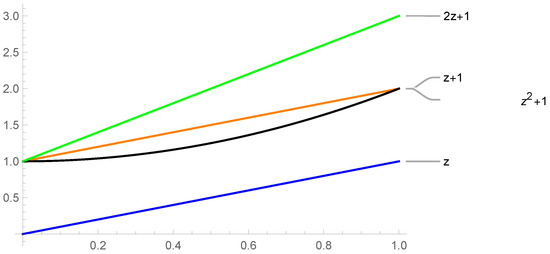

Figure 1.
The figure illustrates the correctness of -order relationships defined in Definition 1.
Theorem 1
(See [28]). Let be defined as for every and are Riemann integrable () over interval . Then, we said that Ψ is over , and
It is most efficient to carry integrals and derivatives to fractional orders or orders other than integers and natural numbers. We describe the idea of the () integral operator to facilitate discussions of fractional integrals.
Definition 2.
Let . The integrals and of order and are defined as:
and
Corollary 1
(See [14]). Let be given by , with , then
and
Theorem 2
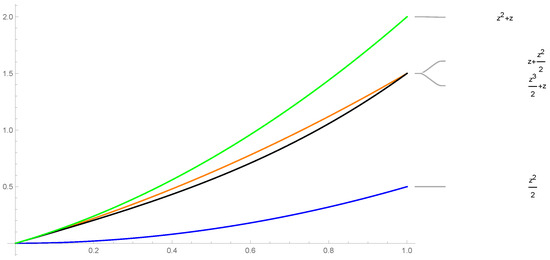

Figure 2.
The figure illustrates the validity of Theorem 2.
We will use some interesting examples to demonstrate the above theorem.
Example 1.
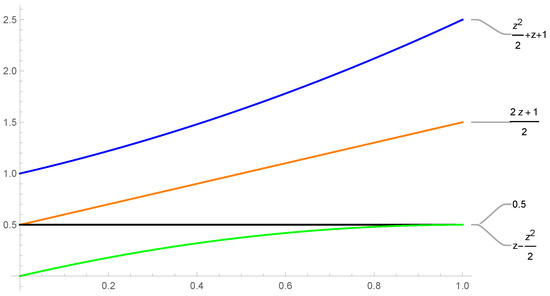

Figure 3.
.
From Definition 1, one has , ∀ .
Since,
and
From Theorem 2, we have
Definition 3
([28]). Let and a function is said to be a harmonically h-convex function, or that , if ∀ and one has
If in (1) ≤ is altered with ≥, then it is called harmonical h-concave function or
The following is the newly introduced class of harmonic-convex () for order relations:
Definition 4
([22]). Let and a function is harmonically -h-convex function, or that , if ∀ and one has
Example 2.
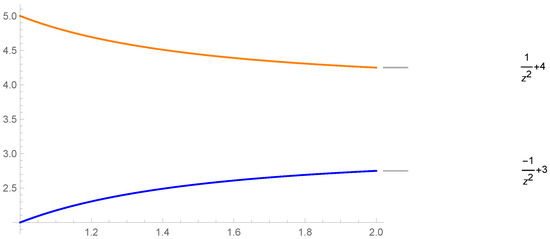
Consider and for all If is defined as (Figure 4).

Figure 4.
In the above figure, is shown as blue and as orange, respectively.
Then,
It is obvious are harmonically h-convex functions over .
Remark 1.
- If , Definition 4 assimilates harmonic -P-function.
- If , Definition 4 assimilates harmonic -h-Godunova–Levin function.
- If , Definition 4 assimilates harmonic -s-convex function.
- If , Definition 4 assimilates harmonic -s-Godunova–Levin function.
3. Main Results
Our goal in this section is to prove some inequalities of Hermite–Hadamard type for set-valued harmonically -h-convex mappings involving fractional integrals.
Theorem 3.
Let be () such that and with If , then the following inequality holds:
Proof.
Since is a harmonically -h-convex function, one has
Substitute and in (4); we have
Multiplying by in (5) and integrating over one has
From Theorem 3, we have
Similarly, one has
Hence, by the inequality (6), we obtain
As a result, first inequality (12) is proven. In order to prove its other side from definition, we have
and
Multiplying by in (9) and integrating over one has
As a result, the proof has been completed. □
Remark 2.
- (i)
- If and with , then we obtain the following output, see Ref. [32].
- (ii)
- If and , then we obtain the following output, see Ref. [33].
Example 3.
Let , and ∀ . If is defined as
then, we have
and
Consequently, Theorem 3 is verified.
Theorem 4.
Let be () such that and with If , then the following inequality holds:
where
and
Example 4.
Let , and ∀ . If are defined as
then, we have
and
Consequently, Theorem 4 is verified.
Theorem 5.
Let be () such that and with If , then the following inequality holds:
Proof.
For one has
Since , one has
Multiplying by in (24) and integrating over one has
Inequality (25) was achieved by changing the integrating variable:
□
Example 5.
Let , and ∀ . If are defined as
then, we have
and
Consequently, Theorem 5 is verified.
Theorem 6.
Let be () such that and with If , then the following inequality holds:
Proof.
Since , one has
For and we obtain
Similarly, we obtain
Example 6.
Let , and ∀ . If are defined as
then, we have
and
Consequently, Theorem 6 is verified.
Theorem 7.
Let be () such that and with If , then the following inequality holds:
Proof.
Since , one has
and
Similarly, we obtain
Multiplying by in (36) and integrating over one has
By using Theorem 3 in relation (37), we obtain our desired inequality. □
Example 7.
Let , and ∀ . If are defined as
then, we have
and
Consequently, Theorem 7 is verified.
Theorem 8.
Let be () such that and with If , then the following inequality holds:
Proof.
Since , one has
For and we obtain
Multiplying by in (39) and integrating over one has
Using Theorem 3 in the relation (40), we have
Similarly, we obtain
As a result, the first inequality (38) is proven. In order to prove the second inequality, since is a harmonically -h-convex function, one has
and
Multiplying by in (43) and integrating over one has
Inequality (38) was achieved by changing the integrating variable. □
Example 8.
Let , and ∀ . If are defined as
Then, all the assumptions of Theorem (8) are satisfied.
Theorem 9.
Let be () such that and with If , then the following inequality holds:
Proof.
Since , one has
For and we have
Multiplying by in (45) and integrating over we have
By using Theorem 3 in the relation (46), we have
Similarly, we obtain
As a result, the first inequality (44) is proven. In order to prove the second inequality, since is a harmonically -h-convex function, one has
and
Multiplying by in (49) and integrating over one has
As a result, the proof has been completed. □
Example 9.
Let , and ∀ . If are defined as
Then, all the assumptions of Theorem (9) are satisfied.
Theorem 10.
Let be () such that and with If , then the following inequality holds:
4. Conclusions
In this work, we construct some Hermite–Hadamard inequalities in a novel manner using harmonical convex functions via Riemann–Liouville integral operator. We do this by using the set-valued mappings for center and radius order. We can evaluate Hermite–Hadamard inequalities from a new angle by combining these ideas. Since it is well known that this fractional integral generalizes the conventional Riemann integral, in this study we generalize various previous findings. A few striking examples are also provided to demonstrate the validity of the conclusions that have been proven. More investigation into equivalent inequalities using different integral operators and convexity types will be fascinating. Additionally, readers will have to construct these findings using fuzzy environments, time scale calculus, and coordinates.
Author Contributions
Conceptualization, W.A. and Y.A.; investigation, W.A.; methodology, W.A. and Y.A.; validation, W.A.; visualization, Y.A.; writing—original draft, W.A.; writing review and editing, W.A. and Y.A. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through large group Research Project under grant number RGP2/366/44.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Baleanu, D.; Jajarmi, A.; Mohammadi, H. A new study on the mathematical modelling of human liver with Caputo–Fabrizio fractional derivative. Chaos Solitons Fractals 2020, 134, 109705. [Google Scholar] [CrossRef]
- Shaked, M.; Shanthikumar, J.G. Stochastic Convexity and Its Applications. Adv. Appl. Probab. 1988, 20, 427–446. [Google Scholar] [CrossRef]
- Sunaga, T. Theory of an interval algebra and its application to numerical analysis. J. Ind. Appl. Math. 2009, 26, 125–143. [Google Scholar] [CrossRef]
- Snyder, J.M. Interval analysis for computer graphics. In Proceedings of the 19th Annual Conference on Computer Graphics and Interactive Techniques, Chicago, IL, USA, 27–31 July 1992; pp. 121–130. [Google Scholar]
- Zhang, X.; Shabbir, K.; Afzal, W.; Xiao, H.; Lin, D. Hermite–Hadamard and Jensen-Type Inequalities via Riemann Integral Operator for a Generalized Class of Godunova–Levin Functions. J. Math. 2022, 2022, e3830324. [Google Scholar] [CrossRef]
- Wang, J.R.; Feckan, M. Fractional Hermite–Hadamard Inequalities; de Gruyter: Berlin, Germany, 2018; Volume 22. [Google Scholar]
- Işcan, I. Hermite–Hadamard’s inequalities for preinvex functions via fractional integrals and related fractional inequalities. arXiv 2012, arXiv:1204.0272. [Google Scholar]
- Pachpatte, B.G. On some inequalities for convex functions. RGMIA Res. 2003, 6, 1–9. [Google Scholar]
- Chen, F. A note on Hermite–Hadamard inequalities for products of convex functions via Riemann–Liouville fractional integrals. Italian J. Pure Appl. Math. 2014, 33, 299–306. [Google Scholar]
- Khan, M.B.; Zaini, H.G.; Santos-García, G. Riemann–Liouville Fractional Integral Inequalities for Generalized Harmonically Convex Fuzzy-Interval-Valued Functions. Int. J. Comput. Intell. Syst. 2022, 15, 28. [Google Scholar] [CrossRef]
- Shi, F.; Ye, G.; Zhao, D.; Liu, W. Some fractional Hermite–Hadamard type inequalities for interval-valued functions. Mathematics 2020, 8, 534. [Google Scholar] [CrossRef]
- Dragomir, S.S. Hermite–Hadamard type inequalities for generalized Riemann–Liouville fractional integrals of h-convex functions. Math. Methods Appl. Sci. 2021, 44, 2364–2380. [Google Scholar] [CrossRef]
- Khan, M.B.; Macías-Díaz, J.E.; Treanțǎ, S.; Soliman, M.S.; Zaini, H.G. Hermite–Hadamard Inequalities in Fractional Calculus for Left and Right Harmonically Convex Functions via Interval-Valued Settings. Fractal Fract. 2022, 6, 178. [Google Scholar] [CrossRef]
- Afzal, W.; Shabbir, K.; Arshad, M.; Asamoah, J.K.K.; Galal, A.M. Some Novel Estimates of Integral Inequalities for a Generalized Class of Harmonical Convex Mappings by Means of Center-Radius Order Relation. J. Math. 2023, 2023, 188–192. [Google Scholar] [CrossRef]
- Sharma, N.; Mishra, R.; Hamdi, A. Hermite–Hadamard Type Integral Inequalities for Multidimensional General h-Harmonic Preinvex Stochastic Processes. Commun.-Stat.-Theory Methods 2022, 51, 6719–6740. [Google Scholar] [CrossRef]
- Chen, J.L. Certain generalized Riemann–Liouville fractional integrals inequalities based on exponentially (h,m)-preinvexity. J. Math. Anal. Appl. 2023, 1, 127731. [Google Scholar] [CrossRef]
- Awan, M.U.; Akhtar, N.; Iftikhar, S.; Noor, M.A.; Chu, Y.-M. New Hermite–Hadamard Type Inequalities for n-Polynomial Harmonically Convex Functions. J. Inequal. Appl. 2020, 2020, 125. [Google Scholar] [CrossRef]
- Viloria, J.M.; Cortez, M.V. Hermite–Hadamard Type Inequalities for Harmonically Convex Functions on n-Coordinates. Appl. Math. Inf. Sci. Lett. 2018, 6, 53–58. [Google Scholar] [CrossRef] [PubMed]
- Kunt, M.; İşcan, İ.; Yazıcı, N.; Gözütok, U. On New Inequalities of Hermite–Hadamard–Fejer Type for Harmonically Convex Functions via Fractional Integrals. arXiv 2016, arXiv:1409.5243. [Google Scholar] [CrossRef] [PubMed]
- Bin-Mohsin, B.; Awan, M.U.; Noor, M.A.; Riahi, L.; Noor, K.I.; Almutairi, B. New Quantum Hermite–Hadamard Inequalities Utilizing Harmonic Convexity of the Functions. IEEE Access 2019, 7, 20479–20483. [Google Scholar] [CrossRef]
- Afzal, W.; Abbas, M.; Hamali, W.; Mahnashi, A.M.; Sen, M.D.L. Hermite–Hadamard-Type Inequalities via Caputo–Fabrizio Fractional Integral for h-Godunova–Levin and (h1,h2)-Convex Functions. Fractal Fract. 2023, 7, 687. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, C.; Zhou, Y. New Generalized Hermite–Hadamard Type Inequalities and Applications to Special Means. J. Inequal. Appl. 2013, 2013, 325. [Google Scholar] [CrossRef]
- Abbas, M.; Afzal, W.; Botmart, T.; Galal, A.M. Jensen, Ostrowski and Hermite–Hadamard Type Inequalities for h-Convex Stochastic Processes by Means of Center-Radius Order Relation. AIMS Math. 2023, 8, 16013–16030. [Google Scholar] [CrossRef]
- Rostamian Delavar, M.; De La Sen, M. Some Generalizations of Hermite–Hadamard Type Inequalities. SpringerPlus 2016, 5, 1661. [Google Scholar] [CrossRef]
- Sharma, N.; Singh, S.K.; Mishra, S.K.; Hamdi, A. Hermite–Hadamard-Type Inequalities for Interval-Valued Preinvex Functions via Riemann–Liouville Fractional Integrals. J. Inequal. Appl. 2021, 2021, 98. [Google Scholar] [CrossRef]
- Lai, K.K.; Bisht, J.; Sharma, N.; Mishra, S.K. Hermite–Hadamard-Type Fractional Inclusions for Interval-Valued Preinvex Functions. Mathematics 2022, 10, 264. [Google Scholar] [CrossRef]
- Bhunia, A.K.; Samanta, S.S. A study of interval metric and its application in multi-objective optimization with interval objectives. Comput. Ind. Eng. 2014, 74, 169–178. [Google Scholar] [CrossRef]
- Liu, W.; Shi, F.; Ye, G.; Zhao, D. The Properties of Harmonically cr-h-Convex Function and Its Applications. Mathematics 2022, 10, 2089. [Google Scholar] [CrossRef]
- Saeed, T.; Afzal, W.; Abbas, M.; Treanţă, S.; De la Sen, M. Some New Generalizations of Integral Inequalities for Harmonical cr-(h1,h2)-Godunova-Levin Functions and Applications. Mathematics 2022, 10, 4540. [Google Scholar] [CrossRef]
- Afzal, W.; Abbas, M.; Macías-Díaz, J.E.; Treanta, S. Some H-Godunova–Levin Function Inequalities Using Center Radius (cr) Order Relation. Fractal Fract. 2022, 6, 518. [Google Scholar] [CrossRef]
- Vivas-Cortez, M.; Ramzan, S.; Awan, M.U.; Javed, M.Z.; Khan, A.G.; Noor, M.A. I.V-CR-γ-Convex Functions and Their Application in Fractional Hermite–Hadamard Inequalities. Symmetry 2023, 15, 1405. [Google Scholar] [CrossRef]
- Işcan, İ.; Wu, S. Hermite–Hadamard type inequalities for harmonically convex functions via fractional integrals. Appl. Math. Comput. 2014, 238, 237–244. [Google Scholar] [CrossRef]
- Chen, F. Extensions of the Hermite–Hadamard Inequality for Harmonically Convex Functions via Fractional Integrals. Appl. Math. Comput. 2015, 268, 121–128. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).