Change-Point Detection in the Volatility of Conditional Heteroscedastic Autoregressive Nonlinear Models
Abstract
:1. Introduction
2. Model and Assumptions
2.1. Notation and Assumptions
- (A1)
- The common fourth order moment of the is finite.
- (A2)
- The function is twice continuously differentiable, a.e., with respect to in some neighborhood of .
- The function is twice continuously differentiable, a.e., with respect to in some neighborhood of .
- There exists a positive function such that , and
- (A3)
- There exists a positive function such that , and for all , and ,
- (A4)
- The sequence is stationary and satisfies either of the following two conditions:
- -mixing with mixing coefficient satisfying and for some ;
- -mixing with mixing coefficient satisfying and for some .
2.2. Parameter Estimation
2.2.1. Conditional Least-Squares Estimation
- and attains a relative minimum at ;
- assuming fixed, and attains a relative minimum at .
3. Change-Point Study
3.1. Change-Point Test and Change Location Estimation
3.2. Asymptotics
3.2.1. Asymptotic Distribution of the Test Statistic
- 1.
- ;
- 2.
- ,
3.2.2. Rate of Convergence of the Change Location Estimator
3.2.3. Limit Distribution of the Location Estimator
4. Practical Consideration
| Algorithm 1 Change-point location estimation |
|
4.1. Example 1
4.2. Example 2
4.3. Comparison with Some Recent Algorithms
4.4. Application to Real Data
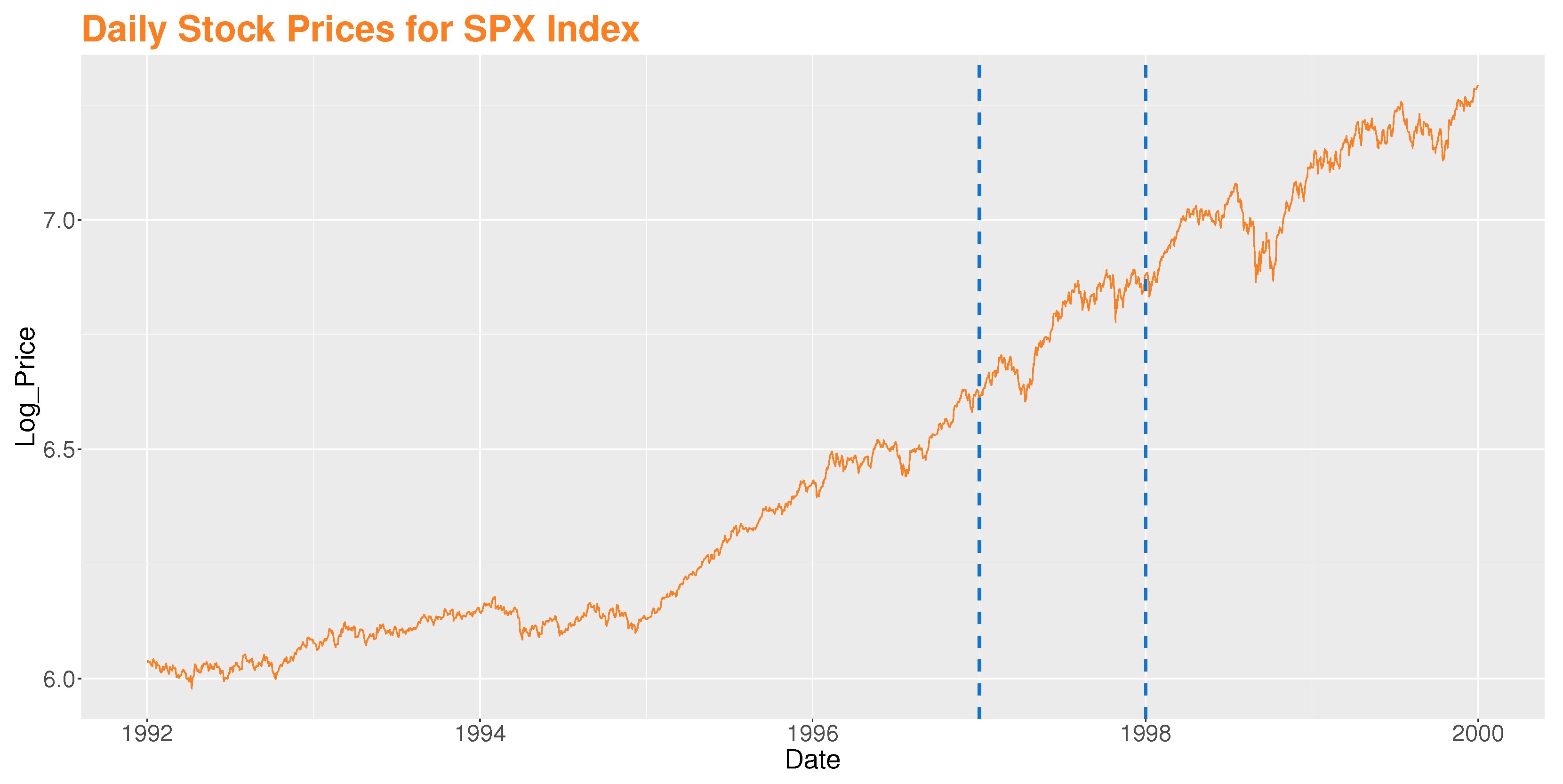
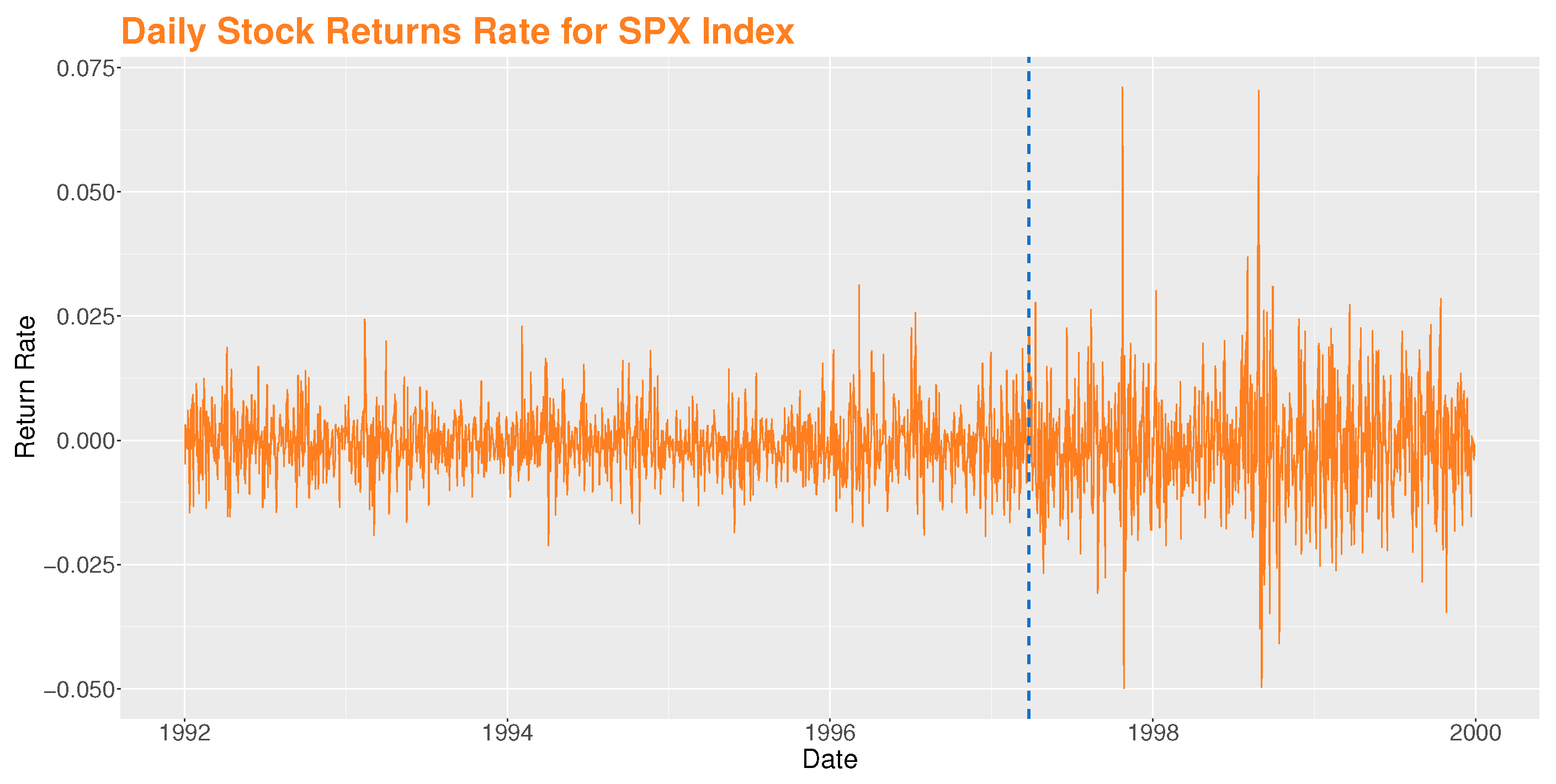
4.4.1. USA Stock Market
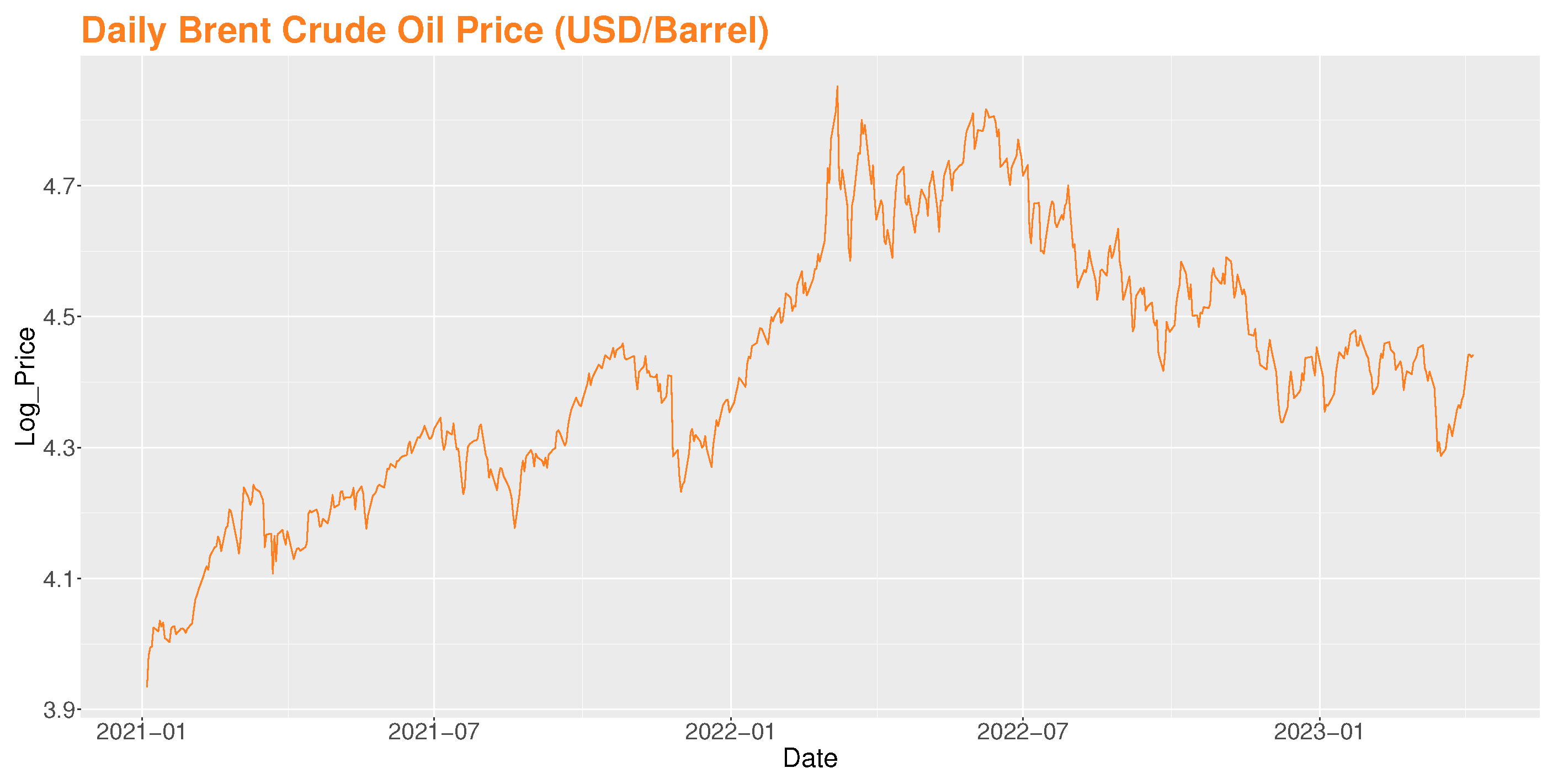
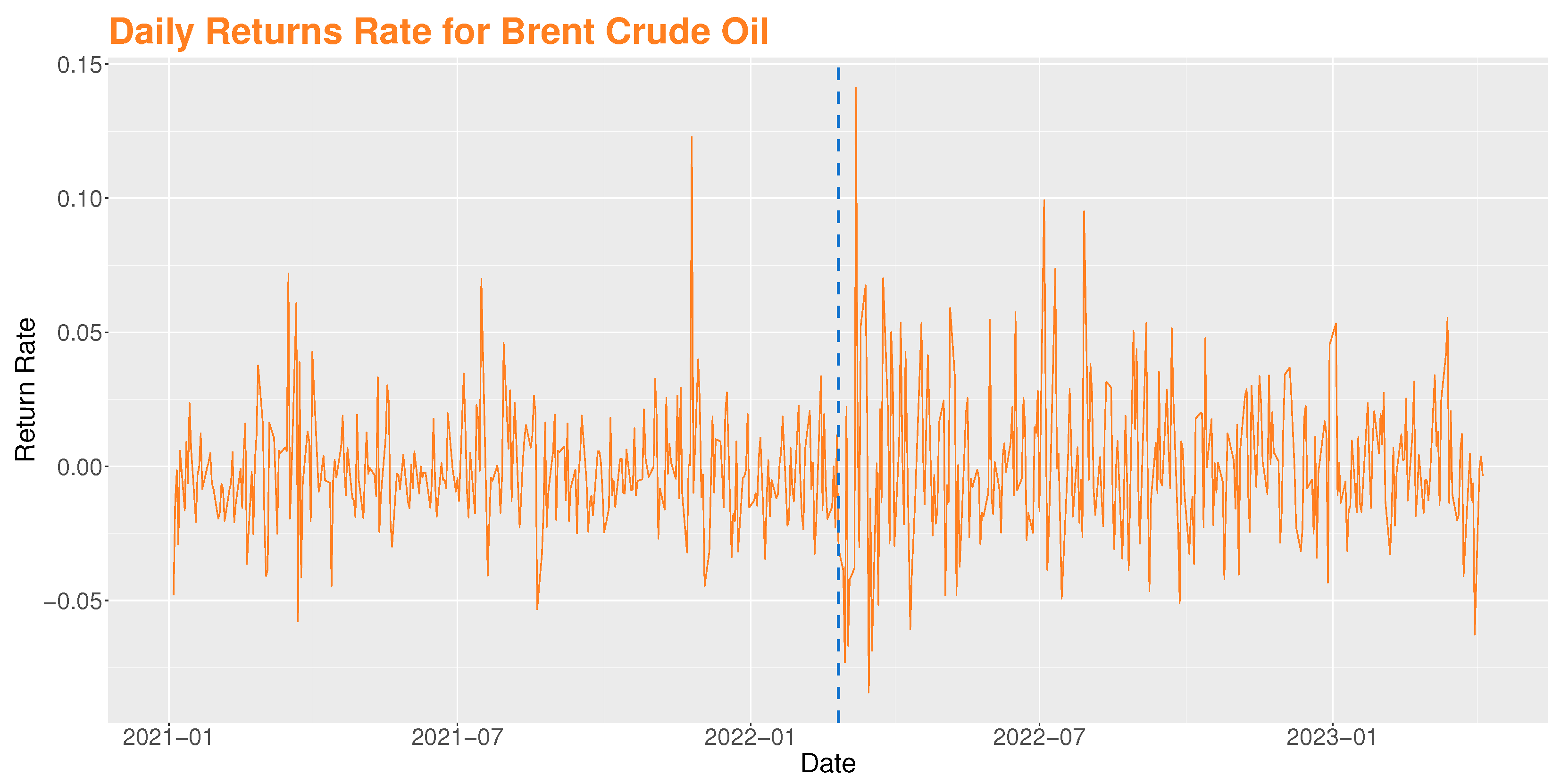
4.4.2. Brent Crude Oil
4.4.3. Comparison with WBS and ICSS
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Preliminary Results
Appendix A.2. Proofs of Theorems
Appendix A.2.1
Appendix A.2.2
Appendix A.2.3
Appendix A.3. Proof of Propositions
References
- Hocking, T.D.; Schleiermacher, G.; Janoueix-Lerosey, I.; Boeva, V.; Cappo, J.; Delattre, O.; Bach, F.; Vert, J.P. Learning smoothing models of copy number profiles using breakpoint annotations. BMC Bioinform. 2013, 14, 164. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Wright, A.; Hauskrecht, M. Change-point detection method for clinical decision support system rule monitoring. Artif. Intell. Med. 2018, 91, 49–56. [Google Scholar] [CrossRef]
- Lavielle, M.; Teyssiere, G. Adaptive detection of multiple change-points in asset price volatility. In Long Memory in Economics; Springer: Berlin/Heidelberg, Germany, 2007; pp. 129–156. [Google Scholar]
- Frick, K.; Munk, A.; Sieling, H. Multiscale change point inference. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2014, 76, 495–580. [Google Scholar] [CrossRef]
- Bai, J.; Perron, P. Estimating and Testing Linear Models with Multiple Structural Changes. Econometrica 1998, 66, 47–78. [Google Scholar] [CrossRef]
- Page, E.S. Continuous inspection schemes. Biometrika 1954, 41, 100–115. [Google Scholar] [CrossRef]
- Page, E. A test for a change in a parameter occurring at an unknown point. Biometrika 1955, 42, 523–527. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change-point problem. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Lombard, F. Rank tests for changepoint problems. Biometrika 1987, 74, 615–624. [Google Scholar] [CrossRef]
- Scariano, S.M.; Watkins, T.A. Nonparametric point estimators for the change-point problem. Commun. Stat. Theory Methods 1988, 17, 3645–3675. [Google Scholar] [CrossRef]
- Bryden, E.; Carlson, J.B.; Craig, B. Some Monte Carlo Results on Nonparametric Changepoint Tests; Federal Reserve Bank of Cleveland: Cleveland, OH, USA, 1995. [Google Scholar]
- Bhattacharya, P.; Zhou, H. Nonparametric Stopping Rules for Detecting Small Changes in Location and Scale Families. In From Statistics to Mathematical Finance; Springer: Cham, Switzerland, 2017; pp. 251–271. [Google Scholar]
- Hinkley, D.V. Inference about the change-point in a sequence of random variables. Biometrika 1970, 57, 1–17. [Google Scholar] [CrossRef]
- Hinkley, D.V. Time-ordered classification. Biometrika 1972, 59, 509–523. [Google Scholar] [CrossRef]
- Yao, Y.C.; Davis, R.A. The asymptotic behavior of the likelihood ratio statistic for testing a shift in mean in a sequence of independent normal variates. Sankhyā Indian J. Stat. Ser. A 1986, 48, 339–353. [Google Scholar]
- Csörgö, M.; Horváth, L. Nonparametric tests for the changepoint problem. J. Stat. Plan. Inference 1987, 17, 1–9. [Google Scholar] [CrossRef]
- Chen, J.; Gupta, A. Change point analysis of a Gaussian model. Stat. Pap. 1999, 40, 323–333. [Google Scholar] [CrossRef]
- Horváth, L.; Steinebach, J. Testing for changes in the mean or variance of a stochastic process under weak invariance. J. Stat. Plan. Inference 2000, 91, 365–376. [Google Scholar] [CrossRef]
- Antoch, J.; Hušková, M. Permutation tests in change point analysis. Stat. Probab. Lett. 2001, 53, 37–46. [Google Scholar] [CrossRef]
- Hušková, M.; Meintanis, S.G. Change point analysis based on empirical characteristic functions. Metrika 2006, 63, 145–168. [Google Scholar] [CrossRef]
- Zou, C.; Liu, Y.; Qin, P.; Wang, Z. Empirical likelihood ratio test for the change-point problem. Stat. Probab. Lett. 2007, 77, 374–382. [Google Scholar] [CrossRef]
- Gombay, E. Change detection in autoregressive time series. J. Multivar. Anal. 2008, 99, 451–464. [Google Scholar] [CrossRef]
- Berkes, I.; Gombay, E.; Horváth, L. Testing for changes in the covariance structure of linear processes. J. Stat. Plan. Inference 2009, 139, 2044–2063. [Google Scholar] [CrossRef]
- Inclan, C.; Tiao, G.C. Use of cumulative sums of squares for retrospective detection of changes of variance. J. Am. Stat. Assoc. 1994, 89, 913–923. [Google Scholar]
- Fryzlewicz, P.; Subba Rao, S. Multiple-change-point detection for auto-regressive conditional heteroscedastic processes. J. R. Stat. Soc. Ser. B Stat. Methodol. 2014, 76, 903–924. [Google Scholar] [CrossRef]
- Härdle, W.; Tsybakov, A. Local polynomial estimators of the volatility function in nonparametric autoregression. J. Econom. 1997, 81, 223–242. [Google Scholar] [CrossRef]
- Härdle, W.; Tsybakov, A.; Yang, L. Nonparametric vector autoregression. J. Stat. Plan. Inference 1998, 68, 221–245. [Google Scholar] [CrossRef]
- Bardet, J.M.; Wintenberger, O. Asymptotic normality of the Quasi Maximum Likelihood Estimator for multidimensional causal processes. Ann. Stat. 2009, 37, 2730–2759. [Google Scholar] [CrossRef]
- Bardet, J.M.; Kengne, W.; Wintenberger, O. Multiple breaks detection in general causal time series using penalized quasi-likelihood. Electron. J. Stat. 2012, 6, 435–477. [Google Scholar] [CrossRef]
- Bardet, J.M.; Kengne, W. Monitoring procedure for parameter change in causal time series. J. Multivar. Anal. 2014, 125, 204–221. [Google Scholar] [CrossRef]
- Ngatchou-Wandji, J. Estimation in a class of nonlinear heteroscedastic time series models. Electron. J. Stat. 2008, 2, 40–62. [Google Scholar] [CrossRef]
- Bai, J. Least squares estimation of a shift in linear processes. J. Time Ser. Anal. 1994, 15, 453–472. [Google Scholar] [CrossRef]
- Hawkins, D.M. Testing a sequence of observations for a shift in location. J. Am. Stat. Assoc. 1977, 72, 180–186. [Google Scholar] [CrossRef]
- Csörgö, M.; Horváth, L. Limit Theorems in Change-Point Analysis; Wiley: Hoboken, NJ, USA, 1997. [Google Scholar]
- Joseph, N.W.; Echarif, E.; Harel, M. On change-points tests based on two-samples U-Statistics for weakly dependent observations. Stat. Pap. 2022, 63, 287–316. [Google Scholar]
- Antoch, J.; Hušková, M.; Veraverbeke, N. Change-point problem and bootstrap. J. Nonparametr. Stat. 1995, 5, 123–144. [Google Scholar] [CrossRef]
- Bhattacharya, P.K. Maximum likelihood estimation of a change-point in the distribution of independent random variables: General multiparameter case. J. Multivar. Anal. 1987, 23, 183–208. [Google Scholar] [CrossRef]
- Picard, D. Testing and estimating change-points in time series. Adv. Appl. Probab. 1985, 17, 841–867. [Google Scholar] [CrossRef]
- Yao, Y.C. Approximating the distribution of the maximum likelihood estimate of the change-point in a sequence of independent random variables. Ann. Stat. 1987, 15, 1321–1328. [Google Scholar] [CrossRef]
- Taniguchi, M.; Kakizawa, Y. Asymptotic theory of estimation and testing for stochastic processes. In Asymptotic Theory of Statistical Inference for Time Series; Springer: New York, NY, USA, 2000; pp. 51–165. [Google Scholar]
- Ngatchou-Wandji, J. Checking nonlinear heteroscedastic time series models. J. Stat. Plan. Inference 2005, 133, 33–68. [Google Scholar] [CrossRef]
- Fryzlewicz, P. Wild Binary Segmentation for multiple change-point detection. Ann. Stat. 2014, 42, 2243–2281. [Google Scholar] [CrossRef]
- Baranowski, R.; Chen, Y.; Fryzlewicz, P. not: Narrowest-over-Threshold Change-Point Detection, R package version 1; CRAN: Vienna, Austria, 2019. [Google Scholar]
- Kouamo, O.; Moulines, E.; Roueff, F. Testing for homogeneity of variance in the wavelet domain. Depend. Probab. Stat. 2010, 200, 175. [Google Scholar]
- Gan, S.; Qiu, D. On the Hájek-Rényi inequality. Wuhan Univ. J. Nat. Sci. 2007, 12, 971–974. [Google Scholar] [CrossRef]
- Billingsley, P. Convergence of Probability Measures; John Wiley: New York, NY, USA, 1968. [Google Scholar]
- Doukhan, P.; Portal, F. Principe d’invariance faible pour la fonction de répartition empirique dans un cadre multidimensionnel et mélangeant. Probab. Math. Stat. 1987, 8, 117–132. [Google Scholar]
- Wooldridge, J.M.; White, H. Some invariance principles and central limit theorems for dependent heterogeneous processes. Econom. Theory 1988, 4, 210–230. [Google Scholar] [CrossRef]
- Hall, P.; Heyde, C.C. Martingale Limit Theory and Its Application; Academic Press: Cambridge, MA, USA, 1980. [Google Scholar]
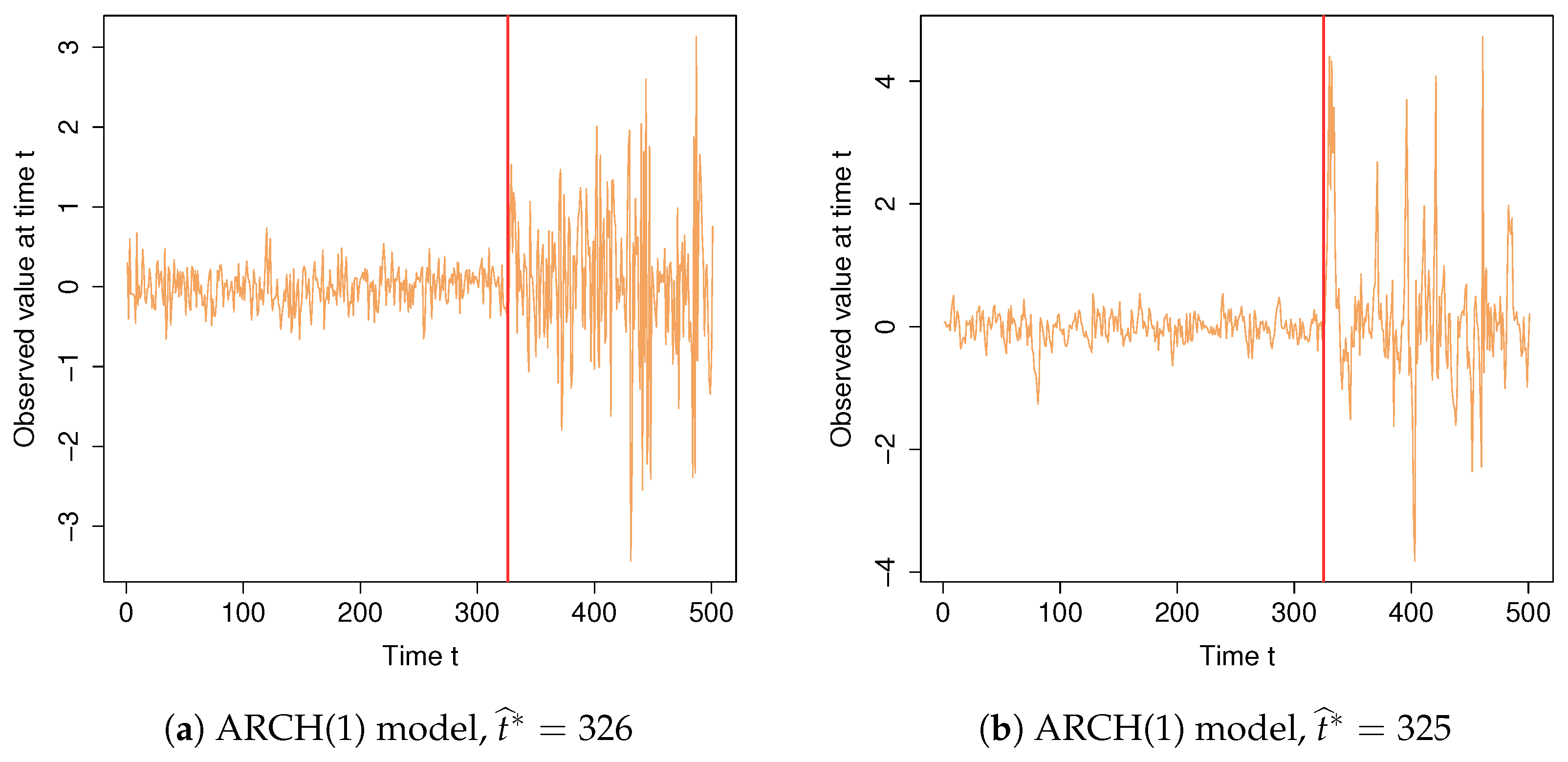
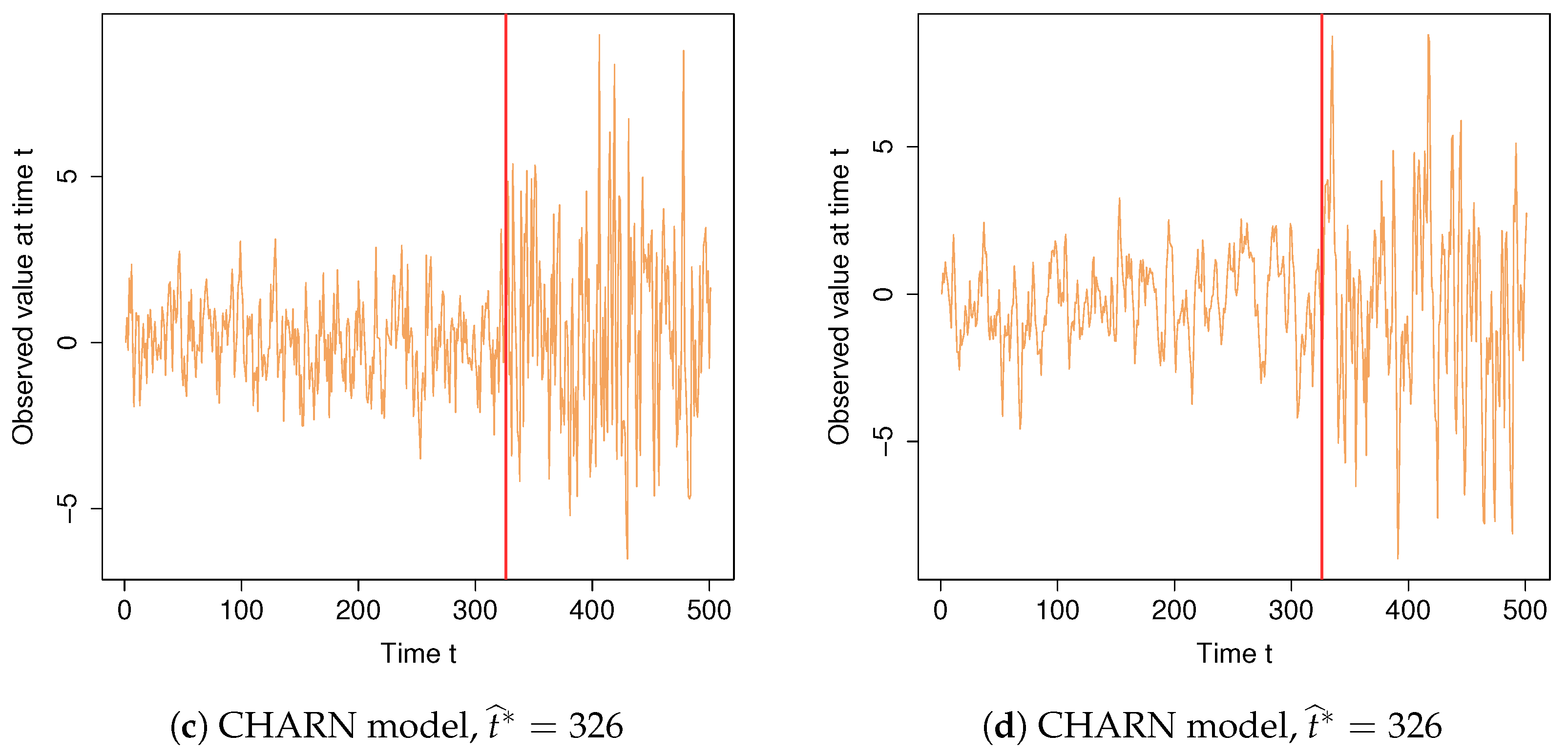
| ϕ | n | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SE | Bias | SE | Bias | SE | Bias | |||||
| 0.3 | 500 | 181 | 4.9667 | 0.1120 | 277 | 3.4284 | 0.0540 | 384 | 3.3993 | 0.0180 |
| 1000 | 287 | 3.8961 | 0.0370 | 522 | 2.4946 | 0.0220 | 767 | 2.8024 | 0.0170 | |
| 5000 | 1264 | 0.6270 | 0.0028 | 2516 | 0.6260 | 0.0032 | 3765 | 0.8172 | 0.0030 | |
| 10,000 | 2517 | 0.4398 | 0.0017 | 5015 | 0.4131 | 0.0015 | 7515 | 0.4701 | 0.0015 | |
| 0.80 | 500 | 137 | 1.8286 | 0.0240 | 258 | 0.9659 | 0.0160 | 383 | 1.0514 | 0.0160 |
| 1000 | 257 | 0.5079 | 0.0070 | 507 | 0.6687 | 0.0070 | 757 | 0.6378 | 0.0070 | |
| 5000 | 1256 | 0.1874 | 0.0012 | 2506 | 0.1750 | 0.0012 | 3755 | 0.1602 | 0.0010 | |
| 10,000 | 2506 | 0.1230 | 0.0006 | 5006 | 0.1388 | 0.0006 | 7505 | 0.1169 | 0.0005 | |
| 1.5 | 500 | 130 | 0.8538 | 0.0100 | 254 | 0.4724 | 0.0080 | 379 | 0.4611 | 0.0080 |
| 1000 | 253 | 0.2662 | 0.0030 | 504 | 0.2884 | 0.0040 | 753 | 0.2562 | 0.0030 | |
| 5000 | 1254 | 0.1344 | 0.0008 | 2503 | 0.1053 | 0.0006 | 3754 | 0.1174 | 0.0008 | |
| 10,000 | 2504 | 0.0880 | 0.0004 | 5004 | 0.0842 | 0.0004 | 7504 | 0.0753 | 0.0004 | |
| ϕ | n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SE | Bias | SE | Bias | SE | Bias | SE | Bias | ||||||
| 0.3 | 5000 | 1265 | 0.6091 | 0.0030 | 1286 | 2.6225 | 0.0072 | 3766 | 0.6596 | 0.0032 | 3776 | 1.2243 | 0.0052 |
| 10,000 | 2516 | 0.4471 | 0.0016 | 2525 | 0.7136 | 0.0025 | 7515 | 0.4182 | 0.0015 | 7523 | 0.6563 | 0.0023 | |
| 0.8 | 5000 | 1256 | 0.1701 | 0.0012 | 1260 | 0.2760 | 0.0020 | 3756 | 0.1818 | 0.0012 | 3760 | 0.2870 | 0.0020 |
| 10,000 | 2506 | 0.1482 | 0.0006 | 2510 | 0.1907 | 0.0010 | 7506 | 0.1338 | 0.0006 | 7509 | 0.1835 | 0.0009 | |
| 1.5 | 5000 | 1254 | 0.1165 | 0.0008 | 1256 | 0.1835 | 0.0012 | 3754 | 0.1154 | 0.0008 | 3756 | 0.1784 | 0.0012 |
| 10,000 | 2503 | 0.0807 | 0.0003 | 2506 | 0.1284 | 0.0006 | 7504 | 0.0776 | 0.0004 | 7506 | 0.1263 | 0.0006 | |
| ϕ | n | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SE | Bias | SE | Bias | SE | Bias | |||||
| 0.3 | 500 | 182 | 4.9959 | 0.1140 | 280 | 3.2396 | 0.0600 | 387 | 3.0412 | 0.0180 |
| 1000 | 298 | 4.3560 | 0.0480 | 525 | 2.6278 | 0.0250 | 770 | 2.3343 | 0.0200 | |
| 5000 | 1267 | 1.7941 | 0.0034 | 2517 | 0.7852 | 0.0034 | 3767 | 0.7948 | 0.0034 | |
| 10,000 | 2517 | 0.4716 | 0.0017 | 5016 | 0.4454 | 0.0016 | 7513 | 0.4245 | 0.0013 | |
| 0.8 | 500 | 139 | 2.0945 | 0.0280 | 259 | 1.0386 | 0.0180 | 384 | 0.9061 | 0.0180 |
| 1000 | 259 | 1.1755 | 0.00900 | 506 | 0.4205 | 0.0060 | 757 | 0.5427 | 0.0070 | |
| 5000 | 1256 | 0.1780 | 0.0012 | 2506 | 0.1713 | 0.0012 | 3757 | 0.2107 | 0.0014 | |
| 10,000 | 2506 | 0.1304 | 0.0006 | 5007 | 0.1375 | 0.0007 | 7506 | 0.1236 | 0.0006 | |
| 1.5 | 500 | 135 | 1.8053 | 0.0200 | 256 | 0.9248 | 0.0120 | 382 | 0.7279 | 0.0140 |
| 1000 | 255 | 0.3217 | 0.0050 | 505 | 0.3138 | 0.0050 | 755 | 0.4666 | 0.0050 | |
| 5000 | 1254 | 0.1469 | 0.0008 | 2505 | 0.1378 | 0.0010 | 3754 | 0.1325 | 0.0008 | |
| 10,000 | 2505 | 0.1010 | 0.0005 | 5004 | 0.0912 | 0.0004 | 7504 | 0.0915 | 0.0004 | |
| 0.25 | 0.50 | 0.75 | 0.25 | 0.50 | 0.75 | 0.25 | 0.50 | 0.75 | 0.25 | 0.50 | 0.75 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.051 | 0.048 | 0.05 | 0.05 | |||||||||
| 0.03 | 0.145 | 0.147 | 0.131 | 0.121 | 0.115 | 0.109 | 0.093 | 0.089 | 0.083 | 0.071 | 0.077 | 0.056 | |
| 0.05 | 0.150 | 0.151 | 0.150 | 0.124 | 0.120 | 0.115 | 0.098 | 0.090 | 0.085 | 0.085 | 0.084 | 0.060 | |
| 0.08 | 0.157 | 0.177 | 0.158 | 0.147 | 0.153 | 0.131 | 0.118 | 0.100 | 0.096 | 0.090 | 0.090 | 0.070 | |
| 0.1 | 0.191 | 0.198 | 0.177 | 0.170 | 0.174 | 0.136 | 0.145 | 0.167 | 0.101 | 0.100 | 0.110 | 0.098 | |
| 0.3 | 0.249 | 0.296 | 0.214 | 0.271 | 0.358 | 0.248 | 0.458 | 0.530 | 0.371 | 0.685 | 0.750 | 0.610 | |
| 0.5 | 0.344 | 0.465 | 0.315 | 0.421 | 0.609 | 0.433 | 0.765 | 0.891 | 0.780 | 0.974 | 0.998 | 0.992 | |
| 0.7 | 0.413 | 0.561 | 0.422 | 0.591 | 0.803 | 0.616 | 0.932 | 0.978 | 0.971 | 0.995 | 0.998 | 0.998 | |
| 0.9 | 0.477 | 0.710 | 0.532 | 0.708 | 0.887 | 0.787 | 0.971 | 0.996 | 0.993 | 0.998 | 0.999 | 0.999 | |
| 1.1 | 0.577 | 0.806 | 0.654 | 0.808 | 0.946 | 0.897 | 0.985 | 0.998 | 0.999 | 0.999 | 1.000 | 1.000 | |
| 1.3 | 0.634 | 0.838 | 0.721 | 0.863 | 0.964 | 0.952 | 0.990 | 0.999 | 0.999 | 1.000 | 1.000 | 1.000 | |
| 1.5 | 0.640 | 0.860 | 0.800 | 0.907 | 0.967 | 0.967 | 0.997 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| Methods | |||||||
|---|---|---|---|---|---|---|---|
| LS | 100 | 39 | 70 | 31 | 79 | 28 | 78 |
| WBS | 46∣43 | 87∣90 | 38∣39 | 82∣80 | 29∣30 | 78∣76 | |
| NOT | 51∣55 | 96 | 38∣42 | 79∣82∣91∣94 | 38∣35 | 78∣82 | |
| ICSS | 42∣48 | 68 | 31∣43 | 78∣81 | 33∣41 | 78∣97 | |
| LS | 200 | 57 | 145 | 54 | 157 | 52 | 155 |
| WBS | 70∣66 | 175∣177 | 62∣59 | 171∣167 | 58∣57 | 159∣158 | |
| NOT | 66∣70∣77 | 175∣190∣194 | 67∣70 | 158∣161 | 64∣68 | 155∣162 | |
| ICSS | 66∣87 | 80∣159 | 61∣76∣87 | 159 | 59∣66∣170∣187 | 156∣173 | |
| S&P 500 Stock Prices | Brent Crude Oil Prices | |
|---|---|---|
| Methods | ||
| LS | 26 March 1997 | 25 February 2022 |
| WBS | 12 May 1997 | 26 January 2022 |
| ICSS | 22 December 1998 ∣ 26 January 1998 | 14 January 2022 |
| 20 April 1995 ∣ 14 November 1996 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arrouch, M.S.E.; Elharfaoui, E.; Ngatchou-Wandji, J. Change-Point Detection in the Volatility of Conditional Heteroscedastic Autoregressive Nonlinear Models. Mathematics 2023, 11, 4018. https://doi.org/10.3390/math11184018
Arrouch MSE, Elharfaoui E, Ngatchou-Wandji J. Change-Point Detection in the Volatility of Conditional Heteroscedastic Autoregressive Nonlinear Models. Mathematics. 2023; 11(18):4018. https://doi.org/10.3390/math11184018
Chicago/Turabian StyleArrouch, Mohamed Salah Eddine, Echarif Elharfaoui, and Joseph Ngatchou-Wandji. 2023. "Change-Point Detection in the Volatility of Conditional Heteroscedastic Autoregressive Nonlinear Models" Mathematics 11, no. 18: 4018. https://doi.org/10.3390/math11184018
APA StyleArrouch, M. S. E., Elharfaoui, E., & Ngatchou-Wandji, J. (2023). Change-Point Detection in the Volatility of Conditional Heteroscedastic Autoregressive Nonlinear Models. Mathematics, 11(18), 4018. https://doi.org/10.3390/math11184018






