Development of a Composite Implicit Time Integration Scheme for Three-Dimensional Discontinuous Deformation Analysis
Abstract
1. Introduction
2. Fundamentals of 3D DDA and Time Integration Scheme
2.1. Block Deformation and Displacement
2.2. Simultaneous Equilibrium Equations with the CAI Scheme
2.3. Problems of the CAI Scheme concerning Time Step in the Traditional DDA
- (1)
- If the time step size is larger than a certain value, the assumption that the acceleration is a constant within a time step may be incorrect. As shown in Figure 1, the acceleration at the end of time step t0 + Δ is equal to or approximately equal to the acceleration at the beginning of time step t0, which leads to linear velocity and quadratic displacement. There can be no doubt that this is errorless or the numerical error is small. However, when a larger time step size is adopted, the acceleration may be variable, and the results of the DDA computation will be inaccurate. The numerical error will grow as the calculation step size increases. Meanwhile, the effect of the inertia force on the block movement may be weakened or even ignored within a larger time step.
- (2)
- If the time step size is too small, the square terms Δ2 ((6)) on the right side of the equal sign are ignored, and the inertia force has a great influence on the diagonal entries [Kii] of the global stiffness matrix ((9)). These also bring to DDA computational inaccuracy and even a high computational cost.
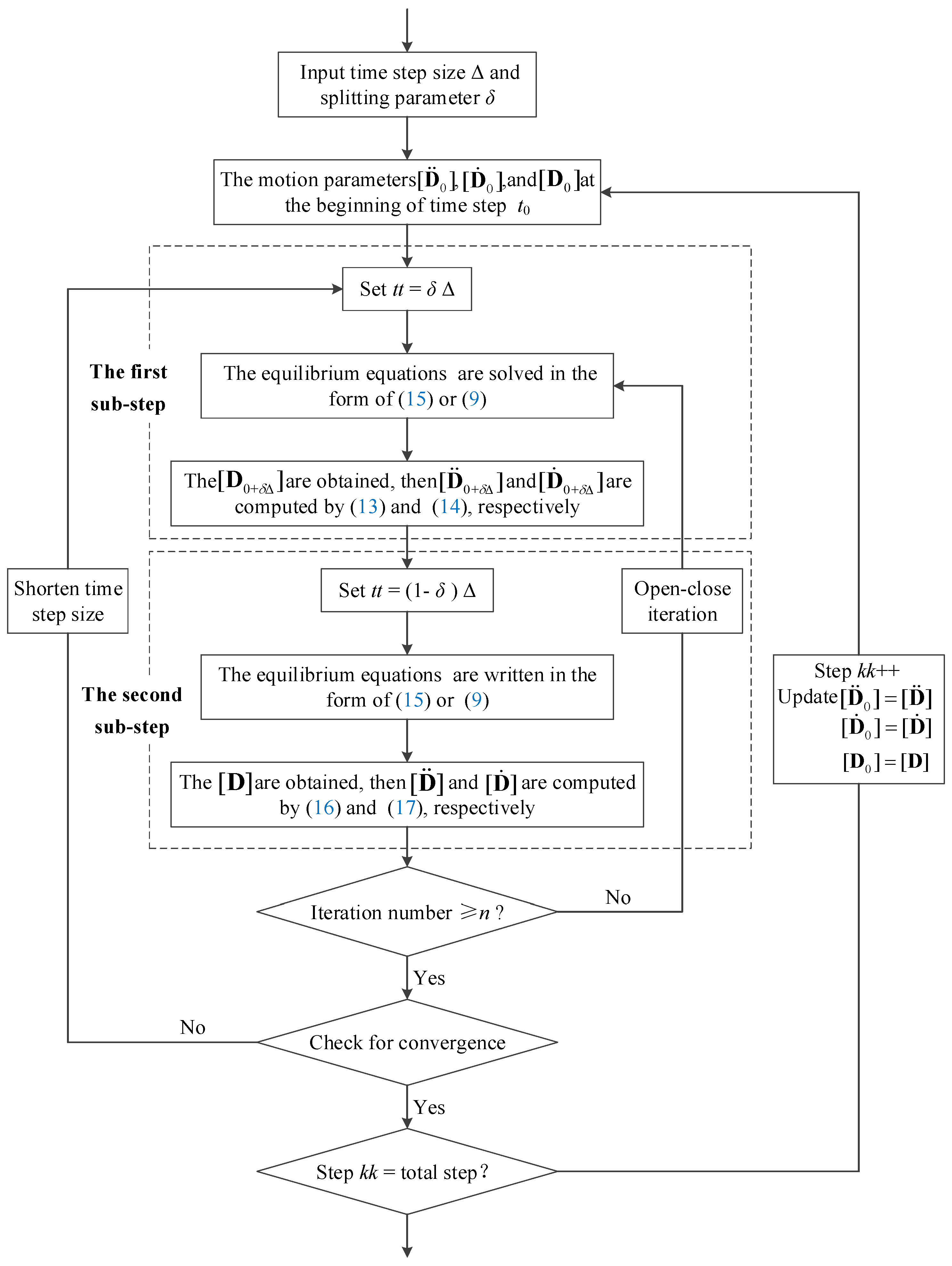
3. CITI Scheme for 3D DDA
3.1. Trapezoidal Rule
3.2. Three-Point Backward Euler Method
3.3. Implementation in 3D DDA
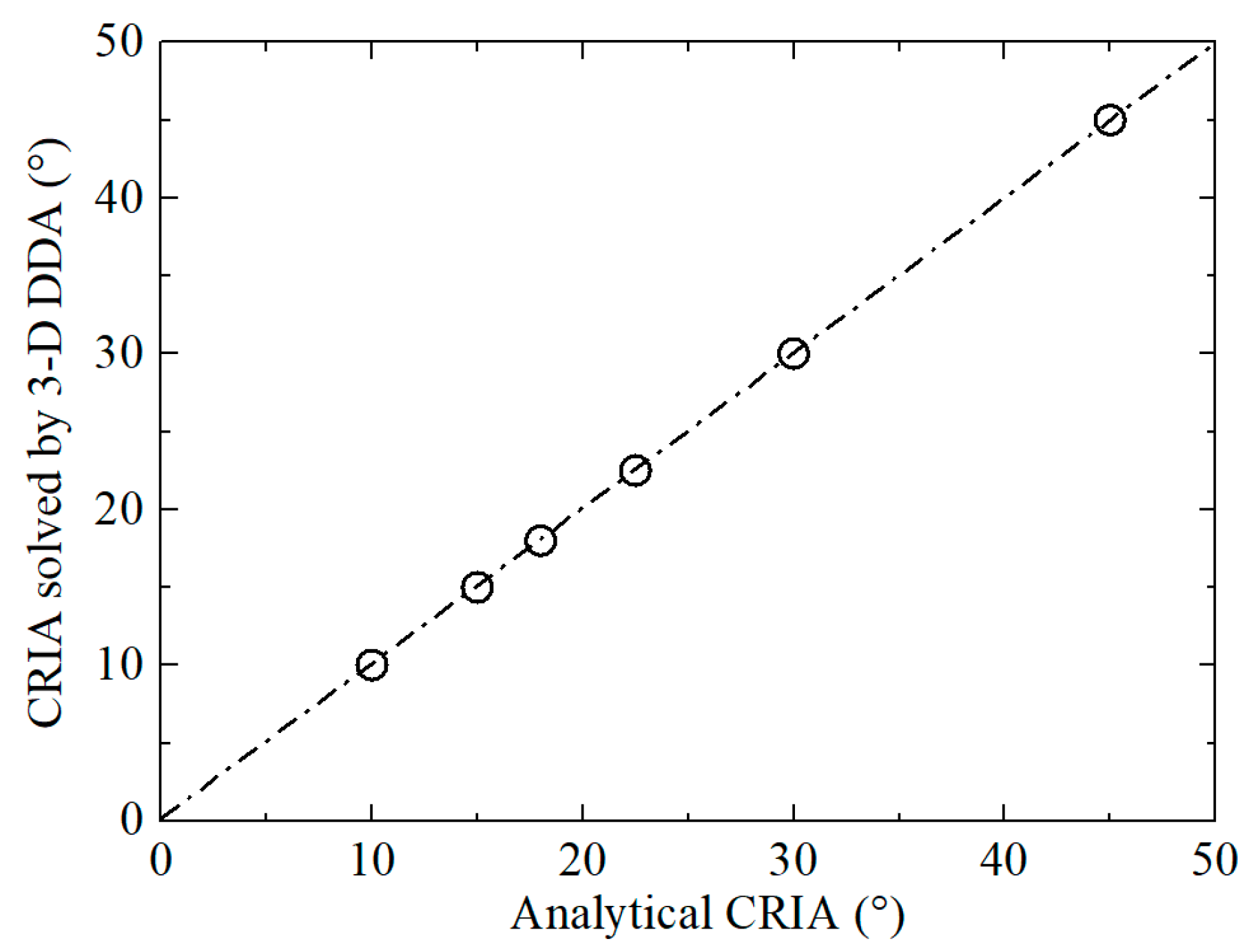
4. Verifications of the Developed 3D DDA Method
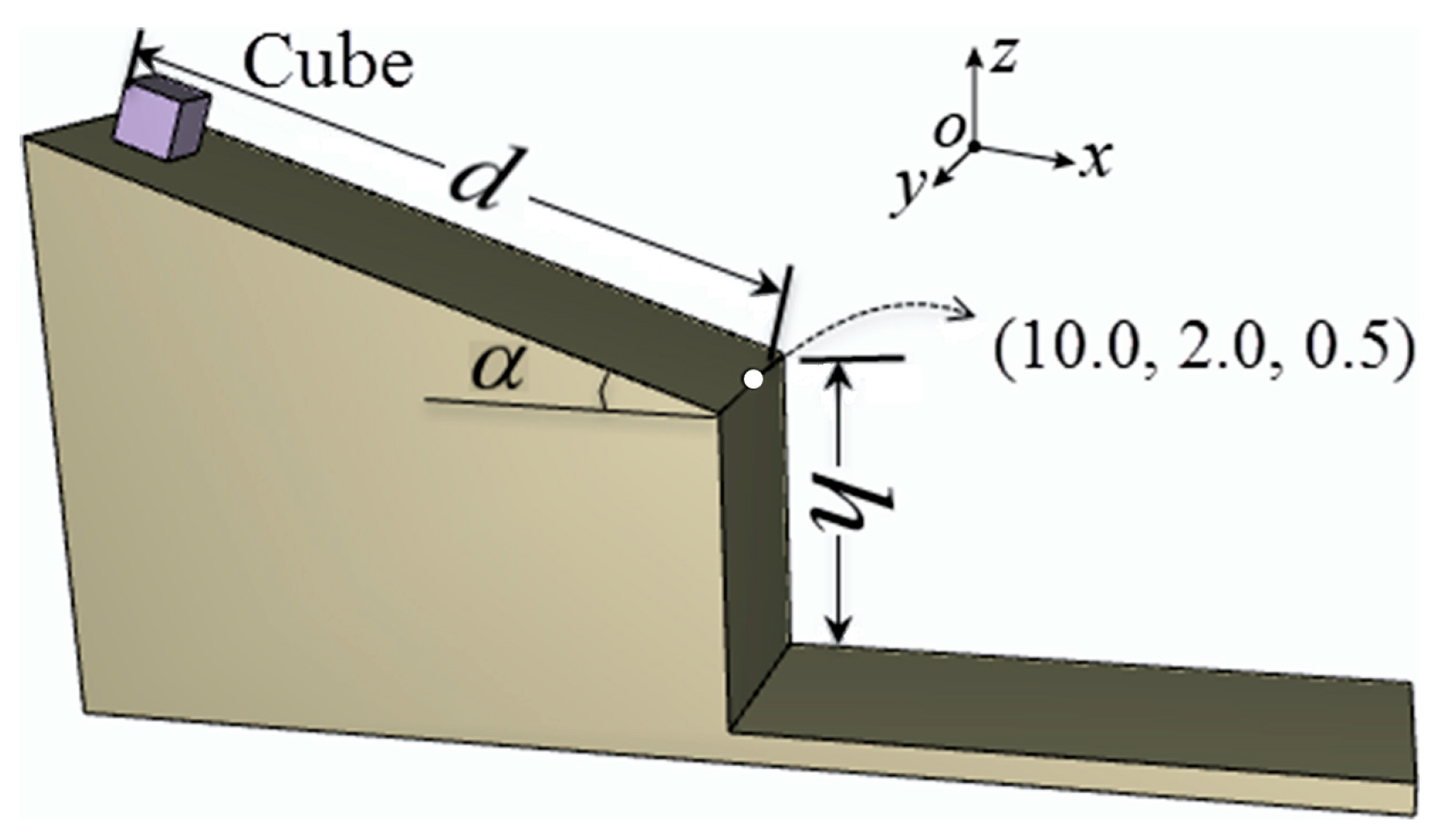
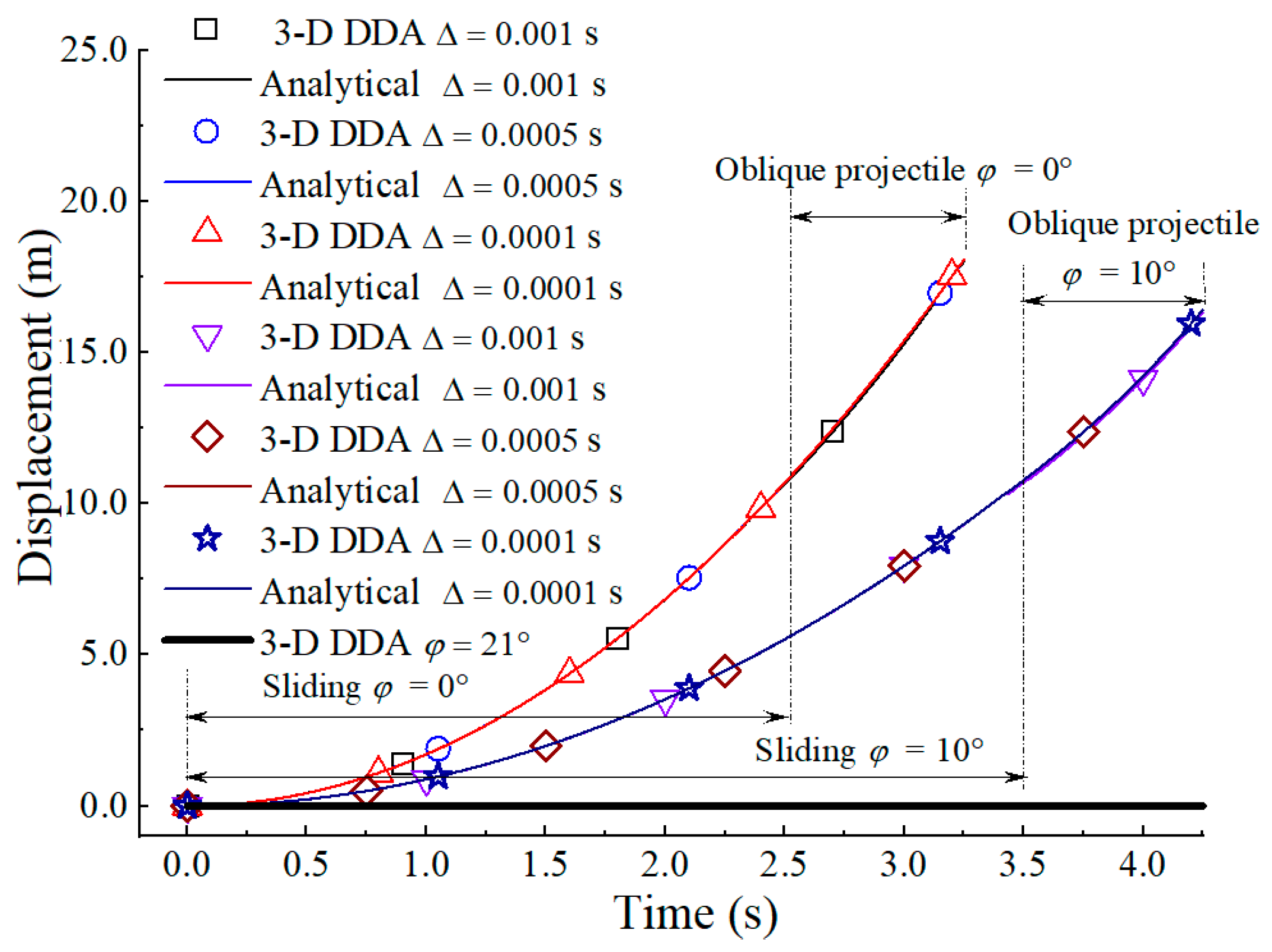
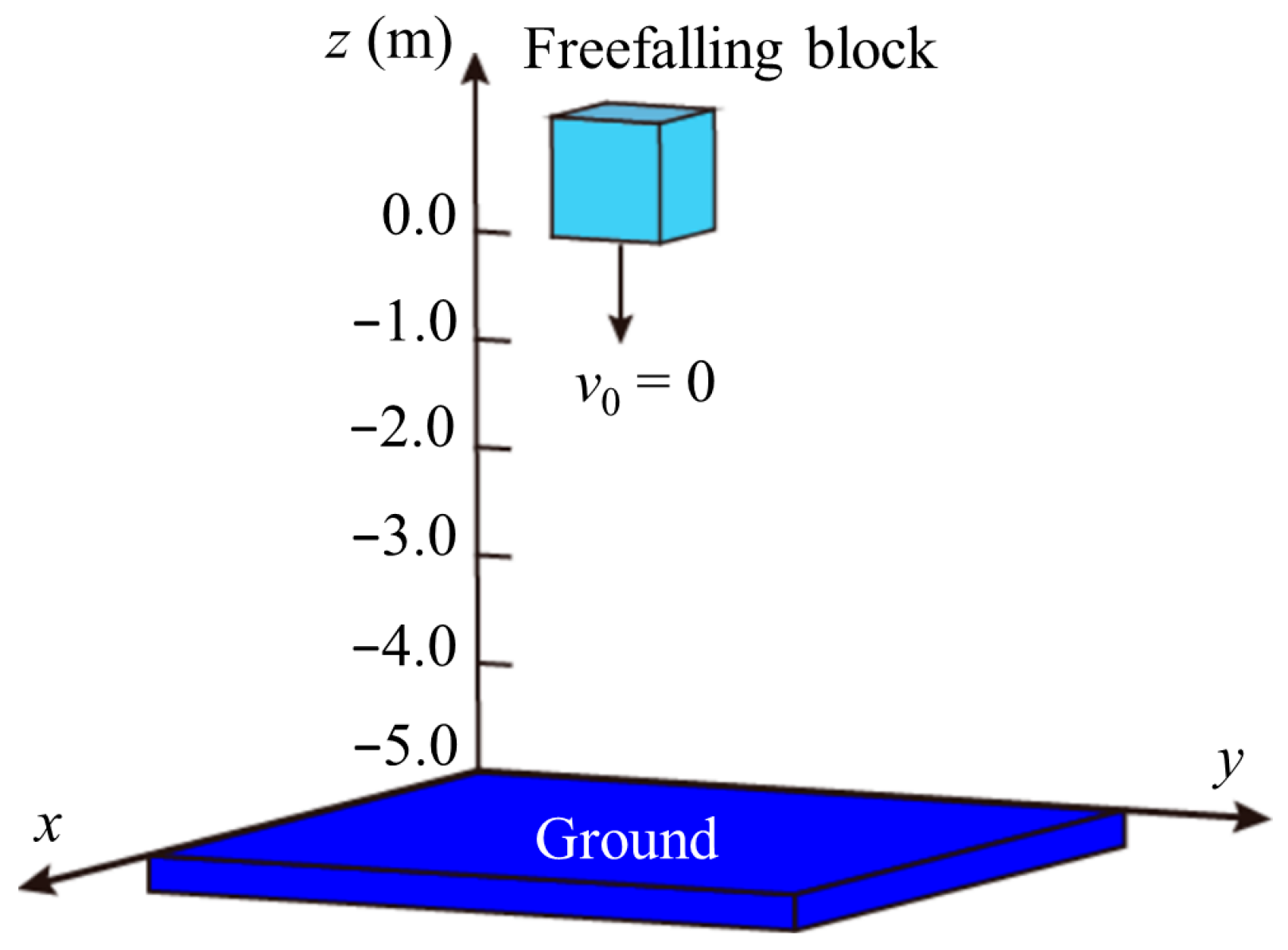
4.1. Freefalling, Sliding, and Oblique Projectile
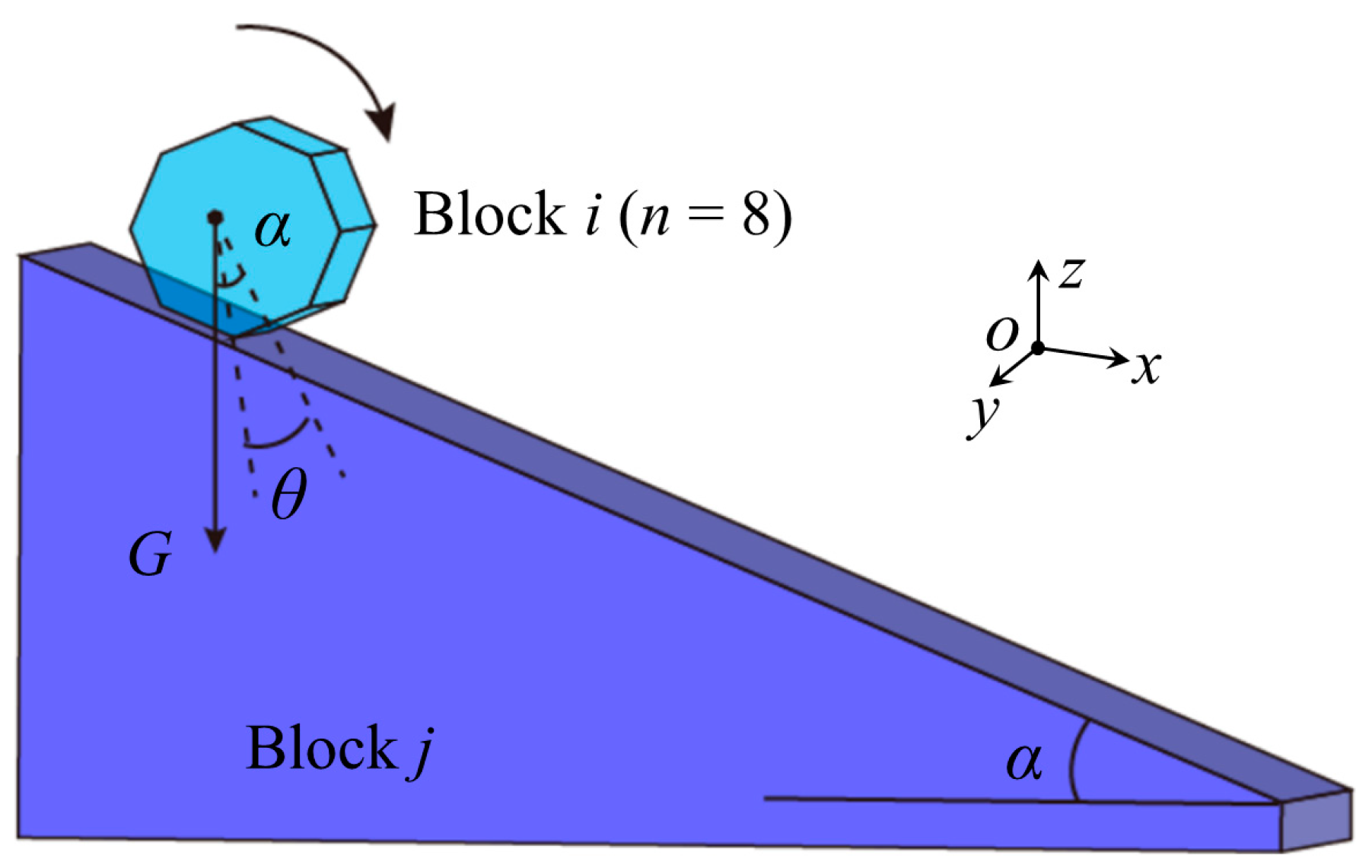
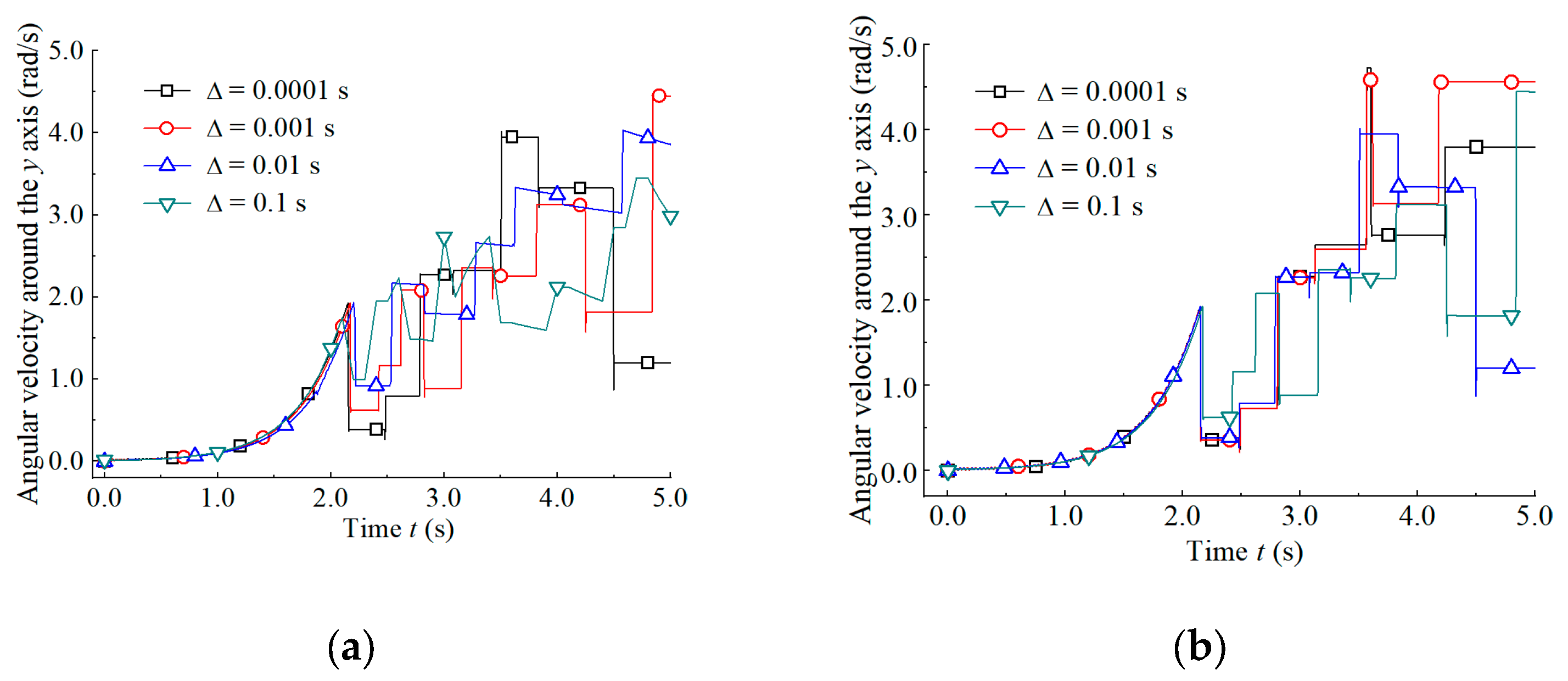
4.2. Rolling
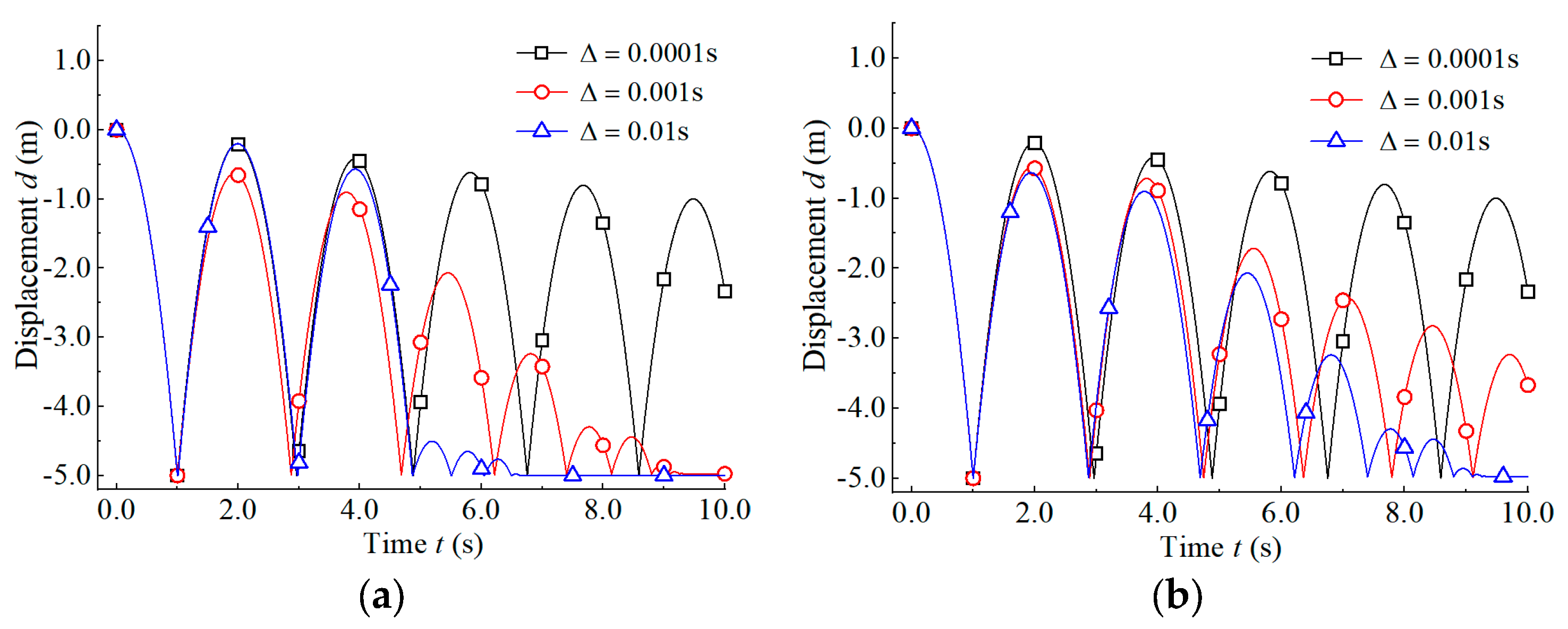
4.3. Bouncing
- (1)
- When a small time step size (e.g., Δ = 0.0001 s) was adopted, the calculation results of the two schemes were similar, and the corresponding bouncing displacements were rarely dissipated with the collision with the ground, whose change trends were basically consistent. When a large time step size (e.g., Δ = 0.001 s) was adopted, the bouncing displacement was completely dissipated to rest at about 8.9 s with the CAI scheme, whereas with the CITI scheme, the bouncing displacement was slowly dissipated and there was still large bouncing displacement until 10.0 s.
- (2)
- When a larger time step size (e.g., Δ = 0.01 s) was adopted, with the CAI scheme, the amplitudes of bouncing displacement were close to the ones when a small time step (e.g., Δ = 0.0001 s) was adopted before the third collision with the ground. However, upon the third collision with the ground, the amplitude of bouncing displacement sharply decayed, and then, the bouncing displacement was dissipated to be resting at 6.2 s. With the CITI scheme, the amplitudes of bouncing displacement decayed gradually with the collision between the block and the ground.
- (3)
- For the CAI scheme, the change of the decay trend of bouncing displacement was significant with the increase of the time step size (e.g., from 0.0001 s to 0.01 s), and even the decay was abrupt when a larger time step size (e.g., Δ = 0.01 s) was adopted. For the CITI scheme, the bouncing displacement gradually attenuated, and this trend can be maintained even if the time step size is large, which conforms to the phenomenon of elastic cases encountered in practice and is also correct. Thus, the CITI scheme is more suitable for bouncing calculation and was less constrained by the time step.
- (4)
- From the perspective of damping, on the one hand, the algorithm damping of the CAI scheme was larger than the CITI scheme under the same large time step, so that the energy dissipation and bouncing displacement decay of the CAI scheme were faster than the CITI scheme. On the other hand, the larger the time step used in both the CAI scheme and the CITI scheme, the greater the algorithm damping used in DDA, the faster the energy dissipation and the bouncing displacement attenuation were. One of the possible reasons is that the effect of the inertia force on block movement is weakened within a larger time step.
5. Numerical Examples
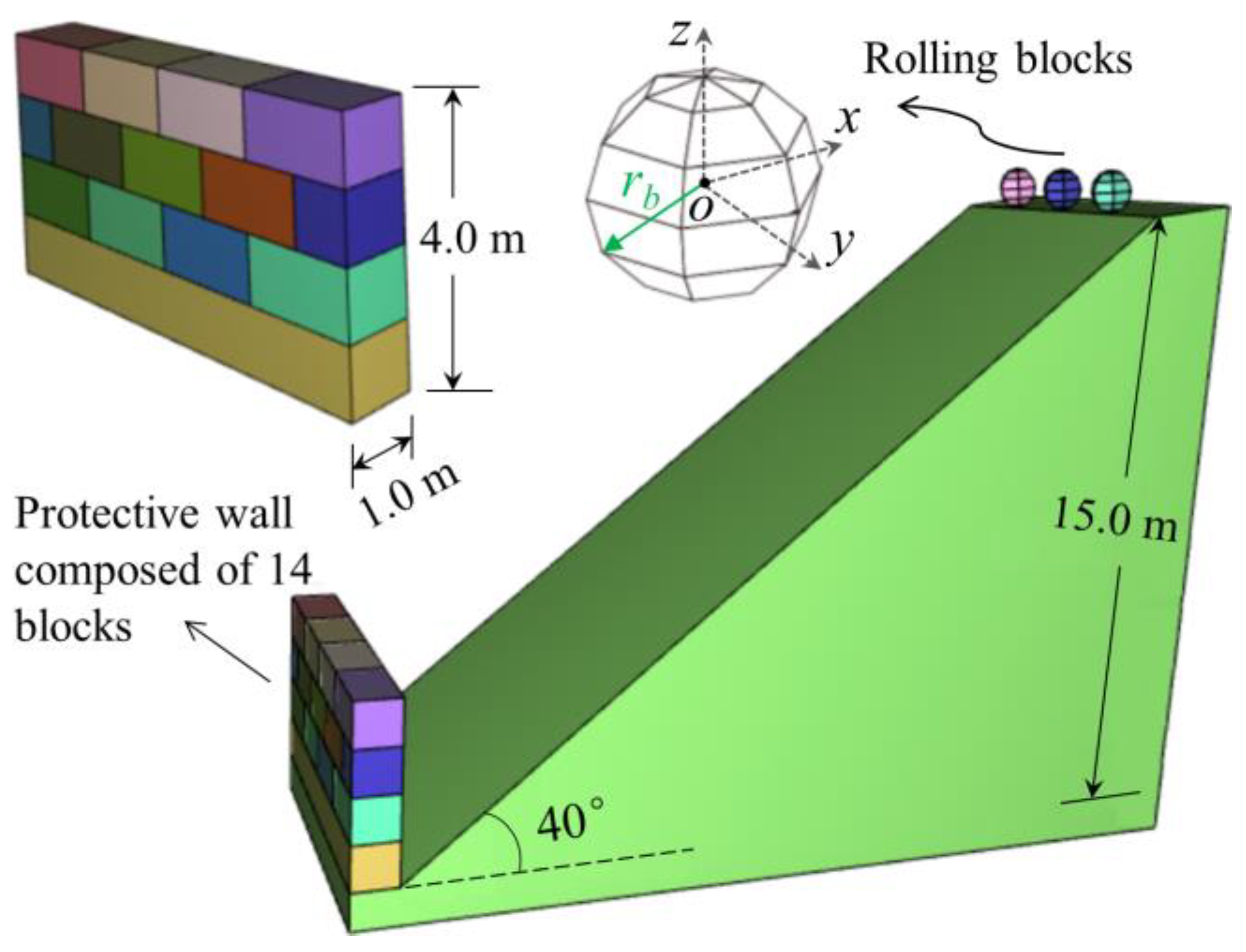
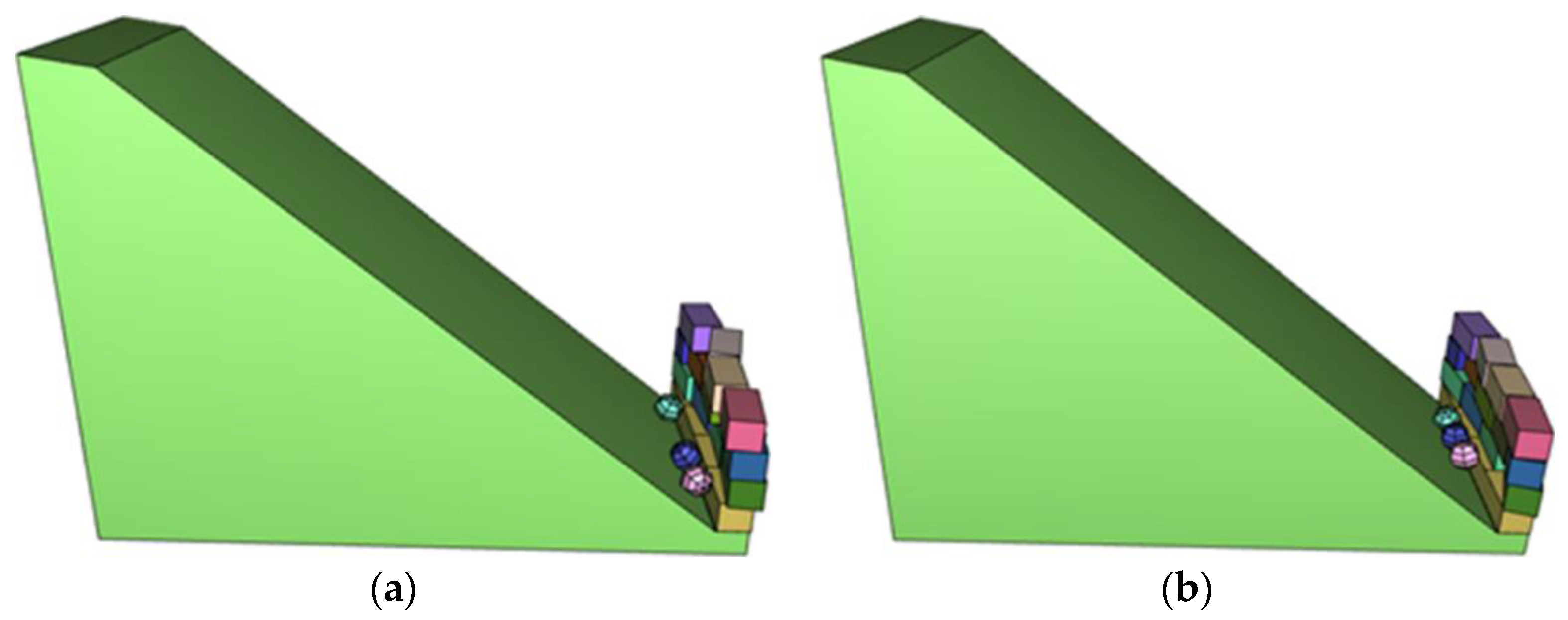
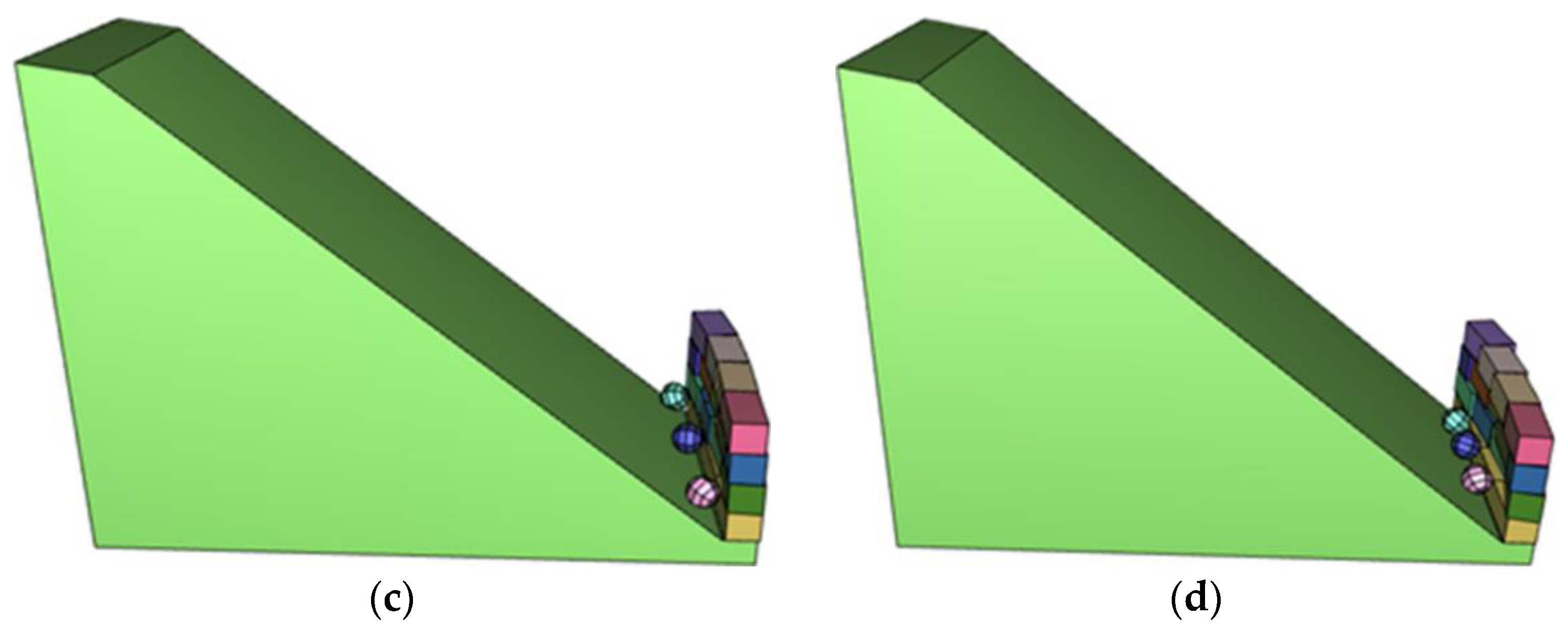
5.1. Collision between Rolling Blocks and Protective Wall
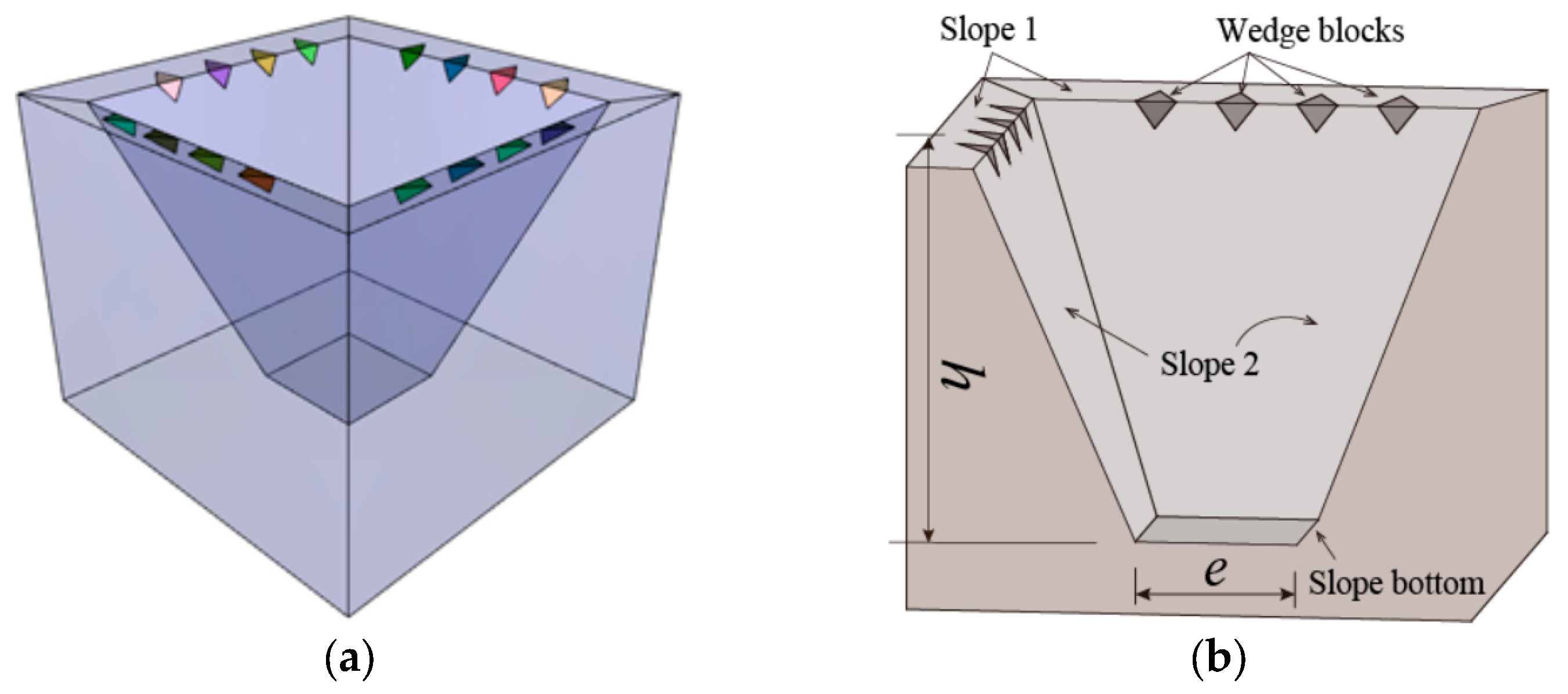
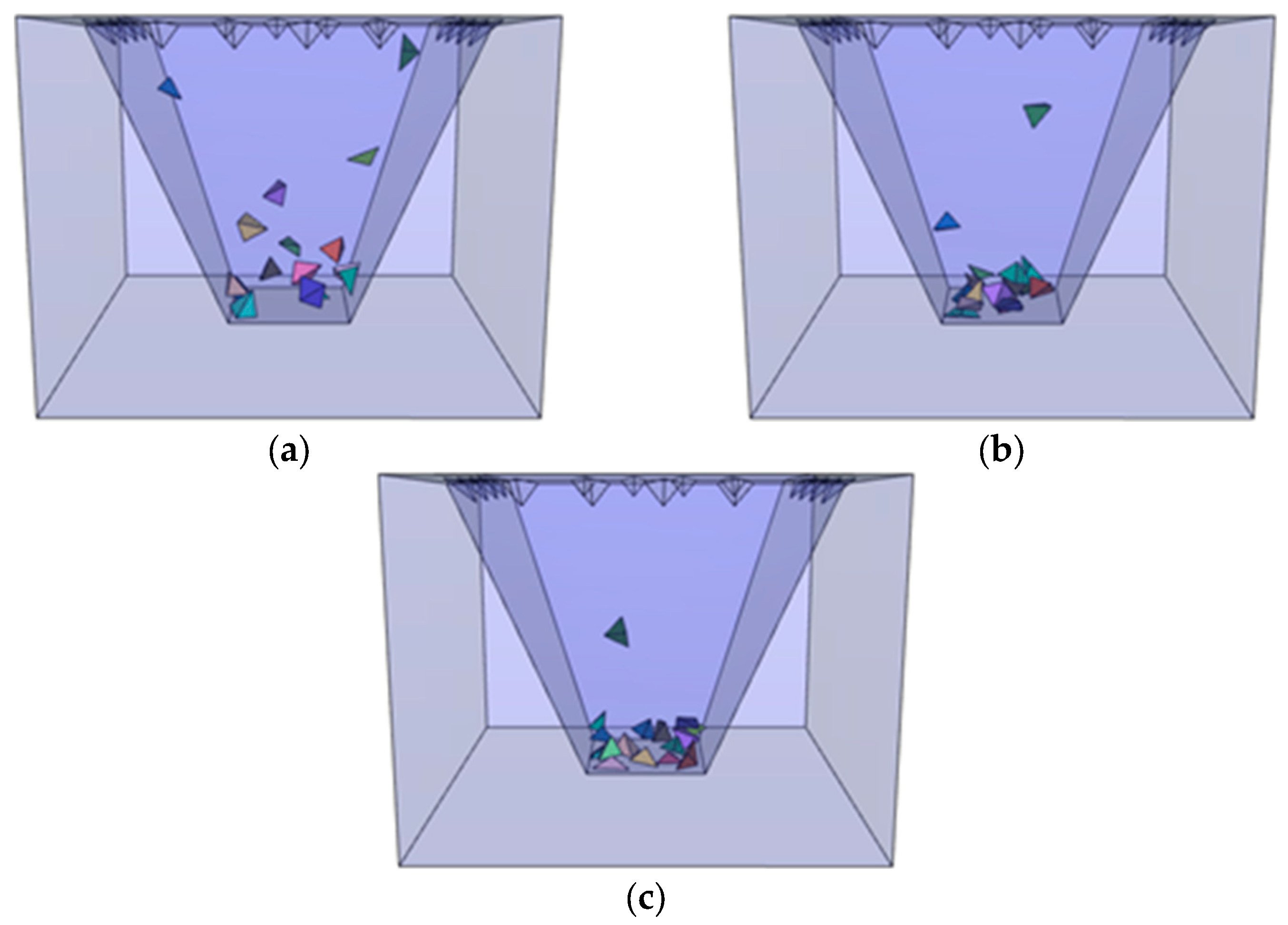
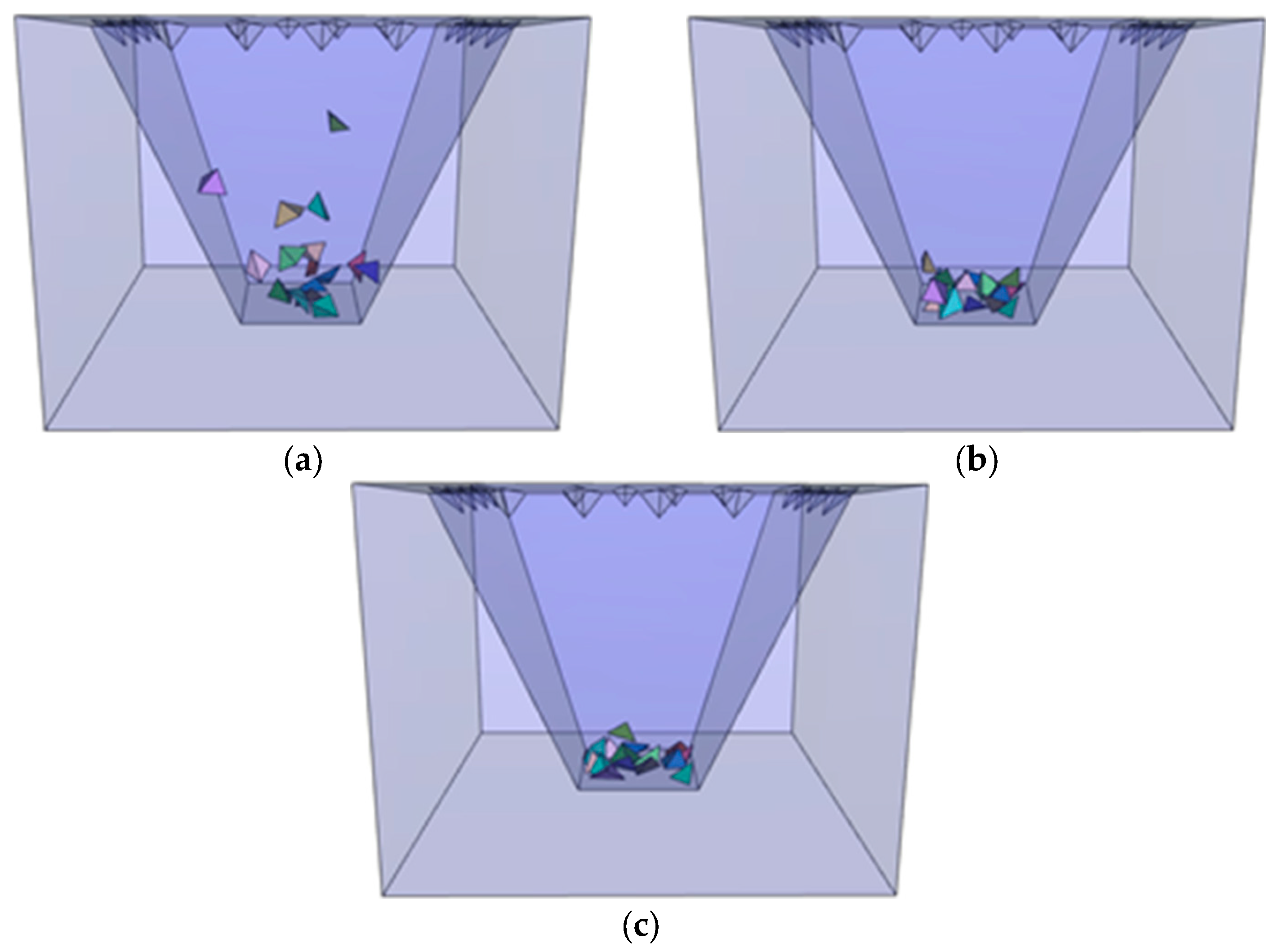
5.2. Wedge Failure
6. Conclusions
- (1)
- The basic idea of the CITI scheme is easy to understand, and the algorithm can be easily implemented into the 3D DDA program.
- (2)
- The CITI scheme can effectively compute the large displacement and deformation of block systems and can solve the nonlinear dynamic failure problems of rock slopes. The computational results of the CITI scheme may be more conservative than those of the CAI scheme.
- (3)
- For a large time step size, the CITI scheme can capture the nonlinear nature of the DDA computation; its results were still stable, and its computational accuracy was higher than the CAI scheme. The CITI scheme expands the value range of the time step size and reduces the numerical error brought by a large time step size. The CITI scheme is more applicable to variable acceleration motion than the CAI scheme.
- (4)
- The CITI scheme is more time-consuming than the CAI scheme in terms of computational efficiency, because there are two sub-steps involved within each time step. Especially, when the number of blocks was large, the computational efficiency reduced obviously.
- (5)
- No matter what integration schemes 3D DDA adopts, the larger the time step, the greater the damping, the faster the energy dissipation, and the shorter the time becoming stable are. For the CITI scheme, the damping is related to the splitting parameter δ, i.e., the greater the splitting parameter, the greater the damping is.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shi, G.H. Discontinuous Deformation Analysis: A New Numerical Model for the Statics and Dynamics of Block Systems. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1988. [Google Scholar]
- Kim, Y.I.; Amadei, B.; Pan, E. Modeling the effect of water, excavation sequence and rock reinforcement with discontinuous deformation analysis. Int. J. Rock Mech. Min. Sci. 1999, 36, 949–970. [Google Scholar] [CrossRef]
- Tian, Q.; Zhao, Z.; Bao, H. Block fracturing analysis using nodal-based discontinuous deformation analysis with the double minimization procedure. Int. J. Numer. Anal. Meth. Geomech. 2014, 38, 881–902. [Google Scholar] [CrossRef]
- Ni, K.S.; Yang, J.; Ning, Y.J.; Kang, G. A modified sub-block DDA fracturing modelling method for rock. Eng. Anal. Bound. Elem. 2020, 111, 154–166. [Google Scholar] [CrossRef]
- Hatzor, Y.H.; Talesnick, M.; Tsesarsky, M. Continuous and discontinuous stability analysis of the bell-shaped caverns at Bet Guvrin, Israel. Int. J. Rock Mech. Min. Sci. 2002, 39, 867–886. [Google Scholar] [CrossRef]
- Sitar, N.; MacLaughlin, M.M.; Doolin, D.M. Influence of kinematics on landslide mobility and failure mode. J. Geotech. Geoenviron. Eng. 2005, 131, 716–728. [Google Scholar] [CrossRef]
- Rizzi, E.; Rusconi, F.; Cocchetti, G. Analytical and numerical DDA analysis on the collapse mode of circular masonry arches. Eng. Struct. 2014, 60, 241–257. [Google Scholar] [CrossRef]
- Chen, K.T.; Wu, J.H. Simulating the failure process of the Xinmo landslide using discontinuous deformation analysis. Eng. Geol. 2018, 239, 269–281. [Google Scholar] [CrossRef]
- Cheng, Y.M. Advancements and improvement in discontinuous deformation analysis. Comput. Geotech. 1998, 22, 153–163. [Google Scholar] [CrossRef]
- Grayeli, R.; Mortazavi, A. Discontinuous deformation analysis with second-order finite element meshed block. Int. J. Numer. Anal. Meth. Geomech. 2006, 30, 1545–1561. [Google Scholar] [CrossRef]
- Bao, H.R.; Zhao, Z.Y. The vertex-to-vertex contact analysis in the two-dimensional discontinuous deformation analysis. Adv. Eng. Softw. 2012, 45, 1–10. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Xu, Q.; Chen, G.Q.; Zhao, J.X.; Zheng, L. Extension of discontinuous deformation analysis and application in cohesive-frictional slope analysis. Int. J. Rock Mech. Min. Sci. 2014, 70, 533–545. [Google Scholar]
- Xia, M.Y.; Chen, G.Q.; Guo, L.X. Improvement of vertex-to-vertex contact processing in two-dimensional DDA. Comput. Geotech. 2021, 135, 104200. [Google Scholar]
- Miki, S.; Sasaki, T.; Koyama, T.; Nishiyama, S.; Ohnishi, Y. Development of coupled discontinuous deformation analysis and numerical manifold method (NMM-DDA). Int. J. Comput. Meth. 2010, 7, 131–150. [Google Scholar]
- Kaidi, S.; Rouainia, M.; Ouahsine, A. Stability of breakwaters under hydrodynamic loading using a coupled DDA/FEM approach. Ocean Eng. 2012, 55, 62–70. [Google Scholar]
- Wang, W.; Chen, G.Q.; Zhang, Y.B.; Zheng, L.; Zhang, H. Dynamic simulation of landslide dam behavior considering kinematic characteristics using a coupled DDA-SPH method. Eng. Anal. Bound. Elem. 2017, 80, 172–183. [Google Scholar]
- Shi, G.H. Three-Dimensional Discontinuous Deformation Analysis. In Proceedings of the 4th International Conference on Analysis of Discontinuous Deformation, Glasgow, UK, 6–8 June 2001; pp. 1–21. [Google Scholar]
- Yeung, M.R.; Jiang, Q.H.; Sun, N. A model of edge-to-edge contact for three dimensional discontinuous deformation analysis. Comput. Geotech. 2007, 34, 175–186. [Google Scholar]
- Keneti, A.R.; Jafari, A.; Wu, J.H. A new algorithm to identify contact patterns between convex blocks for three-dimensional discontinuous deformation analysis. Comput. Geotech. 2008, 35, 746–759. [Google Scholar]
- Beyabanaki, S.A.R.; Mikola, R.G.; Biabanaki, S.O.R.; Mohammadi, S. New point-to-face contact algorithm for 3-D contact problems using the augmented Lagrangian method in 3-D DDA. Geomech. Geoeng. 2009, 4, 221–236. [Google Scholar]
- Zhang, H.; Liu, S.G.; Zheng, L.; Zhong, G.H.; Lou, S.; Han, Z. Extensions of edge-to-edge contact model in three-dimensional discontinuous deformation analysis for friction analysis. Comput. Geotech. 2016, 71, 261–275. [Google Scholar]
- Wang, X.; Wu, W.; Zhu, H.H.; Lin, J.S.; Zhang, H. Acceleration of contact detection between arbitrarily shaped polyhedra based on multi-cover methods in three dimensional discontinuous deformation analysis. Int. J. Rock Mech. Min. Sci. 2020, 132, 104387. [Google Scholar]
- Fan, H.Y.; Li, L.P.; Liu, H.; Ni, J.; Cheng, S.; Zhou, H. Parametric research on the time step and spring stiffness in three-dimensional discontinuous deformation analysis method. Int. J. Numer. Anal. Meth. Geomech. 2022, 46, 2603–2619. [Google Scholar] [CrossRef]
- Jiang, Q.H.; Yeung, M.R. A model of point-to-face contact for three-dimensional discontinuous deformation analysis. Rock Mech. Rock Eng. 2004, 37, 95–116. [Google Scholar]
- Huang, G.H.; Xu, Y.Z.; Chen, X.F.; Ma, J.J.; Zhang, S. An efficient contact search algorithm for three-dimensional sphere discontinuous deformation analysis. Int. J. Comput. Meth. 2021, 18, 2050044. [Google Scholar] [CrossRef]
- Ishikawa, T.; Miura, S.; Ohnishi, Y. Influence of input parameters on energy loss in free fall tests with DDA. In Proceedings of the 7th International Conference on Analysis of Discontinuous Deformation, Honolulu, HI, USA, 10–12 December 2005; pp. 147–158. [Google Scholar]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. Proc. ASCE 1959, 83, 67–94. [Google Scholar] [CrossRef]
- Wilson, E.L. A Computer Program for the Dynamic Stress Analysis of Underground Structures, SEL; Technical Report 68-1; University of California: Berkeley, CA, USA, 1968. [Google Scholar]
- Hilber, H.M.; Hughes, T.J.R.; Taylor, R.L. Improved numerical dissipation for time integration algorithms in structural dynamics. Earthq. Eng. Struct. Dyn. 1977, 5, 283–292. [Google Scholar] [CrossRef]
- Bazzi, G.; Anderheggen, E. The ρ-family of algorithms for time-step integration with improved numerical dissipation. Earthq. Eng. Struct. Dyn. 1982, 10, 537–550. [Google Scholar] [CrossRef]
- Chung, J.; Hulbert, G.M. A time integration algorithm for structural dynamics with improved numerical dissipation: The generalized-α method. J. Appl. Mech. 1993, 60, 371–375. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, D.; Liu, Y. Degenerated shell element with composite implicit time integration scheme for geometric nonlinear analysis. Int. J. Numer. Meth. Eng. 2016, 105, 483–513. [Google Scholar]
- Bathe, K.J.; Baig, M.M.I. On a composite implicit time integration procedure for nonlinear dynamics. Comput. Struct. 2005, 83, 2513–2524. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Liu, D. Accuracy of a composite implicit time integration scheme for structural dynamics. Int. J. Numer. Meth. Eng. 2017, 109, 368–406. [Google Scholar]
- Kazancı, Z.; Bathe, K.J. Crushing and crashing of tubes with implicit time integration. Int. J. Impact Eng. 2012, 42, 80–88. [Google Scholar] [CrossRef]
- Bathe, K.J.; Noh, G. Insight into an implicit time integration scheme for structural dynamics. Comput. Struct. 2012, 98, 1–6. [Google Scholar] [CrossRef]
- Noh, G.; Ham, S.; Bathe, K.J. Performance of an implicit time integration scheme in the analysis of wave propagations. Comput. Struct. 2013, 123, 93–105. [Google Scholar] [CrossRef]
- Alireza, B.; Reza, A. Nonlinear dynamic analysis of unsymmetric layered composite shells. Compos. Struct. 2023, 307, 116627. [Google Scholar]
- Klarmann, S.; Wagner, W. Enhanced studies on a composite time integration scheme in linear and non-linear dynamics. Comput. Mech. 2015, 55, 455–468. [Google Scholar] [CrossRef][Green Version]
- Chen, G.Q.; Zheng, L.; Zhang, Y.B.; Wu, J. Numerical simulation in rockfall analysis: A close comparison of 2-D and 3-D DDA. Rock Mech. Rock Eng. 2013, 46, 527–541. [Google Scholar] [CrossRef]
- Gu, J.; Zhao, Z. Considerations of the discontinuous deformation analysis on wave propagation problems. Int. J. Numer. Anal. Meth. Geomech. 2009, 33, 1449–1465. [Google Scholar] [CrossRef]
- Yagoda-Biran, G.; Hatzor, Y.H. Benchmarking the numerical discontinuous deformation analysis method. Comput. Geotech. 2016, 71, 30–46. [Google Scholar] [CrossRef]
- Zhao, X.F.; Fang, X.S.; Wang, Y. Narrow-phase collision detection based on DDA. In Proceedings of the 8th International Conference on Analysis of Discontinuous Deformation, Beijing, China, 14–19 August 2007; pp. 95–99. [Google Scholar]
- Lin, S.Z.; Xie, Z.Q. Performance of DDA time integration. Sci. China Tech. Sci. 2005, 58, 1558–1566. [Google Scholar] [CrossRef]
- Tang, C.A.; Tang, S.B.; Gong, B.; Bai, H.M. Discontinuous deformation and displacement analysis: From continuous to discontinuous. Sci. China Tech. Sci. 2015, 58, 1567–1574. [Google Scholar] [CrossRef]
- Collatz, L. The Numerical Treatment of Differential Equations, 3rd ed.; Springer: New York, NY, USA, 1966. [Google Scholar]
- Liu, G.Y. Research on 3D DDA Contact Model and Slope Rolling Rock Failure Law. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2019. [Google Scholar]


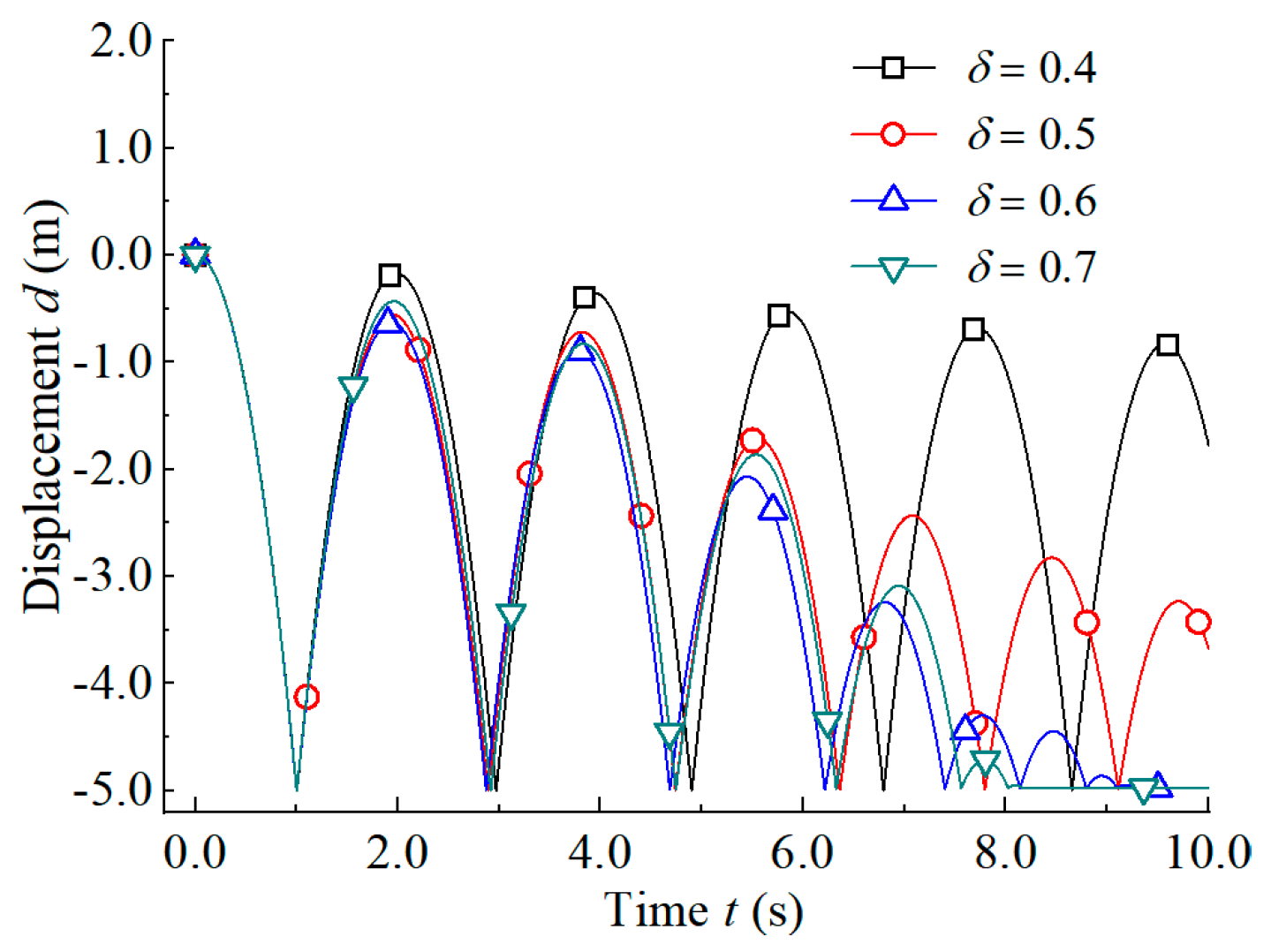


| Integration Schemes | CAI Scheme | CITI Scheme | ||
|---|---|---|---|---|
| δ = 0.5 | δ = 0.6 | δ = 0.7 | ||
| Time | 6.55 s | 6.70 s | 6.45 s | 6.15 s |
| Integration Schemes | CAI Scheme | CITI Scheme | ||
|---|---|---|---|---|
| δ = 0.5 | δ = 0.6 | δ = 0.7 | ||
| Time | 29.0 s | 30.5 s | 28.5 s | 23.5 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Liu, J.; Luo, S.; Bo, W.; Kang, J.; Miao, J. Development of a Composite Implicit Time Integration Scheme for Three-Dimensional Discontinuous Deformation Analysis. Mathematics 2023, 11, 3881. https://doi.org/10.3390/math11183881
Liu G, Liu J, Luo S, Bo W, Kang J, Miao J. Development of a Composite Implicit Time Integration Scheme for Three-Dimensional Discontinuous Deformation Analysis. Mathematics. 2023; 11(18):3881. https://doi.org/10.3390/math11183881
Chicago/Turabian StyleLiu, Guoyang, Junjie Liu, Shouyi Luo, Wu Bo, Jiashuo Kang, and Jianbin Miao. 2023. "Development of a Composite Implicit Time Integration Scheme for Three-Dimensional Discontinuous Deformation Analysis" Mathematics 11, no. 18: 3881. https://doi.org/10.3390/math11183881
APA StyleLiu, G., Liu, J., Luo, S., Bo, W., Kang, J., & Miao, J. (2023). Development of a Composite Implicit Time Integration Scheme for Three-Dimensional Discontinuous Deformation Analysis. Mathematics, 11(18), 3881. https://doi.org/10.3390/math11183881





