Language-Based Opacity Verification in Partially Observed Petri Nets through Linear Constraints
Abstract
:1. Introduction
- We define the concept of secret observation sequences, by considering a case where a secret involves numerous transition sequences yielding the same observation. This concept decreases the effort required to check language opacity in a POPN, by avoiding redundant explorations.
- We identify two language-based opacity properties, called consistency and non-secrecy properties; we separately check each property; then, we provide necessary and sufficient conditions to check language-based opacity, by defining and solving an ILPP.
- Finally, we extend the above results from a centralized framework to a decentralized framework with a coordinator, where more than one intruder observes the system.
2. Preliminaries
2.1. Petri Nets
2.2. Partially Observed Petri Nets
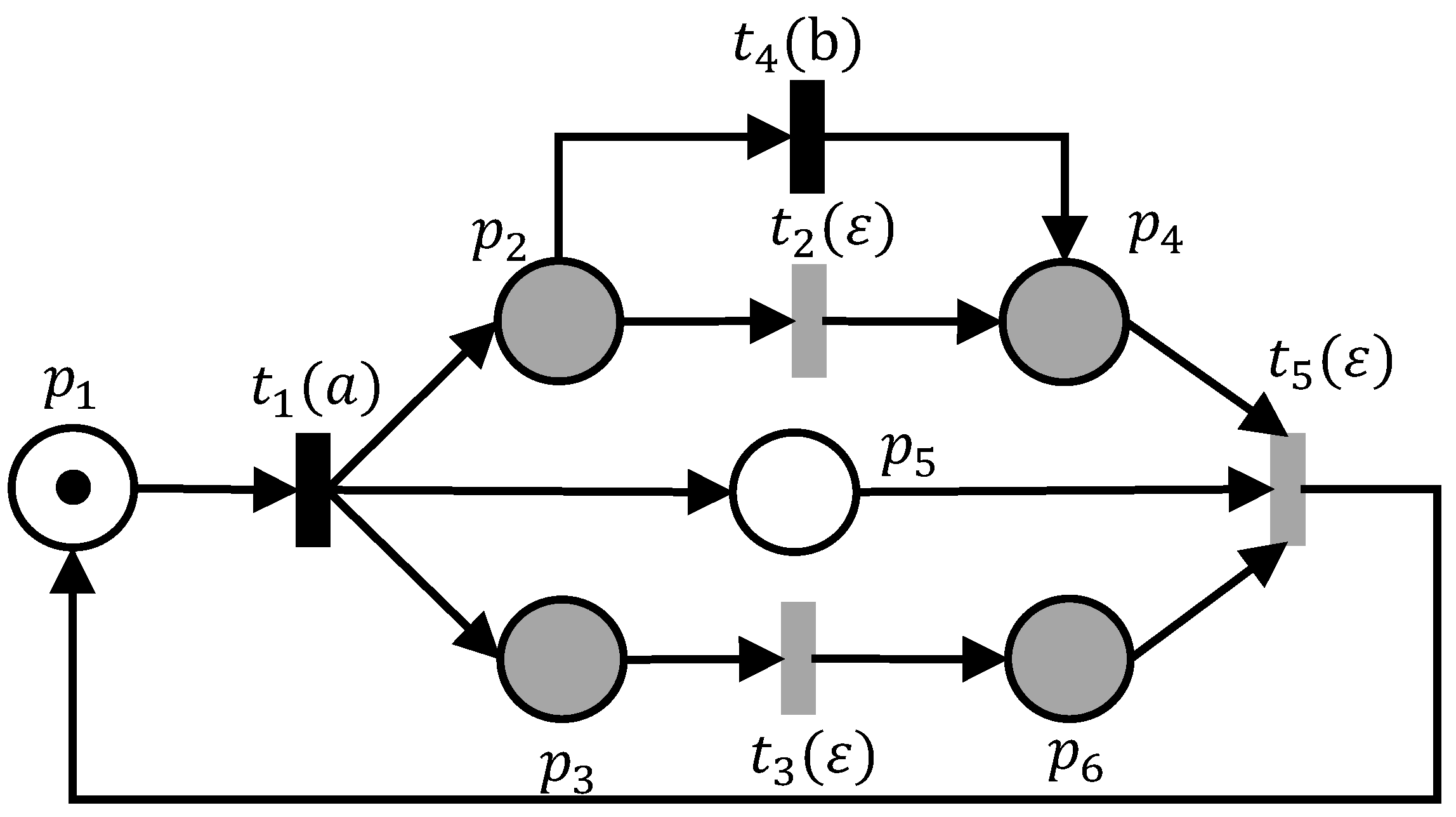
3. Quasi-Unobservable and Discernible Transitions
4. Language-Based Opacity
- Consistency property: ;
- Non-secrecy property: .
5. Mathematical Characterization of LBO
5.1. Consistency Assurance
- , ;
- , ;
- Constraints (3.a) represent the state equation;
- Constraints (3.b) represent the enabling condition of discernible transitions;
- Constraints (3.c) represent the token variation generated by firing and ;
- Constraints (3.d) define a mutual exclusion condition, to prevent firing more than one discernible transition.
5.2. Non-Secrecy Assurance
5.3. Complexity Analysis and Comparison
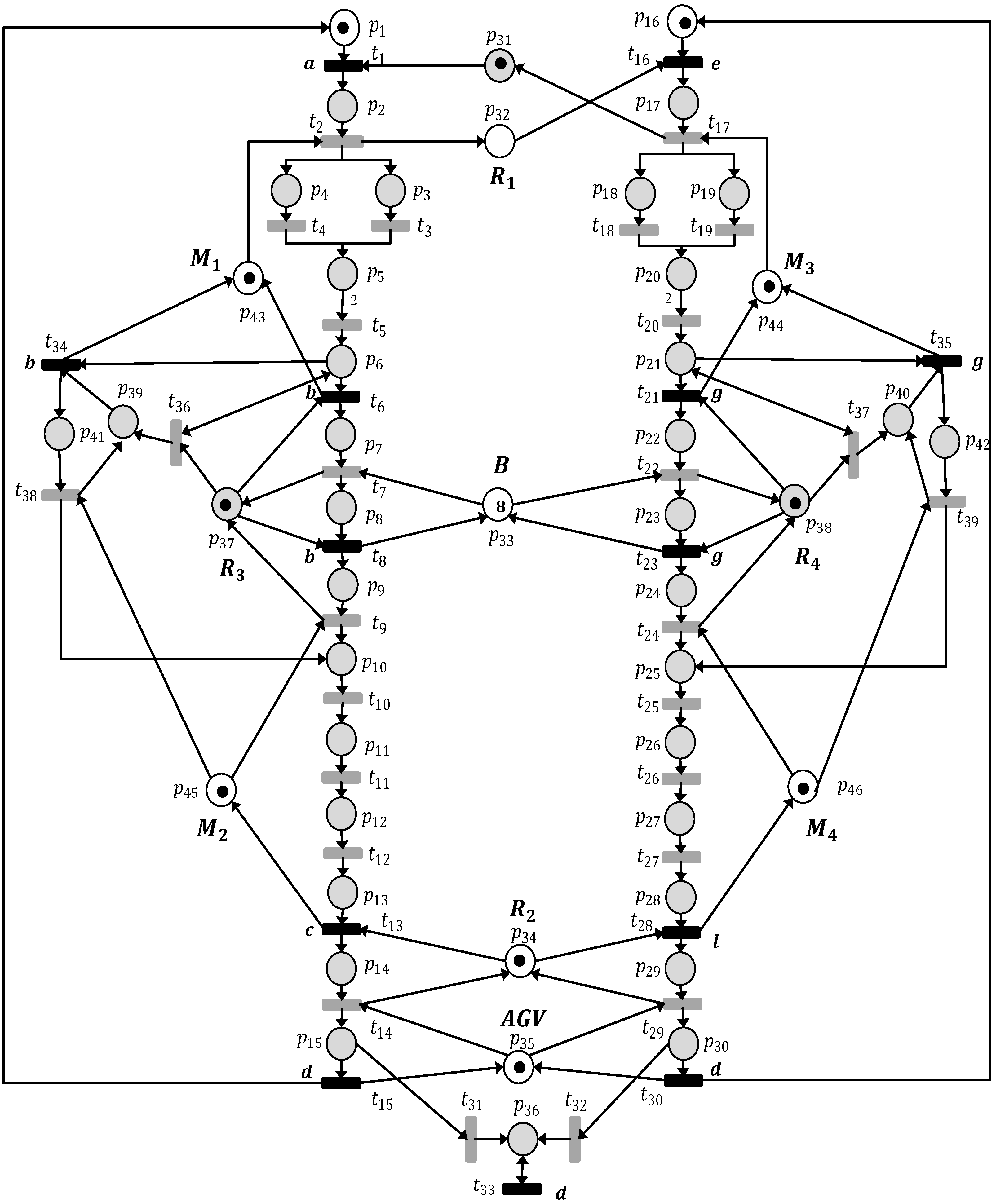
6. Experimental Results: A Manufacturing System
7. LBO in Decentralized Setting
7.1. Decentralized Opacity with Coordinator
- A1:
- Each intruder has full understanding of the system’s structure and initial marking, but uses his own sensor configuration to track its evolution, where , such that if the observable place by intruder j corresponds to place and to 0, otherwise, and where is a local labeling function, such that if and , otherwise.
- A2:
- An observable place is observed by at least one local intruder, i.e., .
- A3:
- A discernible transition is discerned by at least one local intruder, i.e., .
- A4:
- Let be an ordering relation defined between sensor configurations, such that if intruder j observes more than intruder i, i.e., if .
- R1:
- The -induced subnet and the -induced subnet are acyclic for any local intruder .
- R2:
- The general estimation is .
- R3:
- The more an intruder observes, the better its estimation will be, i.e., if, for all , .
- R4:
- The coordinator collects the event sequence estimation generated by each intruder without delay.
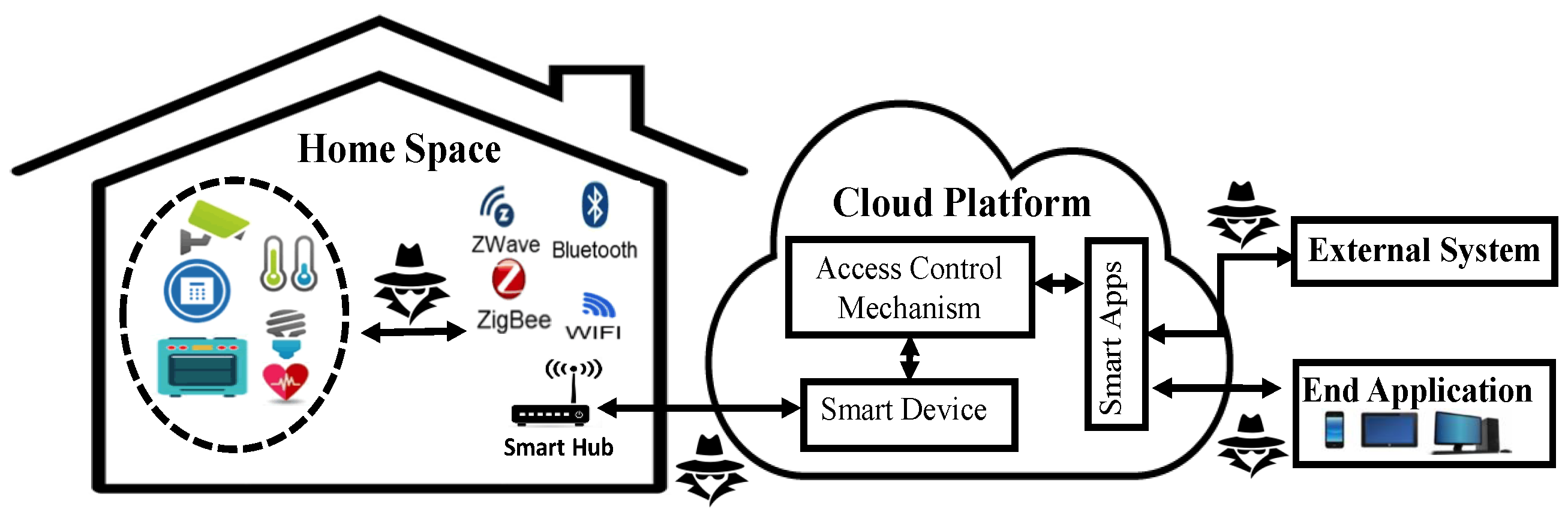
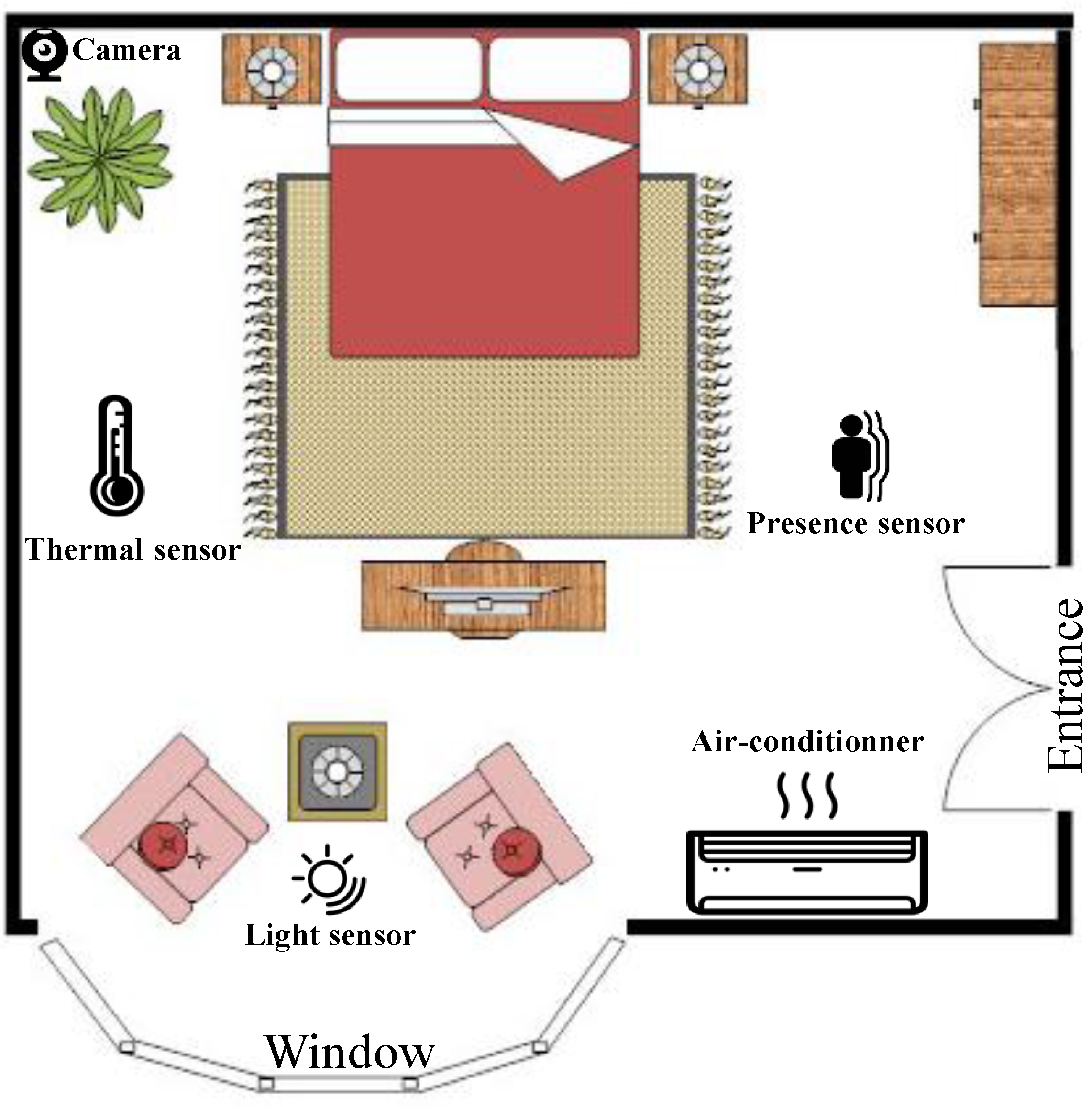
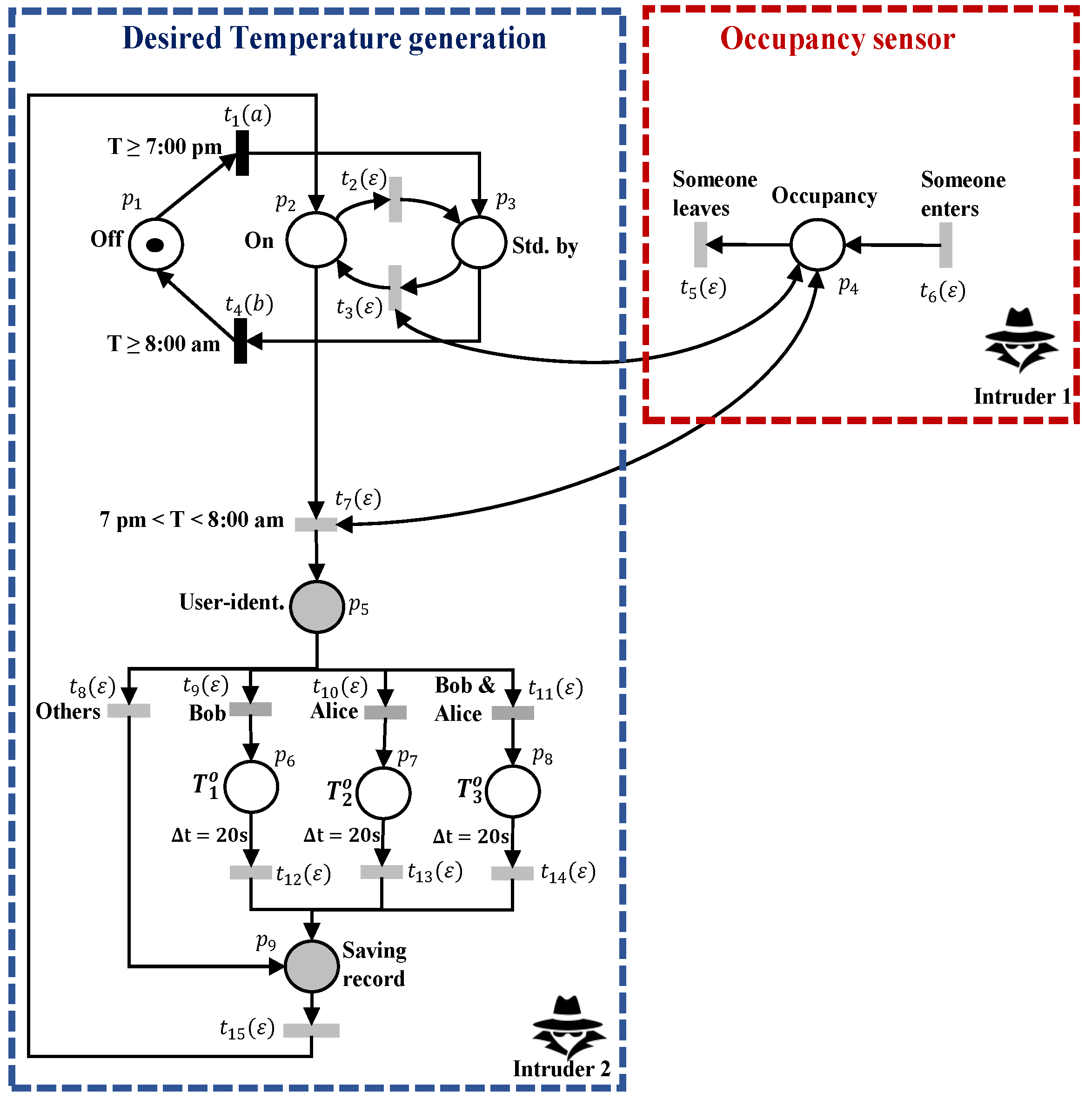
7.2. Study Case: Temperature Control System
- Bob is identified (transition ); then, his preferred reference temperature (place ) will be displayed.
- Alice is identified (transition ) in the room. In this case, the preferred reference temperature will be (place ).
- Bob and Alice are simultaneously present in the room (transition ); then, the reference temperature (place ), on which Bob and Alice have agreed, will be displayed.
- Neither Bob nor Alice is identified (transition ).
8. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gaudin, B.; Marchand, H. Supervisory control and deadlock avoidance control problem for concurrent discrete event systems. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 12–15 December 2005; pp. 2763–2768. [Google Scholar]
- Jiao, T.; Wonham, W. Composite supervisory control for symmetric discrete-event systems. Int. J. Control 2020, 93, 1630–1636. [Google Scholar] [CrossRef]
- Bryans, J.W.; Koutny, M.; Mazaré, L.; Ryan, P.Y. Opacity generalised to transition systems. In Proceedings of the International Workshop on Formal Aspects in Security and Trust, Newcastle upon Tyne, UK, 18–19 July 2005; pp. 81–95. [Google Scholar]
- Basile, F.; De Tommasi, G.; Sterle, C. Non-interference enforcement in bounded Petri nets. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami Beach, FL, USA, 17–19 December 2018; pp. 4827–4832. [Google Scholar]
- Lin, F. Opacity of discrete event systems and its applications. Automatica 2011, 47, 496–503. [Google Scholar] [CrossRef]
- Lafortune, S.; Lin, F.; Hadjicostis, C.N. On the history of diagnosability and opacity in discrete event systems. Annu. Rev. Control 2018, 45, 257–266. [Google Scholar] [CrossRef]
- Saadaoui, I.; Li, Z.; Wu, N. Current-state opacity modelling and verification in partially observed Petri nets. Automatica 2020, 116, 108907. [Google Scholar] [CrossRef]
- Ben-Kalefa, M.; Lin, F. Opaque superlanguages and sublanguages in discrete event systems. Cybern. Syst. 2016, 47, 392–426. [Google Scholar] [CrossRef]
- Badouel, E.; Bednarczyk, M.; Borzyszkowski, A.; Caillaud, B.; Darondeau, P. Concurrent secrets. Discret. Event Dyn. Syst. 2007, 17, 425–446. [Google Scholar] [CrossRef]
- Tong, Y.; Ma, Z.; Li, Z.; Seactzu, C.; Giua, A. Verification of language-based opacity in Petri nets using verifier. In Proceedings of the American Control Conference, Boston, MA, USA, 6–8 July 2016; pp. 757–763. [Google Scholar]
- Cong, X.; Fanti, M.P.; Mangini, A.M.; Li, Z. On-line verification of current-state opacity by Petri nets and integer linear programming. Automatica 2018, 94, 205–213. [Google Scholar] [CrossRef]
- Wu, Y.C.; Lafortune, S. Comparative analysis of related notions of opacity in centralized and coordinated architectures. Discret. Event Dyn. Syst. 2013, 23, 307–339. [Google Scholar] [CrossRef]
- Basile, F.; De Tommasi, G. An algebraic characterization of language-based opacity in labeled Petri nets. IFAC-PapersOnLine 2018, 51, 329–336. [Google Scholar] [CrossRef]
- Paoli, A.; Lin, F. Decentralized opacity of discrete event systems. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 6083–6088. [Google Scholar]
- Lin, F.; Wonham, W.M. Decentralized supervisory control of discrete-event systems. Inf. Sci. 1988, 44, 199–224. [Google Scholar] [CrossRef]
- Ramadge, P.J.; Wonham, W.M. The control of discrete event systems. Proc. IEEE 1989, 77, 81–98. [Google Scholar] [CrossRef]
- Tripakis, S.; Rudie, K. Decentralized Observation of Discrete-Event Systems: At Least One Can Tell. IEEE Control Syst. Lett. 2022, 6, 1652–1657. [Google Scholar] [CrossRef]
- Saadaoui, I.; Li, Z.; Wu, N.; Khalgui, M. Depth-first search approach for language-based opacity verification using Petri nets. IFAC-PapersOnLine 2020, 53, 378–383. [Google Scholar] [CrossRef]
- Silva, M.; Terue, E.; Colom, J.M. Linear algebraic and linear programming techniques for the analysis of place/transition net systems. In Proceedings of the Advanced Course on Petri Nets, Dagstuhl, Germany, 7–18 October 1996; pp. 309–373. [Google Scholar]
- Cabasino, M.P.; Giua, A.; Pocci, M.; Seatzu, C. Discrete event diagnosis using labeled Petri nets. An application to manufacturing systems. Control Eng. Pract. 2011, 19, 989–1001. [Google Scholar] [CrossRef]

| Variable | Type | Size | Range | Total |
|---|---|---|---|---|
| Integer | ||||
| Integer | ||||
| Integer | k ∈ {1, …, } | |||
| Integer | k ∈ {1, …, } | |||
| Integer | k ∈ {1, …, nd} | |||
| Integer | k ∈ {1, …, nd} | |||
| Binary | k ∈ {1, …, } | |||
| Binary | k ∈ {1, …, nd} | |||
| U | Integer | 1 | ||
| Integer | ||||
| Binary | k ∈ {1, …, Li} | |||
| Integer | ||||
| Binary | 1 | |||
| Binary | 1 | |||
| Binary | 1 |
| Constraint Set | Sub-Constraints | Extent | Range | Total |
|---|---|---|---|---|
| f | 1 | 1 | 1 | 1 |
| 3.a | m | 1 | m | |
| 3.b | m | |||
| 3.c | j ∈ {1 … ho} | mo·ho | ||
| 3.d | 2 | |||
| 8.a1 | ||||
| 8.b1 | ||||
| 8.a2 | 1 | 1 | ||
| 8.b2 | 1 | 1 | ||
| 8.a3 | 2 | k {1 …nu} | ||
| 8.b3 | 2 | k {1 …nd} | ||
| 8.c1 | m | |||
| 8.c2 | m | r ∈ {1 … Li} | ||
| 8.c3 | 1 | |||
| 8.c4 | 1 | |||
| 8.c5 | 1 | 1 | ||
| 8.d | 1 | 1 |
| Framework | Graph | Secret Nature | Complexity | |
|---|---|---|---|---|
| [5] | Automaton | No | Labels | Exponential |
| [10] | LPN | Yes | Observable transitions | Exponential |
| [13] | LPN | No | Labels | NP-hard |
| Proposed approach | POPN | No | Transitions | NP-hard |
| Value | ||
|---|---|---|
| Value | |
|---|---|
| Intruder | Projection of | Projection of |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | a |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saadaoui, I.; Labed, A.; Li, Z.; El-Sherbeeny, A.M.; Du, H. Language-Based Opacity Verification in Partially Observed Petri Nets through Linear Constraints. Mathematics 2023, 11, 3880. https://doi.org/10.3390/math11183880
Saadaoui I, Labed A, Li Z, El-Sherbeeny AM, Du H. Language-Based Opacity Verification in Partially Observed Petri Nets through Linear Constraints. Mathematics. 2023; 11(18):3880. https://doi.org/10.3390/math11183880
Chicago/Turabian StyleSaadaoui, Ikram, Abdeldjalil Labed, Zhiwu Li, Ahmed M. El-Sherbeeny, and Huiran Du. 2023. "Language-Based Opacity Verification in Partially Observed Petri Nets through Linear Constraints" Mathematics 11, no. 18: 3880. https://doi.org/10.3390/math11183880
APA StyleSaadaoui, I., Labed, A., Li, Z., El-Sherbeeny, A. M., & Du, H. (2023). Language-Based Opacity Verification in Partially Observed Petri Nets through Linear Constraints. Mathematics, 11(18), 3880. https://doi.org/10.3390/math11183880







