Abstract
The coronavirus disease (COVID-19) outbreak has prompted various industries to embark on digital transformation efforts, with software playing a critical role. Ensuring the reliability of software is of the utmost importance given its widespread use across multiple industries. For example, software has extensive applications in areas such as transportation, aviation, and military systems, where reliability problems can result in personal injuries and significant financial losses. Numerous studies have focused on software reliability. In particular, the software reliability growth model has served as a prominent tool for measuring software reliability. Previous studies have often assumed that the testing environment is representative of the operating environment and that software failures occur independently. However, the testing and operating environments can differ, and software failures can sometimes occur dependently. In this study, we propose a new model that assumes uncertain operating environments and dependent failures. In other words, the model proposed in this study takes into account a wider range of environments. The numerical examples in this study demonstrate that the goodness of fit of the new model is significantly better than that of the existing SRGM. Additionally, we show the utilization of the sequential probability ratio test (SPRT) based on the new model to assess the reliability of the dataset.
Keywords:
software reliability growth model; nonhomogeneous Poisson process; uncertain operating environment; dependent failure; sequential probability ratio test MSC:
94-10
1. Introduction
A software reliability growth model (SRGM) is employed to assess the reliability and quality of software products. This enables consumers to evaluate products by referring to reliability information, and developers can efficiently manage development plans based on reliability considerations. For instance, using the mean value function m(t), it is possible to predict the number of failures at a future time point t. Additionally, it can be used to establish policies for determining the optimal release timing for selling products. In other words, the SRGM is used as a tool for predicting the number of failures in future time periods, predicting product reliability, determining release policies, and estimating development costs. A software reliability growth model is represented by a mean value function m(t) that exhibits unique characteristics. The form of m(t) varies depending on the assumed environments (such as the development, testing, and operating phases). Although there have been numerous studies on software reliability models, it is generally observed that software defects and failures do not occur at regular time intervals. In response to this, existing SRGMs predominantly adopt a nonhomogeneous Poisson process (NHPP) framework. NHPP SRGMs provide a mathematical framework for handling software reliability and are widely utilized due to their versatility in various applications. Previous NHPP software reliability models were primarily built on the assumptions that any faults detected during the testing phase are promptly resolved without any debugging delays, no new faults are introduced, and the software systems deployed in real-world environments are either identical to or closely resemble those used during development and testing.
Most SRGMs generally follow a NHPP and assume that the testing environments are the same as the operating environments, and failures occur independently. In addition, SRGM modeling studies consider assumptions such as debugging environments, testing coverage function, total number of faults, and fault detection rate function. Huang et al. [1] introduced an NHPP SRGM that considered imperfect debugging, various errors, and change-points during the testing phase. Lou et al. [2] discussed a generalized NHPP SRGM with imperfect debugging. Imperfect debugging refers to the state in which not all faults or bugs within the software are eliminated when they occur. Chiu et al. [3] proposed an SRGM in which the number of potential errors fluctuates throughout the debugging period. Gupta et al. [4] introduced a model that considered the coverage factor and power functions in development environments. Zhang et al. [5] proposed a model that introduced new errors during the debugging period owing to imperfect debugging. Nguyen et al. [6] developed a new NHPP SRGM with an S-shaped fault detection rate function having three parameters.
Uncertain operating environments refer to the actual environment in which consumers use the software, including factors such as the operating system, background environments, hardware specifications, etc. This encompasses various scenarios and possibilities. Pradhan et al. [7,8,9,10] developed a model that incorporated an S-shaped inflection as the testing coverage function and considered uncertain operating environments. Environment factors (EFs) refer to various internal and external environments such as testing environments, programming tools, programming effort, program structure, hardware specifications, etc. The testing environment is also not consistent. Haque et al. [11] considered uncertain testing environments such as testing effort, testing skills, and testing coverage. Chatterjee et al. [12] studied the randomness effort using uncertain testing environments and operating environments. The NHPP SRGM studies mentioned earlier assumed independent failures. Sometimes, software failures can occur dependently due to interactions among EFs. Lee et al. [13] and Kim et al. [14] assumed that failures occurred dependently.
SRGMs can be used not only to determine reliability but also to plan release or warranty policies. Raheem et al. [15] devised an optimal release policy based on an SRGM considering imperfect debugging. Minamino et al. [16] and Ke et al. [17] introduced an optimal release policy based on a change-point model. Several studies have been conducted on software reliability using various approaches. Saxena et al. [18], Kumar et al. [19], and Garg et al. [20] developed criteria to assess the goodness of fit of SRGMs. These criteria were derived from a combination of the entropy principle and existing evaluation measures. Several studies have focused on criteria evaluating the reliability of the software and hardware. Yaghoobi [21] proposed two multicriteria decision-making methods for comparing SRGMs. Zhu [22] introduced the concept of complex reliability, which considered both hardware and software components, and proposed maintenance policies applicable to such systems. Several recent software reliability studies have employed machine-learning and deep-learning techniques [23,24,25,26].
Hypothesis testing is worth considering to determine software reliability. However, classical hypothesis testing requires large datasets, which is often a limitation because most software failure datasets are small. To address this issue, we introduce the sequential probability ratio test (SPRT) pioneered by Wald [27], which enables testing with small datasets. Unlike traditional statistical hypothesis testing, the SPRT provides test results at each data collection point, saving time and reducing the cost of data collection by drawing conclusions with less data. In other words, the SPRT is an efficient hypothesis-testing method in terms of time and cost. Stieber [28] successfully applied Wald’s SPRT to ensure software reliability. In this study, we extend the SPRT methodology to estimate software reliability.
The aim of this study is as follows: First, we present a new SRGM that considers both uncertain operating environments and dependent failures. Most of the SRGM research assumes either uncertain operating environments or only considers fault dependency. However, in this study, we develop a model that takes both assumptions into account. Subsequently, we evaluate the performance of each model using real datasets. Numerical examples demonstrate that the proposed model outperforms other models that solely account for uncertain operating environments or dependent failures. This provides a more accurate prediction of the number of failures. Additionally, we demonstrate the effectiveness of the SPRT by utilizing optimal assumption cases based on our proposed model. This allows testers to determine when to stop testing based on the software reliability.
In Section 2, we provide the basic background of NHPP SRGMs and introduce the existing NHPP SRGM models as well as the model proposed in this paper. The SPRT procedure is outlined in Section 3. Section 4 presents the datasets and criteria used in this numerical study. We compare the fit of each model to the datasets and apply the SPRT. In Section 5, we discuss the results of the numerical example. Finally, Section 6 presents the conclusions of this study.
2. Software Reliability Growth Model
2.1. Nonhomogeneous Poisson Process
Most SRGMs assume the nonhomogeneous Poisson process (NHPP), which can be represented by the following equation:
It characterizes the cumulative number of failures, denoted as , up to a given execution time t. The mean value function m(t) represents the expected cumulative number of failures at time t. The function m(t) can be obtained by integrating the intensity function from 0 to t as follows:
The reliability function based on the NHPP can be expressed as follows using m(t) [29]. The reliability function R(t) is defined as the probability that there are no failures in the time interval (0, t), given by
Equation (3) means the probability that a software error does not occur in the interval (0, t). If t + x is given, then the software reliability can be expressed as a conditional probability as in Equation (4).
Here, is the probability that a software error does not occur in the interval (t, t + x), where , . The density function of x is given by
where .
2.2. Existing SRGMs
The mean value function m(t) of the NHPP SRGM is obtained by solving a differential equation. The form of the mean value function depends on the assumptions and specific environments being studied. The commonly used differential equation is as follows [30]:
where the function and represents the expected number of initial failures and newly introduced errors until the start point of testing period and represents the failure detection rate per fault.
This paper presents a specific software reliability model with consideration of the uncertainty of the operating environment based on the work by Pham [26].
The NHPP SRGM is typically characterized by a differential equation that is widely recognized in the field. To account for the uncertain operating conditions considered in this study, the mean value function of the proposed model is obtained as follows [31]:
where η is a random variable. In order to explain the uncertain operating environment, this equation utilizes the random variable η, which has a .
2.3. Proposed Model
Most existing NHPP SRGMs assume that testing and operating environments are the same and that failures occur independently. However, sometimes software failures occur dependently, and the operating environments may differ from the testing environments. For example, if an error occurs in a particular class within a program code, then it may cause errors in other classes that refer to the affected class. Conflicts between program codes due to background processes can potentially impact other codes. These situations lead to the occurrence of dependent failures. Furthermore, constructing a testing environments that consider all operating environments is difficult for testers. The operating environment means the environment in which consumers use the software, including hardware specifications (CPU, GPU, RAM, etc.), operating systems (Window, Mac, Linux, etc.), and various concurrently running programs in the background. The proposed model considers dependent failures and uncertain operating environments. Quantifying the operating environments numerically is difficult. So, looking at Equation (7), the uncertain operating environments are represented by η, the random variable. The assumption of dependent failure occurrences is represented by the parameters of the gamma distribution followed by η, which will be discussed in detail when explaining Equation (10).
In this paper, we propose a model that incorporates both uncertain operating environments and dependent failures. The inclusion of the latter is motivated by the need to consider situations in which failures can propagate from one component to another. With the functions and , we can obtain the mean value function m(t) from Equation (7), as shown below:
The proposed model has five parameters, namely b, c, α, β, and N. In Equation (10), the parameters α and β are also the parameters of , which is the gamma distribution, where η represents the uncertain operating environments in Equation (7).
The assumption of dependent failures in the proposed model arises from the interdependence of model parameters. Specifically, the values of and in Equation (10) depend on the probability distribution of η, which characterizes the uncertain operating environments. As these parameters appear in Equation (7), which expresses the failure detection rate, the assumption of dependent failures is a natural consequence of the model design. Therefore, the correlation between model parameters is a crucial factor that underlies the assumption of dependent failures.
Table 1 lists the mean value functions for the existing NHPP SRGMs and the proposed model. Each model is referred to by abbreviations of its characteristics or author names. DPF1 and DPF2 assume dependent failures, whereas the others assume independent failures. VTUB assumes uncertain operating environments, whereas the proposed model (NEW) assumes dependent failures and uncertain operating environments.

Table 1.
Mean value functions for the existing NHPP SRGMs and the proposed model.
3. Sequential Probability Ratio Test
Wald’s SPRT is widely used as a hypothesis-testing technique [27]. It tests the probability ratios of two hypotheses, and , against a predetermined threshold value at each time point. The SPRT algorithm is iterative and requires additional data collection and testing if the probability ratio falls within a certain acceptance region (A and B). Equation (11) expresses the relationship between and and the thresholds A and B.
where and are constants used to determine the acceptance and rejection of the null hypothesis . If , then is rejected. If , then is accepted.
Moreover, A and B depend on and , as shown in Equations (11) and (12). Here, and β are type 1 and type 2 errors, respectively. In other words, is the producer’s risk, and is the consumer’s risk.
The values of A and B depend on the prespecified risk probabilities, α and β, which represent type 1 (producer’s risk) and type 2 (consumer’s risk) errors and are typically set to 0.05 or 0.1, respectively. The upper line that determines rejection is called , and the lower line that determines acceptance is called are represented as follows:
where , , and are given as follows
Figure 1 shows the reliable region of SPRT. If the data value (blue dot) at a certain time point exists within the reliable region, then it is labeled as “Continue”. If the value is outside the region, then a conclusion of “Reject” or “Accept” is made.
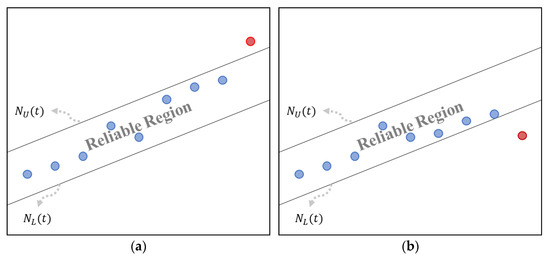
Figure 1.
Reliable region of SPRT: (a) rejection at the final time point (red dot); (b) acceptance at the final time point (red dot).
Stieber [28] applied the SPRT to estimate the reliability of NHPP SRGMs, which involved redefining the probability ratios and of Equation (11) in terms of the mean value function m(t). Here, and are expressed as follows:
The constant B of Equation (11) is on the left side of Equation (17), whereas the constant A of Equation (11) is on the right side of Equation (17). In addition, in Equation (17) is the probability ratio .
4. Numerical Example
In this section, we fit the proposed model and existing models with actual data to estimate the criteria and compare their goodness of fit. We apply the sequential probability ratio test (SPRT) to evaluate the reliability of the data set. Firstly, we fit the data set to each model (mean value function) and estimate the parameters of each model using the least-squares estimation (LSE) method. Then, we calculate the criteria using the estimated parameter values () and compare the goodness of fit. Lastly, we construct an equidistant scale for the parameter set of the proposed model and determine the threshold for the SPRT test based on this parameter set. Finally, we examine the results of applying SPRT to Dataset 1.
4.1. Datasets
We employed two datasets to compare the goodness of fit of the different models [29]. The first dataset (Table 2) was collected by ABC Software Company. The project team comprised a unit manager, one user interface software engineer, and ten software engineers/testers. The dataset was observed over a period of 12 weeks (the unit of time in the table is weeks), and 55 failures were observed during this time.

Table 2.
Dataset 1 (the unit of time is weeks).
The second dataset (Table 3) was collected from a real-time command and control system developed by Bell Laboratories. The failure data corresponds to the observed failures during system testing, and 136 failures were recorded within a period of 25 h.

Table 3.
Dataset 2 (the unit of time is hours).
4.2. Criteria
Different criteria have been suggested for evaluating how well a model fits the data [9]. This study discusses 10 criteria (MSE, PRR, PP, SAE, R2, AIC, PRV, RMSPE, MAE, and MEOP) to compare the proposed model with 10 existing NHPP SRGMs.
Table 4 presents various criteria used to evaluate the goodness of fit of different NHPP SRGMs and the proposed model. These criteria measure the distance or error between the predicted number of failures based on the mean value function of the model, denoted as , and the actual observed data, denoted as . The number of data points is represented as n, and the number of parameters in the model is represented as m. The shorter the distance between the predicted and actual values, the better the mean value function of the model is at predicting the number of failures in the dataset.

Table 4.
Criteria.
The criteria used in the evaluation include the following: The MSE considers the number of parameters in the model, and the number of data points used to measure the distance between the predicted and actual values. The PRR measures the distance between the predicted and actual values while considering the value predicted by the model. The PP measures the distance between the predicted and actual values while considering only the actual data. The SAE measures the total distance between the predicted and actual values.
The coefficient of determination (R2) is a measure of the regression fit. It represents the proportion of the regression sum of squares to the total sum of squares in the model. The closer the value is to 1, the better the fit of the model.
The AIC is a statistical measure that evaluates the ability of a model to fit the data. The likelihood function () of the model is maximized, and the AIC is adjusted for the number of parameters in the model. Typically, a model with more parameters has a better fit; however, the AIC prevents overfitting by penalizing models with too many parameters. Specifically, the AIC is calculated as the log-likelihood function () plus a penalty term that depends on the number of parameters in the model. The likelihood function () and the log-likelihood function () are defined as follows:
The PRV, also known as variation or variance, calculates the standard deviation of the prediction bias; a smaller value indicates a better model fit. The bias is defined as . The RMSPE determines the closeness of the predicted value to the actual data, considering bias and the PRV. The MAE measures the mean absolute error between the predicted value and the actual data. The MEOP calculates the SAE with the predicted value of the model.
In summary, the goodness of fit of a model can be evaluated using 10 criteria. A larger value of R2 indicates a better fit of the model. Other criteria, such as the MSE, PRR, PP, SAE, AIC, PRV, RMSPE, MAE, and MEOP, indicate the degree of closeness between the predicted and actual values in comparison with other models on the same dataset. In general, smaller values for these criteria suggest a better fit of the model.
4.3. Results of Goodness of Fit
Table 5 and Table 6 present the estimated parameters of the models, which are obtained through the application of least-squares estimation.

Table 5.
Parameters estimation of Dataset 1.

Table 6.
Parameters estimation of Dataset 2.
Table 7 and Table 8 present the estimated criteria values of the models for the two datasets. For Dataset 1, the proposed model shows the smallest MSE, PRR, PP, SAE, AIC, RMSPE, MAE, and MEOP at 1.7560, 0.0078, 0.0079, 9.0969, 57.1869, 1.0571, 1.0571, and 1.2996, respectively. The proposed model shows the largest R2 at 0.9956 and the second smallest PRV at 59.6115. For Dataset 2, the proposed model shows the smallest MSE, PRR, PP, SAE, AIC, PRV, RMSPE, MAE, and MEOP at 7.2890, 0.0163, 0.0161, 45.6681, 116.7360, 122.8303, 2.4646, 2.4646, and 2.2834, respectively. The proposed model shows the largest R2 at 0.9936. The results indicate that the proposed model performs better than the other models in predicting the cumulative number of failures in the datasets.

Table 7.
Comparison of the criteria values of the models for Dataset 1.

Table 8.
Comparison of the criteria values of the models for Dataset 2.
The MSE, PRR, and PP are particularly commonly used criteria. Figure 2 and Figure 3 show the top three models for the criteria (MSE, PRR, and PP) in Table 7 and Table 8. In Figure 2, the goodness of fit of the proposed model for Dataset 1 is better than that of the DPF1 and DPF2 models, which assume only dependent failures. Similarly, Figure 3 shows that the goodness of fit of the proposed model for Dataset 2 is better than that of the VTUB model, which assumes only uncertain operating environments. Thus, the proposed model, which considers both dependent failures and uncertain operating environments, is a reasonable approach for studying software reliability.
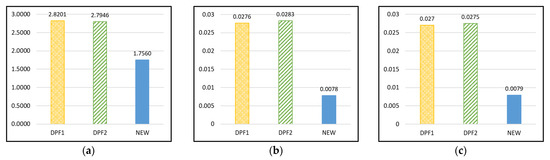
Figure 2.
The top three models of main criteria values for Dataset 1: (a) MSE; (b) PRR; (c) PP.
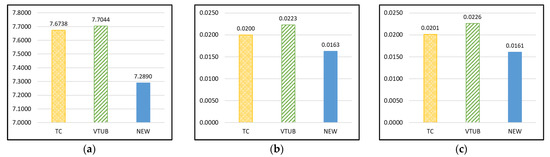
Figure 3.
The top three models of main criteria values for Dataset 2: (a) MSE; (b) PRR; (c) PP.
4.4. Results of SPRT
As the model proposed herein is the best fit for the datasets, we propose a method for measuring reliability by applying the SPRT based on the proposed model. Dataset 1 is used in this study. To test reliability, the SPRT is used on individual parameters or a set of parameters. For the proposed model, applying the SPRT to the parameters and β can lead to sensitivity issues and potentially skew the SPRT results. Therefore, the SPRT is applied specifically to parameters b, N, and c.
Equation (20) shows the null and alternative hypotheses, and , created based on the interval scale of the parameter groups. The parameters (, , , , and ) represent , whereas is represented by (, , , , and ). The values of and are calculated as and , respectively, where is set as the percentile of the parameter value. For instance, when is considered to be 1% of each parameter value, is computed as , and is calculated as . Similarly, percentile values are used to determine the interval scales (, , , and ) for N and c. The values and in Equation (20) are substituted into Equation (17) and based on whether satisfies Equation (17), the conclusion is reached as “Continue” if it is satisfied. If is smaller than the left term of Equation (17), then it is concluded as “Acceptance”. If is bigger than the right term of Equation (17), it is concluded as “Rejection”.
To compare the SPRT results, various cases of are considered in this study, and Table 9 presents 30 cases of values for , , and .

Table 9.
Estimation parameters of Dataset 1.
Table 10, Table 11, Table 12, Table 13, Table 14 and Table 15 show the SPRT results for Dataset 1. The SPRT results from case 1 to case 20 are “Continue.” This indicates “after collecting data for the next time point, and test for the next time point.” From case 21 to case 30, the results are “Reject” at which indicates “stop data collection, and reject the reliability.” If the result is “Accept”, then this indicates “stop the data collection, and accept the reliability”. As the value of increases, the area of acceptance and rejection increases, and as the value of decreases, the area of “Continue” increases. Therefore, determining an appropriate level of is important for the SPRT.

Table 10.
Comparison of SPRT results for Dataset 1 (Cases 1–5).

Table 11.
Comparison of SPRT results for Dataset 1 (Cases 6–10).

Table 12.
Comparison of SPRT results for Dataset 1 (Cases 11–15).

Table 13.
Comparison of SPRT cases for Dataset 1 (Cases 16–20).

Table 14.
Comparison of SPRT cases for Dataset 1 (Cases 21–25).

Table 15.
Comparison of SPRT cases for Dataset 1 (Cases 26–30).
From Section 2.1, we can estimate reliability function of Dataset 1, where x is given as 0.1. Figure 4 shows the results. In Figure 4, it can be observed that the reliability sharply decreases until just before time point 5. This is estimated to be due to the rapid increase in the number of failures in Dataset 1, as indicated in Table 2. The SPRT results (cases 21–30) concluded the rejection of product reliability at the 6th time point, which aligns with the substantial number of failures in Dataset 1 up to the 6th time point. Although Dataset 1 in this study is tested for 12 weeks, according to the results of SPRT, it can be concluded that testing should be discontinued at the 6th week and efforts should be made to improve reliability.
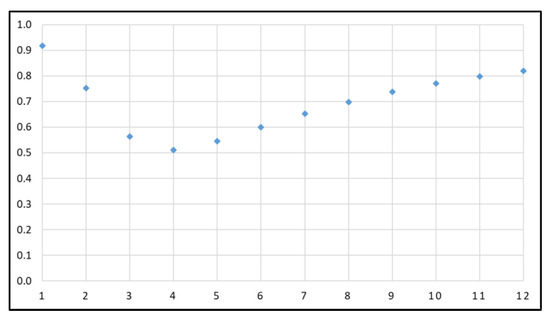
Figure 4.
Reliability function of Dataset 1.
5. Discussion
Most NHPP SRGMs assume that the testing environment is the same as the operating environment or that software failures occur independently. In this study, we propose a new NHPP SRGM that assumes uncertain operating environments and dependent failures. The results of numerical examples demonstrate the superiority of the proposed model over the models that consider only uncertain operating environments (VTUB) or only dependent failures (DPF 1 and DPF 2). Thus, the proposed model estimates the number of failures better than the existing NHPP SRGMs. This study also demonstrates how we can estimate software reliability using the proposed model by applying the SPRT. As the value of increases, the “Continue” region becomes narrower, and the “Accept/Reject” regions become wider. Therefore, it is important to choose an appropriate level of , and further research on this matter is needed. Wood [43] explained that SRGMs can be used to predict the number of failures and provide software reliability to consumer. This study illustrates that the proposed model can be utilized in real environments.
6. Conclusions
This study had two objectives. First, we proposed a model that considered both dependent failures and uncertain operating environments. The results of the numerical examples demonstrated that the proposed model exhibited a significantly better fit than the models that considered only dependent failures (DPF 1 and DPF 2) or uncertain operating environments (VTUB).
Second, by leveraging the proposed model, we introduced a method for assessing software reliability through the application of the SPRT. Specifically, although the dataset was actually tested for 12 weeks, according to the results of the SPRT, testing was discontinued at the 6th week, and it was concluded that measures should be taken to improve the reliability. From the dataset and the values of the reliability function, it was observed that the number of failures in the observed dataset until a certain time point was higher than the number of failures after that point. In other words, even with a limited dataset, this study achieved the goal of an early reliability assessment by applying the SPRT. Further studies that link the SPRT with future software release policies will contribute to efficient development planning processes.
Author Contributions
Conceptualization, H.P.; funding acquisition, I.C.; software, D.L.; writing—original draft, D.L.; writing—review and editing, I.C. and H.P. All three authors contributed equally to this study. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Basic Science Research Program of the National Research Foundation of Korea (NRF), funded by the Ministry of Education (NRF-2021R1F1A1048592 and 2021R1A6A3A01086716).
Data Availability Statement
The data that support the findings of this study are openly available in reference number [29].
Acknowledgments
Many thanks to the reviewers for careful reading and valuable comments which improved the paper representation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huang, Y.-S.; Chiu, K.-C.; Chen, W.-M. A software reliability growth model for imperfect debugging. J. Syst. Softw. 2022, 188, 111267. [Google Scholar] [CrossRef]
- Luo, H.; Xu, L.; He, L.; Jiang, L.; Long, T. A Novel Software Reliability Growth Model Based on Generalized Imperfect Debugging NHPP Framework. IEEE Access 2023, 11, 71573–71593. [Google Scholar] [CrossRef]
- Chiu, K.C.; Huang, Y.S.; Huang, I.C. A study of software reliability growth with imperfect debugging for time-dependent potential errors. Int. J. Ind. Eng.-Theory Appl. Pract. 2019, 26. [Google Scholar] [CrossRef]
- Gupta, R.; Jain, M.; Jain, A. Software Reliability Growth Model in Distributed Environment Subject to Debugging Time Lag; Springer: Berlin/Heidelberg, Germany, 2019; pp. 105–118. [Google Scholar] [CrossRef]
- Zhang, C.; Yuan, Y.; Jiang, W.; Sun, Z.; Ding, Y.; Fan, M.; Li, W.; Wen, Y.; Song, W.; Liu, K. Software Reliability Model Related to Total Number of Faults under Imperfect Debugging; Springer: Berlin/Heidelberg, Germany, 2022; pp. 48–60. [Google Scholar] [CrossRef]
- Nguyen, H.C.; Huynh, Q.T. New non-homogeneous Poisson process software reliability model based on a 3-parameter S-shaped function. IET Softw. 2022, 16, 214–232. [Google Scholar] [CrossRef]
- Pradhan, V.; Dhar, J.; Kumar, A.; Bhargava, A. An S-Shaped Fault Detection and Correction SRGM Subject to Gamma-Distributed Random Field Environment and Release Time Optimization; Springer: Berlin/Heidelberg, Germany, 2020; pp. 285–300. [Google Scholar]
- Pradhan, S.K.; Kumar, A.; Kumar, V. A Testing Coverage Based SRGM Subject to the Uncertainty of the Operating Environment. In Proceedings of the 1st International Online Conference on Mathematics and Applications, online, 1–15 May 2023; MDPI: Basel, Switzerland, 2023; p. 44. [Google Scholar]
- Pradhan, S.K.; Kumar, A.; Kumar, V. A New Software Reliability Growth Model with Testing Coverage and Uncertainty of Operating Environment. Comput. Sci. Math. Forum. 2023, 7, 44. [Google Scholar] [CrossRef]
- Pradhan, V.; Dhar, J.; Kumar, A. Testing coverage-based software reliability growth model considering uncertainty of operating environment. Syst. Eng. 2023, 26, 449–462. [Google Scholar] [CrossRef]
- Haque, M.A.; Ahmad, N. Software reliability modeling under an uncertain testing environment. Int. J. Model. Simul. 2023, 1–7. [Google Scholar] [CrossRef]
- Chatterjee, S.; Saha, D.; Sharma, A.; Verma, Y. Reliability and optimal release time analysis for multi up-gradation software with imperfect debugging and varied testing coverage under the effect of random field environments. Ann. Oper. Res. 2022, 312, 65–85. [Google Scholar] [CrossRef]
- Lee, D.H.; Chang, I.H.; Pham, H. Software Reliability Model with Dependent Failures and SPRT. Mathematics 2020, 8, 1366. [Google Scholar] [CrossRef]
- Kim, Y.S.; Song, K.Y.; Pham, H.; Chang, I.H. A Software Reliability Model with Dependent Failure and Optimal Release Time. Symmetry 2022, 14, 343. [Google Scholar] [CrossRef]
- Raheem, A.R.; Akthar, S.; Rafi, S.M. An Imperfect Debugging Software Reliability Growth Model: Optimal Release Problems through Warranty Period based on Software Maintenance Cost Model. Rev. Geintec 2021, 11, 4623–4631. [Google Scholar] [CrossRef]
- Minamino, Y.; Inoue, S.; Yamada, S. Change-point–based software reliability modeling and its application for software development management. In Recent Advancements in Software Reliability Assurance; CRC Press: Boca Raton, FL, USA, 2019; pp. 59–92. [Google Scholar]
- Ke, S.Z.; Huang, C.Y. Software reliability prediction and management: A multiple change-point model approach. Qual. Reliab. Eng. Int. 2020, 36, 1678–1707. [Google Scholar] [CrossRef]
- Saxena, P.; Kumar, V.; Ram, M. A novel CRITIC-TOPSIS approach for optimal selection of software reliability growth model (SRGM). Qual. Reliab. Eng. Int. 2022, 38, 2501–2520. [Google Scholar] [CrossRef]
- Kumar, V.; Saxena, P.; Garg, H. Selection of optimal software reliability growth models using an integrated entropy–Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS) approach. In Mathematical Methods in the Applied Sciences; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Garg, R.; Raheja, S.; Garg, R.K. Decision Support System for Optimal Selection of Software Reliability Growth Models Using a Hybrid Approach. IEEE Trans. Reliab. 2022, 71, 149–161. [Google Scholar] [CrossRef]
- Yaghoobi, T. Selection of optimal software reliability growth model using a diversity index. Soft Comput. 2021, 25, 5339–5353. [Google Scholar] [CrossRef]
- Zhu, M. A new framework of complex system reliability with imperfect maintenance policy. Ann. Oper. Res. 2022, 312, 553–579. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, C. Software reliability prediction using a deep learning model based on the RNN encoder–decoder. Reliab. Eng. Syst. Saf. 2018, 170, 73–82. [Google Scholar] [CrossRef]
- San, K.K.; Washizaki, H.; Fukazawa, Y.; Honda, K.; Taga, M.; Matsuzaki, A. Deep Cross-Project Software Reliability Growth Model Using Project Similarity-Based Clustering. Mathematics 2021, 9, 2945. [Google Scholar] [CrossRef]
- Li, L. Software reliability growth fault correction model based on machine learning and neural network algorithm. Microprocess. Microsyst. 2021, 80, 103538. [Google Scholar] [CrossRef]
- Banga, M.; Bansal, A.; Singh, A. Implementation of machine learning techniques in software reliability: A framework. In Proceedings of the 2019 International Conference on Automation, Computational and Technology Management (ICACTM), London, UK, 24–26 April 2019; IEEE: New York, NY, USA, 2019; pp. 241–245. [Google Scholar] [CrossRef]
- Wald, A. Sequential Analysis; Dover Publications: Mineola, NY, USA, 2004; ISBN 978-0-486-61579-0. [Google Scholar]
- Stieber, H.A. Statistical quality control: How to detect unreliable software components. In Proceedings of the Eighth International Symposium on Software Reliability Engineering, Albuquerque, NM, USA, 2–5 November 1997; IEEE Computer Society: Washington, DC, USA, 1997; pp. 8–12. [Google Scholar]
- Pham, H. System Software Reliability; Springer: London, UK, 2006. [Google Scholar]
- Pham, H.; Nordmann, L.; Zhang, X. A general imperfect-software-debugging model with S-shaped fault-detection rate. IEEE Trans. Reliab. 1999, 48, 169–175. [Google Scholar] [CrossRef]
- Pham, H. A new software reliability model with Vtub-shaped fault-detection rate and the uncertainty of operating environments. Optimization 2014, 63, 1481–1490. [Google Scholar] [CrossRef]
- Yamada, S.; Ohba, M.; Osaki, S. S-shaped reliability growth modeling for software fault detection. IEEE Trans. Reliab. 1983, 32, 475–484. [Google Scholar] [CrossRef]
- Goel, A.L.; Okumoto, K. Time-Dependent Error-Detection Rate Model for Software Reliability and Other Performance Measures. IEEE Trans. Reliab. 1979, 28, 206–211. [Google Scholar] [CrossRef]
- Yamada, S.; Ohba, M.; Osaki, S. S-shaped Software Reliability Growth Models and Their Applications. IEEE Trans. Reliab. 1984, 33, 289–292. [Google Scholar] [CrossRef]
- Yamada, S.; Tokuno, K.; Osaki, S. Imperfect debugging models with fault introduction rate for software reliability assessment. Int. J. Syst. Sci. 1992, 23, 2241–2252. [Google Scholar] [CrossRef]
- Pham, H.; Zhang, X. An NHPP Software Reliability Model and Its Comparison. Int. J. Reliab. Qual. Saf. Eng. 1997, 04, 269–282. [Google Scholar] [CrossRef]
- Chang, I.H.; Pham, H.; Lee, S.W.; Song, K.Y. A testing-coverage software reliability model with the uncertainty of operating environments. Int. J. Syst. Sci. Oper. Logist. 2014, 1, 220–227. [Google Scholar] [CrossRef]
- Song, K.Y.; Chang, I.H.; Pham, H. A software reliability model with a Weibull fault detection rate function subject to operating environments. Appl. Sci. 2017, 7, 983. [Google Scholar] [CrossRef]
- Li, Q.; Pham, H. A testing-coverage software reliability model considering fault removal efficiency and error generation. PLoS ONE 2017, 12, e0181524. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Pillai, K.; Sukumaran Nair, V.S. A model for software development effort and cost estimation. IEEE Trans. Softw. Eng. 1997, 23, 485–497. [Google Scholar] [CrossRef]
- Anjum, M.; Haque, M.A.; Ahmad, N. Analysis and ranking of software reliability models based on weighted criteria value. Int. J. Inf. Technol. Comput. Sci. 2013, 5, 1–14. [Google Scholar] [CrossRef]
- Wood, A. Software Reliability Growth Models; TANDEM Technical Report; Tandem Computers: Cupertino, CA, USA, 1996; Volume 96. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).