LASSO and Elastic Net Tend to Over-Select Features

Abstract

Machine learning methods have been a standard approach to select features that are associated with an outcome and to build a prediction model when the number of candidate features is large. LASSO is one of the most popular approaches to this end. The LASSO approach selects features with large regression estimates, rather than based on statistical significance, that are associated with the outcome by imposing an $L_1$-norm penalty to overcome the high dimensionality of the candidate features. As a result, LASSO may select insignificant features while possibly missing significant ones. Furthermore, from our experience, LASSO has been found to select too many features. By selecting features that are not associated with the outcome, we may have to spend more cost to collect and manage them in the future use of a fitted prediction model. Using the combination of $L_1$- and $L_2$-norm penalties, elastic net (EN) tends to select even more features than LASSO. The overly selected features that are not associated with the outcome act like white noise, so that the fitted prediction model may lose prediction accuracy. In this paper, we propose to use standard regression methods, without any penalizing approach, combined with a stepwise variable selection procedure to overcome these issues. Unlike LASSO and EN, this method selects features based on statistical significance. Through extensive simulations, we show that this maximum likelihood estimation-based method selects a very small number of features while maintaining a high prediction power, whereas LASSO and EN make a large number of false selections to result in loss of prediction accuracy. Contrary to LASSO and EN, the regression methods combined with a stepwise variable selection method is a standard statistical method, so that any biostatistician can use it to analyze high-dimensional data, even without advanced bioinformatics knowledge.

1. Introduction

Big data usually have a large number of features, also called predictors or covariates, that are potentially associated with an outcome, so that they require new analysis methods [1]. Such big data are called high-dimensional data. Machine learning (ML) methods have been widely used to build prediction models from high-dimensional data, in place of traditional statistical methods. However, it still needs more investigations to recognize their superiority over the standard statistical methods for the analysis of clinical big data. In this paper, we assume that only a small number of candidate features are associated with the outcome.

Least absolute shrinkage and selection operator (LASSO: [2]) has been popularly used for prediction model fitting since it can be used for any types of regression models depending on the type of outcome variable. There are some issues with LASSO. LASSO tends to over-select features, so that the selected features with insignificant or no association with the outcome will play the role of noise in the fitted prediction model and lower the prediction accuracy. If a fitted prediction model includes a large number of features, it often incurs additional cost. For example, suppose that we want to develop a model to predict patients’ outcomes based on gene expression data. At the development stage, we usually use commercial microarray chips with thousands of genes. Once a prediction model is fitted, we usually develop customized chips including only the genes selected for the fitted prediction model to increase the assay accuracy and lower the price of chips [3]. If the number of selected genes is too large, the decrease in price of the customized chips and the increase in assay accuracy can be minimal while sacrificing prediction performance due to falsely selected genes. As another example, suppose that we want to develop a model to predict the shopping behavior of customers using big data for a retailer (e.g., https://www.sprintzeal.com). Once a prediction model is fitted, the retailer using the fitted model will have to keep collecting the features included in the fitted model and manage them to increase the sales volume. In this case, if the number of selected features is too large, these activities can be unnecessarily costly. As in the microarray example, falsely selected features will also result in the loss of prediction accuracy.

Using the $L_1$-norm penalty, LASSO selects features based on the size of regression coefficients, rather than their statistical significance associated with the outcome variable. We standardize feature observations in an effort to make the distributions of features similar and to make the variable selection based on the size of regression coefficients as similar as that based on the statistical significance [4]. However, no known standardization method removes this issue completely, especially when the features have different variable types. For example, if some features are continuous and some are binary, then it is impossible to make the distributions the same by any standardization or transformation, so that the fitted prediction model can include insignificant features while missing some significant ones. Elastic net (EN: [5]) uses a combination of $L_1$-norm and $L_2$-norm penalties, which is less strict than the $L_1$-norm penalty, so that it has more serious problems in these issues.

As an alternative to LASSO and EN, we investigate the use of a standard (un-penalized) regression method combined with a stepwise variable selection procedure to develop a prediction model from high-dimensional data. While the penalized ML methods provide 0-shrinkage estimators, even for a reduced model [6], regression methods equipped with the stepwise variable selection procedure provide the standard maximum likelihood estimators. Furthermore, unlike LASSO and EN, the standard regression methods provide the statistical significance of the regression coefficients for the features included in fitted prediction models with standardization of feature distributions.

There have been numerous items in the literature comparing the performance between logistic regression and some ML methods and claiming that the latter do not have better prediction performance than the former [7,8,9,10,11,12,13]. Most of these findings, however, are anecdotal in the sense that their conclusions are based on real-data analyses, without any systematic simulation studies. While these publications are limited to classification problems using binary outcomes, Kattan [14] compared the performance of ML methods for survival outcomes with that of Cox’s regression method [15] using three urological data sets. For all of the real data sets, the numbers of cases are large, but those of features are not so big that they are not high-dimensional data. Although this type of data may have a big size due to the large number of cases, we do not have any difficulty in analyzing them using a standard regression method. Limited to real-data analyses only, these studies do not provide systemic evaluation of machine learning methods for high-dimensional data.

There have been some publications comparing stepwise selection and LASSO, and our paper extends their findings. Hastie et al. [16] conducted extensive simulations to compare the prediction accuracy of forward stepwise variable selection and LASSO for standard linear regression with a continuous outcome. There are some studies that use real data sets to compare the prediction performance of stepwise variable selection procedure, LASSO and EN [17,18]. Our paper conducts extensive simulations and real-data analysis to compare both variable selection and prediction performance for high-dimensional data. While the above studies consider prediction performance only, we also investigate over-selection issue in regression models for binary and time-to-event outcomes. The previous studies used stepwise procedure, selecting the final model based on model fitting criteria such as R-square or AIC/BIC, while ours is based on p-values to control the significance level of selected features.

In this paper, we compare the variable selection performance of LASSO and EN with the standard statistical regression methods combined with a stepwise variable selection procedure. We conduct extensive simulations for binary outcomes using logistic regression and survival outcomes using the Cox regression model. The performance of the prediction methods are evaluated by mean true selections and mean total selections from training sets and measures of association between fitted prediction model and observed outcome for both training and validation sets. We demonstrate these comparisons using a real data set. Through these numerical studies, We find that LASSO and EN tend to over-select features, while prediction accuracy is no better than that of the standard regression methods equipped with stepwise variable selection, which selects a much smaller number of features.

2. Materials and Methods

We compare the performance of the stepwise method, LASSO, and EN using simulations and analysis of real data by Farrow et al. [19]. We briefly review these prediction methods and the parameters to measure their performance.

The traditional generalized linear model for binary outcomes is logistic regression with stepwise variable selection (L-SVS) and that for time-to-event outcomes is Cox regression with stepwise variable selection (C-SVS). Suppose that there are n subjects, and we observe an outcome variable y and m features $(x_1,\dots ,x_m)$ from each subject. The resulting data will look like $\{y_i,(x_{1i},\dots ,x_{mi}), i=1,\dots ,n\}$. For high-dimensional data, m is much bigger than n, while the number of features that are truly associated with the outcome, denoted as $m_1$, is often small. We will consider a hold-out method to partition the whole data set into training and a validation sets.

2.1. Statistical Models

For $k\ll n$, let $Z={(z_{\tilde{1}},\dots ,z_{\tilde{k}})}^T$ denote a subset of the features that are possibly related with an outcome variable, and $\beta ={({\beta }_{\tilde{1}},\dots ,{\beta }_{\tilde{k}})}^T$ their regression coefficients.

2.1.1. Logistic Regression

The logistic regression method is popularly used to associate a binary outcome y taking 0 or 1 with features [20]. For $P(y=1)\equiv p_{{\beta }_0,\beta }\left(Z\right)$, a logistic regression model is given as

$$\log \frac{p_{{\beta }_0,\beta }\left(Z\right)}{1-p_{{\beta }_0,\beta }\left(Z\right)}={\beta }_0+{\beta }^{T}Z$$

where ${\beta }_0$ is the intercept term. For given $Z_i$, $y_i$’s are independent Bernoulli random variables with success probabilities, $p_{{\beta }_0,\beta }\left(Z\right)$, regression coefficients $({\widehat{\beta }}_0,{\widehat{\beta }}_{\tilde{1}},\dots ,{\widehat{\beta }}_{\tilde{k}})$ are estimated by maximizing the log-likelihood

$${\ell }_1({\beta }_0,\beta )=\sum _{i=1}^n[y_i\log p_{{\beta }_0,\beta }\left(Z_i\right)+(1-y_i)\log \{1-p_{{\beta }_0,\beta }\left(Z_i\right)\}]$$

with respect to $({\beta }_0,{\beta }_{\tilde{1}},\dots ,{\beta }_{\tilde{k}})$.

2.1.2. Cox’s Proportional Hazards Model (PHM)

The Cox’s PHM is commonly used to relate a survival outcome with covariates. For subject $i(=1,\dots ,n)$, let $y_i$ denote the minimum of survival time and censoring time, and ${\delta }_i$ the event indicator, taking 1 if $y_i$ is the survival time and 0 if $y_i$ is the censoring time. A data set will be summarized as $\{(y_i,{\delta }_i),(z_{1i},\dots ,z_{mi}), i=1,\dots ,n\}$. The basic assumption for survival data is that, for each subject, censoring time is independent of survival time given covariates. Using a Cox’s PHM, we assume that the hazard function, $h_i\left(t\right)$, of subject i’s survival time is expressed as

$$h_i\left(t\right)=h_0\left(t\right)e^{{\beta }^T{Z}_i}$$

at time t, where $h_0\left(t\right)$ denotes the baseline hazard. By Cox [15], the regression coefficients are estimated by maximizing the partial log-likelihood function

$${\ell }_2\left(\beta \right)=\sum _{i=1}^n{\delta }_i\left\{Z_i-\frac{{\sum }_{j=1}^{n}I(y_j\ge y_i)Z_{j}exp\left({\beta }^T{Z}_j\right)}{{\sum }_{j=1}^{n}I(y_j\ge y_i)exp\left({\beta }^T{Z}_j\right)}\right\}$$

where $I(·)$ is the indicator function.

2.1.3. Stepwise Variable Selection (SVS)

One of the challenges of high-dimensional data is that the number of candidate features, m, is much larger than the sample size, n. So, variable selection (or dimension reduction) is a critical procedure in prediction model building using high-dimensional data. Popular variable selection methods for standard regression methods include the forward stepwise procedure (also called SVS in this paper), the backward elimination procedure, and all possible combination procedures. For high-dimensional data, however, backward elimination and all possible combination procedures do not work because the estimation procedure of regression models with a large number of covariates does not converge. SVS is very useful, especially when the number of covariates that are truly associated with the outcome is small. It starts with an empty model (or one with an intercept term only for the logistic regression model) and in each step the most significant covariate is added to the model if its p-value is smaller than ${\alpha }_1$, and the extraneous covariates are eliminated if they become insignificant by adding a new variable (i.e., if their p-values are larger than ${\alpha }_2$). This procedure continues until no more covariates are added to the current model. Before starting an analysis using the stepwise procedure, we pre-specify the alpha levels, ${\alpha }_1$ for insertion and ${\alpha }_2$ for deletion, usually ${\alpha }_1<{\alpha }_2$. By the selection of alpha levels, we can control the significance and number of covariates selected for a prediction model.

Some existing stepwise programs, including SAS, use penalized likelihood criteria such as Akaike information criterion (AIC) or Bayesian information criterion (BIC) instead of specifying the significance level. As such, by these methods, we do not know how significant the selected covariates are and we cannot control the number of selected covariates.

2.2. Machine Learning Methods

2.2.1. LASSO

LASSO [2] is a regularized regression method with an $L_1$-norm penalty to the objective function of traditional regression models. For binary outcomes, LASSO adds an $L_1$-norm penalty term to the negative log-likelihood function for a logistic regression and estimates the regression parameters by minimizing

$$-{\ell }_1({\beta }_0,\beta )+\lambda \left|\right|{\beta }_0,\beta {\left|\right|}_1$$

with respect to $({\beta }_0,\beta ,\lambda )$.

For time-to-event outcomes, LASSO adds an $L_1$-norm penalty to the negative log-partial likelihood function for a PHM and estimates the regression parameters by minimizing

$$-{\ell }_2\left(\beta \right)+{\lambda \left|\right|\beta \left|\right|}_1$$

with respect to $(\beta ,\lambda )$ [21]. In this paper, tuning parameter $\lambda$ is selected to minimize the regularized objective function using an internal cross-validation [2,21].

2.2.2. Elastic Net

EN [5] is a generalized regularized model with both $L_1$- and $L_2$-norm regularization terms added to an objective function. For logistic regression with binary outcomes, the regression parameters are estimated by minimizing

$$-{\ell }_1({\beta }_0,\beta )+{\lambda }_1\left|\right|{\beta }_0{,\beta \left|\right|}_1+{\lambda }_2\left|\right|{\beta }_0,\beta {\left|\right|}_2^2$$

with respect to $({\beta }_0,\beta ,{\lambda }_1,{\lambda }_2)$. For Cox regression with time-to-event outcomes, regression parameters are estimated by minimizing

$$-{\ell }_2\left(\beta \right)+{\lambda }_1{\left|\right|\beta \left|\right|}_1+{\lambda }_2{\left|\right|\beta \left|\right|}_2^2$$

with respect to $(\beta ,{\lambda }_1,{\lambda }_2)$. As in LASSO, in this paper, the tuning parameters $({\lambda }_1,{\lambda }_2)$ are obtained by minimizing the regularized objective function using an internal cross-validation.

2.3. Performance Measurements

In our simulation studies, we evaluate the variable selection performance of prediction methods by total selection (i.e., total number of selected covariates) and true selection (i.e., the number of selected covariates that are truly associated with the outcome). Let $\widehat{\beta }$ denote the vector of estimated regression coefficients and Z the vector of corresponding covariates in the current regression model. Then, $r={\widehat{\beta }}^{T}Z$ represents the risk score of a subject with covariate Z. For a data set with a binary outcome, $\{(y_i,Z_i), i=1,\dots ,n\}$, the precision of a fitted prediction model can be evaluated by the AUC of an ROC curve generated by $\{(y_i,r_i), i=1,\dots ,n\}$, where $r_i={\widehat{\beta }}^T{Z}_i$. A large AUC close to 1 means good accuracy of the fitted prediction model. On the other hand, for a data set with a survival outcome, $\{(y_i,{\delta }_i),Z_i, i=1,\dots ,n\}$, the precision of a fitted prediction model can be evaluated by calculating Harrell’s concordance C-index between $(y_i,{\delta }_i)$ and $r_i={\widehat{\beta }}^T{Z}_i$. For a survival outcome, we also calculate −log₁₀ (p-value) for the univariate Cox PHM to regress $(y_i,{\delta }_i)$ on $r_i$. A large negative log p-value means a high accuracy of the fitted prediction model.

All modeling and analyses are conducted using open-source R software, R Foundation for Statistical Computing. The simulation is conducted under version 3.6.0 and the real-data analysis is conducted under version 4.2.2. The R packages and functions we use for LASSO is cv.glmnet from glmnet package, and that for EN is trained from the caret package. We developed our R function to perform R-SVS selecting variables based on the significance level of covariates.

3. Results

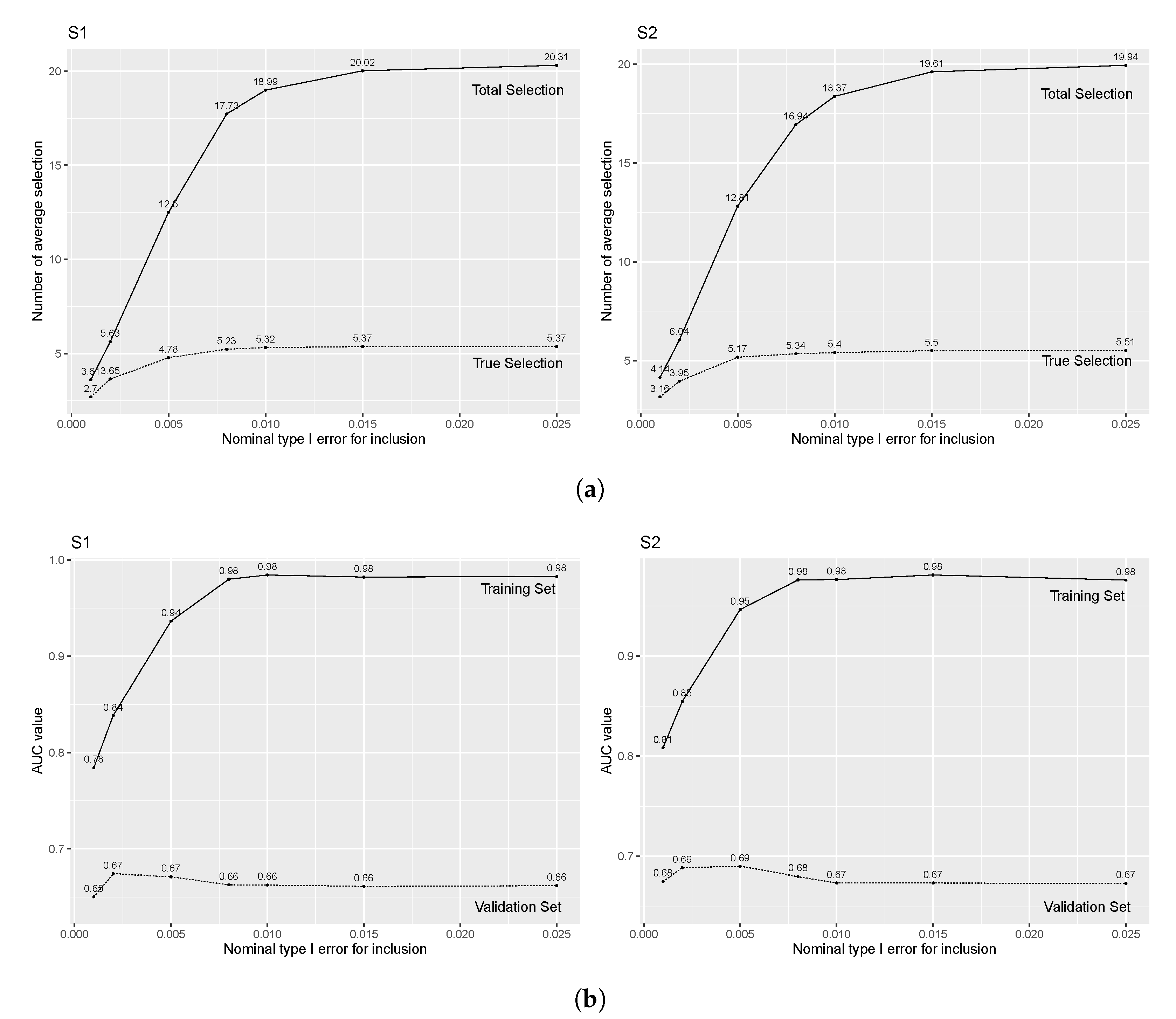
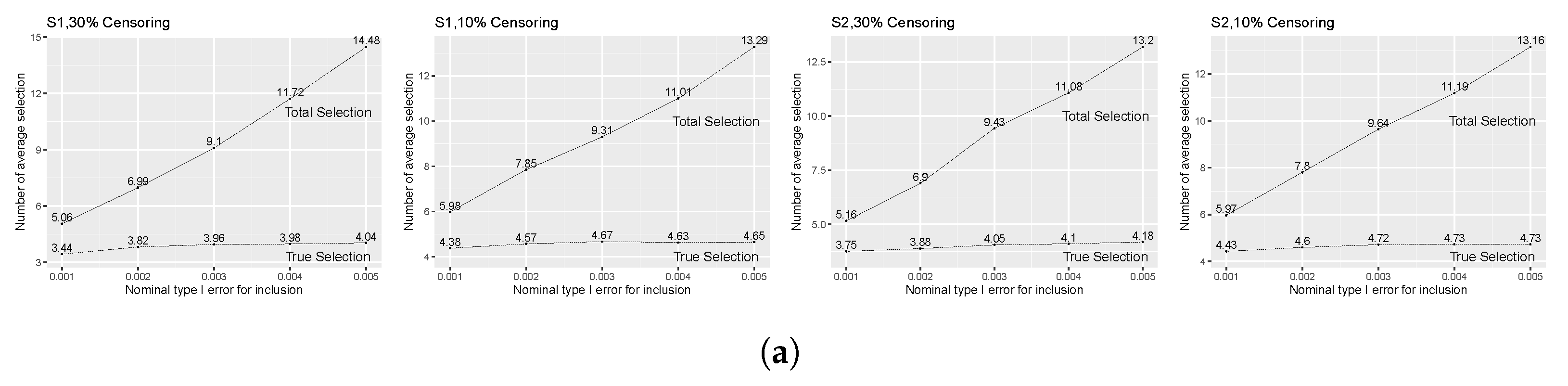
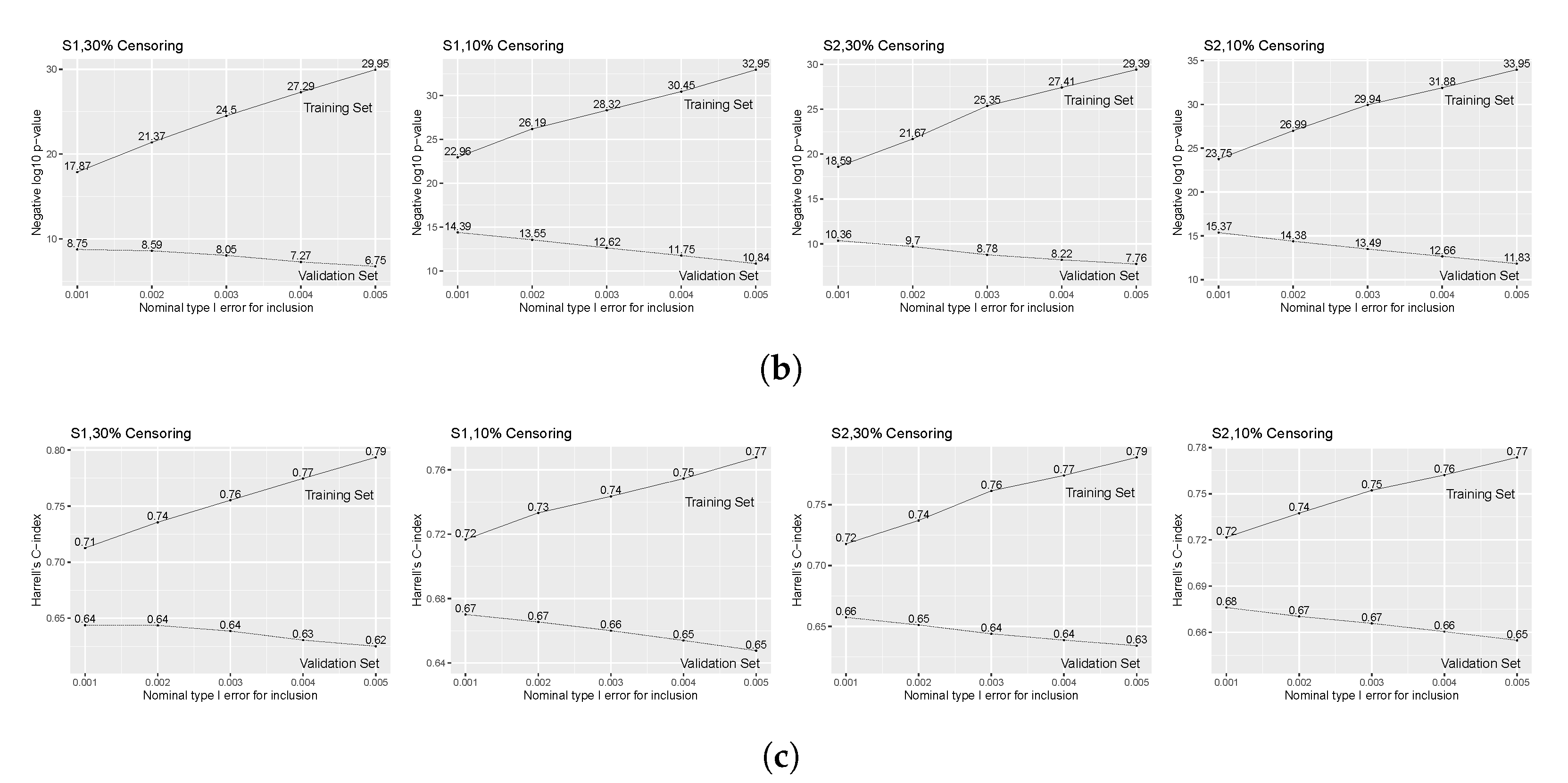
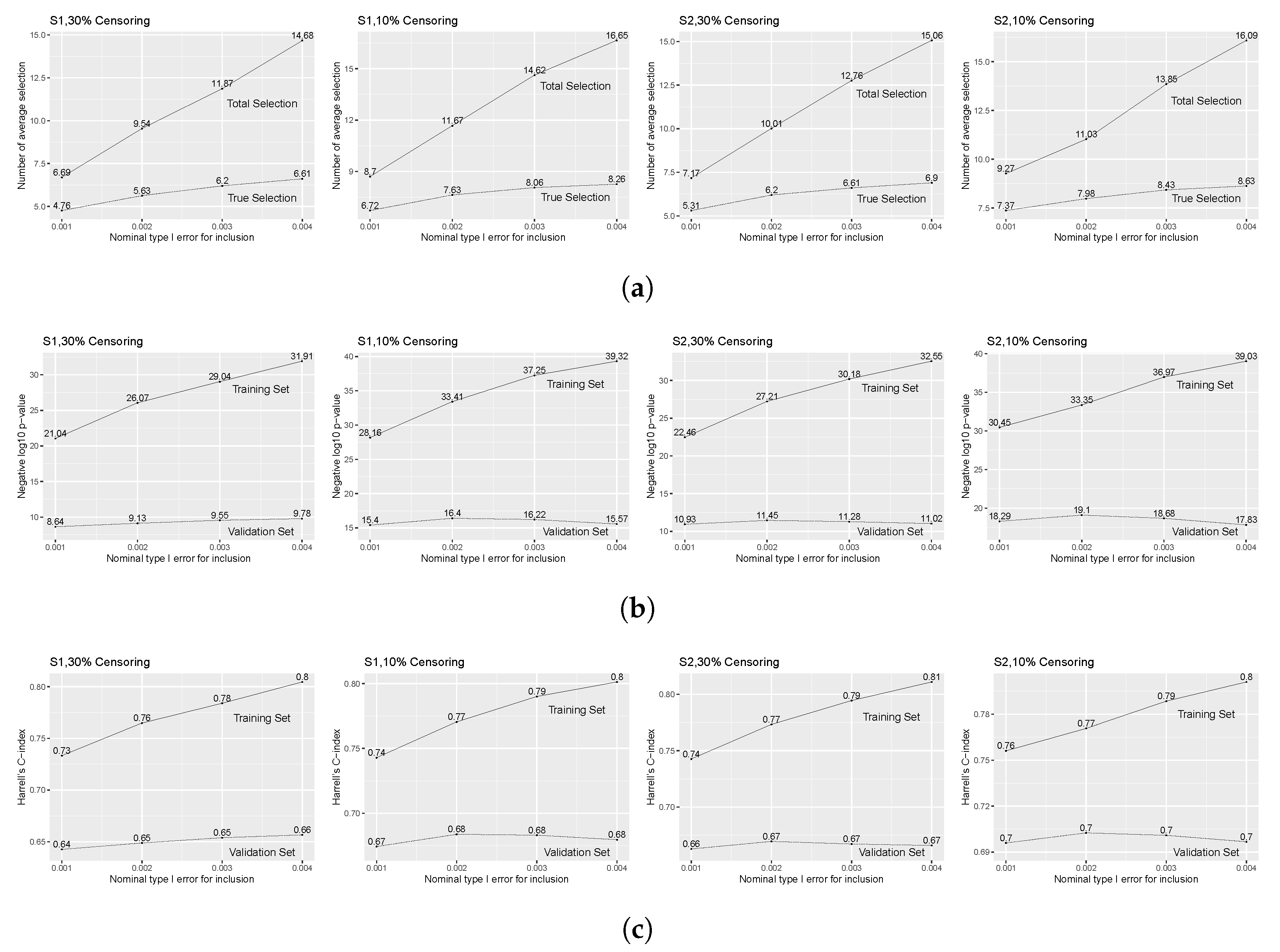
3.1. Impact of Over-Selection

First, we investigate the impact of over-selection on prediction accuracy. Since LASSO and EN do not control the number of selections, we use the standard logistic and Cox regression methods equipped with SVS, called L-SVS and C-SVS, respectively, which can control the number of selections by choosing different alpha levels for insertion and deletion.

We generate $n=400$ samples of $m=1000$ candidate predictors from a multivariate Gaussian distribution with means 0 and variances 1, consisting of 10 independent blocks with a block size of 100. Each block has a compound symmetry correlation structure with a common correlation coefficient $\rho =0.1$. We assume that $m_1=5$ or 10 true predictors of the $m=1000$ candidate predictors are associated with the outcome.

First, we consider a binary outcome case. For subject $i(=1,\dots ,n)$ with true predictors ${\tilde{z}}_i={(z_{\tilde{1}i},\dots ,z_{{\tilde{m}}_{1}i})}^T$, the binary outcome $y_i$ is generated from a Bernoulli distribution with the logistic regression model

$$p_i=P(y_i=1)=\frac{exp({\beta }_0+{\beta }^T{\tilde{z}}_i)}{1+exp({\beta }_0+{\beta }^T{\tilde{z}}_i)},$$

where $\beta ={({\beta }_{\tilde{1}},\dots ,{\beta }_{{\tilde{m}}_1})}^T$ is a vector of regression coefficients corresponding to the true predictors ${\tilde{z}}_i$. We consider two scenarios for choosing true predictors: the first (S1) is to choose all $m_1$ predictors in the first block and the second (S2) is to choose one predictor from each of the $m_1$ different blocks. The true regression coefficients are set at ${\beta }_{\tilde{l}}={(-1)}^{l+1}\ast 0.7, l=0,1,\dots ,m_1$. We use 50–50 hold out, i.e., $n_1=200$ samples for training and the remaining $n_2=200$ samples for validation.

We apply L-SVS to each training set to fit a prediction model and count the total selection and the true selection included in the fitted model. Let Z denote the vector of predictors selected for the fitted model and $\widehat{\beta }$ the vector of corresponding regression estimates. We estimate the AUC of the ROC curve using the fitted risk score $r_i={\widehat{\beta }}^T{Z}_i$ and binary outcome $y_i$ using the training set and the validation set. We repeat this simulation $N=100$ times and calculate mean total selection and true selection for the training sets and the mean AUC for the training and validation sets. Note that the AUC for a training set measures how well the estimated prediction model fits the training data. Due to the over-fitting, the estimated model tends to fit the training set better by including more predictors in the model, so that the AUC from a training set does not measure the real prediction accuracy of a fitted model [22]. Instead, the true prediction accuracy of a fitted model will be measured by the AUC from an independent validation set. We use SVS with various ${\alpha }_1$ levels for inclusion by keeping the ${\alpha }_2$ value for deletion twice the size of ${\alpha }_1$, i.e., ${\alpha }_2=2{\alpha }_1$.

For $m_1=5$, Figure 1a presents mean true selection (dotted line) and total selection (solid line) from the training sets, and Figure 1b presents mean AUC for the validation sets (dotted line) and training sets (solid line). We find that mean total and true selections quickly increases by increasing ${\alpha }_1$ level up to 0.01, but becomes stable after that. Even though we increase ${\alpha }_1$ over the 0.01 level, L-SVS will not select much more predictors. On the other hand, from Figure 1b, the prediction models fit the training sets better (i.e., mean AUC increases) by increasing ${\alpha }_1$ level, and the models select more predictors. However, the prediction accuracy (AUC for validation sets) decreases for ${\alpha }_1>0.002$, probably because of the large number of falsely selected predictors. We observe similar results under (S1) and (S2) settings.

When $m_1=10$, we observe similar results from Figure 2. The only difference is that, with a larger number of true predictors, the proportion of false selections is smaller (Figure 2a) than when $m_1=5$ (Figure 1a), so that the prediction accuracy decreases rather slowly than when $m_1=5$ after around ${\alpha }_1=0.005$ (Figure 2b).

For simulations on survival outcomes, we generate covariate vectors as in the binary outcome case. For subject $i(=1,\dots ,n)$ with true predictors $z_i={(z_{\tilde{1}i},\dots ,z_{{\tilde{m}}_{1}i})}^T$, the hazard rate of the survival time is given as

$$h_i\left(t\right)=h_0{e}^{{\beta }^T{z}_i}$$

where $\beta ={({\beta }_{\tilde{1}},\dots ,{\beta }_{{\tilde{m}}_1})}^T$ is a vector of the regression coefficients for the true predictors $z_i$.

We set ${\beta }_{\tilde{l}}={(-1)}^{l+1}\ast 0.4, l=1,2,\dots ,m_1$ and $h_0=0.1$ under both (S1) and (S2). We assume $m_1=5$ or 10 true predictors. Censoring times are generated from a uniform distribution, $U(0,a)$ for 30% of censoring for a selected accrual period a. With the accrual period a fixed, we also generate 10% of censoring from $U(a,a+b)$ by a selected additional follow-up period b. We apply C-SVS to each training set. Let Z denote the vector of predictors selected by C-SVS and $\widehat{\beta }$ the vector of their regression estimates. We count the total selections and true selections for the fitted prediction model. We fit a univariate Cox regression of the survival outcome $(y_i,{\delta }_i)$ on a covariate $r_i={\widehat{\beta }}^T{Z}_i$ using each of the training and validation sets and calculate the p-value. We also estimate the association between the risk score $r_i$ and the outcome $(y_i,{\delta }_i)$ by Harrell’s C-index using each of the training and validation sets. Note that large −${\log }_{10}$ p-value and C-index from the training set mean that the prediction model fits the training set well, while those from a validation set mean that the fitted prediction model has a high accuracy. From $N=100$ simulation replications, we calculate the mean total and true selections from the training sets and the mean −${\log }_{10}$ p-value and C-index from training and validation sets. C-SVS is performed using various ${\alpha }_1$ values with ${\alpha }_2=2{\alpha }_1$.

Figure 3 reports the simulation results for $m_1=5$ for a range of ${\alpha }_1$ values. From Figure 3a, we find that the true selection is slightly higher, with 10% censoring for both (S1) and (S2) models. For both (S1) and (S2) and both 30% and 10% censoring, mean total and true selections increase in ${\alpha }_1$, so that −${\log }_{10}$ p-value and C-index increase for the training sets, as demonstrated by the solid lines in Figure 3b,c. By increasing ${\alpha }_1$, however, the number of false selections also increases, so that −${\log }_{10}$ p-value and C-index decrease for the validation sets, as demonstrated by the dotted lines in Figure 3b,c. That is, over-selection lowers the accuracy of fitted prediction models.

Figure 4 reports the simulation results for $m_1=10$. The mean total and true selections (Figure 4a), and −${\log }_{10}$ p-value and C-index for training sets (the solid lines of Figure 4b,c) increase in ${\alpha }_1$ as in the case of $m_1=5$. With a larger number of true predictors, however, due to the increase in the proportion of false selections, the prediction accuracy, that is measured by −${\log }_{10}$ p-value and C-index in the validation sets (the dotted lines of Figure 4b,c), decreases after a brief increase up to ${\alpha }_1=0.002$, except for model (S1) with 10% of censoring.

3.2. Comparison of Prediction Methods

Using the simulation data sets for Figure 1 and Figure 2, we compare the performance of LASSO, EN, and L-SVS with $({\alpha }_1,{\alpha }_2)=(0.002,0.004)$. By applying each of these prediction methods to each training set, we estimate the same performance measures of Figure 1 and Figure 2. The simulation results are summarized in

Table 1. Binary outcome: Simulation results (mean total selections and true selections from training sets, and mean AUC from training and validation sets) of the three prediction methods with $m_1(=5 \mathrm{or} 10)$ true covariates and with S1 and S2 models. L-SVS (logistic regression with stepwise variable selection) uses $({\alpha }_1,{\alpha }_2)=(0.002,0.004)$.

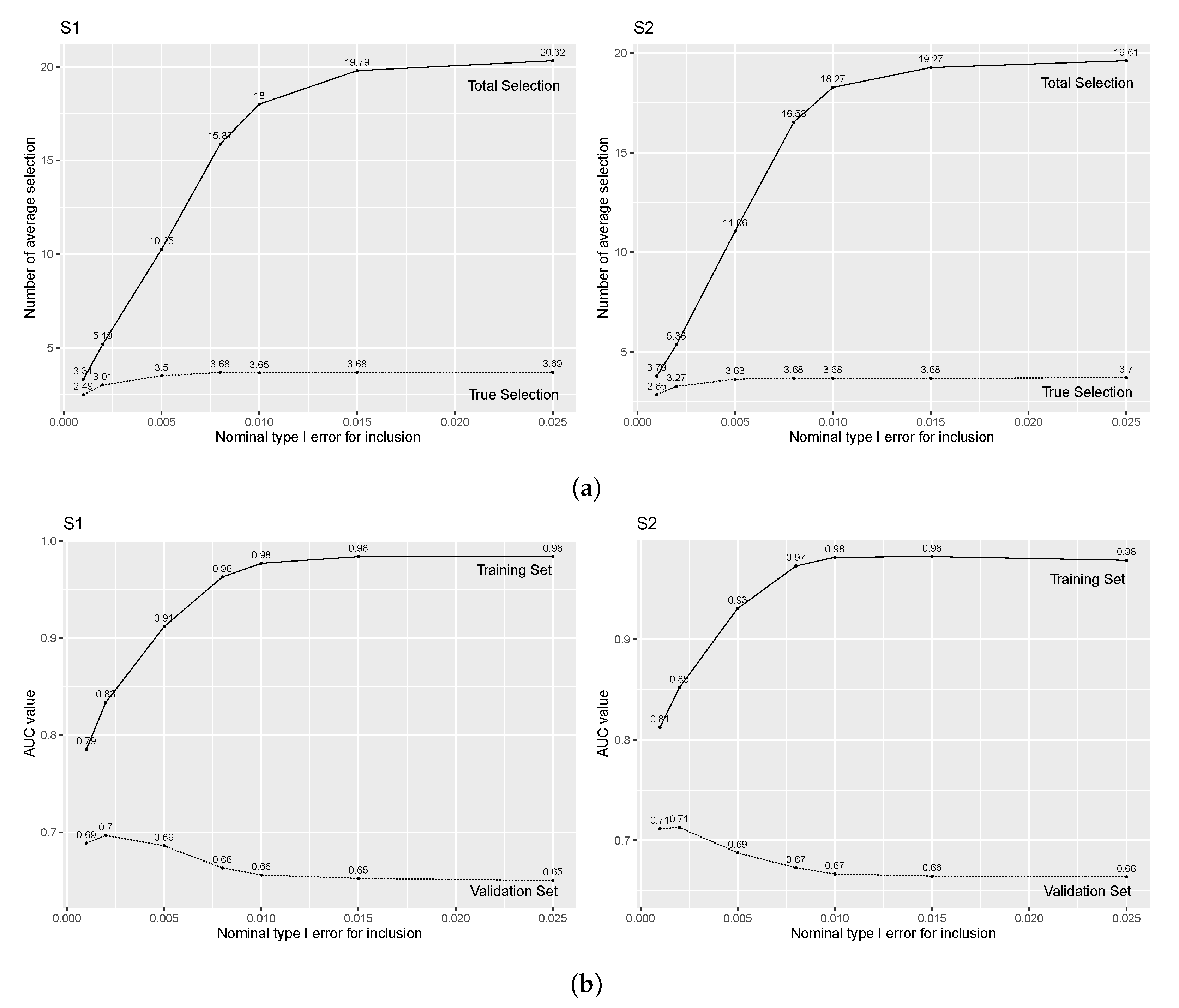
	(S1)			(S2)
	LASSO	EN	L-SVS	LASSO	EN	L-SVS
	(i) $m_1=5$
Total Selections	31.15	74.59	5.32	28.59	56.61	5.32
True Selections	4.03	4.49	3.25	4.28	4.60	3.25
AUC-Training	0.92	0.95	0.84	0.92	0.95	0.85
AUC-Validation	0.70	0.69	0.71	0.72	0.71	0.71
	(ii) $m_1=10$
Total Selections	34.64	101.47	5.63	44.56	84.76	6.88
True Selections	6.73	7.92	3.60	7.76	8.19	4.31
AUC-Training	0.92	0.96	0.83	0.96	0.97	0.87
AUC-Validation	0.69	0.68	0.67	0.73	0.72	0.70

. Since the $L_1$-norm penalty is stricter than the $L_2$-norm penalty, LASSO has smaller true selections than EN, which employs a combination of $L_1$- and $L_2$-norm penalties. Note that LASSO and EN select a large number of predictors, while L-SVS selects only slightly over 5 predictors in total. By selecting a large number of predictors, the two ML methods have a slightly larger true selection and slightly better fitting (i.e., a larger AUC) than L-SVS for the training sets. For validation sets, however, AUCs of the ML methods are no larger than that of L-SVS. We have this kind of results because the large false selections of the ML methods act like error terms and lower the prediction accuracy. L-SVS has better (or comparable under S2) prediction accuracy, even with a slightly smaller number of true selections (and much smaller total selections under S2) than LASSO and EN. Overall, we have similar simulation results between (S1) and (S2). In conclusion, we find that good fitting (large AUC of training sets) is not necessarily translated into high prediction accuracy (large AUC of validation sets) because of the increased false selections. With a larger number of true predictors ($m_1=10$), the mean true selection increases, but the mean false selection increases as well, so that the prediction accuracy is about the same as that for $m_1=5$.

Using the simulation data for Figure 3 and Figure 4, we compare the performance of LASSO, EN, and C-SVS with $({\alpha }_1,{\alpha }_2)=(0.001,0.002)$ for survival outcomes.

Table 2. Survival outcome: Simulation results (mean total selections and true selections from training sets, and mean −${\log }_{10}$p-value and C-index from both training and validation sets) of the three prediction methods with $m_1=5$ or 10 true covariates with (S1) and (S2) models. C-SVS (Cox regression with stepwise variable selection) uses $({\alpha }_1,{\alpha }_2)=(0.001,0.002)$.

	(S1)			(S2)
	LASSO	EN	C-SVS	LASSO	EN	C-SVS
	(i) $m_1=5$ & 30% Censoring
Total Selections	16.51	24.30	4.80	19.28	25.89	5.37
True Selections	4.11	4.46	3.53	4.45	4.53	3.78
−${\log }_{10}$ p-value (training)	22.79	26.25	17.32	25.76	28.24	19.68
−${\log }_{10}$ p-value (validation)	9.06	8.76	9.79	10.45	10.20	10.41
C-index (training)	0.74	0.76	0.71	0.76	0.77	0.73
C-index (validation)	0.64	0.64	0.65	0.66	0.66	0.66
	(ii) $m_1=5$ & 10% Censoring
Total Selections	20.16	23.89	5.74	20.96	25.00	5.86
True Selections	4.61	4.82	4.44	4.78	4.82	4.43
−${\log }_{10}$ p-value (training)	27.60	29.72	22.51	29.73	31.61	23.83
−${\log }_{10}$ p-value (validation)	12.89	12.88	14.95	14.66	14.39	15.69
C-index (training)	0.74	0.75	0.71	0.75	0.76	0.72
C-index (validation)	0.66	0.66	0.67	0.67	0.67	0.68
	(iii) $m_1=10$ & 30% Censoring
Total Selections	26.68	36.83	6.57	30.35	37.73	7.85
True Selections	7.52	8.26	4.89	8.44	8.61	5.69
−${\log }_{10}$ p-value (training)	30.12	34.26	20.61	34.18	36.50	24.90
−${\log }_{10}$ p-value (validation)	9.89	9.87	9.07	13.07	12.87	11.48
C-index (training)	0.78	0.81	0.73	0.81	0.82	0.76
C-index (validation)	0.66	0.66	0.64	0.69	0.69	0.67
	(iv) $m_1=10$ & 10% Censoring
Total Selections	29.46	36.69	8.52	32.47	37.53	9.65
True Selections	8.56	8.85	6.69	9.10	9.32	7.71
−${\log }_{10}$ p-value (training)	36.21	38.68	27.61	39.76	41.38	32.14
−${\log }_{10}$ p-value (validation)	14.77	14.44	15.62	18.44	18.26	19.54
C-index (training)	0.78	0.79	0.74	0.80	0.80	0.76
C-index (validation)	0.67	0.67	0.68	0.70	0.70	0.70

reports the simulation results. As in the binary outcome case, the two ML methods have much larger mean total selection and slightly larger true selection compared to C-SVS. With a lower censoring (10%), each method has larger mean total and true selections, better model fitting (in terms of −${\log }_{10}$ p-value and C-index for training sets), and higher prediction accuracy (in terms of −${\log }_{10}$ p-value and C-index for validation sets). Between models (S1) and (S2), with 30% of censoring, the prediction methods tend to have slightly larger mean total and true selections, and larger negative log10 (p-value) and C-index for both training and validation sets for model (S2). However, with 10% of censoring, these measures are similar between (S1) and (S2). The mean total and true selections are larger with $m_1=10$ than with $m_1=5$. Between the two ML methods, LASSO has slightly higher prediction accuracy (in terms of −${\log }_{10}$ p-value and C-index for validation sets) than EN overall, probably due to the higher over-selection of EN. In spite of the slightly lower true selection, C-SVS has higher prediction accuracy than the two ML methods with 10% of censoring or with $m_1=5$, (S2), and 30% of censoring. Under the other simulation settings, the three prediction methods have similar prediction accuracy.

3.3. Real-Data Analysis

Farrow et al. [19] used the Nanostring nCounter PanCancer Immune Profiling Panel to quantify the expression level of 730 immune-related genes in sentinel lymph node (SLN) specimens from $n=60$ patients (31 positive, 29 negative) from a retrospective melanoma cohort. Since a significant proportion of patients experience recurrence of melanoma after surgery, early detection of poor prognosis and adjuvant therapy may eliminate residual disease and improve the patients’ prognosis. We want to predict SLN positivity and recurrence-free survival (RFS) using the microarray data and baseline characteristics such as gender, age at surgery, and use of additional treatment (add_trt).

For the binary outcome of SLN positivity, we randomly partition the 60 patients into a training set and a validation set so that the two sets have a similar number of SLN positive and negative cases. We apply LASSO, EN, and L-SVS with $({\alpha }_1,{\alpha }_2)=(0.05,0.1)$ to the training set. Figure 5 reports the ROC curves for the training set and validation set. Due to over-fitting, all three methods have large AUCs for the training set. For the validation set, however, EN has a smaller AUC than the other methods, while L-SVS has the largest AUC.

Table 3. Analysis results of Farrow et al. data on SLN positivity.

Method	# Selected Features	AUC
		Training	Validation	Selected Features
LASSO	13	1.0000	0.6619	add_trt, GE_CCL1, GE_CLEC6A,
				GE_HLA_DQA1, GE_IL1RL1, GE_IL25,
				GE_MAGEA12, GE_MASP1, GE_MASP2,
				GE_PRAME, GE_S100B, GE_SAA1,
				GE_USP9Y
Elastic Net	13	1.0000	0.6381	add_trt, GE_CCL1, GE_CLEC6A,
				GE_HLA_DQA1, GE_IL1RL1, GE_IL1RL2,
				GE_IL25, GE_MASP1, GE_MASP2,
				GE_PRAME, GE_S100B, GE_SAA1,
				GE_USP9Y
L-SVS	4	0.9833	0.6905	add_trt, GE_IL1RL1, GE_IL17F, GE_IL1RL2

presents more analysis results. While L-SVS selects only four covariates (two of which are also selected by LASSO and three of which are also selected by EN) as significant predictors, it has the highest prediction accuracy (AUC-validation) among the three prediction methods. LASSO and EN select the same number of predictors, but slightly different sets. The data analysis is conducted under the system x86_64-w64-mingw32/x64 (64-bit) using open-source R software version 4.2.2, and the computing time of the LASSO, EN, and stepwise methods are 0.47 s, 3.74 s, and 9.44 s, respectively. It is expected that L-SVS takes the most time since it performs hypothesis testing during each round of variable selection.

For the time-to-event endpoint of RFS, we randomly partition the 60 patients into a training set and a validation set so that the two sets have a similar number of events and censored cases. We apply EN, LASSO, and C-SVS with $({\alpha }_1,{\alpha }_2)=(0.025,0.05)$ to the training set. The analysis results are reported in

Table 4. Analysis results of Farrow et al. data on recurrence-free survival.

Method	# Selected Features	−${\log }_{10}$ p-Value		C-Index
		Training	Validation	Training	Validation
LASSO	5	3.7153	1.3623	0.8848	0.6959
Elastic Net	11	3.8872	1.1965	0.9058	0.6701
C-SVS	4	3.1182	1.4518	0.9634	0.6907
	Selected Features
LASSO	add_trt, GE_CCL3, GE_CCL4, GE_IL17A, GE_NEFL
Elastic Net	add_trt, GE_CCL3, GE_CCL4, GE_CRP, GE_CXCL1,
	GE_CXCR4, GE_HLA_DRB4, GE_IL17A, GE_IL8,
	GE_MAGEA12, GE_NEFL
C-SVS	add_trt, GE_NEFL, GE_IFNL1, GE_MAGEC1

. As in the analysis of SLN positivity, C-SVS selects the smallest number of predictors, but it has the highest prediction accuracy in terms of −${\log }_{10}$ p-value for the validation set among the three methods and higher prediction accuracy than EN in terms of C-index for the validation set. The prediction models by both L-SVS and C-SVS select add_trt and three genes.

In order to see if each prediction method really selects significant features, we fit a multivariate Cox regression model of RFS on the selected features using the training set of Farrow et al. data [19] and summarize the result in

Table 5. Multivariate Cox regression on recurrence-free survival using the training set of Farrow et al. data.

LASSO			Elastic Net			C-SVS
Feature	Coef.	p-Value	Feature	Coef.	p-Value	Feature	Coef.	p-Value
add_trt	4.558	0.004	add_trt	3.021	0.251	add_trt	5.352	0.001
GE_CCL3	3.634	0.153	GE_CCL3	0.094	0.908	GE_NEFL	$-0.119$	0.006
GE_CCL4	1.163	0.563	GE_CCL4	6.818	0.693	GE_IFNL1	0.146	0.003
GE_IL17A	6.268	0.073	GE_CRP	$-9.743$	0.191	GE_MAGEC1	$-0.125$	0.011
GE_NEFL	$-4.561$	0.023	GE_CXCL1	7.499	0.164
			GE_CXCR4	$-9.089$	0.548
			GE_HLA_DRB4	$-1.803$	0.412
			GE_IL17A	5.879	0.202
			GE_IL8	$-1.004$	0.802
			GE_MAGEA12	$-1.258$	0.846
			GE_NEFL	$-1.059$	0.736

. Note that add_trt and GE_NEFL are selected by all three methods, but their significance diminishes for EN, probably because their effects are diluted by many of the less significant features selected together. While LASSO and EN select many insignificant features, C-SVS selects a set of significant features only by using stepwise variable selection procedure.

4. Discussion

LASSO and EN have been widely used to develop prediction models using high-dimensional data. Recent recognition of ML methods prompts collective investment and applications, which not only stimulate the development of clinical medicine but also induce potential overuse risk. Systematic reviews have been conducted to show that LASSO and EN tend to over-select predictors for fitted prediction models. This leads to some additional costs, as discussed in Section 1, and unfavorable prediction accuracy. As an alternative approach, we have investigated standard regression methods combined with SVS (R-SVS) compared with LASSO and EN. Through simulations and real-data analysis, we found that the ML methods do over-select predictors, over-fit training sets, and, consequently, lose prediction accuracy. In contrast, R-SVS selects much smaller number of predictors and fitted prediction models have comparable or better accuracy than LASSO and EN.

Multiple variants of LASSO have been proposed to deal with over-selection issue [6,23,24,25,26], but we have considered the original LASSO in this paper. It is one of the future research topics to compare the performance of these methods. One of the major findings of this paper is that R-SVS produces very efficient prediction models with easy and fast computing, but without these advanced and complicated modifications.

SAS provides variable selection procedures for regression methods based on information (such as AIC and BIC) or R-square only, so that, like LASSO and EN, they can not control the selection of predictors. So, we developed R programs for R-SVS based on the significance level of regression estimates. Even though standard regression methods are not appropriate for high-dimensional data, those combined with SVS work perfectly as the number of true predictors is much smaller than the sample size. Note that the backward deletion method is not appropriate for high-dimensional data because it starts to fit the full model with all candidate predictors. Since regression methods are well developed for any type of outcomes, R-SVS can be used for any type of regression methods. Furthermore, R-SVS is a standard statistical method, so that statisticians without deep knowledge in bioinformatics can use it for prediction model fitting with high-dimensional data. Our R codes for L-SVS and C-SVS are available upon request.

Some may believe that R-SVS methods require much heavier computing than LASSO and EN. Logistic regression or Cox regression with SVS spend most of their running time performing hypothesis testing and the p-values of covariates for inclusion or deletion. The computation of LASSO and EN is slightly faster because they only estimate the regression coefficients without statistical testing. We find that R-SVS has much lower feature selections than LASSO and EN, but its prediction accuracy is as high as or even higher than the latter.

5. Conclusions

Through simulation studies, we have observed that LASSO and EN select a large number of features with a high false selections. Furthermore, through real-data analysis, these popular ML methods select many insignificant features. As a result, their prediction accuracy can be compromised. In contrast, R-SVS selects much fewer features with high true selection rate, and its prediction accuracy is as high as or even higher than the ML methods. R-SVS selects features based on their significance level, so that all of the selected features are statistically significant. R-SVS requires a longer computing time than the ML methods since it estimates regression coefficients and conducts statistical tests, while the ML methods only estimate regression coefficients. However, the difference in computing time will be negligible for real-data analysis. In all, the stepwise regression method, a standard statistical method, can be a viable alternative to the ML methods for prediction model building with high-dimensional data.