Dynamics and Solutions of Higher-Order Difference Equations

Abstract

The invariance method, known as Lie analysis, consists of finding a group of transformations that leave a difference equation invariant. This powerful tool permits one to lower the order, linearize and more importantly, obtain analytical solutions of difference and differential equations. In this study, we obtain the solutions and periodic solutions for some family of difference equations. We achieve this by performing an invariance analysis of this family. Eventually, symmetries are derived and used to construct canonical coordinates required for the derivation of the solutions. Moreover, periodic aspects of these solutions and the stability character of the equilibrium points are investigated.

1. Introduction

In certain cases, difference equations are used to model the evolution of natural phenomena occurring over time. The analysis of difference equations has attracted the attention of many researchers and interesting results have been obtained. The type of difference equations where initial conditions and parameters appearing in the equations are fuzzy numbers, known as fuzzy difference equations, have also been studied and progress has been made [1,2]. In numerous articles that dealt with solutions of difference equations, we noticed the use of proof by induction to show that the presented formulas for the solutions are valid. To the best of our knowledge, the use of Lie analysis to obtain analytic solutions to difference equations is to some extent new. This method, originally applied to differential equations, has recently been applied to difference equations. It traces back to the twentieth century when Maeda [3] proved that, as long as a difference equation admits symmetries, its order can be reduced. Recently, it has been shown, for differential equations, that when symmetries and conservation laws are associated, one may proceed to double reduction [4]. It is now known that this approach works for difference equations [5]. With regard to differential equations, computer packages that generate Lie symmetries have been developed. Regrettably, this is not the case for difference equations. Symmetries of difference equations are mostly computed by hand and frequently involve cumbersome computations.

In this study, unlike in many articles where the change of variables is made by guess work, we employ symmetries to reduce the order of the difference equation

$$\begin{array}{c}\hfill x_{n+6k}=\frac{x_n{x}_{n+k}{x}_{n+2k}}{x_{n+4k}{x}_{n+5k}(A_n+B_n{x}_n{x}_{n+k}{x}_{n+2k}{x}_{n+3k})},\end{array}$$

(1)

via canonical coordinates. We clearly state the link between the symmetries (characteristics) and the new variable (invariant). Note that in (1), $A_n$ and $B_n$ are real sequences and $x_i$, $i=0,1,\cdots ,6k-1$ are the initial conditions. As a matter of choice, some authors prefer the equivalent form

$$\begin{array}{c}\hfill x_n=\frac{x_{n-6k}{x}_{n-5k}{x}_{n-4k}}{x_{n-2k}{x}_{n-k}(a_n+b_n{x}_{n-6k}{x}_{n-5k}{x}_{n-4k}{x}_{n-3k})}\end{array}$$

(2)

of (1). Studies of special cases of (2) can be found in the literature [6] where the authors consider the equation

$$\begin{array}{c}\hfill x_n=\frac{x_{n-6}{x}_{n-5}{x}_{n-4}}{x_{n-2}{x}_{n-1}(a+b{x}_{n-6}{x}_{n-5}{x}_{n-4}{x}_{n-3})}\end{array}$$

(3)

and presented the formula for solutions as well as their asymptotic behavior. For similar studies on difference equations of this form, the reader can refer to [5,6,7,8,9,10,11,12].

The paper is organized as follows. In Section 2, we provide some basic theory needed for finding symmetries of difference equations and the reduction of order. We also discuss some well-known theory on the stability of equilibrium points. In Section 3, we obtain symmetries and solutions of (1). A more detailed study is conducted for some special cases. Section 4 is mainly dedicated to the stability of the equilibrium points and the periodicity aspects of the solutions of (1). Finally, in Section 5, we show that some existing results in the literature are special cases of our findings.

2. Preliminaries

The algorithm for finding symmetries of difference equations is explained at large in [13]. Consider an equation involving some continuous variables $\mathbf{x}=(x_1,\cdots ,x_q)$ and a local diffeomorphism (point transformation): $\mathcal{T}:\mathbf{x}\to \overline{\mathbf{x}}\left(\mathbf{x}\right)$.

Definition 1.

A parameterized set of transformations

$${\mathcal{T}}_{\epsilon }\left(\mathit{x}\right)\equiv \widehat{\mathit{x}}(\mathit{x};\epsilon )$$

(4)

is a one-parameter local Lie group of transformations if the following conditions are satisfied:

1.

${\mathcal{T}}_0$ is the identity map, so that $\widehat{\mathit{x}}=\mathit{x}$ when $\epsilon =0$.

2.

${\mathcal{T}}_{\gamma }{\mathcal{T}}_{\epsilon }={\mathcal{T}}_{\gamma +\epsilon }$ for every $\gamma ,\epsilon$ sufficiently close to 0.

3.

Every ${\widehat{x}}_{\alpha }$ can be represented as a Taylor series in ε, that is,

$${\widehat{x}}_{\alpha }(\mathit{x};\epsilon )=x_{\alpha }+\epsilon {\eta }_{\alpha }\left(\mathit{x}\right)+O\left({\epsilon }^2\right),\alpha =0,1,\cdots ,q.$$

Definition 2.

The infinitesimal generator of the one-parameter Lie group of point transformations (4) is the operator

$$\begin{array}{c}\hfill X=X\left(\mathit{x}\right)=\eta \left(\mathit{x}\right)·\mathrm{\Delta }=\sum _{\alpha =1}^q{\eta }_{\alpha }\left(\mathit{x}\right)\frac{\partial }{\partial x_{\alpha }},\end{array}$$

(5)

and Δ is the gradient operator.

Theorem 1

([13]). $F\left(x\right)$ is invariant under the group of transformations (4) if and only if $XF\left(x\right)=0$.

Suppose a difference equation has the form

$$\begin{array}{c}\hfill x_{n+6k}=\mathcal{A}(n,x_n,x_{n+k},x_{n+2k},x_{n+3k},x_{n+4k},x_{n+5k}),\end{array}$$

(6)

where $\mathcal{A}$ is a known function that satisfies $\partial \mathcal{A}/\partial x_n\ne 0$. As said before, we explore a one-parameter Lie group of point transformations

$$\begin{array}{c}\hfill {\widehat{x}}_n=x_n+\epsilon \eta (n,x_n)\end{array}$$

(7)

where $\epsilon$ represents the group parameter. The function $\eta =\eta (n,x_n)$ is referred to as the characteristic of the Lie group. The infinitesimal generator takes the form

$$\begin{array}{cc}\hfill \mathcal{X}=& \eta (n,x_n)\frac{\partial }{\partial x_n}.\hfill \end{array}$$

(8)

Although the transformation depends on n and $x_n$ only, one needs to investigate how the symmetries affect the other variables appearing in the right hand side of (6), hence the introduction of the prolonged infinitesimal generator X of $\mathcal{X}$:

$$\begin{array}{cc}\hfill X=& \eta (n,x_n)\frac{\partial }{\partial x_n}+\eta (n+k,x_{n+k})\frac{\partial }{\partial x_{n+k}}+\eta (n+2k,x_{n+2k})\frac{\partial }{\partial x_{n+2k}}+\eta (n+3k,x_{n+3k})\frac{\partial }{\partial x_{n+3k}}\hfill \\ & +\eta (n+4k,x_{n+4k})\frac{\partial }{\partial x_{n+4k}}+\eta (n+5k,x_{n+5k})\frac{\partial }{\partial x_{n+5k}}\hfill \end{array}$$

admitted by the group of transformations (7). Accordingly, the infinitesimal condition for invariance is given by $\eta (n+6k,x_{n+6})-X\left(\mathcal{A}\right)=0$, that is,

$$\begin{array}{cc}\hfill & \eta (n+6k,x_{n+6})-\frac{\partial \mathcal{A}}{\partial x_{n+5k}}\eta (n+5k,x_{n+5k})-\frac{\partial \mathcal{A}}{\partial x_{n+4k}}\eta (n+4k,x_{n+4k})-\frac{\partial \mathcal{A}}{\partial x_{n+3k}}\eta (n+3k,x_{n+3k})\hfill \\ & -\frac{\partial \mathcal{A}}{\partial x_{n+2k}}\eta (n+2k,x_{n+2k})-\frac{\partial \mathcal{A}}{\partial x_{n+k}}\eta (n+k,x_{n+k})-\frac{\partial \mathcal{A}}{\partial x_n}\eta (n,x_n)=0\hfill \end{array}$$

(9)

on condition that (6) is satisfied. The functional Equation (9) can be solved for Q after a set of lengthy computations.

The analysis of stability of the equilibrium points will be carried out using the following definitions and theorems. They can be found in [14].

Definition 3.

The equilibrium point $\overline{x}$ of (6) is stable (locally) if for all $ϵ>0,\exists \delta >0$ such that ${\displaystyle \sum _{i=0}^{6k-1}}|x_i-\overline{x}|<\delta \Rightarrow |x_n-\overline{x}|<ϵ$ for all solution ${\left\{x_n\right\}}_{n=0}^{\infty }$ of (6).

Definition 4.

The equilibrium point $\overline{x}$ of (6) is a global attractor if $x_n\to \overline{x}$, as $n\to \infty$, for any solution ${\left\{x_n\right\}}_{n=0}^{\infty }$ of (6).

Definition 5.

The equilibrium point $\overline{x}$ of (6) is globally asymptotically stable if $\overline{x}$ is locally stable and is a global attractor of (6).

We introduce the characteristic equation of (6) of the fixed point $\overline{x}$:

$$\begin{array}{c}\hfill {\lambda }^{6k}-p_{5k}{\lambda }^{5k}-p_{4k}{\lambda }^{4k}-p_{3k}{\lambda }^{3k}-p_{2k}{\lambda }^{2k}-p_k{\lambda }^k-p_0=0\end{array}$$

(10)

where $p_i=\frac{\partial \mathcal{A}}{\partial x_{n+i}}(\overline{x},\cdots ,\overline{x}),i=0,k,2k,3k,4k,5k.$

Theorem 2

([14]). Suppose $\mathcal{A}$ is a smooth function defined on some neighborhood of $\overline{x}$. Then,

(i)

If all the roots, ${\lambda }_i$, of (10) are such that $|{\lambda }_i|<1$, then $\overline{x}$ is locally asymptotically stable.

(ii)

If at least one root of (10) has absolute value greater than one, then $\overline{x}$ is unstable.

Definition 6.

The equilibrium point $\overline{x}$ of (6) is called non-hyperbolic if there exists a root of (10) with absolute value equal to one.

Theorem 3

([14]). Assume $p_0,p_k,p_{2k},p_{4k}$ and $p_{5k}$ are real numbers such that

$$|p_0|+|p_k|+|p_{2k}|+|p_{3k}|+|p_{4k}|+|p_{5k}|<1.$$

Then, the roots of (10) lie inside the open unit disk $\left|\lambda \right|<1$.

3. Symmetries and Solutions

To find symmetries for (1), we apply the condition (9) to (1) as follows:

$$\begin{array}{cc}\hfill & \eta (n+6k,\mathcal{A})+\frac{x_n{x}_{n+k}{x}_{n+2k}{x}_{n+4k}\eta \left(n+5k,x_{n+5k}\right)+x_n{x}_{n+k}{x}_{n+2k}{x}_{n+5k}\eta \left(n+4k,x_{n+4k}\right)}{x_{n+4k}^2{x}_{n+5k}^2\left(A_n+B_n{x}_n{x}_{n+k}{x}_{n+2k}{x}_{n+3k}\right)}\hfill \\ & +\frac{B_n{x_n}^2{x_{n+k}}^2{x_{n+2k}}^2\eta \left(n+3k,x_{n+3k}\right)}{x_{n+4k}{x}_{n+5k}{\left(A_n+B_n{x}_n{x}_{n+k}{x}_{n+2k}{x}_{n+3k}\right)}^2}-\frac{A_n{x}_n{x}_{n+k}\eta \left(n+2k,x_{n+2k}\right)}{x_{n+4k}{x}_{n+5k}{\left(A_n+B_n{x}_n{x}_{n+k}{x}_{n+2k}{x}_{n+3k}\right)}^2}-\hfill \\ & \frac{A_n{x}_n{x}_{n+k}\eta \left(n+k,x_{n+k}\right)}{x_{n+4k}{x}_{n+5k}{\left(A_n+B_n{x}_n{x}_{n+k}{x}_{n+2k}{x}_{n+3k}\right)}^2}-\frac{A_n{x}_{n+k}{x}_{n+2k}\eta \left(n,x_n\right)}{x_{n+4k}{x}_{n+5k}{\left(A_n+B_n{x}_n{x}_{n+k}{x}_{n+2k}{x}_{n+3k}\right)}^2}=0.\hfill \end{array}$$

(11)

We differentiate (11) with respect to $x_n$ viewing $x_{n+4k}$ as a function of $x_n$, $x_{n+k}$, $x_{n+2k}$, $x_{n+3k}$, $x_{n+5k}$ and $\mathcal{A}$. To put it in another way, we apply the differential operator $\frac{\partial }{\partial x_n}-({\mathcal{A}}_{,x_n}/{\mathcal{A}}_{,x_{n+4k}})\frac{\partial }{\partial x_{n+4k}}$ to (11) to obtain (after clearing fractions except for the reciprocal of $x_n$):

$$\begin{array}{cc}\hfill & x_{n+4k}(A_n+B_n{x}_n{x}_{n+k}{x}_{n+2k}{x}_{n+3k}){\eta }^{\prime }(n+4k,x_{n+4k})-(A_n+B_n{x}_n{x}_{n+k}{x}_{n+2k}{x}_{n+3k})\eta (n+4k,\hfill \\ & x_{n+4k})+B_n{x}_n{x}_{n+k}{x}_{n+2k}{x}_{n+4k}\eta (n+3k,x_{n+3k})+B_n{x}_n{x}_{n+k}{x}_{n+3k}{x}_{n+4k}\eta (n+2k,x_{n+2k})\hfill \\ & +B_n{x}_n{x}_{n+2k}{x}_{n+3k}{x}_{n+4k}\eta (n+k,x_{n+k})-x_{n+4k}(A_n+B_n{x}_n{x}_{n+k}{x}_{n+2k}{x}_{n+3k}){\eta }^{\prime }(n,x_n)\hfill \\ & +x_{n+4k}\left(\frac{A_n}{x_n}+2B_n{x}_{n+k}{x}_{n+2k}{x}_{n+3k}\right)\eta (n,x_k)=0.\hfill \end{array}$$

(12)

Observe that ${\mathcal{A}}_{,x}$ denotes the derivative of $\mathcal{A}$ with respect to x and ${}^{\prime }$ represents the derivative with regard to the continuous variable. Next, we differentiate (12) with respect to $x_n$ and we utilize the method of separation to obtain the following system:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{x}_n{x}_{n+k}{x}_{n+2k}{x}_{n+3k}{x}_{n+4k}\hfill & :{\eta }^{\prime \prime \prime }=0\hfill \\ x_{n+4k}\hfill & :{\eta }^{\prime \prime \prime }-\frac{1}{x_n}{\eta }^{″}+\frac{2}{x_n^2}{\eta }^{\prime }-\frac{2}{x_n^3}\eta =0.\hfill \end{array}\right.\end{array}$$

(13)

It is easy to verity that the general solution of the above system is given by

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \eta \left(n,u_n\right)={\lambda }_n{u_n}^2+{\theta }_n{u}_n\end{array}\end{array}$$

(14)

for some arbitrary functions ${\lambda }_n$ and ${\theta }_n$ depending on n. We replace (14) and the corresponding shifts in (11) ($x_{n+6k}$ must also be replaced by its expression in (1)). Clearing fractions and separating with respect to products of $x_{n+i}$, the resulting system of equations reduces to the constraints:

$$\begin{array}{cc}\hfill & {\lambda }_n=0,\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & {\theta }_n+{\theta }_{n+k}+{\theta }_{n+2k}+{\theta }_{n+3k}=0.\hfill \end{array}$$

(16)

The constraint in (16) is a homogeneous linear difference equation with characteristic equation $r^{3k}+r^{2k}+r^k+1=0$ whose solutions are $e^{i\left(\frac{\pi +4p\pi }{2k}\right)}$, $e^{i\left(\frac{2\pi +4p\pi }{2k}\right)}$ and $e^{i\left(\frac{3\pi +4p\pi }{2k}\right)}$ for $p=0,\cdots ,k-1$. Solutions of (16) take the form $r^n$ and using (8), we have $3k$ symmetries given by

$$\begin{array}{cc}\hfill {\mathcal{X}}_{1p}=& e^{in\left(\frac{\pi +4p\pi }{2k}\right)}{x}_n{\partial }_{x_n},{\mathcal{X}}_{2p}=e^{in\left(\frac{2\pi +4p\pi }{2k}\right)}{x}_n{\partial }_{x_n},{\mathcal{X}}_{3p}=e^{in\left(\frac{3\pi +4p\pi }{2k}\right)}{x}_n{\partial }_{x_n},\hfill \end{array}$$

(17)

$p=0,1,\cdots ,k-1$. We construct the canonical coordinate as

$$\begin{array}{c}\hfill S_n=\int \frac{d{x}_n}{{\theta }_n{x}_n}=\frac{1}{{\theta }_n}ln\left|x_n\right|\end{array}$$

(18)

and we set

$$\begin{array}{c}\hfill |V_n|=exp\{-(S_n{\theta }_n+S_{n+k}{\theta }_{n+k}+S_{n+2k}{\theta }_{n+2k}+S_{n+3k}{\theta }_{n+3k})\}.\end{array}$$

(19)

The variable $V_n$ can take the form

$$\begin{array}{c}\hfill V_n=\frac{1}{x_n{x}_{n+k}{x}_{n+2k}{x}_{n+3k}}\end{array}$$

(20)

and, as a matter of fact, is an invariant because

$$\begin{array}{cc}\hfill X\left(V_n\right)=& \left({\theta }_n{x}_n\frac{\partial }{\partial x_n}+{\theta }_{n+k}{x}_{n+k}\frac{\partial }{\partial x_{n+k}}+{\theta }_{n+2k}{x}_{n+2k}\frac{\partial }{\partial x_{n+2k}}+{\theta }_{n+3k}{x}_{n+3k}\frac{\partial }{\partial x_{n+3k}}+\right.\hfill \\ & {\theta }_{n+4k}{x}_{n+4k}\frac{\partial }{\partial x_{n+4k}}+\left.{\theta }_{n+5k}{x}_{n+5k}\frac{\partial }{\partial x_{n+5k}}\right)V_n\hfill \\ \hfill =& \frac{-1}{x_n{x}_{n+k}{x}_{n+2k}{x}_{n+3k}}\left({\theta }_n+{\theta }_{n+k}+{\theta }_{n+2k}+{\theta }_{n+3k}\right)\hfill \\ \hfill =& 0.\hfill \end{array}$$

(21)

Using (1) and (20), we derive the following relations:

$$V_{n+3k}=A_n{V}_n+B_n$$

(22)

and

$$x_{n+4k}=\frac{V_n}{V_{n+k}}{x}_n$$

(23)

from which are obtained

$$\begin{array}{cc}\hfill V_{3kn+j}=& V_j\left(\prod _{k_1=0}^{n-1}{A}_{3k{k}_1+j}\right)+\sum _{m=0}^{n-1}\left(B_{3km+j}\prod _{k_2=m+1}^{n-1}{A}_{3k{k}_2+j}\right),j=0,1,\cdots ,3k-1,\hfill \end{array}$$

(24)

and

$$\begin{array}{cc}\hfill x_{4kn+j}=& x_j\left(\prod _{s=0}^{n-1}\frac{V_{4ks+j}}{V_{4ks+k+j}}\right),j=0,1,\cdots ,4k-1\hfill \end{array}$$

(25)

using simple iterations. Since we do not have an expression for $V_{4ks+i}$, we make use of (25) to obtain the following:

$$\begin{array}{cc}\hfill x_{12kn+j}=& x_j\left(\prod _{s=0}^{3n-1}\frac{V_{4ks+j}}{V_{4ks+k+j}}\right)\hfill \\ \hfill =& x_j\prod _{s=0}^{n-1}\frac{V_{12ks+j}}{V_{12ks+k+j}}\frac{V_{12ks+4k+j}}{V_{12ks+4k+k+j}}\frac{V_{12ks+8k+j}}{V_{12ks+8k+k+j}}\hfill \\ \hfill =& x_j\prod _{s=0}^{n-1}\prod _{r=0}^2\frac{V_{12ks+4kr+j}}{V_{12ks+4kr+k+j}}\hfill \\ \hfill =& x_j\prod _{s=0}^{n-1}\prod _{r=0}^2\frac{V_{3k\left(4s+\lfloor \frac{4kr+j}{3k}\rfloor \right)+\tau (4kr+j)}}{V_{3k\left(4s+\lfloor \frac{4kr+k+j}{3k}\rfloor \right)+\tau (4kr+k+j)}},j=0,1,\cdots ,12k-1.\hfill \end{array}$$

(26)

Observe that the symbol $\lfloor ·\rfloor$ represents the floor function and $\tau \left(q\right)$ is the remainder after division of q by $3k$. It follows that $0\le \tau \left(p\right)\le 3k-1$. Employing (24) in (26), we find that

$$\begin{array}{cc}\hfill & x_{12kn+j}=x_j\prod _{s=0}^{n-1}\prod _{r=0}^2\hfill \\ & \frac{V_{\tau (4kr+j)}\left({\displaystyle \prod _{k_1=0}^{\begin{array}{c}4s-1+\\ \lfloor \frac{4kr+j}{3k}\rfloor \end{array}}}{A}_{3k{k}_1+\tau (4kr+j)}\right)+{\displaystyle \sum _{m=0}^{\begin{array}{c}4s-1+\\ \lfloor \frac{4kr+j}{3k}\rfloor \end{array}}}\left(B_{3km+\tau (4kr+j)}{\displaystyle \prod _{k_2=m+1}^{\begin{array}{c}4s-1+\\ \lfloor \frac{4kr+j}{3k}\rfloor \end{array}}}{A}_{3k{k}_2+\tau (4kr+j)}\right)}{V_{\tau (4kr+k+j)}\left({\displaystyle \prod _{k_1=0}^{\begin{array}{c}4s-1+\\ \lfloor \frac{4kr+k+j}{3k}\rfloor \end{array}}}{A}_{3k{k}_1+\tau (4kr+k+j)}\right)+{\displaystyle \sum _{m=0}^{\begin{array}{c}4s-1+\\ \lfloor \frac{4kr+k+j}{3k}\rfloor \end{array}}}\left(B_{3km+\tau (4kr+k+j)}{\displaystyle \prod _{k_2=m+1}^{\begin{array}{c}4s-1+\\ \lfloor \frac{4kr+k+j}{3k}\rfloor \end{array}}}{A}_{3k{k}_2+\tau (4kr+k+j)}\right)}\hfill \end{array}$$

(27)

where $V_i=1/\left(x_i{x}_{i+k}{x}_{i+2k}{x}_{i+k}\right)$. Equation (27) gives the solution to the difference Equation (1). Naturally, the solution of (2) is deduced from that of (1) by backshifting it $6k$ times. So, using (27), the solution of (2) reads

$$\begin{array}{cc}\hfill & x_{12kn-6k+j}=x_{j-6k}\prod _{s=0}^{n-1}\prod _{r=0}^2\hfill \\ & \frac{v_{\tau (4kr+j)}\left({\displaystyle \prod _{k_1=0}^{\begin{array}{c}4s-1+\\ \lfloor \frac{4kr+j}{3k}\rfloor \end{array}}}{a}_{3k{k}_1+\tau (4kr+j)}\right)+{\displaystyle \sum _{m=0}^{\begin{array}{c}4s-1+\\ \lfloor \frac{4kr+j}{3k}\rfloor \end{array}}}\left(b_{3km+\tau (4kr+j)}{\displaystyle \prod _{k_2=m+1}^{\begin{array}{c}4s-1+\\ \lfloor \frac{4kr+j}{3k}\rfloor \end{array}}}{a}_{3k{k}_2+\tau (4kr+j)}\right)}{v_{\tau (4kr+k+j)}\left({\displaystyle \prod _{k_1=0}^{\begin{array}{c}4s-1+\\ \lfloor \frac{4kr+k+j}{3k}\rfloor \end{array}}}{a}_{3k{k}_1+\tau (4kr+k+j)}\right)+{\displaystyle \sum _{m=0}^{\begin{array}{c}4s-1+\\ \lfloor \frac{4kr+k+j}{3k}\rfloor \end{array}}}\left(b_{3km+\tau (4kr+k+j)}{\displaystyle \prod _{k_2=m+1}^{\begin{array}{c}4s-1+\\ \lfloor \frac{4kr+k+j}{3k}\rfloor \end{array}}}{a}_{3k{k}_2+\tau (4kr+k+j)}\right)}\hfill \end{array}$$

(28)

where $v_i=1/\left(x_{i-6k}{x}_{i-5k}{x}_{i-4k}{x}_{i-5k}\right)$. For 1, k, $3k$-periodic sequences $A_n$ and $B_n$, the solutions simplifies considerably. The following subsection is dedicated to the case where $A_n$ and $B_n$ are 1-periodic.

3.1. The Case $A_n$ and $B_n$ Are 1-Periodic Sequences

Letting $A_n=A$ and $B_n=B$ in (27), we obtain

$$\begin{array}{cc}\hfill x_{12kn+j}=& x_j{\displaystyle \prod _{s=0}^{n-1}}\left(\frac{V_{\tau \left(j\right)}{A}^{4s+\lfloor \frac{j}{3k}\rfloor }+B{\displaystyle \sum _{m=0}^{\begin{array}{c}4s-1+\lfloor \frac{j}{3k}\rfloor \end{array}}}{A}^m}{V_{\tau (j+k)}{A}^{4s+\lfloor \frac{j+k}{3k}\rfloor }+B{\displaystyle \sum _{m=0}^{\begin{array}{c}4s-1+\lfloor \frac{j+k}{3k}\rfloor \end{array}}}{A}^m}\frac{V_{\tau (j+k)}{A}^{4s+1+\lfloor \frac{j+k}{3k}\rfloor }+B{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+\lfloor \frac{j+k}{3k}\rfloor \end{array}}}{A}^m}{V_{\tau (j+2k)}{A}^{4s+1+\lfloor \frac{j+2k}{3k}\rfloor }+B{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+\lfloor \frac{j+2k}{3k}\rfloor \end{array}}}{A}^m}\right.\hfill \\ & \left.\frac{V_{\tau (j+2k)}{A}^{4s+2+\lfloor \frac{j+2k}{3k}\rfloor }+B{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+1+\lfloor \frac{j+2k}{3k}\rfloor \end{array}}}{A}^m}{V_{\tau \left(j\right)}{A}^{4s+3+\lfloor \frac{j}{3k}\rfloor }+B{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+2+\lfloor \frac{j}{3k}\rfloor \end{array}}}{A}^m}\right)\hfill \\ \hfill & =x_j{\displaystyle \prod _{s=0}^{n-1}}\left(\frac{A^{4s+\lfloor \frac{j}{3k}\rfloor }+\frac{B}{V_{\tau \left(j\right)}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+\lfloor \frac{j}{3k}\rfloor -1\end{array}}}{A}^m}{A^{4s+3+\lfloor \frac{j}{3k}\rfloor }+\frac{B}{V_{\tau \left(j\right)}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+2+\lfloor \frac{j}{3k}\rfloor \end{array}}}{A}^m}\frac{A^{4s+1+\lfloor \frac{j+k}{3k}\rfloor }+\frac{B}{V_{\tau (j+k)}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+\lfloor \frac{j+k}{3k}\rfloor \end{array}}}{A}^m}{A^{4s+\lfloor \frac{j+k}{3k}\rfloor }+\frac{B}{V_{\tau (j+k)}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+\lfloor \frac{j+k}{3k}\rfloor -1\end{array}}}{A}^m}\times \right.\hfill \\ \hfill & \left.\frac{A^{4s+2+\lfloor \frac{j+2k}{3k}\rfloor }+\frac{B}{V_{\tau (j+2k)}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+1+\lfloor \frac{j+2k}{3k}\rfloor \end{array}}}{A}^m}{A^{4s+1+\lfloor \frac{j+2k}{3k}\rfloor }+\frac{B}{V_{\tau (j+2k)}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+\lfloor \frac{j+2k}{3k}\rfloor \end{array}}}{A}^m}\right),\hfill \end{array}$$

(29)

$j=0,1,\dots ,12k\dots 1$. However, $j=0,1,\dots ,12k-1$ can take the form $j=3kr+pk+j_1$ with $r=0,1,2,3$; $p=0,1,2$; $j_1=0,1,\dots ,k-1$. Consequently,

$$\begin{array}{cc}\hfill & x_{12kn+3kr+kp+j_1}=x_{3kr+kp+j_1}{\displaystyle \prod _{s=0}^{n-1}}\left(\frac{A^{4s+r}+\frac{B}{V_{pk+j_1}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+\\ r-1\end{array}}}{A}^m}{A^{4s+3+r}+\frac{B}{V_{pk+j_1}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+2\\ +r\end{array}}}{A}^m}\right.\hfill \\ & \left.\frac{A^{4s+1+r+\lfloor \frac{j_1+(p+1)k}{3k}\rfloor }+\frac{B}{V_{\tau (j_1+(p+1)k)}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+r+\\ \lfloor \frac{j_1+(p+1)k}{3k}\rfloor \end{array}}}{A}^m}{A^{4s+r+\lfloor \frac{j_1+(p+1)k}{3k}\rfloor }+\frac{B}{V_{\tau (j_1+(p+1)k)}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+r-1\\ \lfloor \frac{j_1+(p+1)k}{3k}\rfloor \end{array}}}{A}^m}\frac{A^{4s+2+r+\lfloor \frac{j_1+(p+2)k}{3k}\rfloor }+\frac{B}{V_{\tau (j_1+(p+2)k)}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+1+r+\\ \lfloor \frac{j+(p+2)k}{3k}\rfloor \end{array}}}{A}^m}{A^{4s+1+r+\lfloor \frac{j_1+(p+2)k}{3k}\rfloor }+\frac{B}{V_{\tau (j_1+(p+2)k)}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+r+\\ \lfloor \frac{j_1+(p+2)k}{3k}\rfloor \end{array}}}{A}^m}\right).\hfill \end{array}$$

(30)

More explicitly,

$$\begin{array}{cc}\hfill x_{12kn+3kr+j_1}=& x_{3kr+j_1}{\displaystyle \prod _{s=0}^{n-1}}\frac{A^{4s+r}+\frac{B}{V_{j_1}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+\\ r-1\end{array}}}{A}^m}{A^{4s+3+r}+\frac{B}{V_{j_1}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+\\ 2+r\end{array}}}{A}^m}\frac{A^{4s+1+r}+\frac{B}{V_{j_1+k}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+r\end{array}}}{A}^m}{A^{4s+r}+\frac{B}{V_{j_1+k}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+\\ r-1\end{array}}}{A}^m}\frac{A^{4s+2+r}+\frac{B}{V_{j_1+2k}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+\\ 1+r\end{array}}}{A}^m}{A^{4s+1+r}+\frac{B}{V_{j_1+2k}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+r\end{array}}}{A}^m},\hfill \\ \hfill x_{12kn+3kr+k+j_1}=& x_{3kr+k+j_1}{\displaystyle \prod _{s=0}^{n-1}}\left(\frac{A^{4s+r}+\frac{B}{V_{j_1+k}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+\\ r-1\end{array}}}{A}^m}{A^{4s+3+r}+\frac{B}{V_{j_1+k}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+\\ 2+r\end{array}}}{A}^m}\frac{A^{4s+1+r}+\frac{B}{V_{j_1+2k}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+r\end{array}}}{A}^m}{A^{4s+r+2}+\frac{B}{V_{j_1+2k}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+\\ r+1\end{array}}}{A}^m}\right.\hfill \\ & \left.\frac{A^{4s+3+r}+\frac{B}{V_{j_1}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+\\ 2+r\end{array}}}{A}^m}{A^{4s+2+r}+\frac{B}{V_{j_1}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+\\ r+1\end{array}}}{A}^m}\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_{12kn+3kr+2k+j_1}=& x_{3kr+2k+j_1}{\displaystyle \prod _{s=0}^{n-1}}\left(\frac{A^{4s+r}+\frac{B}{V_{j_1+2k}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+r-1\end{array}}}{A}^m}{A^{4s+3+r}+\frac{B}{V_{j_1+2k}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+2+r\end{array}}}{A}^m}\frac{A^{4s+2+r}+\frac{B}{V_{j_1}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+r+1\end{array}}}{A}^m}{A^{4s+r+1}+\frac{B}{V_{j_1}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+r\end{array}}}{A}^m}\right.\hfill \\ & \left.\frac{A^{4s+3+r}+\frac{B}{V_{j_1+k}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+2+r\end{array}}}{A}^m}{A^{4s+2+r}+\frac{B}{V_{j_1+k}}{\displaystyle \sum _{m=0}^{\begin{array}{c}4s+r+1\end{array}}}{A}^m}\right),\hfill \end{array}$$

(31)

for $r=0,1,2,3$; $j_1=0,1,\dots ,k-1$ with $V_n=1/\left(x_n{x}_{n+k}{x}_{n+2k}{x}_{n+3}\right)$. Equations in (31) are given in terms of the first $12k$ terms including the initial conditions. Since one of the aims of the paper is to present the solution in closed-form, we use (1) to provide the expressions of $x_i$, $i=6k+1,\dots ,12k-1$, as follows:

$$\begin{array}{cc}\hfill x_{6k+j_1}=& \frac{x_{j_1}{x}_{j_1+k}{x}_{j_1+2k}}{x_{j_1+4k}{x}_{j_1+5k}\left(A+\frac{B}{V_{j_1}}\right)},x_{7k+j_1}=\frac{x_{3k+j_1}{x}_{j_1+4k}\left(A+\frac{B}{V_{j_1}}\right)}{x_{j_1}\left(A+\frac{B}{V_{j_1+k}}\right)},\hfill \\ \hfill x_{8k+j_1}=& \frac{x_{4k+j_1}{x}_{j_1+5k}\left(A+\frac{B}{V_{j_1+k}}\right)}{x_{k+j_1}\left(A+\frac{B}{V_{j_1+2k}}\right)},x_{9k+j_1}=\frac{x_{j_1}{x}_{j_1+k}\left(A+\frac{B}{V_{j_1+2k}}\right)}{x_{j_1+4k}\left(A^2+(A+1)\frac{B}{V_{j_1}}\right)},\hfill \\ \hfill x_{10k+j_1}=& \frac{x_{j_1+k}{x}_{j_1+2k}\left(A^2+(A+1)\frac{B}{V_{j_1}}\right)}{x_{j_1+5k}\left(A+\frac{B}{V_{j_1}}\right)\left(A^2+(A+1)\frac{B}{V_{j_1+k}}\right)},\hfill \\ \hfill x_{11k+j_1}=& \frac{x_{j_1+3k}{x}_{j_1+4k}{x}_{j_1+5k}\left(A+\frac{B}{V_{j_1}}\right)\left(A^2+(A+1)\frac{B}{V_{j_1+k}}\right)}{x_{j_1}{x}_{j_1+k}\left(A+\frac{B}{V_{j_1+k}}\right)\left(A^2+(A+1)\frac{B}{V_{j_1+2k}}\right)},\hfill \end{array}$$

(32)

for $j_1=0,1,\cdots ,k-1$.

3.1.1. The Case When $A\ne 1$

If $A\ne 1$, (31) simplifies to

$$\begin{array}{cc}\hfill x_{12kn+3kr+j_1}=& x_{3kr+j_1}{\displaystyle \prod _{s=0}^{n-1}}\left[\frac{A^{4s+r}+\frac{B}{V_{j_1}}\left(\frac{1-A^{4s+r}}{1-A}\right)}{A^{4s+3+r}+\frac{B}{V_{j_1}}\left(\frac{1-A^{4s+r+3}}{1-A}\right)}\frac{A^{4s+1+r}+\frac{B}{V_{j_1+k}}\left(\frac{1-A^{4s+r+1}}{1-A}\right)}{A^{4s+r}+\frac{B}{V_{j_1+k}}\left(\frac{1-A^{4s+r}}{1-A}\right)}\right.\hfill \\ & \left.\frac{A^{4s+2+r}+\frac{B}{V_{j_1+2k}}\left(\frac{1-A^{4s+r+2}}{1-A}\right)}{A^{4s+1+r}+\frac{B}{V_{j_1+2k}}\left(\frac{1-A^{4s+r+1}}{1-A}\right)}\right],\hfill \\ \hfill x_{12kn+3kr+k+j_1}=& x_{3kr+k+j_1}{\displaystyle \prod _{s=0}^{n-1}}\left[\frac{A^{4s+r}+\frac{B}{V_{j_1+k}}\left(\frac{1-A^{4s+r}}{1-A}\right)}{A^{4s+3+r}+\frac{B}{V_{j_1+k}}\left(\frac{1-A^{4s+r+3}}{1-A}\right)}\frac{A^{4s+1+r}+\frac{B}{V_{j_1+2k}}\left(\frac{1-A^{4s+r+1}}{1-A}\right)}{A^{4s+r+2}+\frac{B}{V_{j_1+2k}}\left(\frac{1-A^{4s+r+2}}{1-A}\right)}\right.\hfill \\ & \left.\frac{A^{4s+3+r}+\frac{B(1-A^{4s+r+3)}}{V_{j_1}(1-A)}}{A^{4s+2+r}+\frac{B(1-A^{4s+r+2})}{V_{j_1}(1-A)}}\right],\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_{12kn+3kr+2k+j_1}=& x_{3kr+2k+j_1}{\displaystyle \prod _{s=0}^{n-1}}\left[\frac{A^{4s+r}+\frac{B}{V_{j_1+2k}}\left(\frac{1-A^{4s+r}}{1-A}\right)}{A^{4s+3+r}+\frac{B}{V_{j_1+2k}}\left(\frac{1-A^{4s+r+3}}{1-A}\right)}\frac{A^{4s+2+r}+\frac{B}{V_{j_1}}\left(\frac{1-A^{4s+r+2}}{1-A}\right)}{A^{4s+r+1}+\frac{B}{V_{j_1}}\left(\frac{1-A^{4s+r+1}}{1-A}\right)}\right.\hfill \\ & \left.\frac{A^{4s+3+r}+\frac{B(1-A^{4s+r+3})}{V_{j_1+k}(1-A)}}{A^{4s+2+r}+\frac{B(1-A^{4s+r+2})}{V_{j_1+k}(1-A)}}\right]\hfill \end{array}$$

(33)

with $x_{6k},\cdots ,x_{12k-1}$ given in (32).

The case $A=-1$: For this case, after simplification, we have that

$$\begin{array}{cc}\hfill x_{12kn+j_1}=& \frac{x_{j_1}{\left(-1+\frac{B}{V_{j_1+k}}\right)}^n}{{\left(-1+\frac{B}{V_{j_1}}\right)}^n{\left(-1+\frac{B}{V_{j_1+2k}}\right)}^n},x_{12kn+k+j_1}=\frac{x_{k+j_1}{\left(-1+\frac{B}{V_{j_1+2k}}\right)}^n{\left(-1+\frac{B}{V_{j_1}}\right)}^n}{{\left(-1+\frac{B}{V_{j_1+k}}\right)}^n},\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_{12kn+2k+j_1}=& \frac{x_{2k+j_1}{\left(-1+\frac{B}{V_{j_1+k}}\right)}^n}{{\left(-1+\frac{B}{V_{j_1}}\right)}^n{\left(-1+\frac{B}{V_{j_1+2k}}\right)}^n},x_{12kn+3k+j_1}=\frac{x_{3k+j_1}{\left(-1+\frac{B}{V_{j_1+2k}}\right)}^n{\left(-1+\frac{B}{V_{j_1}}\right)}^n}{{\left(-1+\frac{B}{V_{j_1+k}}\right)}^n},\hfill \\ \hfill x_{12kn+4k+j_1}=& \frac{x_{4k+j_1}{\left(-1+\frac{B}{V_{j_1+k}}\right)}^n}{{\left(-1+\frac{B}{V_{j_1}}\right)}^n{\left(-1+\frac{B}{V_{j_1+2k}}\right)}^n},x_{12kn+5k+j_1}=\frac{x_{5k+j_1}{\left(-1+\frac{B}{V_{j_1+2k}}\right)}^n{\left(-1+\frac{B}{V_{j_1}}\right)}^n}{{\left(-1+\frac{B}{V_{j_1+k}}\right)}^n},\hfill \\ \hfill x_{12kn+6k+j_1}=& \frac{x_{j_1}{x}_{j_1+k}{x}_{j_1+2k}{\left(-1+\frac{B}{V_{j_1+k}}\right)}^n}{x_{4k+j_1}{x}_{j_1+5k}{\left(-1+\frac{B}{V_{j_1}}\right)}^{n+1}{\left(-1+\frac{B}{V_{j_1+2k}}\right)}^n},\hfill \\ \hfill x_{12kn+7k+j_1}=& \frac{x_{j_1+3k}{x}_{j_1+4k}{\left(-1+\frac{B}{V_{j_1+2k}}\right)}^n}{x_{j_1}{\left(-1+\frac{B}{V_{j_1+k}}\right)}^{n+1}{\left(-1+\frac{B}{V_{j_1}}\right)}^{-(n+1)}},\hfill \\ \hfill x_{12kn+8k+j_1}=& \frac{x_{j_1+4k}{x}_{j_1+5k}{\left(-1+\frac{B}{V_{j_1+k}}\right)}^{n+1}}{x_{j_1+k}{\left(-1+\frac{B}{V_{j_1}}\right)}^n{\left(-1+\frac{B}{V_{j_1+2k}}\right)}^{n+1}},\hfill \\ \hfill x_{12kn+9k+j_1}=& \frac{x_{j_1}{x}_{j_1+k}{\left(-1+\frac{B}{V_{j_1+k}}\right)}^n}{x_{j_1+4k}{\left(-1+\frac{B}{V_{j_1}}\right)}^n{\left(-1+\frac{B}{V_{j_1+2k}}\right)}^{n-1}},\hfill \\ \hfill x_{12kn+10k+j_1}=& \frac{x_{j_1+k}{x}_{j_1+2k}{\left(-1+\frac{B}{V_{j_1+2k}}\right)}^n}{x_{j_1+5k}{\left(-1+\frac{B}{V_{j_1+k}}\right)}^n{\left(-1+\frac{B}{V_{j_1}}\right)}^{-(n-1)}},\hfill \\ \hfill x_{12kn+11k+j_1}=& \frac{x_{j_1+3k}{x}_{j_1+4k}{x}_{j_1+5k}{\left(-1+\frac{B}{V_{j_1+k}}\right)}^{n-1}}{x_{j_1}{x}_{j_1+k}{\left(-1+\frac{B}{V_{j_1}}\right)}^{n-1}{\left(-1+\frac{B}{V_{j_1+2k}}\right)}^n},\hfill \end{array}$$

(34)

for $j_1=0,1,\dots ,k-1$.

3.1.2. The Case When $A=1$

If $A=1$, Equation (31) reduces to

$$\begin{array}{cc}\hfill x_{12kn+3kr+j_1}=& x_{3kr+j_1}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{(4s+r)B}{V_{j_1}}}{1+\frac{(4s+r+3)B}{V_{j_1}}}\frac{1+\frac{(4s+r+1)B}{V_{j_1+k}}}{1+\frac{(4s+r)B}{V_{j_1+k}}}\frac{1+\frac{(4s+r+2)B}{V_{j_1+2k}}}{1+\frac{(4s+r+1)B}{V_{j_1+2k}}}\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_{12kn+3kr+k+j_1}=& x_{3kr+k+j_1}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{(4s+r)B}{V_{j_1+k}}}{1+\frac{(4s+r+3)B}{V_{j_1+k}}}\frac{1+\frac{(4s+r+1)B}{V_{j_1+2k}}}{1+\frac{(4s+r+2)B}{V_{j_1+2k}}}\frac{1+\frac{(4s+r+3)B}{V_{j_1}}}{1+\frac{(4s+r+2)B}{V_{j_1}}}\hfill \\ \hfill x_{12kn+3kr+2k+j_1}=& x_{3kr+2k+j_1}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{B(4s+r)}{V_{j_1+2k}}}{1+\frac{B(4s+r+3)}{V_{j_1+2k}}}\frac{1+\frac{(4s+r+2)B}{V_{j_1}}}{1+\frac{(4s+r+1)B}{V_{j_1}}}\frac{1+\frac{(4s+r+3)B}{V_{j_1+k}}}{1+\frac{(4s+r+2)B}{V_{j_1+k}}}\hfill \end{array}$$

(35)

with $x_{6k},\dots ,x_{12k-1}$ given in equations in (32). These equations in (35) can be unpacked and presented in the following closed-form:

$$\begin{array}{cc}\hfill x_{12kn+j_1}=& x_{j_1}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{\left(4s\right)B}{V_{j_1}}}{1+\frac{(4s+3)B}{V_{j_1}}}\frac{1+\frac{(4s+1)B}{V_{j_1+k}}}{1+\frac{\left(4s\right)B}{V_{j_1+k}}}\frac{1+\frac{(4s+2)B}{V_{j_1+2k}}}{1+\frac{(4s+1)B}{V_{j_1+2k}}}\hfill \\ \hfill x_{12kn+k+j_1}=& x_{k+j_1}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{\left(4s\right)B}{V_{j_1+k}}}{1+\frac{(4s+3)B}{V_{j_1+k}}}\frac{1+\frac{(4s+1)B}{V_{j_1+2k}}}{1+\frac{(4s+2)B}{V_{j_1+2k}}}\frac{1+\frac{(4s+3)B}{V_{j_1}}}{1+\frac{(4s+2)B}{V_{j_1}}}\hfill \\ \hfill x_{12kn+2k+j_1}=& x_{2k+j_1}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{\left(4s\right)B}{V_{j_1+2k}}}{1+\frac{(4s+3)B}{V_{j_1+2k}}}\frac{1+\frac{(4s+2)B}{V_{j_1}}}{1+\frac{(4s+1)B}{V_{j_1}}}\frac{1+\frac{(4s+3)B}{V_{j_1+k}}}{1+\frac{(4s+2)B}{V_{j_1+k}}}\hfill \\ \hfill x_{12kn+3k+j_1}=& x_{j_1+3k}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{(4s+1)B}{V_{j_1}}}{1+\frac{(4s+4)B}{V_{j_1}}}\frac{1+\frac{(4s+2)B}{V_{j_1+k}}}{1+\frac{(4s+1)B}{V_{j_1+k}}}\frac{1+\frac{(4s+3)B}{V_{j_1+2k}}}{1+\frac{(4s+2)B}{V_{j_1+2k}}}\hfill \\ \hfill x_{12kn+4k+j_1}=& x_{4k+j_1}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{(4s+1)B}{V_{j_1+k}}}{1+\frac{(4s+4)B}{V_{j_1+k}}}\frac{1+\frac{(4s+2)B}{V_{j_1+2k}}}{1+\frac{(4s+3)B}{V_{j_1+2k}}}\frac{1+\frac{(4s+4)B}{V_{j_1}}}{1+\frac{(4s+3)B}{V_{j_1}}}\hfill \\ \hfill x_{12kn+5k+j_1}=& x_{5k+j_1}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{(4s+1)B}{V_{j_1+2k}}}{1+\frac{(4s+4)B}{V_{j_1+2k}}}\frac{1+\frac{(4s+3)B}{V_{j_1}}}{1+\frac{(4s+2)B}{V_{j_1}}}\frac{1+\frac{(4s+4)B}{V_{j_1+k}}}{1+\frac{(4s+3)B}{V_{j_1+k}}}\hfill \\ \hfill x_{12kn+6k+j_1}=& \frac{x_{j_1}{x}_{j_1+k}{x}_{j_1+2k}}{x_{j_1+4k}{x}_{j_1+5k}(1+\frac{B}{V_{j_1}})}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{(4s+2)B}{V_{j_1}}}{1+\frac{(4s+5)B}{V_{j_1}}}\frac{1+\frac{(4s+3)B}{V_{j_1+k}}}{1+\frac{(4s+2)B}{V_{j_1+k}}}\frac{1+\frac{(4s+4)B}{V_{j_1+2k}}}{1+\frac{(4s+3)B}{V_{j_1+2k}}}\hfill \\ \hfill x_{12kn+7k+j_1}=& \frac{x_{3k+j_1}{x}_{j_1+4k}(1+\frac{B}{V_{j_1}})}{x_{j_1}(1+\frac{B}{V_{j_1+k}})}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{(4s+2)B}{V_{j_1+k}}}{1+\frac{(4s+5)B}{V_{j_1+k}}}\frac{1+\frac{(4s+3)B}{V_{j_1+2k}}}{1+\frac{(4s+4)B}{V_{j_1+2k}}}\frac{1+\frac{(4s+5)B}{V_{j_1}}}{1+\frac{(4s+4)B}{V_{j_1}}}\hfill \\ \hfill x_{12kn+8k+j_1}=& \frac{x_{4k+j_1}{x}_{j_1+5k}(1+\frac{B}{V_{j_1+k}})}{x_{k+j_1}(1+\frac{B}{V_{j_1+2k}})}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{(4s+2)B}{V_{j_1+2k}}}{1+\frac{(4s+5)B}{V_{j_1+2k}}}\frac{1+\frac{(4s+4)B}{V_{j_1}}}{1+\frac{(4s+3)B}{V_{j_1}}}\frac{1+\frac{(4s+5)B}{V_{j_1+k}}}{1+\frac{(4s+4)B}{V_{j_1+k}}}\hfill \\ \hfill x_{12kn+9k+j_1}=& \frac{x_{j_1}{x}_{j_1+k}(1+\frac{B}{V_{j_1+2k}})}{x_{j_1+4k}(1+\frac{2B}{V_{j_1}})}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{(4s+3)B}{V_{j_1}}}{1+\frac{(4s+6)B}{V_{j_1}}}\frac{1+\frac{(4s+4)B}{V_{j_1+k}}}{1+\frac{(4s+3)B}{V_{j_1+k}}}\frac{1+\frac{(4s+5)B}{V_{j_1+2k}}}{1+\frac{(4s+4)B}{V_{j_1+2k}}}\hfill \\ \hfill x_{12kn+10k+j_1}=& \frac{x_{j_1+k}{x}_{j_1+2k}(1+\frac{2B}{V_{j_1}})}{x_{j_1+5k}(1+\frac{B}{V_{j_1}})(1+\frac{2B}{V_{j_1+k}})}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{(4s+3)B}{V_{j_1+k}}}{1+\frac{(4s+6)B}{V_{j_1+k}}}\frac{1+\frac{(4s+4)B}{V_{j_1+2k}}}{1+\frac{(4s+5)B}{V_{j_1+2k}}}\frac{1+\frac{(4s+6)B}{V_{j_1}}}{1+\frac{(4s+5)B}{V_{j_1}}}\hfill \\ \hfill x_{12kn+11k+j_1}=& \frac{x_{j_1+3k}{x}_{j_1+4k}{x}_{j_1+5k}(1+\frac{B}{V_{j_1}})(1+\frac{2B}{V_{j_1+k}})}{x_{j_1}{x}_{j_1+k}(1+\frac{B}{V_{j_1+k}})(1+\frac{2B}{V_{j_1+2k}})}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{(4s+3)B}{V_{j_1+2k}}}{1+\frac{(4s+6)B}{V_{j_1+2k}}}\frac{1+\frac{(4s+5)B}{V_{j_1}}}{1+\frac{(4s+4)B}{V_{j_1}}}\frac{1+\frac{(4s+6)B}{V_{j_1+k}}}{1+\frac{(4s+5)B}{V_{j_1+k}}}\hfill \end{array}$$

(36)

for $j_1=0,1,\dots ,k-1$ with $V_i=1/\left(x_i{x}_{i+k}{x}_{i+2k}{x}_{i+3k}\right)$.

4. Periodicity and Behavior of the Solutions

Here, we study the periodicity of the solutions via the formula of the solutions obtained in the previous section and we look at stability of the equilibrium points.

Theorem 4.

The solution $x_n$ of

$$x_{n+6k}=\frac{x_n{x}_{n+k}{x}_{n+2k}}{x_{n+4k}{x}_{n+5k}(A+B{x}_n{x}_{n+k}{x}_{n+2k}{x}_{n+3k})},$$

(37)

where $A\ne 1$ and $B\ne 0$ are real constants, is $4k$-periodic if and only if the initial conditions, $x_i$, satisfy the following conditions:

(i) 

$x_i=x_{i+4k}$.

(ii) 

$x_i{x}_{i+k}{x}_{i+2k}{x}_{n+3k}=(1-A)/B$.

(iii) 

$x_i\ne x_{i+k}$ or $x_i\ne x_{i+2k}$.

Proof. 

Suppose the initial conditions $x_0,\cdots ,x_{6k-1}$ satisfy $x_i=x_{i+4k}$ with $x_i{x}_{i+k}{x}_{i+2k}{x}_{i+3k}=(1-A)/B$. The last condition eliminates k and $2k$-periodicities. Now, thanks to condition $\left(i\right)$, (31) and (32), we have

$$\begin{array}{cc}\hfill x_{4k+i}& =x_i,i=0,\dots ,2k-1;x_{6k+i}=x_{i+2k},i=0,\dots ,6k-1;x_{12kn+i}=x_i,i=0,\dots ,12k-1.\hfill \end{array}$$

This implies that $x_n=x_{n+4k}$ for all n and the solution is periodic with period $4k$. □

Figure 1 shows the graph of (37) for $k=2$ with the initial conditions satisfying the three conditions in Theorem 4. As expected, the solution is 8-periodic.

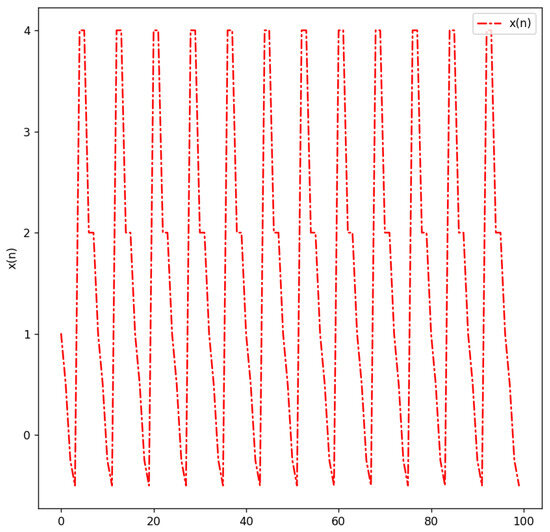
Figure 1. $x_{n+12}=\frac{x_n{x}_{n+2}{x}_{n+4}}{x_{n+8}{x}_{n+10}(2+0.5x_n{x}_{n+2}{x}_{n+4}{x}_{n+6})}$ with $x_0=x_8=1$,  $x_1=x_9=1/2$,  $x_2=x_{10}=-1/4$,  $x_3=x_{11}=-1/2$,  $x_4=4$,  $x_5=4$,  $x_6=2$,  $x_7=2$,  $x_9=1/2$,  $x_{11}=-1/2$.

Figure 2 shows the graph of (37) for $k=2$ with the initial conditions not satisfying one of the three conditions in Theorem 4, condition $\left(ii\right)$ to be specific.

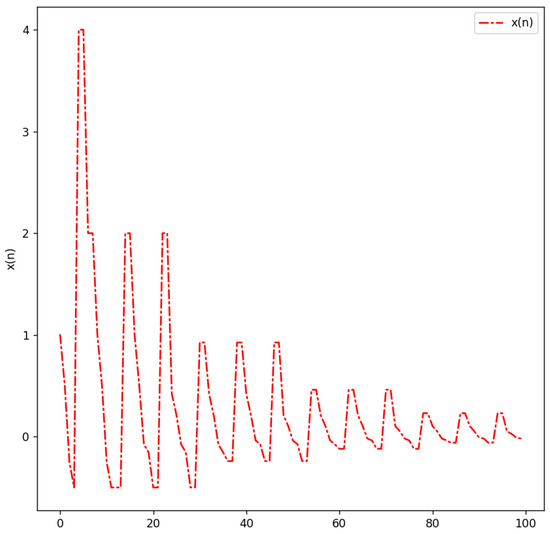
Figure 2. $x_{n+12}=\frac{x_n{x}_{n+2}{x}_{n+4}}{x_{n+8}{x}_{n+10}(2+5x_n{x}_{n+2}{x}_{n+4}{x}_{n+6})}$ with $x_0=1$,  $x_1=1/2$,  $x_2=-1/4$,  $x_3=-1/2$,  $x_4=4$,  $x_5=4$,  $x_6=2$,  $x_7=2$,  $x_8=1$,  $x_9=1/2$,  $x_{10}=-1/4$,  $x_{11}=-1/2$.

Theorem 5.

The solution $x_n$ of (37) is $2k$-periodic if and only if the initial conditions, $x_i$, satisfy the following conditions:

(i) 

$x_i=x_{i+2k}$

(ii) 

$x_i^2{x}_{i+k}^2=(1-A)/B$

(iii) 

$x_i\ne x_{i+k}$.

Proof. 

Suppose the initial conditions satisfy $x_i=x_{i+2k}$ and $x_i^2{x}_{i+k}^2=(1-A)/B$. Condition $\left(iii\right)$ eliminates k-periodicity. Invoking condition $\left(i\right)$, (31) and (32), we have that

$$\begin{array}{cc}\hfill x_{2k+i}& =x_i,i=0,\dots ,4k-1;x_{6k+i}=x_i,i=0,\dots ,6k-1;x_{12kn+i}=x_i,i=0,\dots ,12k-1.\hfill \end{array}$$

Therefore, $x_n=x_{n+2k}$ for all n and the solution is periodic with period $2k$. □

Figure 3 shows the graph of (37) for $k=2$ with the initial conditions satisfying the three conditions in Theorem 5. As expected, the solution is 4-periodic.

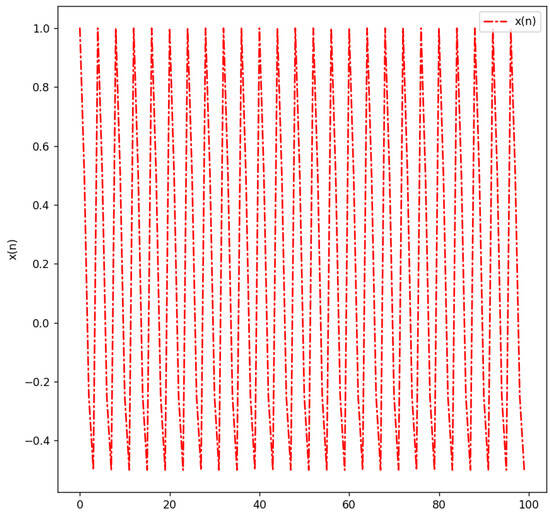
Figure 3. $x_{n+12}=\frac{x_n{x}_{n+2}{x}_{n+2}}{x_{n+8}{x}_{n+10}(2-16x_n{x}_{n+2}{x}_{n+4}{x}_{n+6})}$ with $x_0=x_8=1$,  $x_1=x_9=1/2$,  $x_2=x_{10}=-1/4$,  $x_3=x_{11}=-1/2$,  $x_4=1$,  $x_5=1/2$,  $x_6=-1/4$,  $x_7=-1/2$.

Figure 4 shows the graph of (37) for $k=2$ with the initial conditions not satisfying condition $\left(ii\right)$ in Theorem 5.

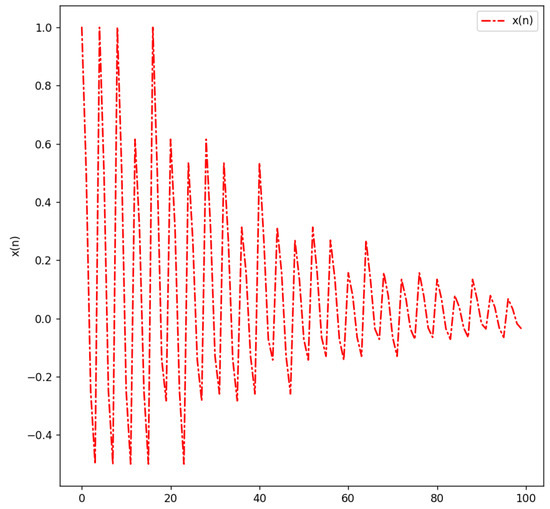
Figure 4. $x_{n+6k}=\frac{x_n{x}_{n+k}{x}_{n+2k}}{x_{n+4k}{x}_{n+5k}(2-6x_n{x}_{n+k}{x}_{n+2k}{x}_{n+3k})}$ with $x_0=x_8=1$,  $x_1=x_9=1/2$,  $x_2=x_{10}=-1/4$,  $x_3=x_{11}=-1/2$,  $x_4=1$,  $x_5=1/2$,  $x_6=-1/4$,  $x_7=-1/2$.

Note that the solution $x_n$ of (37) is not k-periodic when the initial conditions satisfy $x_i=x_{i+k}$ and $x_i^4=(1-A)/B$. In this case, we have a constant sequence. Nevertheless, all the initial conditions being the same does not guarantee the existence of 1-periodic (constant) sequences. We illustrate this in Figure 5 and Figure 6.

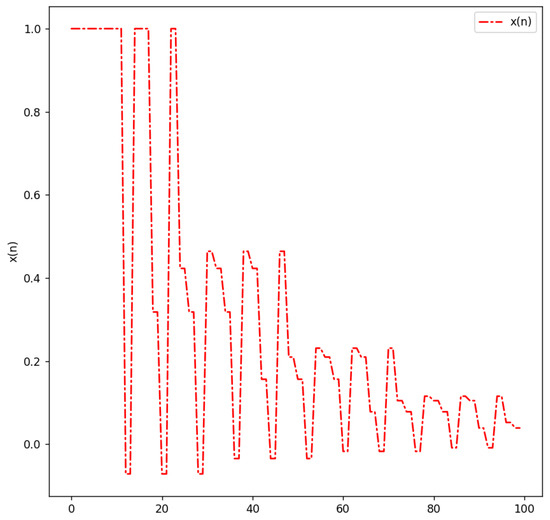
Figure 5. $x_{n+6k}=\frac{x_n{x}_{n+k}{x}_{n+2k}}{x_{n+4k}{x}_{n+5k}(2-16x_n{x}_{n+k}{x}_{n+2k}{x}_{n+3k})}$ with $x_0=x_1=x_2=x_3=x_4=x_5=x_6=x_7=x_8=x_9=x_{10}=x_{11}=1$ not satisfying $x_i^4=(1-A)/B$.

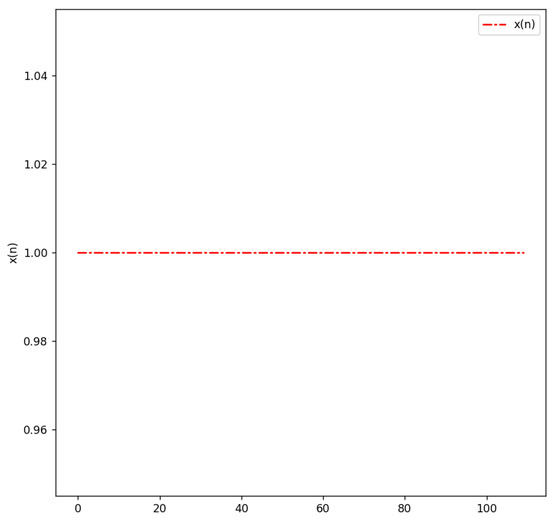
Figure 6. $x_{n+6k}=\frac{x_n{x}_{n+k}{x}_{n+2k}}{x_{n+4k}{x}_{n+5k}(2-1x_n{x}_{n+k}{x}_{n+2k}{x}_{n+3k})}$ with $x_0=x_1=x_2=x_3=x_4=x_5=x_6=x_7=x_8=x_9=x_{10}=x_{11}=1$ satisfying $x_i^4=(1-A)/B$.

5. Concluding Remarks

Although Equations (1) and (2) are the same, the solution of the later equation is obtained by backshifting the solution of the first equation $6k$ times. For example, when $k=1$ and for constant coefficients, (2) becomes

$$\begin{array}{c}\hfill x_n=\frac{x_{n-6}{x}_{n-5}{x}_{n-4}}{x_{n-2}{x}_{n-1}(A+B{x}_{n-6}{x}_{n-5}{x}_{n-4}{x}_{n-3})}\end{array}$$

and its solution, using (33) and (35), is given by (after backshifting 6 times and remembering that, in this case, $1/V_i=x_i{x}_{i+1}{x}_{i+2}{x}_{i+3}$)

$$\begin{array}{cc}\hfill x_{12kn+3r-6}=& x_{3r-6}{\displaystyle \prod _{s=0}^{n-1}}\left[\frac{A^{4s+r}(1-A-\frac{B}{V_{-6}})+\frac{B}{V_{-6}}}{A^{4s+3+r}(1-A-\frac{B}{V_{-6}})+\frac{B}{V_{-6}}}\frac{A^{4s+1+r}(1-A-\frac{B}{V_{-5}})+\frac{B}{V_{-5}}}{A^{4s+r}(1-A-\frac{B}{V_{-5}})+\frac{B}{V_{-5}}}\right.\hfill \\ & \left.\frac{A^{4s+2+r}(1-A-\frac{B}{V_{-4}})+\frac{B}{V_{-4}}}{A^{4s+1+r}(1-A-\frac{B}{V_{-4}})+\frac{B}{V_{-4}}}\right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_{12kn+3r-5}=& x_{3r-5}{\displaystyle \prod _{s=0}^{n-1}}\left[\frac{A^{4s+r}(1-A-\frac{B}{V_{-5}})+\frac{B}{V_{-5}}}{A^{4s+3+r}(1-A-\frac{B}{V_{-5}})+\frac{B}{V_{-5}}}\frac{A^{4s+1+r}(1-A-\frac{B}{V_{-4}})+\frac{B}{V_{-4}}}{A^{4s+r+2}(1-A-\frac{B}{V_{-4}})+\frac{B}{V_{-4}}}\right.\hfill \\ & \left.\frac{A^{4s+3+r}(1-A-\frac{B}{V_{-6}})+\frac{B}{V_{-6}}}{A^{4s+2+r}(1-A-\frac{B}{V_{-6}})+\frac{B}{V_{-6}}}\right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_{12n+3r-4}=& x_{3r-4}{\displaystyle \prod _{s=0}^{n-1}}\left[\frac{A^{4s+r}(1-A-\frac{B}{V_{-4}})+\frac{B}{V_{-4}}}{A^{4s+3+r}(1-A-\frac{B}{V_{-4}})+\frac{B}{V_{-4}}}\frac{A^{4s+2+r}(1-A-\frac{B}{V_{-6}})+\frac{B}{V_{-6}}}{A^{4s+r+1}(1-A-\frac{B}{V_{-6}})+\frac{B}{V_{-6}}}\right.\hfill \\ & \left.\frac{A^{4s+3+r}(1-A-\frac{B}{V_{-5}})+\frac{B}{V_{-5}}}{A^{4s+2+r}(1-A-\frac{B}{V_{-5}})+\frac{B}{V_{-5}}}\right]\hfill \end{array}$$

when $a\ne 1$; and

$$\begin{array}{cc}\hfill x_{12n+3r-6}=& x_{3r-6}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{B}{V_{-6}}\left(4s+r\right)}{1+\frac{B}{V_{-6}}\left(4s+r+3\right)}\frac{1+\frac{B}{V_{-5}}\left(4s+r+1\right)}{1+\frac{B}{V_{-5}}\left(4s+r\right)}\frac{1+\frac{B}{V_{-4}}\left(4s+r+2\right)}{1+\frac{B}{V_{-4}}\left(4s+r+1\right)}\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_{12n+3r-5}=& x_{3r-5}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{B}{V_{-5}}\left(4s+r\right)}{1+\frac{B}{V_{-5}}\left(4s+r+3\right)}\frac{1+\frac{B}{V_{-4}}\left(4s+r+1\right)}{1+\frac{B}{V_{-4}}\left(4s+r+2\right)}\frac{1+\frac{B}{V_{-6}}\left(4s+r+3\right)}{1+\frac{B}{V_{-6}}\left(4s+r+2\right)}\hfill \end{array}$$

$$\begin{array}{cc}\hfill x_{12n+3r-4}=& x_{3r-4}{\displaystyle \prod _{s=0}^{n-1}}\frac{1+\frac{B}{V_{-4}}\left(4s+r\right)}{1+\frac{B}{V_{-4}}\left(4s+r+3\right)}\frac{1+\frac{B}{V_{-6}}\left(4s+r+2\right)}{1+\frac{B}{V_{-6}}\left(4s+r+1\right)}\frac{1+\frac{B}{V_{-5}}\left(4s+r+3\right)}{1+\frac{B}{V_{-5}}\left(4s+r+2\right)}\hfill \end{array}$$

when $a=1$. This special case was studied in [6]. In fact, setting $n:=n+1$ and $r+2:=j$ yields Theorem 2.1 and Corollaries 2.2 and 2.3 in [6].