Di-Forcing Polynomials for Cyclic Ladder Graphs CL_n

Abstract

The cyclic ladder graph $C{L}_n$ is the Cartesian product of cycles $C_n$ and paths $P_2$, that is $C{L}_n=C_n\times P_2$, $(n\ge 3)$. The di-forcing polynomial of $C{L}_n$ is a binary enumerative polynomial of all perfect matching forcing and anti-forcing numbers. In this paper, we derive recursive formulas for the di-forcing polynomial of cyclic ladder graph $C{L}_n$ by classifying and counting the matching cases of the associated edges of a given vertex, from which we obtain the number of perfect matching, the forcing and anti-forcing polynomials, and the generating function and by computing some di-forcing polynomials of the lower order $C{L}_n$.

1. Introduction

In 1985, when studying the resonance structure of molecules, M. Randić and D.J. Klein [1,2] found that a Kekuler structure of the molecule can be determined via fixed partial double bonds, and the minimum number of double bonds required is called the internal degree of freedom of this Kekuler structure. F. Harary and D.J. Klein [3] called it a perfect matching for the forcing number of the graph. P. Hansen et al. [4] and F. Zhang et al. [5] independently inscribed hexagonal systems with forcing edges using different methods. H. Zhang et al. [6] characterized plane basic bipartite graphs with forcing edges. P. Adams et al. [7] proved that, in a bipartite graph of maximum degree 3, the forcing number that determines a perfect matching for it is NP-complete.

In 2004, P. Adams, M. Mahdian, and E.S. Mahmood [8] defined the forcing spectrum $Spe{c}_f\left(G\right)$ of graph G, which is the set of all perfect matching forcing numbers of graph G. H. Zhang and S. Zhao [9] proposed the forcing polynomial of a graph as a enumerative polynomial for perfect matchings with the same forcing number. In 2009, L. Zeng et al. [10] calculated the forcing number of some fullerene graphs.

In 1997, X. Li [11] studied a hexagonal system with anti-forcing edges. In 2007, D. Vhukičevć and N. Trinajstić [12] presented for the first time the anti-forcing number of a graph from the antithesis of the matching forcing, which they obtained simultaneously for the parallelogram hexagonal system and later calculated for the cata-type hexagonal system. H. Hwang, H. Lei, Y. Yeh, and H. Zhang et al. [13] introduced the concept of an enumerative polynomial—the anti-forcing polynomial for a graph. Q. Yang, H. Zhang, and Y. Lin [14] proved that the anti-forcing number of a fullerene graph is at least 4 and gave a procedure to construct all fullerene graphs with anti-forcing number 4, thus proving that the anti-forcing number of all fullerene graphs of order 26 is 5.

In 2016, H. Lei, Y. Yeh, and H. Zhang [15] introduced the concept of a perfect matching anti-forcing number for the first time; gave the anti-forcing spectrum of the graph; and pointed out that the anti-forcing number given by Vhukičevć and Trinajstić is a perfect matching minimum anti-forcing number, which is consistent with the concept of a perfect matching $\left(e\right)$-forcing of the graph proposed by D.J. Klein [16]. In 2017, L. Shi and H. Zhang [17,18] gave a new upper bound for the maximum anti-forcing number of a graph and proved that the maximum forcing number of a $(4,6)$-fullerene graph is equal to its Clar number and the maximum anti-forcing number is equal to its Fris number. K. Deng and H. Zhang [19,20] defined the anti-forcing spectrum $Spe{c}_{af}\left(G\right)$ of a graph as the set consisting of all perfect matching anti-forcing numbers of G.

In 2018, S. Zhao, H. Zhang [21] computed the anti-forcing polynomials for phenyl systems with forcing edges and benzenoidal parallelograms. Some combinatorial interpretations between the anti-forcing spectra of several classes of ladder graph, Lucas series, and Fibonacci series were obtained by Haiyuan Yao, Jebin Wang, and Zhenyun Han [22,23]. In 2019, S. Zhao and H. Zhang [24] computed the forcing polynomials and anti-forcing polynomials for lattice graphs $P_2\times P_n$ and lattice graphs $P_3\times P_{2n}$. In her PhD thesis, S. Zhao [25] obtained recurrence relations for the forcing polynomials of cata-type hexagonal systems and parallelogram hexagonal systems. In 2021, K. Deng et al. [26] studied the forcing and anti-forcing polynomials for pyrene systems and square lattice subsystems.

In 2022, Yutong Liu, Congcong Ma, and Haiyuan Yao [27] proposed the di-forcing polynomials of graphs. In this paper, we focus on the recurrence relations of di-forcing polynomials of cyclic ladder graph $C{L}_n$.

2. Preliminaries

A graph G is an ordered triple $(V\left(G\right),E\left(G\right),{\xi }_G)$ consisting of a nonempty set $V\left(G\right)$ of vertices; a set $E\left(G\right)$, disjoint from $V\left(G\right)$, of edges; and an incidence function${\xi }_G$ that associates with each edge of G an unordered pair of (not necessarily distinct) vertices of G. If e is an edge and u and v are vertices such that ${\xi }_G\left(e\right)=uv$, then e is said to join u and v; the vertices u and v are called the ends of e. A perfect matching in a graph is a set of independent edges that saturate each vertex.

Let M be a perfect matching of a graph G. If a subset S of M is not contained in any other perfect matchings, then S is called a forcing set of M. The size of the minimum forcing set of M is called the forcing number of M, denoted as $f(G,M)$. Let $S_a\subseteq E\left(G\right)\setminus M$. If M is the only perfect matching in $G-S_a$, then $S_a$ is called the anti-forcing set of M, where $G-S_a$ denotes the remaining spanning subgraph after removing all edges in the set $S_a$ from the graph G. The size of the minimum anti-forcing set of M is called the anti-forcing number of M and is denoted as $af(G,M)$. In addition, we refer to the minimum of all perfect matching forcing numbers in graph G as the minimum forcing number of G, denoted as $f\left(G\right)$. The maximum value of all perfect matching forcing numbers in graph G is called the maximum forcing number of G, denoted as $F\left(G\right)$. Similarly, the minimum and maximum values of all perfect matching anti-forcing in graph G are called the minimum and maximum anti-forcing numbers of G, respectively, and are denoted as $af\left(G\right)$ and $Af\left(G\right)$.

Let M be a perfect matching of a graph G. We say that a cycle C of G is an M-alternating cycle if the edges of the circle C alternate in M and $E\left(G\right)\setminus M$. Let $\mathcal{A}$ be the set of M-alternating cycles. If any two M-alternating cycles in $\mathcal{A}$ do not intersect or only intersect the edge in the matching M, we say that $\mathcal{A}$ is M-compatible and then that any two M-alternating cycles in $\mathcal{A}$ are M-compatible, or simply compatible. Let $c(G,M)$ and $c^{\prime }(G,M)$ be the maximum number of disjoint and compatible M-alternating cycles in the graph G, respectively, and $\mathcal{M}\left(G\right)$ be the set consisting of all perfect matchings of G.

Here is the characterization of a forcing set of M.

Lemma 1 

([28]).  Let M be a perfect matching of a graph G. Then, $S\subseteq M$ is a forcing set of M if and only if S contains at least one matching edge of every M-alternating cycle of G.

Similarly, a conclusion for an anti-forcing set is obtained.

Lemma 2 

([15]).  Let M be a perfect matching of a graph G. Then, $S_a\subseteq E\setminus M$ is an anti-forcing set of M if and only if $S_a$ contains at least one non-matching edge of every M-alternating cycle of G.

In the following, we introduce two enumerative polynomials on the number of forcing and anti-forcing for all perfect matchings of the graph.

Definition 1 

([9]).  The forcing polynomial of G is

$$F(G,x)=\sum _{M\in \mathcal{M}\left(G\right)}{x}^{f(G,M)}=\sum _{i=f\left(G\right)}^{F\left(G\right)}\omega (G,i)x^i,$$

where $\omega (G,i)$ refers to the number of perfect matchings of G with forcing number i.

Definition 2 

([21]).  The anti-forcing polynomial of G is

$$Af(G,x)=\sum _{M\in \mathcal{M}\left(G\right)}{x}^{af(G,M)}=\sum _{i=af\left(G\right)}^{Af\left(G\right)}\mu (G,i)x^i,$$

where $\mu (G,i)$ refers to the number of perfect matchings of G with anti-forcing number i.

Observing a striking similarity between the above two definitions, we naturally combine these two polynomials into a single two-variable polynomial:

Definition 3 

([27]).  Let G be a graph. The di-forcing polynomial of G is

$$Faf(G;x,y)=\sum _{M\in \mathcal{M}\left(G\right)}{x}^{f(G,M)}{y}^{af(G,M)}=\sum _{i,j}\nu (G;i,j)x^i{y}^j,$$

where $\nu (G;i,j)$ refers to the number of perfect matchings of G with forcing number i and anti-forcing number j.

Thus,

$$\left\{\begin{array}{c}F(G,x)=Faf(G;x,1);\hfill \\ Af(G,x)=Faf(G;1,x).\hfill \end{array}\right.$$

Lemma 3 

([27]).  Let G be a graph with a perfect matching M. Let $\mathcal{R}\left(G\right)$ and $s\left(M\right)$ denote the system of distinct representatives of the perfect matching equivalent classes and the cardinality of the equivalent class containing M, respectively. Then,

$$Faf(G;x,y)=\sum _{M\in \mathcal{R}\left(G\right)}s\left(M\right)x^{f(G,M)}{y}^{af(G,M)}.$$

3. Di-Forcing Polynomials for Cyclic Ladder Graphs $C{L}_n$

A ladder graph $L_n$ is shown in Figure 1. The vertices of $L_n$ are denoted $a_1,a_2,\cdots ,a_{n-2},a_{n-1},a_n,$$b_1,b_2,b_3,\cdots ,b_{n-2},b_{n-1},b_n$ from top to bottom and left to right.

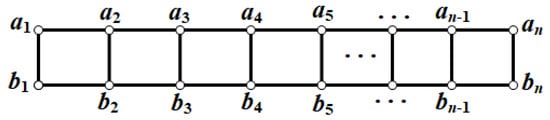
Figure 1. Ladder graph $L_n$.

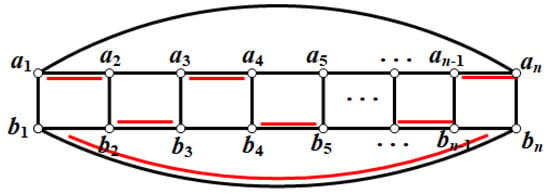
Cyclic ladder graph $C{L}_n$ is a Cartesian product of cycles $C_n$ and paths $P_2$, i.e., $C{L}_n=C_n\times P_n(n\ge 3)$. It can also be obtained from the ladder graph $L_n$ by adding edges $a_1{a}_n$ and $b_1{b}_n$. As shown in Figure 2.

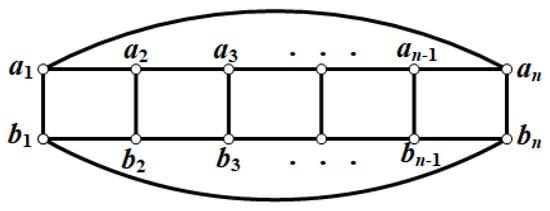
Figure 2. Cyclic ladder graph $C{L}_n$.

In a $C{L}_n$, we call the edges similar to $a_i{b}_i$ vertical edges and the edges similar to $a_i{a}_{i+1}$, $b_i{b}_{i+1}$, $a_1{a}_n$, $b_1{b}_n$ horizontal edges. Let M be a perfect matching of the cyclic ladder graph $C{L}_n$, the edges similar to $a_i{b}_i$ in M are called vertical matching edges, and the edges similar to $a_i{a}_{i+1}$, $b_i{b}_{i+1}$, $a_1{a}_n$, $b_1{b}_n$ are called horizontal matching edges. If $a_i{a}_{i+1},b_i{b}_{i+1}\in M$, we say that the cycle formed with $a_i{a}_{i+1}{b}_{i+1}{b}_i{a}_i$ is a horizontal M-alternating 4-cycle. If $a_i{b}_i,a_{i+1}{b}_{i+1}\in M$, we say that the cycle formed with $a_i{a}_{i+1}{b}_{i+1}{b}_i{a}_i$ is a vertical M-alternating 4-cycle.

Theorem 1 

([29]).  For $n\ge 3$, the number of $C{L}_n$ perfect matching is

$$\left|{\mathcal{M}}_n\right|=\left\{\begin{array}{cc}{l}_n,\hfill & \mathrm{if}2\nmid n,\hfill \\ l_n+2,\hfill & \mathrm{if}2\mid n.\hfill \end{array}\right.$$

In Theorem 1, $l_n=l_{n-1}+l_{n-2}$ is the Lucas series of recurrence relations with initial values $l_0=2,l_1=1$, and its n term sum

$$l_n=\sum _{i=0}^n\frac{n}{n-i}\left(\begin{array}{c}n-i\\ i\end{array}\right).$$

Lemma 4 

([30]).  Let M be any perfect matching of the graph G. Then, $f(G,M)\ge c(G,M).$ In particular, if the graph G is a plane bipartite graph, then $f(G,M)=c(G,M).$

Lemma 5 

([15]).  Let M be any perfect matching of the graph G. Then, $af(G,M)\ge c^{\prime }(G,M).$ In particular, if the graph G is a plane bipartite graph, then $af(G,M)=c^{\prime }(G,M).$

Lemma 6. 

Let M be a perfect matching of $C{L}_n$. Then, there exists a set of maximum disjoint M-alternating cycles that contain all horizontal M-alternating 4-cycles.

Proof. 

Let $\mathcal{A}$ be the set of disjoint M-alternating cycles that contains the maximum number of horizontal M-alternating 4-cycles; then, we assert that $\mathcal{A}$ contains all disjoint horizontal M-alternating 4-cycles.

If M is a perfect matching of all horizontal pairs of matching edges. Let $C_1^{*}$ be an M-alternating cycle that contains $a_1{a}_n$ and $C_2^{*}$ be an M-alternating cycle that contains $b_1{b}_n$. It is easy to prove that if we take the up and down M-alternating cycles, $C_1^{*}$ and $C_2^{*}$, to be a maximum disjoint M-alternating cycles set of M, there are only two $\mathcal{A}$, whereas if we take all horizontal M-alternating 4-cycles to be a maximum disjoint M-alternating cycle set of M, it contains at least two $\mathcal{A}$. This contradicts the way $\mathcal{A}$ is taken, so the assertion holds.

If M is a perfect matching that contains at least one vertical matching edge, assuming that there exists a horizontal M-alternating 4-cycle C not in $\mathcal{A}$, there must exist an M-alternating cycle $C^{*}$ intersecting C. Since the horizontal M-alternating 4-cycle in $C{L}_n$ must occur in pairs in any cycle that intersects it, $C^{*}$ and C share two horizontal matching edges. Hence, $V\left(C\right)\subseteq V\left(C^{*}\right)$, and since $C^{*}$ disjoints with other M-alternating cycles in $\mathcal{A}$,

$${\mathcal{A}}^{\prime }=\left(\mathcal{A}\setminus \left\{C^{*}\right\}\right)\cup \left\{C\right\}$$

is also a maximum disjoint M-alternating cycle set of $C{L}_n$, containing one more horizontal M-alternating 4-cycle C than $\mathcal{A}$. This contradicts the taking of $\mathcal{A}$; therefore, the assertion holds, and thus, the conclusion of the Lemma holds. □

Lemma 7. 

Let M be the perfect matching of $C{L}_n$ consisting of all vertical matching edges, i.e., $M=\left\{\left.a_i{b}_i\right|i=1,2,\dots ,n\right\}$. Then $f(C{L}_n,M)=⌈\frac{n}{2}⌉$.

Proof. 

Let us take the first vertical M-alternating 4-cycle of M as $C_1=a_1{a}_2{a}_1{b}_1{b}_2$. Then, in increasing order from the vertex labeling, take all the remaining vertical M-alternating 4-cycles, denoted as $C_1,C_2,C_3,\cdots ,C_{n-2},C_{n-1},C_n$. Obviously, if n is even, the vertical M-alternating 4-cycles of all odd subscripts disjoint each other because each M-alternating cycle contains at least two matching edges and each vertical M-alternating 4-cycle contains exactly two matching edges. So all the odd subscript M-alternating 4-cycles constitute a maximum number of disjoint M-alternating cycles set, via Lemma 4,

$$f(C{L}_n,M)=c(C{L}_n,M)=\frac{n}{2}.$$

If n is odd taking all the left matching edges of the odd subscript vertical M-alternating 4-cycles and $a_n{b}_n$, we can obtain that a minimum forcing set of M is

$$S=\left\{a_1{b}_1,a_3{b}_3,a_5{b}_5,\cdots ,a_n{b}_n\right\},$$

and it is easy to know that

$$f(C{L}_n,M)=c(C{L}_n,M)+1=\frac{n-1}{2}+1.$$

In summary, then $f(C{L}_n,M)=⌈\frac{n}{2}⌉$. □

Before giving the following lemma 8, we give an example of a perfect matching delete all horizontal M-alternating 4-cycles. Take the example of a perfect matching of $C{L}_9$ (Figure 3).

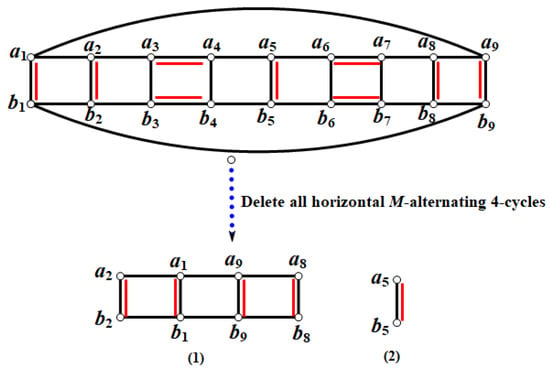
Figure 3. The $C{L}_9$ a perfect matching delete all horizontal M-alternating 4-cycles.

Where (1)–(2) denote the branches following the deletion of all horizontal M-alternating 4-cycles, which are Ladder graphs. In the branches that follow the deletion of all horizontal M-alternating 4-cycles, we call the Ladder graphs that are an odd number of vertically matched edges, odd-length Ladder graphs. In Figure 3, (1) is an even-length ladder graph and (2) is an odd-length ladder graph.

Lemma 8. 

Let M be a perfect matching of $C{L}_n$ containing at least one horizontal M-alternating 4-cycle. Then, the forcing number of M is

$$f(C{L}_n,M)=\frac{n-k_0\left(M\right)}{2},$$

where $k_0\left(M\right)$ denotes the number of branches of the odd-length Ladder subgraph obtained by deleting all horizontal M-alternating 4-cycles (i.e., deleting the four vertices of the horizontal M-alternating 4-cycles) from $C{L}_n$.

Proof. 

By Lemma 6, we can construct a maximum disjoint M-alternating cycle set of $C{L}_n$ containing all horizontal M-alternating 4-cycles, and the remaining M-alternating cycles are disjoint with all horizontal M-alternating 4-cycles, so they can be found in the subgraph obtained by deleting all horizontal M-alternating 4-cycles of $C{L}_n$. Also by Lemma 7, every two vertical matching edges from left to right in each branch form a vertical M-alternating 4-cycle, and their union with the deleted horizontal M-alternating 4-cycles forms a maximum disjoint M-alternating cycles set of $C{L}_n$. Since each odd-length branch wastes one matching edge, $k_0\left(M\right)$ matching edges are wasted in total and each M-alternating cycle in this maximum disjoint M-alternating cycle set is a 4-cycle, which contains exactly two matching edges. In summary, using Lemma 4, we can obtain that

$$f(C{L}_n,M)=c(C{L}_n,M)=\frac{n-k_0\left(M\right)}{2}.$$

□

Note: $L_n$ differs from $C{L}_n$ when deleting horizontal M-alternating 4-cycles in that $L_n$ usually has two branches after deleting the first horizontal M-alternating 4-cycle, while only one branch (ladder graph) appears after $C{L}_n$ deletion. A $C{L}_n$ deletion of the horizontal M-alternating 4-cycles is followed by a ladder graph, so its branches are all planar bipartite graphs.

From Lemmas 7 and 8, we obtain the following two corollaries.

Corollary 1. 

If M is a perfect matching of $C{L}_n$, then $f(C{L}_n,M)=c(C{L}_n,M)$, unless n is odd and M is the perfect matching of all the vertical matching edges. In the latter case, $f(C{L}_n,M)=c(C{L}_n,M)+1$.

Corollary 2. 

Let M be a perfect matching of $C{L}_n$. Then, there exists a maximum disjoint M-alternating cycle set that contains all vertical M-alternating 4-cycles.

Lemma 9 

([29]).  Let M be a perfect matching of $C{L}_n$ containing p vertical matching edges,

$1\le p\le n,p\equiv \left(2\mathrm{mod}\right)n$. Then, the anti-forcing number of M is $\frac{n+p}{2}$.

According to the proof process of Lemma 3.1.1 in [29], we can obtain the following two corollaries.

Corollary 3 

([29]).  The perfect matching of $C{L}_n$ with $2q(<n)$ horizontal matching edges has an anti-forcing number of $n-q$.

Corollary 4. 

Let M be a perfect matching of $C{L}_n$ that does not contain only one vertical matching edge. Then, there exists a maximum compatible M-alternating cycle set that contains all M-alternating 4-cycles (horizontal M-alternating 4-cycles and vertical M-alternating 4-cycles).

If n is even, $C{L}_n$ is a plane bipartite graph, and by Lemma 5, we have $af(C{L}_n,M)=c^{\prime }(C{L}_n,M)$. If n is odd, $C{L}_n$ is not a planar bipartite graph, but still satisfies $af(C{L}_n,M)=c^{\prime }(C{L}_n,M)$ via the proof of Lemma 3.1.1 and Theorem 3.1.4 in the [29], and from the proof procedure of Theorem 3.1.4 in [29], we have the following corollaries.

Lemma 10 

([29]).  Let M be a perfect matching of $C{L}_n$. Then, $af(C{L}_n,M)=c^{\prime }(C{L}_n,M).$

Corollary 5. 

Let M be a perfect matching of $C{L}_n$ containing only paired horizontal matching edges. Then, the anti-forcing number of M is $\frac{n}{2}+2$.

4. Main Conclusions

In the following, we will introduce the definition of a shrinkage M-alternating cycle in a perfect matching of $C{L}_n$.

Let M be a perfect matching of $C{L}_n$. If $a_i{a}_{i+1},b_i{b}_{i+1}\in M$. After deleting the horizontal M-alternating 4-cycle $C=a_i{a}_{i+1}{b}_{i+1}{b}_i{a}_i$ and connecting the edges (non-matching edges) between $a_{i-1}$ and $a_{i+2}$ and between $b_{i-1}$ and $b_{i+2}$, $C{L}_n$ shrinkage to $C{L}_{n-2}$. If $a_i{b}_i,a_{i+1}{b}_{i+1}\in M$, after deleting the vertical M-alternating 4-cycle $C=a_i{a}_{i+1}{b}_{i+1}{b}_i{a}_i$ and connecting the edges (non-matching edges) between $a_{i-1}$ and $a_{i+2}$ and between $b_{i-1}$ and $b_{i+2}$, $C{L}_n$ shrinkage to $C{L}_{n-2}$. If $a_i{b}_i,a_{i+1}{a}_{i+2},b_{i+1}{b}_{i+2}\in M$, after deleting the M-alternating 6-cycle $C=a_i{a}_{i+1}{a}_{i+2}{b}_{i+2}{b}_{i+1}{b}_i{a}_i$ and connecting the edges (non-matching edges) between $a_{i-1}$ and $a_{i+3}$ and between $b_{i-1}$ and $b_{i+3}$, $C{L}_n$ shrinkage to $C{L}_{n-3}$. The above operation after deleting an M-alternating 4-cycle is called a shrinkage M-alternating cycle.

The three perfect matchings shrinkage M-alternating cycles of $C{L}_8$ are shown in Figure 4 (The red line segment indicates that this edge is a matching edge. As below).

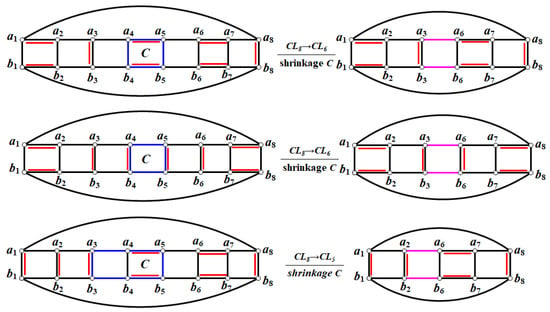
Figure 4. Shrinkage M-alternating cycle for $C{L}_8$.

In the following, we give the main conclusions of this paper.

Theorem 2. 

For $n\ge 6$, the di-forcing polynomial of the $C{L}_n$ satisfies the following recurrence relation:

$$\begin{array}{cc}\hfill Faf(C{L}_n;x,y)& =\left\{\begin{array}{c}(xy+x{y}^2)Faf(C{L}_{n-2};x,y)+x{y}^{2}Faf(C{L}_{n-3};x,y)\hfill \\ + 2x^{\frac{n}{2}}{y}^{\frac{n}{2}}(y-y^3)+2x^2{y}^3(1-xy-x{y}^2),\hfill & if2\mid n,\hfill \\ (xy+x{y}^2)Faf(C{L}_{n-2};x,y)+x{y}^{2}Faf(C{L}_{n-3};x,y)\hfill \\ + 2x^{\frac{n-1}{2}}{y}^{\frac{n-1}{2}}(y-y^3)+x^{\frac{n-1}{2}}{y}^{n-1}(1-x)-2x^3{y}^5,\hfill & if2\nmid n.\hfill \end{array}\right.\hfill \end{array}$$

Proof. 

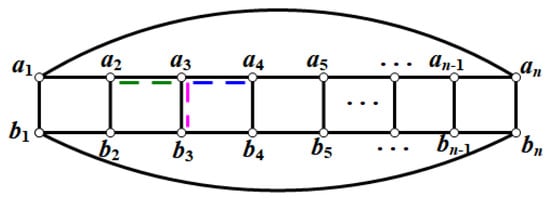
(1) If n is even, let M be any perfect matching of $C{L}_n$, and we discuss the matching based on the vertex $a_3$-associated edges as follows (Figure 5).

Figure 5. Three cases on the associating edge of vertex $a_3$.

Case 1. $a_3{a}_4\in M$.

Subcase 1.1. If $b_2{b}_3\in M$, M is a perfect matching of all horizontal matching edges that are not paired. As shown in Figure 6.

Figure 6. A perfect matching with unpaired horizontal matching edges.

We take a minimum forcing set $S=\left\{a_1{a}_2,b_2{b}_3\right\}$ of M, a maximum disjoint M-alternating cycle set $\mathcal{A}=\left\{C_a,C_b\right\}$, the minimum anti-forcing set

$$S^{\prime }=\left\{a_2{a}_3,a_2{b}_2,b_1{b}_2\right\},$$

a maximum compatible M-alternating cycle set

$${\mathcal{A}}^{\prime }=\left\{C_a,C_b,C_{ab}\right\},$$

where

$$C_a=a_1{a}_2\cdots a_n{a}_1,C_b=b_1{b}_2\cdots b_n{b}_1,C_{ab}=a_1{a}_2{b}_2{b}_3\cdots a_{n-1}{a}_n{b}_n{b}_1{a}_1.$$

Hence, by Corollary 1 and Lemma 10, its partial di-forcing polynomial is

$$x^2{y}^3.$$

Subcase 1.2. If $b_3{b}_4\in M$, then $C_1=a_3{a}_4{b}_4{b}_3{a}_3$ constitutes a horizontal M-alternating 4-cycle.

Subcase 1.2.1. If the numbers of vertical matching edges on the left and right sides of $C_1$ to the number between the next pair of horizontal matching are not all odd or if there is at least one pair of horizontal matching edges on the left side of $C_1$ to the right side, we shrinkage $C_1$. On the one hand, using Lemma 6, there exists a maximum disjoint M-alternating cycle set of $C{L}_n$ contains $C_1$ and the rest of the M-alternating cycles are disjoint from $C_1$, which are found in the subgraphs following the shrinkage of $C{L}_n$ using $C_1$. Hence, $C_1$ contributes 1 to the maximum disjoint M-alternating cycle set, and by Corollary 1, $C_1$ contributes 1 to the forcing number of M. On the other hand, if M is a perfect matching of all horizontal pairs of matching edges, then using Corollary 5, the shrinkage of $C_1$ reduces a pair of horizontal matching edges, the anti-forcing number of a perfect matching of subgraph $C{L}_{n-2}$ can be obtained as $\frac{n}{2}+1$. If M is not a perfect matching of all horizontal pairs of matching edges, using Lemma 9, the anti-forcing number of perfect matching of $C{L}_n$ is

$$n-q,$$

and the shrinkage of $C_1$ reduces $C{L}_n$ via a pair of horizontally matched edges, which leads to the anti-forcing number of a perfect matching of subgraph $C{L}_{n-2}$ being

$$n-q-1.$$

Hence, the anti-forcing number of $C_1$ on M contributes 1. In addition, after the shrinkage of $C_1$, $C{L}_{n-2}$ does not contain a perfect matching for Subcase 1.1.

In summary, there is a partial di-forcing polynomial

$$\begin{array}{c}\hfill xy(Fa{f}_1(C{L}_{n-2};x,y)-x^2{y}^3),\end{array}$$

where the shrinkage subgraphs are not renumbered using the numbering of $C{L}_n$ perfect matching (as below), and it contains the subgraphs $C{L}_{n-2}$ in which the perfect matching is

$$\begin{array}{cc}\hfill & a_2{a}_5,b_2{b}_5\notin M,a_1{a}_2,b_1{b}_2,a_5{a}_6,b_5{b}_6\in M;\hfill \\ & a_2{a}_5,b_2{b}_5\notin M,a_5{a}_6,b_5{b}_6\in M;\hfill \\ & a_2{a}_5,b_2{b}_5\notin M,a_1{a}_2,b_1{b}_2\in M;\hfill \\ & a_2{a}_5,b_2{b}_5\notin M,a_2{b}_2,a_5{b}_5\in M.\hfill \end{array}$$

Subcase 1.2.2. If the numbers of vertical matching edges on the left and right sides of $C_1$ to the number between the next pair of horizontal matching are all odd, since the vertical matching edges on both sides of $C_1$ after the shrinkage of $C_1$ form a new M-alternating 4-cycle, using Corollary 1, the forcing number of $C{L}_n$ does not change before and after the shrinkage. In this situation, we shrinkage the M-alternating 6-cycle formed using $C_2=a_2{b}_2{b}_3{b}_4{a}_4{a}_3{a}_2$. On the one hand, $a_2{b}_2$ in $C_2$ has practically no effect on the forcing number of M. According to Lemma 6, there exists a maximum disjoint M-alternating cycle set of $C{L}_n$ that contains $C_1$ and the rest of the M-alternating cycles are disjoint from $C_1$, which are found in the subgraphs following the shrinkage of $C{L}_n$ via $C_2$. Hence, $C_2$ contributes 1 to the maximum disjoint M-alternating cycle set, and using Corollary 1, $C_2$ contributes 1 to the forcing number of M. On the other hand, using Lemma 9, the anti-forcing number of a perfect matching of $C{L}_n$ is

$$\frac{n+p}{2}.$$

The shrinkage of $C_2$ reduces one pair of horizontal matching edges with one vertical matching edge, and the anti-forcing number of a perfect matching of subgraph $C{L}_{n-2}$ is

$$\frac{(n-3)+(p-1)}{2}=\frac{n+p}{2}-2.$$

Hence, the anti-forcing number of $C_2$ to M contributes 2.

In summary, there is a partial di-forcing polynomial

$$\begin{array}{c}\hfill x{y}^{2}Fa{f}_2(C{L}_{n-3};x,y),\end{array}$$

where it contains the perfect matching of $C{L}_{n-3}$ is

$$a_1{a}_5,b_1{b}_5\notin M,a_5{b}_5\in M.$$

Case 2. $a_3{b}_3\in M$. There are three Subcases, as follows.

Subcase 2.1. If $a_1{a}_2,b_1{b}_2,a_4{b}_4\in M$, then $C_3=a_3{b}_3{b}_4{a}_4{a}_3$ is a vertical M-alternating 4-cycle, and we shrinkage $C_3$. On the one hand, using Corollary 2, there exists a maximum disjoint M-alternating cycle set of $C{L}_n$ contains $C_3$ and the rest of the M-alternating cycles are disjoint from $C_3$, which are found in the subgraphs following the shrinkage of $C{L}_n$ using $C_3$. Hence, $C_3$ contributes 1 to the maximum disjoint M-alternating cycle set, and via Corollary 1, $C_3$ contributes 1 to the forcing number of M. On the other hand, the shrinkage of $C_3$ reduces $C{L}_n$ by two vertical matching edges, and thus according to Lemma 9, the anti-forcing number of a perfect matching of subgraph $C{L}_{n-2}$ is $(\frac{n+p}{2}-2)$. Hence, $C_3$ contributes 2 to the anti-forcing number of M.

In addition, if M is a perfect matching containing only one pair of vertical matching edges, and the rest are all horizontal matching edges, using Corollary 1 and Lemma 9, its di-forcing polynomial is

$$x^{\frac{n}{2}}{y}^{\frac{n}{2}+1}.$$

After the shrinkage of $C_3$, the subgraph $C{L}_{n-2}$ contains a perfect matching with all horizontal matching edges, and its partial di-forcing polynomial is

$$x^{\frac{n}{2}-1}{y}^{\frac{n}{2}+1}.$$

Obviously, there is no change in the number of anti-forcing before and after the shrinkage, so it is not possible to shrinkage $C_3$. On the other hand, after the shrinkage of $C_3$, the subgraph does not contain the perfect matching of Subcase 1.1.

In summary, there is a partial di-forcing polynomial

$$\begin{array}{c}\hfill x{y}^2(Fa{f}_3(C{L}_{n-2};x,y)-x^{\frac{n}{2}-1}{y}^{\frac{n}{2}+1}-x^2{y}^3)+x^{\frac{n}{2}}{y}^{\frac{n}{2}+1},\end{array}$$

where it contains the perfect matching of $C{L}_{n-2}$ is

$$\begin{array}{cc}\hfill & a_2{a}_5,b_2{b}_5\notin M,a_1{a}_2,b_1{b}_2\in M;\hfill \\ & a_3{b}_3,a_4{b}_4\in M,a_i{a}_{i+1},b_i{b}_{i+1}\in M(i=5,6,7,\cdots ,n,1,2).\hfill \end{array}$$

Subcase 2.2. If $a_2{b}_2\in M$, and $a_4{a}_5\in M$ or $a_4{b}_4\in M$, then $C_4=a_2{b}_2{b}_3{a}_3{a}_2$ is a vertical M-alternating 4-cycle, we shrinkage $C_4$. Similarly to the proof process of Subcase 2.1, it can be concluded that there is a partial di-forcing polynomial

$$\begin{array}{c}\hfill x{y}^2(Fa{f}_4(C{L}_{n-2};x,y)-x^{\frac{n}{2}-1}{y}^{\frac{n}{2}+1}-x^2{y}^3)+x^{\frac{n}{2}}{y}^{\frac{n}{2}+1},\end{array}$$

where it contains the perfect matching of $C{L}_{n-2}$, which is

$$\begin{array}{cc}\hfill & a_1{a}_4,b_1{b}_4\notin M,a_4{a}_5,b_4{b}_5\in M;\hfill \\ & a_1{a}_4,b_1{b}_4\notin M,a_4{b}_4\in M;\hfill \\ & a_2{b}_2,a_3{b}_3\in M,a_i{a}_{i+1},b_i{b}_{i+1}\in M(i=4,5,6,\cdots ,n,1).\hfill \end{array}$$

Subcase 2.3. If $a_1{a}_2,a_4{a}_5\in M$, then $C^{\prime }=a_1{a}_2{b}_2{b}_1{a}_1$ is a horizontal M-alternating 4-cycle. Since $a_3{b}_3$ is vertical matching of a single edge, we cannot shrinkage $a_3{b}_3$ directly. In this situation, we shrinkage the M-alternating 6-cycle formed by $C_5=a_1{a}_2{a}_3{b}_3{b}_2{b}_1{a}_1.$ On the one hand, $a_3{b}_3$ in $C_5$ has practically no effect on the forcing number of M. Therefore, according to Lemma 6, there exists a set of maximum disjoint M-alternating cycles of $C{L}_n$ contains $C^{\prime }$ and the rest of the M-alternating cycles are disjoint from $C^{\prime }$, which are found in the subgraphs of the $C{L}_n$ shrinkage after $C_5$. Hence, $C_5$ contributes 1 to the set of maximum disjoint M-alternating cycles of M. Via Corollary 1, the forcing number of $C_5$ to M contributes 1. On the other hand, according to Lemma 9, the anti-forcing number of a perfect matching of $C{L}_n$ is $\frac{n+p}{2}$. The shrinkage of $C_5$ reduces one pair of horizontal matching edges with one vertical matching edge, and the anti-forcing number of a perfect matching of subgraph $C{L}_{n-2}$ is $(\frac{n+p}{2}-2).$ Hence, the anti-forcing number of $C_5$ to M contributes 2.

In summary, there is a partial di-forcing polynomial

$$\begin{array}{c}\hfill x{y}^{2}Fa{f}_5(C{L}_{n-3};x,y)\end{array}$$

where it contains the perfect matching of $C{L}_{n-3}$ is

$$\begin{array}{c}\hfill a_4{a}_n,b_4{b}_n\notin M,a_5{a}_5\in M.\end{array}$$

Case 3. $a_2{a}_3\in M$. From the structure of Cyclic ladder graphs, we easily know that $a_2{a}_3$ is the same as the $a_3{a}_4$ situation, and the proof procedure is similar. Hence, we only state the cases of a perfect matching of the shrinkage subgraphs and their corresponding di-forcing polynomials.

Subcase 3.1. If $b_1{b}_2\in M$, M is a perfect matching of all horizontal matching edges that are not paired, its partial di-forcing polynomial is

$$x^2{y}^3.$$

Subcase 3.2. If $b_2{b}_3\in M$, then $C_6=a_2{a}_3{b}_3{b}_2{a}_2$ is a horizontal M-alternating 4-cycle and $C_7=a_2{a}_3{a}_4{b}_4{b}_3{b}_2{a}_2$ is a vertical M-alternating 4-cycle. It follows from the classification of Subcase 1.2 that we shrinkage $C_6$ and $C_7$, respectively. Different from Subcase 1.2: The number of perfect matchings of all vertical matching edges in $C{L}_n$ is 1, and 1 has been contributed in Subcase 1.2. Hence, for Subcase 3.2, we shrinkage $C_7$ to be a perfect matching of all vertical matching edges in subgraph $C{L}_{n-3}$. From Corollary 1 and Lemma 9, it follows that after shrinkage $C_7$, $C_7$ contributes 1 to the forcing number of M and 2 to the anti-forcing number.

Hence, there is a partial di-forcing polynomial

$$\begin{array}{c}\hfill xy(Fa{f}_6(C{L}_{n-2};x,y)-x^2{y}^3)+x{y}^{2}Fa{f}_7(C{L}_{n-3};x,y)\end{array}$$

where it contains the perfect matching of $C{L}_{n-2}$ is

$$\begin{array}{cc}\hfill & a_1{a}_4\notin M,a_1{a}_n,a_4{a}_5\in M;\hfill \\ & a_1{a}_4\notin M,a_4{a}_5\in M;\hfill \\ & a_1{a}_4\notin M,a_1{a}_n\in M;\hfill \\ & a_1{a}_4\notin M,a_1{b}_1,a_4{b}_4\in M.\hfill \end{array}$$

It contains the perfect matching of $C{L}_{n-3}$, which is

$$\begin{array}{cc}\hfill & a_1{a}_5\notin M,a_i{b}_i\in M(i=5,6,\cdots ,n,1);\hfill \\ & a_1{a}_5,b_1{b}_5\notin M,a_1{b}_1\in M.\hfill \end{array}$$

In summary of Cases 1–3, the di-forcing polynomial of $C{L}_n$ is

$$\begin{array}{cc}\hfill Faf(C{L}_n;x,y)& =xy(Fa{f}_1(C{L}_{n-2};x,y)+Fa{f}_6(C{L}_{n-2};x,y))+x{y}^2(Fa{f}_3(C{L}_{n-2};x,y)\hfill \\ & +Fa{f}_4(C{L}_{n-2};x,y))+x{y}^2(Fa{f}_2(C{L}_{n-3};x,y)+Fa{f}_7(C{L}_{n-3};x,y)\hfill \\ & +Fa{f}_5(C{L}_{n-3};x,y))+2x^{\frac{n}{2}}{y}^{\frac{n}{2}+1}-2x^{\frac{n}{2}}{y}^{\frac{n}{2}+3}+2x^2{y}^3-2x^3{y}^4-2x^3{y}^5.\hfill \end{array}$$

We have verified that

$(Fa{f}_1(C{L}_{n-2};x,y)+Fa{f}_6(C{L}_{n-2};x,y)+2x^2{y}^3)$ just happens to be the di-forcing polynomial of $C{L}_{n-2}$;

$(Fa{f}_3(C{L}_{n-2};x,y)+Fa{f}_4(C{L}_{n-2};x,y)+2x^2{y}^3)$ just happens to be the di-forcing polynomial of $C{L}_{n-2}$;

$(Fa{f}_2(C{L}_{n-3};x,y)+Fa{f}_7(C{L}_{n-3};x,y)+Fa{f}_5(C{L}_{n-3};x,y))$ just happens to be the di-forcing polynomial of $C{L}_{n-3}$.

Hence, we simplify the above equation to obtain the di-forcing polynomial of $C{L}_n$ as

$$\begin{array}{cc}\hfill Faf(C{L}_n;x,y)& =(xy+x{y}^2)Faf(C{L}_{n-2};x,y)+x{y}^{2}Faf(C{L}_{n-3};x,y)\hfill \\ & +2x^{\frac{n}{2}}{y}^{\frac{n}{2}}(y-y^3)+2x^2{y}^3(1-xy-x{y}^2).\hfill \end{array}$$

(2) If n is odd, similar to the above procedure of proving that n is even, the di-forcing polynomial of $C{L}_n$ can be obtained as

$$\begin{array}{cc}\hfill Faf& (C{L}_n;x,y)=xyFaf(C{L}_{n-2};x,y)+x{y}^{2}Faf(C{L}_{n-2};x,y)+x{y}^{2}Faf(C{L}_{n-3};x,y)\hfill \\ & -xy\left(x^{\frac{n-1}{2}}{y}^{n-2}\right)+x^{\frac{n-1}{2}}{y}^{n-1}-x{y}^2\left(2x^{\frac{n-3}{2}}{y}^{\frac{n-1}{2}+1}\right)+2x^{\frac{n-1}{2}}{y}^{\frac{n-1}{2}+1}-x{y}^2\left(2x^2{y}^3\right).\hfill \end{array}$$

Among them, the number of vertical matching edges in $C{L}_n$ is odd if n is odd. The perfect matching contains only one pair of horizontal matching edges, with the rest being all vertical matching, $C{L}_n$ has no change in the number of forcing of M after shrinkage the horizontal M-alternating 4-cycle, so this perfect matching is not included in the subgraph after shrinkage the horizontal M-alternating 4-cycle. Hence, from Lemmas 8 and 9, the partial di-forcing polynomial is

$$\begin{array}{c}\hfill x^{\frac{n-1}{2}}{y}^{n-1}-xy\left(x^{\frac{n-1}{2}}{y}^{n-2}\right).\end{array}$$

On the other hand, if M contains only one vertical matching edge and the rest are perfect matching with all horizontal matching edges, the anti-forcing number of M does not change after shrinkage the M-alternating 6-cycle. Thus, the shrinkage subgraph does not contain perfect matching with all horizontal pairs of matching edges. Since n is odd but $(n-3)$ is even, there is no perfect matching of all horizontal unpairs if n is odd. Hence, using Lemmas 8 and 9, the partial di-forcing polynomial is

$$\begin{array}{c}\hfill 2x^{\frac{n-1}{2}}{y}^{\frac{n-1}{2}+1}-x{y}^2(2x^{\frac{n-3}{2}}{y}^{\frac{n-1}{2}+1}-2x^2{y}^3).\end{array}$$

In summary, by simplifying, the di-forcing polynomial of $C{L}_n$ is

$$\begin{array}{cc}\hfill Faf(C{L}_n;x,y)& =(xy+x{y}^2)Faf(C{L}_{n-2};x,y)+x{y}^{2}Faf(C{L}_{n-3};x,y)\hfill \\ & +2x^{\frac{n-1}{2}}{y}^{\frac{n-1}{2}}(y-y^3)+x^{\frac{n-1}{2}}{y}^{n-1}(1-x)-2x^3{y}^5.\hfill \end{array}$$

Hence, using (1) and (2), for $n\ge 6$, the di-forcing polynomial of $C{L}_n$ satisfies the following recurrence relation:

$$\begin{array}{cc}\hfill Faf(C{L}_n;x,y)& =\left\{\begin{array}{c}(xy+x{y}^2)Faf(C{L}_{n-2};x,y)+x{y}^{2}Faf(C{L}_{n-3};x,y)\hfill \\ + 2x^{\frac{n}{2}}{y}^{\frac{n}{2}}(y-y^3)+2x^2{y}^3(1-xy-x{y}^2),\hfill & \mathrm{if}2\mid n,\hfill \\ (xy+x{y}^2)Faf(C{L}_{n-2};x,y)+x{y}^{2}Faf(C{L}_{n-3};x,y)\hfill \\ + 2x^{\frac{n-1}{2}}{y}^{\frac{n-1}{2}}(y-y^3)+x^{\frac{n-1}{2}}{y}^{n-1}(1-x)-2x^3{y}^5,\hfill & \mathrm{if}2\nmid n.\hfill \end{array}\right.\hfill \end{array}$$

□

In the following, we give important corollaries that follow from Theorem 2.

Corollary 6. 

For $n\ge 4$, the number of perfect matching of $C{L}_n$ is

$$\left|{\mathcal{M}}_n\right|=2\left|{\mathcal{M}}_{n-2}\right|+\left|{\mathcal{M}}_{n-3}\right|-2.$$

Corollary 7. 

For $n\ge 6$, there is

$$\begin{array}{c}\hfill F\left(C{L}_n,x\right)=2xF\left(C{L}_{n-2},x\right)+xF\left(C{L}_{n-3},x\right)+\phi \left(n\right),\end{array}$$

where

$$\begin{array}{c}\hfill \mathit{if}n\mathit{is}\mathit{even},\phi \left(n\right)=2x^2(1-2x);\mathit{if}n\mathit{is}\mathit{odd},\phi \left(n\right)=x^{\frac{n-1}{2}}(1-x)-2x^3.\end{array}$$

Corollary 8. 

For $n\ge 6$, there is

$$\begin{array}{cc}\hfill Af(C{L}_n,x)& =(x+x^2)Af(C{L}_{n-2},x)+x^{2}Af(C{L}_{n-3},x)-2x^5+\psi \left(n\right),\hfill \end{array}$$

where

$$\begin{array}{c}\hfill \mathit{if}n\mathit{is}\mathit{even},\psi \left(n\right)=2(1-x)(x^{\frac{n+2}{2}}(1+x)+x^3);\mathit{if}n\mathit{is}\mathit{odd},\psi \left(n\right)=2x^{\frac{n-1}{2}}(x-x^3).\end{array}$$

Theorem 3. 

The generating function of ${\left\{Faf(C{L}_n;x,y)\right\}}_{n\ge 3}$ is

$$\begin{array}{c}\hfill P(x,y,z)=\frac{D(x,y,z)}{(-1+z)(1+z)(-1+xy{z}^2)(-1+x{y}^2{z}^2)(-1+xy{z}^2(1+y+yz))},\end{array}$$

where

$$\begin{array}{cc}\hfill D(x,y,z)& =-(x{y}^2{z}^3(2x^4{y}^5{z}^7(1+y+yz)+3(-1+z^2)-xy(1+3(2+y)z-(2+y)z^2\hfill \\ & -(4+3y)z^3+(1+y)z^4)+x^3{y}^3{z}^4(-1-2z+z^2+2y^3(-1+z)z{(1+z)}^2\hfill \\ & +y^{2}z(-5-3z+3z^2+z^3)+y(-1-8z-z^2+2z^3))+x^2{y}^2{z}^2(y^{2}z(5+3z-5z^2\hfill \\ & -3z^3)-2(-1-3z+z^2+z^3)+y(1+11z+2z^2-7z^3-z^4)))).\hfill \end{array}$$

Proof. 

From Theorem 2,

$$\begin{array}{cc}\hfill P& (x,y,z)=\sum _{n=3}^{\infty }Faf(C{L}_n;x,y)z^n\hfill \\ & =\sum _{n=3}^{5}Faf(C{L}_n;x,y)z^n+\sum _{n=6}^{\infty }Faf(C{L}_n;x,y)z^n\hfill \\ & =\sum _{n=6}^{\infty }((x{y}^2+xy)Faf(C{L}_{n-2};x,y)+x{y}^{2}Faf(C{L}_{n-3};x,y)-2x^3{y}^5)z^n\hfill \\ & +\sum _{n=3}^{5}Faf(C{L}_n;x,y)z^n+\sum _{n=3}^{\infty }(2x^n{y}^n(y-y^3)+2x^2{y}^3(1-xy))z^{2n}\hfill \\ & +\sum _{n=3}^{\infty }(x^n{y}^{2n}(1-x)+2x^n{y}^n(y-y^3))z^{2n+1}\hfill \\ & =(x{y}^2+xy)\sum _{n=6}^{\infty }Faf(C{L}_{n-2};x,y)z^n+x{y}^2\sum _{n=6}^{\infty }Faf(C{L}_{n-3};x,y)z^n-2x^3{y}^5\sum _{n=6}^{\infty }{z}^n\hfill \\ & +\sum _{n=3}^{\infty }(2x^n{y}^n(y-y^3)+2x^2{y}^3(1-xy))z^{2n}+\sum _{n=3}^{\infty }(x^n{y}^{2n}(1-x)+2x^n{y}^n(y-y^3))z^{2n+1}\hfill \\ & +\sum _{n=3}^{5}Faf(C{L}_n;x,y)z^n\hfill \\ & =(x{y}^2+xy)z^2\sum _{n=3}^{\infty }Faf(C{L}_n;x,y)z^n+x{y}^2{z}^3\sum _{n=3}^{\infty }Faf(C{L}_n;x,y)z^n-2x^3{y}^5\sum _{n=6}^{\infty }{z}^n\hfill \\ & -(x{y}^2+xy)z^{2}Faf(C{L}_3;x,y)z^3+\sum _{n=3}^{\infty }(2x^n{y}^n(y-y^3)+2x^2{y}^3(1-xy))z^{2n}\hfill \\ & +\sum _{n=3}^{\infty }(x^n{y}^{2n}(1-x)+2x^n{y}^n(y-y^3))z^{2n+1}+\sum _{n=3}^{5}Faf(C{L}_n;x,y)z^n\hfill \\ & =((x{y}^2+xy)z^2+x{y}^2{z}^3)\sum _{n=3}^{\infty }Faf(C{L}_n;x,y)z^n+x{y}^2{z}^3(-x^2{y}^2{z}^2+2x{y}^2{z}^2+3x{y}^{2}z\hfill \\ & +2xy{z}^2+6xyz+xy+3)+\frac{2x^3{y}^5{z}^6}{z-1}+\frac{2x^2{y}^3{z}^6(x^2{y}^2{z}^2+x{y}^3(z^2-1)-2xy{z}^2+1)}{(z^2-1)(xy{z}^2-1)}\hfill \\ & +\frac{x^3{y}^4{z}^7(2x{y}^4{z}^2+(x-1)x{y}^3{z}^2-y^2(2x{z}^2+x+1)+2)}{(xy{z}^2-1)(x{y}^2{z}^2-1)}.\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill (1-(x{y}^2+xy)z^2& -x{y}^2{z}^3)\sum _{n=3}^{\infty }Faf(C{L}_n;x,y)z^n\hfill \\ & =x{y}^2{z}^3(-x^2{y}^2{z}^2+2x{y}^2{z}^2+3x{y}^{2}z+2xy{z}^2+6xyz+xy+3)\hfill \\ & +\frac{2x^3{y}^5{z}^6}{z-1}+\frac{2x^2{y}^3{z}^6(x^2{y}^2{z}^2+x{y}^3(z^2-1)-2xy{z}^2+1)}{(z^2-1)(xy{z}^2-1)}\hfill \\ & +\frac{x^3{y}^4{z}^7(2x{y}^4{z}^2+(x-1)x{y}^3{z}^2-y^2(2x{z}^2+x+1)+2)}{(xy{z}^2-1)(x{y}^2{z}^2-1)},\hfill \end{array}$$

simplify to obtain

$$\begin{array}{cc}\hfill & \sum _{n=3}^{\infty }Faf(C{L}_n;x,y)z^n\hfill \\ & =\frac{D(x,y,z)}{(-1+z)(1+z)(-1+xy{z}^2)(-1+x{y}^2{z}^2)(-1+xy{z}^2(1+y+yz))},\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill D(x,y,z)& =-(x{y}^2{z}^3(2x^4{y}^5{z}^7(1+y+yz)+3(-1+z^2)-xy(1+3(2+y)z-(2+y)z^2\hfill \\ & -(4+3y)z^3+(1+y)z^4)+x^3{y}^3{z}^4(-1-2z+z^2+2y^3(-1+z)z{(1+z)}^2\hfill \\ & +y^{2}z(-5-3z+3z^2+z^3)+y(-1-8z-z^2+2z^3))+x^2{y}^2{z}^2(y^{2}z(5+3z-5z^2\hfill \\ & -3z^3)-2(-1-3z+z^2+z^3)+y(1+11z+2z^2-7z^3-z^4)))).\hfill \end{array}$$

□

Note that the di-forcing polynomials for the $C{L}_3$ to $C{L}_{19}$ are listed below:

$$\begin{array}{cc}\hfill Faf(C{L}_3;x,y)& =3x{y}^2+x^2{y}^3.\hfill \\ \hfill Faf(C{L}_4;x,y)& =6x^2{y}^3+3x^2{y}^4.\hfill \\ \hfill Faf(C{L}_5;x,y)& =5x^2{y}^3+5x^2{y}^4+x^3{y}^5.\hfill \\ \hfill Faf(C{L}_6;x,y)& =2x^2{y}^3+3x^2{y}^4+6x^3{y}^4+8x^3{y}^5+x^3{y}^6.\hfill \\ \hfill Faf(C{L}_7;x,y)& =7x^3{y}^4+14x^3{y}^5+7x^3{y}^6+x^4{y}^7.\hfill \\ \hfill Faf(C{L}_8;x,y)& =2x^2{y}^3+8x^3{y}^5+8x^4{y}^5+8x^3{y}^6+14x^4{y}^6+8x^4{y}^7+x^4{y}^8.\hfill \\ \hfill Faf(C{L}_9;x,y)& =9x^4{y}^5+3x^3{y}^6+27x^4{y}^6+27x^4{y}^7+9x^4{y}^8+x^5{y}^9.\hfill \\ \hfill Faf(C{L}_{10};x,y)& =2x^2{y}^3+15x^4{y}^6+10x^5{y}^6+30x^4{y}^7+22x^5{y}^7+15x^4{y}^8+20x^5{y}^8\hfill \\ & +10x^5{y}^9+x^5{y}^{10}.\hfill \\ \hfill Faf(C{L}_{11};x,y)& =11x^5{y}^6+11x^4{y}^7+44x^5{y}^7+11x^4{y}^8+66x^5{y}^8+44x^5{y}^9\hfill \\ & +11x^5{y}^{10}+x^6{y}^{11}.\hfill \\ \hfill Faf(C{L}_{12};x,y)& =2x^2{y}^3+24x^5{y}^7+12x^6{y}^7+3x^4{y}^8+72x^5{y}^8+32x^6{y}^8\hfill \\ & +72x^5{y}^9+40x^6{y}^9+24x^5{y}^{10}+30x^6{y}^{10}+12x^6{y}^{11}+x^6{y}^{12}.\hfill \\ \hfill Faf(C{L}_{13};x,y)& =x^7{y}^{13}+13x^6{y}^{12}+65x^6{y}^{11}+130x^6{y}^{10}+130x^6{y}^9+65x^6{y}^8+13x^6{y}^7\hfill \\ & +26x^5{y}^{10}+52x^5{y}^9+26x^5{y}^8.\hfill \\ \hfill Faf(C{L}_{14};x,y)& =x^7{y}^{14}+14x^7{y}^{13}+42x^7{y}^{12}+70x^7{y}^{11}+70x^7{y}^{10}+44x^7{y}^9+14x^7{y}^8\hfill \\ & +35x^6{y}^{12}+140x^6{y}^{11}+210x^6{y}^{10}+140x^6{y}^9+35x^6{y}^8+14x^5{y}^{10}\hfill \\ & +14x^5{y}^9+2x^2{y}^3.\hfill \\ \hfill Faf(C{L}_{15};x,y)& =x^8{y}^{15}+15x^7{y}^{14}+90x^7{y}^{13}+225x^7{y}^{12}+300x^7{y}^{11}+225x^7{y}^{10}\hfill \\ & +90x^7{y}^9+15x^7{y}^8+50x^6{y}^{12}+150x^6{y}^{11}+150x^6{y}^{10}+50x^6{y}^9+3x^5{y}^{10}.\hfill \\ \hfill Faf(C{L}_{16};x,y)& =x^8{y}^{16}+16x^8{y}^{15}+56x^8{y}^{14}+112x^8{y}^{13}+140x^8{y}^{12}+112x^8{y}^{11}\hfill \\ & +58x^8{y}^{10}+16x^8{y}^9+48x^7{y}^{14}+240x^7{y}^{13}+480x^7{y}^{12}+480x^7{y}^{11}\hfill \\ & +240x^7{y}^{10}+48x^7{y}^9+40x^6{y}^{12}+80x^6{y}^{11}+40x^6{y}^{10}+2x^2{y}^3.\hfill \\ \hfill Faf(C{L}_{17};x,y)& =x^9{y}^{17}+17x^8{y}^{16}+119x^8{y}^{15}+357x^8{y}^{14}+595x^8{y}^{13}+595x^8{y}^{12}\hfill \\ & +357x^8{y}^{11}+119x^8{y}^{10}+17x^8{y}^9+85x^7{y}^{14}+340x^7{y}^{13}+510x^7{y}^{12}\hfill \\ & +340x^7{y}^{11}+85x^7{y}^{10}+17x^6{y}^{12}+17x^6{y}^{11}.\hfill \\ \hfill Faf(C{L}_{18};x,y)& =x^9{y}^{18}+18x^9{y}^{17}+72x^9{y}^{16}+168x^9{y}^{15}+252x^9{y}^{14}+252x^9{y}^{13}\hfill \\ & +168x^9{y}^{12}+74x^9{y}^{11}+18x^9{y}^{10}+63x^8{y}^{16}+378x^8{y}^{15}+945x^8{y}^{14}\hfill \\ & +1260x^8{y}^{13}+945x^8{y}^{12}+378x^8{y}^{11}+63x^8{y}^{10}+90x^7{y}^{14}+270x^7{y}^{13}\hfill \\ & +270x^7{y}^{12}+90x^7{y}^{11}+3x^6{y}^{12}+2x^2{y}^3.\hfill \\ \hfill Faf(C{L}_{19};x,y)& =x^{10}{y}^{19}+19x^9{y}^{18}+152x^9{y}^{17}+532x^9{y}^{16}+1064x^9{y}^{15}+1330x^9{y}^{14}\hfill \\ & +1064x^9{y}^{13}+532x^9{y}^{12}+152x^9{y}^{11}+19x^9{y}^{10}+133x^8{y}^{16}+665x^8{y}^{15}\hfill \\ & +1330x^8{y}^{14}+1330x^8{y}^{13}+665x^8{y}^{12}+133x^8{y}^{11}+57x^7{y}^{14}+114x^7{y}^{13}\hfill \\ & +57x^7{y}^{12}.\hfill \end{array}$$