Non-Convex Optimization: Using Preconditioning Matrices for Optimally Improving Variable Bounds in Linear Relaxations
Abstract
1. Introduction
2. Background
2.1. Intervals
2.2. Linear Systems
3. Example: Contracting a Linear System
4. Toward an Optimal Contraction of Non-Square Linear Systems
4.1. Improving the Gauss-Pivoting Heuristic
4.2. Linear-Based Preconditioning
4.2.1. Minimizing the Size of the Interval Projection
4.2.2. Minimizing/Maximizing the Upper/Lower Bound of the Interval Projection
5. Experiments
5.1. Contracting Power
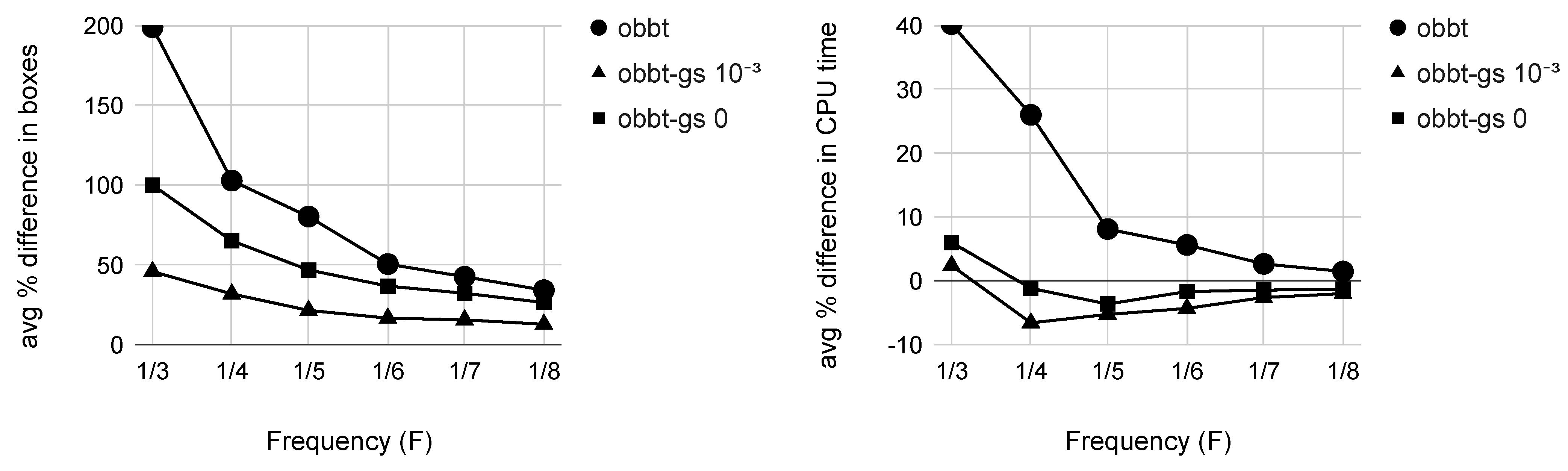
5.2. Sustainability
5.3. Non-Convex Optimization Problems
| Algorithm 1: The obbt-gs contractor for reducing box domains. |
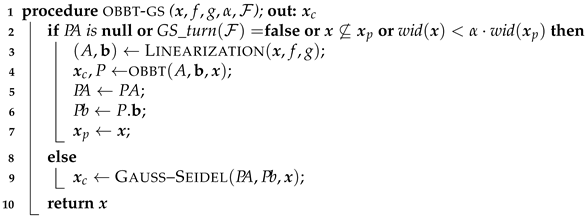 |
- has not been created.
- It is not the turn of applying Gauss–Seidel: the user-defined parameter indicates the frequency of applying Gauss–Seidel instead of obbt. For example, if , then GS_turn returns true once every 5 calls.
- The space related to the current box is not related to the space used for computing the current preconditioning matrix, i.e., . This occurs when the algorithm finishes a branch of the search tree and starts another one.
- The box is too small compared to the last one used for preconditioning, i.e., , with a user-defined parameter.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bertsekas, D. Nonlinear Programming, 3rd ed.; Optimized Computers Series; Athena Scientific: Belmont, MA, USA, 2016; Available online: http://www.athenasc.com/nonlinbook.html (accessed on 1 August 2023).
- Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Araya, I.; Reyes, V. Interval branch-and-bound algorithms for optimization and constraint satisfaction: A survey and prospects. J. Glob. Optim. 2016, 65, 837–866. [Google Scholar] [CrossRef]
- Locatelli, M.; Schoen, F. Global Optimization: Theory, Algorithms and Applications; SIAM: Philadelphia, PA, USA, 2013. [Google Scholar]
- Araya, I.; Trombettoni, G.; Neveu, B. A contractor based on convex interval taylor. In Proceedings of the International Conference on Integration of Artificial Intelligence (AI) and Operations Research (OR) Techniques in Constraint Programming, Nantes, France, 28 May–1 June 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–16. [Google Scholar]
- Adjiman, C.S.; Dallwig, S.; Floudas, C.A.; Neumaier, A. A global optimization method, αBB, for general twice-differentiable constrained NLPs—I. Theoretical advances. Comput. Chem. Eng. 1998, 22, 1137–1158. [Google Scholar] [CrossRef]
- Misener, R.; Floudas, C.A. ANTIGONE: Algorithms for continuous/integer global optimization of nonlinear equations. J. Glob. Optim. 2014, 59, 503–526. [Google Scholar] [CrossRef]
- Belotti, P.; Lee, J.; Liberti, L.; Margot, F.; Wächter, A. Branching and bounds tightening techniques for non-convex MINLP. Optim. Methods Softw. 2009, 24, 597–634. [Google Scholar] [CrossRef]
- Nowak, I.; Vigerske, S. LaGO: A (heuristic) branch and cut algorithm for nonconvex MINLPs. Cent. Eur. J. Oper. Res. 2008, 16, 127–138. [Google Scholar] [CrossRef]
- Achterberg, T. SCIP: Solving constraint integer programs. Math. Program. Comput. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Trombettoni, G.; Ignacio, A.; Neveu, B.; Chabert, G. Inner regions and interval linearizations for global optimization. In Proceedings of the AAAI, San Francisco, CA, USA, 7–11 August 2011. [Google Scholar]
- Gleixner, A.M.; Berthold, T.; Müller, B.; Weltge, S. Three enhancements for optimization-based bound tightening. J. Glob. Optim. 2017, 67, 731–757. [Google Scholar] [CrossRef]
- Cengil, F.; Nagarajan, H.; Bent, R.; Eksioglu, S.; Eksioglu, B. Learning to accelerate globally optimal solutions to the AC Optimal Power Flow problem. Electr. Power Syst. Res. 2022, 212, 108275. [Google Scholar] [CrossRef]
- Suriyanarayana, V.; Tavaslioglu, O.; Patel, A.B.; Schaefer, A.J. DeepSimplex: Reinforcement Learning of Pivot Rules Improves the Efficiency of Simplex Algorithm in Solving Linear Programming Problems. 2019. Available online: https://openreview.net/pdf?id=SkgvvCVtDS (accessed on 29 July 2023).
- Forrest, J.J.; Goldfarb, D. Steepest-edge simplex algorithms for linear programming. Math. Program. 1992, 57, 341–374. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Orden, A.; Wolfe, P. The generalized simplex method for minimizing a linear form under linear inequality restraints. Pac. J. Math. 1955, 5, 183–195. [Google Scholar] [CrossRef]
- Niki, H.; Kohno, T.; Morimoto, M. The preconditioned Gauss–Seidel method faster than the SOR method. J. Comput. Appl. Math. 2008, 219, 59–71. [Google Scholar] [CrossRef]
- Hansen, E.; Walster, G.W. Solving overdetermined systems of interval linear equations. Reliab. Comput. 2006, 12, 239–243. [Google Scholar] [CrossRef]
- Ceberio, M.; Granvilliers, L. Solving nonlinear equations by abstraction, Gaussian elimination, and interval methods. In Proceedings of the International Workshop on Frontiers of Combining Systems, Santa Margherita Ligure, Italy, 8–10 April 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 117–131. [Google Scholar]
- Abdi, H. The method of least squares. Encycl. Meas. Stat. 2007, 1, 530–532. [Google Scholar]
- Golub, G.H.; Reinsch, C. Singular value decomposition and least squares solutions. In Linear Algebra; Springer: Berlin/Heidelberg, Germany, 1971; pp. 134–151. [Google Scholar]
- Jaulin, L.; Kieffer, M.; Didrit, O.; Walter, E.; Jaulin, L.; Kieffer, M.; Didrit, O.; Walter, É. Interval Analysis; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Horáček, J.; Hladík, M. Subsquares approach—A simple scheme for solving overdetermined interval linear systems. In Proceedings of the International Conference on Parallel Processing and Applied Mathematics, Warsaw, Poland, 8–11 September 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 613–622. [Google Scholar]
- Domes, F.; Neumaier, A. Rigorous filtering using linear relaxations. J. Glob. Optim. 2012, 53, 441–473. [Google Scholar] [CrossRef][Green Version]
- Chabert, G.; Jaulin, L. Contractor Programming. Artif. Intell. 2009, 173, 1079–1100. [Google Scholar] [CrossRef]
- Benhamou, F.; Goualard, F.; Granvilliers, L.; Puget, J.F. Revising hull and box consistency. In Proceedings of the International Conference on Logic Programming, Las Cruces, NM, USA, 29 November–4 December 1999; Citeseer: State College, PA, USA, 1999. [Google Scholar]
- Moore, R.E. Methods and Applications of Interval Analysis; SIAM: Philadelphia, PA, USA, 1979. [Google Scholar]
- Ninin, J.; Messine, F.; Hansen, P. A reliable affine relaxation method for global optimization. 4OR 2015, 13, 247–277. [Google Scholar] [CrossRef]
- Shcherbina, O.; Neumaier, A.; Sam-Haroud, D.; Vu, X.H.; Nguyen, T.V. Benchmarking global optimization and constraint satisfaction codes. In Proceedings of the Global Optimization and Constraint Satisfaction: First International Workshop on Global Constraint Optimization and Constraint Satisfaction, COCOS 2002, Valbonne-Sophia Antipolis, France, 15–18 October 2002; Revised Selected Papers 1. Springer: Berlin/Heidelberg, Germany, 2003; pp. 211–222. [Google Scholar]

| Benchmark | n | m | #Nonlinear | Benchmark | n | m | #Nonlinear |
|---|---|---|---|---|---|---|---|
| avgasa | 8 | 10 | 0 | ex8_4_4bis | 5 | 4 | 0 |
| chembis | 11 | 4 | 0 | ex8_4_5 | 15 | 11 | 11 |
| dipigri | 7 | 4 | 4 | ex8_4_5bis | 4 | 1 | 0 |
| dixchlng | 10 | 5 | 5 | ex8_5_1 | 6 | 5 | 2 |
| dualc8 | 8 | 15 | 0 | ex8_5_1-1 | 6 | 5 | 2 |
| ex2_1_7 | 20 | 10 | 0 | ex8_5_1bis | 7 | 6 | 2 |
| ex2_1_8 | 24 | 20 | 0 | ex8_5_2_1 | 6 | 5 | 2 |
| ex2_1_9 | 10 | 1 | 0 | ex8_5_4 | 5 | 4 | 2 |
| ex5_4_4 | 27 | 19 | 6 | ex8_5_5 | 5 | 4 | 2 |
| ex6_1_3 | 12 | 9 | 6 | ex8_5_6 | 6 | 4 | 2 |
| ex6_1_3bis | 6 | 3 | 0 | hhfair | 27 | 25 | 6 |
| ex6_2_10 | 6 | 3 | 0 | hs056 | 7 | 4 | 4 |
| ex6_2_11 | 3 | 1 | 0 | hs100 | 7 | 4 | 4 |
| ex6_2_12 | 4 | 2 | 0 | hs113 | 10 | 8 | 8 |
| ex6_2_14 | 4 | 2 | 0 | hs119 | 16 | 8 | 0 |
| ex6_2_8 | 3 | 1 | 0 | hydro | 30 | 24 | 6 |
| ex7_2_8 | 8 | 4 | 4 | meanvar | 7 | 2 | 0 |
| ex7_3_4bis | 7 | 14 | 2 | schwefel5 | 5 | 5 | 0 |
| ex7_3_5bis | 4 | 6 | 2 | schwefel5-abs | 5 | 5 | 0 |
| ex8_1_3 | 2 | 2 | 0 | srcpm | 38 | 20 | 0 |
| ex8_4_4-1 | 17 | 12 | 12 | srcpm-1 | 39 | 20 | 0 |
| obbt | obbt-gs | obbt-gs | ||||||
|---|---|---|---|---|---|---|---|---|
| Boxes | CPU | Boxes | CPU | t | Boxes | CPU | t | |
| ex6_2_12 | 7854 | 10.8 | 9854 | 11.1 | 3.3% | 10,290 | 10.1 | −6.2% |
| ex6_2_8 | 31,793 | 41.5 | 45,649 | 38.2 | −8.2% | 46,079 | 32.6 | −21.7% |
| ex8_4_4bis | 77,506 | 114 | 114,091 | 99.1 | −13.1% | 120,760 | 87.1 | −26.6% |
| ex8_5_2_1 | 9616 | 23.6 | 13,587 | 21.6 | −8.7% | 14,853 | 19.2 | −18.9% |
| schwefel5−abs | 6329 | 8.6 | 9485 | 6.27 | −27.1% | 11,283 | 7.97 | −7.3% |
| ex6_1_3 | 16,553 | 122 | 22,837 | 112.4 | −7.9% | 21,875 | 93.1 | −23.8% |
| srcpm | 337 | 7.02 | 597 | 6.3 | −10.1% | 600 | 6.30 | −10.3% |
| ex2_1_7 | 2515 | 17.9 | 2939 | 16.3 | −9.0% | 2609 | 15.1 | −15.8% |
| ex8_5_1 | 4135 | 10.1 | 5072 | 7.07 | −30.1% | 4899 | 8.41 | −16.8% |
| dixchlng | 1787 | 8.30 | 1935 | 6.71 | −19.7% | 2158 | 6.51 | −22.1% |
| hs100 | 2667 | 6.75 | 3753 | 5.71 | −15.4% | 4050 | 4.8 | −28.3% |
| hs113 | 4769 | 19.3 | 6817 | 16.3 | −15.9% | 7593 | 15.0 | −22.5% |
| hhfair | 1609 | 21.9 | 2132 | 18.9 | −13.8% | 2185 | 25.2 | 15.4 % |
| dualc8 | 190,092 | 532 | 331,281 | 749 | 40.9% | 322,698 | 611 | 14.9% |
| chembis | 483,627 | 1425 | 802,579 | 1725 | 21.1% | 500,690 | 1462 | 2.6% |
| ex8_4_5 | 16,934 | 216 | 27,942 | 204 | −5.8% | 17,368 | 191 | −11.5% |
| avg: | −8.5% | avg: | −12.7% | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reyes, V.; Araya, I. Non-Convex Optimization: Using Preconditioning Matrices for Optimally Improving Variable Bounds in Linear Relaxations. Mathematics 2023, 11, 3549. https://doi.org/10.3390/math11163549
Reyes V, Araya I. Non-Convex Optimization: Using Preconditioning Matrices for Optimally Improving Variable Bounds in Linear Relaxations. Mathematics. 2023; 11(16):3549. https://doi.org/10.3390/math11163549
Chicago/Turabian StyleReyes, Victor, and Ignacio Araya. 2023. "Non-Convex Optimization: Using Preconditioning Matrices for Optimally Improving Variable Bounds in Linear Relaxations" Mathematics 11, no. 16: 3549. https://doi.org/10.3390/math11163549
APA StyleReyes, V., & Araya, I. (2023). Non-Convex Optimization: Using Preconditioning Matrices for Optimally Improving Variable Bounds in Linear Relaxations. Mathematics, 11(16), 3549. https://doi.org/10.3390/math11163549








