Link Prediction for Temporal Heterogeneous Networks Based on the Information Lifecycle
Abstract
:1. Introduction
- We propose a link prediction framework based on an encoder–decoder for temporal heterogeneous networks, which can achieve more accurate results in practical applications than other frameworks.
- We propose an augmented residual information matrix considering meta-paths that incorporates the law of decreasing information lifecycle into meta-paths. This matrix is used as an input to the encoder to enhance the effective extraction of semantic and structural information.
- Through numerous experiments, we verify that our method is superior to many existing methods in terms of effectiveness.
2. Related Work
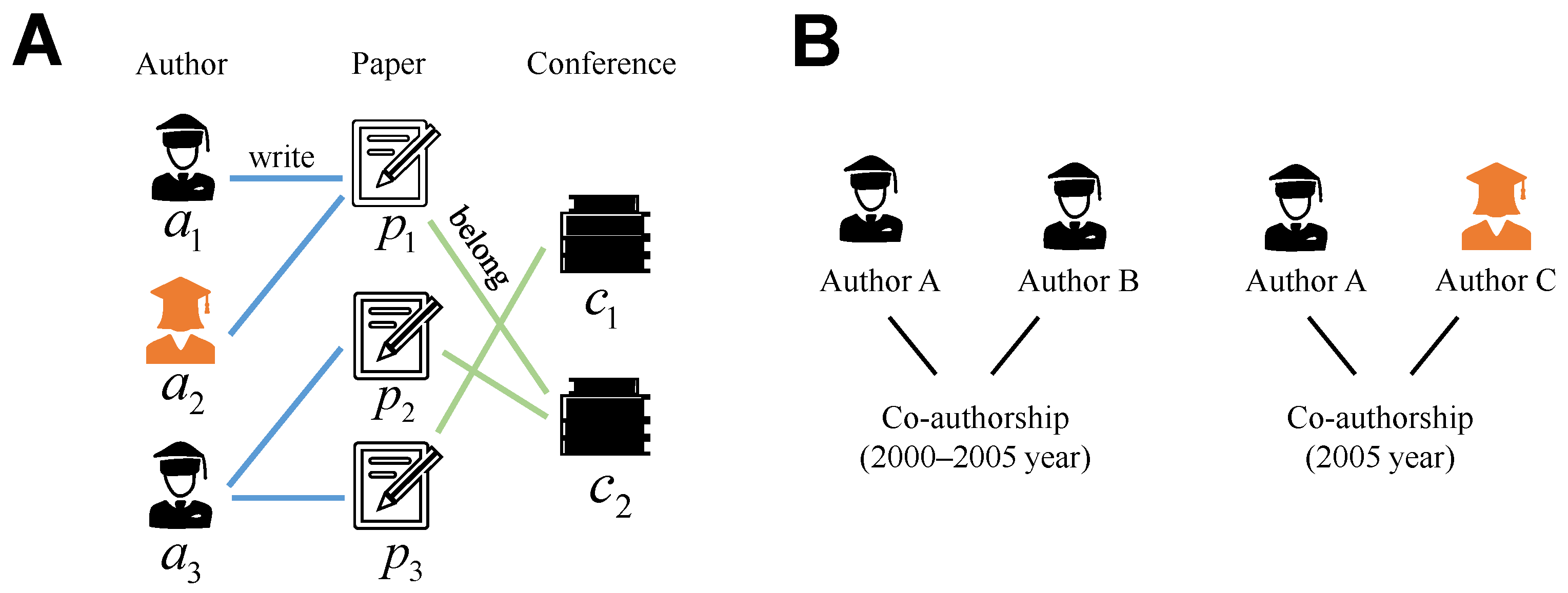
3. Notations and Definitions
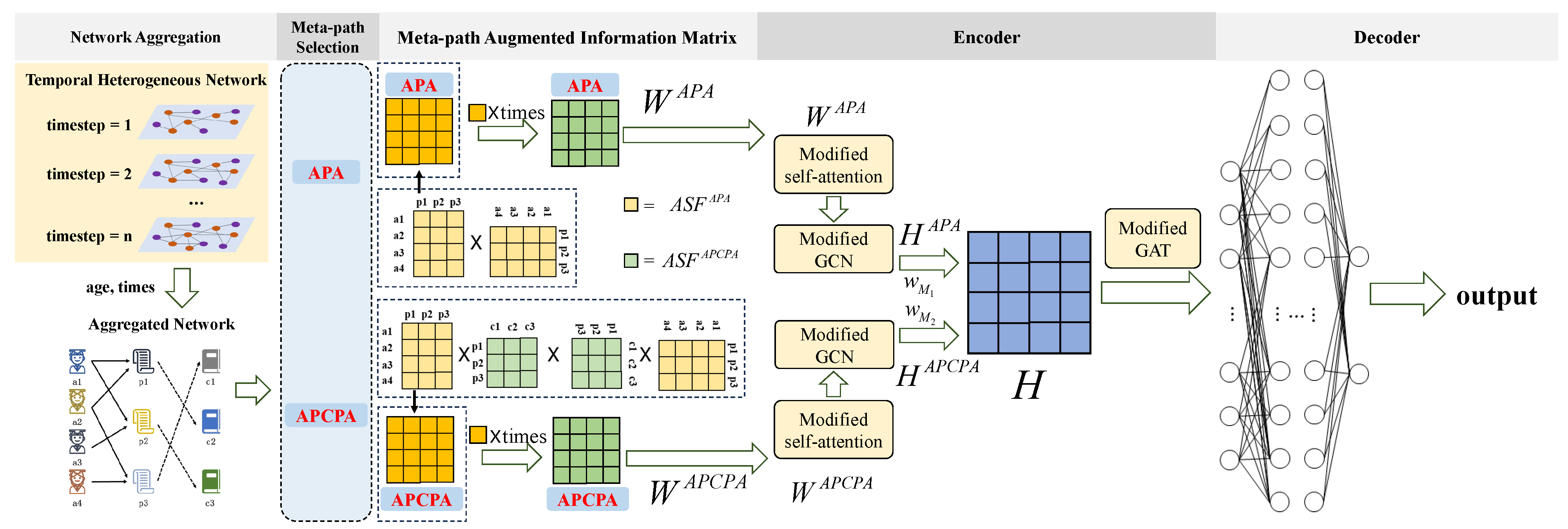
4. The LP-THN Model
4.1. Basic Idea
4.2. Encoder
4.2.1. Modified Self-Attention Mechanism
4.2.2. Modified GCN
4.2.3. Modified GAT
4.3. Decoder
5. Experiments
5.1. Datasets and Settings
5.1.1. Datasets
- AMiner [35] is a scientific research network that contains three types of nodes. We used articles from this network published in five research areas in 9 time slices from 1990 to 1997. We considered two meta-paths: , which denotes author collaborations, and , which denotes author participation in the same conference.
- Last.FM [36] is an online music platform. The network contains 3 types of nodes, and the dataset we used contains partial information generated on the platform during the years 1956, 1947, 1979 and 2005–2010, divided into 5 time slices. We considered two meta-paths: , which indicates that two users listened to the same artist, and , which indicates that two users listened to artists with the same musical style.
- MovieLens [37] is a noncommercial film recommendation platform. The network contains a total of three types of nodes, and the dataset we used contains a portion of the information generated on the site between 1996 and 2018, divided into 8 time slices. We considered two meta-paths: , which indicates that two users have rated the same author, and , which indicates that two users have rated a film on the same topic.
5.1.2. Baselines and Evaluation Metrics
- DeepWalk [12]: node sequences are obtained by a random walk, and the node sequences are then input into Word2vec to obtain low-dimensional embedded representations of the nodes.
- Node2Vec [13]: node sequences are obtained by biased random walk, and the node sequences are used as input to Word2vec to obtain low-dimensional embedded representations of the nodes.
- LINE [15]: node embeddings are learned by maximizing the similarity between a node and its first-order and second-order neighbours.
- M-NMF [14]: based on nonnegative matrix partitioning, which captures the community structure in the graph as well as the similarity between nodes.
- Deeplink [38]: a deep learning method for node embedding representation that uses a deep convolutional neural network to learn node embedding representation.
- Struc2Vec [39]: the context sequence of a node is constructed by traversing the depth-first search path of each node, and the sequence is then fed into Word2vec to obtain the node’s low-dimensional embedding representation.
- Metapath2vec [21]: node sequences are obtained by a random meta-path-based walk, and the sequences are fed into Word2vec to obtain a representation of node embeddings in heterogeneous networks.
5.1.3. Experimental Settings
5.2. Analysis of the Experimental Results
5.2.1. Comparison Experiments
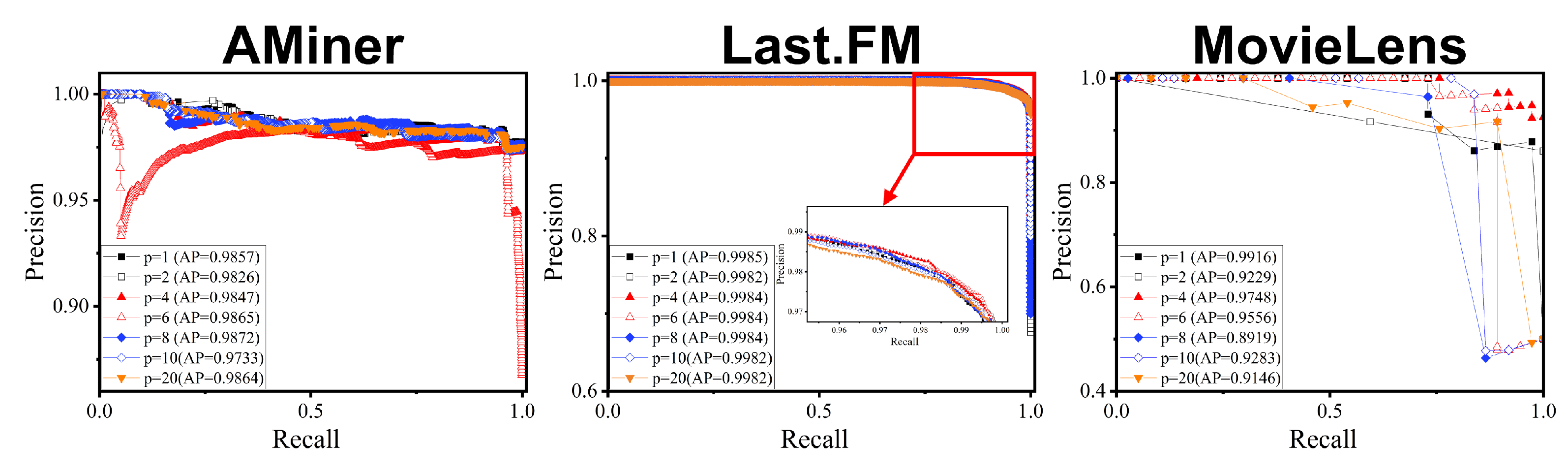
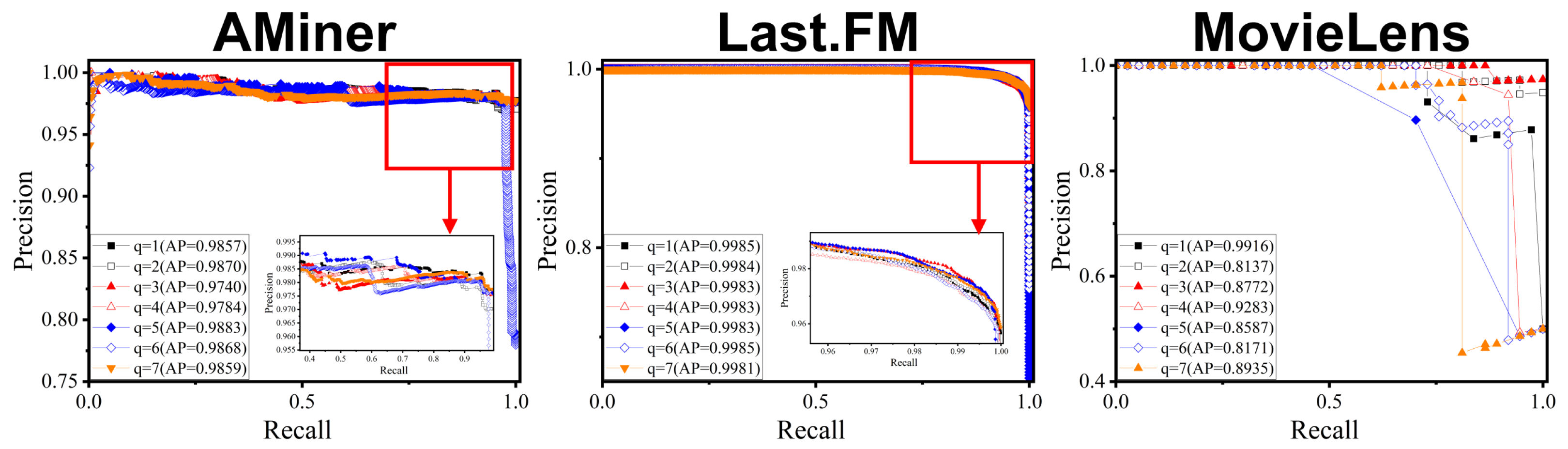
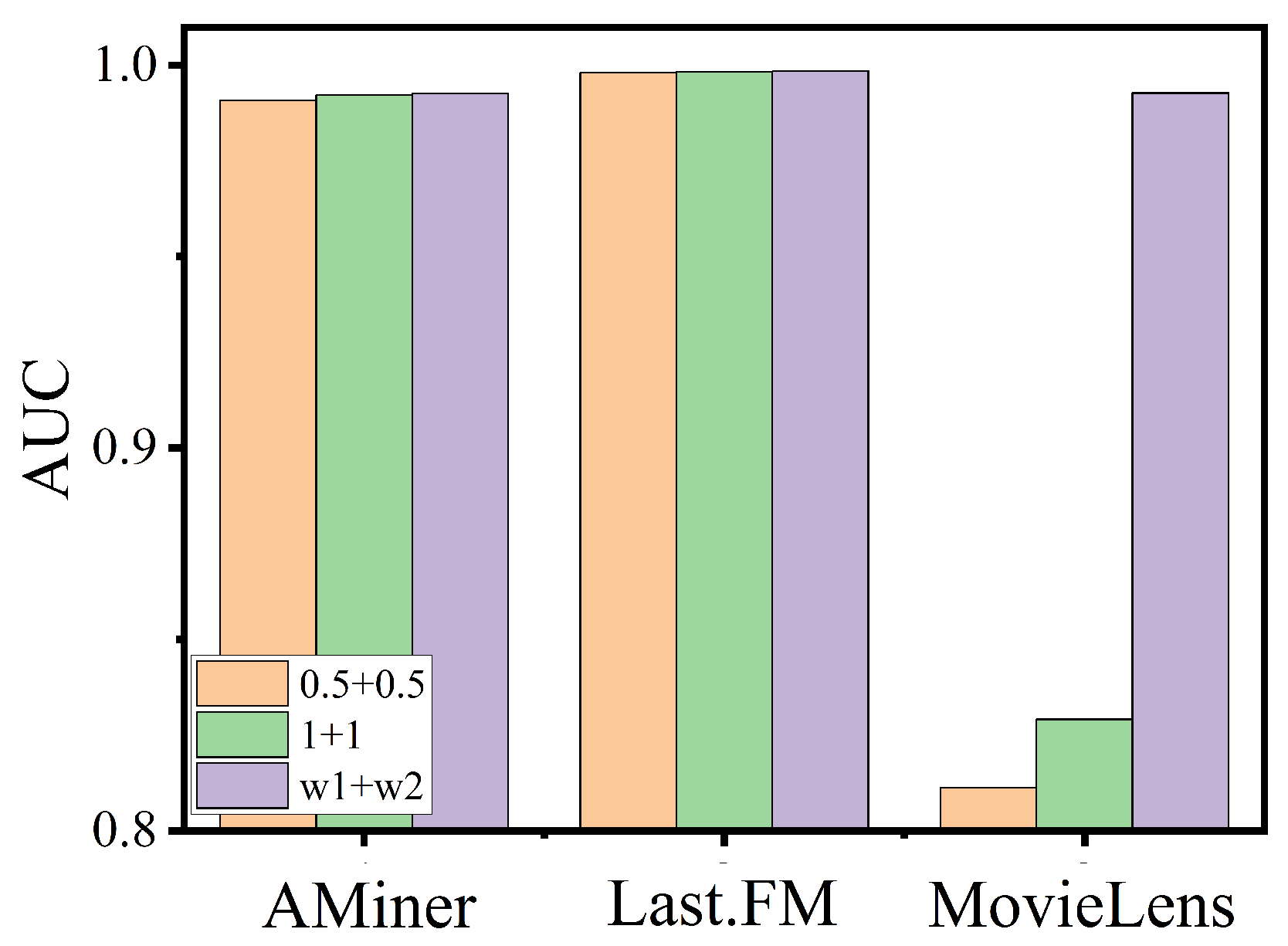
5.2.2. Parameter Sensitivity Analysis
5.2.3. Ablation Experiments
5.2.4. Complexity Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stanfield, Z.; Coşkun, M.; Koyutürk, M. Drug response prediction as a link prediction problem. Sci. Rep. 2017, 7, 40321. [Google Scholar] [CrossRef] [PubMed]
- Nasiri, E.; Berahm, K.; Rostami, M.; Dabiri, M. A novel link prediction algorithm for protein-protein interaction networks by attributed graph embedding. Comput. Biol. Med. 2021, 137, 104772. [Google Scholar] [CrossRef] [PubMed]
- Liben-Nowell, D.; Kleinberg, J. The link prediction problem for social networks. In Proceedings of the Twelfth International Conference on Information and Knowledge Management, New Orleans, LA, USA, 9–11 November 2003; pp. 556–559. [Google Scholar]
- Cho, H.; Yu, Y. Link prediction for interdisciplinary collaboration via co-authorship network. Soc. Netw. Anal. Min. 2018, 8, 1–12. [Google Scholar] [CrossRef]
- Liu, G. An ecommerce recommendation algorithm based on link prediction. Alex. Eng. J. 2022, 61, 905–910. [Google Scholar] [CrossRef]
- Adamic, L.A.; Adar, E. Friends and neighbors on the web. Soc. Net. 2003, 25, 211–230. [Google Scholar] [CrossRef]
- Zhou, T.; Lü, L.; Zhang, Y.C. Predicting missing links via local information. Eur. Phys. J. B 2009, 71, 623–630. [Google Scholar] [CrossRef]
- Katz, L. A new status index derived from sociometric analysis. Psychometrika 1953, 18, 39–49. [Google Scholar] [CrossRef]
- Leicht, E.A.; Holme, P.; Newman, M.E. Vertex similarity in networks. Phys. Rev. E 2006, 73, 026120. [Google Scholar] [CrossRef]
- Fouss, F.; Pirotte, A.; Renders, J.M.; Saerens, M. Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation. IEEE Trans. Knowl. Data Eng. 2007, 19, 355–369. [Google Scholar] [CrossRef]
- Jeh, G.; Widom, J. Simrank: A measure of structural-context similarity. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002; pp. 538–543. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Wang, X.; Cui, P.; Wang, J.; Pei, J.; Zhu, W.; Yang, S. Community preserving network embedding. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. Line: Large-scale information network embedding. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015; pp. 1067–1077. [Google Scholar]
- Scarselli, F.; Gori, M.; Tsoi, A.C. The graph neural network model. IEEE Trans. Neural Net. 2008, 20, 61–80. [Google Scholar] [CrossRef]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. NIPS 2017, 30, 1024–1034. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised, classification, with, graph, convolutional, networks. arXiv 2017, arXiv:1609.02907. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Shi, C.; Wang, R.; Wang, X. Survey on Heterogeneous Information Networks Analysis and Applications. J. Softw. 2022, 33, 598–621. [Google Scholar]
- Dong, Y.; Chawla, N.V.; Swami, A. metapath2vec: Scalable representation learning for heterogeneous networks. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 135–144. [Google Scholar]
- Fu, T.Y.; Lee, W.C.; Lei, Z. Hin2vec: Explore meta-paths in heterogeneous information networks for representation learning. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 1797–1806. [Google Scholar]
- Chang, S.; Han, W.; Tang, J.; Qi, G.J.; Aggarwal, C.C.; Huang, T.S. Heterogeneous network embedding via deep architectures. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 119–128. [Google Scholar]
- Zhang, C.; Song, D.; Huang, C.; Swami, A.; Chawla, N.V. Heterogeneous graph neural network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 793–803. [Google Scholar]
- Shi, C.; Hu, B.; Zhao, W.X.; Philip, S.Y. Heterogeneous information network embedding for recommendation. IEEE Trans. Knowl. Data Eng. 2018, 31, 357–370. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, Q.; Yang, Q.; Wei, W. Temporal link prediction via adjusted sigmoid function and 2-simplex structure. Sci. Rep. 2022, 12, 16585. [Google Scholar] [CrossRef]
- Zou, L.; Zhan, X.X.; Sun, J.; Hanjalic, A.; Wang, H. Temporal network prediction and interpretation. IEEE Trans. Netw. Sci. Eng. 2021, 9, 1215–1224. [Google Scholar] [CrossRef]
- Zhou, L.; Yang, Y.; Ren, X.; Wu, F.; Zhuang, Y. Dynamic network embedding by modeling triadic closure process. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LO, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Nguyen, G.H.; Lee, J.B.; Rossi, R.A.; Ahmed, N.K.; Koh, E.; Kim, S. Continuous-time dynamic network embeddings. In Proceedings of the Companion Proceedings of the Web Conference 2018, Lyon, France, 23–27 April 2018; pp. 969–976. [Google Scholar]
- Rahman, M.; Saha, T.K.; Hasan, M.A.; Xu, K.S.; Reddy, C.K. Dylink2vec: Effective feature representation for link prediction in dynamic networks. arXiv 2018, arXiv:1804.05755. [Google Scholar]
- Abbas, K.; Abbasi, A.; Dong, S.; Niu, L.; Chen, L.; Chen, B. A Novel Temporal Network-Embedding Algorithm for Link Prediction in Dynamic Networks. Entropy 2023, 25, 257. [Google Scholar] [CrossRef]
- Yin, Y.; Ji, L.X.; Zhang, J.P.; Pei, Y.L. DHNE: Network representation learning method for dynamic heterogeneous networks. IEEE Access 2019, 7, 134782–134792. [Google Scholar] [CrossRef]
- Wang, X.; Lu, Y.; Shi, C.; Wang, R.; Cui, P.; Mou, S. Dynamic heterogeneous information network embedding with meta-path based proximity. IEEE Trans. Knowl. Data Eng. 2020, 34, 1117–1132. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. NIPS 2017, 30, 5998–6008. [Google Scholar]
- Tang, J.; Zhang, J.; Yao, L.; Li, J.; Zhang, L.; Su, Z. Arnetminer: Extraction and mining of academic social networks. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 990–998. [Google Scholar]
- Cantador, I.; Brusilovsky, P.; Kuflik, T. Second workshop on information heterogeneity and fusion in recommender systems (HetRec2011). In Proceedings of the Fifth ACM Conference on Recommender Systems, Chicago, IL, USA, 23–27 October 2011; pp. 387–388. [Google Scholar]
- Harper, F.M.; Konstan, J.A. The movielens datasets: History and context. ACM Trans. Interact. Intell. Syst. 2015, 5, 1–19. [Google Scholar] [CrossRef]
- Zhou, F.; Liu, L.; Zhang, K.; Trajcevski, G.; Wu, J.; Zhong, T. Deeplink: A deep learning approach for user identity linkage. In Proceedings of the IEEE INFOCOM 2018-IEEE Conference on Computer Communications, Honolulu, HI, USA, 15–19 April 2018; pp. 1313–1321. [Google Scholar]
- Ribeiro, L.F.; Saverese, P.H.; Figueiredo, D.R. struc2vec: Learning node representations from structural identity. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 385–394. [Google Scholar]



| Datasets | Node Types | #Node | Meta-Path | Time Steps |
|---|---|---|---|---|
| AMiner | Author (A) Paper (P) Conference (C) | 7043 5371 17 | APA APCPA | 9 |
| Last.FM | User (U) Artist (A) Tag (T) | 1234 9438 5472 | UAU UATAU | 5 |
| MovieLens | User (U) Movie (M) Genre (G) | 819 12,677 39 | UMU UMGMU | 8 |
| Datasets | Metric | DeepWalk | Node2Vec | LINE | M-NMF | Deeplink | Struc2Vec | Metapath2vec | LP-THN-1st | LP-THN-2nd | LP-THN |
|---|---|---|---|---|---|---|---|---|---|---|---|
| AMiner | AUC | 0.9380 | 0.9625 | 0.9482 | 0.9415 | 0.9398 | 0.9332 | 0.9623 | 0.9912 | 0.9903 | 0.9934 |
| F1 | 0.9403 | 0.9632 | 09493 | 0.9418 | 0.942 | 0.9358 | 0.9631 | 0.9627 | 0.9355 | 0.9686 | |
| ACC | 0.9380 | 0.9625 | 0.9482 | 0.9415 | 0.9398 | 0.9332 | 0.9624 | 0.9728 | 0.9386 | 0.969 | |
| Last.FM | AUC | 0.8539 | 0.9675 | 0.969 | 0.9223 | 0.9559 | 0.9594 | 0.9667 | 0.9844 | 0.9778 | 0.9848 |
| F1 | 0.8819 | 0.9707 | 0.9717 | 0.9318 | 0.9608 | 0.9638 | 0.9701 | 0.9768 | 0.9721 | 0.9768 | |
| ACC | 0.8604 | 0.9687 | 0.9699 | 0.9249 | 0.9576 | 0.9610 | 0.9680 | 0.9752 | 0.9726 | 0.9761 | |
| MovieLens | AUC | 0.8832 | 0.8576 | 0.9744 | 0.8967 | 0.9068 | 0.9345 | 0.9872 | 0.9913 | 0.9935 | 0.9945 |
| F1 | 0.8861 | 0.8642 | 0.9737 | 0.9000 | 0.9014 | 0.9333 | 0.9867 | 0.9927 | 0.9921 | 0.9981 | |
| ACC | 0.8816 | 0.8553 | 0.9737 | 0.8947 | 0.9079 | 0.9342 | 0.9868 | 0.9933 | 0.9872 | 0.9860 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, J.; Li, J.; Jiang, J. Link Prediction for Temporal Heterogeneous Networks Based on the Information Lifecycle. Mathematics 2023, 11, 3541. https://doi.org/10.3390/math11163541
Cao J, Li J, Jiang J. Link Prediction for Temporal Heterogeneous Networks Based on the Information Lifecycle. Mathematics. 2023; 11(16):3541. https://doi.org/10.3390/math11163541
Chicago/Turabian StyleCao, Jiaping, Jichao Li, and Jiang Jiang. 2023. "Link Prediction for Temporal Heterogeneous Networks Based on the Information Lifecycle" Mathematics 11, no. 16: 3541. https://doi.org/10.3390/math11163541
APA StyleCao, J., Li, J., & Jiang, J. (2023). Link Prediction for Temporal Heterogeneous Networks Based on the Information Lifecycle. Mathematics, 11(16), 3541. https://doi.org/10.3390/math11163541






