2.2. Related Works
Over the past few decades, researchers have made significant advancements in developing software reliability growth models by exploring various ideas and approaches. One notable contribution in this field is the work of Pham and Nordmann, who introduced a general framework for constructing new SRGMs [
5]. This framework has served as a foundation for interpreting several existing software reliability models. Within this framework, two concepts play vital roles in the construction of an SRGM: the expected number of initial faults (NIF) present in the software at the beginning of the testing phase and the fault detection rate (FDR), which represents the rate at which failures are detected over time. In the context of software debugging, both NIF and FDR can be treated as either constant or varying in a time-dependent manner.
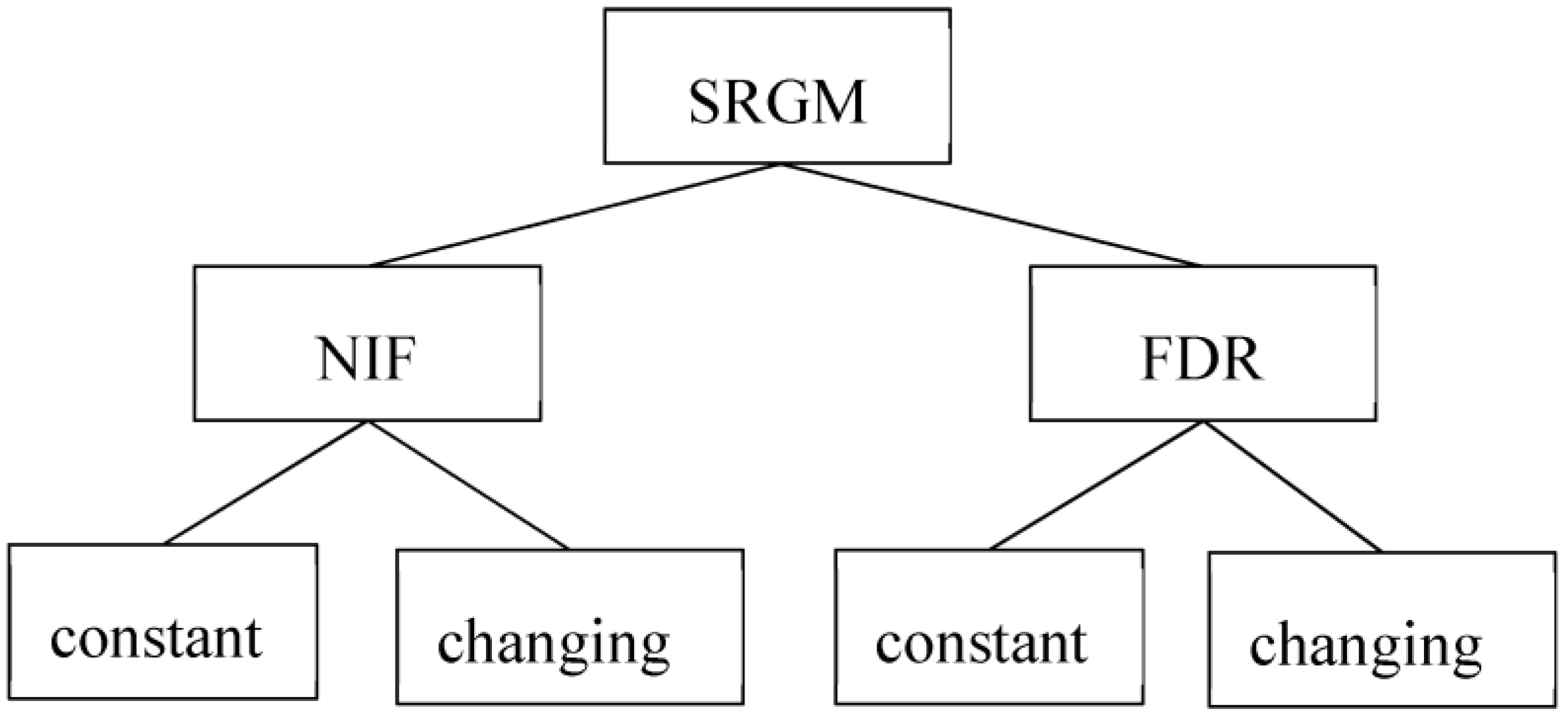
Figure 2 categorizes this group of SRGMs based on whether the NIF and FDR are considered constant or subject to change. This figure helps to provide a clearer understanding of the different models within this family.
In models with constant NIF, it is assumed that when a fault is detected, it is immediately removed by the testers, and no new errors are introduced in the process. Consequently, the software’s initial defects remain unchanged throughout the debugging phase. On the other hand, in software reliability models with changing NIF, it is acknowledged that new faults may be introduced during the testing phase. This means that the total number of defects in the software is not constant and comprises both the initial faults and the additional faults introduced during the debugging process. This assumption recognizes the possibility of testers unintentionally introducing new errors while attempting to fix existing defects.
The FDR is a significant indicator of the effectiveness of the testing phase. It is influenced by various factors, including the expertise of testers, testing techniques employed, and the selection of test cases. The FDR can remain constant or vary among faults depending on the software reliability model. In the case of a constant FDR, it is assumed that all defects in the software have an equal probability of being detected throughout the testing period. This implies that the FDR remains consistent over time, irrespective of the specific characteristics of the faults.
Conversely, in models with a time-dependent FDR, the function may exhibit increasing or decreasing trends as time progresses. This variation acknowledges the dynamic nature of the testing process, where the effectiveness of fault detection can be influenced by factors such as the testing team’s expertise, the program’s size, and the software’s testability. By incorporating the concept of a changing FDR, software reliability models can better reflect the complexities and uncertainties inherent in real-world testing scenarios. Recognizing the dependence of the FDR on various factors enables researchers to develop more accurate models and gain deeper insights into the dynamics of software reliability assessment.
- A.
SRGMs with constant NIF and constant/changing FDR
The Goel–Okumoto model [
6] is a widely referenced example of an NHPP model with constant NIF and FDR. More SRGMs with constant NIF and changing FDR have been proposed in the literature. These models consider learning phenomena, time resources, testing coverage, and environmental uncertainties. Yamada et al. [
7] introduced the concept of a learning process in software testing, where testers gradually improve their skills and familiarity with the software products. They formulated an increasing FDR with a hyperbolic function to represent the learning rate of testers and proposed the delayed S-shaped model. Ohba [
8] considered the learning process of testers during the testing phase and defined the FDR using a non-decreasing logistic S-shaped curve, leading to the development of the inflection S-shaped model. Yamada and Osaki [
9] considered the consumption of time resources and proposed the exponential testing effort and Rayleigh testing effort models. Pham [
1] introduced the imperfect fault detection (IFD) model, which incorporates a changing FDR that combines fault introduction with the phenomenon of testing coverage. This model allows for a more realistic representation of the testing process. Song et al. [
10] considered the impact of testing coverage uncertainty or randomness in the operating environment. They proposed a new NHPP software reliability model with constant NIF and changing FDR regarding a testing coverage function, considering the uncertainty associated with operational environments.
- B.
SRGMs with changing NIF and constant/changing FDR
More SRGMs with time-dependent changing NIF function and constant/changing FDR have been proposed in the literature. For example, Yamada et al. [
11] proposed two imperfect debugging models assuming the NIF function to be an exponential or linear function of the testing time, respectively, and FDR to be constant. Pham and Zhang [
12] developed an imperfect debugging model considering an exponential function of testing time for NIF and a non-decreasing S-shaped function for FDR. Pham et al. [
13] proposed an imperfect SRGM with NIF function to be linear and FDR S-shaped of the testing time. Li and Pham [
14] introduced a new, changing NIF model, and FDR is expressed as a testing coverage function. In their model, they also assumed that when a software failure is detected, immediate debugging starts, and either the total number of faults is reduced by one with probability p or the total number of faults remains the same with probability 1-p.
- C.
Other SRGMs
Many imperfect SRGMs do not fit the above framework precisely and use other approaches. For example, Chiu et al. [
15] proposed a model that considers the influential factors for finding errors in software, including the autonomous errors-detected and learning factors. They proposed an FDR function including two factors representing the exponential-shaped and the S-shaped types of behaviors. Iqbal et al. [
16] investigated the impact of two learning effect factors: autonomous and acquired learning, which are gained after repeated experience/observation of the testing/debugging process by the tester/debugger in an SRGM. Wang et al. [
17] proposed an imperfect software debugging model that considers a log-logistic distribution function for NIF, which can capture the increasing and decreasing characteristics of the fault introduction rate per fault. They reason imperfect software debugging models proposed in the literature generally assume a constantly or monotonically decreasing fault introduction rate per fault. These models cannot adequately describe the fault introduction process in a practical test. Wang and Wu [
18] proposed a nonlinear NHPP imperfect software debugging model by considering that fault introduction is a nonlinear process. Al-Turk and Al-Mutairi [
19] developed an SRGM based on one-parameter Lindley distribution, which is modified by integrating two learning effects of the autonomous error-detected factor and the learning factor. These studies highlight the ongoing efforts to refine SRGMs by considering real-world scenarios and addressing the critical aspects of the software testing and debugging processes. Huang et al. [
20] developed an NHPP model considering both human factors (learning effect of the debugging process) and the nature of errors, such as varieties of errors and change points, during the testing period to extend the practicability of SRGMs. Verma et al. [
21] proposed an SRGM by considering conditions of error generation, fault removal efficiency (FRE), imperfect debugging parameter, and fault reduction factor (FRF). The error generation, imperfect debugging, and FRE parameters have been assumed to be constant, while FRF is time dependent and modeled using exponential, Weibull, and delayed s-shaped distribution functions. Luo et al. [
22] recently proposed a new SRGM with a changing NIF and FDR represented by an exponential decay function of testing time.
Each category of SRGMs has its own set of advantages and disadvantages. On one end of the spectrum, SRGMs with a changing NIF and FDR tend to have more parameters, as they incorporate various assumptions to yield a more realistic representation of the underlying processes. However, this realism comes at the cost of increased complexity. Complex models may require more resources, such as time and memory, to appropriately evaluate. While the abundance of parameters offers flexibility, it also leads to higher computational overhead.
In contrast, SRGMs with a constant NIF and FDR follow a simpler approach, resulting in fewer parameters and more straightforward models. A simpler model is generally easier to comprehend, interpret, and implement. Despite potentially sacrificing some level of realism, the simplicity of such models can prove advantageous, especially when computational efficiency and ease of use are significant considerations.