Improvement of Constructal Optimization for “Volume-Point” Heat Conduction Based on Uniformity Principle of Temperature Difference Fields
Abstract
1. Introduction
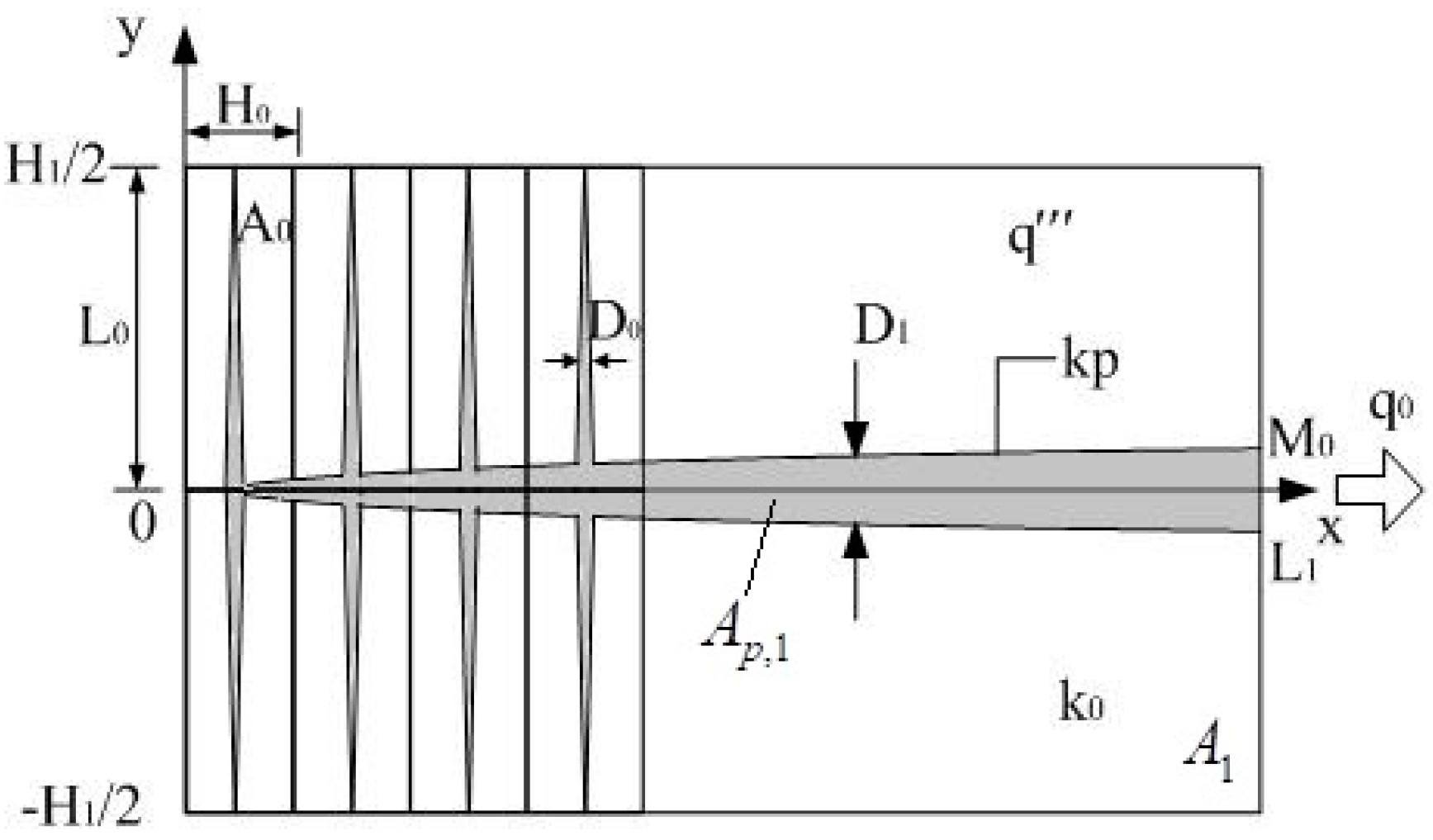
2. Constructal Heat Conduction Optimization Based on the Uniformity Principle of TDFs
2.1. Element Area
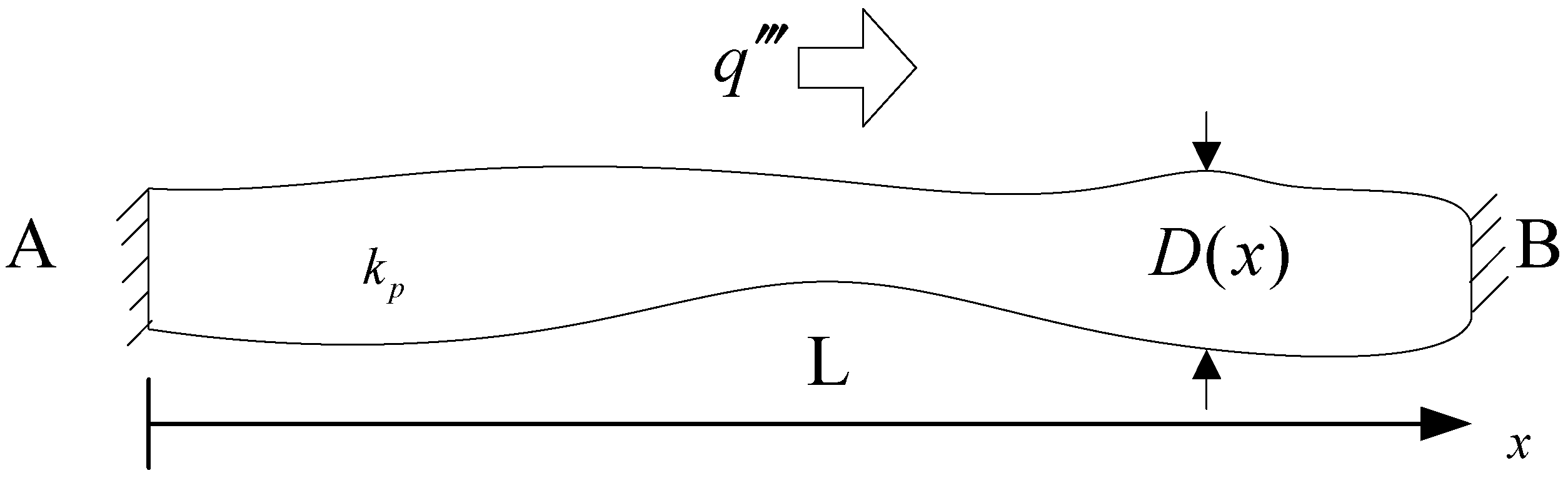
2.2. First-Order Construct
2.3. Second-Order Construct
3. Comparison and Analyses
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Area (m2) |
| a | Aspect ratio of element |
| C | Constant |
| Cr | Heat capacity rate ratio |
| D | Width of high-conductivity path (m) |
| EDR (W•K) | |
| H | Width of the area (m) |
| Heat conductivity of the volume (W/(m•K)) | |
| Heat conductivity of the path (W/(m•K)) | |
| Ratio of high to low thermal conductivity | |
| L | Length of the area (m) |
| M0 | Heat sink point |
| Ntu | Number of heat transfer units |
| n | Number of constituted construct |
| Heat generating rate (W/m2) | |
| T | Temperature (K) |
| Temperature difference (K) | |
| Dimensionless minimum average temperature difference | |
| Dimensionless maximum average temperature difference | |
| Greek symbols | |
| Lagrange function | |
| Area ratio (-) | |
| Lagrange multiplier | |
| Subscripts | |
| h | Optimization for minimum EDR |
| max | Maximum |
| min | Minimum |
| mm | Twice minimum value |
| mmm | Thrice minimum values |
| opt | Optimal |
| p | High-conductivity path |
| T | Optimization for minimum peak temperature |
| 0, 1, 2,…,i | Construct order |
References
- Waldrop, M.M. The chips are down for Moore’s law. Nature 2016, 530, 144–147. [Google Scholar] [CrossRef] [PubMed]
- van Erp, R.; Soleimanzadeh, R.; Nela, L.; Kampitsis, G.; Matioli, E. Co-designing electronics with microfluidics for more sustainable cooling. Nature 2020, 585, 211–216. [Google Scholar] [PubMed]
- He, Z.; Yan, Y.; Zhang, Z. Thermal management and temperature uniformity enhancement of electronic devices by micro heat sinks: A review. Energy 2021, 216, 119223. [Google Scholar]
- Ebadian, M.A.; Lin, C.X. A review of high-heat-flux heat removal technologies. Trans. ASME J. Heat Transfer. 2011, 133, 110801. [Google Scholar]
- Dadsetani, R.; Salimpour, M.R.; Tavakoli, M.R.; Goodarzi, M.; Filho, E.P.B. Thermal and mechanical design of reverting microchannels for cooling disk-shaped electronic parts using constructal theory. Int. J. Numer. Method H. 2020, 30, 245–265. [Google Scholar]
- You, J.; Feng, H.J.; Chen, L.G.; Xie, Z. Constructal design and experimental validation of a non-uniform heat generation body with rectangular cross-section and parallel circular fluid channels. Int. J. Heat Mass Tran. 2020, 148, 119028. [Google Scholar]
- Kim, K.-S.; Won, M.-H.; Kim, J.-W.; Back, B.-J. Heat pipe cooling technology for desktop PC CPU. Appl. Therm. Eng. 2003, 23, 1137–1144. [Google Scholar] [CrossRef]
- Qu, P.; Cheng, J.; Chen, Y.; Li, Y.; Li, W.; Tao, H. Numerical and experimental investigation on heat transfer of multi-heat sources mounted on a fined radiator within embedded heat pipes in an electronic cabinet. Int. J. Therm. Sci. 2023, 183, 107833. [Google Scholar]
- Liu, Z.H.; Zeng, X.; Zhao, W.K.; Gao, Y.; Sun, Y. A topology optimization design of three-dimensional cooling plate for the thermal homogeneity of lithium-ion batteries. Energy Convers. Manag. 2022, 14, 100215. [Google Scholar]
- Fawaz, A.; Hua, Y.; Le Corre, S.; Fan, Y.; Luo, L. Topology optimization of heat exchangers: A review. Energy 2022, 252, 124053. [Google Scholar]
- Xia, Z.Z.; Cheng, X.G.; Li, Z.X.; Guo, Z.Y. Bionic optimization of heat transport paths for heat conduction problems. J. Enhanc. Heat Transf. 2004, 11, 119–132. [Google Scholar] [CrossRef]
- Akhlaghi, N.; Najafpour-Darzi, G. A comprehensive review on biological hydrogen production. Int. J. Hydrogen Energy 2020, 45, 22492–22512. [Google Scholar] [CrossRef]
- Ghodoossi, L. Thermal and hydrodynamic analysis of a fractal microchannel network. Energy Convers. Manag. 2005, 46, 771–778. [Google Scholar] [CrossRef]
- Liu, F.; Zhu, R.S.; Jing, D.L. Hydraulic and thermal performances of tree-like convergent microchannel heat sinks. Fractals 2022, 30, 2250096. [Google Scholar]
- Bejan, A. Constructal-theory network of conducting paths for cooling a heat generating volume. Trans. ASME J. Heat Transfer. 1997, 40, 799–816. [Google Scholar]
- Bejan, A. Street network theory of organization in nature. J. Adv. Transp. 1996, 30, 85–107. [Google Scholar] [CrossRef]
- Bejan, A.; Lorente, S. The constructal law and the evolution of design in nature. Phys. Life Rev. 2011, 8, 209–240. [Google Scholar] [CrossRef]
- Chen, L.; Feng, H.; Xie, Z.; Sun, F. Progress of constructal theory in China over the past decade. Int. J. Heat Mass Tran. 2019, 130, 393–419. [Google Scholar]
- Bejan, A. Heat Transfer: Evolution, Design and Performance; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Bejan, A. Theory of Flow Access with Apparent Obstacles: Cascades, Jumps, Roll Waves, and Turbulence. ASME Open J. Eng. 2022, 1, 011048. [Google Scholar]
- Ledezma, G.A.; Bejan, A.; Errera, M.R. Constructal tree networks for heat transfer. J. Appl. Phys. 1997, 82, 89–100. [Google Scholar] [CrossRef]
- Wei, S.; Chen, L.; Sun, F. The volume-point constructal optimization for discrete variable cross-section conducting path. Appl. Energy 2009, 86, 1111–1118. [Google Scholar] [CrossRef]
- Wei, S.; Chen, L.; Sun, F. Constructal optimization of discrete and continuous-variable cross-section conducting path based on entransy dissipation rate minimization. Sci. China Technol. Sci. 2010, 53, 1666–1677. [Google Scholar]
- Ghodoossi, L.; Egrican, N. Conductive cooling of triangular shaped electronics using constructal theory. Energy Convers. Manag. 2004, 45, 811–828. [Google Scholar] [CrossRef]
- Fagundes, T.M.; Yaghoobian, N.; Rocha, L.A.O. Constructal design of branched conductivity pathways inserted in a trapezoidal body: A numerical investigation of the effect of body shape on optimal pathway structure. Proc. Rom. Acad. Ser. A Math. Phys. Tech. Sci. Inform. Sci. 2018, 18, 297–302. [Google Scholar]
- Liu, H.L.; Li, B.T.; Hong, J. Generating constructal-conduction-networks for cooling discs at macro and micro scales. Int. Comm. Heat Mass. 2019, 109, 104318. [Google Scholar] [CrossRef]
- Li, Y.; Feng, M. Optimal design of conductive natural branched pathways for cooling a heat-generating volume. Heat Transfer. 2021, 50, 2571–2591. [Google Scholar] [CrossRef]
- Hajmohammadi, M.; Abianeh, V.A.; Moezzinajafabadi, M.; Daneshi, M. Fork-shaped highly conductive pathways for maximum cooling in a heat generating piece. Appl. Therm. Eng. 2013, 61, 228–235. [Google Scholar] [CrossRef]
- Lorenzini, G.; Biserni, C.; Rocha, L. Constructal design of X-shaped conductive pathways for cooling a heat-generating body. Int. J. Heat Mass Trans. 2013, 58, 513–520. [Google Scholar] [CrossRef]
- Lu, Z.; Zhang, K.; Liu, J.; Li, F. Effect of branching level on the performance of constructal theory based Y-shaped liquid cooling heat sink. Appl. Therm. Eng. 2020, 168, 114824. [Google Scholar] [CrossRef]
- Hajmohammadi, M.; Shariatzadeh, O.J.; Moulod, M.; Nourazar, S. Phi and Psi shaped conductive routes for improved cooling in a heat generating piece. Int. J. Therm. Sci. 2014, 77, 66–74. [Google Scholar] [CrossRef]
- Wu, W.; Chen, L.; Sun, F. Improvement of tree-like network constructal method for heat conduction optimization. Sci. China Ser. E Technol. Sci. 2006, 49, 332–341. [Google Scholar] [CrossRef]
- Wu, W.; Chen, L.; Xie, Z.; Sun, F. Improvement of constructal tree-like network for “volume-point” heat conduction with variable cross-section conducting path and without the premise of optimal last-order construct. Int. Comm. Heat Mass. 2015, 67, 97–103. [Google Scholar] [CrossRef]
- Wei, S.; Chen, L.; Sun, F. Constructal entransy dissipation minimization for “volume-point” heat conduction without the premise of optimized last-order construct. Int. J. Exergy 2010, 7, 627–639. [Google Scholar]
- Chen, S.; Miguel, A.F.; Aydin, M. Constructal design in the cooling and hydraulic performance of tube heat sinks. Int. Comm. Heat Mass. 2021, 129, 105668. [Google Scholar] [CrossRef]
- Wu, Z.; Feng, H.; Chen, L.; Xie, Z.; Cai, C. Pumping power minimization of an evaporator in ocean thermal energy conversion system based on constructal theory. Energy 2019, 181, 974–984. [Google Scholar]
- Mosa, M.; Labat, M.; Lorente, S. Constructal design of flow channels for radiant cooling panels. Int. J. Therm. Sci. 2019, 145, 106052. [Google Scholar] [CrossRef]
- Hajmohammadi, M.R.; Bahrami, M.; Ahmadian-Elmi, M. Thermal performance improvement of microchannel heat sinks by utilizing variable cross-section microchannels filled with porous media. Int. Comm. Heat Mass. 2021, 126, 105360. [Google Scholar]
- Gosselin, L.; Bejan, A. Constructal heat trees at micro and nanoscales. J. Appl. Phys. 2004, 96, 5852–5859. [Google Scholar] [CrossRef]
- You, J.; Feng, H.; Chen, L.; Xie, Z. Constructal optimization for “disc-point” heat conduction with nonuniform heat generation. Int. J. Heat Mass Trans. 2019, 134, 1191–1198. [Google Scholar]
- Samal, B.; Barik, A.K.; Awad, M.M. Thermo-fluid and entropy generation analysis of newly designed loops for constructal cooling of a square plate. Appl. Thermal Eng. 2019, 156, 250–262. [Google Scholar]
- Zhu, H.; Chen, L.; Ge, Y.; Feng, H. Constructal entropy generation rate minimization of heat conduction for leaf-shaped quadrilateral heat generation body. Eur. Phys. J. Plus 2022, 137, 275. [Google Scholar]
- Dadsetani, R.; Sheikhzadeh, G.A.; Safaei, M.R.; Leon, A.S.; Goodarzi, M. Cooling enhancement and stress reduction optimization of disk-shaped electronic components using nanofluids. Symmetry 2020, 12, 931. [Google Scholar] [CrossRef]
- Chen, C.; You, J.; Feng, H.; Chen, L. A multi-objective study on the constructal design of non-uniform heat generating disc cooled by radial- and dendritic-pattern cooling channels. Sci. China Technol. Sci. 2021, 64, 729–744. [Google Scholar]
- Guo, Z.-Y.; Zhou, S.-Q.; Li, Z.-X.; Chen, L.-G. Uniformity principle of temperature difference field in heat exchanger. Sci. China Ser. E 1996, 26, 25–31. (In Chinese) [Google Scholar]
- Guo, Z.; Zhou, S.; Li, Z.; Chen, L. Theoretical analysis and experimental confirmation of the uniformity principle of temperature difference field in heat exchanger. Int. J. Heat Mass Trans. 2002, 45, 2119–2127. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, Q.; Liang, X. Analyses of entransy dissipation, entropy generation and entransy-dissipation-based thermal resistance on heat exchanger optimization. Appl. Therm. Eng. 2012, 38, 31–39. [Google Scholar]
- Fu, R.H.; Zhang, X. A rigorous proof for the uniformity principle of temperature difference field in heat exchanger with deductive method. Int. J. Heat Mass Trans. 2017, 114, 135–144. [Google Scholar]
- Guo, Z.; Zhu, H.; Liang, X. Entransy-A physical quantity describing heat transfer ability. Int. J. Heat Mass Trans. 2007, 50, 2545–2556. [Google Scholar] [CrossRef]
- Chen, X.; Liang, X. Uniformity principle of temperature difference field in heat transfer optimization. Chin. Phys. B 2019, 28, 064402. [Google Scholar] [CrossRef]


| Construct Order i | ||||||
|---|---|---|---|---|---|---|
| Element area | ||||||
| First-order construct | 2 | 1/2 | ||||
| Second- and higher-order constructs | Degenerate into first-order construct | |||||
| Construct Order i | ||||||
|---|---|---|---|---|---|---|
| Element area | ||||||
| First-order construct | 2 | 1/2 | ||||
| Second- and higher-order construct | Degenerate into first-order construct | |||||
| Construct Order i | ||||||
|---|---|---|---|---|---|---|
| Element area | ||||||
| First-order construct | 2 | 1/2 | ||||
| Second- and higher-order construct | Degenerate into first-order construct | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, S.; Wang, D. Improvement of Constructal Optimization for “Volume-Point” Heat Conduction Based on Uniformity Principle of Temperature Difference Fields. Mathematics 2023, 11, 3466. https://doi.org/10.3390/math11163466
Wei S, Wang D. Improvement of Constructal Optimization for “Volume-Point” Heat Conduction Based on Uniformity Principle of Temperature Difference Fields. Mathematics. 2023; 11(16):3466. https://doi.org/10.3390/math11163466
Chicago/Turabian StyleWei, Shuhuan, and Dini Wang. 2023. "Improvement of Constructal Optimization for “Volume-Point” Heat Conduction Based on Uniformity Principle of Temperature Difference Fields" Mathematics 11, no. 16: 3466. https://doi.org/10.3390/math11163466
APA StyleWei, S., & Wang, D. (2023). Improvement of Constructal Optimization for “Volume-Point” Heat Conduction Based on Uniformity Principle of Temperature Difference Fields. Mathematics, 11(16), 3466. https://doi.org/10.3390/math11163466





