On the Fundamental Diagram for Freeway Traffic: Exploring the Lower Bound of the Fitting Error and Correcting the Generalized Linear Regression Models
Abstract
1. Introduction
2. Correcting Generalized Linear Regression Models
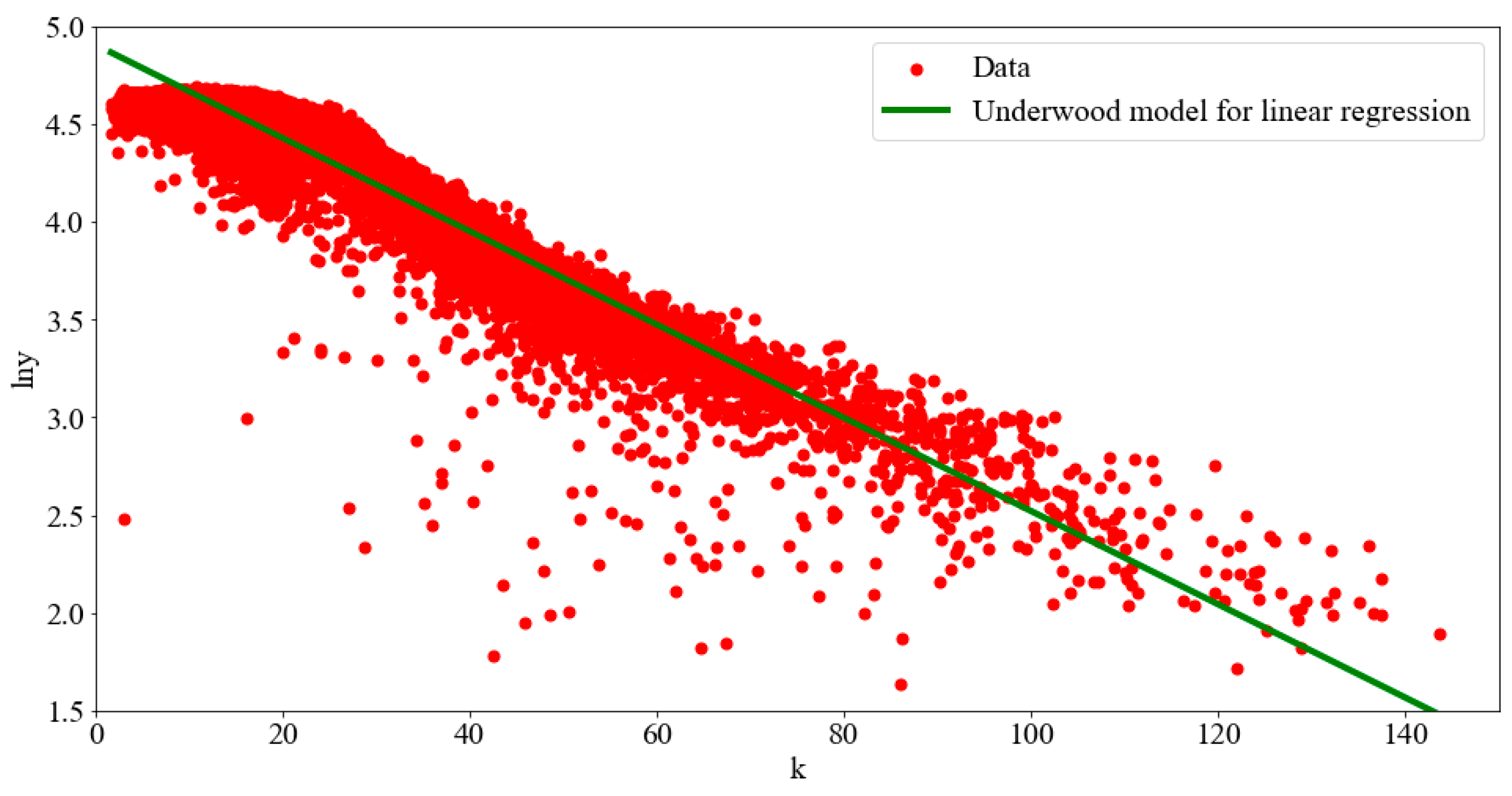
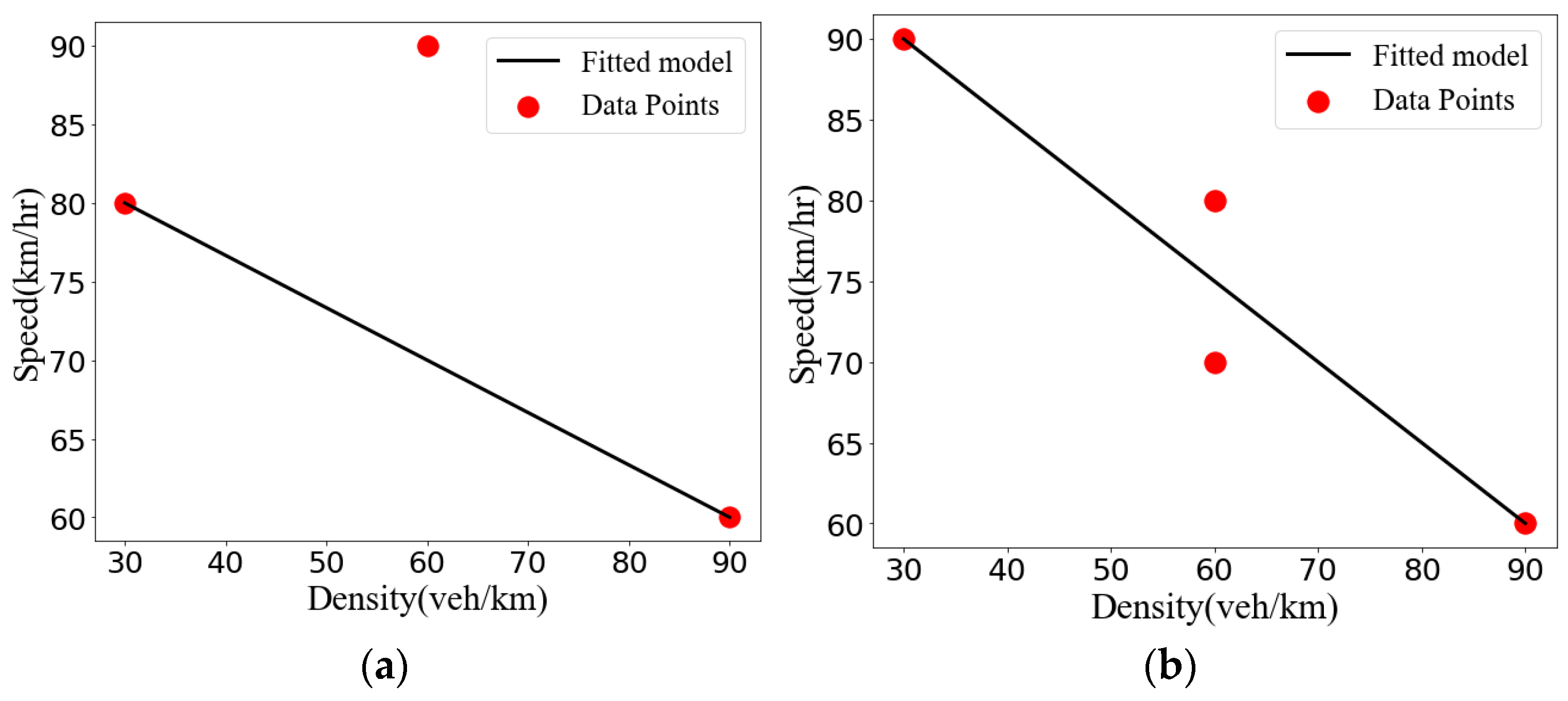
2.1. Analysis
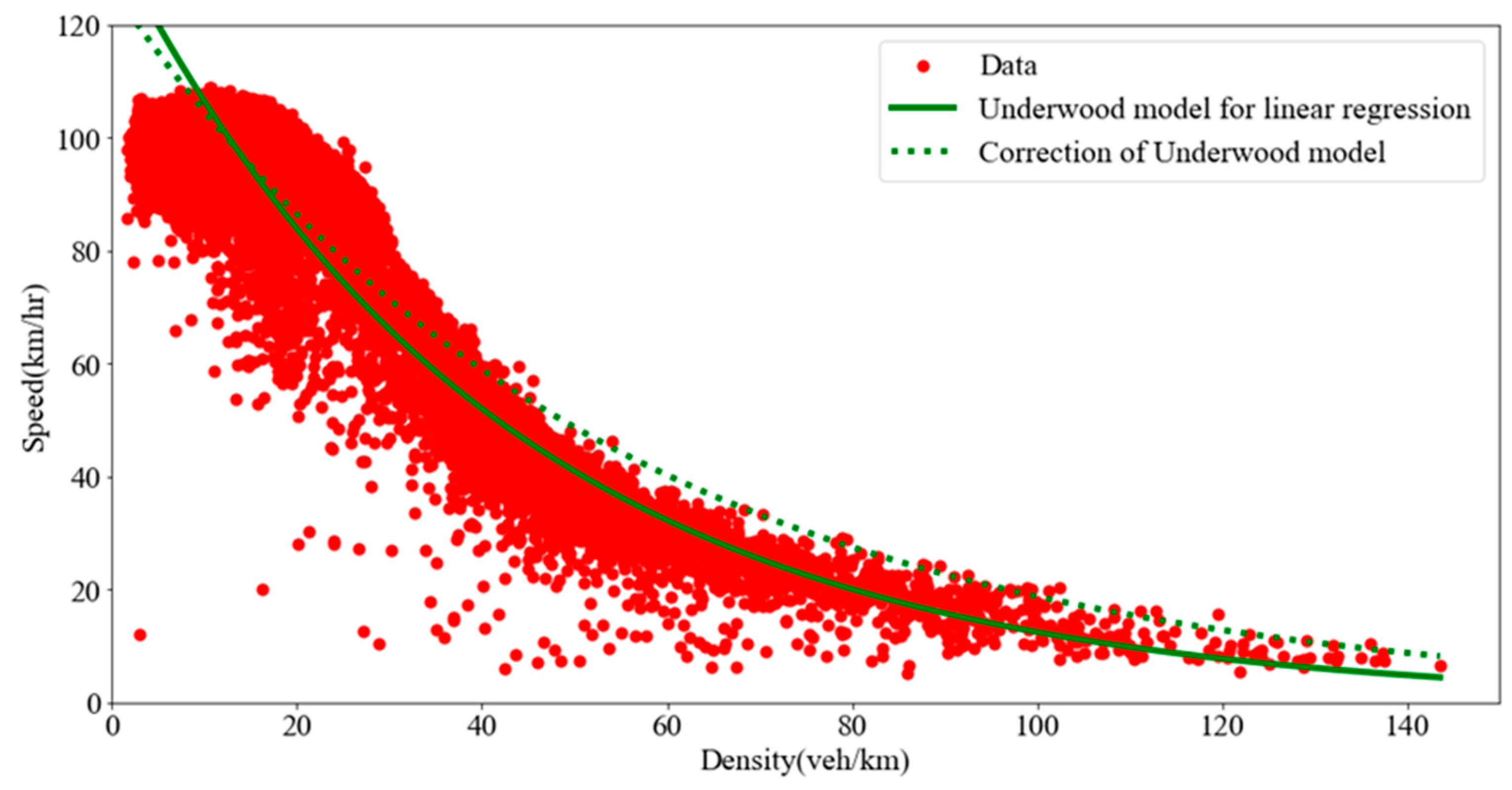
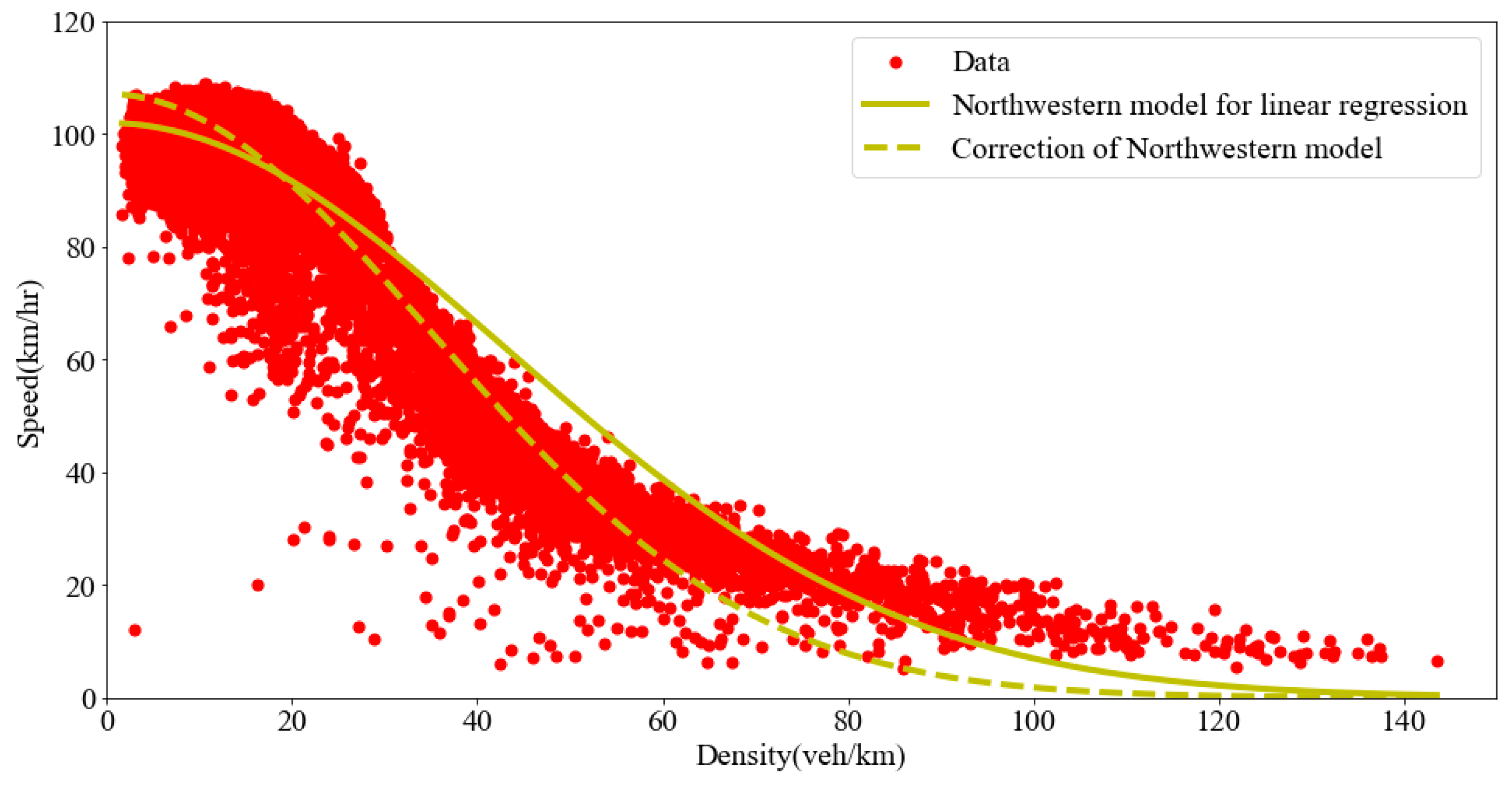
2.2. Correction
| Algorithm 1: An enumeration algorithm. |
| Input: A set of candidate pairs of parameters . Output: The minimum MSE, the optimal values of parameters. denotes the MSE value of the pair of parameters ; the minimum MSE and its corresponding optimal parameters are denoted as , , . Initialize the , , . For do: For do: Calculate the MSE value for the pair of parameters . If do: , , End if End for End for |
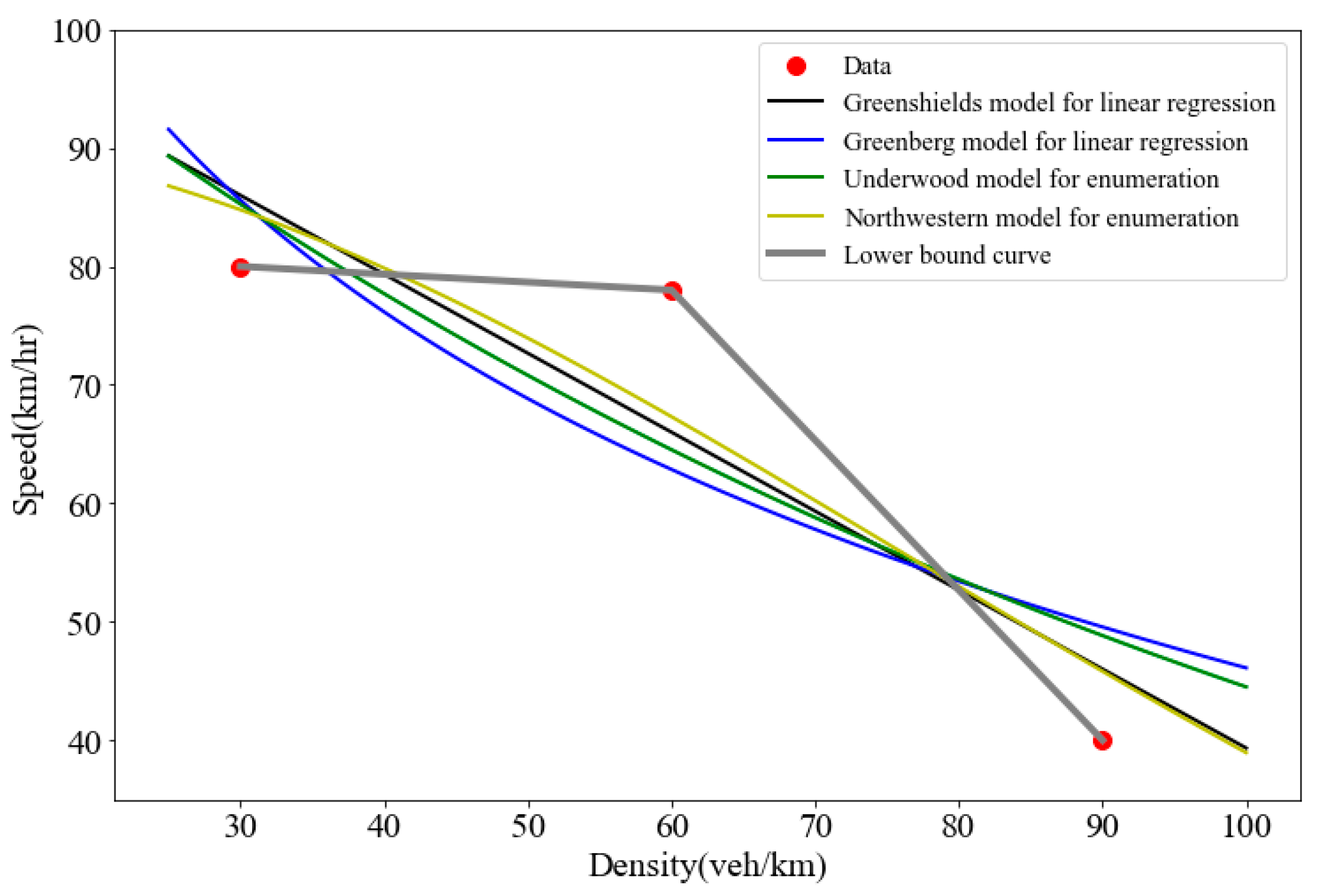
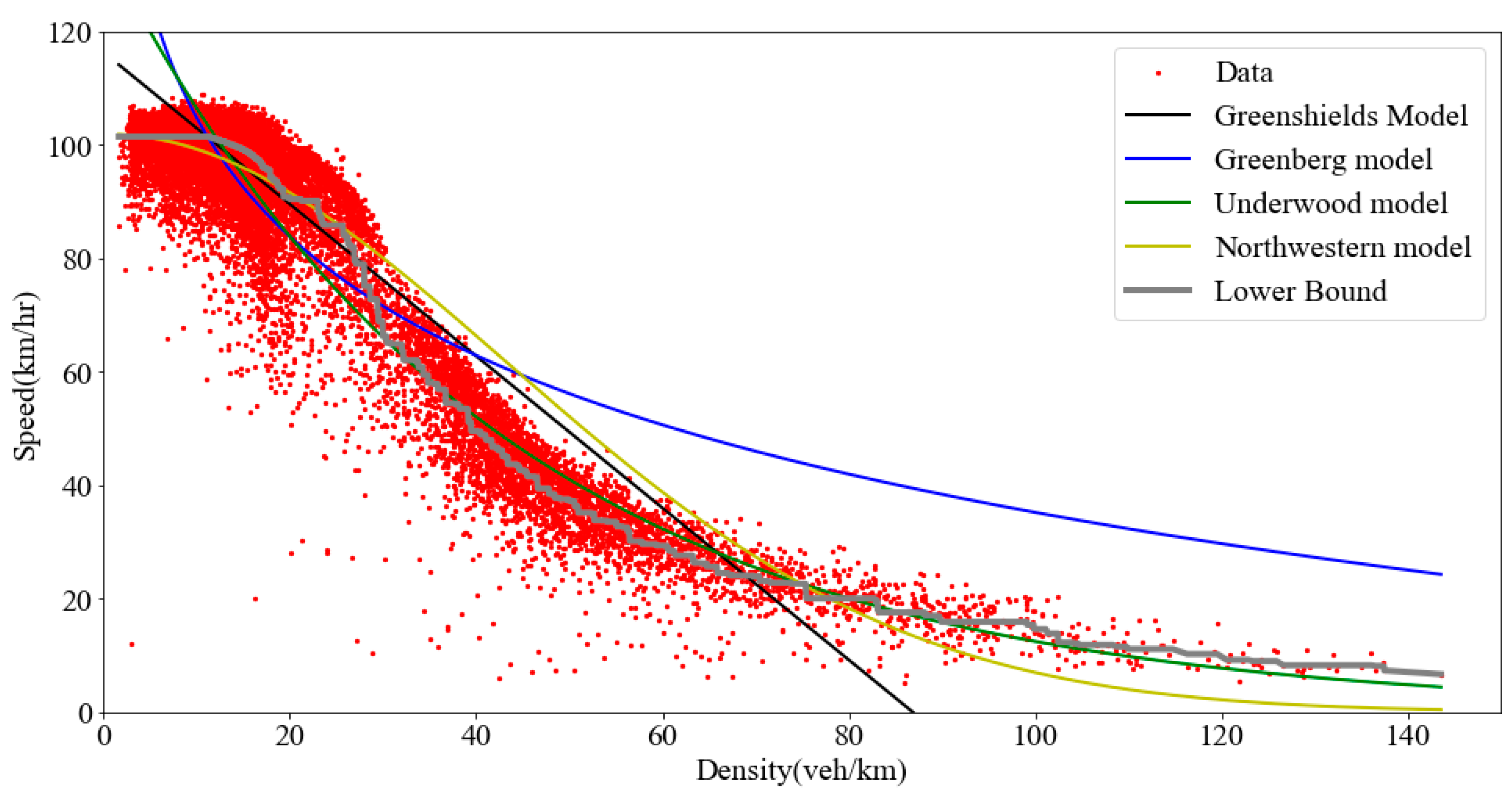
3. Lower Bound of the Fitting Error of Existing Models
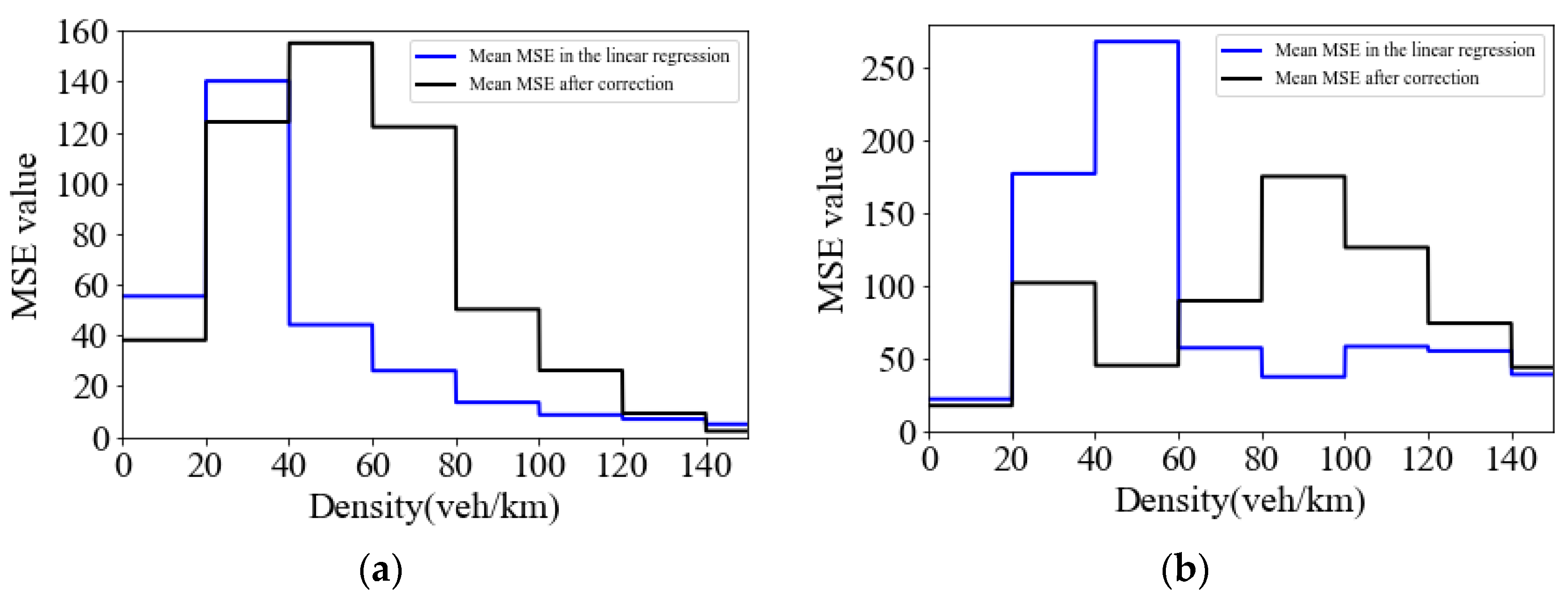
3.1. MSE Values of Existing Models
3.2. Quadratic Programming Model
3.3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Greenshields, B.D.; Bibbins, J.R.; Channing, W.S.; Miller, H.H. A study of traffic capacity. Highw. Res. Board Proc. 1935, 14, 448–477. [Google Scholar]
- Haight, F.A. Mathematical Theories of Traffic Flow; Academic Press: London, UK, 1963. [Google Scholar]
- Greenberg, H. An analysis of traffic flow. Oper. Res. 1959, 7, 255–275. [Google Scholar] [CrossRef]
- Edie, L.C. Car-following and steady state theory for non-congested traffic. Oper. Res. 1961, 9, 66–76. [Google Scholar] [CrossRef]
- Underwood, R.T. Speed, Volume, and Density Relationship: Quality and Theory of Traffic Flow; Yale Bureau of Highway Traffic: New Haven, CT, USA, 1961; pp. 141–188. [Google Scholar]
- Newell, G.F. Nonlinear effects in the dynamics of car following. Oper. Res. 1961, 9, 209–229. [Google Scholar] [CrossRef]
- Kerner, B.S.; Konhäuser, P. Structure and parameters of clusters in traffic flow. Phys. Rev. 1994, 50, 54–83. [Google Scholar] [CrossRef]
- Del Castillo, J.M.; Benítez, F.G. On the functional form of the speed-density relationship—I: General theory. Transp. Res. Part B Methodol. 1995, 29, 373–389. [Google Scholar] [CrossRef]
- Del Castillo, J.M.; Benítez, F.G. On the functional form of the speed-density relationship—II: Empirical investigation. Transp. Res. Part B Methodol. 1995, 29, 391–406. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.M. Fundamental diagram of traffic flow: New identification scheme and further evidence from empirical data. Transp. Res. Rec. 2001, 2011, 50–59. [Google Scholar] [CrossRef]
- Wu, N. A new approach for modelling of fundamental diagrams. Transp. Res. Part A Policy Pract. 2002, 36, 867–884. [Google Scholar] [CrossRef]
- MacNicholas, M.J. A simple and pragmatic representation of traffic flow. In Symposium on The Fundamental Diagram: 75 Years; Transportation Introduction Research Board: Woods Hole, MA, USA, 2008. [Google Scholar]
- Wang, H.; Li, H.; Chen, Q.; Ni, D. Logistic modeling of the equilibrium speed–density relationship. Transp. Res. Part A Policy Pract. 2011, 45, 554–566. [Google Scholar] [CrossRef]
- Wu, X.; Liu, H.X.; Geroliminis, N. An empirical analysis on the arterial fundamental diagram. Transp. Res. Part B Methodol. 2011, 45, 255–266. [Google Scholar] [CrossRef]
- Dervisoglu, G. Automatic Calibration of Freeway Models with Model-Based Sensor Fault Detection; University of California: Berkeley, CA, USA, 2012. [Google Scholar]
- Keyvan-Ekbatani, M.; Kouvelas, A.; Papamichail, I.; Papageorgiou, M. Exploiting the fundamental diagram of urban networks for feedback-based gating. Transp. Res. Part B Methodol. 2012, 46, 1393–1403. [Google Scholar] [CrossRef]
- Keyvan-Ekbatani, M.; Papageorgiou, M.; Papamichail, I. Urban congestion gating control based on reduced operational network fundamental diagrams. Transp. Res. Part C Emerg. Technol. 2013, 33, 74–87. [Google Scholar] [CrossRef]
- Keyvan-Ekbatani, M.; Papageorgiou, M.; Knoop, V.L. Controller design for gating traffic control in presence of time-delay in urban road networks. Transp. Res. Part C Emerg. Technol. 2015, 59, 308–322. [Google Scholar] [CrossRef]
- Qu, X.; Wang, S.; Zhang, J. On the fundamental diagram for freeway traffic: A novel calibration approach for single-regime models. Transp. Res. Part B Methodol. 2015, 73, 91–102. [Google Scholar] [CrossRef]
- Drake, J.S.; Schofer, J.L.; May, A.D. A statistical analysis of speed–density hypotheses. Highway Res. Rec. 1967, 154, 112–117. [Google Scholar]
- Fan, S.; Seibold, B. Data-fitted first-order traffic models and their second-order generalizations. Transport. Res. Rec. 2013, 2391, 32–43. [Google Scholar] [CrossRef]
- Qu, X.; Zhang, J.; Wang, S. On the stochastic fundamental diagram for freeway traffic: Model development, analytical properties, validation, and extensive applications. Transp. Res. Part B Methodol. 2017, 104, 256–271. [Google Scholar] [CrossRef]
- Wang, S.; Chen, X.; Qu, X. Model on empirically calibrating stochastic traffic flow fundamental diagram. Commun. Transp. Res. 2021, 1, 100015. [Google Scholar] [CrossRef]
- Bramich, D.M.; Menéndez, M.; Ambühl, L. Fitting empirical fundamental diagrams of road traffic: A comprehensive review and comparison of models using an extensive data set. IET Intell. Transp. Syst. 2022, 23, 14104–14127. [Google Scholar] [CrossRef]
- Jabeena, M. Comparative study of traffic flow models and data retrieval methods from video graphs. Int. J. Eng. Res. Appl. 2013, 3, 1087–1093. [Google Scholar]
- Li, Y.; Lu, H.; Bian, C.; Sui, Y.G. Traffic speed-flow model for the mix traffic flow on Beijing urban expressway. In Proceedings of the 2009 International Conference on Measuring Technology and Mechatronics Automation, Zhangjiajie, China, 11–12 April 2009; Volume 3, pp. 641–644. [Google Scholar]
- Banos, A.; Corson, N.; Lang, C.; Marilleau, N.; Taillandier, P. Multiscale modeling: Application to traffic flow. Agent-Based Spat. Simul. NetLogo 2017, 2, 37–62. [Google Scholar]
- Anuar, K.; Habtemichael, F.; Cetin, M. Estimating traffic flow rate on freeways from probe vehicle data and fundamental diagram. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Gran Canaria, Spain, 15–18 September 2015; pp. 2921–2926. [Google Scholar]
- Wang, H.; Ni, D.; Chen, Q.Y.; Li, J. Stochastic modelling of the equilibrium speed-density relationship. J. Adv. Transp. 2013, 47, 126–150. [Google Scholar] [CrossRef]
- Zhang, J.; Qu, X.; Wang, S. Reproducible generation of experimental data sample for calibrating traffic flow fundamental diagram. Transport. Res. Part A Policy Pract. 2018, 111, 41–52. [Google Scholar] [CrossRef]
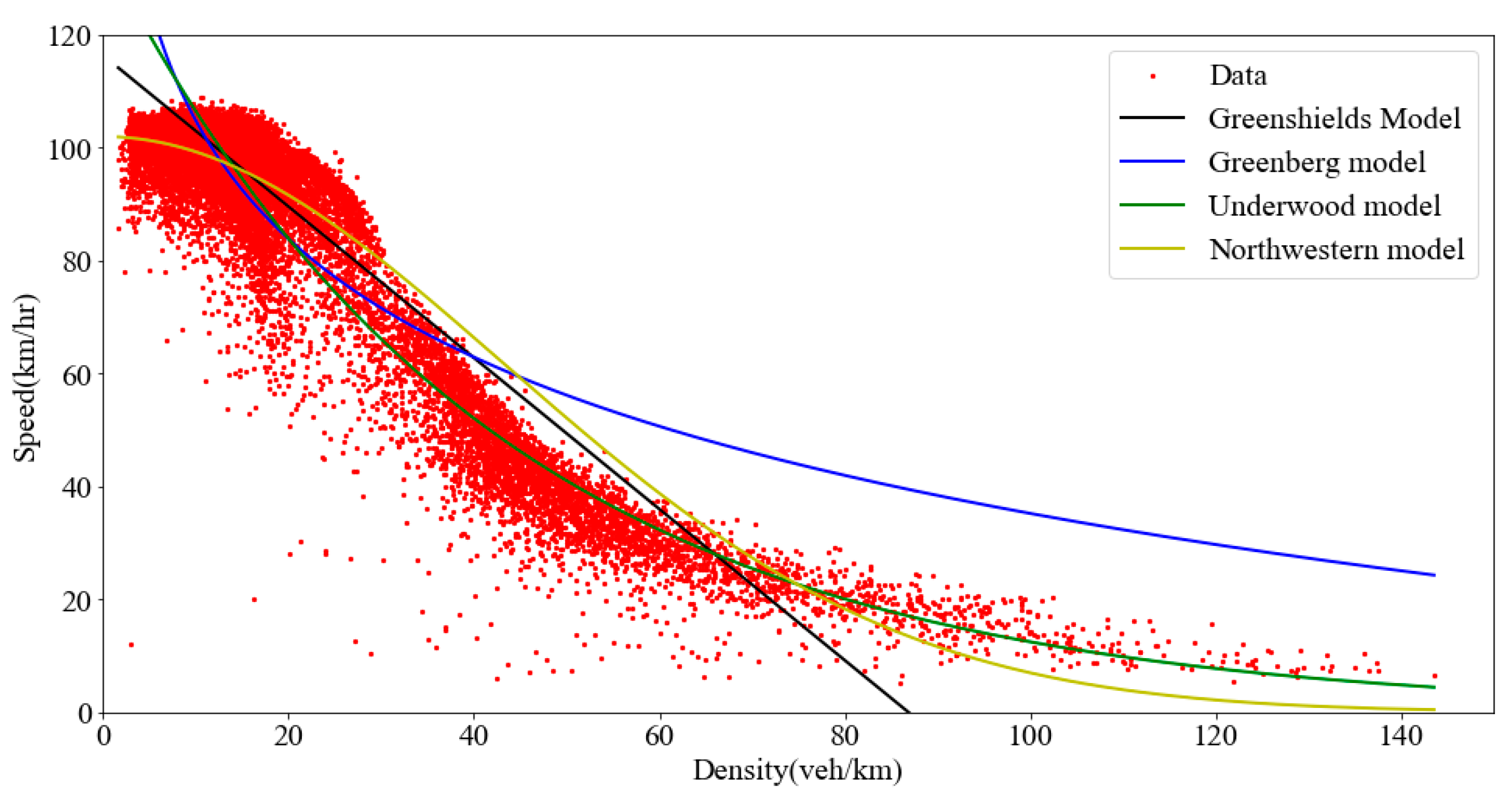
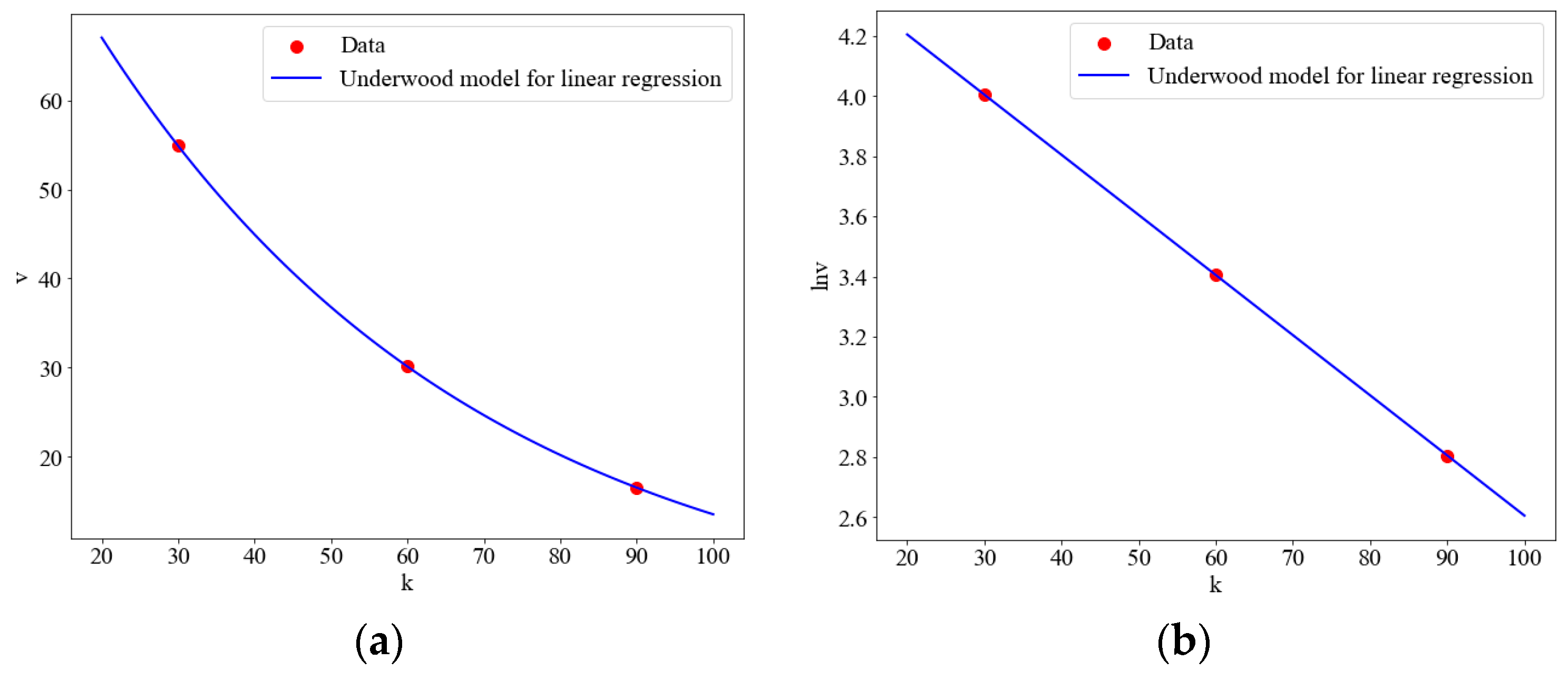
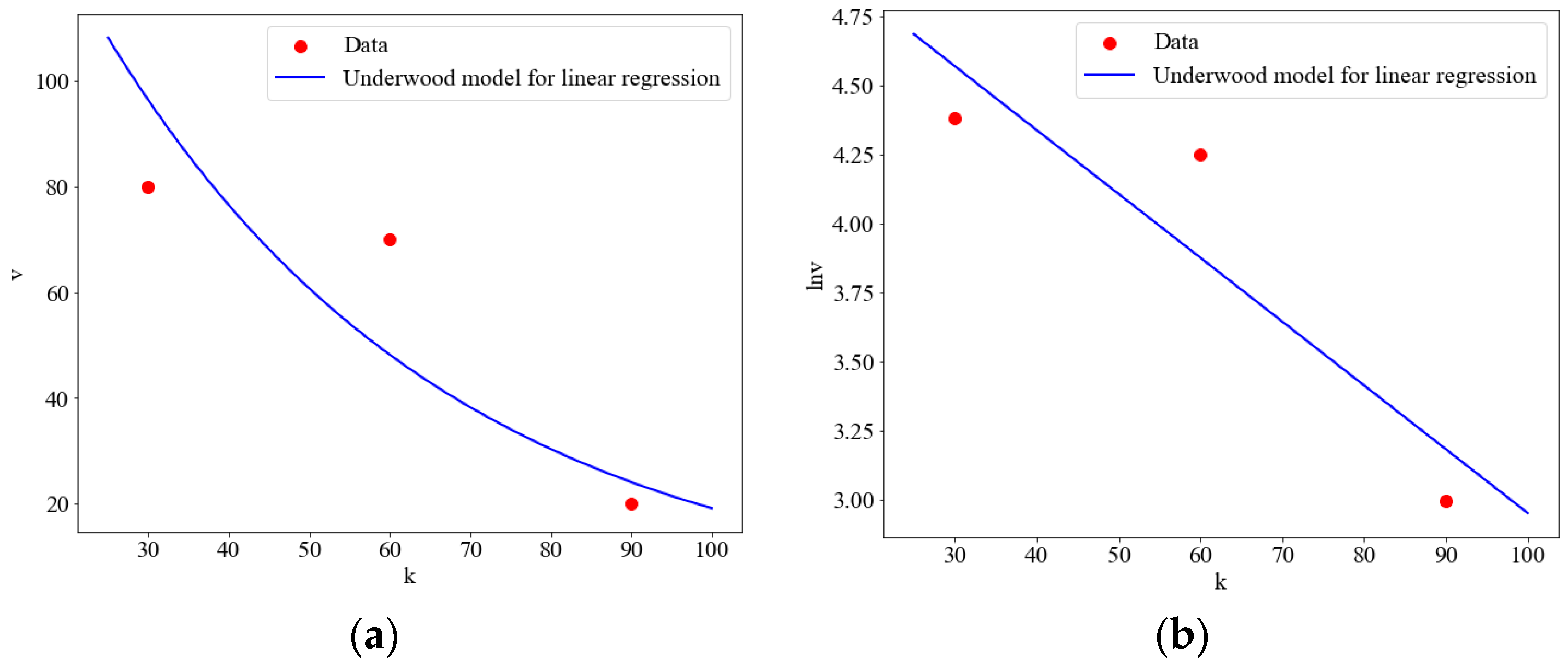
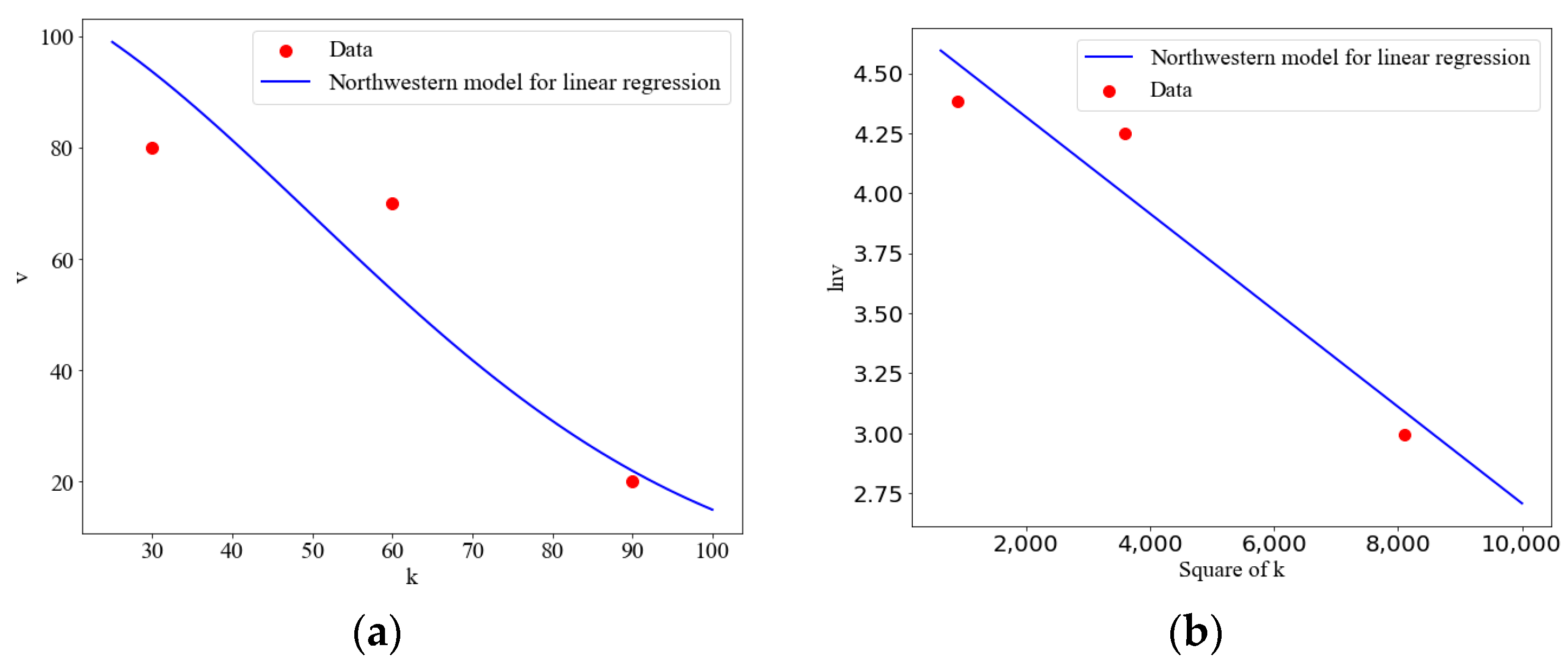


| Models | Function | Parameters |
|---|---|---|
| Greenshields [1] | , | |
| Greenberg [3] | , | |
| Underwood [5] | , | |
| Northwestern [20] | , |
| Models | Function | Transformation | Original MSE | Corrected MSE |
|---|---|---|---|---|
| Greenshields (Greenshields et al., 1935) [1] | , | 46.727 | 46.727 | |
| Greenberg (1959) [3] | , | 107.948 | 107.948 | |
| Underwood (1961) [5] | , | 59.4544 | 50.3609 | |
| Northwestern (Drake et al., 1967) [20] | , | 44.3233 | 25.9371 |
| Models | Corrected MSE |
|---|---|
| Greenshields (Greenshields et al., 1935) [1] | 72.0000 |
| Greenberg (1959) [3] | 117.3113 |
| Underwood (1961) [5] | 95.7534 |
| Northwestern (Drake et al., 1967) [20] | 57.0006 |
| Models | MSE | Relative Gap |
|---|---|---|
| Greenshields [1] | 46.7270 | 137.603% |
| Greenberg [3] | 107.9480 | 457.583% |
| Underwood [5] | 50.3609 | 160.129% |
| Northwestern [20] | 25.9371 | 33.973% |
| Average value | 57.8053 | 197.322% |
| Sample Size | MSE Values for Linear Regression | MSE Values after Correction | MSE Values for Lower Bound | Relative Gap for Linear Regression | Relative Gap for Corrected Results | |
|---|---|---|---|---|---|---|
| 1 | 100 | 79.266 | 67.860 | 24.084 | 229.126% | 181.766% |
| 2 | 100 | 44.656 | 43.402 | 10.827 | 312.444% | 300.863% |
| 3 | 500 | 62.533 | 50.326 | 14.262 | 338.467% | 252.871% |
| 4 | 500 | 68.246 | 58.360 | 18.631 | 266.316% | 213.249% |
| 5 | 1000 | 57.880 | 48.574 | 16.318 | 254.691% | 197.667% |
| 6 | 1000 | 53.204 | 44.782 | 12.246 | 334.443% | 265.675% |
| 7 | 5000 | 61.323 | 51.584 | 19.455 | 215.196% | 165.137% |
| 8 | 5000 | 58.771 | 50.546 | 18.529 | 217.175% | 172.787% |
| 9 | 10,000 | 59.292 | 50.461 | 19.010 | 211.899% | 165.446% |
| 10 | 10,000 | 60.492 | 51.296 | 19.657 | 207.732% | 160.950% |
| 11 | 30,000 | 59.321 | 49.987 | 18.852 | 214.672% | 165.157% |
| 12 | 30,000 | 59.220 | 50.062 | 19.505 | 203.620% | 156.668% |
| Sample Size | MSE Values for Linear Regression | MSE Values after Correction | MSE Values for Lower Bound | Relative Gap for Linear Regression | Relative Gap for Corrected Results | |
|---|---|---|---|---|---|---|
| 1 | 100 | 26.520 | 26.288 | 15.640 | 69.562% | 68.082% |
| 2 | 100 | 99.182 | 65.021 | 24.821 | 299.583% | 161.955% |
| 3 | 500 | 29.822 | 24.064 | 16.680 | 78.787% | 44.271% |
| 4 | 500 | 43.881 | 29.784 | 17.6181 | 149.064% | 69.054% |
| 5 | 1000 | 38.354 | 23.915 | 15.793 | 142.859% | 51.433% |
| 6 | 1000 | 49.473 | 23.244 | 14.825 | 233.723% | 56.790% |
| 7 | 5000 | 52.530 | 28.479 | 20.810 | 152.427% | 36.852% |
| 8 | 5000 | 49.058 | 27.132 | 19.101 | 156.829% | 42.045% |
| 9 | 10,000 | 40.869 | 24.552 | 17.541 | 132.990% | 39.969% |
| 10 | 10,000 | 46.855 | 25.510 | 18.658 | 151.124% | 36.722% |
| 11 | 30,000 | 43.821 | 26.410 | 19.684 | 122.624% | 34.172% |
| 12 | 30,000 | 43.286 | 26.440 | 19.655 | 120.226% | 34.521% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shangguan, Y.; Tian, X.; Jin, S.; Gao, K.; Hu, X.; Yi, W.; Guo, Y.; Wang, S. On the Fundamental Diagram for Freeway Traffic: Exploring the Lower Bound of the Fitting Error and Correcting the Generalized Linear Regression Models. Mathematics 2023, 11, 3460. https://doi.org/10.3390/math11163460
Shangguan Y, Tian X, Jin S, Gao K, Hu X, Yi W, Guo Y, Wang S. On the Fundamental Diagram for Freeway Traffic: Exploring the Lower Bound of the Fitting Error and Correcting the Generalized Linear Regression Models. Mathematics. 2023; 11(16):3460. https://doi.org/10.3390/math11163460
Chicago/Turabian StyleShangguan, Yidan, Xuecheng Tian, Sheng Jin, Kun Gao, Xiaosong Hu, Wen Yi, Yu Guo, and Shuaian Wang. 2023. "On the Fundamental Diagram for Freeway Traffic: Exploring the Lower Bound of the Fitting Error and Correcting the Generalized Linear Regression Models" Mathematics 11, no. 16: 3460. https://doi.org/10.3390/math11163460
APA StyleShangguan, Y., Tian, X., Jin, S., Gao, K., Hu, X., Yi, W., Guo, Y., & Wang, S. (2023). On the Fundamental Diagram for Freeway Traffic: Exploring the Lower Bound of the Fitting Error and Correcting the Generalized Linear Regression Models. Mathematics, 11(16), 3460. https://doi.org/10.3390/math11163460










