Abstract
When we apply comparative phylogenetic analyses to genome data, it poses a significant problem and challenge that some of the given species (or taxa) often have missing genes (i.e., data). In such a case, we have to impute a missing part of a gene tree from a sample of gene trees. In this short paper, we propose a novel method to infer the missing part of a phylogenetic tree using an analogue of a classical linear regression in the setting of tropical geometry. In our approach, we consider a tropical polytope, a convex hull with respect to the tropical metric closest to the data points. We show a condition that we can guarantee that an estimated tree from the method has at most a Robinson–Foulds (RF) distance of four from the ground truth, and computational experiments with simulated data and empirical data from Clavicipitaceae, which contains more than 4000 genes, show the method works well.
MSC:
92B15
1. Introduction
Due to new technology, today we are able to generate sequences from the genome with lower cost. However, at the same time, we have a great challenge to analyze large scale datasets from genome sequences. In phylogenomics, a new field that applies tools from phylogenetics to genome datasets, we often conduct comparative phylogenetic analyses, that is, to compare evolutionary histories among a set of taxa between different genes from the genome (for example, see [1]). However, we often face the problem in this process that some taxa in the dataset have missing gene(s) [2,3]. When this happens, systematists infer missing part of a gene tree from other gene trees using a supervised learning method, such as the linear regression model.
A phylogenetic tree is a weighted tree which represents evolutionary history of a given set of taxa (or species). In phylogenetic trees, leaves represent species or taxa in the present time which we can observe and internal nodes in the tree, which represent ancestors of the species, do not have any labels. A gene tree is a phylogenetic tree reconstructed from an alignment of a gene in a genome. Gene trees with the same set of species or taxa do not have to have the same tree topology since each gene might have different mutation rates due to the selection pressures, etc. [4]. In a comparative phylogenetic analysis, we often compare gene trees (for example, we compare how they are different, how their mutation rates are different, and often we are interested in inferring the species tree).
To infer a missing part of a gene tree, we often apply a supervised method to regress the missing part. In this process, first, we compute an unique vector representation of each gene tree. Then we infer the missing components of the vector of the tree from the vectors computed from other gene trees in a dataset using a regression model, such as a multiple linear regression [3].
However, a set of all such vectors realizing all possible phylogenetic trees, which is called a space of phylogenetic trees, is not Euclidean. In fact, a space of phylogenetic trees is an union of polyhedral cones with a large co-dimension, so this is not even convex in terms of Euclidean metrics. Therefore, it is not appropriate to apply classical regression models, such as linear regression or neural networks, since they assume convexity in terms of Euclidean geometry. Thus, in this short paper, we propose an analogue of a classical multiple linear regression in the setting of tropical geometry with the max-plus algebra—an application of tropical polytopes to infer the missing part of a phylogenetic tree.
Equidistant trees are used to model gene trees under the multi-species coalescent model [4]. Therefore, in this paper, we focus on an equidistant tree, which is a rooted phylogenetic tree such that the total weight on an unique path from its root to each leaf is the same, and we focus on the space of all possible equidistant trees. It is well-known that the space of all possible equidistant trees is a tropical Grassmannian, which means that it is a tropically linear space with respect to the tropical metric [5,6,7]. Therefore, with the tropical metric with the max-plus algebra, we can conduct statistical analyses using tropical linear algebra, which is an analogue of a classical linear algebra. In fact, there has been much development in statistical learning over the space of phylogenetic trees using tools from tropical geometry [7,8,9,10,11,12].
Since a tropical polytope is tropically convex and since the space of equidistant trees is tropically convex, if all vertices are equidistant trees, then a tropical polytope is contained in the space of equidistant trees. Thus, in this paper, we propose to use a tropical polytope over the space of equidistant trees to infer missing part of a phylogenetic trees. This proposed method has basically four main step: (1) compute induced trees on the set of leaves which we observe in T, a tree with missing leaf (leaves) from a training set; (2) compare T with these induced trees; (3) compute a tropical polytope with trees with full set of leaves whose induced trees have closest tree topologies with T; and (4) project T onto the tropical polytope computed in step (3).
In Section 2, we discuss basics from tropical geometry and in Section 3, we discuss basics from phylogenetics. In Section 4, we show our novel method to impute a missing part of a phylogenetic tree. Then, in Section 5, we show a theoretical condition of T that the worst case scenario for the estimated tree via our method has the Robinson–Foulds distance at most 4. Then, Section 6 shows computational experiments of our method against other methods including a multiple linear regression and our method performs well.
2. Basics in Tropical Geometry
In this section, we discuss basics from tropical geometry. We consider the tropical projective torus, where is the vector with all ones in . Basically this means that any vectors in is invariant with , i.e., for any element . For more details, see [13,14].
Under the tropical semiring , the tropical arithmetic operations of addition and multiplication are defined as:
For any scalars and for any vectors , we have tropical scalar multiplication and tropical vector addition defined as:
Definition 1.
Suppose we have a set . If
for any and for any , then S is called tropically convex. Suppose we have a finite subset . Then, the smallest tropically-convex subset containing V is called the tropical convex hull or tropical polytope of V. can also be written as:
A tropical line segment, , between two points is a tropical convex hull of .
Example 1.
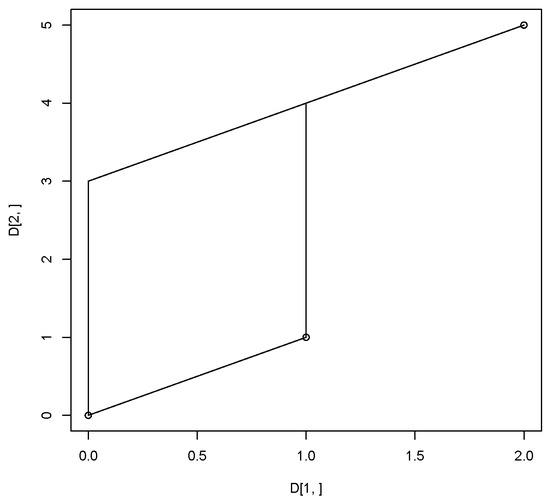
Suppose we have three points . Then the tropical convex hull of these three points is shown in Figure 1.

Figure 1.
Tropical polytope of three points .
Remark 1.
By the definition, if a set is tropically convex, then a tropical line segment between any two points in S must be contained in S.
Definition 2.
For any points , the tropical metric), , between v and w is defined as:
Example 2.
Suppose we have points . Then we have the distance between these two points in terms of the tropical metric is
Definition 3.
Let and let be a tropical polytope with its vertex set V. For , let
Then is a projection onto P with the property such that
for all .
Example 3.
Suppose we have three points . Also suppose the tropical convex hull P of these three points. Suppose we have a point . Then,
Thus, we have
Thus, .
3. Basics in Phylogenetic Trees
Let . A phylogenetic tree T on is a weighted tree of m leaves with the labels and internal nodes in the tree not labeled. A subtree in T on is a subtree of T with leaves a. An equidistant tree on is a rooted phylogenetic tree on such that the total weight on the path from its root to each leaf i in has the same distance for each . In this paper, we assume on equidistant trees.
In order to conduct a statistical analysis, we have to convert a phylogenetic tree into a vector. Here, we discuss one way to convert a phylogenetic tree into a vector.
Definition 4.
Suppose we have a dissimilarity map such that
If there exists a phylogenetic tree on such that is the total weight on the unique path from a leaf to a leaf , then we call D as a tree metric.
Remark 2.
Since a tree metric of a phylogenetic tree on is symmetric and its diagonal is 0, we consider an upper triangular matrix of the tree metric and we consider the upper triangular matrix of the tree metric as a vector in .
Definition 5.
Let be a metric over , namely, D is a map from to such that
Suppose D is a metric on . Then if D satisfies
is attained at least twice for any , then D is called an ultrametric.
Example 4.
Suppose we have and
Then, D is an ultrametric.
It is well-known that if we have an ultrametric on , then there is an unique equidistant tree on by the following theorem:
Theorem 1
([15]). Suppose we have an equidistant tree T with a leaf label set and suppose for all is the distance from a leaf i to a leaf j. Then, D is an ultrametric if and only if T is an equidistant tree on .
Therefore by Theorem 1, in this paper, we consider the set of ultrametrics, , on m as the space of equidistant trees on .
Definition 6.
Let such that and . Suppose we have an equidistant phylogenetic tree T with the leave set . A clade of T with leaves is an equidistant tree on x constructed from T by adding all common ancestral interior nodes of any combinations of only leaves x and excluding common ancestors including any leaf from in T, and all edges in T connecting to these ancestral interior nodes and leaves x.
Definition 7.
For a rooted phylogenetic tree, a nearest neighbor interchange (NNI) is an operation of a phylogenetic tree to change its tree topology by picking three mutually exclusive leaf sets and changing a tree topology of the clade, possibly the whole tree, consisting with three distinct clades with leaf sets , , and .
Remark 3.
Since there are three possible ways of connecting three distinct clades, NNI possibly creates two new tree topologies on .
Definition 8.
Suppose we have rooted phylogenetic trees on . The Robinson–Foulds (RF) distance is the number of operations that the subtree of has the same tree topology as the subtree of by removing a leaf of and the subtree of has the same tree topology as the subtree of by removing a leaf of .
Remark 4.
The Robinson–Foulds distance is always divisible by 2.
Remark 5.
One can see that the Robinson–Foulds distance between two trees which is one NNI move apart is 2.
4. Method
In this section, we introduce a method to infer a missing part of an equidistant tree using tools from tropical geometry. Let be the Robinson–Foulds distance between and . The algorithm on this method is shown in Algorithm 1.
| Algorithm 1: Imputation with a tropical polytope |
 |
5. Theoretical Results
Let such that and . Let be a sample of equidistant trees with m leaves. Let for be an equidistant tree with x by dropping tips y from , i.e., is an induced tree on a.
Theorem 2.
Suppose is a sample of equidistant trees with and let such that is a subtree on x which is an equidistant tree with x by dropping tips y from and is an subgraph graph with y by adding all common ancestral interior nodes of any combinations of only leaves x and excluding common ancestors including any leaf from in for . Suppose and have the same tree topology for . If are clade in for and is also a clade in T, then an estimated tree via our method with the tropical polytope and T differ at most the Robinson–Foulds distance = 4.
Proof.
Since are connected trees for , forms a clade in for . Also is a connected tree, so that is also a clade in T. This means that and for any have only one NNI move distance. Since and have the same tree topology and since is also a clade in T, , and T differ only by one NNI move distance. Note that and have at most the Robinson–Foulds distance = 2 since and have just one NNI move difference, and so as with T. Let be an ultrametric form a tree for . Then, take any tropical line segment . Since and have just one NNI move difference, by Theorem 8 in [16], any tree topology of the tree realized from an ultrametric in has the same tree topology of or . Since P is tropically convex, any point in P is a tropically convex combination of for . Thus, the tree topology of the tree realized by an ultrametric in P has at most one NNI move different. Since the estimate , and any tree realized from an ultrametric in P to T has at most 2 NNI move difference. Thus, we have the result. □
6. Computational Experiments
In this section, we apply this method to simulated data sets and compare its performance with the baseline model, which uses means of each missing element in an ultrametric computed from a tree, and the multiple linear regression model proposed by Yasui et al. in [3].
6.1. Simulated Data
To assess a performance of this method, we use simulated datasets generated from the multi-species coalescent model using the software Mesquite [17].
Under the multi-species coalescent model, there are two parameters: species depth and effective population size . In this paper, we fix the effective population size as and we vary as we vary the ratio
6.2. Experimental Design
Here we vary . For this experiment, we fix the number of leaves as 10. Therefore . For each value of R, we generate a random species tree via the Yule model first. Then we generate the set of 1000 gene trees from the multi-species coalescent model given the species tree. Therefore, for each R, we have a simulated dataset with size 1000.
Note that when R is larger we have tighter constraints to gene tree topologies by its species tree. Therefore, we do not have large variance for generating gene trees so that it is easier to estimate the missing part of a gene tree. On the other hand, if we have small R, then we have a large variance for gene tree topologies, the coalescent model is becoming more like a random process [4].
For estimating the performance of our method when we vary the number of leaves missing, we set three different cases: one leaf out of 10 leaves is removed, two leaves out of 10 leaves are removed, and three leaves out of 10 leaves are removed. For each scenario in terms of R and in terms of the number of leaves removed, we pick 200 random observations from the data set of 1000 trees as a test set.
To compare the performance of our method, we use the baseline model, i.e., we fill missing values of an ultrametric by taking the mean of observations with the full set of leaves and the multiple linear regression model proposed by Yasui et al. [3]. For the multiple linear regression model, we set a missing element as a response variable and observed elements in an ultrametric as predictors [3].
6.3. Results
To assess a performance of our method against the baseline and the method proposed by Yasui et al., we use the Robinson–Foulds distance between an estimated tree and T. The results are shown in Table 1 and Figure 2. Note that the smaller the Robinson–Foulds distance between two trees, the closer their tree topologies are. When the Robinson–Foulds distance is 0, their tree topologies are the same. Figure 3 shows that the performance of the baseline and the performance of the linear regression model have very similar results for one, two, and three, the number of leaves removed and all ratio of R.

Table 1.
These numbers shown in this table are average Robinson–Foulds distances between estimated trees and true trees. For each category, we infer 200 trees from 800 trees. The smaller the Robinson–Foulds distance is, the better the performance.
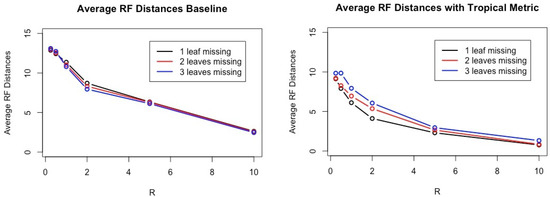
Figure 2.
This figure shows performance on the baseline (Left) and our method using a tropical poltyope (Right). For each category, we infer 200 trees from 800 trees. The x-axis represents the ratio R and the y-axis shows the average Robinson–Foulds distances between estimated trees and true trees for 200 trees. The smaller the Robinson–Foulds distance is, the better the performance.
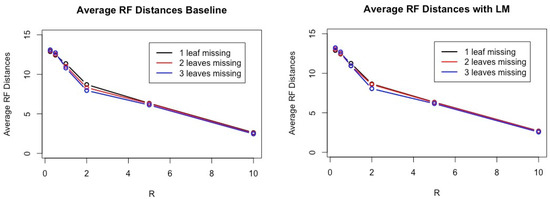
Figure 3.
This figure shows performance on the baseline model (left) and linear regression models (Right). For each category, we infer 200 trees from 800 trees. The x-axis represents the ratio R and the y-axis shows the average Robinson–Foulds distances between estimated trees and true trees for 200 trees. The smaller the Robinson–Foulds distance is, the better the performance. As one can see, these results are very close to each other for all R.
According to computational experiments with simulated datasets shown in Table 1 and Figure 2, our method has smaller Robinson–Foulds distances in any cases compared to other methods. It is interesting that the number of leaves removed seems to greatly affect the results in general while R clearly affects performances of all three methods compared.
If we have only one missing leaf and larger R, often the average Robinson–Foulds distances between inferred trees and true trees is less than 1 because we have often the condition satisfied in Theorem 2 due to very high constraints on tree topologies of gene trees.
7. Application to Empirical Data
7.1. Empirical Dataset
We apply our imputation method to a set of annotated genomes of the fungal family, Clavicipitaceae from [18]. Kang et al. annotated genome sequences for 12 species from the fungal family Clavicipitaceae with MAKER. The 12 species in Clavicipitaceae include Epichloë festucae Fl1 (designated E0894), Aciculosporium take (A7993), Atkinsonella texensis B6155, Balansia obtecta B249 (B0249), Claviceps purpurea 20.1 (C0201), Epichloë amarillans E4668, Epichloë inebrians E818 (E0818), Epichloë glyceriae E277 (E0277), Epichloë mollis AL9923 (E3601), Epichloë typhina subsp. poae E5819, Metarhizium robertsii ARSEF 23 (M0023), and Periglandula ipomoeae P4806. For details on phylogenetic reconstructions on this dataset, see [18]. In this dataset there are 3408 house keeping genes out of 4268 genes. Among them 860 gene trees, including gene trees for ergot alkaloid biosynthesis (EAS) genes have missing leaf (leaves).
7.2. Results
After imputation, we apply the tropical kernel density estimator (KDE) [19] to find possible outlier(s) from the dataset. With the significance level and bandwidth estimated by the nearest neighbors, we found 43 possible outliers including 12 core housekeeping genes and a mating type gene (mtAC) with those of the five EAS genes, easG, easC, easD, cloA, and easA.
Since the tropical polytope defined by the set of all house keeping genes with full leaves is in dimension. Thus, in order to visualize the tropical polytope we apply a tropical principal component analysis (PCA) developed by Yoshida et al. [7,8]. We use the tropical PCA to visualize in the two dimension shown in Figure 4.
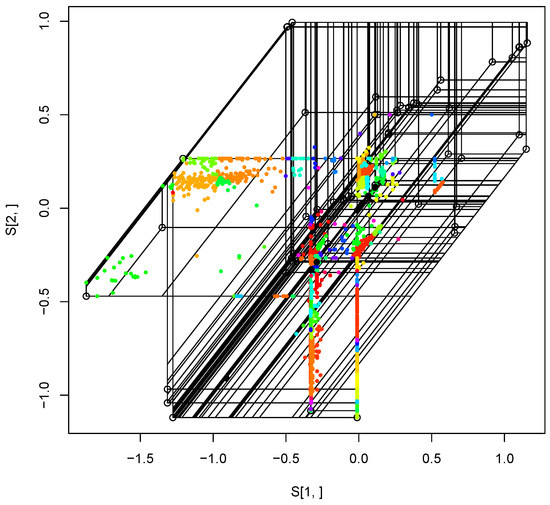
Figure 4.
The tropical polytope of gene trees for the housekeeping genes. Black points in the figures are outliers found by the tropical KDE. In order to visualize this, we apply the tropical PCA. Each color represents an unique tree topology.
8. Discussion
In this short paper, we show a novel method to impute a missing part of an equidistant tree on using a tropical polytope, which is an analogue of a linear regression in the setting of tropical geometry. From simulated data generated from the multi-species coalescent model, we show that this method works very well. In addition, we show a condition that the estimate tree and the true tree have at most a Robinson–Foulds distance of 4 (Theorem 2).
In order to demonstrate our method, we apply it to simulated data as well as an empirical data from Clavicipitaceae. This dataset contains more than 4000 genes and 860 out of 4268 gene trees miss some of leaves. Some trees miss 8 out of 12 tips. Then, we apply the tropical KDE developed by [19] to find outlying gene trees and the results are consistent with the conclusion in [18].
In the future, we can investigate applying the “tropical principal component analysis (PCA)” proposed by Yoshida, et al. in [8] to an imputation of trees since the classical PCA can be viewed as a multivariate linear regression model with orthogonal projections.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The author declare no conflict of interest.
References
- Koonin, E.; Puigbó, P.; Wolf, Y. Comparison of phylogenetic trees and search for a central trend in the “forest of life”. J. Comput. Biol. 2011, 18, 917–924. [Google Scholar] [CrossRef] [PubMed]
- Peters, C.; Geary, M.; Nelson, H.; Rusk, B.; von Hardenberg, A.; Muir, A.P. Phylogenetic placement and life history trait imputation for Grenada Dove Leptotila wellsi, Generalized fuzzy trees. Int. J. Comput. Intell. Syst. 2023, 10, 711–720. [Google Scholar]
- Yasui, N.; Vogiatzis, C.; Yoshida, R.; Fukumizu, K. imPhy: Imputing Phylogenetic Trees with Missing Information Using Mathematical Programming. IEEE/ACM Trans. Comput. Biol. Bioinform. 2020, 17, 1222–1230. [Google Scholar] [CrossRef] [PubMed]
- Maddison, W. Gene Trees in Species Trees. Syst. Biol. 1997, 46, 523–536. [Google Scholar] [CrossRef]
- Ardila, F.; Klivans, C.J. The Bergman Complex of a Matroid and Phylogenetic Trees. J. Comb. Theory Ser. B 2006, 96, 38–49. [Google Scholar] [CrossRef]
- Speyer, D.; Sturmfels, B. Tropical mathematics. Math. Mag. 2009, 82, 163–173. [Google Scholar] [CrossRef]
- Page, R.; Yoshida, R.; Zhang, L. Tropical principal component analysis on the space of phylogenetic trees. Bioinformatics 2020, 36, 4590–4598. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, R.; Zhang, L.; Zhang, X. Tropical Principal Component Analysis and its Application to Phylogenetics. arXiv 2017, arXiv:1710.02682. [Google Scholar] [CrossRef] [PubMed]
- Monod, A.; Lin, B.; Yoshida, R.; Kang, Q. Tropical Geometry of Phylogenetic Tree Space: A Statistical Perspective. 2019. Available online: https://arxiv.org/pdf/1805.12400.pdf (accessed on 27 June 2023).
- Lin, B.; Sturmfels, B.; Tang, X.; Yoshida, R. Convexity in Tree Spaces. SIAM J. Discret. Math. 2017, 3, 2015–2038. [Google Scholar] [CrossRef]
- Yoshida, R. Tropical Balls and its Applications to K Nearest Neighbor over the Space of Phylogenetic Trees. Mathematics 2021, 9, 779. [Google Scholar] [CrossRef]
- Yoshida, R. Tropical Data Science over the Space of Phylogenetic Trees. In IntelliSys 2021: The Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2021; Volume 295, Chapter 26; pp. 340–361. [Google Scholar]
- Joswig, M. Essentials of Tropical Combinatorics; Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 2021. [Google Scholar]
- Maclagan, D.; Sturmfels, B. Introduction to Tropical Geometry; American Mathematical Society: Providence, RI, USA, 2015; Volume 161. [Google Scholar]
- Buneman, P. A note on the metric properties of trees. J. Comb. Theory Ser. B 1974, 17, 48–50. [Google Scholar] [CrossRef]
- Yoshida, R.; Cox, S. Tree Topologies along a Tropical Line Segment. Vietnam J. Math. 2022, 50, 395–419. [Google Scholar] [CrossRef]
- Maddison, W.P.; Maddison, D. Mesquite: A Modular System for Evolutionary Analysis. Version 2.72.. 2009. Available online: http://mesquiteproject.org (accessed on 28 June 2023).
- Kang, Q.; Schardl, C.; Moore, N.; Yoshida, R. CURatio: Genome-wide phylogenomic analysis method using ratios of total branch lengths. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018, 17, 981–989. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, R.; Miura, K.; Barnhill, D.; Howe, D. Tropical Density Estimation of Phylogenetic Trees. 2022. Available online: https://arxiv.org/abs/2206.04206 (accessed on 30 June 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).