Abstract
Feature selection is a widely utilized technique in educational data mining that aims to simplify and reduce the computational burden associated with data analysis. However, previous studies have overlooked the high costs involved in acquiring certain types of educational data. In this study, we investigate the application of a multi-objective gray wolf optimizer (GWO) with cost-sensitive feature selection to predict students’ academic performance in college English, while minimizing both prediction error and feature cost. To improve the performance of the multi-objective binary GWO, a novel position update method and a selection mechanism for a, b, and d are proposed. Additionally, the adaptive mutation of Pareto optimal solutions improves convergence and avoids falling into local traps. The repairing technique of duplicate solutions expands population diversity and reduces feature cost. Experiments using UCI datasets demonstrate that the proposed algorithm outperforms existing state-of-the-art algorithms in hypervolume (HV), inverted generational distance (IGD), and Pareto optimal solutions. Finally, when predicting the academic performance of students in college English, the superiority of the proposed algorithm is again confirmed, as well as its acquisition of key features that impact cost-sensitive feature selection.
Keywords:
feature selection; multi-objective gray wolf optimizer; cost-sensitive; academic performance MSC:
68Txx
1. Introduction
Data mining is used to discover useful information or obtain meaningful insights from big data [1], and the application of educational data mining (EDM) has attracted a great deal of attention. EDM is an effective tool for identifying hidden patterns in educational data, predicting academic performance and enhancing learning/teaching environments [2,3]. Machine learning techniques enhance the abilities of EDM and allow educators and institutions to make data-driven decisions [4].
Academic performance is closely related to the efforts of students, as well as their emotional state, self-regulation behavior, and levels of knowledge, and serves as a crucial indicator for evaluating students’ learning [5,6]. Predicting academic performance using EDM processing technology may be of great benefit for teachers seeking to develop plans and promote individualized education [7]. Such predictions may offer valuable insights into growth trajectories behind the learning processes of students, with potentially substantial theoretical and practical implications for education informatization. However, it is a complex task to identify the factors which influence students’ academic performance. Original academic data contain numerous irrelevant and redundant features which affect prediction results [8]. Feature selection minimizes feature redundancy without loss of critical data [9,10], and it is well-suited for predicting the academic performance of students.
Feature selection methods are categorized into supervised, unsupervised, and semi-supervised feature selection from the availability of classification labels [11]; they are also divided into filter, wrapper, and embedded methods, where the main differences among the three relate to the integration of feature selection and the classification learning algorithm [12]. The filter method runs quickly but exhibits a significant evaluation deviation compared with other learning algorithms. On the other hand, the wrapper method produces high accuracy for learning algorithms but runs slowly.
Most feature selection algorithms assume that data are readily available in a database and can be obtained without cost [13,14]. However, in real-world applications, feature cost is a crucial requirement that cannot be overlooked. Costs include not only the expenditure of money, but also the investment of time and other valuable resources required to acquire the necessary data. In the application of academic performance prediction, although most features may be freely acquired through the learning management system (LMS), there are some features that involve significant cost such as statistics on the study time and classroom performance of students. Taking this into account, in this study we investigate a cost-sensitive feature selection algorithm for predicting students’ academic performance in college English. Our main contributions are as follows:
- Propose a new position update method of binary gray wolf optimizer (GWO) to balance exploration and exploitation.
- Propose an adaptive mutation of Pareto solutions to increase exploitation space and convergence.
- Propose a repairing strategy of duplicate solutions to improve the diversity of solutions and reduce feature cost.
- Propose a multi-objective cost-sensitive feature selection for predicting students’ academic performance in college English which may be adapted for real-world applications.
The structure of this paper is organized as follows: Section 2 introduces research works related to the present study; Section 3 presents the proposed multi-objective binary GWO (MRGWO); Section 4 completes its experimental validation; and Section 5 predicts students’ academic performance in college English. In Section 6, a brief conclusion is provided.
2. Related Works
2.1. The Prediction of Students’ Academic Performance Based on Multi-Objective Feature Selection
Predicting students’ academic performance through feature selection offers a number of potential benefits, including a reduction in time complexity, and the creation of easily understandable learning models. Decision trees have been proven to be a highly effective method for classification and regression, and they exhibit a considerable number of advantages relating to efficiency, simplicity, flexibility, and interpretability. In this regard, the configuration of parameters has a substantial impact on the construction of the optimal tree in terms of accuracy and size. Kostopoulos et al. provided a highly accurate and interpretable classification tree for the early prediction of students at risk of failure in university courses [15], and thus helped to promote effective interventions and other supportive actions to motivate students and improve their performance.
González-Gallardo et al. used econometric techniques and an interval multi-objective programming method to analyze trade-offs among four indicators that measured different aspects of students’ happiness [16]. They defined a linear programming model in which emotion, motivation, belongingness, and bullying were objectives; the model used ideal preferences to investigate the situation of students with the highest levels of happiness in Spain and Finland.
Oscar et al. estimated four econometric models (mathematics scores, reading scores, and the percentages of students achieving a certain threshold in both subjects) in which students’ academic performance was regressed on their satisfaction with different aspects of the teaching process [17]. These multi-objective models optimized the performance and satisfaction of students. A decomposition-based multi-objective genetic algorithm was used to address the problem, and various scalar functions were employed to generate approximations to Pareto optimal rank.
Lee et al. applied the multi-objective value-added measures (MOVAM) algorithm to evaluate and improve the effectiveness of schools in academic and social–emotional learning [18]. Their results revealed that the types had a weak impact on schools and that their benefit patterns were different. The comparison indicated that schools should improve academic and social–emotional learning through the collaboration of key organizations and teaching conditions. In addition, because students’ academic performance is also related to the teaching environment, the design of educational buildings and the indoor environment were also optimized to improve performance [19,20].
2.2. Multi-Objective Cost-Sensitive Feature Selection
Feature selection is an important data-preprocessing technique in classification problems such as bioinformatics and signal processing. In many cases, users are interested not only in maximizing classification performance but also in minimizing the cost that may be associated with certain features [21,22,23]. Zhang et al. were the first to study multi-objective particle swarm optimization (PSO) for cost-sensitive feature selection [24]. To enhance the search ability of the proposed algorithm, they used probability-based coding, efficient hybrid operators, crowding distance, external profiles, and Pareto dominance relationships.
Liao et al. proposed a multi-granularity feature selection that simultaneously selects the optimal feature subset and the optimal data granularity to minimize the total cost of mixed data [25]. An adaptive neighborhood model first generated particles based on the types of features and various variable cost settings in practical situations were then considered.
An and Zhou suggested a cost-sensitive feature selection method with hierarchical random forest [26]. Unlike with commonly used algorithms, the cost of features was incorporated into the construction process of the decision tree, and both the cost and performance of each feature were optimized simultaneously. In addition, the hierarchical sample method improved the performance of feature subsets on high-dimensional data.
Because different features involve costs, the problem of cost-sensitive feature selection has become increasingly important in real-world applications. To meet the various requirements of decision makers, Zhang et al. introduced a multi-objective feature selection method [27]. Two new operators were used to obtain a subset of non-dominated features with great distribution and convergence where the leader archive and the external archive enhanced the search ability of different kinds of bees.
For feature selection with fuzzy cost, Hu et al. introduced a fuzzy multi-objective feature selection based on PSO [28]. The proposed method developed a fuzzy dominance relation to compare the superiority of candidate particles, and it defined a fuzzy crowding distance measure to prune elite profiles and determine the global leader of particles. In addition, a tolerance coefficient ensured that the obtained Pareto optimal solutions satisfied the preferences of decision makers.
Research on multi-objective academic performance has primarily focused on maximizing students’ happiness and prediction accuracy, while cost-sensitive feature selection has not yet received attention. GWO is an evolutionary algorithm (EA) with fast convergence and few parameters, but there is currently a lack of reports of research which specifically investigates the application of multi-objective GWO for cost-sensitive feature selection.
2.3. Gray Wolf Optimizer
Wolves have a very strict social hierarchy, similar to a pyramid structure. GWO simulates the behaviors of gray wolves such as searching and hunting for food and determining a social hierarchy. In GWO, the first three optimal solutions are named , , and . The remaining candidates are collectively referred to as wolves , which update their positions through the positions of , , and . Wolves first determine their distances from , , and using calculations expressed in Equations (1)–(9), and positions are then updated as in Equation (10). Figure 1 is the flowchart of GWO.
where , , and are the positions of , and , respectively; , , and mean the distances between , , , and i; and are two random values within [0, 1]; and a decreases linearly from 2 to 0.
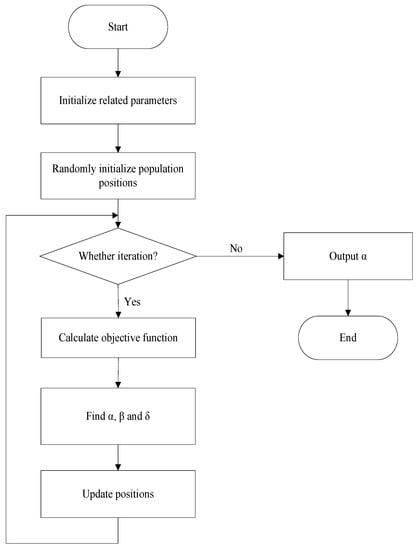
Figure 1.
The flowchart of GWO.
3. Multi-Objective Gray Wolf Optimizer for Cost-Sensitive Feature Selection
MRGWO incorporates the concept of NSGA-III (Non-dominated Sorting Genetic Algorithm III) to select the next generation by reference points. Its flowchart is presented in Figure 2. To improve the performance of multi-objective binary GWO, a new position update approach and a selection method of Pareto solutions are proposed (see Section 3.2 and Section 3.3). Pareto solutions do not adopt the update positions of GWO, but employ adaptive mutation to explore their neighboring space (see Section 3.4). If a new solution duplicates previous solutions, it attempts to repair (see Section 3.5).
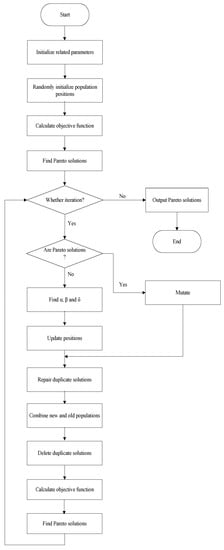
Figure 2.
The flowchart of MRGWO.
3.1. Problem Description
In feature selection, “0” means an unselected feature and “1” denotes a selected feature. Cost-sensitive feature selection has two optimization objectives, minimum classification error and feature cost. Therefore, it is formulated as a multi-objective problem, as shown in Equation (11):
where x is a binary string whose length equals the number of features; indicates the classification error of x; and is the acquired cost of x.
where n is the length of x and is the cost of feature i.
3.2. Binary Gray Wolf Optimizer
In GWO, A controls exploration and exploitation, and its value is defined by a. Due to stochasticity, the range of A varies in the interval [−2, 2]. Exploration is promoted when A > 1 or A < −1, while exploitation is emphasized when −1 < A < 1.
In the initial stage of GWO, wolves are far away from , , and , so is relatively large. As the optimization progresses, wolves gradually converge towards the optimal solution and becomes smaller. In binary GWO [29], the transfer function is responsible for mapping continuous space to binary space, but it ignores the impact on binary GWO. Consequently, the position of binary GWO biases towards 1 at the initial phase and 0 at the later stage. The algorithm does not produce a good balance between exploration and exploitation, so we propose an improved binary GWO, as expressed in Equation (14).
where ; d is the dimension; denotes the current iteration.
3.3. The Selection of , , and
In GWO, , , and guide wolves towards their prey, while in multi-objective binary GWO, there are generally non-dominated solutions. A selection method of , , and is proposed for the following two situations:
- (1)
- The number of non-dominated solutions is greater than or equal to 3.
In this situation, , , and come from non-dominated solutions. To balance the exploration and exploitation of MRGWO, in the early stage of the algorithm, the Euclidean distances between , , and are as large as possible, i.e., chooses the first strongly non-dominated solution. selects a non-dominated solution far from , and is a non-dominated solution far from both and . In the later stage, non-dominated solutions with strong dominance are selected in preference. In MRGWO, a solution’s dominance criterion is determined by the number of solutions it dominates.
- (2)
- The number of non-dominated solutions is less than 3.
This situation suggests that the population is too convergent or that the Pareto front exhibits significant irregularities. Therefore, it is crucial to expand the search region of the population, especially for unexplored space. Initially, the search space of the population is established as the central region. is responsible for searching this region, and finds the direction away from it (the solution far from the center), as shown in Figure 3. In the later stage, solutions with strong dominance are selected in preference.
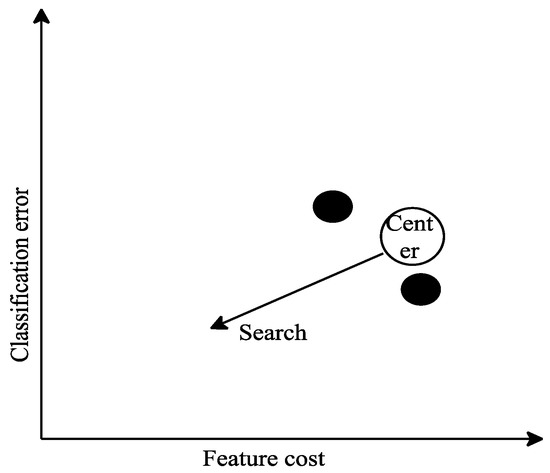
Figure 3.
The selection of , , and in MRGWO.
3.4. The Adaptive Mutation of Pareto Optimal Solutions
According to Equations (1)–(6), will be very small when , , and update their positions. They have a high probability of switching positions, as can be understood from Equation (14). An adaptive mutation method is proposed to enhance the exploitation ability around Pareto optimal solutions.
Mutation step size plays a vital role in search behavior. A large size leads to exploration and preventing the algorithm from getting stuck in local optima, but hinders population convergence. A small size encourages exploitation but causes the population to fall into local optima. Algorithm 1 describes the adaptive mutation method used in MRGWO to balance exploration and exploitation. If we suppose that the number of features is N, then the computation complexity of Algorithm 1 is O() and its space complexity is O(1).
| Algorithm 1: Mutation |
 |
At least two features undergo mutation during each iteration, where one feature with low cost is selected, and another feature with high cost is unselected. The probability of mutation decreases linearly from 0.5 to 0. This adaptive mutation method improves local search and saves feature cost.
3.5. Repairing Duplicate Solutions
Binary EAs are limited to positions that only take values 0 or 1. Unfortunately, this constraint reduces the diversity of the population and results in the presence of duplicate solutions. Traditional approaches remove all duplicate solutions, but they also reduce the selected population size (especially when the number of duplicate solutions is excessive).
If a solution duplicates with another solution, MRGWO first tries to eliminate the selected feature with the highest cost; if it also duplicates with other solutions, MRGWO then proceeds to choose the unselected feature with the lowest cost. MRGWO repeats the above steps again to exit to avoid unnecessary waste of computational resources.
As illustrated in Figure 4, if we assume that duplicates with other solutions, it is necessary to perform repairing operations on . Here, {, , , } are the selected features. The strategy first tries to reduce feature cost. If has the highest cost among the selected features, it repairs to an unselected feature. If there are still duplicates after repairing, it then chooses the least costly of the unselected features {, , , , , , } to improve the classification accuracy. Because has the lowest cost, it is selected to repair . The repairing solution reduces the cost of the selected features, and increases both the search space and population diversity.
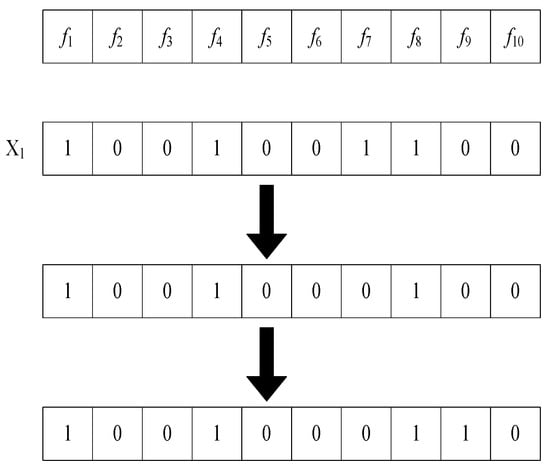
Figure 4.
An example for repairing duplicate solutions.
The time complexity of MRGWO is O(m*m*N*T*+m**T), where T is the number of iterations, m is the population size, and represents the computational time of the objective function.
4. Experimental Results and Analysis
To validate the performance of MRGWO, we conducted a comparative analysis with MODSSA [30], MOGWO [31], and MBPSO [24]. Each algorithm was executed 20 times, with 100 iterations each time. The population size was 30. Their main parameters are presented in Table 1. We use K-nearest neighbor (KNN) as the classifier (K = 5) and 10-fold cross-validation to evaluate the constructed models.

Table 1.
The main parameter setting of the compared algorithms.
4.1. Benchmark Datasets
A total of seven datasets from the UCI repository [32] were used to test the algorithms, and Table 2 provides a brief description of these. The feature cost is within [0, 1], randomly generated by the random function.

Table 2.
UCI datasets.
4.2. Experimental Analysis
- 1.
- Hypervolume (HV)
Table 3 displays the HV values of MRGWO and the compared algorithms; AVG and STD represent the mean and variance, respectively, of the experimental results. Table 3 clearly illustrates that MRGWO achieves the best HV values in the seven UCI datasets with feature dimensions ranging from 13 to 56. MRGWO searches for more solutions in both low- and high-dimensional space and exhibits strong local search ability.

Table 3.
The HV values of the compared algorithms.
To further verify the performance of the algorithms, two non-parametric validation methods, the Wilcoxon rank-sum test and the Friedman test, are used to confirm the validity of the experimental data. The corresponding results are presented in the last three rows of Table 3. “>”, “=”, and “<” indicate significantly better, similar, and worse results. The Wilcoxon rank-sum test reveals that MRGWO has excellent performance across all seven datasets, while the other algorithms have statistically significant differences compared to MRGWO in the datasets. The average ranks of MODSSA, MOGWO, MBPSO, and MRGWO obtained from the Friedman test are 2.9, 4, 2.1, and 1, respectively, and the p-value is less than 0.05. This suggests that MRGWO is superior to other multi-objective algorithms in the benchmark datasets. In summary, Table 3 clearly demonstrates the superiority of MRGWO in HV, as supported by the results of both the Wilcoxon rank-sum test and the Friedman test.
- 2.
- Inverted generational distance (IGD)
Table 4 provides the experimental results of the multi-objective algorithms in IGD and their Wilcoxon rank-sum and Friedman tests. The findings depicted in Table 4 demonstrate that MRGWO outperforms other algorithms in IGD, and that it has excellent performance in Bands, Hcvdat, Lung Cancer, Voting, and Waveform. MBPSO outperforms MRGWO in Heart and Lymphography. The Wilcoxon rank-sum reveals that MRGWO and MBPSO have similar statistical data in Bands, Heart, Lymphography, and Voting, while MODSSA and MOGWO do not perform as well as MRGWO and MRPSO in IGD. The average ranks of MODSSA, MOGWO, MBPSO, and MRGWO obtained from the Friedman test are 3.4, 3.6, 1.7, and 1.3, respectively, with a p-value of 6.34 × 10−4. These results, and those obtained using non-parametric methods, confirm the superiority of MRGWO in IGD.

Table 4.
The IGD values of the compared algorithms.
HV, IGD, and non-parametric statistical analysis evidenced that MRGWO exhibits exceptional convergence and distribution, and it successfully balances the exploration and exploitation of multi-objective feature selection.
- 3.
- Pareto solutions
The final Pareto optimal solutions consist of the non-dominated solutions acquired from all algorithms running 20 times; Figure 5 shows the Pareto solutions obtained by the algorithms.
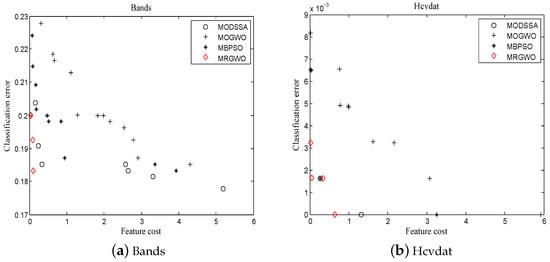
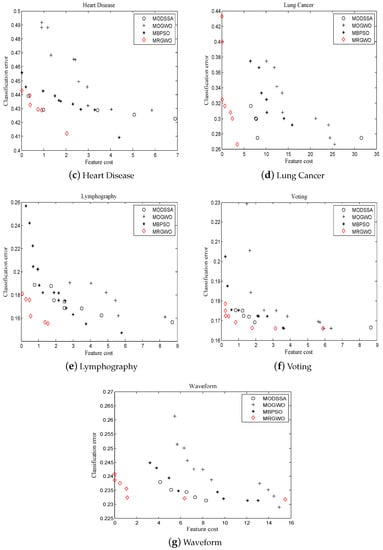
Figure 5.
Pareto optimal sets found by the compared algorithms.
In Bands, MRGWO obtains three optimal solutions in the low-cost space. MODSSA and MBPSO perform well in the high-cost space, and they search for solutions in more space. Although the solutions of MOGWO are widely distributed, they have high classification errors. In Hcvdat, the multi-objective algorithms acquire few Pareto solutions because of the limited feature cost space. MRGWO has four optimal solutions. Interestingly, MRGWO, MODSSA, and MBPSO find solutions with zero classification error, but MRGWO utilizes the lowest feature cost. On the other hand, MOGWO acquires more solutions, but its classification quality is poor. The performance of the algorithms in Heart Disease is average. MRGWO obtains a large number of solutions in the low-cost space. MBPSO and MOGWO search many medium-cost solutions, but the classification errors of MOGWO are greater than those of MBPSO. The solutions of MODSSA present great diversity and classification ability.
In Lung Cancer, MRGWO obtains Pareto solutions in the low-cost space. Although MODSSA, MOGWO, and MBPSO attempt to use more feature cost combinations, their final classification performance is not as excellent as MRGWO. In Lymphography, both MRGWO and MBPSO perform exceptionally well. Especially in the low-cost space, MRGWO outperforms other algorithms, while MBPSO has advantages in the high-cost space. In Voting, the solutions have great distribution, and MRGWO exhibits excellent classification ability in the feature cost space. Although MODSSA, MOGWO, and MBPSO also obtain many solutions, their classification performance is inferior to MRGWO.
In Waveform, MRGWO obtains five optimal solutions in the low-cost space and many more optimal solutions in the medium- and high-cost spaces. The solutions of MODSSA, MOGWO, and MBPSO predominantly concentrate in the medium- and high-feature-cost spaces. The performance of MOGWO is inferior to the other algorithms, but it achieves the highest cost to obtain the lowest classification error.
The Pareto optimal solutions found by the multi-objective algorithms highlight that MRGWO achieves the best classification accuracy with low feature cost, and that its optimal solutions have great distribution. MRGWO utilizes mutation and repairing duplicate solutions to search in more space.
Table 5 presents the average running time of the algorithms. It can be seen that MRGWO generally requires more time in the datasets, compared with MODSSA, MOGWO, and MBPSO. In feature selection, the classifier is a key factor affecting algorithmic performance. Although the Pareto solutions of MRGWO are superior to those of other multi-objective algorithms, when searching for solutions with more feature cost, the mutation method and the repeated solution repair strategy will increase the time complexity of MRGWO. Finally, because Waveform has the largest data size, while Lung Cancer has the fewest samples, the algorithms spent the most time in Waveform and the least time in Lung Cancer.

Table 5.
The average running time of the compared algorithms (second).
5. The Prediction of Students’ Academic Performance in College English
In light of the findings reported above, we conducted an academic performance prediction of the final English grades of sophomore students at a Chinese university.
5.1. Data Description
The data (LMX) consisted of various demographic, academic, behavioral, and family features collected from the Academic Affairs Office, Student Affairs Office, Network Information Center, and Library based on student ID, as illustrated in Table 6. In line with practice in European countries, the academic performance of students was evaluated using five levels: A (Excellent), B (Good), C (Satisfactory), D (Pass), and E (Fail). A total of 14 attributes were collected per student. Before training our model, we started by cleaning and organizing the data. Fortunately, there were only a few instances of missing or incorrect data, so we removed them without affecting the overall data distribution. We also converted nominal data into numeric data via One-Hot encoding. Because demographic and academic features are easily accessible through information systems, their cost of acquisition is low. However, the acquisition of some behavioral and family features needs to be carried out manually, and this incurs high cost. There were about 500 data points used in the investigation, and the cost of corresponding features was 0.1, 0.1, 0.1, 0.1, 0.1, 0.4, 0.35, 0.1, 0.1, 0.35, 0.3, 0.4, 0.4, and 0.4.

Table 6.
The details of students’ information.
5.2. Cost-Sensitive Students’ Academic Performance in College English
As can be seen from Figure 6, MRGWO produced the best performance in HV, followed by MODSSA, MBPSO, and MOGWO. Through the Wilcoxon rank-sum test, we found that there are statistical differences in the experimental data between MRGWO and the other algorithms. The HV indicated that MRGWO has a better performance in terms of diversity and coverage of the Pareto front, while MRGWO effectively balanced the selected features and their cost.
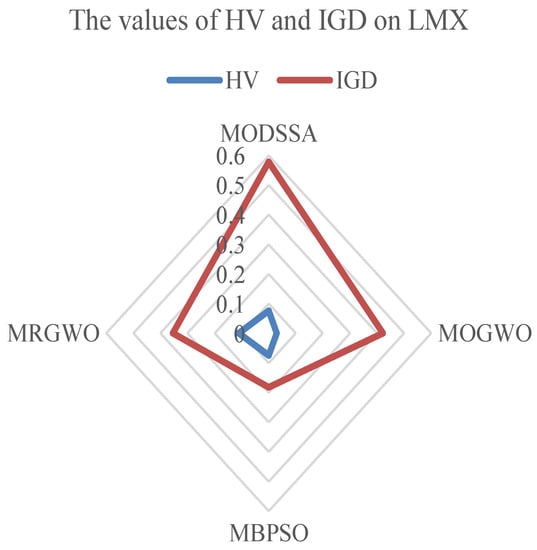
Figure 6.
The values of HV and IGD on LMX.
The IGD values of MODSSA, MOGWO, MBPSO, and MRGWO were 0.5788, 0.4216, 0.1823, and 0.3539, respectively. Although MRGWO was superior to the other compared algorithms, the rank sum revealed no statistically significant difference between MBPSO and MRGWO in IGD. MRGWO had the advantages of convergence and coverage. Based on the results obtained from HV, IGD, and statistical analysis, MRGWO exhibited the most favorable performance. The proposed method effectively expanded the search space of multi-objective algorithms and provides diverse solutions in academic performance.
From Figure 7, it is concluded that the number of Pareto optimal solutions of MRGWO was fewer than those of MODSSA, MOGWO, and MBPSO. However, MRGWO used low feature cost and obtained low classification errors. MODSSA also acquired low cost, but the errors were higher than those of MRGWO. MOGWO and MBPSO sought to use more feature cost, yet their solutions were not as favorable as those of MRGWO. Figure 7 reveals that MRGWO is suitable for LMX and that it effectively balances feature cost and classification accuracy in multi-objective feature selection.
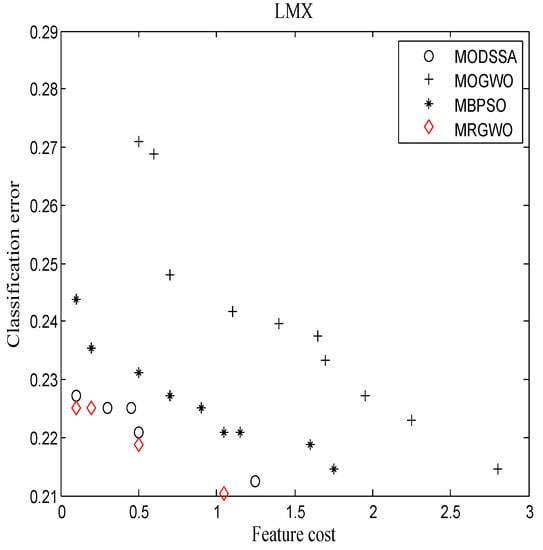
Figure 7.
The Pareto solutions on LMX.
The average running time of MODSSA, MOGWO, MBPSO, and MRGWO is 171.0017, 175.4042, 173.1825, and 131.0683, respectively. It is worth noting that MRGWO demonstrated the most efficient performance in computational time. On the other hand, MODSSA, MOGWO, and MBPSO exhibited comparable computational time. Because MRGWO attempted to achieve classification with fewer features, this advantage contributed to its superior operational efficiency, compared with the other algorithms.
In MRGWO, the commonly utilized features included , , , , and . In MODSSA, the selected features contained , , , , , , and . MOGWO employed , , , , , and to implement classification. In MBPSO, the most frequently selected features were , , , and .
The features selected by these algorithms imply that demographic and academic features play a significant role in determining the multi-objective performance of students in college English. Because the features of behavior and family involve high feature cost, they tend to be unselected.
In cost-sensitive multi-objective academic performance, the cost of feature selection is a key factor affecting classification, and this contradicts some conclusions drawn from previous studies using single-objective methods [2].
5.3. Discussion
In the past, most educational research has focused on which features affect students’ academic performance and has ignored the cost of acquiring these features. Although the gender and origin of students can quickly be obtained from the information system, the acquisition of behavioral and family features involves high cost. In this study, we identified features with low feature cost based on students’ academic performance. Our findings will provide valuable support to governments and policymakers by assisting in monitoring performance, formulating policies, setting targets, evaluating outcomes, and implementing educational reforms to address challenges in the education system. During this research, we integrated different feature selection methods with machine learning models to achieve efficient and effective results.
Our results demonstrate that students’ academic performance can be effectively predicted using only a small number of features. This information is valuable for teachers seeking to quickly identify students with below- or above-average academic motivation. Furthermore, such data-driven studies can help higher education institutions establish learning analytics frameworks and aid in decision-making processes.
The findings of the present study may be specific to the particular schools and contexts used in the research; generalizing the results to other schools or regions might require further investigation. The results are affected by both the completeness of data and by feature cost. In the future, we can use more data sources, dimensions and metrics to test these algorithms. Investigating how cultural, social, and economic factors influence academic performance could help in the development of targeted strategies for diverse student populations.
6. Conclusions
To assist educators in making decisions and implementing effective interventions, we employed a multi-objective binary GWO (MRGWO) algorithm to evaluate the prediction of students’ academic performance in college English and the cost of selected features. The position update and the selection of optimal solutions balanced global search and local search. Additionally, the mutation of Pareto optimal solutions and the repairing of duplicate solutions expanded population diversity and reduced both feature cost and classification error. In the UCI datasets, the experiments with MODSSA, MOGWO, and MBPSO showed that MRGWO had significant advantages in HV, IGD, and Pareto optimal solutions. In predicting academic performance in college English, MRGWO also demonstrated excellent performance. These results indicate that the proposed algorithm is suitable for multi-objective cost-sensitive feature selection in students’ academic performance. In future research, we may consider applying the proposed ideas to other EAs to expand possible areas of application.
Author Contributions
Conceptualization, L.Y. and P.H.; Formal analysis, L.Y. and S.-C.C.; Methodology, L.Y., S.-C.C. and J.-S.P.; Software, L.Y. and P.H.; Writing—original draft, L.Y.; Writing—review and editing, P.H., S.-C.C. and J.-S.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Henan Provincial Philosophy and Social Science Planning Project (2022BJJ076), and the Henan Province Key Research and Development and Promotion Special Project (Soft Science Research) (222400410105).
Data Availability Statement
Data are available on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Morales, M.; Salmerón, A.; Maldonado, A.D.; Masegosa, A.R.; Rumí, R. An Empirical Analysis of the Impact of Continuous Assessment on the Final Exam Mark. Mathematics 2022, 10, 3994. [Google Scholar] [CrossRef]
- Yağcı, M. Educational data mining: Prediction of students’ academic performance using machine learning algorithms. Smart Learn. Environ. 2022, 9, 11. [Google Scholar] [CrossRef]
- Thakur, N. A large-scale dataset of Twitter chatter about online learning during the current COVID-19 Omicron wave. Data 2022, 7, 109. [Google Scholar] [CrossRef]
- Cerquitelli, T.; Meo, M.; Curado, M.; Skorin-Kapov, L.; Tsiropoulou, E.E. Machine Learning Empowered Computer Networks. Comput. Networks 2023, 230, 109807. [Google Scholar] [CrossRef]
- Chicharro, F.I.; Giménez, E.; Sarría, Í. The enhancement of academic performance in online environments. Mathematics 2019, 7, 1219. [Google Scholar] [CrossRef]
- Segura, M.; Mello, J.; Hernández, A. Machine Learning Prediction of University Student Dropout: Does Preference Play a Key Role? Mathematics 2022, 10, 3359. [Google Scholar] [CrossRef]
- Liu, C.; Wang, H.; Yuan, Z. A Method for Predicting the Academic Performances of College Students Based on Education System Data. Mathematics 2022, 10, 3737. [Google Scholar] [CrossRef]
- Ali, M.A.; PP, F.R.; Abd Elminaam, D.S. An Efficient Heap Based Optimizer Algorithm for Feature Selection. Mathematics 2022, 10, 2396. [Google Scholar] [CrossRef]
- Pan, J.S.; Hu, P.; Snášel, V.; Chu, S.C. A survey on binary metaheuristic algorithms and their engineering applications. Artif. Intell. Rev. 2023, 56, 6101–6167. [Google Scholar] [CrossRef]
- Pan, J.S.; Zhang, L.G.; Wang, R.B.; Snášel, V.; Chu, S.C. Gannet optimization algorithm: A new metaheuristic algorithm for solving engineering optimization problems. Math. Comput. Simul. 2022, 202, 343–373. [Google Scholar] [CrossRef]
- Tanwar, A.; Alghamdi, W.; Alahmadi, M.D.; Singh, H.; Rana, P.S. A Fuzzy-Based Fast Feature Selection Using Divide and Conquer Technique in Huge Dimension Dataset. Mathematics 2023, 11, 920. [Google Scholar] [CrossRef]
- Lee, J.; Jang, H.; Ha, S.; Yoon, Y. Android malware detection using machine learning with feature selection based on the genetic algorithm. Mathematics 2021, 9, 2813. [Google Scholar] [CrossRef]
- Hu, P.; Pan, J.S.; Chu, S.C.; Sun, C. Multi-surrogate assisted binary particle swarm optimization algorithm and its application for feature selection. Appl. Soft Comput. 2022, 121, 108736. [Google Scholar] [CrossRef]
- Hu, P.; Pan, J.S.; Chu, S.C. Improved binary grey wolf optimizer and its application for feature selection. Knowl. Based Syst. 2020, 195, 105746. [Google Scholar] [CrossRef]
- Kostopoulos, G.; Fazakis, N.; Kotsiantis, S.; Sgarbas, K. Multi-objective Optimization of C4. 5 Decision Tree for Predicting Student Academic Performance. In Proceedings of the 2019 10th International Conference on Information, Intelligence, Systems and Applications (IISA), Patras, Greece, 15–17 July 2019; IEEE: Patras, Greece; pp. 1–4. [Google Scholar]
- González-Gallardo, S.; Ruiz, A.B.; Luque, M. Analysis of the well-being levels of students in spain and finland through interval multiobjective linear programming. Mathematics 2021, 9, 1628. [Google Scholar] [CrossRef]
- Marcenaro-Gutiérrez, O.D.; González-Gallardo, S.; Luque, M. Evaluating the potential trade-off between students’ satisfaction and school performance using evolutionary multiobjective optimization. Rairo-Oper. Res. 2021, 55, S1051–S1067. [Google Scholar] [CrossRef]
- Lee, J.; Kim, T.; Su, M. Reassessing school effectiveness: Multi-objective value-added measures (MOVAM) of academic and socioemotional learning. Stud. Educ. Eval. 2021, 68, 100972. [Google Scholar] [CrossRef]
- Acosta-Acosta, D.F.; El-Rayes, K. Optimal design of classroom spaces in naturally-ventilated buildings to maximize occupant satisfaction with human bioeffluents/body odor levels. Build. Environ. 2020, 169, 106543. [Google Scholar] [CrossRef]
- Hwang, R.L.; Liao, W.J.; Chen, W.A. Optimization of energy use and academic performance for educational environments in hot-humid climates. Build. Environ. 2022, 222, 109434. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Wang, G.G. Improved differential evolution using two-stage mutation strategy for multimodal multi-objective optimization. Swarm Evol. Comput. 2023, 78, 101232. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, G.G. Improved NSGA-III using transfer learning and centroid distance for dynamic multi-objective optimization. Complex Intell. Syst. 2021, 9, 1143–1164. [Google Scholar] [CrossRef]
- Wang, G.G.; Gao, D.; Pedrycz, W. Solving multiobjective fuzzy job-shop scheduling problem by a hybrid adaptive differential evolution algorithm. IEEE Trans. Ind. Inform. 2022, 18, 8519–8528. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.W.; Cheng, J. Multi-objective particle swarm optimization approach for cost-based feature selection in classification. IEEE/ACM Trans. Comput. Biol. Bioinform. 2015, 14, 64–75. [Google Scholar] [CrossRef] [PubMed]
- Liao, S.; Zhu, Q.; Qian, Y.; Lin, G. Multi-granularity feature selection on cost-sensitive data with measurement errors and variable costs. Knowl. Based Syst. 2018, 158, 25–42. [Google Scholar] [CrossRef]
- An, C.; Zhou, Q. A cost-sensitive feature selection method for high-dimensional data. In Proceedings of the 2019 14th International Conference on Computer Science & Education (ICCSE), Toronto, ON, Canada, 19–21 August 2019; IEEE: Toronto, ON, Canada; pp. 1089–1094. [Google Scholar]
- Zhang, Y.; Cheng, S.; Shi, Y.; Gong, D.W.; Zhao, X. Cost-sensitive feature selection using two-archive multi-objective artificial bee colony algorithm. Expert Syst. Appl. 2019, 137, 46–58. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, Y.; Gong, D. Multiobjective particle swarm optimization for feature selection with fuzzy cost. IEEE Trans. Cybern. 2020, 51, 874–888. [Google Scholar] [CrossRef]
- Panwar, L.K.; Reddy, S.; Verma, A.; Panigrahi, B.K.; Kumar, R. Binary grey wolf optimizer for large scale unit commitment problem. Swarm Evol. Comput. 2018, 38, 251–266. [Google Scholar] [CrossRef]
- Aljarah, I.; Habib, M.; Faris, H.; Al-Madi, N.; Heidari, A.A.; Mafarja, M.; Abd Elaziz, M.; Mirjalili, S. A dynamic locality multi-objective salp swarm algorithm for feature selection. Comput. Ind. Eng. 2020, 147, 106628. [Google Scholar] [CrossRef]
- Al-Tashi, Q.; Abdulkadir, S.J.; Rais, H.M.; Mirjalili, S.; Alhussian, H.; Ragab, M.G.; Alqushaibi, A. Binary multi-objective grey wolf optimizer for feature selection in classification. IEEE Access 2020, 8, 106247–106263. [Google Scholar] [CrossRef]
- Lichman, M. UCI Machine Learning Repository; University of California, School of Information and Computer Science: Irvine, CA, USA, 2013; Available online: http://archive.ics.uci.edu/ml (accessed on 2 June 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).