Multiple-Image Encryption Scheme Based on an N-Dimensional Chaotic Modular Model and Overlapping Block Permutation–Diffusion Using Newly Defined Operation
Abstract
1. Introduction
2. N-Dimensional Modular Chaotic Model
2.1. Construction of ND-CMCM
2.2. Examples of the Proposed Chaotic Model
2.2.1. 2D Logistic–PWLCM Coupled Modular Map
2.2.2. 3D Cubic–Fraction–IST Coupled Modular Map
2.2.3. 4D ICMIC–ICMIC–1DSP–1DCP Coupled Modular Map
3. Performance Analysis of New Systems
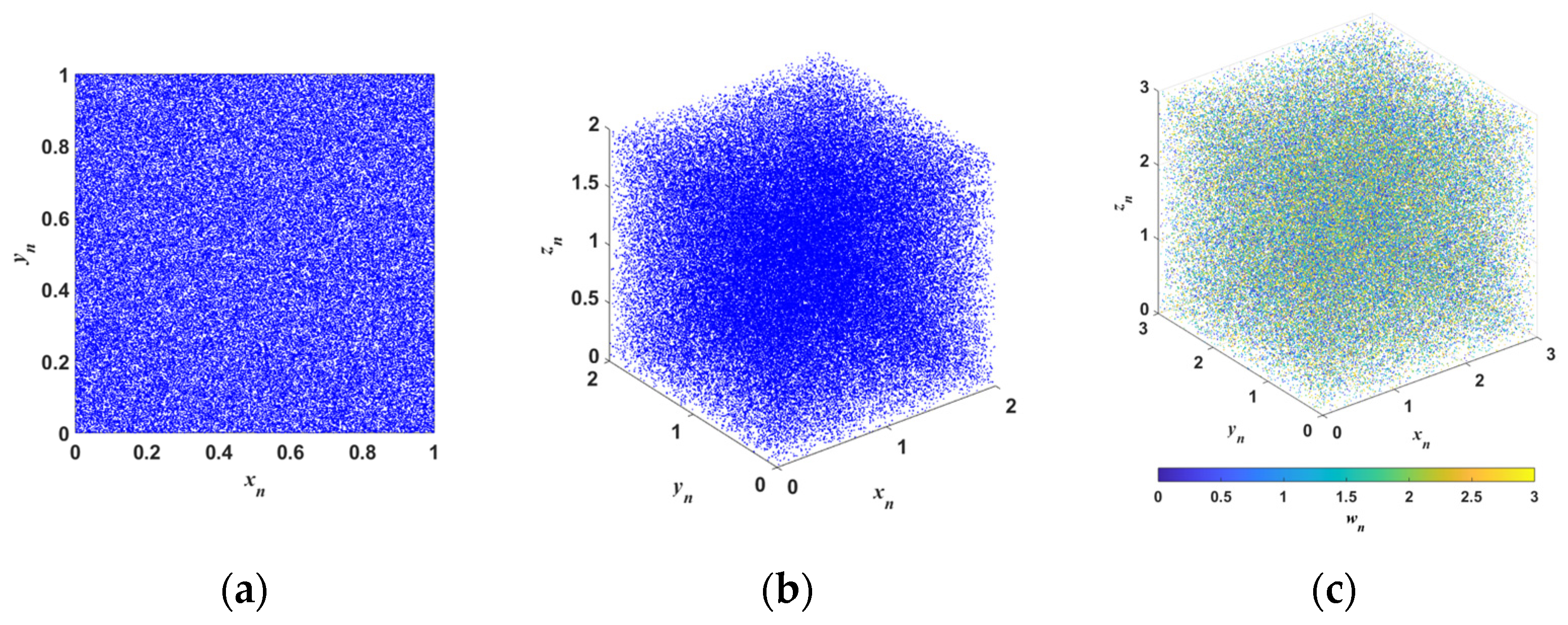
3.1. Bifurcation Diagram and Phase Diagram
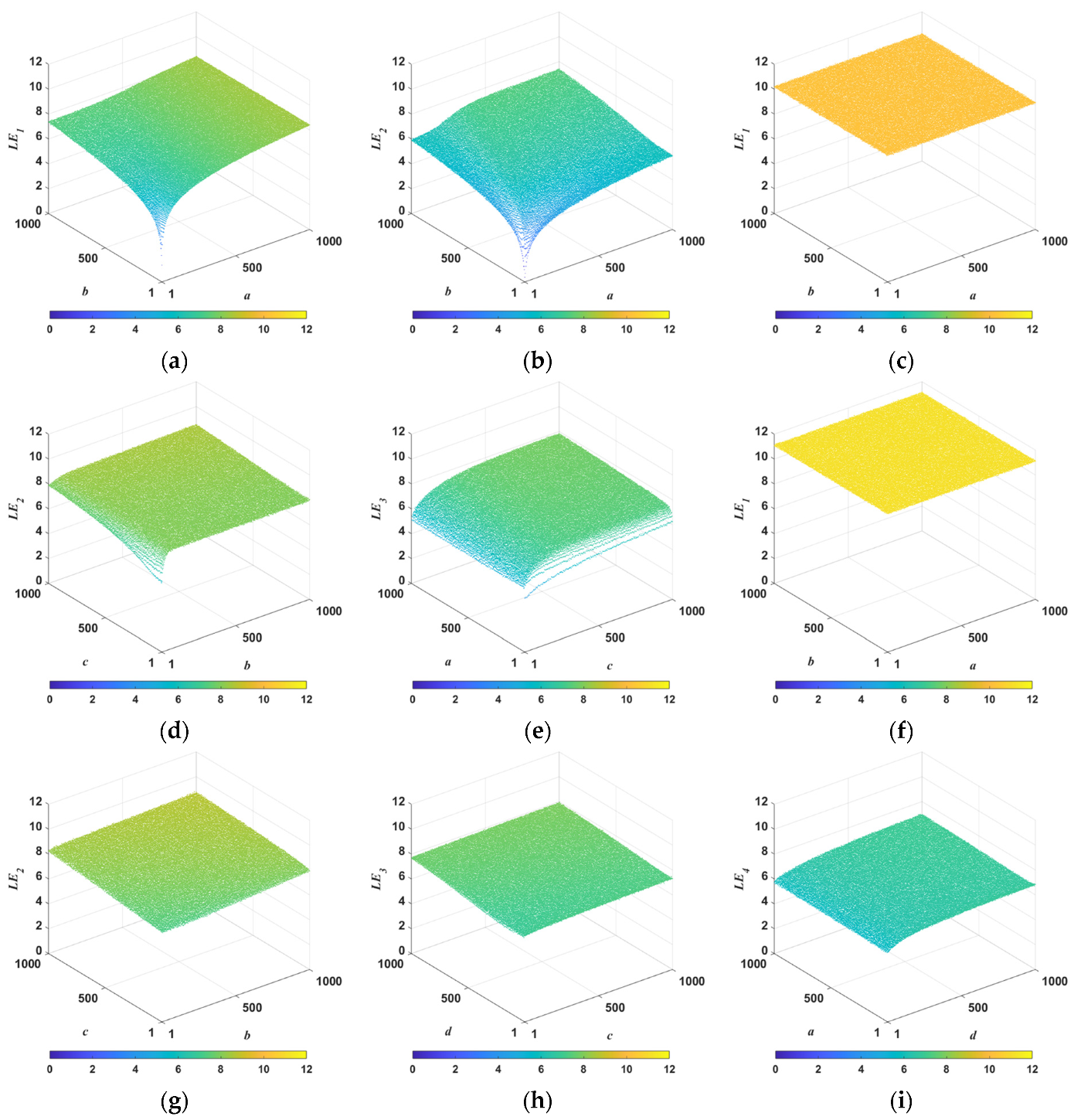
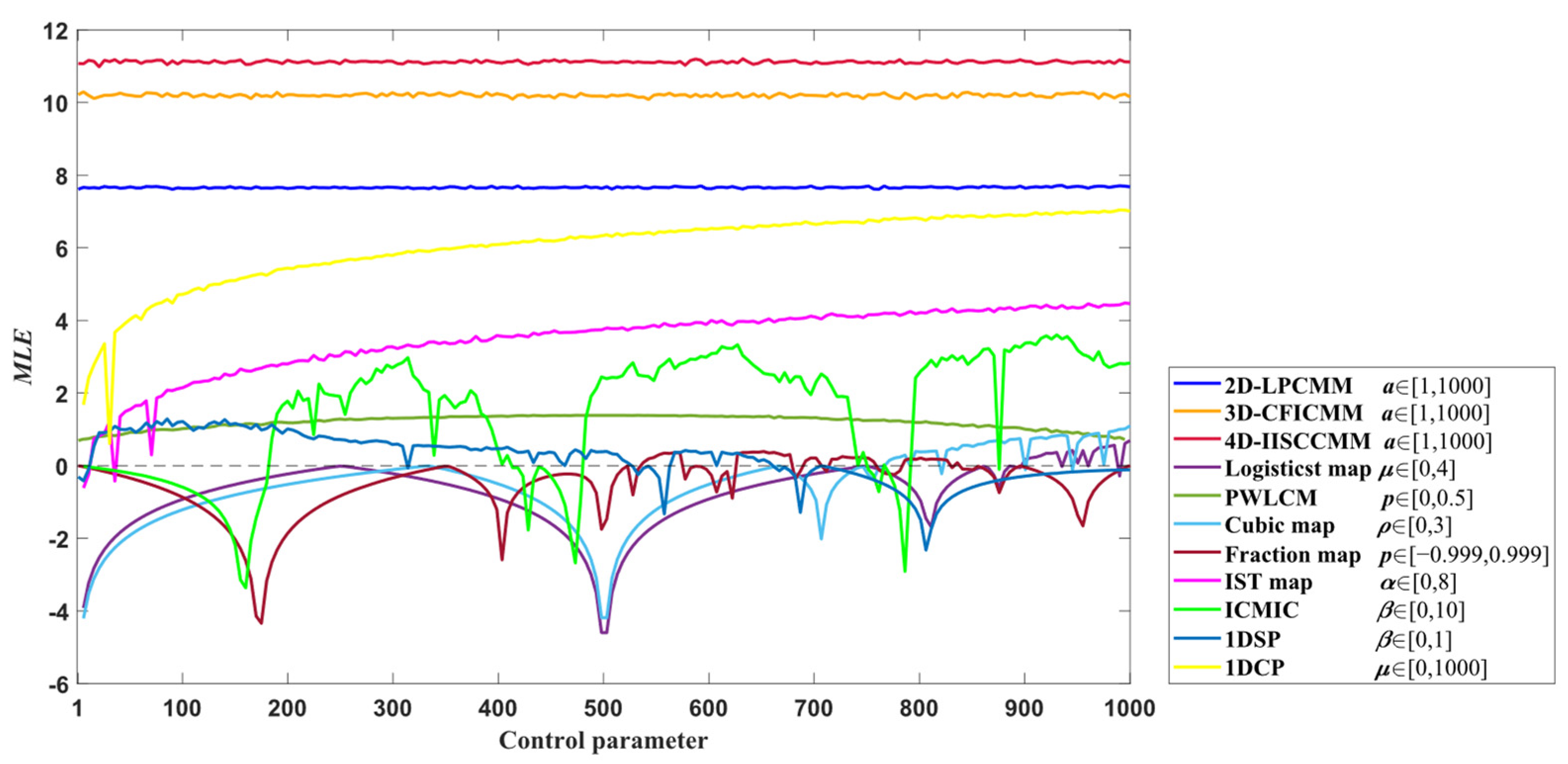
3.2. Lyapunov Exponent
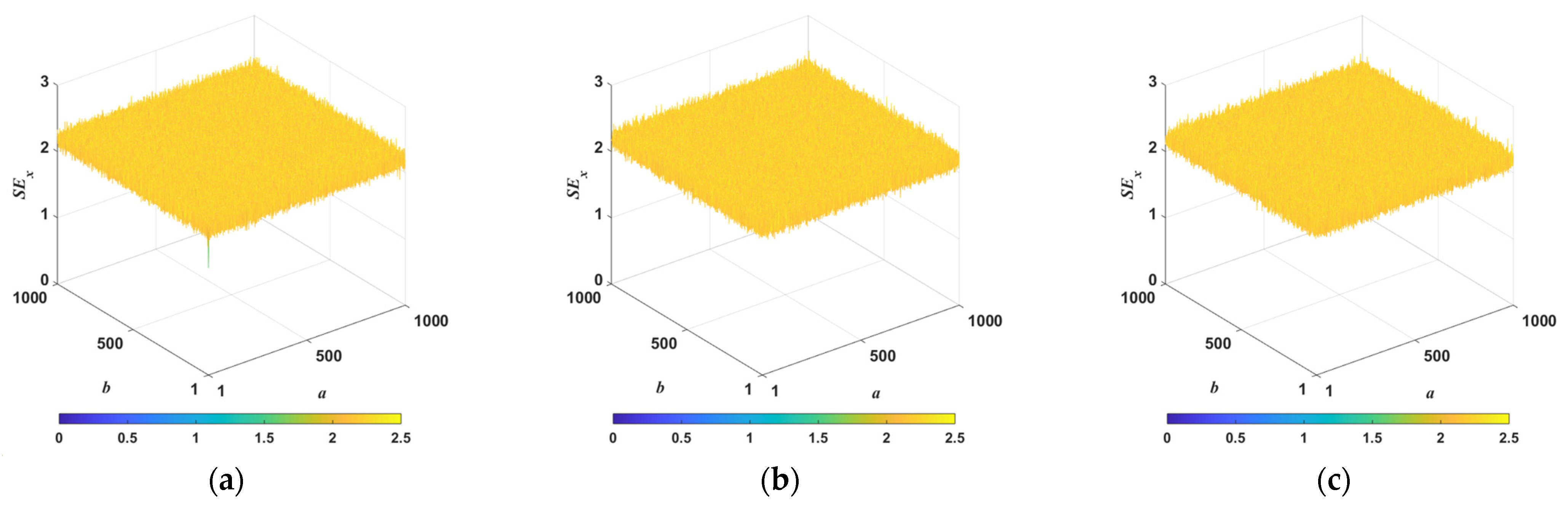
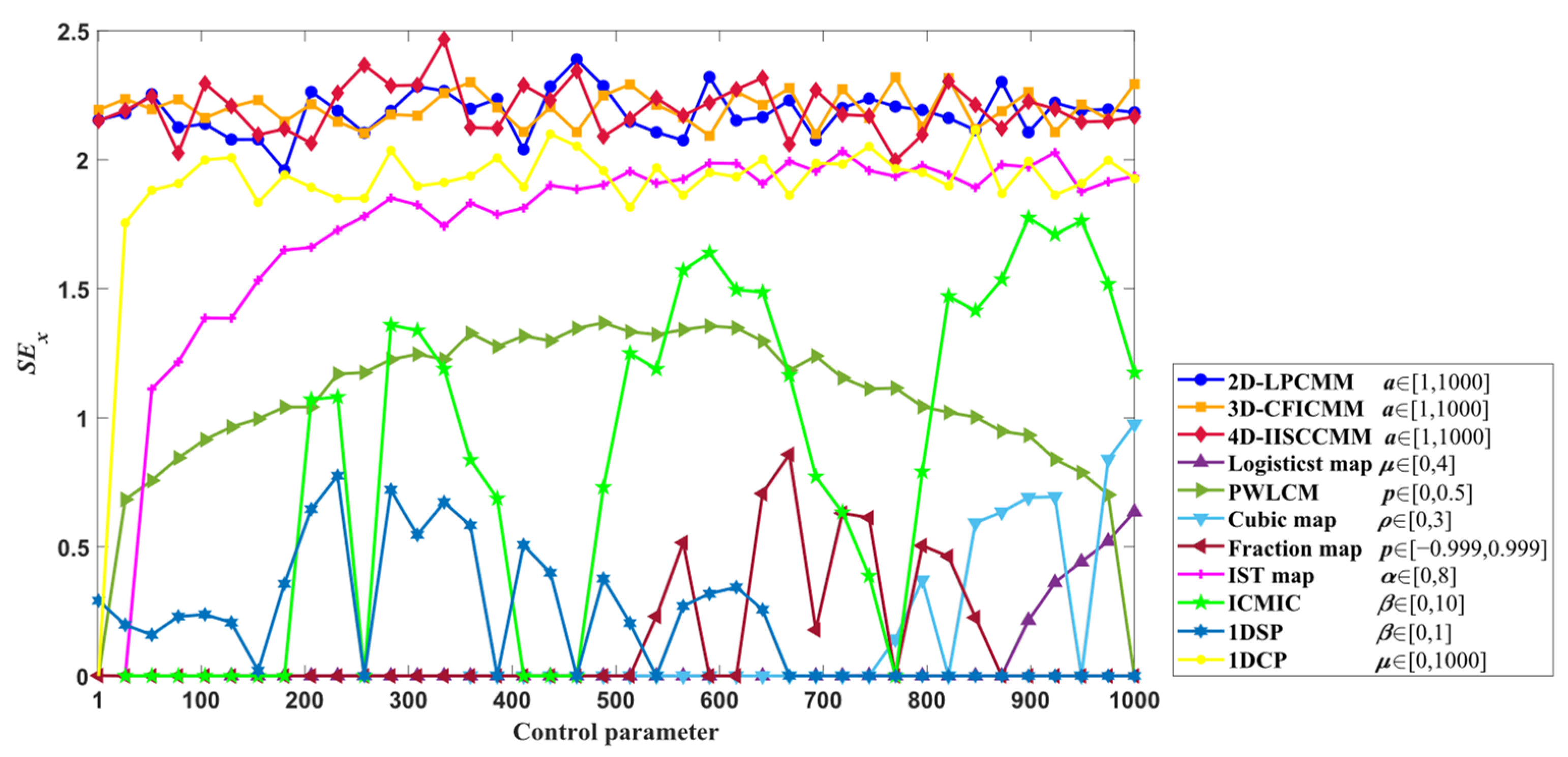
3.3. Sample Entropy
4. Proposed Encryption Algorithm
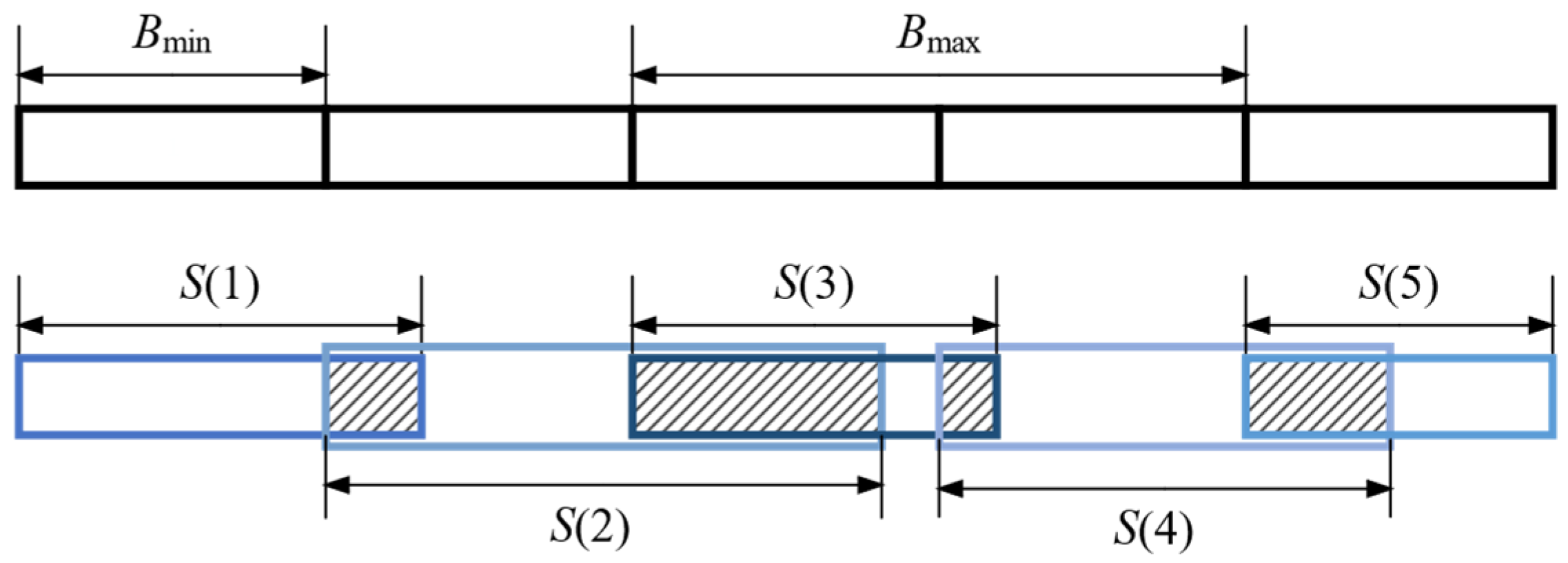
4.1. Overlapping Block
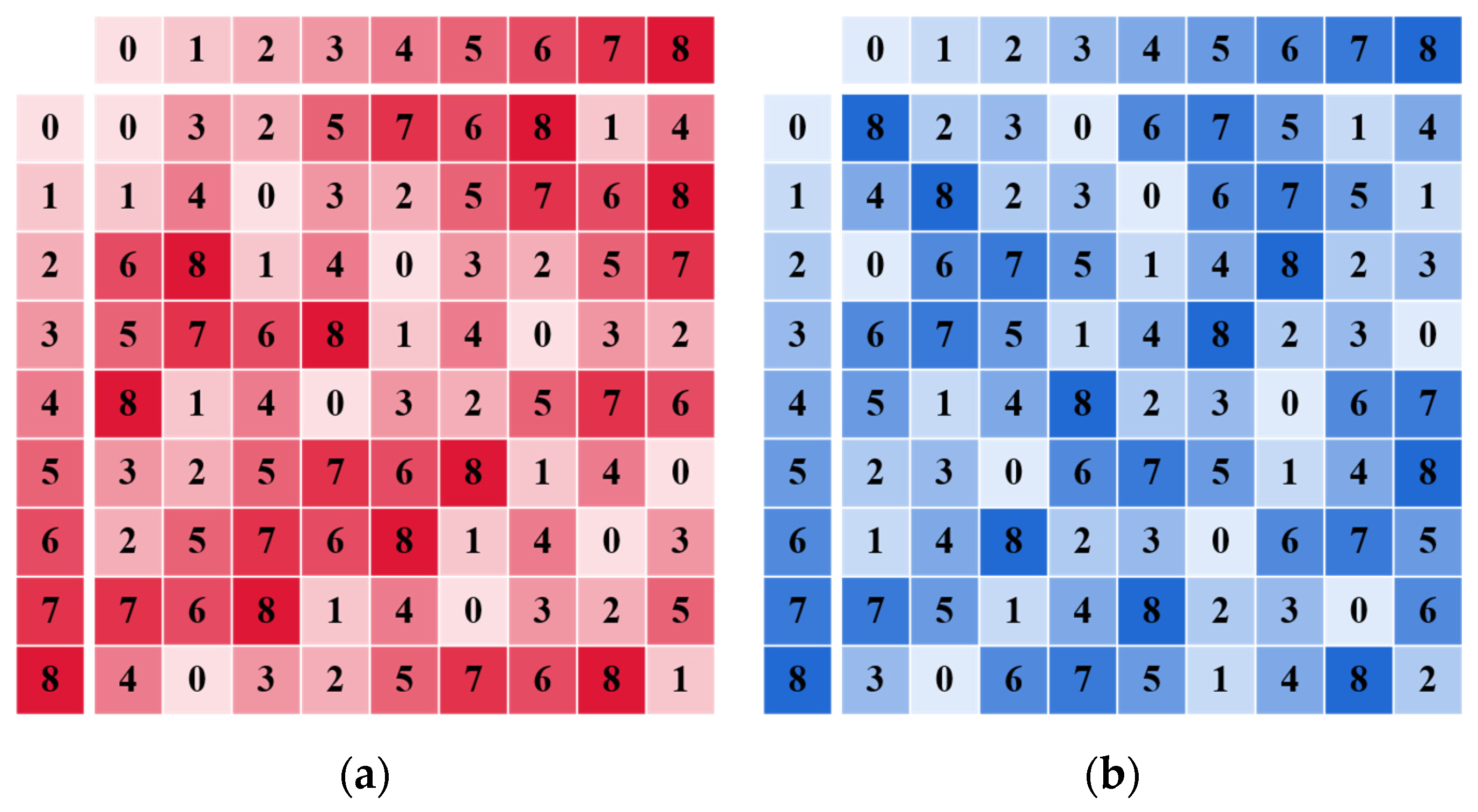
4.2. Newly Defined Operations Based on Latin Squares and Lookup Table
| Algorithm 1 Pseudo-code for generating Latin squares | |
| Input: chaotic sequences Q1 and Q2 of length n Output: nth order Latin square L | |
| 1: | [~,I1] = sort(Q1); |
| 2: | [~,I2] = sort(Q2); |
| 3: | I1 = I1 − 1; |
| 4: | for i = 0 to n − 1 |
| 5: | L(i + 1,:) = circshift(I1,I2(i + 1)); |
| 6: | end for |
| Algorithm 2 Pseudo-code for generating reverse Latin squares | |
| Input: nth Latin square L Output:nth reverse Latin square L’ | |
| 1: | for i = 0 to n − 1 |
| 2: | for j = 0 to n − 1 |
| 3: | L’(L(i + 1,j + 1) + 1,j + 1) = i; |
| 4: | end for |
| 5: | end for |
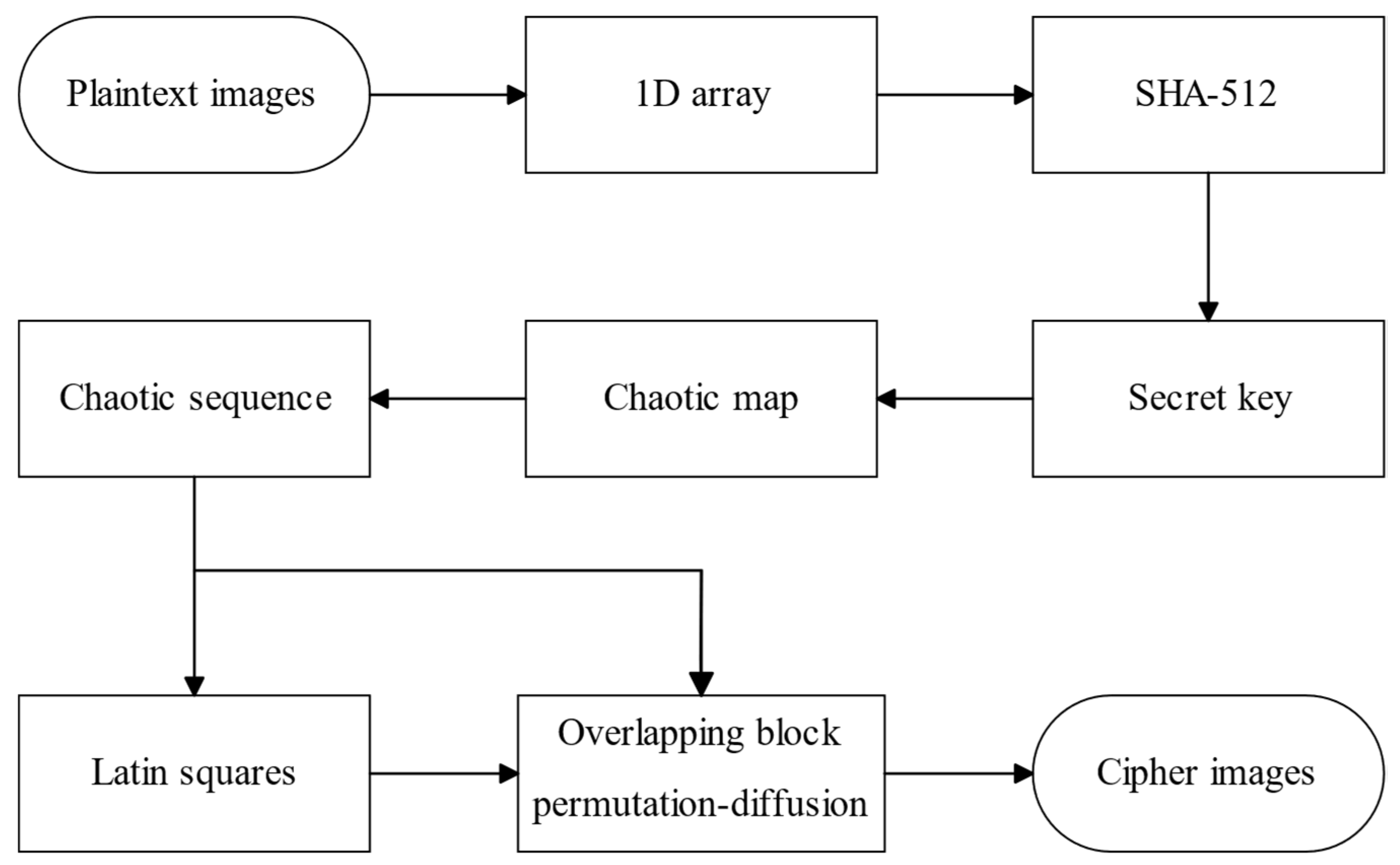
4.3. Encryption Process
4.3.1. Generation of Secret Key and Chaotic Sequences
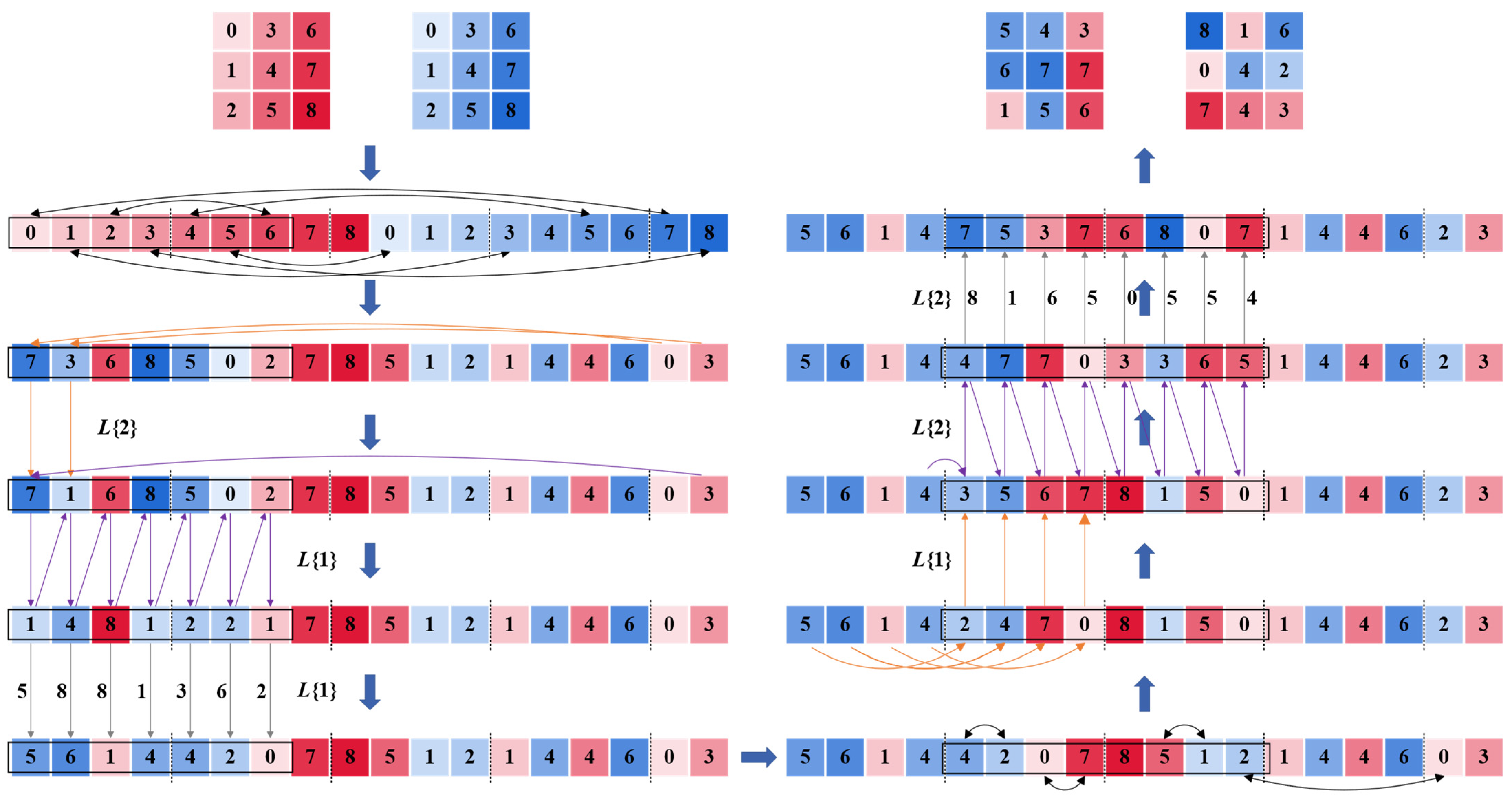
4.3.2. Overlapping Block Permutation–Diffusion
| Algorithm 3 Pseudo-code for index processing | |
| Input: E, A Output: E1, A1 | |
| 1: | Temp = [E A]; |
| 2: | Temp = unique(Temp,’stable’); |
| 3: | Stemp = length(Temp); |
| 4: | if mod(Stemp,2) = 1 |
| 5: | Temp(end) = []; |
| 6: | Stemp = Stemp − 1; |
| 7: | end if |
| 8: | E1 = Temp(1: Stemp/2); |
| 9: | A1 =Temp(Stemp/2 + 1:end); |
| Algorithm 4 Pseudo-code for forward permutation–diffusion | |
| Input: P, Blen, Bmin, S1, CS3, CS4, CS5, CS9, CS10, CS13, Output: P | |
| 1: | Ct = 1; Plen = Blen; |
| 2: | for i = 1 to Bn |
| 3: | if Plen < S1(i) |
| 4: | S = Plen; |
| 5: | end if |
| 6: | L1 = mod(ceil(CS3(i) × 1014),Lnum) + 1; L2 = mod(ceil(CS4(i) × 1014),Lnum) + 1; |
| 7: | L3 = mod(ceil(CS5(i) × 1014),Lnum) + 1; E = mod(ceil(CS9(Ct:Ct + S − 1) × 1014),Plen) + 1; |
| 8: | D = mod(ceil(CS10(Ct:Ct + S − 1) × 1014),256); Ct = Ct + S; |
| 9: | A = 1 to S; |
| 10: | [E1,A1] = Algorithm 2(E,A); E1 =E1 + (i − 1) × Bmin; A1 =A1 + (i − 1) × Bmin; |
| 11: | P(E1)⇔P(A1) |
| 12: | if i > 1 |
| 13: | if Plen > Bmin |
| 14: | P((i − 1) × Bmin + 1:i × Bmin) = LL(P((i − 1) × Bmin + 1:i × Bmin),P((i − 2) × Bmin + 1:(i − 1) × Bmin),L{L1}); |
| 15: | else |
| 16: | P((i − 1) × Bmin + 1:end)= LL(P((i − 1) × Bmin + 1:end),P((i − 2) × Bmin + 1:(i − 1) × Bmin),L{L1}); |
| 17: | end if |
| 18: | for k = 1 to S |
| 19: | P((i − 1) × Bmin + k) = LL(P((i − 1) × Bmin + k),P((i − 1) × Bmin + k − 1),L{L2}); |
| 20: | end for |
| 21: | else |
| 22: | P(1:Blen − ((Bn − 1) × Bmin)) = LL(P(1:Blen − ((Bn − 1) × Bmin)),P((Bn − 1) × Bmin + 1:end), L{L1}); |
| 23: | P(1) = LL(P(1),P(Bn),L{L2}); |
| 24: | for k = 2 to S |
| 25: | P(k) = LL(P(k),P(k − 1),L{L2}); |
| 26: | end for |
| 27: | end if |
| 28: | P((i − 1) × Bmin + 1:(i − 1) × Bmin + S) = LL(P((i − 1) × Bmin + 1:(i − 1) × Bmin + S),D,L{L3}); |
| 29: | Plen = Plen − Bmin; |
| 30: | end for |
4.4. Decryption Process
5. Experimental Results and Security Analysis
5.1. Key Space Analysis
5.2. Key Sensitivity Analysis
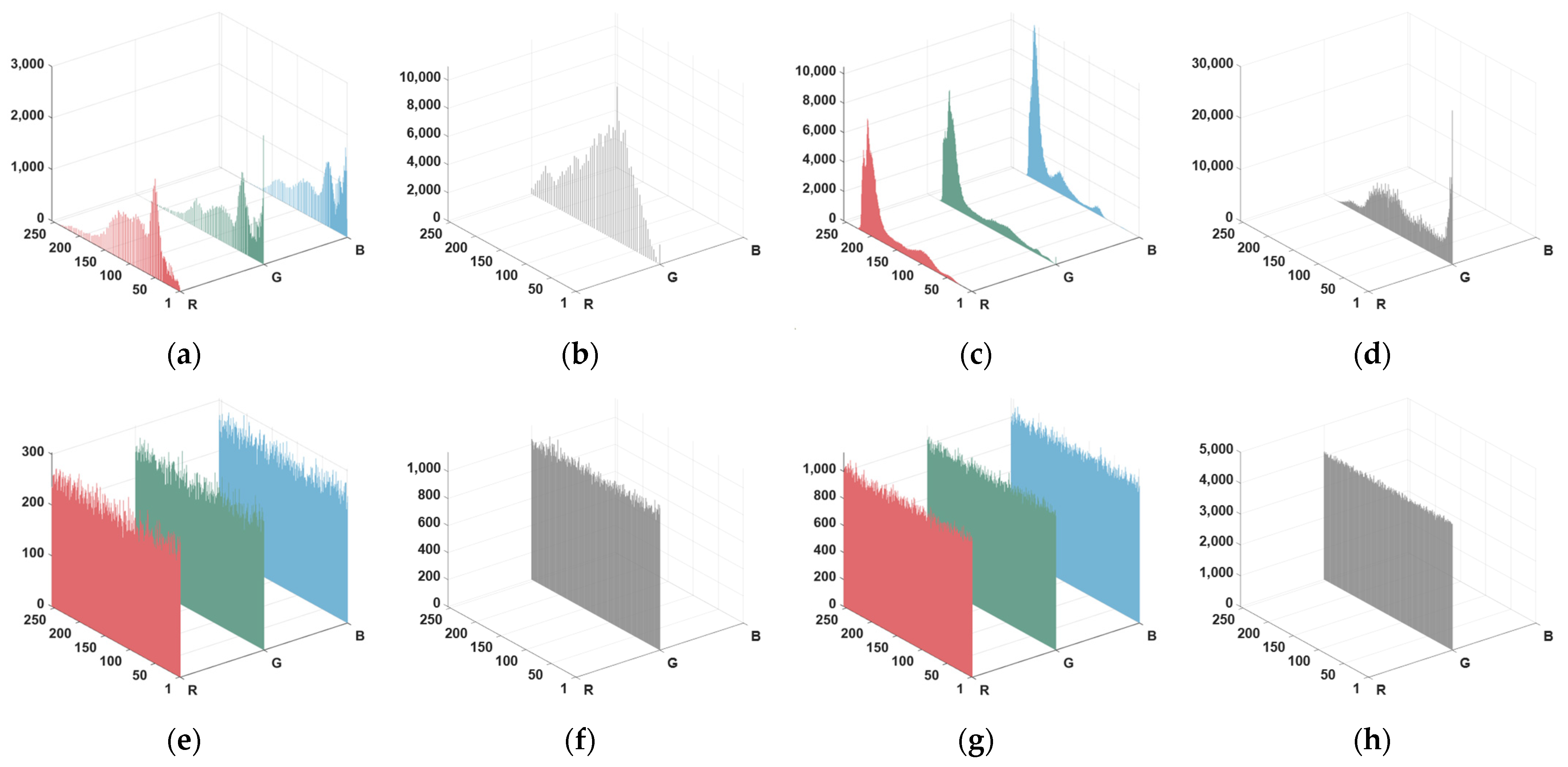
5.3. Histogram Analysis
5.4. Chosen Plaintext Attack Analysis
5.5. Differential Attack Analysis
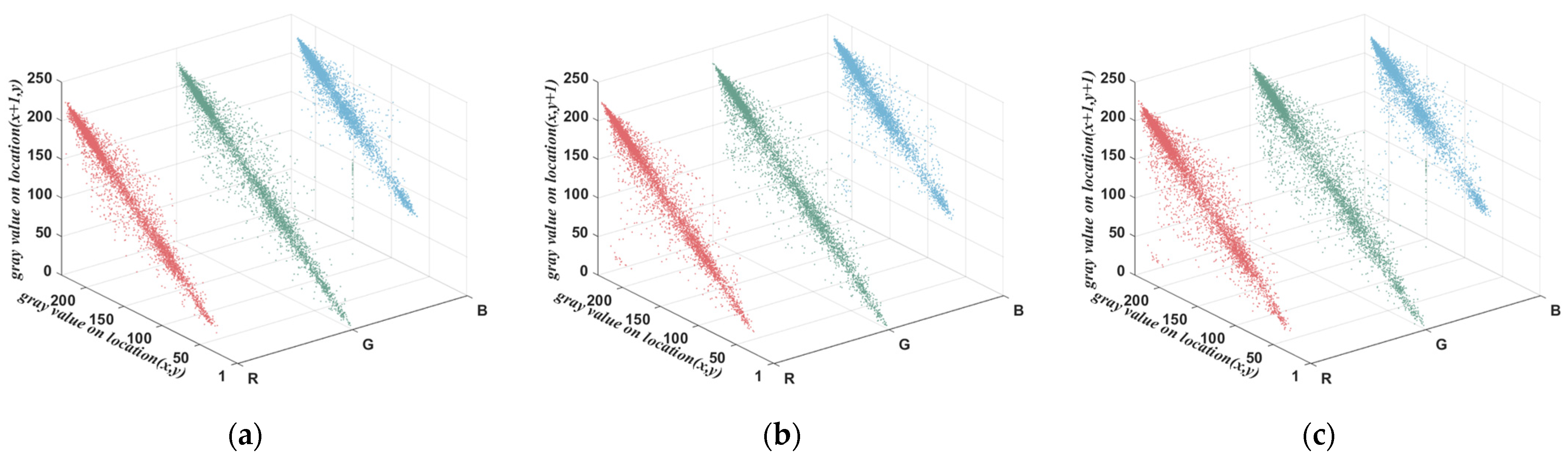
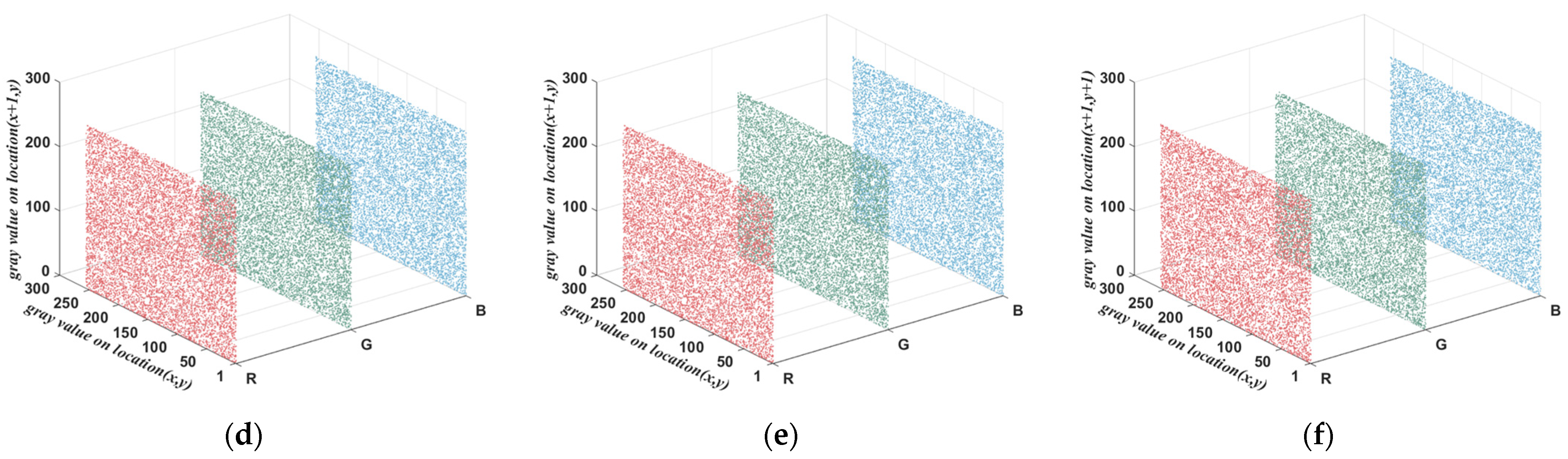
5.6. The Correlation between Adjacent Pixels Analysis
5.7. Information Entropy Analysis
5.8. Robustness Analysis
5.9. Speed Analysis
5.10. Comparison with Other Schemes
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, N.-R.; Tong, L.-J.; Zou, W.-P. Multi-image encryption scheme with quaternion discrete fractional Tchebyshev moment transform and cross-coupling operation. Signal Process. 2023, 211, 109107. [Google Scholar] [CrossRef]
- Xian, Y.; Wang, X. Fractal sorting matrix and its application on chaotic image encryption. Inf. Sci. 2021, 547, 1154–1169. [Google Scholar] [CrossRef]
- Duan, C.-F.; Zhou, J.; Gong, L.-H.; Wu, J.-Y.; Zhou, N.-R. New color image encryption scheme based on multi-parameter fractional discrete Tchebyshev moments and nonlinear fractal permutation method. Opt. Lasers Eng. 2022, 150, 106881. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, Z.; Li, X.; Wu, M.; Wang, X.; Dong, Y. Quantum Image Encryption Based on Quantum Image Decomposition. Int. J. Theor. Phys. 2021, 60, 2930–2942. [Google Scholar] [CrossRef]
- Guo, L.; Du, H.; Huang, D. A quantum image encryption algorithm based on the Feistel structure. Quantum Inf. Process. 2022, 21, 20. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Q. Compressed phase coding-based optical image encryption. Optik 2023, 278, 170744. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, X.; Jin, M.; Zhang, L.; Xu, B. Optical image encryption based on two-channel detection and deep learning. Opt. Lasers Eng. 2023, 162, 107415. [Google Scholar] [CrossRef]
- Kumar, K.; Roy, S.; Rawat, U.; Malhotra, S. IEHC: An efficient image encryption technique using hybrid chaotic map. Chaos Solitons Fractals 2022, 158, 111994. [Google Scholar] [CrossRef]
- Chen, J.; Chen, L.; Zhang, L.Y.; Zhu, Z.-l. Medical image cipher using hierarchical diffusion and non-sequential encryption. Nonlinear Dyn. 2019, 96, 301–322. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, B.; Zhou, Y. Sine Chaotification Model for Enhancing Chaos and Its Hardware Implementation. IEEE Trans. Ind. Electron. 2019, 66, 1273–1284. [Google Scholar] [CrossRef]
- Wang, R.; Li, M.-Y.; Luo, H.-J. Exponential sine chaotification model for enhancing chaos and its hardware implementation. Chin. Phys. B 2022, 31, 080508. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, B.; Zhang, Y.; Zhou, Y. Modular chaotification model with FPGA implementation. Sci. China-Technol. Sci. 2021, 64, 1472–1484. [Google Scholar] [CrossRef]
- Hua, Z.; Zhang, Y.; Zhou, Y. Two-Dimensional Modular Chaotification System for Improving Chaos Complexity. IEEE Trans. Signal Process. 2020, 68, 1937–1949. [Google Scholar] [CrossRef]
- Zhou, Z.; Xu, X.; Yao, Y.; Jiang, Z.; Sun, K. Novel multiple-image encryption algorithm based on a two-dimensional hyperchaotic modular model. Chaos Solitons Fractals 2023, 173, 113630. [Google Scholar] [CrossRef]
- Teng, L.; Wang, X.; Yang, F.; Xian, Y. Color image encryption based on cross 2D hyperchaotic map using combined cycle shift scrambling and selecting diffusion. Nonlinear Dyn. 2021, 105, 1859–1876. [Google Scholar] [CrossRef]
- Sun, J. 2D-SCMCI Hyperchaotic Map for Image Encryption Algorithm. IEEE Access 2021, 9, 59313–59327. [Google Scholar] [CrossRef]
- Gao, X. Image encryption algorithm based on 2D hyperchaotic map. Opt. Laser Technol. 2021, 142, 107252. [Google Scholar] [CrossRef]
- Patro, K.A.K.; Acharya, B. An efficient dual-layer cross-coupled chaotic map security-based multi-image encryption system. Nonlinear Dyn. 2021, 104, 2759–2805. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Li, H.; Zhou, Y. Visual image encryption scheme based on inter-intra-block scrambling and weighted diffusion. Vis. Comput. 2023. [Google Scholar] [CrossRef]
- Peng, Y.; Lan, Z.; Sun, K.; Xu, W. A simple color image encryption algorithm based on a discrete memristive hyperchaotic map and time-controllable operation. Opt. Laser Technol. 2023, 165, 109543. [Google Scholar] [CrossRef]
- Wang, X.; Xu, X.; Sun, K.; Jiang, Z.; Li, M.; Wen, J. A color image encryption and hiding algorithm based on hyperchaotic system and discrete cosine transform. Nonlinear Dyn. 2023, 111, 14513–14536. [Google Scholar] [CrossRef]
- Li, T.; Zhang, D. Hyperchaotic Image Encryption Based on Multiple Bit Permutation and Diffusion. Entropy 2021, 23, 510. [Google Scholar] [CrossRef] [PubMed]
- Qiu, H.; Xu, X.; Jiang, Z.; Sun, K.; Xiao, C. A color image encryption algorithm based on hyperchaotic map and Rubik’s Cube scrambling. Nonlinear Dyn. 2022, 110, 2869–2887. [Google Scholar] [CrossRef]
- Zhu, S.; Deng, X.; Zhang, W.; Zhu, C. Image Encryption Scheme Based on Newly Designed Chaotic Map and Parallel DNA Coding. Mathematics 2023, 11, 103340. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, X.; Zhao, X. Image encryption algorithm based on improved Zigzag transformation and quaternary DNA coding. J. Inf. Secur. Appl. 2022, 70. [Google Scholar] [CrossRef]
- Wei, D.; Jiang, M.; Deng, Y. A secure image encryption algorithm based on hyper-chaotic and bit-level permutation. Expert Syst. Appl. 2023, 213, 119074. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y. Design of image cipher using block-based scrambling and image filtering. Inf. Sci. 2017, 396, 97–113. [Google Scholar] [CrossRef]
- Wang, R.; Deng, G.-Q.; Duan, X.-F. An image encryption scheme based on double chaotic cyclic shift and Josephus problem. J. Inf. Secur. Appl. 2021, 58, 102699. [Google Scholar] [CrossRef]
- Wang, X.; Liu, P. A New Image Encryption Scheme Based on a Novel One-Dimensional Chaotic System. IEEE Access 2020, 8, 174463–174479. [Google Scholar] [CrossRef]
- Xu, Q.; Sun, K.; He, S.; Zhu, C. An effective image encryption algorithm based on compressive sensing and 2D-SLIM. Opt. Lasers Eng. 2020, 134, 106178. [Google Scholar] [CrossRef]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Li, S.J.; Chen, G.R.; Mou, X.Q. On the dynamical degradation of digital piecewise linear chaotic maps. Int. J. Bifurc. Chaos 2005, 15, 3119–3151. [Google Scholar] [CrossRef]
- Yuan, X.; Zhao, J.; Yang, Y.; Wang, Y. Hybrid parallel chaos optimization algorithm with harmony search algorithm. Appl. Soft Comput. 2014, 17, 12–22. [Google Scholar] [CrossRef]
- Chang, L.; Lu, J.A.; Deng, X.M. A new two-dimensional discrete chaotic system with rational fraction and its tracking and synchronization. Chaos Solitons Fractals 2005, 24, 1135–1143. [Google Scholar] [CrossRef]
- Belazi, A.; Kharbech, S.; Aslam, M.N.; Talha, M.; Xiang, W.; Iliyasu, A.M.; Abd El-Latif, A.A. Improved Sine-Tangent chaotic map with application in medical images encryption. J. Inf. Secur. Appl. 2022, 66, 103131. [Google Scholar] [CrossRef]
- Chen, C.; Sun, K.; He, S. A class of higher-dimensional hyperchaotic maps. Eur. Phys. J. Plus 2019, 134, 410. [Google Scholar] [CrossRef]
- Mansouri, A.; Wang, X. A novel one-dimensional sine powered chaotic map and its application in a new image encryption scheme. Inf. Sci. 2020, 520, 46–62. [Google Scholar] [CrossRef]
- Talhaoui, M.Z.; Wang, X.; Midoun, M.A. A new one-dimensional cosine polynomial chaotic map and its use in image encryption. Vis. Comput. 2021, 37, 541–551. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y.; Noonan, J.P.; Agaian, S. Design of image cipher using latin squares. Inf. Sci. 2014, 264, 317–339. [Google Scholar] [CrossRef]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI randomness tests for image encryption. Cyber J. Multidiplinary J. Ence Technol. J. Sel. Areas Telecommun. 2011. [Google Scholar]
- Liu, C.; Ding, Q. A Color Image Encryption Scheme Based on a Novel 3D Chaotic Mapping. Complexity 2020, 2020, 3837209. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, Y. Multiple-image encryption algorithm based on the 3D scrambling model and dynamic DNA coding. Opt. Laser Technol. 2021, 141, 107073. [Google Scholar] [CrossRef]
- Sun, X.; Shao, Z.; Shang, Y.; Liang, M.; Yang, F. Multiple-image encryption based on cascaded gyrator transforms and high-dimensional chaotic system. Multimed. Tools Appl. 2021, 80, 15825–15848. [Google Scholar] [CrossRef]
- Patro, K.A.K.; Soni, A.; Netam, P.K.; Acharya, B. Multiple grayscale image encryption using cross -coupled chaotic maps. J. Inf. Secur. Appl. 2020, 52, 102470. [Google Scholar] [CrossRef]
- Gao, X.; Mou, J.; Banerjee, S.; Cao, Y.; Xiong, L.; Chen, X. An effective multiple-image encryption algorithm based on 3D cube and hyperchaotic map. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 1535–1551. [Google Scholar] [CrossRef]
- Wang, X.; Liu, H. Cross-plane multi-image encryption using chaos and blurred pixels. Chaos Solitons Fractals 2022, 164, 112586. [Google Scholar] [CrossRef]
- Gaffar, A.; Joshi, A.B.; Singh, S.; Mishra, V.N.; Rosales, H.G.; Zhou, L.; Dhaka, A.; Mishra, L.N. A Technique for Securing Multiple Digital Images Based on 2D Linear Congruential Generator, Silver Ratio, and Galois Field. IEEE Access 2021, 9, 96125–96150. [Google Scholar] [CrossRef]
- Ye, H.-S.; Zhou, N.-R.; Gong, L.-H. Multi-image compression-encryption scheme based on quaternion discrete fractional Hartley transform and improved pixel adaptive diffusion. Signal Process. 2020, 175. [Google Scholar] [CrossRef]
- Ul Haq, T.; Shah, T. Algebra-chaos amalgam and DNA transform based multiple digital image encryption. J. Inf. Secur. Appl. 2020, 54, 102592. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, J.; Liu, D.; Wang, X. A Multiple-Medical-Image Encryption Method Based on SHA-256 and DNA Encoding. Entropy 2023, 25, 898. [Google Scholar] [CrossRef] [PubMed]









| Key Type | Image | Size | Level 1 | Level 2 | Level 3 | |||
|---|---|---|---|---|---|---|---|---|
| NPCR (%) | UACI (%) | NPCR (%) | UACI (%) | NPCR (%) | UACI (%) | |||
| Key generated by SHA-512 | 5.1.11 | 256 × 256 × 1 | 99.6184 | 33.4516 | 99.6120 | 33.4797 | 99.6445 | 33.5498 |
| 1.1.01 | 512 × 512 × 1 | 99.6088 | 33.4600 | 99.6132 | 33.4604 | 99.6235 | 33.5580 | |
| 1.3.01 | 1024 × 1024 × 1 | 99.6108 | 33.4651 | 99.6078 | 33.4424 | 99.6058 | 33.4144 | |
| 4.1.01 | 256 × 256 × 3 | 99.6049 | 33.4838 | 99.6119 | 33.4793 | 99.5900 | 33.4514 | |
| 4.2.01 | 512 × 512 × 3 | 99.6146 | 33.4744 | 99.6131 | 33.4682 | 99.6260 | 33.4593 | |
| 2.2.01 | 1024 × 1024 × 3 | 99.6087 | 33.4596 | 99.6102 | 33.4637 | 99.6088 | 33.4732 | |
| Pure black | 512 × 512 × 3 | 99.6084 | 33.4465 | 99.6111 | 33.4456 | 99.6241 | 33.4705 | |
| Mean | - | 99.6107 | 33.4630 | 99.6113 | 33.4627 | 99.6175 | 33.4824 | |
| Customized key | 5.1.12 | 256 × 256 × 1 | 99.5911 | 33.2539 | 99.6030 | 33.5674 | 99.6124 | 33.5947 |
| 5.2.10 | 512 × 512 × 1 | 99.5975 | 33.3703 | 99.6088 | 33.4564 | 99.6029 | 33.4332 | |
| 5.3.01 | 1024 × 1024 × 1 | 99.6031 | 33.4669 | 99.6107 | 33.4592 | 99.6011 | 33.4326 | |
| 4.1.05 | 256 × 256 × 3 | 99.5967 | 33.4399 | 99.6014 | 33.4807 | 99.6282 | 33.4856 | |
| 4.2.05 | 512 × 512 × 3 | 99.6015 | 33.4614 | 99.6084 | 33.4686 | 99.6160 | 33.4847 | |
| 6.2.02 | 1024 × 1024 × 3 | 99.6111 | 33.4849 | 99.6099 | 33.4630 | 99.6044 | 33.4669 | |
| Pure white | 512 × 512 × 3 | 99.6168 | 33.4971 | 99.6032 | 33.4590 | 99.6170 | 33.4838 | |
| Mean | - | 99.6025 | 33.4249 | 99.6065 | 33.4792 | 99.6117 | 33.4831 | |
| Image | Size | Direction | Plaintext Image | Ciphertext Image | ||
|---|---|---|---|---|---|---|
| Level 1 | Level 2 | Level 3 | ||||
| 4.1.01 | 256 × 256 × 3 | H | 0.9679 | −0.0032 | 0.0040 | 0.0019 |
| V | 0.9588 | 0.0065 | 0.0068 | 0.0067 | ||
| D | 0.9447 | 0.0019 | −0.0010 | 0.0028 | ||
| 5.2.10 | 512 × 512 × 1 | H | 0.9317 | 0.0199 | −0.0054 | −0.0022 |
| V | 0.9435 | −0.0029 | 0.0000 | 0.0063 | ||
| D | 0.9036 | −0.0075 | 0.0003 | 0.0009 | ||
| 4.2.05 | 512 × 512 × 3 | H | 0.9604 | 0.0022 | −0.0044 | −0.0015 |
| V | 0.9543 | 0.0066 | 0.0036 | 0.0009 | ||
| D | 0.9251 | 0.0027 | −0.0011 | −0.0014 | ||
| 5.3.01 | 1024 × 1024 × 1 | H | 0.9818 | −0.0062 | 0.0051 | 0.0001 |
| V | 0.9769 | 0.0074 | 0.0005 | −0.0018 | ||
| D | 0.9665 | 0.0087 | 0.0047 | 0.0001 | ||
| Pure black | 512 × 512 × 3 | H | - | −0.0045 | −0.0020 | −0.0014 |
| V | - | 0.0082 | 0.0005 | −0.0065 | ||
| D | - | 0.0066 | 0.0040 | −0.0013 | ||
| Image | Size | PI | CI | Image | Size | PI | CI | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Level 1 | Level 2 | Level 3 | Level 1 | Level 2 | Level 3 | ||||||
| 5.1.11 | 256 × 256 × 1 | 6.4523 | 7.9971 | 7.9975 | 7.9978 | 5.1.12 | 256 × 256 × 1 | 6.8981 | 7.9977 | 7.9981 | 7.9979 |
| 1.1.01 | 512 × 512 × 1 | 6.7057 | 7.9993 | 7.9992 | 7.9994 | 5.2.10 | 512 × 512 × 1 | 7.0686 | 7.9993 | 7.9992 | 7.9993 |
| 1.3.01 | 1024 × 1024 × 1 | 7.6702 | 7.9998 | 7.9998 | 7.9998 | 5.3.01 | 1024 × 1024 × 1 | 7.2428 | 7.9999 | 7.9998 | 7.9998 |
| 4.1.01 | 256 × 256 × 3 | 5.7056 | 7.9990 | 7.9992 | 7.9992 | 4.1.05 | 256 × 256 × 3 | 6.6639 | 7.9998 | 7.9998 | 7.9998 |
| 4.2.01 | 512 × 512 × 3 | 7.4404 | 7.9997 | 7.9998 | 7.9998 | 4.2.05 | 512 × 512 × 3 | 7.6133 | 7.9999 | 7.9999 | 7.9999 |
| 2.2.01 | 1024 × 1024 × 3 | 7.5237 | 7.9999 | 7.9999 | 7.9999 | 6.2.02 | 1024 × 1024 × 3 | 6.5786 | 7.9999 | 7.9999 | 7.9999 |
| Pure black | 512 × 512 × 3 | 0 | 7.9997 | 7.9998 | 7.9998 | Pure white | 512 × 512 × 3 | 0 | 7.9998 | 7.9998 | 7.9998 |
| Size | Level 1 | Level 2 | Level 3 | |||
|---|---|---|---|---|---|---|
| Time (s) | Time (s/Unit) | Time (s) | Time (s/Unit) | Time (s) | Time (s/Unit) | |
| 256 × 256 × 1 | 0.064 | 0.064 | 0.121 | 0.121 | 0.229 | 0.229 |
| 512 × 512 × 1 | 0.226 | 0.057 | 0.337 | 0.084 | 0.749 | 0.187 |
| 1024 × 1024 × 1 | 0.807 | 0.050 | 1.161 | 0.073 | 2.502 | 0.156 |
| 256 × 256 × 3 | 0.171 | 0.057 | 0.264 | 0.088 | 0.579 | 0.193 |
| 512 × 512 × 3 | 0.624 | 0.052 | 0.886 | 0.074 | 1.944 | 0.162 |
| 1024 × 1024 × 3 | 2.221 | 0.046 | 3.153 | 0.066 | 6.626 | 0.138 |
| Mean | - | 0.054 | - | 0.084 | - | 0.178 |
| Scheme | NPCR (%) | UACI (%) | Correlation | IE | Time (s/Unit) | ||
|---|---|---|---|---|---|---|---|
| Horizontal | Vertical | Diagonal | |||||
| Ref. [18] | 99.6229 | 33.4809 | 0.0019 | 0.0012 | 0.0020 | 7.9994 | - |
| Ref. [43] | 99.6060 | 33.5126 | −0.0003 | 0.0011 | 0.0013 | 7.9998 | 0.107 |
| Ref. [44] | - | - | 0.0044 | −0.0050 | −0.0002 | - | 0.515 |
| Ref. [45] | 99.6167 | 33.4772 | −0.0036 | −0.0049 | −0.0023 | 7.9993 | - |
| Ref. [46] | 99.6200 | 33.4600 | 0.0013 | 0.0009 | −0.0018 | 7.9999 | 0.540 |
| Ref. [47] | 99.6085 | 33.4634 | 0.0011 | 0.0008 | 0.0015 | 7.9993 | 0.320 |
| Ref. [48] | 99.6012 | 33.4418 | 0.0015 | −0.0002 | −0.0004 | 7.9996 | 0.503 |
| Ref. [49] | 99.6077 | 33.4399 | −0.0016 | 0.0057 | −0.0189 | 7.9996 | 1.711 |
| Ref. [50] | 99.6367 | 33.3733 | 0.0116 | 0.0057 | 0.0039 | 7.9994 | - |
| Ref. [51] | 99.6174 | 33.4657 | −0.0164 | 0.0056 | 0.0289 | 7.9993 | 0.123 |
| Level 1 | 99.6107 | 33.4630 | 0.0022 | 0.0066 | 0.0027 | 7.9993 | 0.054 |
| Level 2 | 99.6113 | 33.4627 | −0.0044 | 0.0036 | −0.0011 | 7.9994 | 0.084 |
| Level 3 | 99.6175 | 33.4824 | −0.0015 | 0.0009 | −0.0014 | 7.9994 | 0.178 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Xu, X.; Jiang, Z.; Sun, K. Multiple-Image Encryption Scheme Based on an N-Dimensional Chaotic Modular Model and Overlapping Block Permutation–Diffusion Using Newly Defined Operation. Mathematics 2023, 11, 3373. https://doi.org/10.3390/math11153373
Zhou Z, Xu X, Jiang Z, Sun K. Multiple-Image Encryption Scheme Based on an N-Dimensional Chaotic Modular Model and Overlapping Block Permutation–Diffusion Using Newly Defined Operation. Mathematics. 2023; 11(15):3373. https://doi.org/10.3390/math11153373
Chicago/Turabian StyleZhou, Ziqi, Xuemei Xu, Zhaohui Jiang, and Kehui Sun. 2023. "Multiple-Image Encryption Scheme Based on an N-Dimensional Chaotic Modular Model and Overlapping Block Permutation–Diffusion Using Newly Defined Operation" Mathematics 11, no. 15: 3373. https://doi.org/10.3390/math11153373
APA StyleZhou, Z., Xu, X., Jiang, Z., & Sun, K. (2023). Multiple-Image Encryption Scheme Based on an N-Dimensional Chaotic Modular Model and Overlapping Block Permutation–Diffusion Using Newly Defined Operation. Mathematics, 11(15), 3373. https://doi.org/10.3390/math11153373






