Author Contributions
Conceptualization, J.A. and H.W.G.; methodology, R.B.A.-V. and H.W.G.; software, J.A. and E.C.-O.; validation, R.B.A.-V., O.V. and H.W.G.; formal analysis, R.B.A.-V., E.C.-O. and H.W.G.; investigation, J.A.; writing—original draft preparation, J.A. and R.B.A.-V.; writing—review and editing, R.B.A.-V., E.C.-O. and O.V.; funding acquisition, O.V. and H.W.G. All authors have read and agreed to the published version of the manuscript.
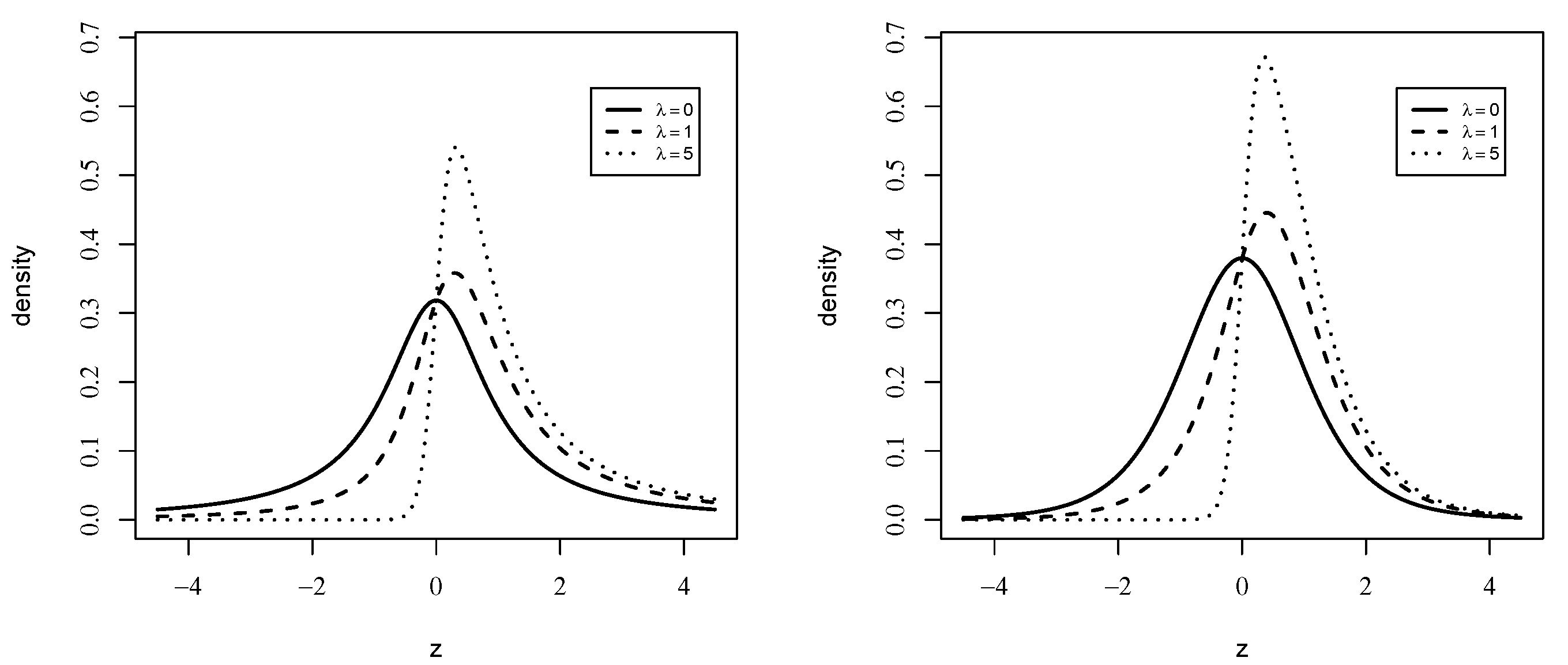
Figure 1.
Different plots of the pdf of the MStN distribution for different values of when (left panel) and (right panel).
Figure 1.
Different plots of the pdf of the MStN distribution for different values of when (left panel) and (right panel).
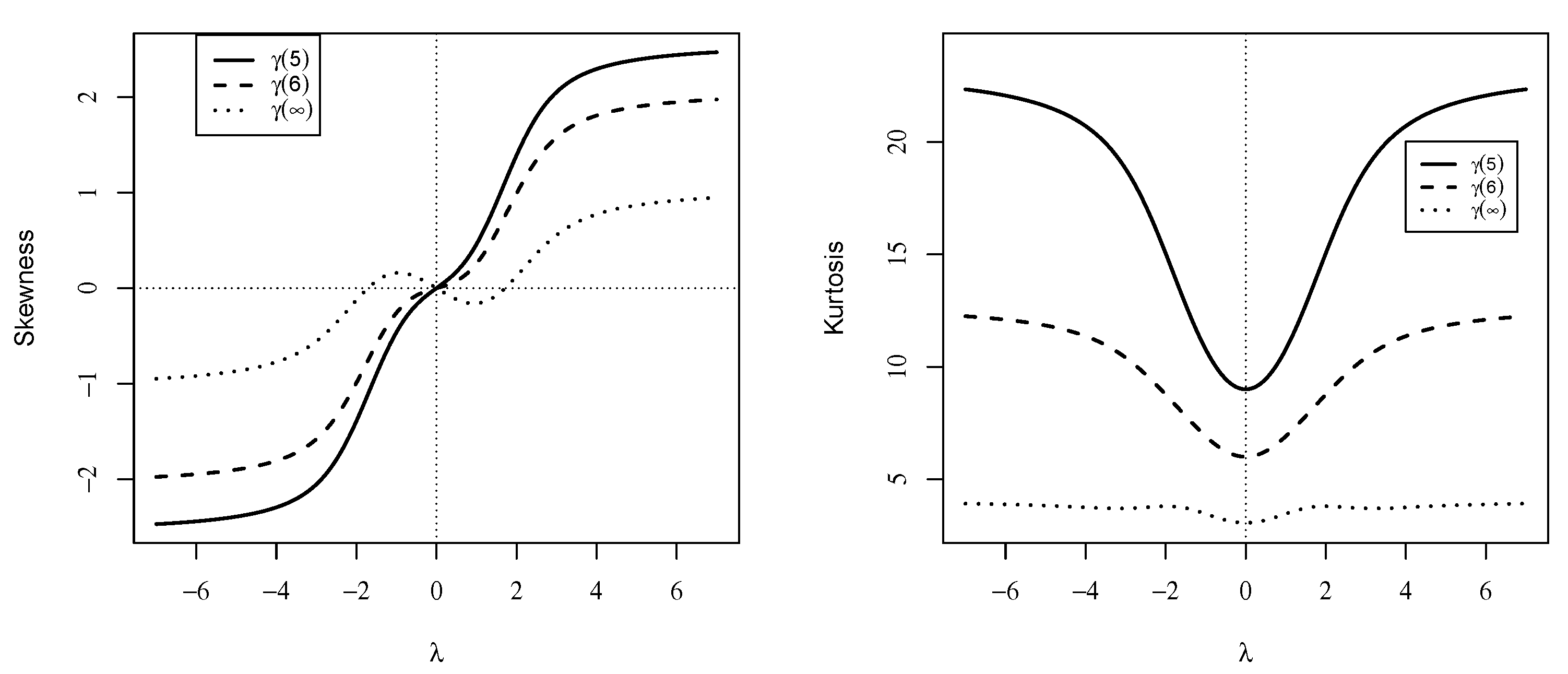
Figure 2.
Skewness and kurtosis coefficients for the MStN model.
Figure 2.
Skewness and kurtosis coefficients for the MStN model.
Figure 3.
Graph of the function .
Figure 3.
Graph of the function .
Figure 4.
Probability of divergence for the ML estimate of for the MStN model when (left panel) and (right panel).
Figure 4.
Probability of divergence for the ML estimate of for the MStN model when (left panel) and (right panel).
Figure 5.
Modified function (left panel) and integrated modified function (right panel) for SN (dashed line), MStN with (solid line) and (thick solid line) and MSN (dotted line).
Figure 5.
Modified function (left panel) and integrated modified function (right panel) for SN (dashed line), MStN with (solid line) and (thick solid line) and MSN (dotted line).
Figure 6.
Histogram of the nickel concentration data together with the pdf of MSN model (dotted) and MStN (solid).
Figure 6.
Histogram of the nickel concentration data together with the pdf of MSN model (dotted) and MStN (solid).
Figure 7.
QQ plots for MStN and MSN distributions.
Figure 7.
QQ plots for MStN and MSN distributions.
Figure 8.
Empirical cdf (ogive) versus theoretical cdf for the MStN and MSN models.
Figure 8.
Empirical cdf (ogive) versus theoretical cdf for the MStN and MSN models.
Figure 9.
Histogram of the plasma concentration of betacarotene data with the pdf of the MSN (dotted) and MStN (continuous) models.
Figure 9.
Histogram of the plasma concentration of betacarotene data with the pdf of the MSN (dotted) and MStN (continuous) models.
Figure 10.
QQ plots for MStN and MSN distributions.
Figure 10.
QQ plots for MStN and MSN distributions.
Figure 11.
Empirical cdf (ogive) versus theoretical cdf for the MStN and MSN models.
Figure 11.
Empirical cdf (ogive) versus theoretical cdf for the MStN and MSN models.
Table 1.
Skewness and kurtosis ranges for different values of .
Table 1.
Skewness and kurtosis ranges for different values of .
| Skewness Range | Kurtosis Range |
|---|
| 5 | (−2.550, 2.550) | (9.00, 23.109) |
| 7 | (−1.798, 1.798) | (5.000, 9.461) |
| 9 | (−1.539, 1.539) | (4.200, 7.054) |
| 11 | (−1.407, 1.407) | (3.857, 6.082) |
| 13 | (−1.326, 1.326) | (3.667, 5.561) |
| 15 | (−1.272, 1.272) | (3.545, 5.237) |
| 17 | (−1.233, 1.233) | (3.462, 5.017) |
| 19 | (−1.204, 1.204) | (3.400, 4.857) |
| ∞ | (−0.995, 0.995) | (3.000, 3.869) |
Table 2.
ML estimate of and empirical (theoretical) percentage of cases when it exists: this results in 5000 iterations from the model.
Table 2.
ML estimate of and empirical (theoretical) percentage of cases when it exists: this results in 5000 iterations from the model.
| | | | | |
|---|
| | a | | a | | a | |
| 5 | 3 | 6.99 | 70.68 (71.04) | 7.00 | 95.10 (95.49) | 5.82 | 99.74 (99.80) |
| | 5 | 7.17 | 71.48 (72.28) | 7.00 | 95.36 (95.95) | 5.86 | 99.90 (99.84) |
| | 10 | 7.06 | 74.52 (73.24) | 6.97 | 96.24 (96.29) | 5.83 | 99.84 (99.86) |
| 10 | 3 | 11.52 | 45.62 (45.09) | 14.58 | 77.32 (77.66) | 13.73 | 95.18 (95.01) |
| | 5 | 12.31 | 46.44 (46.15) | 15.00 | 79.08 (78.72) | 13.64 | 96.16 (95.47) |
| | 10 | 12.67 | 47.26 (47.00) | 14.38 | 80.40 (79.55) | 13.88 | 95.54 (95.82) |
Table 3.
Bias of , and , and percentages of cases when exists: results in 5000 iterations from the distribution.
Table 3.
Bias of , and , and percentages of cases when exists: results in 5000 iterations from the distribution.
| n | | | Bias () | Bias () | a | |
|---|
| 50 | 5 | 3 | 0.003 | 0.006 | 6.860 | 83.78 |
| 100 | 5 | 3 | −0.005 | 0.010 | 6.797 | 96.98 |
| 200 | 5 | 3 | −0.001 | 0.003 | 5.665 | 99.88 |
| 50 | 10 | 3 | 0.016 | −0.010 | 11.052 | 61.80 |
| 100 | 10 | 3 | 0.004 | 0.001 | 13.499 | 85.24 |
| 200 | 10 | 3 | 0.000 | 0.002 | 13.211 | 97.60 |
| 50 | 5 | 5 | 0.003 | 0.004 | 6.840 | 85.54 |
| 100 | 5 | 5 | −0.001 | 0.000 | 6.637 | 97.52 |
| 200 | 5 | 5 | −0.001 | 0.003 | 5.666 | 99.96 |
| 50 | 10 | 5 | 0.016 | −0.011 | 11.254 | 61.96 |
| 100 | 10 | 5 | 0.004 | −0.003 | 13.645 | 86.08 |
| 200 | 10 | 5 | 0.001 | −0.001 | 12.845 | 98.00 |
| 50 | 5 | 10 | 0.008 | −0.006 | 6.798 | 87.10 |
| 100 | 5 | 10 | 0.000 | 0.001 | 6.525 | 98.22 |
| 200 | 5 | 10 | 0.000 | 0.002 | 5.641 | 99.94 |
| 50 | 10 | 10 | 0.017 | −0.015 | 11.404 | 65.28 |
| 100 | 10 | 10 | 0.002 | −0.001 | 13.621 | 87.80 |
| 200 | 10 | 10 | −0.001 | 0.000 | 13.200 | 98.20 |
Table 4.
Bias of and , empirical coverage of 0.95CI based on and empirical (theoretical) percentage of cases when exists: results in 5000 iterations from the distribution.
Table 4.
Bias of and , empirical coverage of 0.95CI based on and empirical (theoretical) percentage of cases when exists: results in 5000 iterations from the distribution.
| n | | | Bias( a | Bias( | | |
|---|
| 20 | 5 | 3 | 1.867 | −1.583 | 0.94 | 71.64 (71.04) |
| 50 | 5 | 3 | 1.754 | −0.298 | 0.95 | 95.06 (95.49) |
| 100 | 5 | 3 | 0.788 | −0.030 | 0.95 | 99.82 (99.80) |
| 20 | 10 | 3 | 1.991 | −6.034 | 0.90 | 44.78 (45.09) |
| 50 | 10 | 3 | 4.299 | −2.866 | 0.94 | 76.80 (77.66) |
| 100 | 10 | 3 | 3.856 | −0.694 | 0.94 | 94.84 (95.01) |
| 20 | 5 | 5 | 2.148 | −1.513 | 0.94 | 72.62 (72.28) |
| 50 | 5 | 5 | 1.802 | −0.293 | 0.95 | 96.48 (95.95) |
| 100 | 5 | 5 | 0.815 | −0.004 | 0.95 | 99.80 (99.84) |
| 20 | 10 | 5 | 2.197 | −5.949 | 0.90 | 46.46 (46.15) |
| 50 | 10 | 5 | 4.116 | −2.751 | 0.94 | 79.38 (78.72) |
| 100 | 10 | 5 | 3.862 | −0.626 | 0.95 | 95.38 (95.47) |
| 20 | 5 | 10 | 2.177 | −1.479 | 0.94 | 72.82 (73.24) |
| 50 | 5 | 10 | 2.103 | −0.236 | 0.96 | 96.64 (96.29) |
| 100 | 5 | 10 | 0.776 | 0.018 | 0.95 | 99.90 (99.86) |
| 20 | 10 | 10 | 2.274 | −5.888 | 0.91 | 47.42 (47.00) |
| 50 | 10 | 10 | 4.169 | −2.626 | 0.94 | 79.18 (79.55) |
| 100 | 10 | 10 | 4.338 | −0.600 | 0.95 | 95.88 (95.82) |
Table 5.
Bias of , , and , empirical coverage of 0.95 CI based on and empirical percentage of cases when exists: results in 5000 iterations from the model.
Table 5.
Bias of , , and , empirical coverage of 0.95 CI based on and empirical percentage of cases when exists: results in 5000 iterations from the model.
| n | | | Bias () | Bias () | Bias () | Bias () | | |
|---|
| 50 | 5 | 3 | 0.004 | 0.005 | 1.889 | −0.898 | 0.93 | 84.24 |
| 100 | 5 | 3 | −0.002 | 0.005 | 1.617 | −0.306 | 0.94 | 97.42 |
| 200 | 5 | 3 | −0.001 | 0.004 | 0.712 | −0.106 | 0.95 | 99.84 |
| 50 | 10 | 3 | 0.017 | −0.008 | 1.097 | −3.971 | 0.87 | 61.86 |
| 100 | 10 | 3 | 0.004 | −0.003 | 3.301 | −1.699 | 0.91 | 85.40 |
| 200 | 10 | 3 | 0.001 | 0.000 | 3.188 | −0.534 | 0.94 | 97.96 |
| 50 | 5 | 5 | 0.004 | 0.002 | 1.828 | −0.855 | 0.94 | 86.70 |
| 100 | 5 | 5 | −0.002 | 0.005 | 1.755 | −0.255 | 0.94 | 97.58 |
| 200 | 5 | 5 | −0.001 | 0.002 | 0.628 | −0.098 | 0.95 | 99.78 |
| 50 | 10 | 5 | 0.016 | −0.013 | 1.185 | −3.842 | 0.87 | 63.74 |
| 100 | 10 | 5 | 0.005 | −0.002 | 3.736 | −1.508 | 0.92 | 86.72 |
| 200 | 10 | 5 | 0.000 | 0.000 | 3.053 | −0.401 | 0.94 | 97.78 |
| 50 | 5 | 10 | 0.006 | −0.003 | 1.832 | −0.813 | 0.92 | 86.84 |
| 100 | 5 | 10 | 0.000 | 0.002 | 1.523 | −0.245 | 0.95 | 98.00 |
| 200 | 5 | 10 | 0.000 | 0.000 | 0.578 | −0.108 | 0.94 | 99.94 |
| 50 | 10 | 10 | 0.014 | −0.013 | 1.530 | −3.689 | 0.88 | 64.18 |
| 100 | 10 | 10 | 0.004 | −0.002 | 3.622 | −1.311 | 0.92 | 86.40 |
| 200 | 10 | 10 | 0.002 | −0.002 | 2.700 | −0.450 | 0.93 | 98.06 |
Table 6.
Descriptive statistics of the nickel concentration dataset.
Table 6.
Descriptive statistics of the nickel concentration dataset.
| Data | n | | s | | |
|---|
| Nickel | 86 | | | | |
Table 7.
ML estimates of the parameters of the MStN model when is known together with the maximum of the log-likelihood function.
Table 7.
ML estimates of the parameters of the MStN model when is known together with the maximum of the log-likelihood function.
| | | | |
|---|
| 13.092 | 6.284 | 0.954 | 1 | −343.057 |
| 8.676 | 11.182 | 2.235 | 2 | −338.775 |
| 7.083 | 13.767 | 2.994 | 3 | −338.260 |
| 6.335 | 15.345 | 3.492 | 4 | −338.483 |
| 5.858 | 16.458 | 3.875 | 5 | −338.864 |
| 21.439 | 11.410 | −0.518 | 6 | −349.399 |
Table 8.
Parameter estimates, standard errors, and AIC for SN, MSN, and MStN distributions.
Table 8.
Parameter estimates, standard errors, and AIC for SN, MSN, and MStN distributions.
| MLE | SN | MSN | MStN |
|---|
| 2.625 (1.136) | 2.571 (1.260) | 7.083 (1.402) |
| 24.968 (1.913) | 25.027 (2.153) | 13.767 (1.838) |
| 10.261 (4.751) | 10.619 (5.239) | 2.994 (0.789) |
| - | - | 3 |
| −344.762 | −344.769 | −338.260 |
| AIC | 693.524 | 693.538 | 682.520 |
Table 9.
ML estimate and modified ML estimate of , , for the MStN distribution.
Table 9.
ML estimate and modified ML estimate of , , for the MStN distribution.
| | | | | |
|---|
| 7.083 (1.402) | 13.767 (1.838) | 2.994 (0.789) | - | −338.260 | - |
| 7.083 (1.447) | 13.767 (1.843) | - | 2.838 (0.731) | - | −338.305 |
Table 10.
Confidence interval for .
Table 10.
Confidence interval for .
| MLE | | | |
|---|
| IC | (1.696, 4.292) | (1.373, 4.615) | (1.158, 4.830) |
| IC* | (1.635, 4.040) | (1.336, 4.339) | (1.137, 4.539) |
Table 11.
Descriptive statistics of the plasma concentration of betacarotene.
Table 11.
Descriptive statistics of the plasma concentration of betacarotene.
| Data | n | | s | | |
|---|
| Betaplasma | 315 | | | | |
Table 12.
ML estimates of the parameters of the MStN model when and its maximum log-likelihood function are known.
Table 12.
ML estimates of the parameters of the MStN model when and its maximum log-likelihood function are known.
| | | | |
|---|
| 64,737 | 74,446 | 2514 | 1 | −1.931,939 |
| 52,120 | 107,392 | 3946 | 2 | −1.917,631 |
| 45,800 | 127,352 | 5081 | 3 | −1.918,405 |
| 42,250 | 140,472 | 5930 | 4 | −1.921,499 |
| 39,815 | 150,177 | 6608 | 5 | −1.924,907 |
Table 13.
Parameter estimates, standard errors, , AIC, and BIC for the SN, MSN, and MStN distributions.
Table 13.
Parameter estimates, standard errors, , AIC, and BIC for the SN, MSN, and MStN distributions.
| MLE | SN | MSN | MStN |
|---|
| 21.332 (5.180) | 21.332 (5.170) | 52.120(5.686) |
| 248.613 (10.510) | 248.594 (10.505) | 107.391(8.519) |
| 18.834(6.968) | 18.954(6.971) | 3.945(0.728) |
| - | - | 2 |
| −1976.317 | −1976.319 | −1917.631 |
| AIC | 3956.634 | 3956.638 | 3839.262 |
| BIC | 3969.896 | 3969.896 | 3852.520 |