1. Introduction
In recent years, with the rapid growth of commodity consumption, the market environment and industrial structure have changed greatly, and the logistics and transportation problems have become more and more complex. The logistics industry is facing a major challenge of reducing logistics and transportation costs and improving transportation efficiency, and the traditional single transportation method has been difficult to meet the multifaceted needs of the market. Multimodal transport relies on two or more modes of transport and integrates the characteristics of various modes of transport, which can improve transport efficiency and reduce transport costs, and has become the focus of scholars’ research [
1]. The core problem of multimodal transport is the optimization of transport routes and the choice of transport mode, which restrict each other and profoundly affect the interests of logistics enterprises and customers through transportation cost and time. Therefore, it is of great practical significance for the development of the logistics industry to study the problem of multimodal transportation route planning and provide effective solutions.
Aiming at the multimodal transportation route planning problem, scholars at home and abroad have conducted much research [
2,
3]. However, most research conducted by scholars focuses on multimodal transportation path planning in deterministic environments, and there is less research in uncertain environments. In practice, the process of cargo transportation will be affected by various uncertain factors. For example, the uncertainty of transportation and transfer time caused by road conditions and road section damage, the lack of effective information communication between customers and carriers, or the enterprise’s demand prediction to determine the cargo transportation plan, but the forecast results can hardly accurately reflect the demand uncertainty caused by the fluctuation of cargo demand [
4]. If these uncertainties are not taken into account, transportation costs and risks will increase, and the quality of transportation services will be affected. Although some scholars have considered the uncertainty of the transportation process, these models involve only one source of uncertainty. Considering multiple uncertainties at the same time better reflects the actual transportation scenarios, thus improving the reliability of multimodal route optimization results [
5]. This paper combines the uncertainty of customer demand and the uncertainty of transportation time to model multimodal transportation to provide more reliable multimodal transportation path solutions.
Demand uncertainty can be described by fuzzy programming and stochastic programming [
6,
7]. However, stochastic programming requires a large amount of historical order data to fit probability distributions of uncertain parameters [
8]. In most cases, there are not enough or unreliable data to model multimodal transport using stochastic programming. In practice, decision-makers are more likely to give their estimates of uncertain parameters, and it is more feasible to use fuzzy programming to solve uncertainty. Therefore, this paper uses fuzzy programming to represent the uncertainty of demand. In terms of time uncertainty, scholars have also done a lot of research. For example, Adil et al. [
9] used fuzzy stochastic programming to describe transportation time and established a fuzzy stochastic optimization model for multimodal transportation. Demir et al. [
10] used sampling averaging to represent the uncertainty in transportation time and demonstrated the advantages of the stochastic approach in achieving robust transportation plans. In addition, the uncertainty of transport time and transshipment time can also be fitted through common random distribution [
11], and the modelling difficulty is lower than other methods. To facilitate the solution of the model, this paper uses normal and uniform distributions to describe the uncertainty of transportation time and transshipment time, respectively.
Improving transportation efficiency is an important goal for carriers to fulfil transportation orders, which can improve the service level by enhancing the timeliness of transportation. The time window is an effective way to seek on-time delivery and reduce transportation costs in transportation planning. Most of the literature constructs a hard time window constraint [
12,
13]; that is, the completion of a transportation order must fall within its time window. Otherwise, it is regarded as a failure. However, the hard time window may cause the problem to be difficult to solve, or the optimal solution cannot be found [
14], so it is more appropriate to establish a soft time window. In this case, there is an inventory cost for early arrival and a penalty cost for late arrival. In addition, considering only the time window of the destination simplifies the model research, but in practice, each intermediate node may have different time window requirements [
15]. The multimodal routes can be better optimized if the time windows of the nodes in the multimodal network are considered. Therefore, this paper introduces a mixed-time window constraint, i.e., the intermediate node time window is set as a soft time window, which allows goods to arrive earlier or later, while the endpoint is set as a hard time window, in which goods must arrive within the range, making the model more consistent with the actual situation.
Many studies have planned multimodal transport routes to minimize cost and time without considering the impact of carbon emissions. As green transportation is getting more and more attention from the government, the issue of carbon emission has become a hot topic of research in recent years. Compared with a single mode of transportation, multimodal transportation can significantly reduce carbon emissions. Incorporating carbon emissions into multimodal transport route planning can further stimulate its potential. According to the current research, carbon emissions can be combined into the total cost through carbon tax [
16] or optimized as an independent target in the model [
17]. However, Sun et al. [
18] pointed out that carbon tax is not applicable in practice and will lead to relatively high emission costs in some paths. Therefore, it is more reliable to optimize carbon emission as an independent objective [
19]. Moreover, multi-objective optimization can balance sub-objectives to meet actual needs and has been widely used in decision-making [
20]. Therefore, this paper establishes a multi-objective optimization model with transportation cost, time, and carbon emission as the objectives.
The multi-objective optimization models usually have infinitely many Pareto optimal solutions and need to combine the user preferences for each objective to determine a single suitable solution [
21]. The weighted sum method is a classical method for multi-objective optimization [
22], and its effectiveness in solving multi-objective optimization models, especially preference models, has been verified [
23]. Therefore, this paper chooses the weighted sum method to solve the multimodal transport model. The weighted sum method solves the multi-objective model by converting the multi-objective optimization problem into a single-objective problem by assigning the corresponding weights to different objectives and solving it by an optimization algorithm [
23]. However, the setting of weight coefficients is highly subjective, and it is difficult to determine the appropriate weights for each objective based on preferences [
24]. Fixed weights tend to discard the optimal solution of the whole system and cause unnecessary losses. It is necessary to automatically adjust the weights of each objective during the optimization process by an appropriate and effective method to seek the relevant equilibrium among the objectives and converge to the optimal solution in dynamic optimization. Game theory is an effective method to deal with the interaction of multiple objectives and has been widely used in some complex optimization problems between various fields [
25]. Therefore, this paper combines the game theory method with the weighted sum method to propose a cooperative game theory-based multi-objective optimization method for multimodal transportation. In the process of algorithm optimization, each objective is as far away from its worst result as possible, and the weights of each objective are dynamically adjusted in the optimization process by the game theory method without prior knowledge to obtain the best multimodal transportation path scheme.
After the weight of each object is dynamically updated by the cooperative game theory method, it can be solved by the optimization algorithm. The multi-objective optimization model of multimodal transport established in this paper involves many intermediate variables and is a typical NP-hard problem [
26], which is computationally intensive and not suitable for solving using mathematical planning and exact solution methods [
11]. The excellent performance of the heuristic algorithm in combinatorial optimization makes it widely used in multimodal cargo transportation optimization [
27]. Among them, the particle swarm algorithm (PSO) has the characteristics of fast convergence ability and computational simplicity [
28,
29] and has some advantages over other evolutionary algorithms in terms of implementation difficulty, algorithm parameter setting, and optimization search [
30]. Therefore, in this paper, PSO is chosen as the solution algorithm for the multimodal transport model.
In this study, our main contributions are:
To solve the problem of multimodal transport path planning under uncertain environments, a multi-objective fuzzy nonlinear programming model considering mixed-time window constraints is established.
To make the model solvable, the fuzzy expected value method and the fuzzy chance-constrained programming method are used to de-fuzzify the established multi-objective fuzzy programming model and obtain the deterministic parameters of the model.
Combining the game theory method with the weighted sum method, a multi-objective optimization method of multimodal transport based on cooperative game theory is proposed. The weights of each objective are dynamically adjusted in the algorithm optimization process through cooperative game theory to obtain the optimal path of multimodal transportation.
This paper is organized as follows:
Section 2 develops a multi-objective optimization model for multimodal transportation considering multiple uncertainty factors under a mixed-time window constraint.
Section 3 defuzzifies the multi-objective fuzzy programming model and presents the algorithms used to solve the multimodal multi-objective model. The model and algorithm proposed in this paper are verified in a real combined transport network in
Section 4, and the relevant results are analyzed.
Section 5 summarizes the full work and provides an outlook for future work.
5. Conclusions and Future Work
In this paper, a multi-objective fuzzy nonlinear programming model considering mixed time window constraints is established to solve the problem of multimodal transport path planning under an uncertain environment, taking cost, time, and carbon emission as optimization objectives. Then, the fuzzy expected value method and the fuzzy chance-constrained programming method are used to de-fuzzify the multi-objective fuzzy programming model, and the deterministic parameters of the model are obtained. To solve the model, a multi-objective optimization method of multimodal transport based on cooperative game theory is proposed. The game theory method is combined with the weighted sum method, and the weight of each objective is dynamically adjusted in the algorithm optimization process through cooperative game theory to obtain the optimal multimodal transport path. Finally, the effectiveness of the proposed algorithm is verified in a real combined transport network.
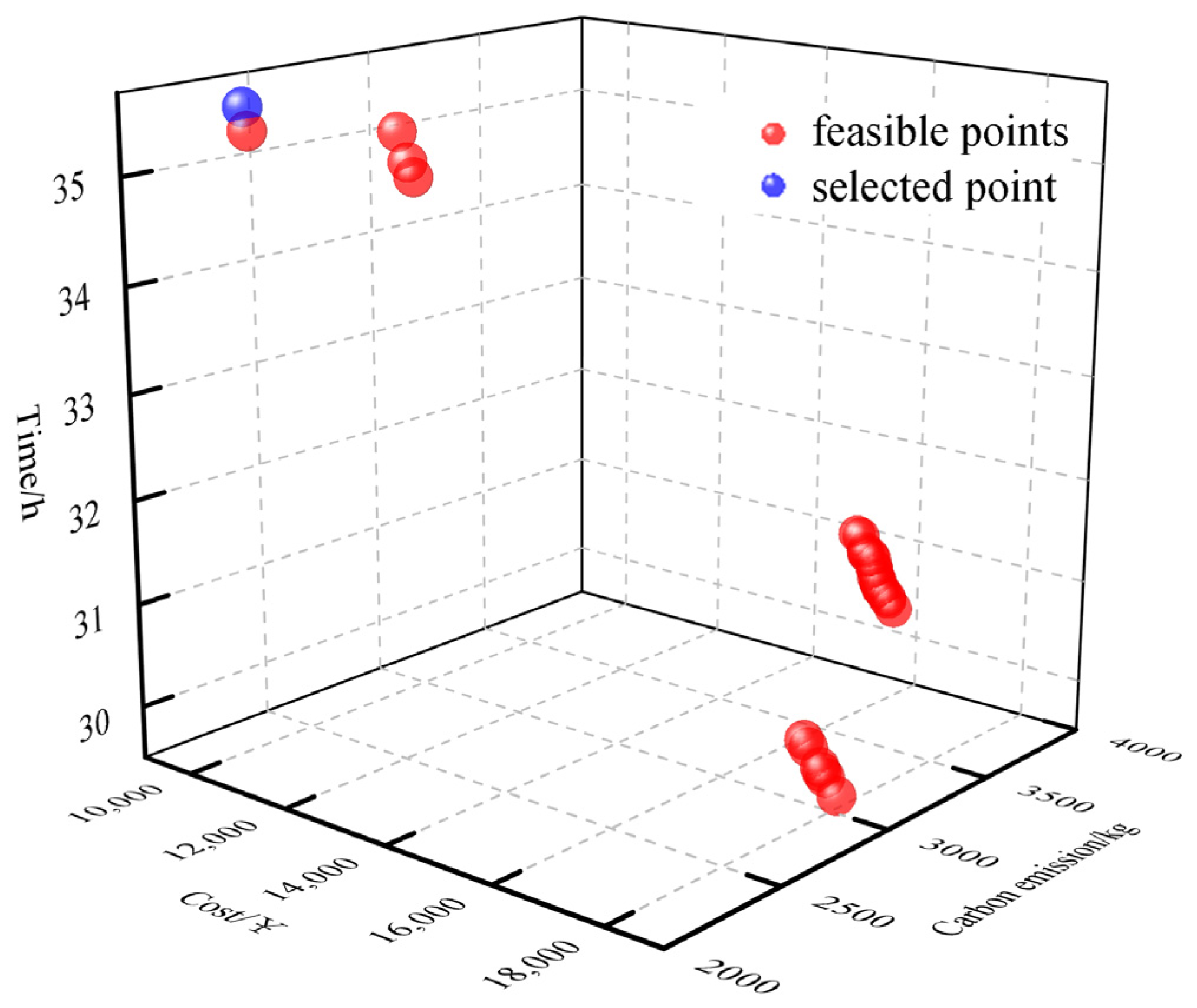
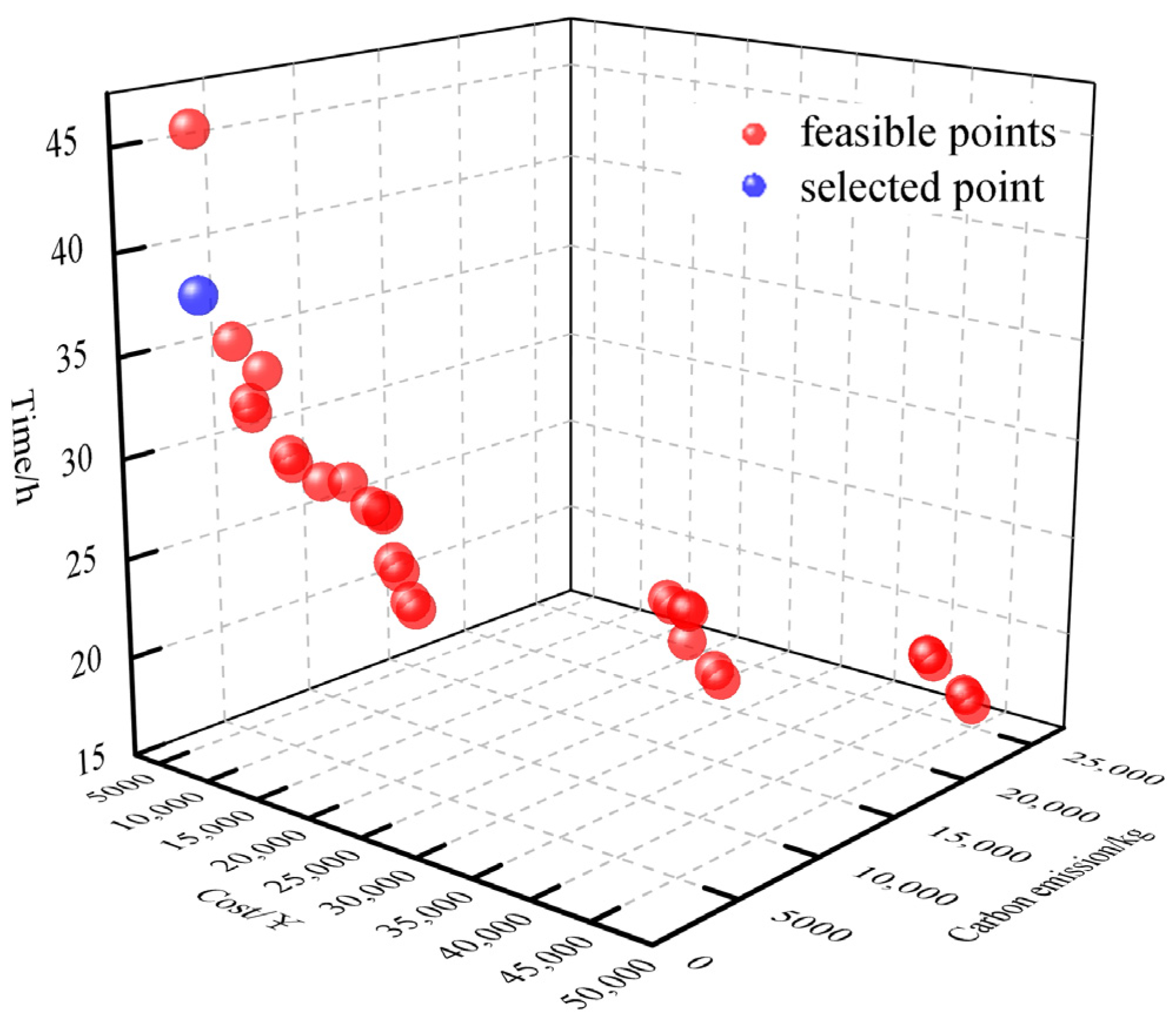
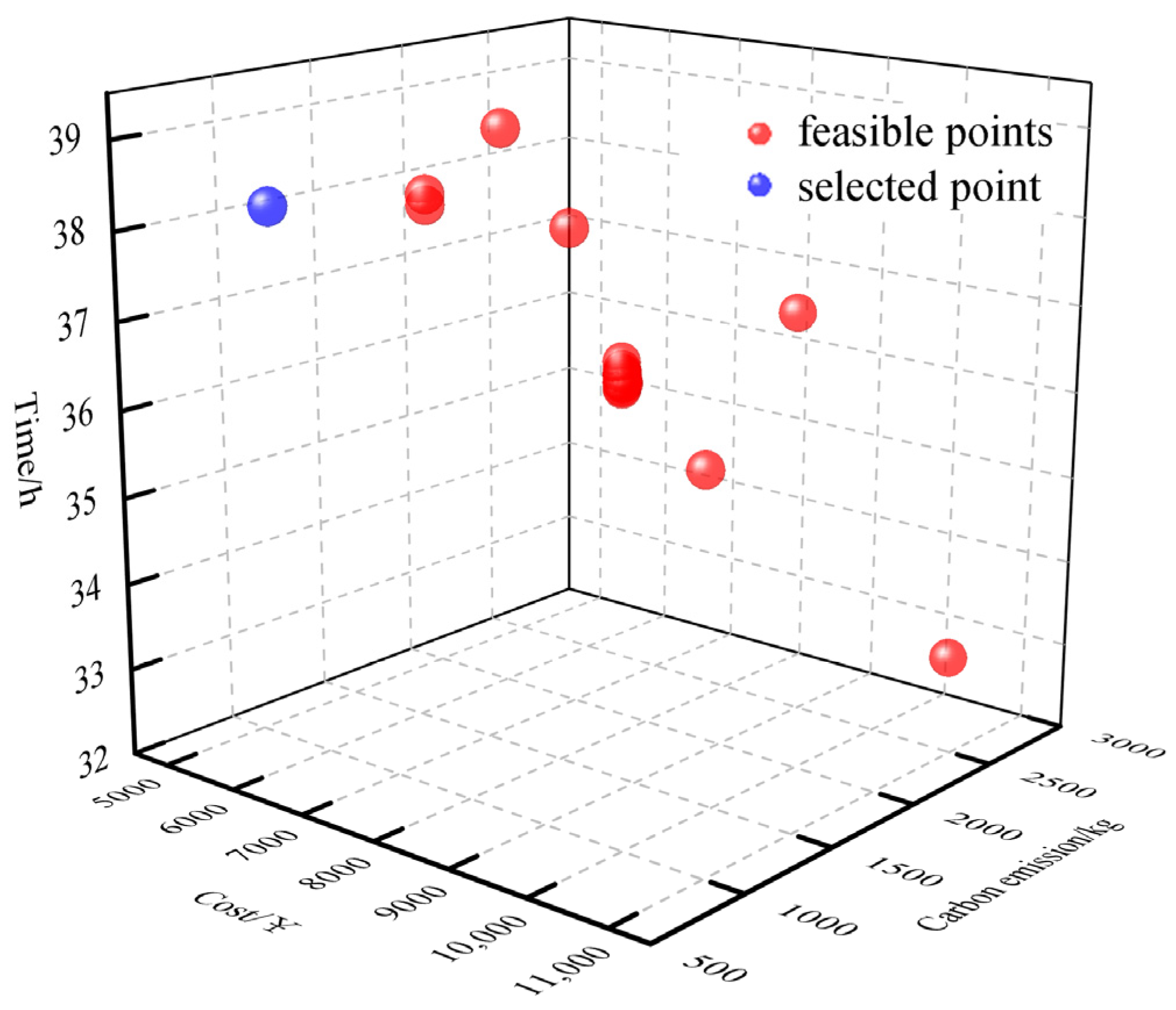
The experiment results show that the method of dynamically adjusting weights by cooperative game theory effectively improves the performance of the weighted sum method, and the obtained results are overall better than those using a fixed combination of weights. In addition, compared with MOPSO and NSGA-II, the proposed algorithm has a better optimization effect and can combine the decision-makers’ preference for the goal well to obtain the optimal path that meets the requirements of the time window, effectively reducing transportation costs and carbon emissions and promoting the development of green transportation. The effectiveness of the weighted sum method in the multi-objective preference model is further proved.
Finally, this paper analyzes the influence of uncertainty factors on multimodal route planning results. The results show that demand uncertainty has a more obvious influence on the optimization results of the multimodal transport model than time uncertainty. It is necessary to consider the uncertainty factor in the model when performing multimodal transport route planning. By taking uncertainties into account, the robustness and accuracy of route planning results can be improved, thus providing a more reliable and efficient solution for multimodal transport services.
In addition, through the analysis of route optimization results, it can be seen that railway transportation plays a significant role in reducing transportation costs and carbon emissions. Therefore, in future work, we will further explore the impact of the railway on the multimodal transport structure, and we will consider more uncertainty factors in the model to better simulate the real transportation environment, as well as find other methods to solve the multi-objective problem and provide more reliable multimodal transportation path solutions.