Abstract
Given several nonnegative matrices with a single pattern of allocation among their zero/nonzero elements, the average matrix should have the same pattern, too. This is the first tenet of the pattern-multiplicative average (PMA) concept, while the second one suggests the multiplicative (or geometric) nature of averaging. The original concept of PMA was motivated by the practice of matrix population models as a tool to assess the population viability from long-term monitoring data. The task has reduced to searching for an approximate solution to an overdetermined system of polynomial equations for unknown elements of the average matrix (G), and hence to a nonlinear constrained minimization problem for the matrix norm. Former practical solutions faced certain technical problems, which required sophisticated algorithms but returned acceptable estimates. Now, we formulate (for the first time in ecological modeling and nonnegative matrix theory) the PMA problem as an eigenvalue approximation one and reduce it to a standard problem of linear programing (LP). The basic equation of averaging also determines the exact value of λ1(G), the dominant eigenvalue of matrix G, and the corresponding eigenvector. These are bound by the well-known linear equations, which enable an LP formulation of the former nonlinear problem. The LP approach is realized for 13 fixed-pattern matrices gained in a case study of Androsace albana, an alpine short-lived perennial, monitored on permanent plots over 14 years. A standard software routine reveals the unique exact solution, rather than an approximate one, to the PMA problem, which turns the LP approach into ‘’the best of versatile optimization tools”. The exact solution turns out to be peculiar in reaching zero bounds for certain nonnegative entries of G, which deserves modified problem formulation separating the lower bounds from zero.
Keywords:
matrix population model; Androsace albana; life cycle graph; population projection matrix; matrix average; constrained optimization; linear programming; exact solution MSC:
15B48; 90C08; 90C26; 92D25; 92-10
1. Introduction
Pattern-multiplicative average (PMA) of nonnegative matrices is a concept motivated in the field of matrix population models by the need to assess the viability of a local population from the outcome of its long-term monitoring. Matrix population models represent a wide and rapidly growing area of applications [1,2], where the theory of nonnegative matrices applies to population dynamics [3]. When biologists study a population of a plant or animal species and observe the population at discrete time moments, they classify individuals according to an observable trait such as age, body size, ontogenetic stage, etc., and divide the entire range of trait values into certain discrete classes, thus dealing with a discrete population structure [4]. It is expressed mathematically as a vector x(t) ∈ (n ≥ 2) representing the (absolute or relative) abundances of n class-specific groups of individuals, whereafter the matrix population model is a system of first-order difference equations,
linking the population vector at the next moment, t + 1, to that at the current one, t.
x(t + 1) = L(t) x(t), t = 0, 1, 2, …,
Matrix L(t) is therefore called the population projection matrix (PPM) [4], despite the projection term having quite another meaning in matrix algebra [5]. All the matrix entries are nonnegative and called vital rates as they have a certain demographic sense [4]. The pattern of how zero/nonzero elements are arranged within the matrix is associated, in a unique way, to what is called the life cycle graph (ibidem) as it bears the biological knowledge of how the individuals grow/develop for one time step and provide for the population recruitment.
Being nonnegative, the PPM becomes a legal target for the Perron–Frobenius Theorem [5,6], whereby a rich repertoire of model properties and population characteristics can be obtained after the PPM has been calibrated from data [4,7]. In particular, the dominant eigenvalue, λ1 > 0, of matrix L(t) serves as a “measure of how the local population is adapted to the environment where and when the data have been mined to calibrate the PPM” [8] (p. 1). When the data are of the “identified individuals” type [4], a great advantage of MPMs is that the calibration can be performed just from two successive observations, thus meeting Equation (1) and yielding a time-dependent L(t). Correspondingly, the adaptation measure, λ1, inherits the time dependence, and the great advantage turns dialectically into a great problem or challenge when the task is to assess the adaptation from a time series of observation data, hence from a finite set of one-step PPMs.
The historically first response to the challenge was grounded on the theory of random sequences of vectors L(t) x(t), t → ∞ [9,10,11,12], and it has led to what is now called the stochastic growth rate of a population in a randomly changing environment (see [4] and refs therein). Another more recent approach reverts the task just to averaging a given number, say M (M ≥ 2), of one-step PPMs and calculating the dominant eigenvalue, λ1(G), of the average matrix G. Letter “G” here bears a hint to the geometric (or multiplicative) nature of averaging, and the hint will be revealed further in Section 2.2. This approach has led to a concept that was proposed 5 years ago with regard to matrix population models [13], and the task of averaging was reduced to a constrained nonlinear minimization problem for the matrix norm [8,13] (see Section 2.3). The norm has however not appeared quite fit for global optimization but required versatile optimization tools [14] to solve the problem.
This paper aims at expanding those “versatile optimization tools” with another target of optimization, namely, the deviation of λ1(Gopt) from the ideal calculable λ1(G) (Section 2.4). The approach originates from the fact the ideal λ1(G) is known:
where Prod denotes the product of M one-step PPMs. This leads to a problem that appears to be formalizable as a standard problem of linear programming (LP), and hence solvable by standard routines. The solution is exemplified by a case study of monitoring a local population of an alpine short-lived perennial for 13 years [15] (Section 2.1). Section 2.3 and Section 2.4 contain, respectively, a short presentation of the published “versatile optimization tools” and an in-depth one of the original LP approach. The outcomes of both are presented in Section 3, enabling the comparison of results, which reveals a surprising contrast and induces certain comments (Section 4), in particular, on how general the proposed LP technique might be.
λ1(G) = (Prod)1/M,
2. Materials and Methods
2.1. Case Study
A local population of Androsace albana, an alpine short-lived perennial plant species, was monitored on permanent sample plots once a year [15] for 14 years (2009–2022). Although A. albana actually reproduces by seeds, the stage of dormant seeds was deliberately excluded from the life cycle graph by ontogenetic stages as the seed-related vital rates cannot be reliably estimated in the field [16]. Later, we proved such an exclusion to be correct within the integer-valued formalism [17], which can always be applied for the “identified individuals” data. The life cycle graph looks, correspondingly, as shown in Figure 1, with the “virtual” rather than real recruitment arcs. These three arcs ingo, respectively, to three early stages because the newly recruited plants can be observed in any of them at the moment of observation.
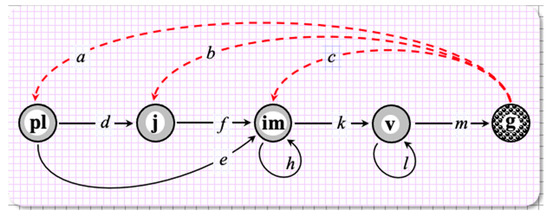
Figure 1.
A. albana life cycle graph by ontogenetic stages: pl, plantules; j, juvenile plants; im, immature plants; v, adult vegetative plants; and g, generative plants. Dashed arrows correspond to “virtual” reproduction (adapted from [15]).
Now, we have x(t) ∈ , and the natural order of components in x(t) leads to the following PPM pattern:
with 10 vital rates to be calibrated. The calibration for 13 successive pairs of observation years results in 13 annual PPMs, L(t) = [lij(t)], presented in Table 1. Each of them obeys Equation (1). There are 6 annual PPMs with λ1(L(t)) > 1 and 7 of those with λ1(L(t)) < 1, so that even an “educated guess” of what should be λ1(G), the dominant eigenvalue of the average matrix, remains uncertain.

Table 1.
Outcome of PPM calibration for A. albana based on 2009–2022 data (updating Table 2 from [15]).
2.2. Pattern-Multiplicative Average of Annual PPMs
The logic of PMA ensues from the following apparent observation: given the 13 annual PPMs calibrated according to Equation (1) (Table 1), we have the initial population structure projected to the terminal one,
by
the product of 13 annual PPMS in chronological order.
x(2022) = L(2021) L(2020) … L(2009) x(2009),
Prod = L(2021) L(2020) … L(2009),
x(2022) = Prod x(2009).
Because the average matrix ought to perform absolutely the same when raised to the 13th power, we have the following basic equation of averaging,
which justifies Equation (2) of the Introduction. As is noted ibidem, a routine extraction of the 13th root from a given, even positive, Prod can hardly return a nonnegative matrix, nor guarantee the fixed pattern (3) for the root.
G13 = Prod,
A workaround leads to solving matrix Equation (6) as a system of scalar polynomial equations for unknown matrix elements. In fact, there are 5 × 5 − 10 = 15 elements that are prescribed to be zero by pattern (3), while the corresponding 15 scalar equations bind the unknown elements too, in addition to the 10 equations for the 10 unknowns. It means that Equation (6) is overdetermined as a system of scalar equations; hence, it may have an exact solution only under special relations between the equations depriving those extra 15 ones of their independence. There is no reason however to seek this kind of relation among the PPMs, so that Equation (6), the basic equation of averaging, has no solution over the set of the pattern (3) PPMs.
The simple and clear logic of PPM averaging thus faces a principal obstacle in matrix algebra, and a workaround comes to an approximate solution.
2.3. Approximate PMA as a Nonlinear Constrained Minimization Problem
Any approximation invokes the question of how close the approximate solution is to the exact one. Although the latter is unknown, the equivalent form of Equation (6),
just illustrates the ideal, yet unreachable, closeness as a 5 × 5 matrix of zeros. Retaining the same notation G = [gij] for the approximate average matrix, we can see the elements of G13 as certain polynomials of the 5 × 13 = 65th degree. If we consider the quality of approximation to be a scalar value, then it should be the error of approximation. The error can be measured as the (squared) matrix norm, whereby we come to the following nonlinear minimization problem:
G13 − Prod = 0,
Here, defines the problem to be a constrained one as it represents the constraints that ensue from the logics of averaging: the average vital rates should not be less nor greater than those fixed in observations. In matrix terms, it means that each entry of the annual PPM has to lie within the bounds defined by the minimal value and the maximal one among the 13 annual values of that entry. In formal terms,
(see Table 2).

Table 2.
Bounds for the 10 unknown variables ensuing from 13 annual PPMs (Table 1).
Table 2.
Bounds for the 10 unknown variables ensuing from 13 annual PPMs (Table 1).
| Minimal | Vital Rate | Maximal |
|---|---|---|
| 4/3 | a | 49 |
| 3 | b | 85 |
| 0 | c | 25 |
| 0 | d | 7/15 |
| 0 | e | 1 |
| 1/49 | f | 7/9 |
| 0 | h | 2/3 |
| 6/95 | k | 5/6 |
| 8/25 | l | 22/23 |
| 1/35 | m | 5/15 |
So, we come to the constrained nonlinear minimization problem (8 and 9), where the bounds of B are defined in Table 2. Both standard routines for global optimization [18] and more sophisticated ones [14] can be applied for solving the problem (8 and 9).
2.4. Approximate PMA as an Eigenvalue-Constrained Optimization Problem
Noted in the Introduction, expression (2) is actually a simple algebraic consequence of (6), the basic equation of averaging, that would be true if the exact solution existed. Since it does not exist, another measure of approximation quality can be found by the following speculations.
Suppose v is a dominant eigenvector of the average matrix G, i.e., we have
G v = λ1(G) v.
Acting by operator G successively on both sides of Equation (10), we obtain
(G)2 v = λ1(G)2 v,
(G)3 v = λ1(G)3 v,
…,
(G)13 v = λ1(G)13 v.
(G)3 v = λ1(G)3 v,
…,
(G)13 v = λ1(G)13 v.
In combination with the averaging Equations (6) and (11), it signifies that v is a dominant eigenvector of the matrix product, Prod, too. Hereby, the other measure of an approximation error is
which can be calculated from the data presented in Table 1. The optimal solution should be searched for among those matrices G that have the same eigenvector v. To exemplify how matrices of a single pattern with different eigenvalues may have the same dominant eigenvector is a student-level exercise (a hint to the solution in Appendix A).
|λ1(G) − ρ0|, where ρ0 = ρ(Prod)
To be unique, this eigenvector, v*, can, for instance, be expressed in percent and calculated like the vectors x* presented in Table 1. It can thereafter serve as a constraint in the search of approximation among various λ1 values associated with a single v*. (To give an example of a matrix eigenvalue being nonlinear as a function of matrix elements is another exercise). Hence, we have a nonlinear minimization problem again. However, the change of variables, a beloved mathematical trick,
turns the problem into a linear one. More specifically, it turns the task into the following two linear problems: to maximize the λ1(G) when ρ0 ≥ λ1(G) and to minimize it when λ1(G) ≥ ρ0.
y = |λ1(G) − ρ0|,
Moreover, vector v* = [v1, v2, …, v5], the known positive eigenvector of G, and its dominant eigenvalue λ1(G) are bound by definition to the matrix equation
Gv* = λ1(G)v*.
With due regard to the fixed pattern (3) and with omitting subscript 1 at λ1, this matrix equation reduces to the five scalar linear equations for a, b, … , l, m, λ:
av5 − λv1 = 0,
bv5 + dv1 − λv2 = 0,
cv5 + ev1+ fv2+ hv3 − λv3 = 0,
kv3 + lv4 − λv4 = 0,
mv4 − λv5 = 0,
i.e., for the ten unknown entries of G and the 11th formal variable λ.
bv5 + dv1 − λv2 = 0,
cv5 + ev1+ fv2+ hv3 − λv3 = 0,
kv3 + lv4 − λv4 = 0,
mv4 − λv5 = 0,
i.e., for the ten unknown entries of G and the 11th formal variable λ.
The 11th variable has its own bounds: as the dominant eigenvalue of the average matrix, the unknown λ has to locate within the following bounds,
to be determined from Table 1. The two specific problems specify these bounds further:
Finally, we have the following problem formulation:
where x = [a, b, …, l, m, λ]T, while the polygons (p = 1, 2) are defined in (15) and the equality-type constraints (14). The two inner problems (16) represent the standard LP ones to be solved by standard software routines, such as the function linprog in MATLAB® [19] (technical details in Appendix B).
3. Results
3.1. Case Study Outcome
Calibrated with absolute accuracy, 13 annual PPMs for A. albana are presented in Table 1 with their dominant eigenvalues and corresponding eigenvectors.
3.2. Pattern-Multiplicative Averaging as an Approxiation Problem
The logics of approximate PMA have been implemented as problem settings in Section 2.3 and Section 2.4. Matrix Prod (4), the product of 13 annual PPMs, is too cumbersome to be presented here in its original rational form. Its numerical form up to the 15th significant digit is shown in Table 3 together with the dominant eigenvalue and the corresponding eigenvector.

Table 3.
Numerical inputs for the optimization problems.
3.3. Minimizing the Approximation Error as a Matrix Norm
The solution to the constraint minimization problem (8) has been obtained in [14] by the “versatile optimization tools” (Table 4) for the case of 12 annual PPMs. The quality of approximation ranges from 0.002374 to 0.002379 as a function of the optimization method (ibidem). In the format of Table 1, the obtained average matrices are presented in Table 4.

Table 4.
Solutions to the PMA problem by various optimization techniques (adapted from [14]).
3.4. Eigenvalue-Constrained Optimization Problem
Solutions to the problem (14–16) are shown in Table 5.

Table 5.
Solutions to the PMA problem by the LP technique.
The solutions to the two optimization problems look indistinguishable within the publication format allowed, and they are really different at the 16th decimal digit alone, which may well be attributed to the computer round-off errors. It means that both problems have the same unique optimal solution, i.e., the corresponding vertex is in common of the polygons B1 and B2.
4. Discussion and Conclusions
The case study practice has not motivated any logics of PMA beyond the population structure projection from the initial vector to the terminal one, i.e., Equations (4) and (5). Therefore, we deal here with single-objective problems alone (in the terminology of [20]). Once having been formulated in mathematical terms [13], this objective comes immediately to the difference norm as the distance between two matrices following the fundamental of real analysis [21]. However, even the squared matrix norm has required “versatile optimization tools” [14] to achieve even moderate approximation quality in the corresponding nonlinear constrained minimization problem (Table 4).
Besides the moderate approximation quality, the basin-hopping global search, as an essential part of the “versatile optimization tools”, leaves no chance for the results being quantitatively reproducible as it is essentially stochastic [22]. In contrast, the LP approach is essentially deterministic [23]; hence, the results in Section 3.4 can be reproduced any number of times.
What does not contrast the LP approach to the PMA task is the eigenvalue optimization problem being nonlinear, too. Because the matrix eigenvalue in general and the dominant eigenvalue in particular are not linear as a function of matrix elements (see Appendix A), the use of linear programming seems paradoxical at first glance. However, besides the trick with a change of variables (13), the very nature of eigenvalue–eigenvector relations is linear, resulting in the linear relationships among the matrix elements and the linear equality-type constraints in the LP setting. The trick has nevertheless failed to cheat a software routine formality, namely, to express the loss function as a linear combination of formal variables at fixed coefficients (see Appendix B). The reason is quite evident: function (12) is not a linear function, albeit consisting of two linear parts.
These two parts have logically resulted in the two adjacent LP problems differing in the range (15) of the lambda alone. They both yield a single solution surprisingly coincident with the ideal λ1(G) (Table 5). On the one hand, the theory of linear programming is known to admit nonunique solutions [23]. On the other, different matrices might well have the same dominant eigenvector (see Appendix A) in our practical case, too. Fortunately, the solution returned by the routine has turned out to be unique, hence the unique, best solution to the averaging problem.
Moreover, this best solution is absolutely accurate (Table 5), thus turning a solution to the approximate PMA problem into the exact one and suggesting the best alternative to our former ecological practice [8,15,16]. Therefore, it makes no sense to quantitatively compare the outcomes of the “versatile optimization tools” and the LP approach—the comparison should rather be qualitative, with an obvious conclusion, thus denying any possible reproaches to comparing the case of 12 annual PPMs [14] with the current case of 13 PPMs.
The only “spoon of tar” in this “barrel of honey” is due to certain zeros in the optimal solution, i.e., zero entries to the average matrix G. While there are in total 4 vital rates that have zero minimal values among the 13 annual ones (Table 2), 3 of them, namely, for c, d, e, (Figure 1), are reached by the “ideal” solution (Table 5). The shares of c = 0, d = 0, and d = 0 in the set of 13 annual PPMs (Table 1) are equal, respectively, to 9/13, 7/14, and 1/13 (Appendix C). Whether the average matrix should take into account the most frequent zeros or all of them is a dialectical issue. The paradigm of biological diversity in general and the concept of polyvariant ontogeny [24,25] in particular dictate retaining all the links in the life cycle graph (Figure 1), hence the absence of occasional zeros in the average matrix.
Therefore, an optimistic mathematical hypothesis is that the same absolute result can be obtained in the eigenvalue-constrained optimization problem when we substitute the minimal positive bounds for the zero ones. Testing this hypothesis might be an object of further studies.
Note also that the LP technique presented in Section 2.4 for a specific case study is general enough to be applied for any finite set of irreducible nonnegative fixed-pattern matrices, the specificity being only confined to the bounds and equality-type constraints. While the task is always to find the best approximation, the supertask is to motivate younger mathematicians to give a theoretical explanation of why the best approximation turns into the exact solution.
Funding
This research was supported by the Russian Scientific Foundation, grant number 22-24-00628.
Data Availability Statement
The field data supporting reported results can be found in the sources referred throughout this paper.
Acknowledgments
The author thanks Vladimir Yu. Protasov for the idea to formulate the PMA task as an LP problem. Programming and calculations were implemented in MATLAB® R2021b.
Conflicts of Interest
The author declares no conflict of interests with himself. The funder had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A
Exercise 1. Exemplify how matrices with a fixed pattern and different eigenvalues may have the same dominant eigenvector. Hint: Consider an imprimitive Leslie matrix with the pattern of
and double it.
Exercise 2. Exemplify the matrix eigenvalue being nonlinear as a function of matrix elements. Hint: See matrix (A1).
Appendix B
Using MATLAB®, we have logically reformulated the LP problem in matrix terms and in the terms of problems (14)–(16). The corresponding solver linprog [19] finds the minimum in a problem specified by
Here, vectors are defined as
matrix A and vector b represent the inequality-type constraints (empty in our case), Aeq and beq the equality-type constraints:
and vectors lb and ub, the lower and upper bounds, respectively, for x, are given in Table 2, lacking them for λ, the last component. Extracted from Table 1, these bounds for λ1(G) are
x = [a, b, …, l, m, λ]T, yT = [0, 0, …, 0, 1];
0.3988 ≤ λ ≤ 1.5779.
Specified in accordance with (15), these bounds split to
where ρ0 is given in Table 3. Correspondingly, the pair of lb and ub split to the following ones,
where
0.3988 ≤ λ ≤ ρ0 and ρ0 ≤ λ ≤ 1.5779,
lb, ub1 and lb2, ub,
ub111 = lb211 = ρ0
Following (A2)–(A7) and the syntax of linprog [19], we input the following two calls:
which return what is shown in Table 5.
[xopt1, yval1] = linprog(y1, [], [], Aeq, beq, lb, ub1);
[xopt2, yval2] = linprog(y2, [], [], Aeq, beq, lb2, ub),
Appendix C
To determine how many zeros there are among particular entries into a fixed place, say (3, 5), at all the 13 given matrices, we first arrange them as a 3D MATLAB® array [26] named All13L. Second, we calculate the frequency of zeros at that place by means of the built-in MATLAB® function nnz [27] and the following line:
>> sym(13 - nnz(All13L(3, 5, :)))/13,
ans = 9/13.
- Similar lines for the places of (2, 1) and (3, 1) return, respectively, 7/13 and 1/13.
References
- COMADRE. Available online: https://compadre-db.org/Data/Comadre (accessed on 30 May 2023).
- COMPADRE. Available online: https://compadre-db.org/Data/Compadre (accessed on 30 May 2023).
- Berman, A.; Plemmons, R.J. Nonnegative Matrices in the Mathematical Sciences; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar]
- Caswell, H. Matrix Population Models: Construction, Analysis and Interpretation, 2nd ed.; Sinauer Associates: Sunderland, MA, USA, 2001. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Gantmacher, F.R. Matrix Theory; Chelsea Publ.: New York, NY, USA, 1959. [Google Scholar]
- Logofet, D.O.; Salguero-Gómez, R. Novel challenges and opportunities in the theory and practice of matrix population modelling: An editorial for the special feature “Theory and Practice in Matrix Population Modelling”. Ecol. Model. 2021, 443, 109457. [Google Scholar] [CrossRef]
- Logofet, D.O. Does averaging overestimate or underestimate population growth? It depends. Ecol. Model. 2019, 411, 108744. [Google Scholar] [CrossRef]
- Cohen, J.E. Comparative statics and stochastic dynamics of age-structured populations. Theor. Popul. Biol. 1979, 16, 159–171. [Google Scholar] [CrossRef] [PubMed]
- Tuljapurkar, S.D.; Orzack, S.H. Population dynamics in variable environments I. Long-run growth rates and extinction. Theor. Popul. Biol. 1980, 18, 314–342. [Google Scholar] [CrossRef]
- Tuljapurkar, S.D. Demography in stochastic environments. II. Growth and convergence rates. J. Math. Biol. 1986, 24, 569–581. [Google Scholar] [CrossRef] [PubMed]
- Tuljapurkar, S.D. Population Dynamics in Variable Environments; Lecture Notes in Biomathematics; Springer: Berlin, Germany, 1990; Volume 85. [Google Scholar] [CrossRef]
- Logofet, D.O. Averaging the population projection matrices: Heuristics against uncertainty and nonexistence. Ecol. Complex. 2018, 33, 66–74. [Google Scholar] [CrossRef]
- Protasov, V.Y.; Zaitseva, T.I.; Logofet, D.O. Pattern-multiplicative average of nonnegative matrices: When a constrained minimization problem requires versatile optimization tools. Mathematics 2022, 10, 4417. [Google Scholar] [CrossRef]
- Logofet, D.O.; Golubyatnikov, L.L.; Kazantseva, E.S.; Belova, I.N.; Ulanova, N.G. Thirteen years of monitoring an alpine short-lived perennial: Novel methods disprove the former assessment of population viability. Ecol. Model. 2023, 477, 110208. [Google Scholar] [CrossRef]
- Logofet, D.O.; Kazantseva, E.S.; Belova, I.N.; Onipchenko, V.G. How long does a short-lived perennial live? A modelling approach. Biol. Bul. Rev. 2018, 8, 406–420. [Google Scholar] [CrossRef]
- Logofet, D.O.; Kazantseva, E.S.; Onipchenko, V.G. Seed bank as a persistent problem in matrix population models: From uncertainty to certain bounds. Ecol. Modell. 2020, 438, 109284. [Google Scholar] [CrossRef]
- MathWorks. Documentation. Available online: https://www.mathworks.com/help/gads/globalsearch.html?s_tid=doc_ta (accessed on 30 May 2023).
- MathWorks. Documentation. Available online: https://www.mathworks.com/help/optim/ug/linprog.html?s_tid=doc_ta (accessed on 30 May 2023).
- Deb, K.; Roy, P.C.; Hussein, R. Surrogate modeling approaches for multiobjective optimization: Methods, taxonomy, and results. Math. Comput. Appl. 2021, 26, 5. [Google Scholar] [CrossRef]
- Krantz, S.G. Real Analysis and Foundations, 5th ed.; CRC Press: BoicaRaton, FL, USA, 2022; pp. 325–413. [Google Scholar]
- Robert, C.P.; Casella, G. Monte Carlo Statistical Methods, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar] [CrossRef]
- Luenberger, D.G. Introduction to Linear and Non-linear Programming; Addison-Wesley: Reading, MA, USA, 1973. [Google Scholar]
- Zhukova, L.A. Polyvariance of the meadow plants. In Zhiznennye Formy v Ekologii i Sistematike Rastenii (Life Forms in Plant Ecology and Systematics); Mosk. Gos. Pedagog. Inst.: Moscow, Russia, 1986; pp. 104–114. [Google Scholar]
- Zhukova, L.A. Populyatsionnaya Zhizn’ Lugovykh Rastenii (Population Life of Meadow Plants); Lanar: Yoshkar-Ola, Russia, 1995. [Google Scholar]
- MathWorks. Documentation. Available online: https://www.mathworks.com/help/matlab/math/multidimensional-arrays.html (accessed on 30 May 2023).
- MathWorks. Documentation. Available online: https://www.mathworks.com/help/matlab/ref/nnz.html?s_tid=doc_ta (accessed on 30 May 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).