Compact Integer Programs for Depot-Free Multiple Traveling Salesperson Problems
Abstract
1. Introduction
2. Related Work
2.1. TSP and SmTSP
2.2. mTSP from 1960 to 1975
2.3. mTSP from 1976 to 1995
2.4. mTSP from 1996 to 2005
2.5. mTSP from 2006 to Date
2.6. Approximation Algorithms
2.7. When Depots Are Unknown or Unnecessary
- Closed paths (CP).
- Open paths (OP).
- Minsum objective function.
- Minmax objective function.
- Bounding constraints:
- -
- Lower bound on the number of vertices per path.
- -
- Upper bound on the number of vertices per path.
3. Integer Programs for DFTSP
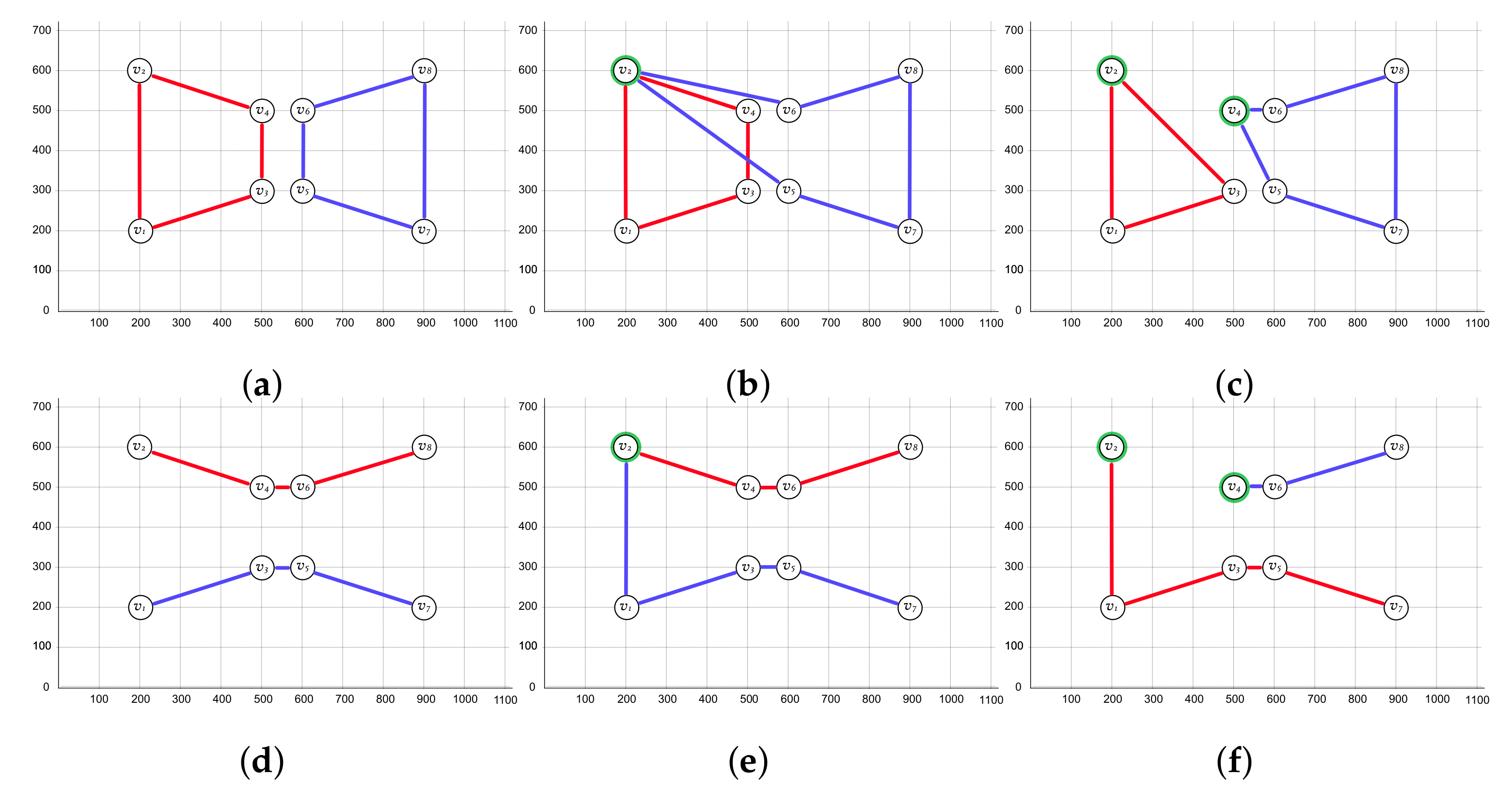
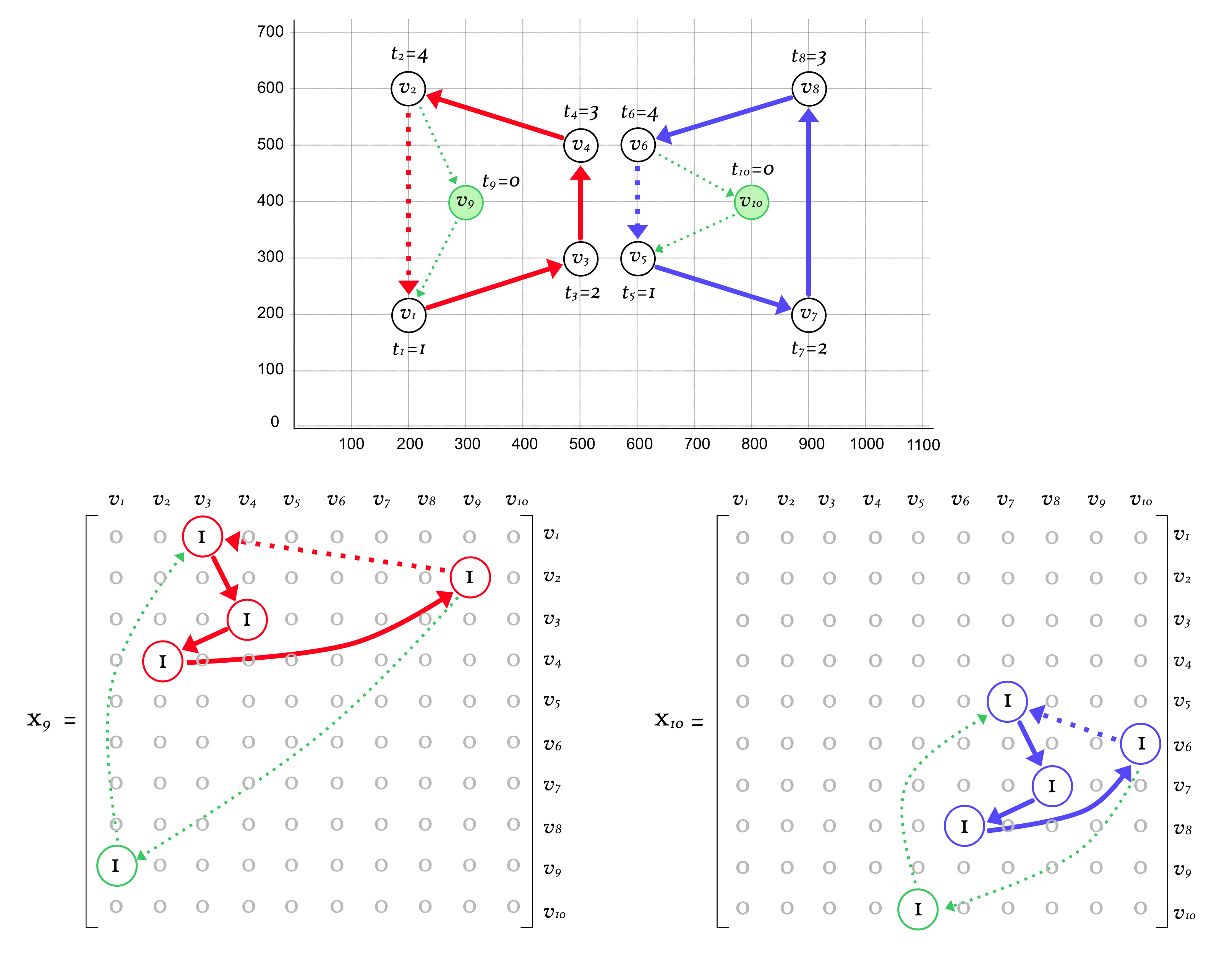
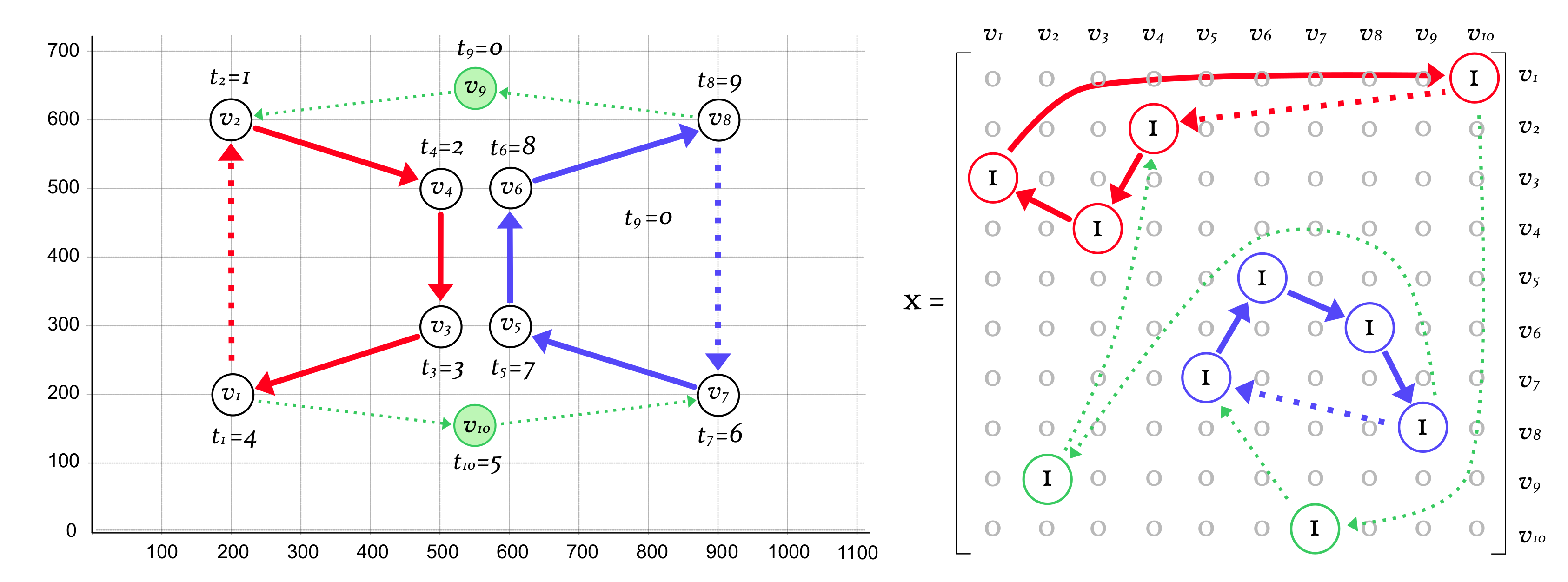
3.1. Based on FD-MmTSP
- If , then .
- This case corresponds to the vertices non-adjacent to any dummy depot in any path. In Figure 3, these are , , , and .
- If and , then .
- This case corresponds to the first vertex visited by each salesperson after leaving its dummy depot. In Figure 3, these are and .
- If and , then .
- This case corresponds to the last vertex visited by each salesperson before returning to its dummy depot. In Figure 3, these are and .
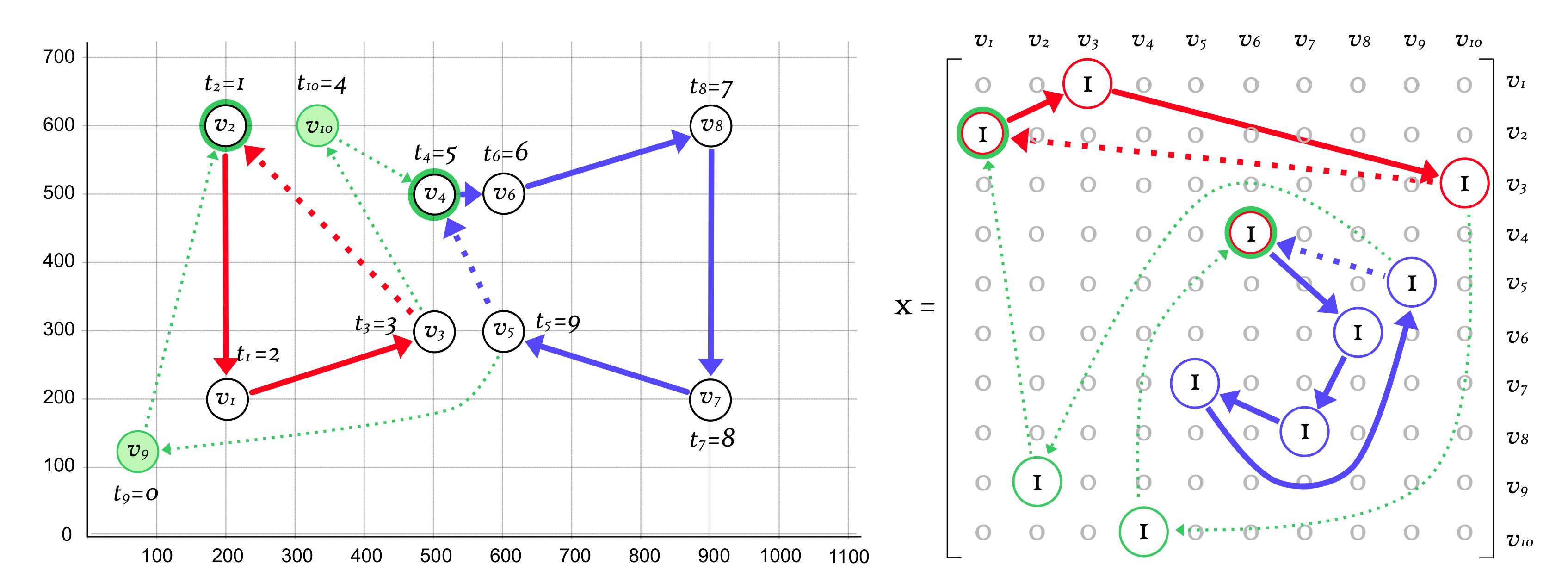
3.2. More Compact Programs for DFmTSP
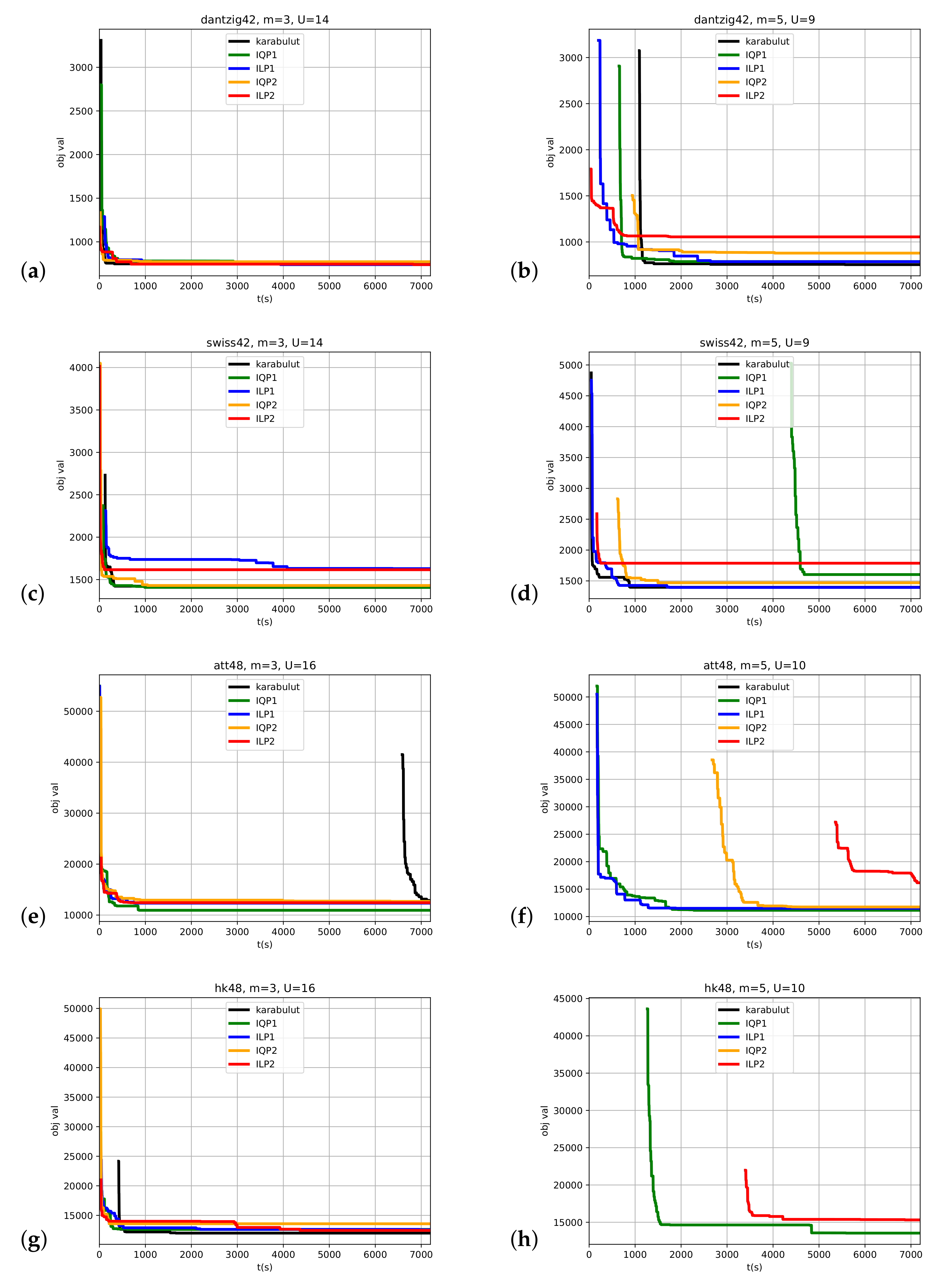
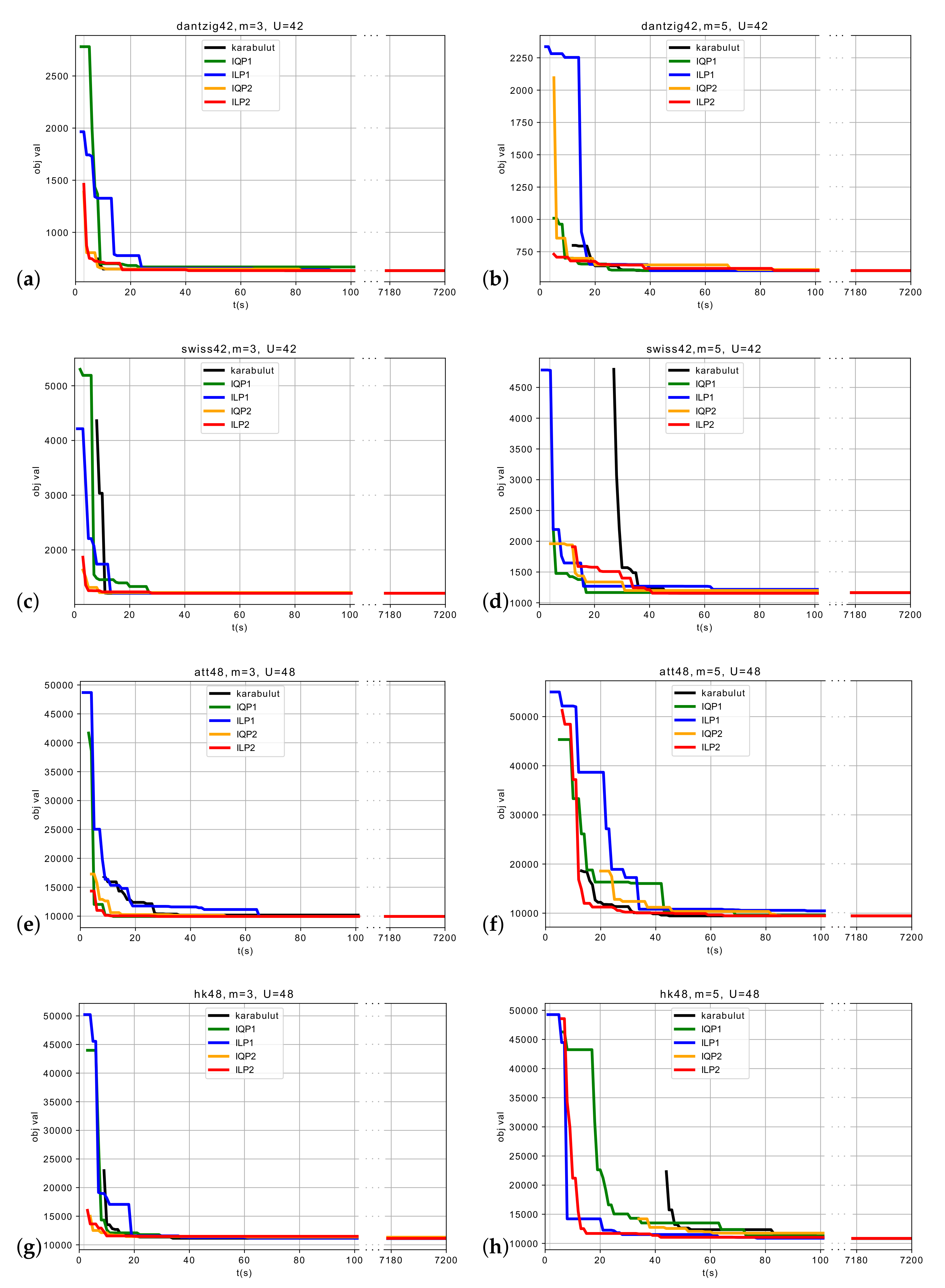
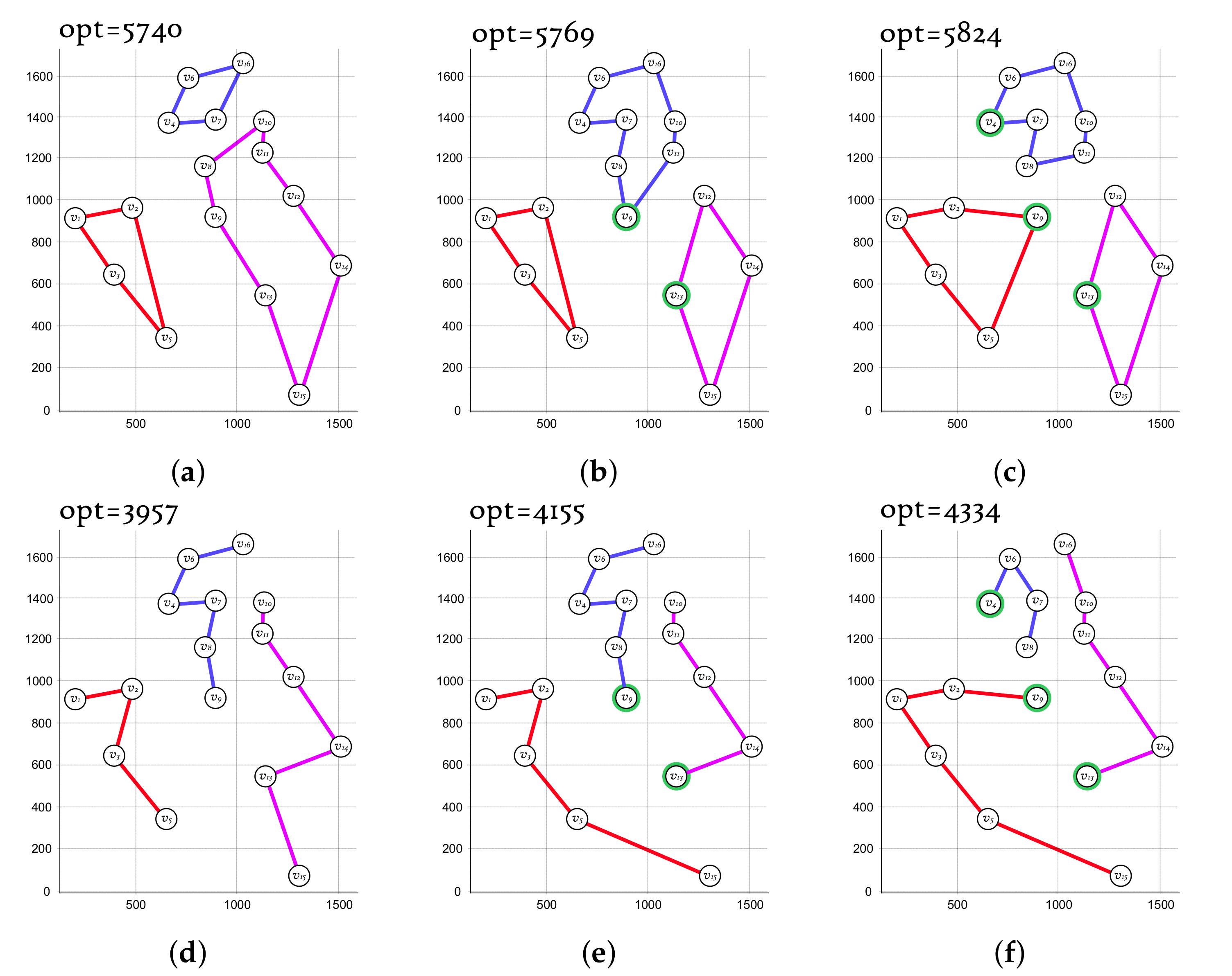
4. Empirical Tests
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CP | Closed paths |
| CP-DFmTSP | Closed-paths depot-free multiple traveling salesperson problem |
| CP-FD-MmTSP | Closed-paths fixed-destination multiple-depots multiple traveling salesperson problem |
| DF | Depot free |
| DFmTSP | Depot-free multiple traveling salesperson problem |
| FD-MmTSP | Fixed-destination multiple-depots multiple traveling salesperson problem |
| ILP | Integer linear program |
| IP | Integer program |
| IQP | Integer quadratic program |
| M | Multiple depots |
| MmTSP | Multiple-depots multiple traveling salesperson problem |
| mTSP | Multiple traveling salesperson problem |
| NFD-MmTSP | Non-fixed-destination multiple-depots multiple traveling salesperson problem |
| OP | Open paths |
| OP-DFmTSP | Open-paths depot-free multiple traveling salesperson problem |
| S | Single-depot |
| SECs | Subtour elimination constraints |
| SmTSP | Single-depot multiple traveling salesperson problem |
| TSP | Traveling salesperson problem |
Appendix A
References
- Cheikhrouhou, O.; Khoufi, I. A comprehensive survey on the Multiple Traveling salesman Problem: Applications, approaches and taxonomy. Comput. Sci. Rev. 2021, 40, 100369. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Fulkerson, D.R.; Johnson, S.M. Solution of a Large-Scale Traveling-Salesman Problem; RAND Corporation: Santa Monica, CA, USA, 1954; pp. 393–410. [Google Scholar]
- Dantzig, G.B.; Fulkerson, D.R.; Johnson, S.M. On a linear-programming, combinatorial approach to the traveling-salesman problem. Oper. Res. 1959, 7, 58–66. [Google Scholar] [CrossRef]
- Miller, C.E.; Tucker, A.W.; Zemlin, R.A. Integer programming formulation of traveling salesman problems. J. ACM 1960, 7, 326–329. [Google Scholar] [CrossRef]
- Svestka, J.A.; Huckfeldt, V.E. Computational Experience with an M-salesperson Traveling salesman Algorithm. Manag. Sci. 1973, 19, 790–799. [Google Scholar] [CrossRef]
- Bektas, T. The multiple traveling salesman problem: An overview of formulations and solution procedures. Omega 2006, 34, 209–219. [Google Scholar] [CrossRef]
- Kara, I.; Bektas, T. Integer linear programming formulations of multiple salesman problems and its variations. Eur. J. Oper. Res. 2006, 174, 1449–1458. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Ramser, J.H. The Truck Dispatching Problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Mor, A.; Speranza, M.G. Vehicle routing problems over time: A survey. 4OR-Q J. Oper. Res. 2020, 18, 129–149. [Google Scholar] [CrossRef]
- Bellmore, M.; Hong, S. Transformation of multisalesperson problem to the standard traveling salesman problem. J. ACM 1974, 21, 500–504. [Google Scholar] [CrossRef]
- Gavish, B. A note on the formulation of the m-salesman traveling salesperson problem. Manag. Sci. 1976, 22, 704–705. [Google Scholar] [CrossRef]
- Svestka, J.A. Response to A note on the formulation of the m-salesman traveling salesperson problem. Manag. Sci. 1976, 22, 706. [Google Scholar] [CrossRef]
- Hong, S.; Padberg, M.W. A note on the symmetric multiple traveling salesman problem with fixed charges. Oper. Res. 1977, 25, 871–874. [Google Scholar] [CrossRef]
- Gavish, B.; Graves, S.C. The Travelling Salesman Problem and Related Problems; Massachusetts Institute of Technology, Operations Research Center: Cambridge, MA, USA, 1978. [Google Scholar]
- Rao, M.R. A note on the multiple traveling salesmen problem. Oper. Res. 1980, 28, 628–632. [Google Scholar] [CrossRef]
- Discenza, J.H. A more compact formulation of the symmetric multiple traveling salesman problem with fixed charges. Networks 1981, 11, 73–75. [Google Scholar] [CrossRef]
- Jonker, R.; Volgenant, T. An improved transformation of the symmetric multiple traveling salesman problem. Oper. Res. 1988, 36, 163–167. [Google Scholar] [CrossRef]
- Guoxing, Y. Transformation of multidepot multisalesmen problem to the standard travelling salesman problem. Eur. J. Oper. Res. 1995, 81, 557–560. [Google Scholar] [CrossRef]
- Wacholder, E.; Han, J.; Mann, R.C. A neural network algorithm for the multiple traveling salesmen problem. Biol. Cybern. 1989, 61, 11–19. [Google Scholar] [CrossRef]
- Laporte, G.; Yves, N. A cutting planes algorithm for the m-salesmen problem. J. Oper. Res. Soc. 1980, 31, 1017–1023. [Google Scholar] [CrossRef]
- Ali, A.I.; Kennington, J.L. The asymmetric M-travelling salesmen problem: A duality based branch-and-bound algorithm. Discret. Appl. Math. 1986, 13, 259–276. [Google Scholar]
- Ali, A.; Kennington, J. The M-Travelling Salesmen Problem; Department of Operations Research, Southern Methodist University: Dallas, TX, USA, 1980. [Google Scholar]
- Gavish, B.; Srikanth, K. An optimal solution method for large-scale multiple traveling salesmen problems. Oper. Res. 1986, 34, 698–717. [Google Scholar] [CrossRef]
- Potvin, J.Y.; Lapalme, G.; Rousseau, J.M. A generalized k-opt exchange procedure for the MTSP. INFOR Inf. Syst. Oper. Res. 1989, 27, 474–481. [Google Scholar] [CrossRef]
- Hsu, C.Y.; Tsai, M.H.; Chen, W.M. A study of feature-mapped approach to the multiple travelling salesmen problem. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Singapore, 11–14 June 1991; pp. 1589–1592. [Google Scholar]
- Gromicho, J.; Paixão, J.; Bronco, I. Exact solution of multiple traveling salesman problems. In Combinatorial Optimization; Akgül, M., Hamacher, H.W., Tüfekçi, S., Eds.; NATO ASI Series; Springer: Berlin/Heidelberg, Germany, 1992; Volume 82, pp. 291–292. ISBN 978-3-642-77489-8. [Google Scholar]
- Russell, R.A. An Effective Heuristic for the M-Tour Traveling salesman Problem with Some Side Conditions. Oper. Res. 1977, 25, 517–524. [Google Scholar] [CrossRef]
- França, P.M.; Gendreau, M.; Laporte, G.; Müller, F.M. The m-traveling salesman problem with minmax objective. Transp. Sci. 1995, 29, 267–275. [Google Scholar] [CrossRef]
- Modares, A.; Somhom, S.; Enkawa, T. A self-organizing neural network approach for multiple traveling salesman and vehicle routing problems. Int. Trans. Oper. Res. 1999, 6, 591–606. [Google Scholar] [CrossRef]
- Somhom, S.; Modares, A.; Enkawa, T. Competition-based neural network for the multiple travelling salesmen problem with minmax objective. Comput. Oper. Res. 1999, 26, 395–407. [Google Scholar] [CrossRef]
- Faigl, J.; Kulich, M.; Preucil, L. Multiple traveling salesmen problem with hierarchy of cities in inspection task with limited visibility. In Proceedings of the 5th Workshop on Self-Organizing Maps, Paris, France, 5–8 September 2005; pp. 91–98. [Google Scholar]
- Tang, L.; Liu, J.; Rong, A.; Yang, Z. A multiple traveling salesman problem model for hot rolling scheduling in Shanghai Baoshan Iron & Steel Complex. Eur. J. Oper. Res. 2000, 124, 267–282. [Google Scholar]
- Sofge, D.; Schultz, A.; De Jong, K. Evolutionary Computational Approaches to Solving the Multiple Traveling salesman Problem Using a Neighborhood Attractor Schema. In Applications of Evolutionary Computing; Cagnoni, S., Gottlieb, J., Hart, E., Middendorf, M., Raidl, G.R., Eds.; EvoWorkshops, Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2279, pp. 153–162. ISBN 978-3-540-43432-0. [Google Scholar]
- Carter, A.E. Design and Application of Genetic Algorithms for the Multiple Traveling Salesperson Assignment Problem. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 21 April 2003. [Google Scholar]
- Song, C.H.; Lee, K.; Lee, W.D. Extended simulated annealing for augmented TSP and multi-salesmen TSP. In Proceedings of the International Joint Conference on Neural Networks, Portland, OR, USA, 20–24 July 2003; pp. 2340–2343. [Google Scholar]
- Bugera, V. Properties of No-Depot MIN-MAX 2-Traveling-salesmen Problem. In Recent Developments in Cooperative Control and Optimization; Murphey, S., Pardalos, R., Cagnoni, P.M., Eds.; Cooperative Systems; Springer: Boston, MA, USA, 2004; Volume 3, pp. 45–59. ISBN 978-1-4613-7947-8. [Google Scholar]
- Byungsoo, N. Heuristic Approaches for No-Depot k-Traveling Salesmen Problem with a Minmax Objective. Master’s Thesis, Texas A&M University, College Station, TX, USA, May 2006. [Google Scholar]
- Hou, M.; Liu, D. A novel method for solving the multiple traveling salesmen problem with multiple depots. Chin. Sci. Bull. 2012, 57, 1886–1892. [Google Scholar] [CrossRef]
- Wang, X.; Liu, D.; Hou, M. A novel method for multiple depot and open paths, Multiple Traveling salesmen Problem. In Proceedings of the IEEE 11th International Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 31 January–2 February 2013. [Google Scholar]
- Vandermeulen, I.; Groß, R.; Kolling, A. Balanced Task Allocation by Partitioning the Multiple Traveling Salesperson Problem. In Proceedings of the 18th International Conference on Autonomous Agents and MultiAgent Systems, Montréal, QC, Canada, 13–17 May 2019. [Google Scholar]
- Zheng, J.; Hong, Y.; Xu, W.; Li, W.; Chen, Y. An effective iterated two-stage heuristic algorithm for the multiple Traveling Salesmen Problem. Comput. Oper. Res. 2022, 143, 105772. [Google Scholar] [CrossRef]
- Sundar, K.; Rathinamm, S. An exact algorithm for a heterogeneous, multiple depot, multiple traveling salesman problem. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 July 2015. [Google Scholar]
- Yadlapalli, S.; Malik, W.A.; Darbha, S.; Pachter, M. A Lagrangian-based algorithm for a Multiple Depot, Multiple Traveling salesmen Problem. Nonlinear Anal. Real World Appl. 2009, 10, 1990–1999. [Google Scholar] [CrossRef]
- Bektas, T. Formulations and Benders decomposition algorithms for multidepot salesmen problems with load balancing. Eur. J. Oper. Res. 2012, 216, 83–93. [Google Scholar] [CrossRef]
- Aguayo, M.M.; Sarin, S.C.; Sherali, H.D. Solving the Single and Multiple Asymmetric Traveling Salesmen Problems by Generating Subtour Elimination Constraints from Integer Solutions. IISE Trans. 2018, 50, 45–53. [Google Scholar] [CrossRef]
- Campuzano, G.; Obreque, C.; Aguayo, M.M. Accelerating the Miller–Tucker–Zemlin model for the asymmetric traveling salesman problem. Expert Syst. Appl. 2020, 148, 113229. [Google Scholar] [CrossRef]
- Benavent, E.; Martínez, A. Multi-depot Multiple TSP: A polyhedral study and computational results. Ann. Oper. Res. 2013, 207, 7–25. [Google Scholar] [CrossRef]
- Oberlin, P.; Rathinam, S.; Darbha, S. A transformation for a Multiple Depot, Multiple Traveling Salesperson Problem. In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009. [Google Scholar]
- Sarin, S.C.; Sherali, H.D.; Judd, J.D.; Tsai, P.F.J. Multiple asymmetric traveling salesmen problem with and without precedence constraints: Performance comparison of alternative formulations. Comput. Oper. Res. 2014, 51, 64–89. [Google Scholar] [CrossRef]
- Assaf, M.; Ndiaye, M. A transformation for multiple depot multiple traveling salesman problem. In Proceedings of the International Conference on Engineering & MIS (ICEMIS), Monastir, Tunisia, 8–10 May 2017. [Google Scholar]
- Assaf, M. Transformations for Variants of the Travelling Salesman Problem and Applications. Master’s Thesis, American University of Sharjah, Sharjah, United Arab Emirates, April 2017. [Google Scholar]
- Kitjacharoenchai, P.; Ventresca, M.; Moshref-Javadi, M.; Lee, S.; Tanchoco, J.M.A.; Brunese, P.A. Multiple traveling salesman problem with drones: Mathematical model and heuristic approach. Comput. Ind. Eng. 2019, 129, 14–30. [Google Scholar] [CrossRef]
- Aguayo, M.M.; Avilés, F.N.; Sarin, S.C.; Sherali, H.D. A Two-Index Formulation for the Fixed-Destination Multi-Depot Asymmetric Travelling Salesman Problem and Some Extensions. Informatica 2022, 33, 671–692. [Google Scholar] [CrossRef]
- Kivelevitch, E.H.; Cohen, K.; Kumar, M. A binary programming solution to the min-max multiple-depots, multiple traveling salesman problem. In Proceedings of the AIAA Infotech@Aerospace (I@A) Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar]
- Qu, H.; Yu, Z.; Tang, H. A columnar competitive model for solving multi-traveling salesman problem. Chaos Solitons Fractals 2007, 31, 1009–1019. [Google Scholar] [CrossRef]
- Matsuura, T.; Numata, K. Solving Min-Max Multiple Traveling salesman Problems by Chaotic Neural Network. In Proceedings of the International Symposium on Nonlinear Theory and Its Applications, Luzern, Switzerland, 14–18 September 2014. [Google Scholar]
- Carter, A.E.; Ragsdale, C.T. A new approach to solving the multiple traveling salesperson problem using genetic algorithms. Eur. J. Oper. Res. 2006, 175, 246–257. [Google Scholar] [CrossRef]
- Brown, E.C.; Ragsdale, C.T.; Carter, A.E. A grouping genetic algorithm for the multiple traveling salesperson problem. Int. J. Inf. Technol. Decis. Mak. 2007, 6, 333–347. [Google Scholar] [CrossRef]
- Sze, S.N.; Tiong, W.K. A Comparison between Heuristic and Meta-Heuristic Methods for Solving the Multiple Traveling salesman Problem. Int. J. Math. Comput. Sci. 2007, 1, 13–16. [Google Scholar]
- Zhao, F.; Dong, J.; Li, S.; Yang, X. An improved genetic algorithm for the multiple traveling salesman problem. In Proceedings of the Chinese Control and Decision Conference, Yantai, China, 2–4 July 2008. [Google Scholar]
- Singh, A.; Baghel, A.S. A new grouping genetic algorithm approach to the multiple traveling salesperson problem. Soft Comput. 2009, 13, 95–101. [Google Scholar] [CrossRef]
- Zhou, W.; Li, Y. An improved genetic algorithm for multiple traveling salesman problem. In Proceedings of the 2nd International Asia Conference on Informatics in Control, Automation and Robotics, Wuhan, China, 6–7 March 2010. [Google Scholar]
- Chen, S.H.; Chen, M.C. Operators of the Two-Part Encoding Genetic Algorithm in Solving the Multiple Traveling salesmen Problem. In Proceedings of the International Conference on Technologies and Applications of Artificial Intelligence, Chung Li, Taiwan, 11–13 November 2011. [Google Scholar]
- Király, A.; Abonyi, J. Optimization of Multiple Traveling salesmen Problem by a Novel Representation Based Genetic Algorithm. In Intelligent Computational Optimization in Engineering. Studies in Computational Intelligence; Köppen, M., Schaefer, G., Abraham, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 366, pp. 241–269. ISBN 978-3-642-21704-3. [Google Scholar]
- Sedighpour, M.; Yousefikhoshbakht, M.; Darani, N.M. An Effective Genetic Algorithm for Solving the Multiple Traveling salesman Problem. J. Optim. Ind. Eng. 2011, 8, 73–79. [Google Scholar]
- Yu, Q.; Wang, D.; Lin, D.; Li, Y.; Wu, C. A Novel Two-Level Hybrid Algorithm for Multiple Traveling Salesman Problems. In Advances in Swarm Intelligence. ICSI 2012. Lecture Notes in Computer Science; Tan, Y., Shi, Y., Ji, Z., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7331, pp. 497–503. ISBN 978-3-642-30975-5. [Google Scholar]
- Yuan, S.; Skinner, B.; Huang, S.; Liu, L. A new crossover approach for solving the multiple travelling salesmen problem using genetic algorithms. Eur. J. Oper. Res. 2013, 228, 72–82. [Google Scholar] [CrossRef]
- Hosseinabadi, A.A.R.; Kardgar, M.; Shojafar, M.; Shamshirband, S.; Abraham, A. GELS-GA: Hybrid metaheuristic algorithm for solving Multiple Travelling salesman Problem. In Proceedings of the 14th International Conference on Intelligent Systems Design and Applications, Okinawa, Japan, 28–30 November 2014. [Google Scholar]
- Alves, R.M.F.; Lopes, C.R. Using genetic algorithms to minimize the distance and balance the routes for the multiple Traveling salesman Problem. In Proceedings of the IEEE Congress on Evolutionary Computation, Sendai, Japan, 25–28 May 2015. [Google Scholar]
- Bolaños, R.I.; Toro, E.M.; Granada, M. A population-based algorithm for the multi travelling salesman problem. Int. J. Ind. Eng. Comput. 2016, 7, 245–256. [Google Scholar] [CrossRef]
- Lu, Z.; Zhang, K.; He, J.; Niu, Y. Applying K-means Clustering and Genetic Algorithm for Solving MTSP. In Proceedings of the 11th International Conference, BIC-TA, Xi’an, China, 28–30 October 2016. [Google Scholar]
- Lo, K.M.; Yi, W.Y.; Wong, P.K.; Leung, K.S.; Leung, Y.; Mak, S.T. A Genetic Algorithm with New Local Operators for Multiple Traveling salesman Problems. Int. J. Comput. Intell. Syst. 2018, 11, 692–705. [Google Scholar] [CrossRef]
- Singh, D.R.; Singh, M.K.; Singh, T.; Prasad, R. Genetic Algorithm for Solving Multiple Traveling Salesmen Problem using a New Crossover and Population Generation. Comput. Sist. 2018, 22, 491–503. [Google Scholar] [CrossRef]
- Xu, X.; Yuan, H.; Liptrott, M.; Trovati, M. Two phase heuristic algorithm for the multiple-travelling salesman problem. Soft Comput. 2018, 22, 6567–6581. [Google Scholar] [CrossRef]
- Zhou, H.; Song, M.; Pedrycz, W. A comparative study of improved GA and PSO in solving multiple traveling salesmen problem. Appl. Soft Comput. 2018, 64, 564–580. [Google Scholar] [CrossRef]
- Harrath, Y.; Salman, A.F.; Alqaddoumi, A.; Hasan, H.; Radhi, A. A novel hybrid approach for solving the multiple traveling salesmen problem. Arab. J. Basic Appl. Sci. 2019, 26, 103–112. [Google Scholar] [CrossRef]
- Jiang, C.; Wan, Z.; Peng, Z. A new efficient hybrid algorithm for large scale multiple traveling salesman problems. Expert Syst. Appl. 2020, 139, 112867. [Google Scholar] [CrossRef]
- Al-Furhud, M.A.; Ahmed, Z.H. Experimental Study of a Hybrid Genetic Algorithm for the Multiple Travelling salesman Problem. Math. Probl. Eng. 2020, 2020, 3431420. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, X.; Li, H.; Jin, H. An Improved Partheno-Genetic Algorithm With Reproduction Mechanism for the Multiple Traveling Salesperson Problem. IEEE Access 2020, 8, 102607–102615. [Google Scholar] [CrossRef]
- Singamsetty, P.; Thenepalle, J.K. An efficient genetic algorithm for solving open multiple travelling salesman problem with load balancing constraint. Decis. Sci. Lett. 2021, 10, 525–534. [Google Scholar] [CrossRef]
- Al-Taani, A.T.; Al-Alfifi, L.M. Solving the Multiple Traveling Salesman Problem Using Memetic Algorithm. Artif. Intell. Evol. 2022, 3, 27–40. [Google Scholar] [CrossRef]
- Lou, P.; Xu, K.; Yan, J.; Xiao, Z. An Improved Partheno-Genetic Algorithm for Open Path Multi-Depot Multiple Traveling Salesmen Problem. J. Phys. Conf. Ser. 2021, 1848, 012002. [Google Scholar] [CrossRef]
- Chandran, N.; Narendran, T.T.; Ganesh, K. A clustering approach to solve the multiple travelling salesmen problem. Int. J. Ind. Syst. Eng. 2006, 1, 372–387. [Google Scholar] [CrossRef]
- Junjie, P.; Dingwei, W.; Preucil, L. An Ant Colony Optimization Algorithm for Multiple Travelling salesman Problem. In Proceedings of the First International Conference on Innovative Computing, Beijing, China, 30 August–1 September 2006. [Google Scholar]
- Liu, W.; Li, S.; Zhao, F.; Zheng, A. An ant colony optimization algorithm for the Multiple Traveling Salesmen Problem. In Proceedings of the 4th IEEE Conference on Industrial Electronics and Applications, Xi’an, China, 25–27 May 2009. [Google Scholar]
- Ghafurian, S.; Javadian, N. An ant colony algorithm for solving fixed destination multi-depot multiple traveling salesmen problems. Appl. Soft Comput. 2011, 11, 1256–1262. [Google Scholar] [CrossRef]
- Yousefikhoshbakht, M.; Sedighpour, M. A combination of sweep algorithm and elite ant colony optimization for solving the multiple traveling salesman problem. Proc. Rom. Acad. -Ser. Math. Physics, Tech. Sci. Inf. Sci. 2012, 13, 295–301. [Google Scholar]
- Lu, L.C.; Yue, T.W. Mission-oriented ant-team ACO for min–max MTSP. Appl. Soft Comput. 2019, 76, 436–444. [Google Scholar] [CrossRef]
- Farisi, O.I.R.; Setiyono, B.; Danandjojo, R.I. A hybrid approach to multi-depot multiple traveling salesman problem based on firefly algorithm and ant colony optimization. Int. J. Artif. Intell. (IJ-AI) 2021, 10, 910–918. [Google Scholar] [CrossRef]
- Costa-Salas, Y.J.; Abreu-Ledón, R.; Coello-Machado, J.I.; Nowé, A. Multi-type ant colony system for solving the multiple traveling salesman problem. Rev. TéCnica Fac. Ing. Univ. Del Zulia 2012, 35, 311–320. [Google Scholar]
- Necula, R.; Breaban, M.; Raschip, M. Performance Evaluation of Ant Colony Systems for the Single-Depot Multiple Traveling Salesman Problem. In Hybrid Artificial Intelligent Systems; Onieva, E., Santos, I., Osaba, E., Quintián, H., Corchado, E., Eds.; Springer: Cham, Switzerland, 2015; Volume 9121, pp. 257–268. ISBN 978-3-319-19643-5. [Google Scholar]
- Kivelevitch, E.; Cohen, K.; Kumar, M. A Market-based Solution to the Multiple Traveling salesmen Problem. J. Intell. Robot. Syst. 2013, 72, 21–40. [Google Scholar] [CrossRef]
- Scott, D.; Manyam, S.G.; Casbeer, D.W.; Kumar, M. Market Approach to Length Constrained Min-Max Multiple Depot Multiple Traveling Salesman Problem. In Proceedings of the 2020 American Control Conference, Denver, CO, USA, 1–3 July 2020. [Google Scholar]
- Larki, H.; Yousefikhoshbakht, M. Solving the Multiple Traveling salesman Problem by a Novel Meta-heuristic Algorithm. J. Optim. Ind. Eng. 2014, 16, 55–63. [Google Scholar]
- Rostami, A.S.; Mohanna, F.; Keshavarz, H.; Hosseinabadi, A.A.R. Solving Multiple Traveling Salesman Problem using the Gravitational Emulation Local Search Algorithm. Appl. Math. Inf. Sci. 2015, 2, 699–709. [Google Scholar]
- Soylu, B. A general variable neighborhood search heuristic for multiple traveling salesmen problem. Comput. Ind. Eng. 2015, 90, 390–401. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Y.; Lin, Y. Memetic algorithm based on sequential variable neighborhood descent for the minmax multiple traveling salesman problem. Comput. Ind. Eng. 2017, 106, 105–122. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, H.; Xu, M.; Shen, F. Hybrid genetic algorithm with variable neighborhood search for multi-scale multiple bottleneck traveling salesmen problem. Future Gener. Comput. Syst. 2021, 114, 229–242. [Google Scholar] [CrossRef]
- Wang, M.; Xin, B.; Wang, Q. A general variable neighborhood search for the multiple depots multiple traveling salesmen problem. In Proceedings of the The International Workshop on Advanced Computational Intelligence and Intelligent Informatics (IWACIII2021), Beijing, China, 31 October–3 November 2021. [Google Scholar]
- Venkatesh, P.; Singh, A. Two metaheuristic approaches for the multiple traveling salesperson problem. Appl. Soft Comput. 2015, 26, 74–89. [Google Scholar] [CrossRef]
- Chen, Y.; Jia, Z.; Ai, X.; Yang, D.; Yu, J. A modified two-part wolf pack search algorithm for the multiple traveling salesmen problem. Appl. Soft Comput. 2017, 61, 714–725. [Google Scholar] [CrossRef]
- Alazzam, H.; Alsmady, A.; Mardini, W. Solving Multiple Traveling salesmen Problem using Discrete Pigeon Inspired Optimizer. In Proceedings of the 11th International Conference on Information and Communication Systems (ICICS), Irbid, Jordan, 7–9 April 2020. [Google Scholar]
- Hu, Y.; Yao, Y.; Lee, W.S. A reinforcement learning approach for optimizing multiple traveling salesman problems over graphs. Knowl.-Based Syst. 2020, 204, 106244. [Google Scholar] [CrossRef]
- Karabulut, K.; Öztop, H.; Kandiller, L.; Tasgetiren, M.F. Modeling and optimization of multiple traveling salesmen problems: An evolution strategy approach. Comput. Oper. Res. 2021, 129, 105192. [Google Scholar] [CrossRef]
- He, P.; Hao, J.-K. Memetic search for the minmax multiple traveling salesman problem with single and multiple depots. Eur. J. Oper. Res. 2023, 307, 1055–1070. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, X.; Dong, Y.; Xie, J.; Xie, G.; Xu, X. A novel state transition simulated annealing algorithm for the multiple traveling salesmen problem. J. Supercomput. 2021, 77, 11827–11852. [Google Scholar] [CrossRef]
- Hamza, A.; Darwish, A.H.; Rihawi, O. A new local search for the bees algorithm to optimize multiple traveling salesman problem. Intell. Syst. Appl. 2023, 18, 200242. [Google Scholar] [CrossRef]
- Averbakh, I.; Berman, O. A heuristic with worst-case analysis for minimax routing of two travelling salesmen on a tree. Discret. Appl. Math. 1996, 68, 17–32. [Google Scholar] [CrossRef]
- Averbakh, I.; Berman, O. (p-1)(p+1)-approximate algorithms for p-traveling salesmen problems on a tree with minmax objective. Discret. Appl. Math. 1997, 75, 201–216. [Google Scholar] [CrossRef]
- Nagamoshi, H.; Okada, K. A faster 2-approximation algorithm for the minmax p-traveling salesmen problem on a tree. Discret. Appl. Math. 2004, 140, 103–114. [Google Scholar] [CrossRef]
- Rathinam, S.; Sengupta, R. Lower and Upper Bounds for a Symmetric Multiple Depots, Multiple Travelling salesman Problem; Research Report, UCB-ITS-RR-2006-2; Institute of Transportation Studies, University of California at Berkeley: Berkeley, CA, USA, 2006. [Google Scholar]
- Xu, Z.; Rodrigues, B. A 3/2-Approximation Algorithm for Multiple Depot Multiple Traveling salesman Problem. In Lecture Notes in Computer Science; Kaplan, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6139, pp. 127–138. ISBN 978-3-642-13730-3. [Google Scholar]
- Xu, Z.; Xu, L.; Rodrigues, B. An analysis of the extended Christofides heuristic for the k-depot TSP. Oper. Res. Lett. 2011, 39, 218–223. [Google Scholar] [CrossRef]
- Xu, Z.; Rodrigues, B. An extension of the Christofides heuristic for the generalized multiple depot multiple traveling salesmen problem. Eur. J. Oper. Res. 2017, 257, 735–745. [Google Scholar] [CrossRef]
- Xu, L.; Xu, Z.; Xu, D. Exact and approximation algorithms for the min–max k-traveling salesmen problem on a tree. Eur. J. Oper. Res. 2013, 227, 284–292. [Google Scholar] [CrossRef]
- Pérez-Escalona, P.; Rapaport, I.; Soto, J.; Vidal, I. The Multiple Traveling Salesman Problem on Spiders. In Proceedings of the 47th International Conference on Current Trends in Theory and Practice of Computer Science, SOFSEM, Bolzano-Bozen, Italy, 25–29 January 2021. [Google Scholar]
- He, P.; Hao, J.-K. Hybrid search with neighborhood reduction for the multiple traveling salesman problem. Comput. Oper. Res. 2022, 142, 105726. [Google Scholar] [CrossRef]
- Mantha, B.R.K.; Jung, M.K.; García de Soto, B.; Menassa, C.C.; Kamat, V.R. Generalized task allocation and route planning for robots with multiple depots in indoor building environments. Autom. Constr. 2020, 119, 103359. [Google Scholar] [CrossRef]
- Gurobi Optimization, LLC Gurobi Optimizer Reference Manual. 2022. Available online: https://www.gurobi.com (accessed on 20 June 2023).
- Reinelt, G. TSPLIB—A traveling salesman problem library. ORSA J. Comput. 2021, 3, 376–384. [Google Scholar] [CrossRef]
- Ransikarbum, K.; Wattanasaeng, N.; Madathil, S.C. Analysis of multi-objective vehicle routing problem with flexible time windows: The implication for open innovation dynamics. J. Open Innov. Technol. Mark. Complex. 2023, 9, 100024. [Google Scholar] [CrossRef]
- Zhou, H.; Qin, H.; Cheng, C.; Rousseau, L.-M. An exact algorithm for the two-echelon vehicle routing problem with drones. Transp. Res. Part B Methodol. 2023, 168, 124–150. [Google Scholar] [CrossRef]
- Sar, K.; Ghadimi, P. A systematic literature review of the vehicle routing problem in reverse logistics operations. Comput. Ind. Eng. 2023, 177, 109011. [Google Scholar] [CrossRef]
- Moghdani, R.; Salimifard, K.; Demir, E.; Benyettou, A. The green vehicle routing problem: A systematic literature review. J. Clean. Prod. 2023, 279, 123691. [Google Scholar] [CrossRef]
- Menchaca-Méndez, A.; Montero, E.; Flores-Garrido, M.; Miguel-Antonio, L. An algorithm to compute time-balanced clusters for the delivery logistics problem. Eng. Appl. Artif. Intell. 2023, 111, 104795. [Google Scholar] [CrossRef]


| Main Scope | mTSP | Reference |
|---|---|---|
| Integer programming | S M DF | [4,5,6,10,11,12,13,14,15,16,17,18,19,20,21,22,49] [6,15,18,42,44,47,48,50,51,52,53,54] [36,51,104] |
| Exact algorithm | S M DF | [14,20,23,45,46] [42,43,44,45,47,115] - |
| Heuristic | S M DF | [19,24,25,26,27,40,41] [38,39,40] [37,40] |
| Metaheuristic | S | [28,29,30,31,34,35,55,56,57,58,59,60,61,62,63,64,65,67,68,69,70,71,72,73,74,76,78,80,81] |
| [83,84,85,87,88,90,91,94,95,96,97,98,100,101,102,103,104,105,107,117] | ||
| M DF | [82,86,88,89,92,93,99,104,105,118] [32,33,66,75,77,79,104,106] | |
| Approximation algorithm | S M DF | [108,116] [108,110,111,112,113,114,115] [109] |
| Instance | n | m | U | Karabulut et al. [104] | IQP1 | ILP1 | IQP2 | ILP2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| dantzig42 | 42 | 3 | 14 | 748 | 320 | 18% | 772 | 2914 | 24% | 739 | 3934 | 21% | 772 | 1125 | 24% | 739 | 6823 | 21% |
| 5 | 9 | 754 | 5559 | 21% | 787 | 1843 | 34% | 786 | 2639 | 34% | 879 | 4030 | 43% | 1055 | 1763 | 52% | ||
| swiss42 | 42 | 3 | 14 | 1410 | 5682 | 17% | 1407 | 1155 | 21% | 1629 | 6377 | 33% | 1430 | 1043 | 24% | 1616 | 107 | 33% |
| 5 | 9 | 1397 | 886 | 19% | 1603 | 4673 | 38% | 1394 | 1741 | 26% | 1470 | 1493 | 37% | 1787 | 246 | 48% | ||
| att48 | 48 | 3 | 16 | 12,557 | 7200 | 25% | 10,941 | 859 | 17% | 12,339 | 777 | 26% | 12,683 | 6329 | 31% | 12,432 | 668 | 28% |
| 5 | 10 | - | - | - | 11,149 | 2272 | 27% | 11,505 | 1884 | 28% | 11,748 | 4602 | 33% | 16,160 | 7129 | 52% | ||
| gr48 | 48 | 3 | 16 | 5337 | 4452 | 13% | 5213 | 2881 | 15% | 5478 | 528 | 21% | 5423 | 1724 | 23% | 6030 | 5921 | 30% |
| 5 | 10 | - | - | - | 7009 | 6895 | 45% | 5530 | 7184 | 30% | 6696 | 2286 | 44% | 7060 | 4639 | 47% | ||
| hk48 | 48 | 3 | 16 | 11,999 | 1656 | 9% | 12,620 | 663 | 20% | 12,568 | 6956 | 19% | 13,576 | 643 | 26% | 12,456 | 4357 | 20% |
| 5 | 10 | - | - | - | 13,546 | 5583 | 33% | - | - | - | - | - | - | 15,316 | 6864 | 42% | ||
| Instance | n | m | U | Karabulut et al. [104] | IQP1 | ILP1 | IQP2 | ILP2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| dantzig42 | 42 | 3 | 42 | 633 | 74 | 0% | 633 | 206 | 5.69% | 633 | 91 | 7.11% | 633 | 100 | 3.95% | 633 | 40 | 3.79% |
| 5 | 42 | 604 | 84 | 0% | 604 | 36 | 4.64% | 604 | 38 | 14.07% | 604 | 135 | 15.07% | 605 | 83 | 13.22% | ||
| swiss42 | 42 | 3 | 42 | 1208 | 188 | 0% | 1208 | 89 | 2.15% | 1208 | 27 | 1.57% | 1208 | 203 | 9.11% | 1208 | 27 | 9.27% |
| 5 | 42 | 1155 | 50 | 1.47% | 1155 | 413 | 5.11% | 1155 | 812 | 5.63% | 1167 | 2200 | 19.37% | 1155 | 60 | 17.49% | ||
| att48 | 48 | 3 | 48 | 9946 | 442 | 4.25% | 9946 | 11 | 5.81% | 9946 | 85 | 4.83% | 9946 | 51 | 7.57% | 9946 | 26 | 7.51% |
| 5 | 48 | 9448 | 43 | 2.64% | 9448 | 182 | 13.52% | 9448 | 400 | 13.79% | 9448 | 85 | 15.81% | 9448 | 2000 | 14.73% | ||
| gr48 | 48 | 3 | 48 | 4761 | 201 | 1.70% | 4761 | 96 | 3.91% | 4761 | 27 | 6.87% | 4761 | 1369 | 8.36% | 4761 | 227 | 8.25% |
| 5 | 48 | 4544 | 113 | 0% | 4544 | 207 | 8.78% | 4558 | 71 | 7.79% | 4735 | 171 | 18.59% | 4558 | 2829 | 14.26% | ||
| hk48 | 48 | 3 | 48 | 11,101 | 115 | 0% | 11,101 | 335 | 2.08% | 11,101 | 206 | 2.20% | 11,332 | 3037 | 10.98% | 11,134 | 1950 | 8.45% |
| 5 | 48 | 10,834 | 164 | 0% | 10,834 | 919 | 6.98% | 10,834 | 786 | 7.30% | 10,888 | 1524 | 17.20% | 10,967 | 127 | 17.42% | ||
| IP | Section | Objective Function | Binary Variables | Constraints |
|---|---|---|---|---|
| IQP1 | Section 3.1 | quadratic | ||
| ILP1 | linear | |||
| IQP2 | Section 3.2 | quadratic | ||
| ILP2 | linear |
| IP | Dummy Depots | CP | OP | Minsum | Minmax | L | U | FD-M+DF |
|---|---|---|---|---|---|---|---|---|
| IQP1 | m | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | |
| ILP1 | m | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| IQP2 | m | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | ||
| ILP2 | m | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cornejo-Acosta, J.A.; García-Díaz, J.; Pérez-Sansalvador, J.C.; Segura, C. Compact Integer Programs for Depot-Free Multiple Traveling Salesperson Problems. Mathematics 2023, 11, 3014. https://doi.org/10.3390/math11133014
Cornejo-Acosta JA, García-Díaz J, Pérez-Sansalvador JC, Segura C. Compact Integer Programs for Depot-Free Multiple Traveling Salesperson Problems. Mathematics. 2023; 11(13):3014. https://doi.org/10.3390/math11133014
Chicago/Turabian StyleCornejo-Acosta, José Alejandro, Jesús García-Díaz, Julio César Pérez-Sansalvador, and Carlos Segura. 2023. "Compact Integer Programs for Depot-Free Multiple Traveling Salesperson Problems" Mathematics 11, no. 13: 3014. https://doi.org/10.3390/math11133014
APA StyleCornejo-Acosta, J. A., García-Díaz, J., Pérez-Sansalvador, J. C., & Segura, C. (2023). Compact Integer Programs for Depot-Free Multiple Traveling Salesperson Problems. Mathematics, 11(13), 3014. https://doi.org/10.3390/math11133014








