A New Method for Commercial-Scale Water Purification Selection Using Linguistic Neural Networks
Abstract
1. Introduction
1.1. A Brief Review of the Development of Neural Networks and Their Types
1.2. A Brief Review of Feed-Forward Neural Networks and Their Uses
1.3. A Brief Review of Activation Function and Its Importance
- We expand the concept of a feed-forward neural network to incorporate a feed-forward double-hierarchy linguistic neural network using Yager–Dombi operators;
- We develop a fuzzy neural network for the selection of water purification methods using a double-hierarchy linguistic neural network and use it for the selection of water purification methods;
- We extend the Yager–Dombi operations to aggregate a double hierarchy for fuzzy information.
1.4. Motivation behind the Study
- To extend the concept of fuzzy neural networks to incorporate double-hierarchy linguistic neural networks;
- To combine existing aggregation operators to create a new aggregation operator;
- To develop a fuzzy neural network for the selection of water purification methods;
- To extend the Yager–Dombi operations to aggregate double-hierarchy fuzzy information.
1.5. Contribution of the Study
- We develop new t-norms and their operations by using the Yager and Dombi t-norms and discuss their relationships;
- The developed t-norms are further expanded to aggregation operators to develop a new set of double-hierarchy linguistic terms;
- The proposed aggregation is necessary for artificial neural networks. Therefore, we integrate the proposed aggregation operators into the hidden layers of a linguistic neural network;
- We develop a new approach to linguistic neural networks and linguistic decision models using linguistic neural networks;
- The proposed linguistic decision model, based on a linguistic neural network, is applied to water-purification procedure-selection problems;
2. Fundamental Concept
3. Yager–Dombi Operators for DHLTSs
4. Activation Functions and Neural Network Systems
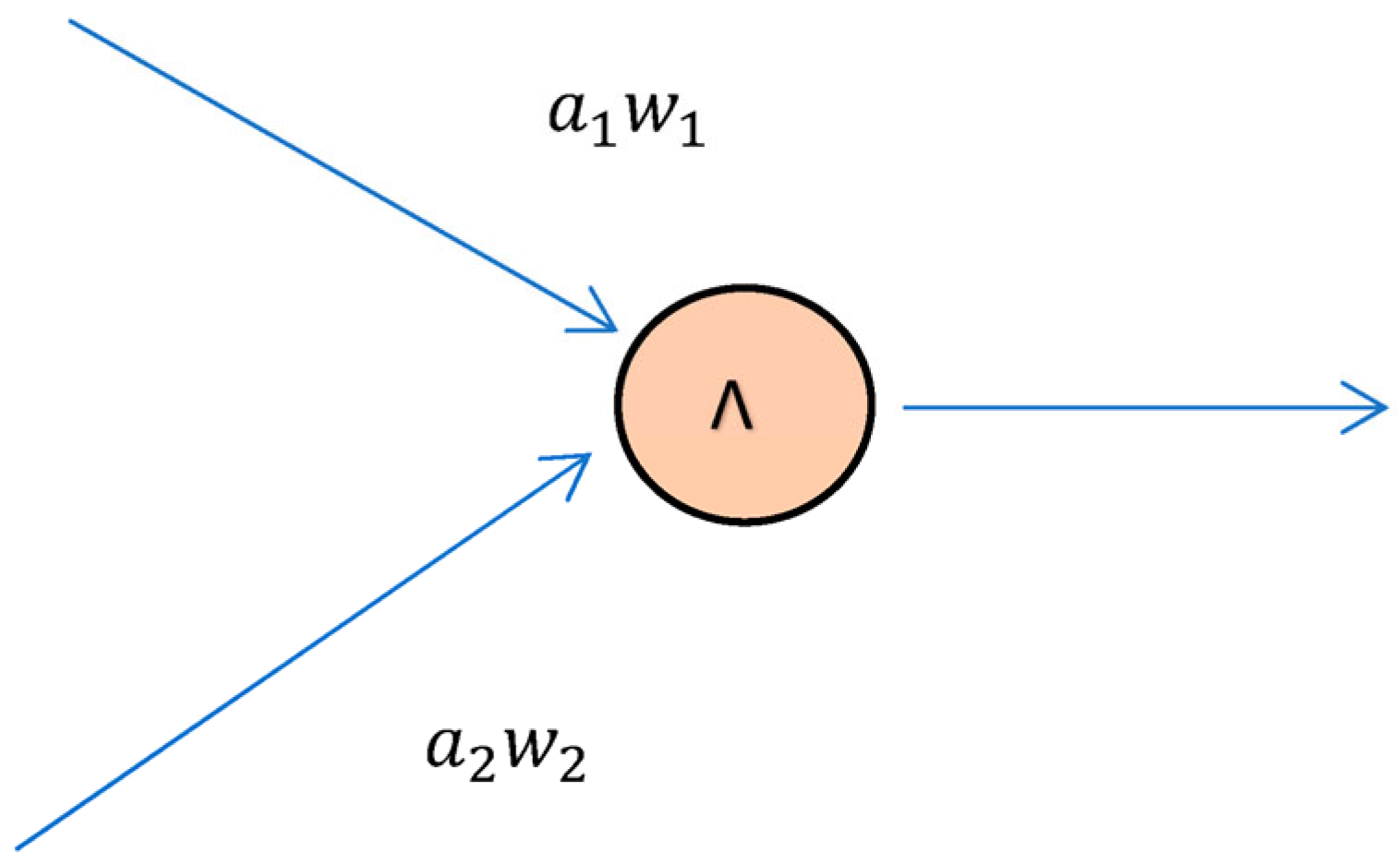
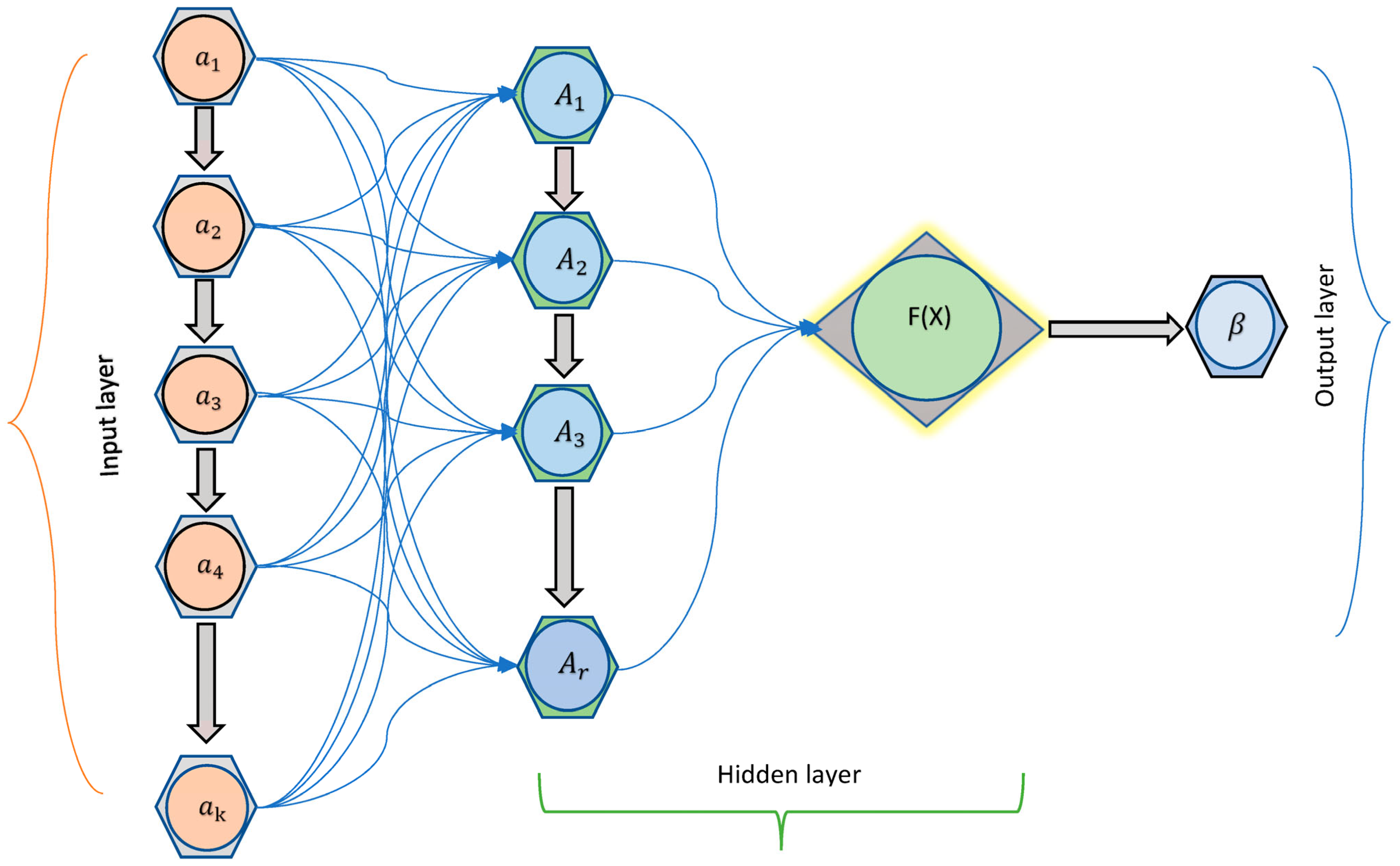
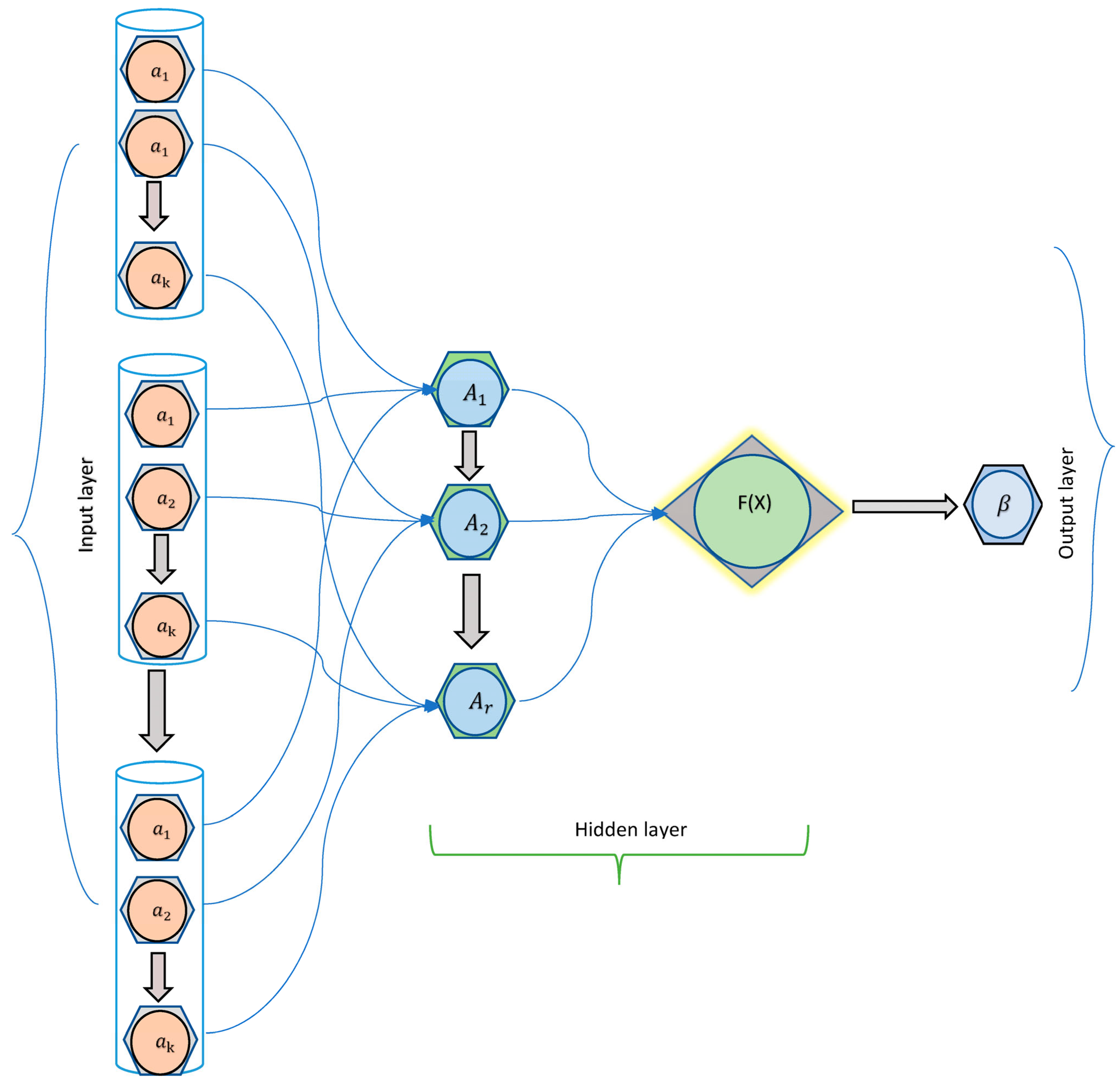
5. The Output of Neural Networks Using Yager–Dombi Operators
- To evaluate the entropy of the information provided by the experts in the form of matrices, we use the following equation:
- 2.
- We obtain the final criteria weight vector as follows:
Output of Feed-Forward Double-Hierarchy Linguistic Term Neural Networks
6. Numerical Example
- (1)
- : Chlorination: Chlorination is a process that uses chlorine to disinfect water. Chlorine is added to water, which kills the harmful bacteria and viruses present in it. This method is effective in killing most of the disease-causing pathogens;
- (2)
- : Reverse Osmosis: In the reverse osmosis (RO) process, a semi-permeable membrane is utilized to filter out dissolved particles, contaminants, and minerals from water. It is a highly effective method of water purification and is commonly used in households and industries;
- (3)
- : Ultraviolet Purification: UV purification uses ultraviolet light to kill bacteria, viruses, and other microorganisms present in water. It is an effective method of water purification and does not use any chemicals;
- (4)
- : Filtration: Filtration is a process that removes impurities from water by passing it through a porous material. Sediments, dirt, and other bigger particles can be effectively removed from water with this technique;
- (5)
- : Coagulation and sedimentation: Chemicals such as alum are added to water to cause impurities to clump together and settle at the bottom of a tank, which can then be removed through sedimentation;
- (6)
- : Boiling: By bringing water to a boil for at least one minute, the majority of disease-causing organisms can be killed;
- (7)
- : Distillation: Water is heated during distillation, and the steam is subsequently condensed back into water. Minerals, chemicals, and bacteria are just a few of the impurities that can be removed by using this method.
- : Economic factors: Economic factors can have a significant impact on water purification, as the process of treating and purifying water can be expensive and require significant investments in infrastructure, technology, and human resources. One major economic factor that can affect water purification is the availability and cost of resources such as energy, chemicals, and materials needed for the purification process;
- : Socio-political factors: The socio-political environment can have a significant impact on water purification. Governments have an obligation to make sure that their populations have access to safe drinking water since access to clean water is a fundamental human right. However, the provision of clean water can be influenced by a variety of socio-political factors, such as social factors, public health, and political instability, among others;
- : Environmental factors: There are many environmental factors that can affect water purification, including temperature, chemicals, turbidity, and climate change. Overall, environmental factors can have a significant impact on water purification and must be taken into account when designing and implementing water purification systems;
- : Type of Contaminants: The type and concentration of contaminants present in the water will also affect the purification process. Different treatment processes are better suited for removing different types of contaminants, such as chemicals, microbes, or sediments;
- : Water Quality Standards: The level of purity required for the final product will affect the purification process. Different industries and applications have different standards for water quality, which will influence the choice of treatment process and the extent of purification required.
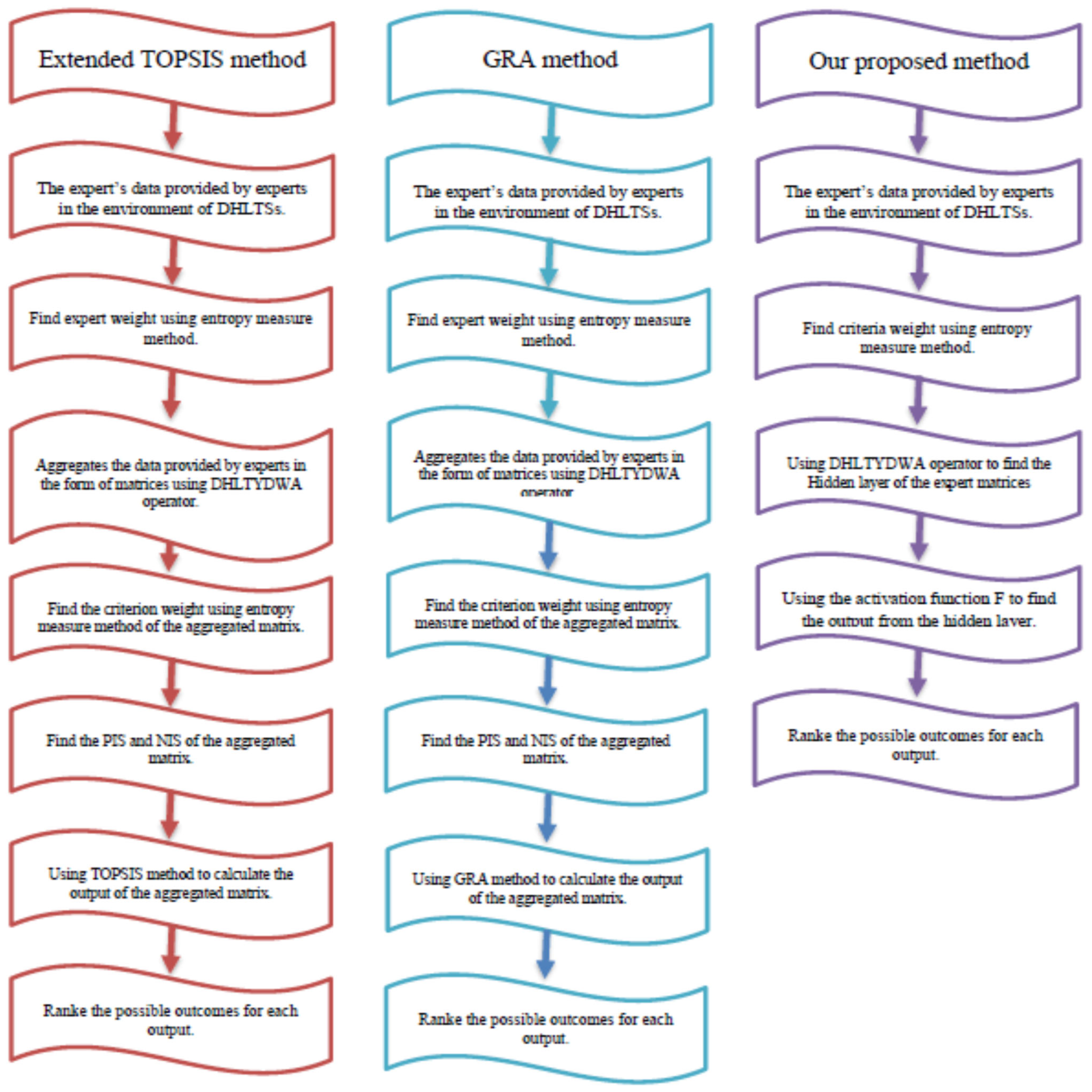
7. Verification of Our Proposed Method
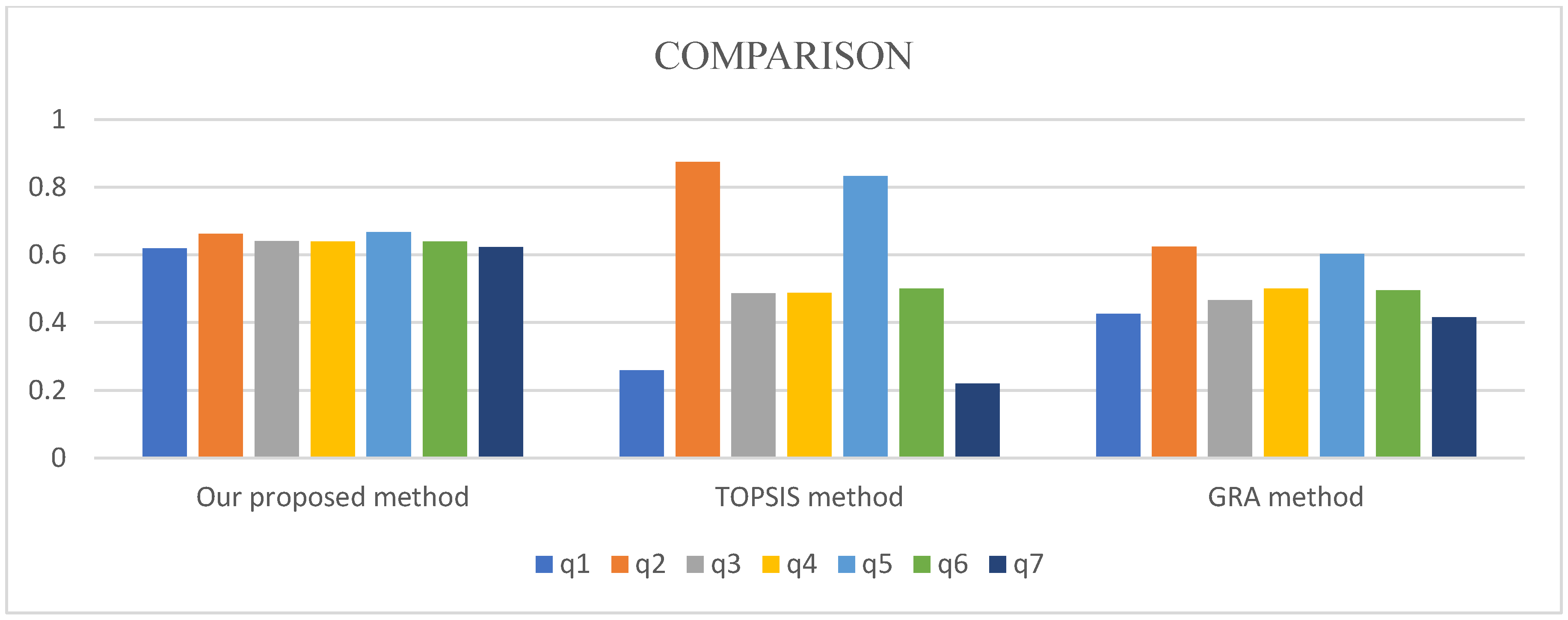
8. Discussion and Comparison
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Razi, M.A.; Athappilly, K. A comparative predictive analysis of neural networks (NNs), nonlinear regression and classification and regression tree (CART) models. Expert Syst. Appl. 2005, 29, 65–74. [Google Scholar] [CrossRef]
- Coats, P.K.; Fant, L.F. Recognizing financial distress patterns using a neural network tool. Financ. Manag. 1993, 1993, 142–155. [Google Scholar] [CrossRef]
- Ceylan, H.; Bayrak, M.B.; Gopalakrishnan, K. Neural Networks Applications in Pavement Engineering: A Recent Survey. Int. J. Pavement Res. Technol. 2014, 7, 434–444. [Google Scholar]
- Sarvamangala, D.R.; Kulkarni, R.V. Convolutional neural networks in medical image understanding: A survey. Evol. Intell. 2022, 15, 1–22. [Google Scholar] [CrossRef]
- Fang, C.; Dong, H.; Zhang, T. Mathematical models of overparameterized neural networks. Proc. IEEE 2021, 109, 683–703. [Google Scholar] [CrossRef]
- Mitchell, J.M.O. Classical statistical methods. Mach. Learn. Neural Stat. Classif. 1994, 1994, 17–28. [Google Scholar]
- Koh, J.; Lee, J.; Yoon, S. Single-image deblurring with neural networks: A comparative survey. Comput. Vis. Image Underst. 2021, 203, 103134. [Google Scholar] [CrossRef]
- Alshehri, S.A. Neural network technique for image compression. IET Image Process. 2016, 10, 222–226. [Google Scholar] [CrossRef]
- Yen, Y.; Fanty, M.; Cole, R. Speech recognition using neural networks with forward-backward probability generated targets. In Proceedings of the 1997 IEEE International Conference on Acoustics, Speech, and Signal Processing, Munich, Germany, 21–24 April 1997; Volume 4, pp. 3241–3244. [Google Scholar]
- Collobert, R.; Weston, J. A unified architecture for natural language processing: Deep neural networks with multitask learning. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 160–167. [Google Scholar]
- Ma, Q. Natural language processing with neural networks. In Proceedings of the Language Engineering Conference, Hyderabad, India, 13–15 December 2002; pp. 45–56. [Google Scholar]
- Rani, S.; Kumar, P. Deep learning based sentiment analysis using convolution neural network. Arab. J. Sci. Eng. 2019, 44, 3305–3314. [Google Scholar] [CrossRef]
- Chen, P.; Sun, Z.; Bing, L.; Yang, W. Recurrent attention network on memory for aspect sentiment analysis. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, Copenhagen, Denmark, 7–11 September 2017; pp. 452–461. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1998; Volume 326. [Google Scholar]
- Yoo, P.D.; Kim, M.H.; Jan, T. Machine learning techniques and use of event information for stock market prediction: A survey and evaluation. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Sydney, Australia, 29 November–1 December 2006; Volume 2, pp. 835–841. [Google Scholar]
- Adya, M.; Collopy, F. How effective are neural networks at forecasting and prediction? A review and evaluation. J. Forecast. 1998, 17, 481–495. [Google Scholar] [CrossRef]
- Zaghloul, W.; Lee, S.M.; Trimi, S. Text classification: Neural networks vs support vector machines. Ind. Manag. Data Syst. 2009, 109, 708–717. [Google Scholar] [CrossRef]
- Naseer, M.; Minhas, M.F.; Khalid, F.; Hanif, M.A.; Hasan, O.; Shafique, M. Fannet: Formal analysis of noise tolerance, training bias and input sensitivity in neural networks. In Proceedings of the 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 9–13 March 2020; pp. 666–669. [Google Scholar]
- Shin, K.S.; Lee, T.S.; Kim, H.J. An application of support vector machines in bankruptcy prediction model. Expert Syst. Appl. 2005, 28, 127–135. [Google Scholar] [CrossRef]
- Sterling, A.J.; Zavitsanou, S.; Ford, J.; Duarte, F. Selectivity in organocatalysis—From qualitative to quantitative predictive models. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2021, 11, e1518. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Wang, Y.; Lombardi, F.; Han, J. A survey of stochastic computing neural networks for machine learning applications. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 2809–2824. [Google Scholar] [CrossRef]
- Schwendicke, F.A.; Samek, W.; Krois, J. Artificial intelligence in dentistry: Chances and challenges. J. Dent. Res. 2020, 99, 769–774. [Google Scholar] [CrossRef]
- Ossowska, A.; Kusiak, A.; Świetlik, D. Artificial intelligence in dentistry—Narrative review. Int. J. Environ. Res. Public Health 2022, 19, 3449. [Google Scholar] [CrossRef]
- Drakopoulos, G.; Giannoukou, I.; Mylonas, P.; Sioutas, S. The converging triangle of cultural content, cognitive science, and behavioral economics. In Artificial Intelligence Applications and Innovations, Proceedings of theAIAI 2020 IFIP WG 12.5 International Workshops: MHDW 2020 and 5G-PINE 2020, Neos Marmaras, Greece, 5–7 June 2020, Proceedings 16; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 200–212. [Google Scholar]
- Bebis, G.; Georgiopoulos, M. Feed-forward neural networks. IEEE Potentials 1994, 13, 27–31. [Google Scholar] [CrossRef]
- Medsker, L.R.; Jain, L.C. Recurrent neural networks. Des. Appl. 2001, 5, 64–67. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Lange, S.; Riedmiller, M. Deep auto-encoder neural networks in reinforcement learning. In Proceedings of the 2010 International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Chao, J.; Shen, F.; Zhao, J. Forecasting exchange rate with deep belief networks. In Proceedings of the 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 1259–1266. [Google Scholar]
- Zavadskas, E.K.; Mardani, A.; Turskis, Z.; Jusoh, A.; Nor, K.M. Development of TOPSIS method to solve complicated decision-making problems—An overview on developments from 2000 to 2015. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 645–682. [Google Scholar] [CrossRef]
- Wei, G.W. GRA method for multiple attribute decision making with incomplete weight information in intuitionistic fuzzy setting. Knowl.-Based Syst. 2010, 23, 243–247. [Google Scholar] [CrossRef]
- Guitouni, A.; Martel, J.M. Tentative guidelines to help choosing an appropriate MCDA method. Eur. J. Oper. Res. 1998, 109, 501–521. [Google Scholar] [CrossRef]
- Elliott, D.L. A Better Activation Function for Artificial Neural Networks; Institute for Systems Research, Harvard University: College Park, MA, USA, 1993. [Google Scholar]
- Schmidt-Hieber, J. Nonparametric Regression Using Deep Neural Networks with ReLU Activation Function. 2020. Available online: https://arxiv.org/abs/1708.06633 (accessed on 30 May 2023).
- Yin, X.; Goudriaan, J.A.N.; Lantinga, E.A.; Vos, J.A.N.; Spiertz, H.J. A flexible sigmoid function of determinate growth. Ann. Bot. 2003, 91, 361–371. [Google Scholar] [CrossRef] [PubMed]
- Zamanlooy, B.; Mirhassani, M. Efficient VLSI implementation of neural networks with hyperbolic tangent activation function. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2013, 22, 39–48. [Google Scholar] [CrossRef]
- Kamruzzaman, J. Arctangent activation function to accelerate backpropagation learning. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2002, 85, 2373–2376. [Google Scholar]
- Montavon, G.; Samek, W.; Müller, K.R. Methods for interpreting and understanding deep neural networks. Digit. Signal Process. 2018, 73, 1–15. [Google Scholar] [CrossRef]
- Sideris, A.; Orita, K. Structured learning in feedforward neural networks with application to robot trajectory control. In Proceedings of the 1991 IEEE International Joint Conference on Neural Networks, Singapore, 18–21 November 1991; pp. 1067–1072. [Google Scholar]
- Sharma, S.; Mehra, R. Implications of pooling strategies in convolutional neural networks: A deep insight. Found. Comput. Decis. Sci. 2019, 44, 303–330. [Google Scholar] [CrossRef]
- Garg, H.; Shahzadi, G.; Akram, M. Decision-making analysis based on Fermatean fuzzy Yager aggregation operators with application in COVID-19 testing facility. Math. Probl. Eng. 2020, 2020, 7279027. [Google Scholar] [CrossRef]
- Akram, M.; Khan, A.; Borumand Saeid, A. Complex Pythagorean Dombi fuzzy operators using aggregation operators and their decision-making. Expert Syst. 2021, 38, e12626. [Google Scholar] [CrossRef]
- Ye, F. An extended TOPSIS method with interval-valued intuitionistic fuzzy numbers for virtual enterprise partner selection. Expert Syst. Appl. 2010, 37, 7050–7055. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. Int. J. Bioautomation 2016, 20, 1. [Google Scholar]
- Li, X.; Xu, Z.; Wang, H. Three-way decisions based on some Hamacher aggregation operators under double hierarchy linguistic environment. Int. J. Intell. Syst. 2021, 36, 7731–7753. [Google Scholar] [CrossRef]
- Cheng, F.; Liang, H.; Niu, B.; Zhao, N.; Zhao, X. Adaptive neural self-triggered bipartite secure control for nonlinear MASs subject to DoS attacks. Inf. Sci. 2023, 631, 256–270. [Google Scholar] [CrossRef]
| 0.738521429 | 0.326423333 | 0.212368533 | 0.136978263 | 0.1258662 | |
| 0.969678667 | 0.368916545 | 0.333768273 | 0.154811222 | 0.095050909 | |
| 0.570108667 | 0.487515667 | 0.185739733 | 0.104634095 | 0.087066391 | |
| 2.278308762 | 1.182855545 | 0.731876539 | 0.396423581 | 0.3079835 | |
| 0.694964668 | 0.541884482 | 0.422591636 | 0.283884909 | 0.235464362 |
| DHLTYDWA | 0.61904 | 0.66270 | 0.64047 | 0.63911 | 0.66773 | 0.63961 | 0.62284 |
| DHLTYDOWA | 0.62006 | 0.66972 | 0.64923 | 0.63942 | 0.67406 | 0.64974 | 0.62513 |
| DHLTYDHWA | 0.51688 | 0.52162 | 0.51856 | 0.51912 | 0.52149 | 0.51857 | 0.51747 |
| 0.21584 | 0.03857 | 0.14964 | 0.14933 | 0.04855 | 0.14578 | 0.22714 | |
| 0.07570 | 0.27066 | 0.1419 | 0.14222 | 0.24299 | 0.14576 | 0.0644 | |
| output | 0.25967 | 0.87526 | 0.48672 | 0.48781 | 0.83347 | 0.49997 | 0.22089 |
| raking | 0.87526 | 0.83347 | 0.49997 | 0.48781 | 0.48672 | 0.25967 | 0.22089 |
| 0.58842 | 0.87869 | 0.642025 | 0.70632 | 0.86793 | 0.66403 | 0.60736 | |
| 0.79424 | 0.52724 | 0.73448 | 0.70624 | 0.57306 | 0.677098 | 0.85416 | |
| output | 0.42557 | 0.62499 | 0.46642 | 0.50003 | 0.60231 | 0.49513 | 0.41556 |
| raking | 0.62499 | 0.60231 | 0.50003 | 0.49513 | 0.46642 | 0.42557 | 0.41556 |
| DHLTYDWA | |
| DHLTYDOWA | |
| DHLTYDHWA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdullah, S.; Almagrabi, A.O.; Ali, N. A New Method for Commercial-Scale Water Purification Selection Using Linguistic Neural Networks. Mathematics 2023, 11, 2972. https://doi.org/10.3390/math11132972
Abdullah S, Almagrabi AO, Ali N. A New Method for Commercial-Scale Water Purification Selection Using Linguistic Neural Networks. Mathematics. 2023; 11(13):2972. https://doi.org/10.3390/math11132972
Chicago/Turabian StyleAbdullah, Saleem, Alaa O. Almagrabi, and Nawab Ali. 2023. "A New Method for Commercial-Scale Water Purification Selection Using Linguistic Neural Networks" Mathematics 11, no. 13: 2972. https://doi.org/10.3390/math11132972
APA StyleAbdullah, S., Almagrabi, A. O., & Ali, N. (2023). A New Method for Commercial-Scale Water Purification Selection Using Linguistic Neural Networks. Mathematics, 11(13), 2972. https://doi.org/10.3390/math11132972






