Leader-Follower Quasi-Consensus of Multi-Agent Systems with Packet Loss Using Event-Triggered Impulsive Control

Abstract

This paper focuses on the leader–follower quasi-consensus problem of multi-agent systems, considering the practical communication scenarios which involve packet loss. The phenomenon of packet loss is described in terms of the packet loss rate. A novel hybrid event-triggered impulsive control strategy is proposed, the Lyapunov stability theory is employed to derive sufficient conditions for realizing the leader–follower quasi-consensus, and the exclusion of Zeno behavior is demonstrated. Finally, a numerical simulation example is provided to verify the effectiveness of the proposed approach. The simulation results indicate that the packet loss rate is closely related to the control gain and the maximum triggered interval, specifically because as the packet loss rate increases, the trigger frequency also increases.

1. Introduction

Inspired by biological collectives, researchers have introduced the concept of multi-agent systems (MASs) [1]. These systems, also known as “systems of systems”, are large-scale, complex structures consisting of numerous distributed, semi-autonomous, or autonomous subsystems (agents) interconnected through networks [2]. As time advances, multi-agent systems have become a prominent field within the study of complex systems science [3]. In recent years, complex network theory has received tremendous attention from numerous researchers as a powerful tool for investigating complexity science and complex systems [4,5,6]. Multi-agent systems are typical complex systems. Drawing inspiration from current theories on complex dynamic networks, multi-agent systems can be modeled as complex dynamic networks in which nodes denote individual agents, edges connecting nodes represent cooperation or communication relationships between agents, and the dynamic characteristics of nodes characterize the motion properties of the agent system.

With the development of communication network technology, research on MASs has garnered increasing attention [7,8] and has been extensively applied in various fields, including unmanned aircraft formations, robotic cooperative control, and sensor networks [9,10,11]. Currently, the main research problems in control of multi-agent systems include tracking control, formation control, swarm control, flocking control, rendezvous control, controllability, and consensus. Among them, the consensus problem of multi-agent systems is a fundamental issue. Consensus refers to the convergence of the states of all agents in a multi-agent system to a common value over time. Furthermore, leader–follower consensus occurs when a goal-oriented leader exists for all other agents to follow [12]. On the other hand, the definition of consensus fails to hold when MASs are impacted by external disturbances that limit the consensus error within a measurable range, which is called quasi-consensus [13].

Over the past two decades, numerous control protocols have been developed to ensure consensus, such as classic state/output feedback, adaptive control, sampled-data control, and impulsive control. These protocols have been widely employed in the literature to study the consensus problem of MASs [14,15,16,17]. Impulsive control protocols based on impulsive systems which are characterized by abrupt changes in their evolution at certain instant, have been proposed by scholars [18]. As a powerful non-continuous control method, impulsive control is a control strategy that only applies control at certain discrete sampling points [19,20,21,22] to change the system state, as compared to continuous control methods such as state feedback control [23]. Impulsive control is considered an effective control strategy [24] because it has significant advantages over complex systems that cannot tolerate or receive continuous control inputs [25]. Under the action of impulsive control, MASs will undergo instantaneous jumps at impulsive instants, which not only improves the robustness of the information transmission in networks [26]. Therefore, it has attracted the attention of many researchers and has been widely applied in various systems, including MASs, national capital market regulation and management, and power system regulation [27,28,29].

However, the impulsive control employed in the aforementioned literature was implemented with prescribed periods or under dwell-time conditions, which may lead to resource wastage [30,31,32]. To prevent unnecessary control, reduce communication bandwidth requirements, and enhance resource utilization, event-triggered impulsive control (ETIC) is introduced. In this case, the controller, benefiting from the event-triggered mechanism (ETM), operates only when specific conditions are met. Furthermore, Zeno behavior, where an infinite number of events occur in a finite-time interval, can significantly degrade the performance and stability of a system, and therefore, it is crucial due to the excitability of the execution equipment [33]. Owing to these advantages, ETIC has been widely used in MASs [34,35,36] and applied in some industrial control investigations such as Wind Power Systems [37,38]. For instance, a distributed control mechanism has been proposed in [35] to ensure leader–follower consensus; Ref. [36] has proposed a novel control protocol that combines impulsive control with an event-triggered mechanism to solve the consensus problem for nonlinear multiagent systems under energy consumption constraint; Ref. [37] has studied an event-triggered fuzzy load frequency control for wind power systems with measurement outliers and transmission delays. Moreover, Ref. [38] has investigated a novel adaptive memory-event-triggered mechanism to address the weighted memory-event-triggered $H_{\infty }$ static output control issue for Takagi–Sugeno fuzzy wind turbine systems with uncertainty. However, the influence of disturbances was ignored in the earlier studies. Therefore, in recent years, the design of event-triggered schemes that can resist disturbances has become a research focus [39,40,41,42]. In [41], the authors have introduced a novel event-triggered impulsive mechanism to counteract the effects of external disturbances and derive sufficient conditions for achieving closed-loop system consensus; Ref. [42] has investigated the nonlinear event-triggered closed-loop system with packet loss. Finally, it is worth noting that some parameters, which are relatively conservative due to their anti-disturbance nature, can be relaxed in this paper.

On the other hand, numerous factors influence MASs in engineering applications, particularly packet loss in communication channels due to insufficient power supply, attacks, and other reasons. Information loss may render the control effect ineffective, leading to system performance degradation [43,44,45,46,47]. In most scenarios where network communication transmission distance is short [48,49], the effect of delay on the system can be neglected, but packet loss is ubiquitous and cannot be ignored. Moreover, the unpredictability of network environments often results in random packet loss, with time-varying or uncertain probabilities. Generally, when a MAS experiences packet loss, the random attribute related to packet loss can be characterized using a Bernoulli-distributed random variable.For example, consensus with random packet loss has examined in [46]; Ref. [47] has discussed fixed-time output tracking for high-order MASs with packet loss under directed network topology. Thus, it is crucial to study the packet loss problem. To the best of our knowledge, although consensus with packet loss has been extensively investigated in the literature, most studies concentrate on ETM without considering impulsive effects. Furthermore, there is scarce research on the design of ETIC for leader–follower consensus of MASs under packet loss. Thus, it is crucial to study the leader–follower quasi-consensus of multi-agent systems with packet loss using event-triggered impulsive control. Building on the insights from the preceding discussion, this paper focuses on the consensus problem of leader–follower MASs under ETIC with packet loss. By introducing a novel impulsive mechanism and employing linear matrix inequalities, we establish sufficient conditions for the system to attain quasi-consensus, while also estimating an upper bound on the error. The primary contributions of this paper are twofold:

(1)

To elaborate further, this paper introduces the concept of packet loss rate as a quantitative measure of its impact on consensus. The relationship between the packet loss rate and event-triggered parameters, such as control gain and maximum triggering interval, is also analyzed and revealed. This analysis provides insight into how different event-triggered parameters can be designed based on the packet loss rate to achieve better consensus.

(2)

We develop a novel event-triggered impulsive strategy that eliminates Zeno behavior. Compared with the previous works such as [39,40,41,42], the following advantages of our constructed ETM can be summarized as follows: (1) The adjustable triggering parameter ${\beta }_1,{\beta }_2$ lead to ETM to have a wider range of parameter selection than existing results, making it applicable to more scenarios. (2) The measured error $x\left(t\right)-x\left(t_k\right)$ is not required in this manuscript, making the designed event-triggered impulsive mechanism easier to construct and implement. (3) The designed event-triggering mechanism is formulated in terms of Lyapunov function, which can be applied to different control systems by selecting different Lyapunov functions.

The rest of this paper is structured as follows: Section 2 presents some preliminaries and the system model. Section 3 proposes a novel anti-disturbance event-triggered impulsive strategy and presents the main results. Section 4 provides a simulation example. Finally, Section 5 concludes the paper.

Notation 1. 

In this paper, the following notations are adopted: $\mathbb{R}$, ${\mathbb{R}}^{+}$, and ${\mathbb{N}}^{+}$ denote the sets of real numbers, non-negative real numbers, and positive integers, respectively. ${\mathbb{R}}^n$ and ${\mathbb{R}}^{n\times m}$ denote the n-dimensional and the $n\times m$-dimensional real spaces equipped with the Euclidean norm $|·|$, respectively. For any real numbers a and b, we use $a\vee b$ (resp. $a\wedge b$) to denote the maximum (resp. minimum) value between a and b. For any vector or real matrix U, $\left|U\right|$ denotes its Euclidean and matrix-induced norms, while ${\lambda }_{min}\left(U\right)$ and ${\lambda }_{max}\left(U\right)$ denote the minimum and maximum eigenvalues of matrix U, respectively. We define $\overline{U}=I\otimes U$, where I is a dimension-appropriate unit matrix and ⊗ is the Kronecker product. Additionally, $\mathrm{diag}\{·\}$ denotes the diagonal matrix. $\mathcal{N}:=\{1,2,\cdots ,N\}$ is a finite set, where $N\in {\mathbb{N}}^{+}$. For any continuous function $y:\mathbb{R}\to {\mathbb{R}}^w$, ${\left|y\right|}_h$ denotes its maximum value or supremum on the interval h.

2. Preliminaries

2.1. Graph Theory

MASs can be represented by graph theory, denoted as $G=\{V,E,\mathcal{A}\}$, where $V=\{v_1,v_2,\cdots ,v_N\}$ is the set of nodes, E represents the edges, and $\mathcal{A}={\left[a_{ij}\right]}_{N\times N}$ is the adjacency matrix. N is the number of followers in the system. If there is an edge between agents i and j (where $i\ne j$), there is $a_{ij}=a_{ji}>0$. Otherwise, $a_{ij}=a_{ji}=0$. Define the neighbor node set of $v_i$ as $N_i$ if there exist edges between i and other followers. Additionally, $a_{ii}=0$. The Laplacian matrix is denoted by $L={\left[l_{ij}\right]}_{N\times N}$, where $l_{ii}={\sum }_{j\in N_i}^N{a}_{ij}$ and $l_{ij}=-a_{ij}$ for $i\ne j$. We label the leader as 0, and let the diagonal matrix $C=\mathrm{diag}\{c_1,c_2,\cdots ,c_N\}$ represent the connections between the leader and followers. If there is a directed flow of information from the leader 0 to the follower i, then $c_i>0$. Otherwise, $c_i=0$. Lastly, define $H=L+C$.

2.2. System Description

Consider a system that consists of a leader and N followers, whose dynamics are described as follows:

$$\left\{\begin{array}{c}{\dot{x}}_i\left(t\right)=A\left(t\right)x_i\left(t\right)+Bf(x_i\left(t\right),w_i\left(t\right))+u_i\left(t\right),\hfill \\ {\dot{x}}_0\left(t\right)=A\left(t\right)x_0\left(t\right)+Bf(x_0\left(t\right),w_0\left(t\right)),\hfill \end{array}\right.$$

(1)

where $i\in \mathcal{N}$ and $t\ge t_0$. $x_i\left(t\right)\in {\mathbb{R}}^n$ and $x_0\left(t\right)\in {\mathbb{R}}^n$ are the system states of follower i and the leader, respectively. $w_i\left(t\right)\in {\mathbb{R}}^w$ and $w_0\left(t\right)\in {\mathbb{R}}^w$ are the external perturbations of the follower i and the leader, respectively. $u_i\left(t\right)\in {\mathbb{R}}^n$ is the control input of the follower agent. $A:\mathbb{R}\to {\mathbb{R}}^{n\times n}$ and $B\in {\mathbb{R}}^{n\times m}$ are time-varying and constant matrices, respectively, where $A\left(t\right)=A+MF\left(t\right)Q$ with constant matrices $A,M,Q$ of appropriate dimensions, and $F\left(t\right)$ is a time-varying matrix of proper dimensions that satisfies $F^T\left(t\right)F\left(t\right)\le I$. The function $f:{\mathbb{R}}^n\times {\mathbb{R}}^w\to {\mathbb{R}}^m$ represents the nonlinear property of the system, satisfying $f(0,0)\equiv 0$. Assume that system (1) starts from $t_0$, and the initial states of follower i and the leader are $x_i\left(t_0\right)$ and $x_0\left(t_0\right)$, respectively. Additionally, we define the right upper Dini derivative as $D^{+}V(t,x)=lim{sup}_{h\to 0^{+}}\frac{1}{h}(V(t+h,x+hv(x,w))-V(t,x))$, where $V:{\mathbb{R}}^{+}\times {\mathbb{R}}^n\to {\mathbb{R}}^{+}$ and $v:{\mathbb{R}}^n\times {\mathbb{R}}^w\to {\mathbb{R}}^n$ are the local Lipschitz and nonlinear functions.

In this paper, the control input of the follower i is designed as follows:

$$\begin{array}{c}\hfill u_i\left(t\right)=\sum _{k=1}^{+\infty }{b}_k\left(\sum _{j\in N_i}{a}_{ij}(x_i\left(t\right)-x_j\left(t\right))+c_i(x_i\left(t\right)-x_0\left(t\right))\right)\delta (t-t_k),\end{array}$$

(2)

where $b_k\in \mathbb{R}$ denotes the impulsive control gain; $\delta \left(t\right)$ is the Dirac function. The set $\{t_k,k\in {\mathbb{N}}^{+}\}$ denotes the impulsive instants generated by the ETM.

Let $e_i\left(t\right)=x_i\left(t\right)-x_0\left(t\right)$ denote the system error, and let ${\tilde{w}}_i\left(t\right)=w_i\left(t\right)-w_0\left(t\right)$. We define $g(e_i\left(t\right),{\tilde{w}}_i\left(t\right))=f\left(x_i\left(t\right),w_i\left(t\right)\right)-f\left(x_0\left(t\right),w_0\left(t\right)\right)$. Furthermore, let

$$\begin{array}{cc}\hfill & e\left(t\right)={(e_1^T\left(t\right),e_2^T\left(t\right),...,e_N^T\left(t\right))}^T,\hfill \\ \hfill \tilde{w}& \left(t\right)={({\tilde{w}}_1^T\left(t\right),{\tilde{w}}_2^T\left(t\right),...,{\tilde{w}}_N^T\left(t\right))}^T,\hfill \\ \hfill G(e\left(t\right),\tilde{w}\left(t\right))=& {\left(g^T(e_1\left(t\right),{\tilde{w}}_1\left(t\right)),g^T(e_2\left(t\right),{\tilde{w}}_2\left(t\right)),...,g^T(e_N\left(t\right),{\tilde{w}}_N\left(t\right))\right)}^T.\hfill \end{array}$$

Based on (1) and (2) and the Kronecker product, the following compact error system can be obtained:

$$\left\{\begin{array}{cc}\dot{e}\left(t\right)=\overline{A}\left(t\right)e\left(t\right)+\overline{B}G(e\left(t\right),\tilde{w}\left(t\right)),\hfill & \hfill t\ne t_k,t\ge t_0,\\ \Delta e\left(t\right)=b_k(H\otimes I)e\left(t^{-}\right),\hfill & \hfill t=t_k,k\in {\mathbb{N}}^{+},\end{array}\right.$$

(3)

where $\Delta e\left(t_k\right)=e\left(t_k^{+}\right)-e\left(t_k^{-}\right)$ denotes the jump of system at impulsive instant $t=t_k,k\in {\mathbb{N}}^{+}$. Assume that $e\left(t\right)$ is right-continuous, i.e., $e\left(t_k^{+}\right)=e\left(t_k\right)$, where $e\left(t_k^{+}\right)={lim}_{r\to 0^{+}}e(t_k+r)$ and $e\left(t_k^{-}\right)={lim}_{r\to 0^{-}}e(t_k+r)$. Therefore, further express $e\left(t_k\right)=(I+b_{k}H\otimes I)e\left(t_k^{-}\right)$ holds.

If packet loss happen in the controller, (2) fails to stabilize system (1), i.e., $b_k=0$. To describe this situation, we define the packet loss matrix as follows:

$$\begin{array}{c}\hfill \aleph =\left\{\begin{array}{cc}I+b_{k}H\otimes I,\hfill & \hfill \sigma \left(t_k\right)=1,\\ I,\hfill & \hfill \sigma \left(t_k\right)=0,\end{array}\right.\end{array}$$

(4)

where $\sigma \left(t_k\right)$ is a packet loss indicator function for $t=t_k,k\in {\mathbb{N}}^{+}$. When packet loss occurs, $\sigma =0$. Otherwise, $\sigma =1$.

Based on (4), the error system (3) can be rewritten as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{e}\left(t\right)=\overline{A}\left(t\right)e\left(t\right)+\overline{B}G(e\left(t\right),\tilde{w}\left(t\right)),t\ne t_k,t\ge t_0,\hfill \\ e\left(t\right)=\aleph e\left(t^{-}\right),t=t_k,k\in {\mathbb{N}}^{+}.\hfill \end{array}\right.\end{array}$$

(5)

Remark 1. 

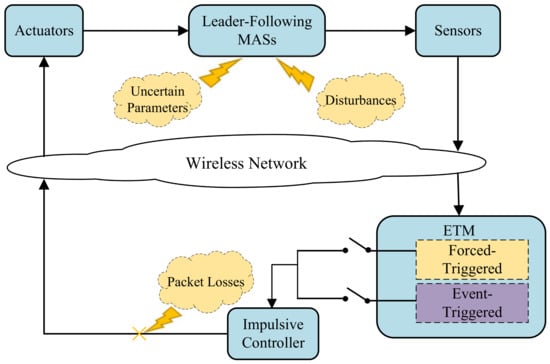
Figure 1 describes the operation of an MAS and its control loop. The system utilizes sensors to collect state information and determine if the triggering conditions have been met. If the conditions are met, the sensor information is transmitted wirelessly to the impulsive controller, which generates a control signal. This signal is then fed back to the system by the actuator, creating a closed-loop control system that stabilizes the system. Moreover, It is noteworthy that in the event triggering mechanism, only one condition will be satisfied between forced-triggered and event-triggered. However, if packet loss occurs during the transmission of the control signal, the signal received by the system may be invalid, causing the system to become unstable. Therefore, it is crucial to ensure the reliability of the wireless network to prevent packet loss and maintain the stability of the system. To summarize, this paragraph highlights the importance of reliable communication in MASs and its significant impact on system stability.

Figure 1. ETIC loop. The thunder symbols represent the impact of external disturbances, data loss, and other factors on the system.

2.3. Definition, Lemma, and Assumption

Definition 1. 

For any initial states $x_i\left(t_0\right)$ and $x_0\left(t_0\right)$, if there exists a positive number E such that when $t\to +\infty$, the error state can eventually converge to a bounded set:

$$\begin{array}{c}\hfill \mathcal{C}=\left\{\left.e\in {\mathbb{R}}^{Nn}\right|\underset{t\to \infty }{lim\; sup}\left|e\left(t\right)\right|\le E\right\},\end{array}$$

then system (1) can achieve the leader–follower quasi-consensus, and E is called the upper bound of the error. Particularly, if E = 0, system (1) can achieve the leader–follower consensus.

Lemma 1. 

For any positive number r, vectors $u\in {\mathbb{R}}^l$ and $v\in {\mathbb{R}}^d$, a positive definite matrix $X\in {\mathbb{R}}^{d\times d}$ and any matrix $Y\in {\mathbb{R}}^{l\times d}$, there holds:

$$\begin{array}{c}\hfill 2u^{T}Yv\le r{u}^{T}YX{Y}^{T}u+r^{-1}{v}^T{X}^{-1}v.\end{array}$$

Assumption A1. 

There exist two positive numbers ${\epsilon }_1$ and ${\epsilon }_2$ such that the nonlinear function $f:{\mathbb{R}}^n\times {\mathbb{R}}^w\to {\mathbb{R}}^m$ in system (1) satisfies the following inequality:

$$\begin{array}{c}\hfill {\left|f(x_1,y_1)-f(x_2,y_2)\right|}^2\le {\epsilon }_1^2{\left|x_1-x_2\right|}^2+{\epsilon }_2^2{\left|y_1-y_2\right|}^2.\end{array}$$

Assumption A2. 

The communication topology of system (1) has a directed spanning tree with the leader agent as the root node.

Assumption A3. 

The external perturbations $w_i\left(t\right)$ and $w_0\left(t\right)$ in system (1) are measurable and bounded. Moreover, assume that ${sup}_{t\ge t_0}\left|\tilde{w}\left(t\right)\right|\le \varpi <+\infty$.

3. Main Results

3.1. Design of Event-Triggered Mechanism

Before giving sufficient conditions for system (1) to achieve the quasi-consensus, a novel ETM is designed as follows:

$$\left\{\begin{array}{cc}\hfill t_k& =min\left\{t_{k-1}+\theta ,t_k^{*}\right\},k\in \mathbb{N},\hfill \\ \hfill t_k^{*}& =inf\left\{t>t_{k-1}|V\left(e\left(t\right)\right)\ge {\beta }_1{e}^{-\gamma (t-t_{k-1})}V\left(e\left(t_{k-1}\right)\right)+{\beta }_2{\left|\tilde{w}\right|}_{[t_0,t]}^2\right\},\hfill \end{array}\right.$$

(6)

where $\theta >0$ is a parameter to be designed, which represents the maximum triggering interval. $\gamma ,{\beta }_1,{\beta }_2>0$ are pre-specified parameters. $V:{\mathbb{R}}^{Nn}\to {\mathbb{R}}^{+}$ is a Lyapunov function, where ${\lambda }_1{\left|e\left(t\right)\right|}^2\le V\left(e\left(t\right)\right)\le {\lambda }_2{\left|e\left(t\right)\right|}^2$ with ${\lambda }_2\ge {\lambda }_1>0$.

Remark 2. 

From ETM (6), it has been shown that the designed ETM has two operation modes: triggering at $t_{k-1}+\theta$ or $t_k^{*}$. The first case uses the maximum trigger interval and generates impulses called forced impulses in this paper. The second case generates impulses called triggered impulses. In the following, sufficient conditions to realize the quasi-consensus as well as consensus are first proved, and exclusion of Zeno behavior is given afterward.

Remark 3. 

In fact, the forced-triggered sequence is involved in the ETM discussed in the article, but there is no upper bound restriction on the maximum triggering interval $\theta$. In other words, the maximum triggering interval is arbitrary and can be designed to suit specific system requirements. The only constraint that needs to be satisfied is that the forced-triggered sequence must have a minimum time interval of $\theta >0$ between consecutive impulses. To provide more detail, a forced impulse sequence is a specific pattern of impulses that are applied to a system under control. These impulses can be generated by the control system to impose a desired behavior or can be applied externally to achieve a particular objective. In the context of the ETM discussed in the article, the forced impulse sequence is used to maintain the stability of the system by triggering impulses at specific instants. In summary, the forced impulse sequence is an essential aspect of the ETM, and its design is flexible, provided that the minimum time interval of $\theta >0$ between consecutive impulses is satisfied. This allows for greater control over the system’s behavior while maintaining its stability.

3.2. Sufficient Condition for Quasi-Consensus

Theorem 1. 

Let Assumptions 1–3 be satisfied, if there exist positive numbers ${\epsilon }_1,{\epsilon }_2$, positive scales ${\mu }_1,\theta ,\chi ,d$, a positive definite matrix $P\in {\mathbb{R}}^{n\times n}$, and positive definite diagonal matrices $R_1,R_2\in {\mathbb{R}}^{n\times n}$ such that

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}\begin{array}{c}\Phi \end{array}& \overline{P}\overline{M}& \overline{P}\overline{B}\\ *& -{\overline{R}}_1& 0\\ *& *& -{\overline{R}}_2\end{array}\right]<0,\end{array}$$

(7)

$$\begin{array}{c}\hfill \left[\begin{array}{cc}-exp\left(-d\right)\overline{P}& I+b_{k}H\otimes I\\ *& -\overline{P}\end{array}\right]<0,\end{array}$$

(8)

$$\begin{array}{c}\hfill ({\mu }_1+1)\theta <(1-\chi )d,\end{array}$$

(9)

where $\Phi ={\overline{A}}^T\overline{P}+\overline{P}\overline{A}+{\overline{Q}}^T{\overline{R}}_1\overline{Q}+{\epsilon }_1^2{\lambda }_{max}\left({\overline{R}}_2\right)-{\mu }_1\overline{P}$. Then system (1) can achieve the leader–follower quasi-consensus under the ETM (6) and the impulsive controller (2). Moreover, the upper boundedness can be estimated as

$$\begin{array}{c}\hfill E=\varpi \sqrt{\frac{{\mu }_2}{{\lambda }_{min}\left(\overline{P}\right)}}.\end{array}$$

Proof. 

Based on the Lyapunov function

$$V\left(e\left(t\right)\right)=e^T\left(t\right)\overline{P}e\left(t\right),$$

derivative along system (5) yields when $t\in [t_{k-1},t_k)$

$$\begin{array}{cc}\hfill D& {}^{+}V\left(e\left(t\right)\right)={\dot{e}}^T\left(t\right)\overline{P}e\left(t\right)+e\left(t\right)\overline{P}\dot{e}\left(t\right)\hfill \\ \hfill & =\left(e^T\left(t\right){\overline{A}}^T\left(t\right)+G^T(t,e\left(t\right),\tilde{w}\left(t\right)){\overline{B}}^T\right)\overline{P}e\left(t\right)+e\left(t\right)\overline{P}\left(\overline{A}\left(t\right)e\left(t\right)+\overline{B}G(e\left(t\right),\tilde{w}\left(t\right))\right),\hfill \end{array}$$

(10)

and it can be observed that $F^T\left(t\right)F\left(t\right)\le I$. Moreover, taking into account Lemma 1 and Assumption 1 leads to the following:

$$\begin{array}{cc}\hfill e^T\left(t\right){\overline{A}}^T\left(t\right)\overline{P}e\left(t\right)& +e\left(t\right)\overline{P}\overline{A}\left(t\right)e\left(t\right)=e^T\left(t\right){\overline{A}}^T\overline{P}e\left(t\right)+e^T\left(t\right){\overline{Q}}^T{\overline{F}}^T\left(t\right){\overline{M}}^T\overline{P}e\left(t\right)\hfill \\ \hfill & +e^T\left(t\right)\overline{P}\overline{A}e\left(t\right)+e^T\left(t\right)\overline{P}\overline{M}\overline{F}\left(t\right)\overline{Q}e\left(t\right)\hfill \\ \hfill & \le e^T\left(t\right)\left({\overline{A}}^T\overline{P}+\overline{P}\overline{A}+\overline{P}\overline{M}{\overline{R}}_1^{-1}{\overline{M}}^T\overline{P}+{\overline{Q}}^T{\overline{F}}^T\left(t\right){\overline{R}}_1\overline{F}\left(t\right)\overline{Q}\right)e\left(t\right)\hfill \\ \hfill & \le e^T\left(t\right)\left({\overline{A}}^T\overline{P}+\overline{P}\overline{A}+\overline{P}\overline{M}{\overline{R}}_1^{-1}{\overline{M}}^T\overline{P}+{\overline{Q}}^T{\overline{R}}_1\overline{Q}\right)e\left(t\right),\hfill \end{array}$$

(11)

and

$$\begin{array}{cc}\hfill & G^T(t,e\left(t\right),\tilde{w}\left(t\right)){\overline{B}}^T\overline{P}e\left(t\right)+e\left(t\right)\overline{P}\overline{B}G(e\left(t\right),\tilde{w}\left(t\right))\hfill \\ \hfill & \le e^T\left(t\right)\overline{P}\overline{B}{\overline{R}}_2^{-1}{\overline{B}}^T\overline{P}e\left(t\right)+G^T(e\left(t\right),\tilde{w}\left(t\right)){\overline{R}}_{2}G(e\left(t\right),\tilde{w}\left(t\right))\hfill \\ \hfill & \le e^T\left(t\right)\left(\overline{P}\overline{B}{\overline{R}}_2^{-1}{\overline{B}}^T\overline{P}+{\epsilon }_1^2{\lambda }_{max}\left({\overline{R}}_2\right)\right)e\left(t\right)+{\epsilon }_2^2{\lambda }_{max}\left({\overline{R}}_2\right){\left|\tilde{w}\right|}_{[t_0,t]}^2.\hfill \end{array}$$

(12)

Inequalities (10) can be rewritten using (11) and (12) as

$$\begin{array}{cc}\hfill D^{+}V\left(e\left(t\right)\right)& \le e^T\left(t\right)({\overline{A}}^T\overline{P}+\overline{P}\overline{A}+\overline{P}\overline{M}{\overline{R}}_1^{-1}{\overline{M}}^T\overline{P}+{\overline{Q}}^T{\overline{R}}_1\overline{Q}+\hfill \\ \hfill & \overline{P}\overline{B}{\overline{R}}_2^{-1}{\overline{B}}^T\overline{P}+{\epsilon }_1^2{\lambda }_{max}\left({\overline{R}}_2\right))e\left(t\right)+{\epsilon }_2^2{\lambda }_{max}\left({\overline{R}}_2\right){\left|\tilde{w}\right|}_{[t_0,t]}^2,\hfill \end{array}$$

and the following inequality can be obtained by employing (7)

$$\begin{array}{c}\hfill D^{+}V\left(e\left(t\right)\right)\le {\mu }_{1}V\left(e\left(t\right)\right)+{\mu }_2{\left|\tilde{w}\right|}_{[t_0,t]}^2,\end{array}$$

(13)

where ${\mu }_2={\epsilon }_2^2{\lambda }_{max}\left(R_2\right)$. According to (13), it can be known that for $t\in [t_{k-1},t_k)$ whenever $V\left(e\left(t\right)\right)\ge {\mu }_2{\left|\tilde{w}\right|}_{[t_0,t]}^2$

$$\begin{array}{c}\hfill D^{+}V\left(e\left(t\right)\right)\le cV\left(e\left(t\right)\right),\end{array}$$

(14)

where $c={\mu }_1+1$. On the other hand, when $t=t_k$, using (8) to obtain

$$\begin{array}{cc}\hfill V\left(e\left(t_k\right)\right)& =e^T\left(t_k^{-}\right){(I+b_{k}H\otimes I)}^T\left(t\right)\overline{P}(I+b_{k}H\otimes I)e\left(t_k^{-}\right),\hfill \\ \hfill & <exp\left(-d\right)V\left(e\left(t_k^{-}\right)\right).\hfill \end{array}$$

Let us assume that $V\left(e\left(t_0\right)\right)>{\mu }_2{\left|\tilde{w}\left(t_0\right)\right|}^2$. If $V\left(e\left(t_0\right)\right)\le {\mu }_2{\left|\tilde{w}\left(t_0\right)\right|}^2$, define $t_0:=t_0^{\prime }$, where $t_0^{\prime }<+\infty$ is an instant such that $V\left(e\left(t_0^{\prime }\right)\right)>{\mu }_2{\left|\tilde{w}\left(t_0^{\prime }\right)\right|}^2$. If $t_0^{\prime }$ does not exist or $t_0^{\prime }=+\infty$, then for any $t\ge t_0$, $V\left(e\left(t\right)\right)\le {\mu }_2|\tilde{w}{\left|[t_0,t]\right|}^2\le {\mu }_2{\varpi }^2$ always holds. As a result, the system (1) can achieve leader–follower quasi-consensus. Define $t_1^{\prime }=inf\{t\ge t_0:V\left(e\left(t\right)\right)\le {\mu }_2|\tilde{w}{|}_{[t_0,t]}^2\}$, that is, $V\left(e\left(t\right)\right)\ge {\mu }_2{\left|\tilde{w}\right|}_{[t_0,t]}^2$ in the interval $[t_0,t_1^{\prime })$. The following two cases are discussed further.

Case 1:

No event occurs in the interval $[t_0,t_1^{\prime })$. For any $t\in [t_0,t_1^{\prime })$, from (14), we have

$$\begin{array}{c}\hfill V\left(e\left(t\right)\right)\le e^{c(t-t_0)}V\left(e\left(t_0\right)\right).\end{array}$$

Case 2:

There are $N(t_1^{\prime },t_0)$ events in the interval $[t_0,t_1^{\prime })$, and the impulsive sequence is assumed to be denoted by $\left\{t_k\right\},k\in \{1,2,\dots ,N(t_1^{\prime },t_0)\}$. When $t\in [t_0,t_1)$, we have $V\left(e\left(t\right)\right)\le e^{c(t-t_0)}V\left(e\left(t_0\right)\right)$. When it comes to $t=t_1$, considering the possible influence of packet loss, from (4) we can obtain

$$\begin{array}{c}\hfill V\left(e\left(t_1\right)\right)\le e^{-\sigma \left(t_1\right)d+c(t_1-t_0)}V\left(e\left(t_0\right)\right).\end{array}$$

Analogously, when $t\in [t_1,t_2)$ we can obtain $V\left(e\left(t\right)\right)\le e^{-\sigma \left(t_1\right)d+c(t-t_0)}V\left(e\left(t_0\right)\right)$, and the following inequality holds at instant $t=t_2$

$$\begin{array}{c}\hfill V\left(e\left(t_2\right)\right)<e^{-(\sigma \left(t_1\right)+\sigma \left(t_2\right))d+c(t_2-t_0)}V\left(e\left(t_0\right)\right).\end{array}$$

When $t\in [t_0,t_1^{\prime })$, it can be obtained by iteration:

$$\begin{array}{cc}\hfill V\left(e\right(t\left)\right)& \le exp\left(-d\sum _{k=1}^{N(t,t_0)}\sigma \left(t_k\right)+c(t-t_0)\right)V\left(e\left(t_0\right)\right)\hfill \\ \hfill & \le e^{-(1-\chi )N(t,t_0)d+c(t-t_0)}V\left(e\left(t_0\right)\right).\hfill \end{array}$$

Since any $t\in [t_0,t_1^{\prime })$, one has ${\sum }_{k=1}^{N(t,t_0)}\sigma \left(t_k\right)=N_l(t,t_0)=(1-\chi )N(t,t_0)$. Moreover, for impulsive sequence $\left\{t_k\right\}$, $k\in \{1,2,\dots ,N(t_1^{\prime },t_0)\}$, the inequality $t-t_0\le \theta (N(t_0,t)+1)$ always holds. Hence, for any $t\in [t_0,t_1^{\prime })$, we have

$$\begin{array}{c}\hfill V\left(e\left(t\right)\right)\le exp(\eta N(t,t_0)+c\theta )V\left(e\left(t_0\right)\right),\end{array}$$

(15)

where $\eta =(\chi -1)d+c\theta <0$. If $t_1^{\prime }=+\infty$, (15) holds for all $t\in [t_0,+\infty )$. Otherwise, divide $(t_1^{\prime },+\infty )$ into multiple intervals: $(t_1^{\prime },+\infty )={\cup }_{l=1}^L[(t_l^{\prime },s_l)\cup [s_l,t_{l+1}^{\prime }]]$ (if $L<+\infty$, let $t_{L+1}^{\prime }:=+\infty$). Hence, when $t\in (t_l^{\prime },s_l)$, we have $V\left(e\left(t\right)\right)\le {\mu }_2{\left|\tilde{w}\right|}_{[t_0,t]}^2$ and when $t\in [s_l,t_{l+1}]$, one has $V\left(e\left(t\right)\right)\ge {\mu }_2{\left|\tilde{w}\right|}_{[t_0,t]}^2$, i.e., (15) holds. Therefore, for any $t\ge t_0$, the following inequality holds:

$$\begin{array}{c}\hfill V\left(e\left(t\right)\right)\le exp(\eta N(t,t_0)+c\theta )V\left(e\left(t_0\right)\right)+{\mu }_2{\left|\tilde{w}\right|}_{[t_0,t]}^2,\end{array}$$

(16)

and as $t\to +\infty$, we can obtain that

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim\; sup}\left|V\left(e\right(t\left)\right)\right|={\mu }_2{\varpi }^2,\end{array}$$

which indicates that

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim\; sup}\left|e\left(t\right)\right|=\varpi \sqrt{\frac{{\mu }_2}{{\lambda }_{min}\left(\overline{P}\right)}}:=E.\end{array}$$

(17)

Therefore, system (1) can achieve the leader–follower quasi-consensus under the ETM (6) and the impulsive controller (2), and the upper boundedness of the error is $E=\varpi \sqrt{{\mu }_2{\lambda }_{min}^{-1}\left(\overline{P}\right)}$.

□

Remark 4. 

Based on (9), it can be verified that $\theta <d(1-\chi ){({\mu }_1+1)}^{-1}$ and $\chi <1-({\mu }_1+1)\theta d^{-1}$. In other words, the maximum triggering interval θ is related to the packet loss rate χ, impulsive strength d and system continuous characteristic ${\mu }_1$. Specifically: (1) A higher packet loss rate leads to more frequent triggering, as the existence of packet loss can cause the desired control to disappear. To ensure the stability of system (3), more impulses are needed at this time. (2) Increasing the impulsive strength d will lead a decrease in the trigger frequency. (3) A larger value of ${\mu }_1$ results in higher triggering frequency (more impulsive control).

3.3. Exclusion of Zeno Behavior

Excluding Zeno behavior is essential, as it can invalidate the theoretical analysis (such as the existence of solutions) and result in excessive waste of communication and computer resources [50]. For instance, Zeno behavior can cause the system to become unstable, as it may result in the accumulation of control impulses in a short interval, leading to system oscillations and even instability; Secondly, Zeno behavior can lead to high control frequency, which can cause wear and tear on mechanical systems, such as actuators, sensors, and other components, leading to increased maintenance requirements.

Theorem 2. 

The ETM (6) does not exist Zeno behavior whenever

$$\begin{array}{c}\hfill \gamma \theta <ln\left({\lambda }_1{\beta }_1\right)-ln\left({\lambda }_2\right).\end{array}$$

Proof. 

Assume that ETM (6) generates the impulsive sequence $\{t_k,k\in {\mathbb{N}}^{+}\}$. Based on the characteristics of ETM (6), the following three cases are discussed:

Case 1:

The impulses corresponding to $\{t_k,k\in {\mathbb{N}}^{+}\}$ are all forced impulses. Since $t_k-t_{k-1}\equiv \theta >0$, Zeno behavior can be excluded naturally.

Case 2:

The impulses corresponding to $\{t_k,k\in {\mathbb{N}}^{+}\}$ are all triggered impulses. It follows from (13) that for $t\in [t_{k-1},t_k),k\in {\mathbb{N}}^{+}$

$$\begin{array}{c}\hfill D^{+}V\left(e\left(t\right)\right)\le {\mu }_{1}V\left(e\left(t\right)\right)+{\mu }_2{\left|\tilde{w}\right|}_{[t_0,t_k]}^2,\end{array}$$

(18)

multiplying both sides of (18) by $e^{-{\mu }_1(t-t_{k-1})}$, we can obtain

$$\begin{array}{c}\hfill D^{+}V\left(e\left(t\right)\right)e^{-{\mu }_1(t-t_{k-1})}\le {\mu }_{1}V\left(e\left(t\right)\right)e^{-{\mu }_1(t-t_{k-1})}+{\mu }_2{\left|\tilde{w}\right|}_{[t_0,t_k]}^2{e}^{-{\mu }_1(t-t_{k-1})},\end{array}$$

integrating which over $t_{k-1}$ to t, we can obtain

$$V\left(e\left(t\right)\right)e^{-{\mu }_1(t-t_{k-1})}{|}_{t_{k-1}}^t\le -\frac{{\mu }_2}{{\mu }_1}{\left|\tilde{w}\right|}_{[t_0,t_k]}^2{e}^{-{\mu }_1(t-t_{k-1})}{|}_{t_{k-1}}^t,$$

i.e.,

$$V\left(e\left(t\right)\right)\le V\left(e\left(t_{k-1}\right)\right)e^{{\mu }_1(t-t_{k-1})}+\frac{{\mu }_2}{{\mu }_1}{\left|\tilde{w}\right|}_{[t_0,t_k]}^2\left(e^{{\mu }_1(t-t_{k-1})}-1\right).$$

(19)

From event-triggered mechanism (6), when $t=t_k$, we have

$$\begin{array}{cc}\hfill V\left(e\left(t_k\right)\right)& ={\beta }_1{e}^{-\gamma (t_k-t_{k-1})}V\left(e\left(t_{k-1}\right)\right)+{\beta }_2{\left|\tilde{w}\right|}_{[t_0,t_k]}^2,\hfill \end{array}$$

(20)

based on (6), (19) and (20), we can obtain

$$\begin{array}{cc}\hfill & {\lambda }_1{\beta }_1{e}^{-\gamma (t_k-t_{k-1})}{\left|\left(e\left(t_{k-1}\right)\right)\right|}^2+{\beta }_2{\left|\tilde{w}\right|}_{[t_0,t_k]}^2\hfill \\ \hfill & \le {\lambda }_2|\left(e\left(t_{k-1}\right)\right){|}^2{e}^{{\mu }_1(t_k-t_{k-1})}+\frac{{\mu }_2}{{\mu }_1}{\left|\tilde{w}\right|}_{[t_0,t_k]}^2\left(e^{{\mu }_1(t_k-t_{k-1})}-1\right),\hfill \end{array}$$

i.e.,

$$\begin{array}{cc}\hfill & \frac{{\lambda }_1}{{\lambda }_2}{\beta }_1{e}^{-\gamma (t_k-t_{k-1})}{\left|\left(e\left(t_{k-1}\right)\right)\right|}^2+\frac{{\beta }_2}{{\lambda }_2}{\left|\tilde{w}\right|}_{[t_0,t_k]}^2\hfill \\ \hfill & \le |\left(e\left(t_{k-1}\right)\right){|}^2{e}^{{\mu }_1(t_k-t_{k-1})}+\frac{{\mu }_2}{{\lambda }_2{\mu }_1}{\left|\tilde{w}\right|}_{[t_0,t_k]}^2\left(e^{{\mu }_1(t_k-t_{k-1})}-1\right),\hfill \end{array}$$

subtracting $|\left(e\left(t_{k-1}\right)\right){|}^2$ from both sides leads

$$\begin{array}{cc}\hfill & \left(\frac{{\lambda }_1}{{\lambda }_2}{\beta }_1{e}^{-\gamma (t_k-t_{k-1})}-1\right){\left|\left(e\left(t_{k-1}\right)\right)\right|}^2+\frac{{\beta }_2}{{\lambda }_2}{\left|\tilde{w}\right|}_{[t_0,t_k]}^2\hfill \\ \hfill & \le |\left(e\left(t_{k-1}\right)\right){|}^2\left(e^{{\mu }_1(t_k-t_{k-1})}-1\right)+\frac{{\mu }_2}{{\lambda }_2{\mu }_1}{\left|\tilde{w}\right|}_{[t_0,t_k]}^2\left(e^{{\mu }_1(t_k-t_{k-1})}-1\right),\hfill \end{array}$$

then we have further inequality:

$$\begin{array}{cc}\hfill \left(\right(\frac{{\lambda }_1}{{\lambda }_2}{\beta }_1& e^{-\gamma (t_k-t_{k-1})}-1)\vee \frac{{\beta }_2}{{\lambda }_2})\left(|\left(e\left(t_{k-1}\right)\right){|}^2+{\left|\tilde{w}\right|}_{[t_0,t_k]}^2\right)\hfill \\ \hfill & \le \left(e^{{\mu }_1(t_k-t_{k-1})}-1\right)\left(1\wedge \frac{{\mu }_2}{{\lambda }_2{\mu }_1}\right)\left(|\left(e\left(t_{k-1}\right)\right){|}^2+{\left|\tilde{w}\right|}_{[t_0,t_k]}^2\right).\hfill \end{array}$$

Given that ${\lambda }_1{{\lambda }_2}^{-1}{\beta }_1{e}^{-\gamma \theta }-1>0$, we can deduce that $\gamma \theta <ln\left({\lambda }_1{\beta }_1\right)-ln\left({\lambda }_2\right)$, in this case, we can further derive that

$$\begin{array}{cc}\hfill (\frac{{\lambda }_1}{{\lambda }_2}{\beta }_1& e^{-\gamma \theta }-1)\vee \frac{{\beta }_2}{{\lambda }_2}\le (e^{{\mu }_1(t_k-t_{k-1})}-1)\left(1\wedge \frac{{\mu }_2}{{\lambda }_2{\mu }_1}\right),\hfill \end{array}$$

from which, we can obtain

$$\begin{array}{c}\hfill t_k-t_{k-1}\ge {{\mu }_1}^{-1}ln\left(\frac{\left({{\lambda }_2}^{-1}{\lambda }_1{\beta }_1{e}^{-\gamma \theta }-1\right)\vee {{\lambda }_2}^{-1}{\beta }_2}{1\wedge {\left({\lambda }_2{\mu }_1\right)}^{-1}{\mu }_2}\right)>0.\end{array}$$

Thus, Zeno behavior is avoided in Case 2.

Case 3:

In this case, $\{t_k,k\in {\mathbb{N}}^{+}\}$ consists of both forced and triggered impulsive instants. Let us assume that there exists Zeno behavior within the interval $[S_1,S_2)$, with $S_2$ being the accumulation point such that $S_2-S_1<\theta$. Consequently, there is no more than one forced impulse within this interval, which we define as the instant $t^{*}$. Given that Zeno behavior is present in the interval $[S_1,S_2)$, all other triggering instants in $(t^{*},S_2)$ are considered triggered impulsive instants. Nevertheless, no Zeno behavior is observed in Case 2, which contradicts the existence of $S_2$. As a result, Zeno behavior can also be ruled out in Case 3. To sum up, if $\gamma \theta <ln\left({\lambda }_1{\beta }_1\right)-ln\left({\lambda }_2\right)$, the ETM (6) does not exist Zeno behavior.

□

Remark 5. 

For the Lyapunov function $V\left(e\left(t\right)\right)=e^T\left(t\right)\overline{P}e\left(t\right)$ in the ETM (6), Zeno behavior can be excluded when $\gamma \theta <ln\left({\lambda }_{min}\left(\overline{P}\right){\beta }_1\right)-ln\left({\lambda }_{max}\left(\overline{P}\right)\right)$. When $\overline{P}$ is an appropriate sized unit matrix, i.e., $V\left(e\left(t\right)\right)=e^T\left(t\right)e\left(t\right)$, substituting which into (18) shows that Zeno behavior can be excluded when $\gamma \theta <ln{\beta }_1$.

Remark 6. 

The ETM constructed in [39,40,41] requires that ${\beta }_2\ge ϵ>0$, but this assumption is not required in our paper. Therefore, the proposed ETM (6) is more general.

4. A Numerical Simulation Example

To verify the proposed results in this paper, we provide a numerical simulation example. We consider the leader–follower MAS with a leader and four followers, whose dynamics are described in system (1), and the communication topology is shown in Figure 2. Based on Figure 2, we obtain the following:

$$\begin{array}{c}\hfill L=\left[\begin{array}{cccc}1& 0& 0& -1\\ 0& 1& -1& 0\\ 0& -1& 2& -1\\ -1& 0& -1& 2\end{array}\right],\end{array}\begin{array}{c}\hfill C=\left[\begin{array}{cccc}1& & & \\ & 0& & \\ & & 0& \\ & & & 0\end{array}\right],\end{array}$$

and we further have

$$\begin{array}{c}\hfill H=\left[\begin{array}{cccc}2& 0& 0& -1\\ 0& 1& -1& 0\\ 0& -1& 2& -1\\ -1& 0& -1& 2\end{array}\right].\end{array}$$

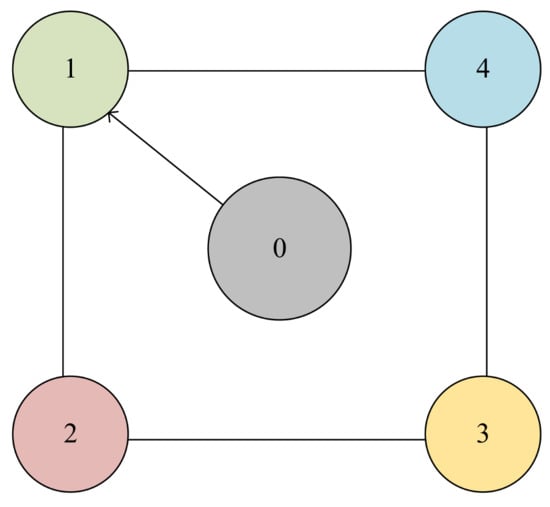
Figure 2. The communication topology.

Let $f(x_j\left(t\right),w_j\left(t\right))=0.5tanh\left(x_j\left(t\right)\right)+0.5tanh\left(w_j\left(t\right)\right)$, for any $j\in \left\{0,1,2,3,4\right\}$. Then, ${\epsilon }_1={\epsilon }_2=0.5$. Moreover, we set $M=0.2I,Q=I$, $F\left(t\right)=\mathrm{diag}\{0.2,-0.5,0.4\}sin\left(t\right)$ and

$$\begin{array}{c}\hfill A=\left[\begin{array}{ccc}-0.87& 0& 0\\ 1& -1& 1\\ 0& -0.62& 0\end{array}\right]\end{array},\begin{array}{c}\hfill B=\left[\begin{array}{ccc}0.21& 0& 0\\ 0& 0.12& 0\\ 0& 0.82& 0.25\end{array}\right].\end{array}$$

Choose the parameters: $b_k\equiv -0.35$, ${\mu }_1=0.4$, which can be solved by linear matrix inequalities as $R_1=3.1404I,R_2=1.5067I,d=0.043$, and

$$\begin{array}{c}\hfill P=\left[\begin{array}{ccc}2.4025& 0.7230& -0.0817\\ 0.7230& 1.4901& -0.8628\\ -0.0817& -0.8628& 2.9833\end{array}\right],\end{array}$$

which indicates that ${\lambda }_1={\lambda }_{min}\left(P\right)=0.408$. In addition, the external disturbance and initial parameters are randomly selected as follows: $t_0=0$,

$$\begin{array}{c}\hfill \\ \hfill & =\left[\begin{array}{ccccc}0.2& 0.5& 0.6& 0.3& 0.1\\ -0.1& 0.4& -0.2& 0.5& -0.2\\ 0.3& 0.4& 0.3& 0.1& 0.3\end{array}\right]\times 0.5cos\left(t\right),\hfill \end{array}$$

and

$$\begin{array}{c}\hfill \\ \hfill & =\left[\begin{array}{ccccc}4.5& 5.5& -1.5& -0.2& 1\\ -3.2& 2.5& -1& -2& -1.5\\ 2& -2.5& 0.5& 2.8& 0.2\end{array}\right].\hfill \end{array}$$

By some calculations, $\varpi =0.4$ and the upper error bound $E=\varpi \sqrt{{\mu }_2{{\lambda }^{-1}}_{min}\left(\overline{P}\right)}=0.6016$.

Assume the system control packet loss rate $\chi =0.5$, and if the parameters of ETM is satisfied for the following conditions: ${\beta }_1=2.6$, $\gamma =1$ and $\theta =0.02<min\{{\gamma }^{-1}ln\left({\lambda }_1{\beta }_1\right),d(1-\chi ){({\mu }_1+1)}^{-1}\}=min\left\{0.059,0.0246\right\}$, Theorems 1 and 2 are applicable. The leader–follower quasi-consensus of system (1) can be realized under the impulsive controller (2) as well as Zeno behavior can be excluded.

Furthermore, by selecting the parameters ${\beta }_2=0.8$ and $\gamma =1$ in the ETM (6), it can be shown in Figure 3a,b that the trajectory of the error state variable and the triggered situations of event impulsive instants can be obtained, respectively. To examine the impact of different control packet loss rates on the triggering instants. Let $\chi =0.01$ and $\chi =0.1$, the triggering instants in these cases are shown in Figure 4a,b, respectively. Through observation, we can see that as the control packet loss rate $\chi$ increases, the number of triggering instants also increases accordingly, while more forced impulse instants are required when the packet loss rate is low.

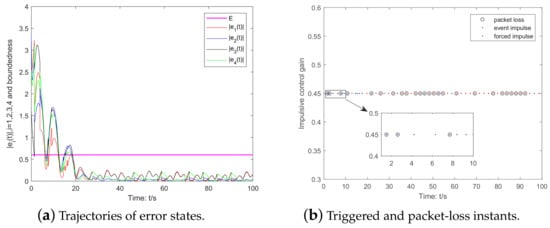
Figure 3. Trajectories of error states and distribution of triggered instants.

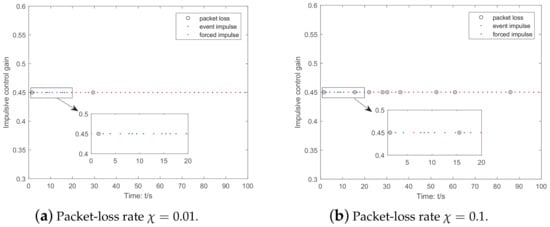
Figure 4. Triggered and packet-loss instants under different packet-loss rates.

Finally, in order to demonstrate the advantages of the proposed method in this paper compared to existing methods, by adjusting the code based on other studies to match the corresponding ETM and parameters, the comparative simulation results obtained are shown in Figure 5. We can conclude that under the premise that both schemes can achieve leader-following quasi-consensus for MAS, the number of triggered impulses in this paper is fewer from observation of Figure 5b,d. In other words, the control cost of the method proposed in this paper is lower, and for the method proposed in this paper, ${\beta }_2$ is a tunable parameter, which allows for a wider range of choices. Moreover, measured error $x\left(t\right)-x\left(t_k\right)$ is not required in this manuscript, making the designed ETM easier to construct and implement. Therefore, the research findings have broader applications.

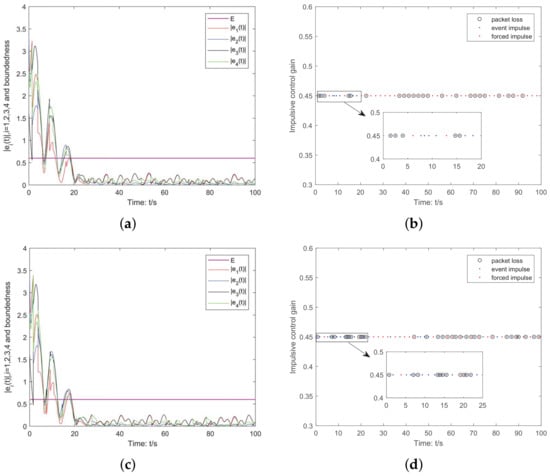
Figure 5. The simulation results of this study with those of existing research. (a) Trajectories of error states for ETM (6). (b) Distribution of triggered instant in this paper. (c) Trajectories of error states for ETM from one existing study. (d) Distribution of triggered instant in one existing study.

5. Conclusions

This paper studies the leader-following quasi-consensus of MASs with packet loss using ETIC. The linear matrix inequality and packet loss rate are used to derive sufficient conditions for the quasi-consensus. Compared to previous works, the strategy in this paper has several advantages, including a wider range of parameter selection due to adjustable triggering parameters, easier construction and implementation due to not requiring the measurement of error, and applicability to different control systems through the use of Lyapunov functions. The results reveal that the packet loss rate is related to factors such as control gain and maximum triggering interval. Therefore, designing different ETM parameters based on the packet loss rate is of great significance. Finally, we provide a numerical simulation example to verify the obtained results. Since time delay is ubiquitous, future works will consider the impact of time delay on system consensus.