Multi-Objective Optimization for Controlling the Dynamics of the Diabetic Population
Abstract
1. Introduction
- (1)
- A multi-objective mathematical model for controlling the dynamics of the diabetic population is introduced;
- (2)
- A discretization of the proposed model is realized based on the trapezoidal rule and the Euler–Cauchy method (we demonstrate that this error is bounded);
- (3)
- Two multi-objective optimizers are used to solve the proposed multi-objective model;
- (4)
- As a first postprocessing phase, FFT convolution is used to clean the noise from the control;
- (5)
- As a second post-processing phase, two soft clustering methods are used to structure the Pareto front.
2. Related Works
3. Methodology Overview
4. Multi-Objective Diabetic Control Model
4.1. Single-Goal Control Model
4.2. Multi-Objective Control Model
- (a)
- The primary methods used were gradient descent algorithms [29];
- (b)
- Dual methods, which exploit convexity to calculate the gradient of the dual max–min, were also used [30];
- (c)
- The substitution and the decomposition Lagrange methods that introduce a copy variable to decompose the initial problem to two sub-problems [31]: the first one does not have any constraints (for which we can use gradient descent, among others) and the second one does not have objective functions (for which we can use back tracking methods, among others).
4.3. Pareto Controls Characterization
5. Smart Algorithms
5.1. Swarm Intelligence Optimizers
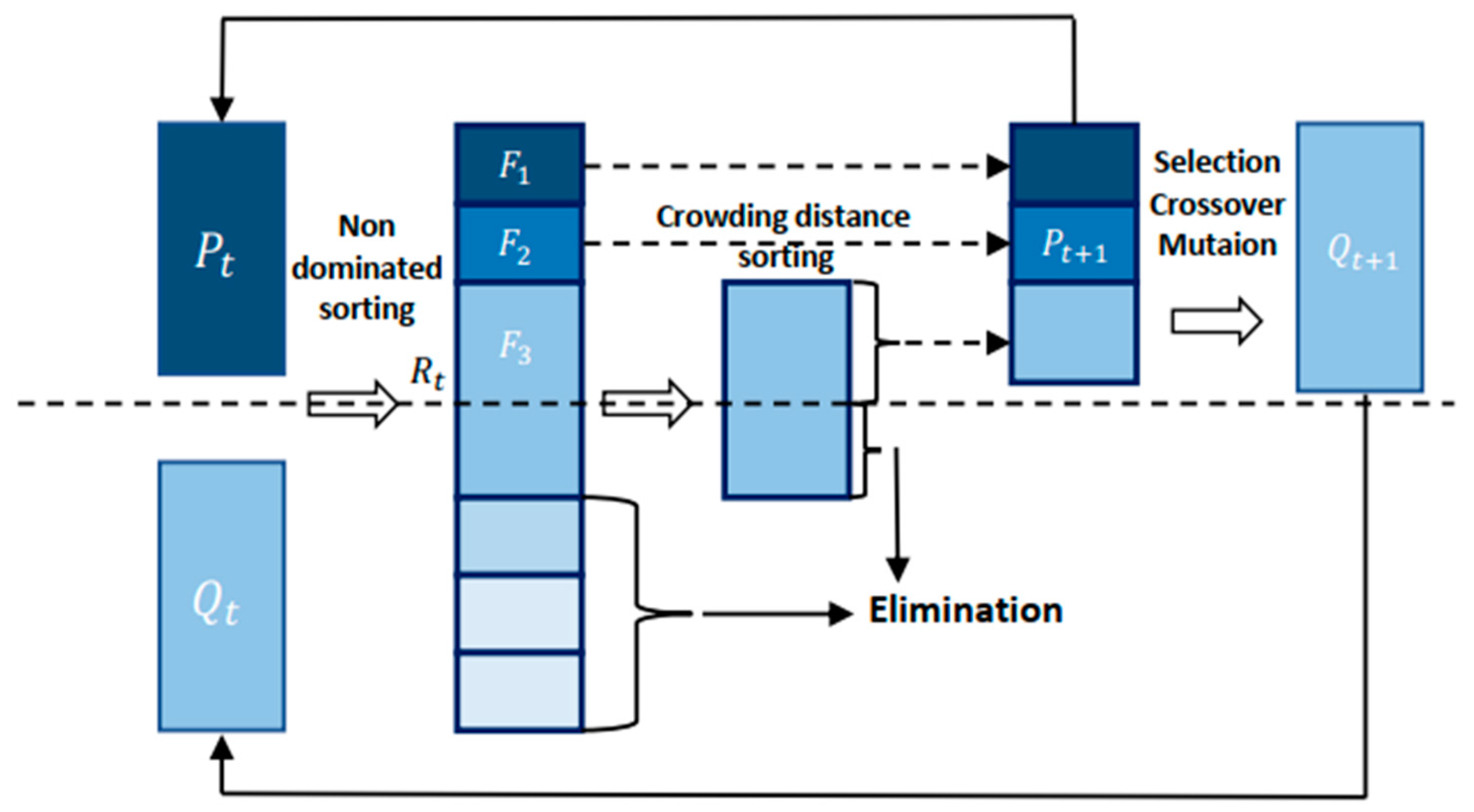
5.1.1. Non-Dominated Sorting Genetic Algorithm II
5.1.2. Multi-Objective Firefly Algorithm
- (a)
- Fireflies have the ability to attract other fireflies, no matter which sex they are.
- (b)
- The attraction is positively proportional to the brightness. If all the fireflies have nearly the same degree of brightness, then one or more fireflies are moving.
- (c)
- The luminosity of a firefly is calculated from the cost function.
5.2. Soft Clustering Algorithms
5.2.1. Gaussian Mixture Model (GMM)
5.2.2. Fuzzy C-Means (FCM)
6. Experimental Results and Discussion
6.1. NSGA-II Combined with Soft Clustering Methods
6.2. MOFA Combined with Soft Clustering Methods
- (a)
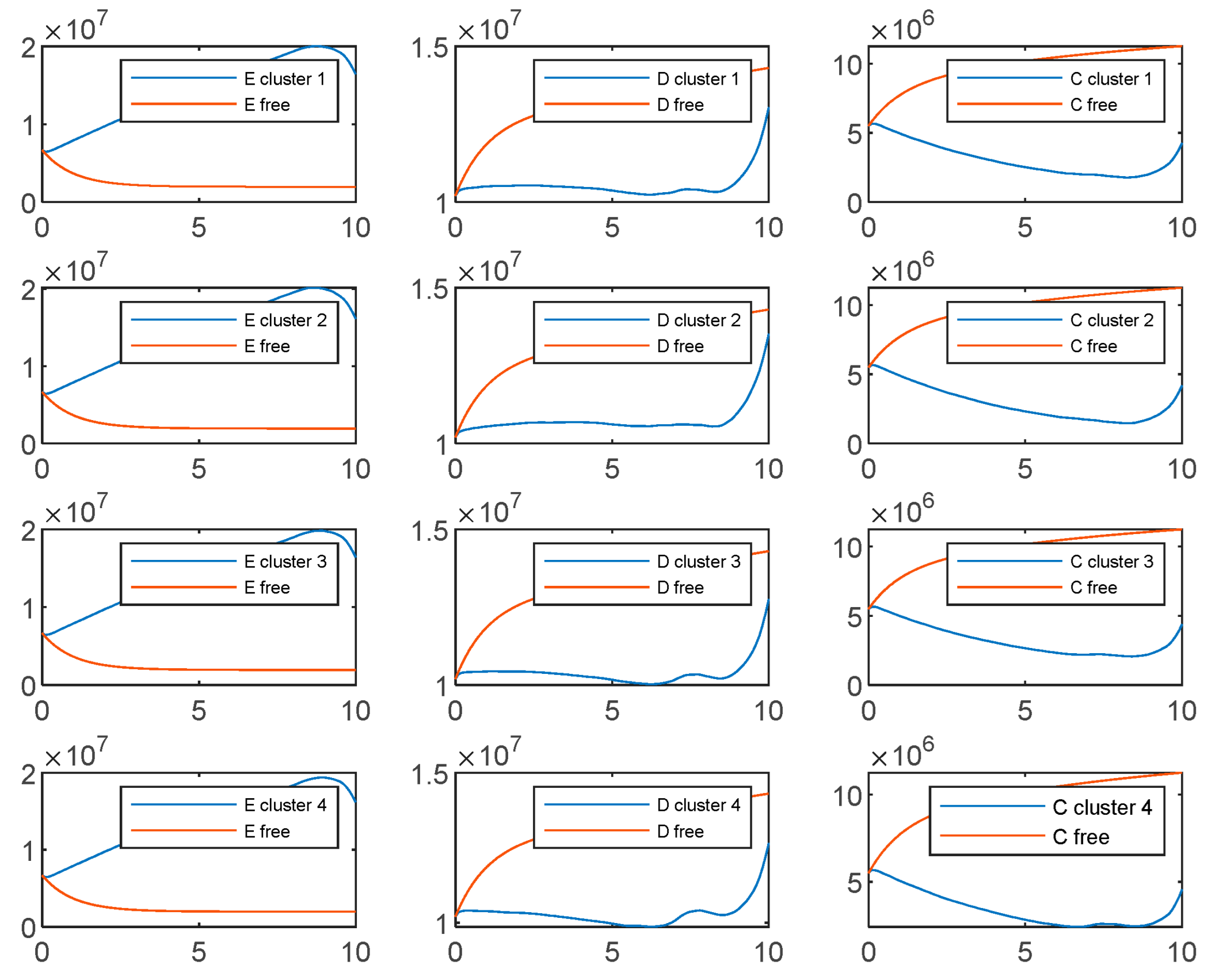
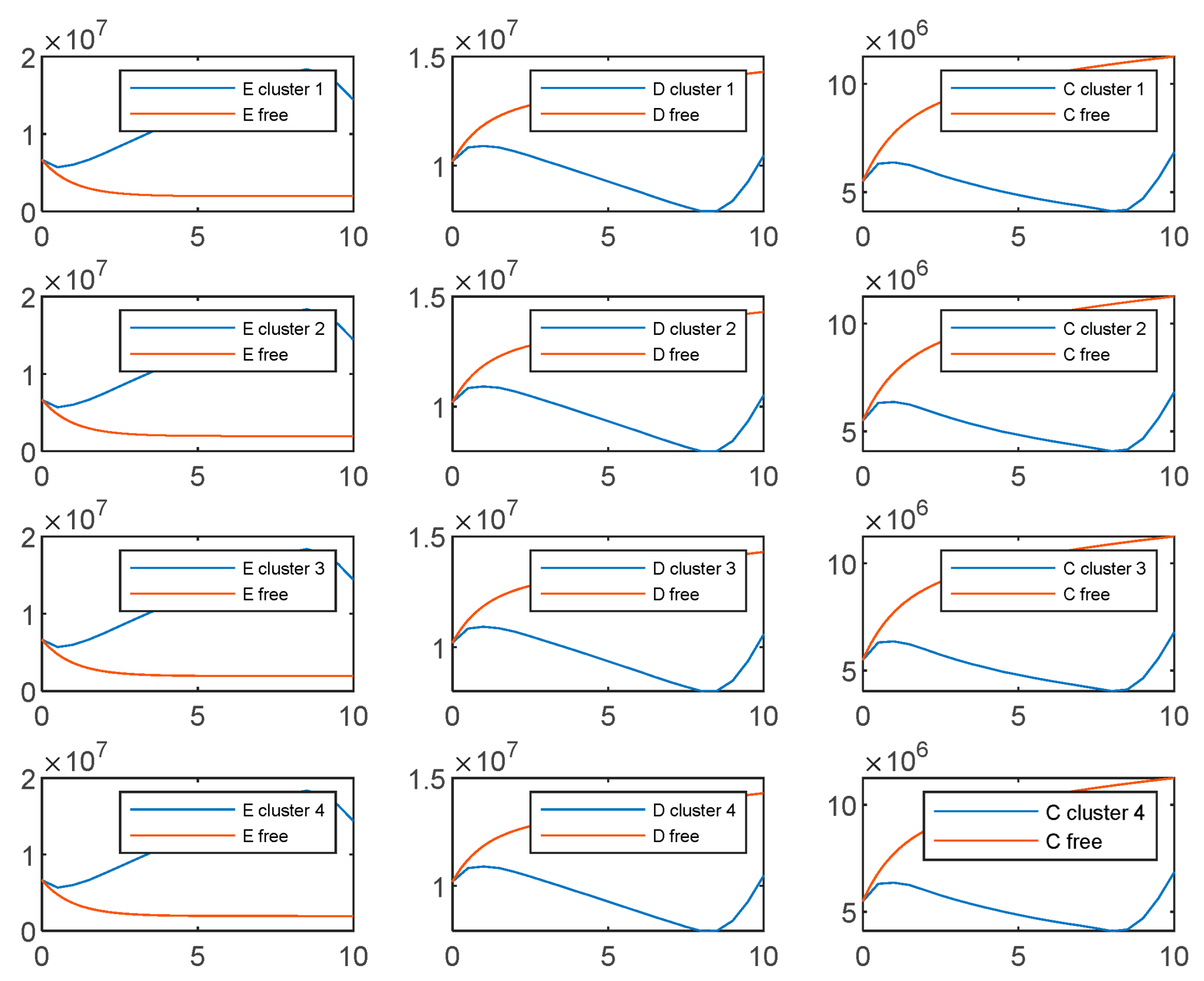
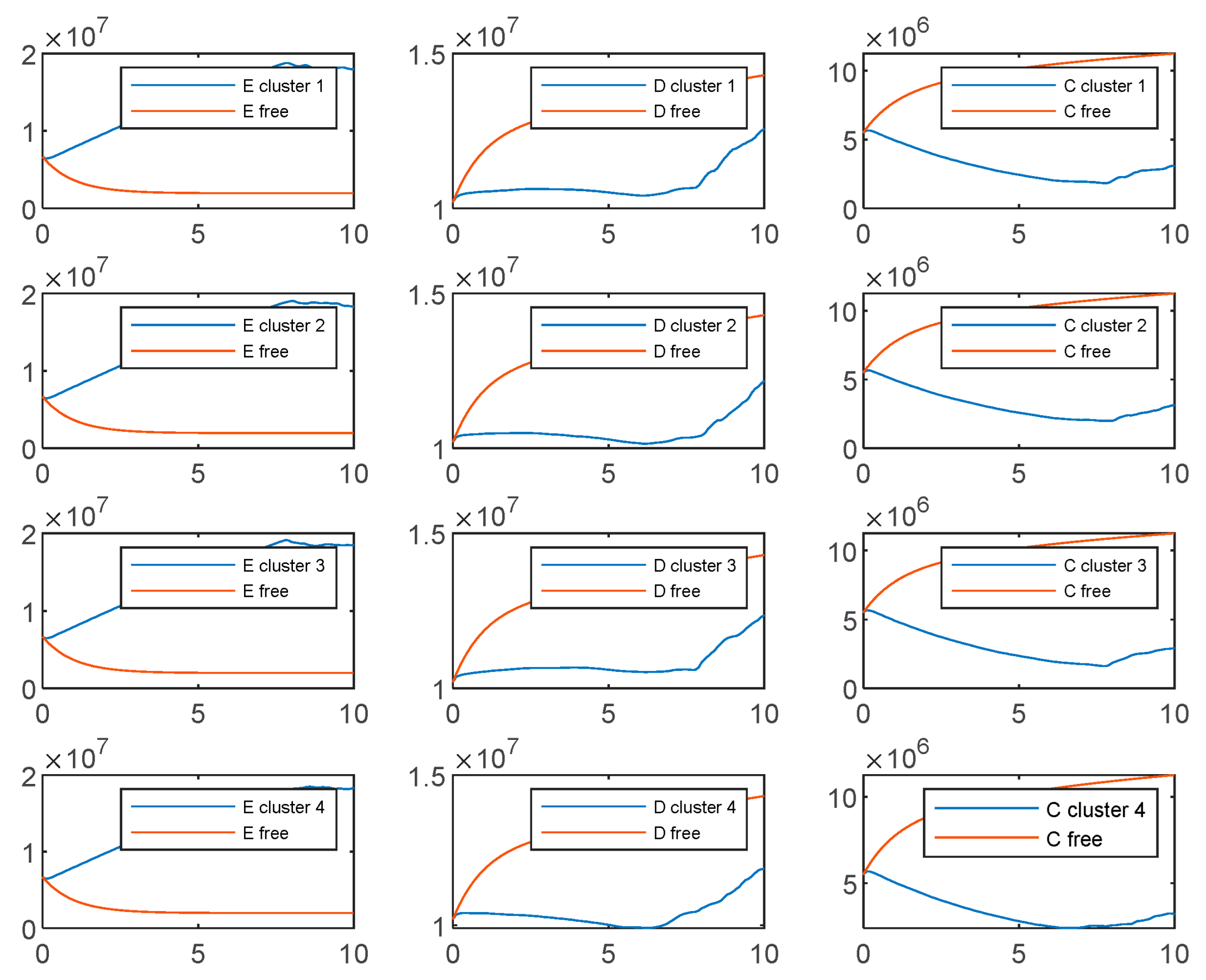
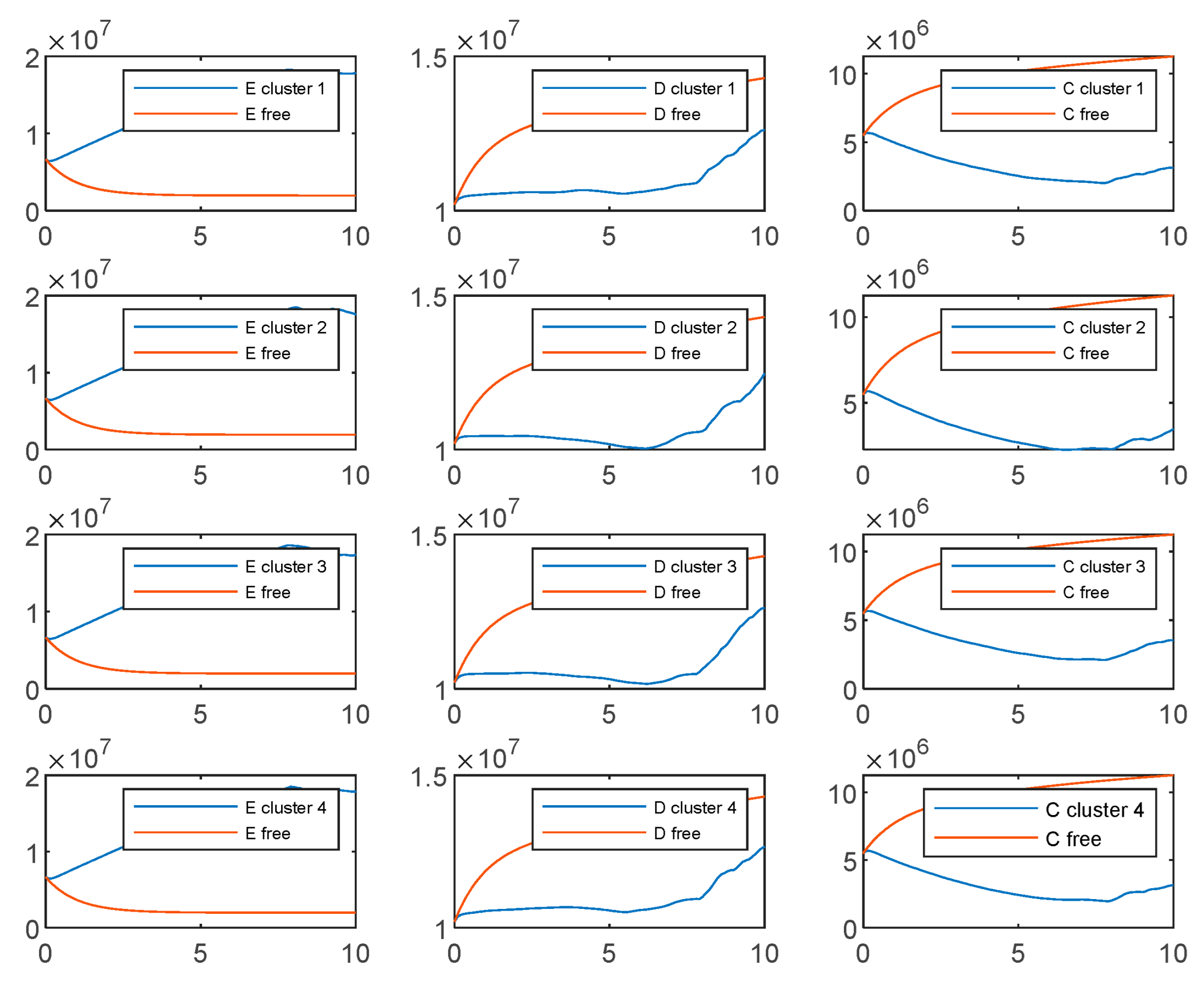
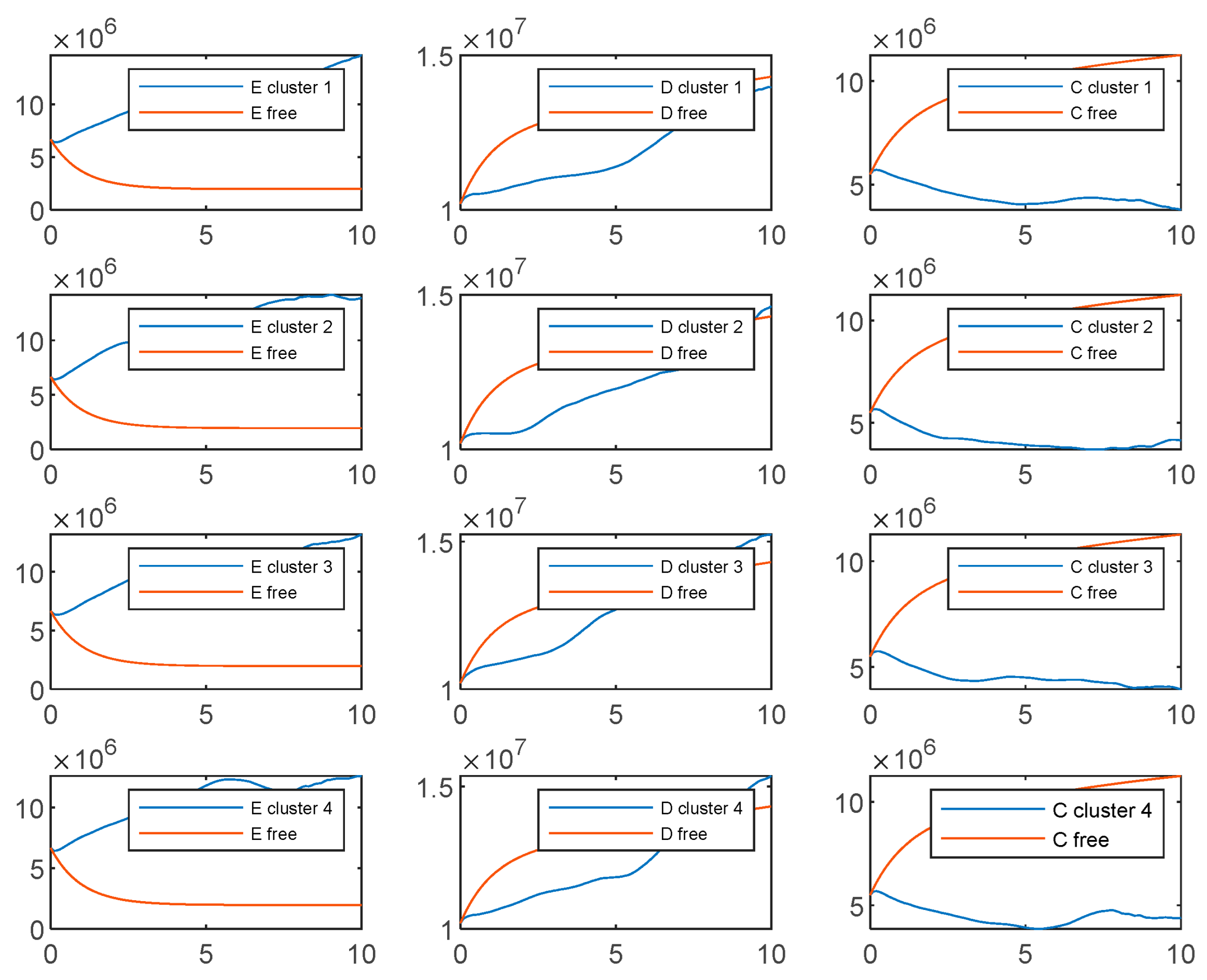
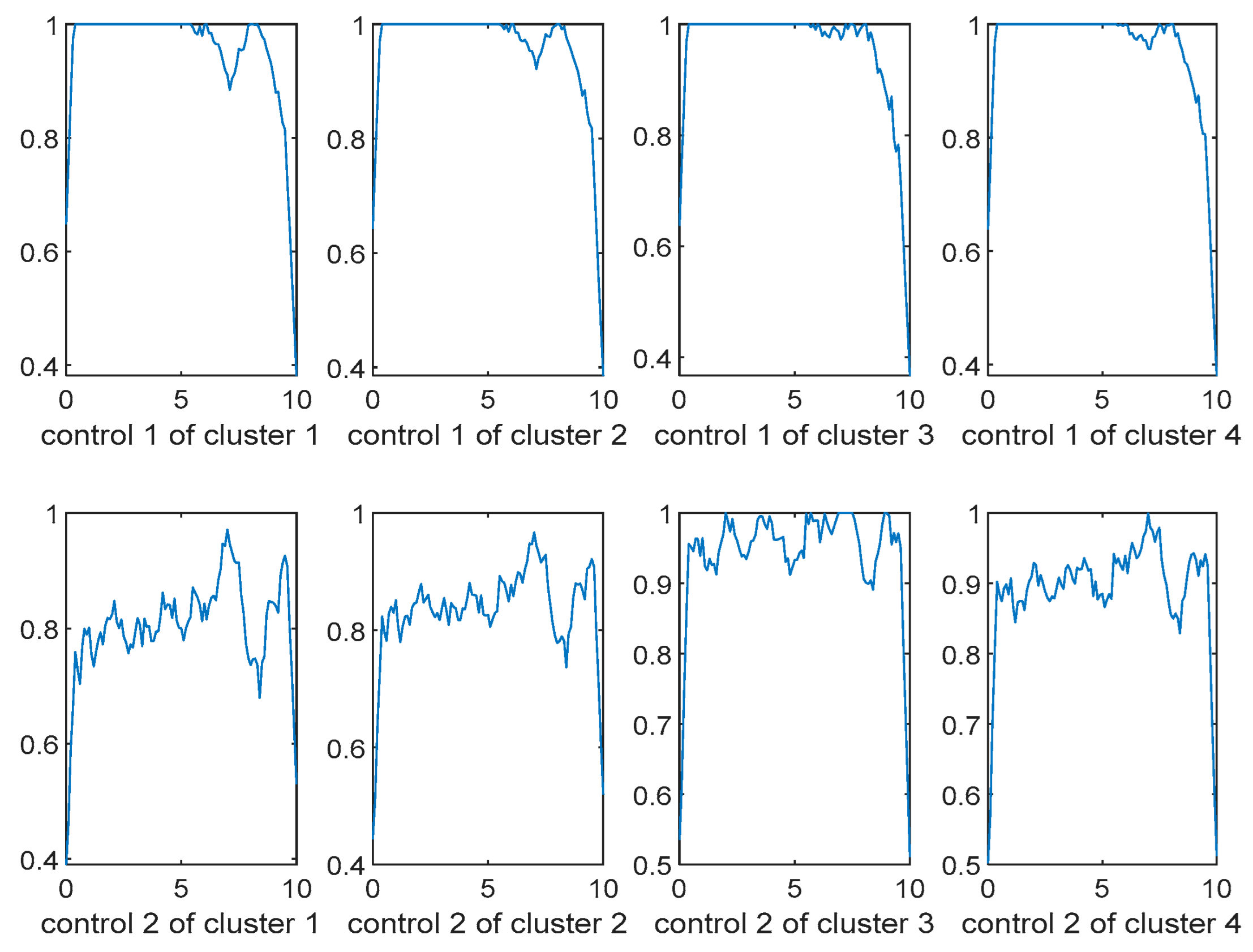
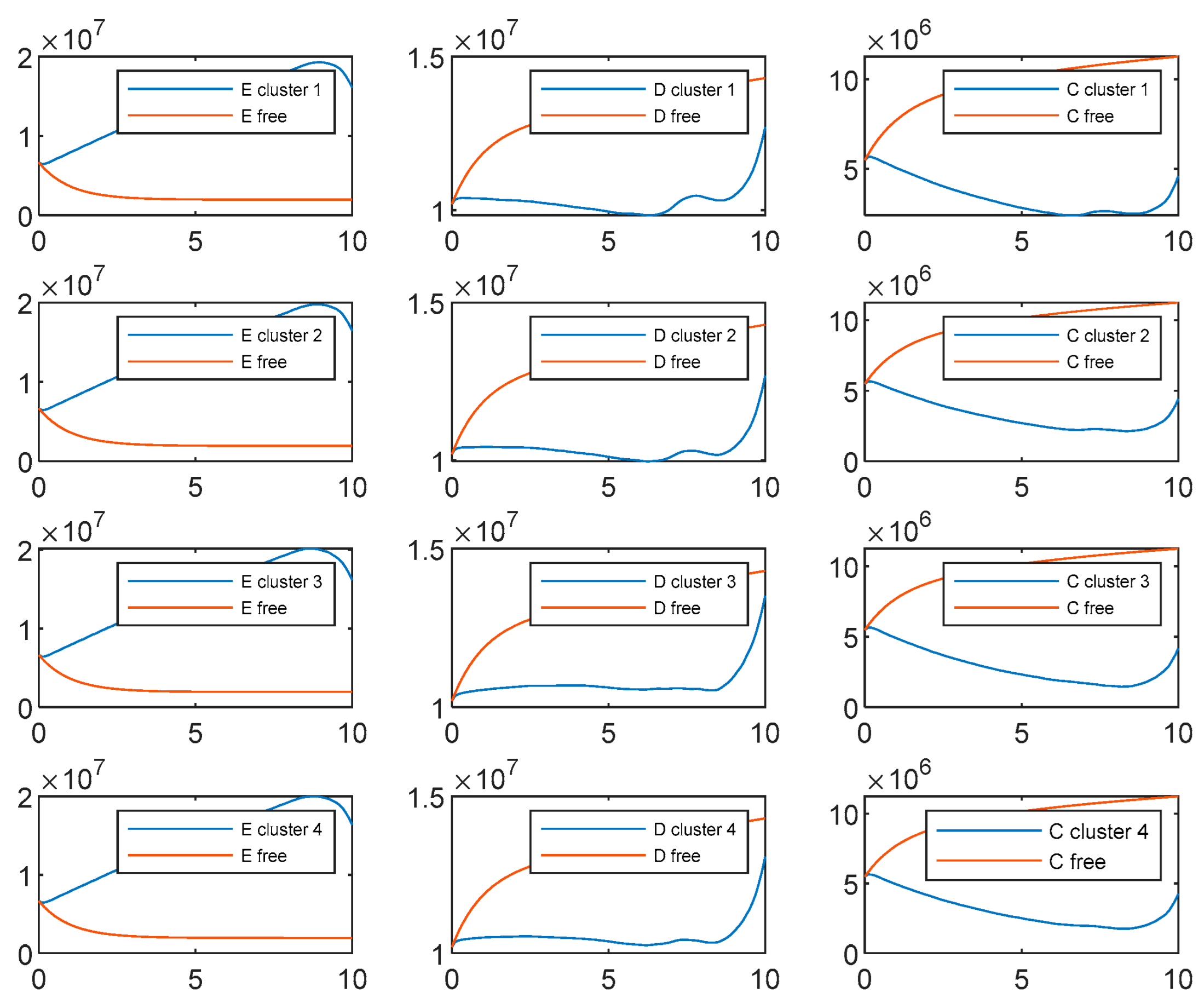
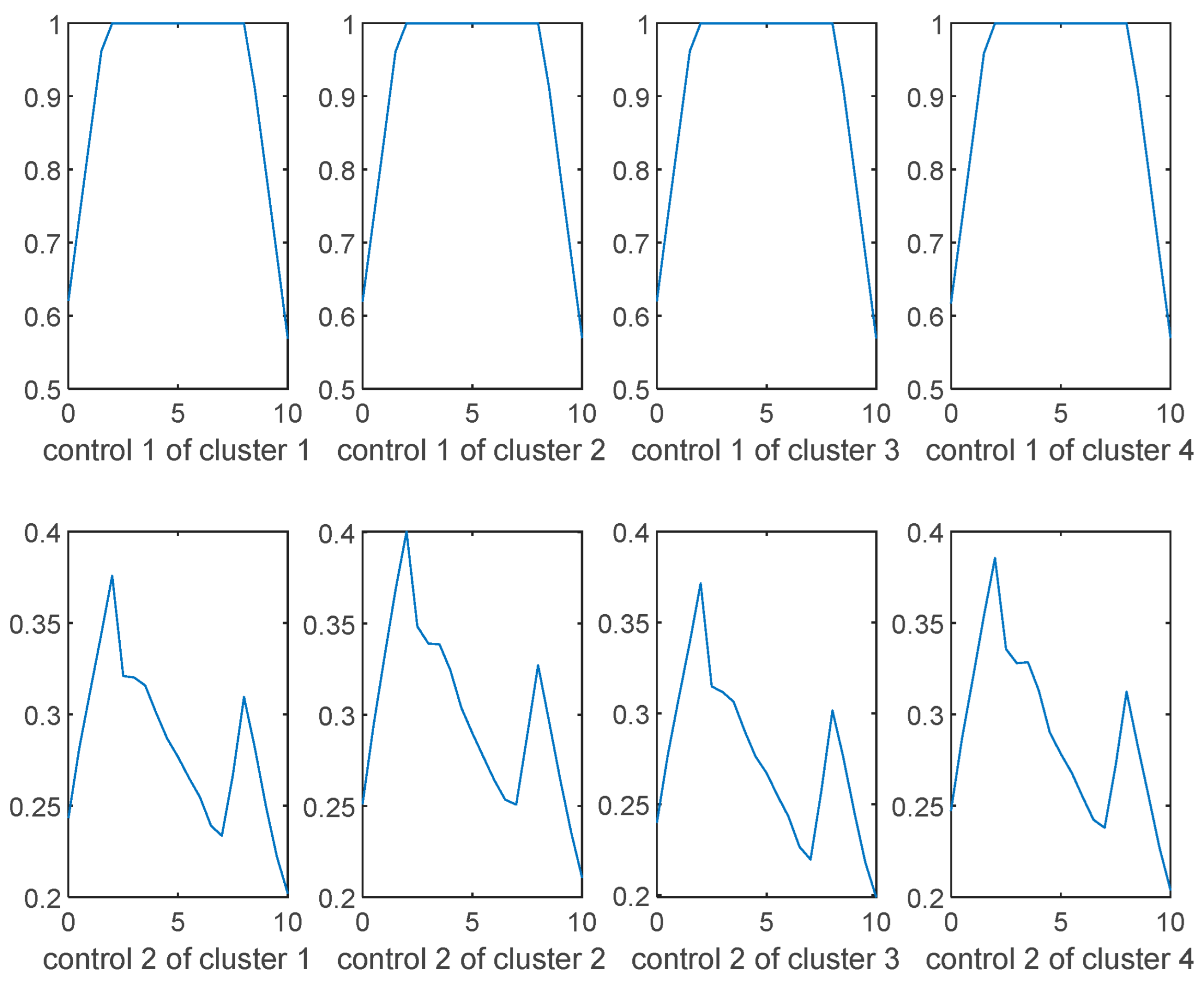
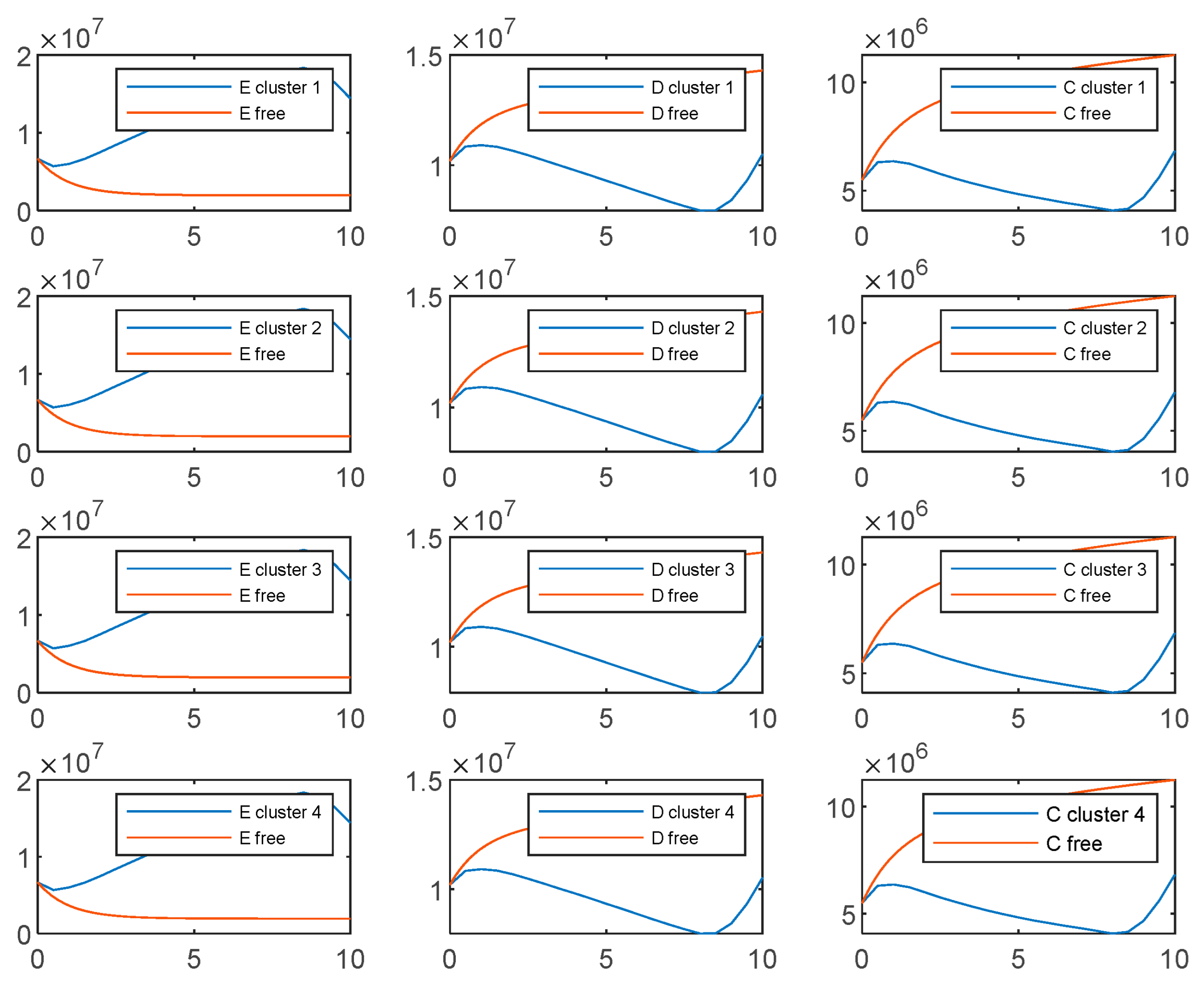
- Considering the experimental results shown in the Figure A1, Figure A2, Figure A3 and Figure A4, we notice that the two soft clustering methods FCM and GMM give approximately the same groups (considering a simple permutation), so we extended the same remarks, conclusions, and recommendations to the other method.
- (b)
- (c)
6.3. Single-Objective vs. Multi-Objective on the Control of the Dynamics of the Diabetic Population Problem (C2D2P)
6.4. Sensitivity of the Proposed System
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A



Appendix B



References
- International Diabetes Federation (IDF). About—Diabetes. Available online: https://idf.org/about-diabetes/facts-figures (accessed on 1 May 2023).
- Abdellatif, E.O.; Karim, E.M.; Hicham, B.; Saliha, C. Intelligent local search for an optimal control of diabetic population dynamics. Math. Model. Comput. Simul. 2022, 14, 1051–1071. [Google Scholar] [CrossRef]
- El Moutaouakil, K.; Ahourag, A.; Chakir, S.; Kabbaj, Z.; Chellack, S.; Cheggour, M.; Baizri, H. Hybrid firefly genetic algorithm and integral fuzzy quadratic programming to an optimal Moroccan diet. Math. Model. Comput. 2023, 10, 338–350. [Google Scholar] [CrossRef]
- Ahourag, A.; El Moutaouakil, K.; Cheggour, M.; Chellak, S.; Baizri, H. Multiobjective optimization to optimal moroccan diet using genetic algorithm. Int. J. Eng. Model. 2023, 36, 67–79. [Google Scholar]
- Ahourag, A.; Chellak, S.; Cheggour, M.; Baizri, H.; Bahri, A. Quadratic programming and triangular numbers ranking to an optimal moroccan diet with minimal glycemic load. Stat. Optim. Inf. Comput. 2023, 11, 85–94. [Google Scholar]
- World Health Organisation. Definition and Diagnosis of Diabetes Mellitus and Intermediate Hyperglycemia; WHO: Geneva, Switzerland, 2016. [Google Scholar]
- IDF Diabetes Atlas, 9th ed.; International Diabetes Federation (IDF): Brussels, Belgium, 2019.
- Kouidere, A.; Khajji, B.; Balatif, O.; Rachik, M. A multi-age mathematical modeling of the dynamics of population diabetics with effect of lifestyle using optimal control. J. Appl. Math. Comput. 2021, 67, 375–403. [Google Scholar] [CrossRef]
- Abdellatif, E.O.; Karim, E.M.; Saliha, C.; Hicham, B. Genetic algorithms for optimal control of a continuous model of a diabetic population. In Proceedings of the 2022 IEEE 3rd International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS), Fez, Morocco, 1–2 December 2022; pp. 1–5. [Google Scholar]
- Li, H.; Peng, R.; Wang, Z. On a diffusive susceptible-infected-susceptible epidemic model with mass action mechanism and birth-death effect: Analysis, simulations, and comparison with other mechanisms. SIAM J. Appl. Math. 2018, 78, 2129–2153. [Google Scholar] [CrossRef]
- Jin, H.Y.; Wang, Z.A. Global stabilization of the full attraction-repulsion keller-segel system. Discret. Contin. Dyn. Syst.—Ser. A 2020, 40, 3509–3527. [Google Scholar] [CrossRef]
- Yuan, M.; Li, Y.; Zhang, L.; Pei, F. Research on intelligent workshop resource scheduling method based on improved NSGA-II algorithm. Robot. Comput. Integr. Manuf. 2021, 71, 102141. [Google Scholar] [CrossRef]
- Ranganathan, S.; Surya Kalavathi, M.; Asir Rajan, C.C. Self-adaptive firefly algorithm based multi-objectives for multi-type FACTS placement. IET Gener. Transm. Distrib. 2016, 10, 2576–2584. [Google Scholar] [CrossRef]
- El Moutaouakil, K.; Yahyaouy, A.; Chellak, S.; Baizri, H. An optimized gradient dynamic-neuro-weighted-fuzzy clustering method: Application in the nutrition field. Int. J. Fuzzy Syst. 2022, 24, 3731–3744. [Google Scholar] [CrossRef]
- Boutayeb, A.; Chetouani, A. A population model of diabetes and pre-diabetes. Int. J. Comput. Math. 2007, 84, 57–66. [Google Scholar] [CrossRef]
- Mahata, A.; Mondal, S.P.; Alam, S.; Chakraborty, A.; De, S.K.; Goswami, A. Mathematical model for diabetes in fuzzy environment with stability analysis. J. Intell. Fuzzy Syst. 2019, 36, 2923–2932. [Google Scholar] [CrossRef]
- Ollerton, R.L. Application of optimal control theory to diabetes mellitus. Int. J. Control 1989, 50, 2503–2522. [Google Scholar] [CrossRef]
- Swan, G.W. An optimal control model of diabetes mellitus. Bull. Math. Biol. 1982, 44, 793–808. [Google Scholar] [CrossRef] [PubMed]
- Makroglou, A.; Karaoustas, I.; Li, J.; Kuang, Y. Delay differential equation models in diabetes modeling. Theor. Biol. Med. Model. 2009. Available online: https://d1wqtxts1xzle7.cloudfront.net/39776544/Delay_differential_equation_models_in_di20151107-11553-9sa4j7-libre.pdf?1446919153=&response-content-disposition=inline%3B+filename%3DDelay_differential_equation_models_in_di.pdf&Expires=1688109253&Signature=gzNPLMm9mZ3KYeZD9wfLLcKorB-7z3XPMW8kUnqEXooVDMVVRyQqbvUD1timDez8PEcjfkgNsLfYgASjLAJ~LP~rY5M7aihIVP5~wu4y5GR29sMBYBgTyszEQSG5g10Gt~LYiWgqbmPcrBXBP7Lcv5rkQkORQzTOxJhWoiRYadd8Hw6kBVlr4mjVPEMHxnQkgp6QEW-qlqF1FUKKG8pxI338xA~bkZDSiDKmGgzvjiEBBcBj3W1LCGQMZh1maPlnmVqaldj8n33dkCEXny5bM-yvEz64JsAJ6my3qC59kctUZR4YwI2rVjKTWhEN4dlD3ogdKkBRNA2bal4vQPpRCA__&Key-Pair-Id=APKAJLOHF5GGSLRBV4ZA (accessed on 1 May 2023).
- Derouich, M.; Boutayeb, A.; Boutayeb, W.; Lamlili, M. Optimal control approach to the dynamics of a population of diabetics. Appl. Math. Sci. 2014, 8, 2773–2782. [Google Scholar] [CrossRef]
- Gumel, A.B.; Shivakumar, P.N.; Sahai, B.M. A mathematical model for the dynamics of HIV-1 during the typical course of infection. Nonlinear Anal. Theory Methods Appl. 2001, 47, 1773–1783. [Google Scholar] [CrossRef]
- Yusuf, T.T. Optimal control of incidence of medical complications in a diabetic patients’ population. FUTA J. Res. Sci. 2015, 11, 180–189. [Google Scholar]
- Permatasari, A.H.; Tjahjana, R.H.; Udjiani, T. Existence and characterization of optimal control in mathematics model of diabetics population. J. Phys. Conf. Ser. 2018, 983, 012069. [Google Scholar] [CrossRef]
- Daud, A.A.M.; Toh, C.Q.; Saidun, S. Development and analysis of a mathematical model for the population dynamics of Diabetes Mellitus during pregnancy. Math. Model. Comput. Simul. 2020, 12, 620–630. [Google Scholar] [CrossRef]
- Kouidere, A.; Balatif, O.; Ferjouchia, H.; Boutayeb, A.; Rachik, M. Optimal control strategy for a discrete time to the dynamics of a population of diabetics with highlighting the impact of living environment. Discret. Dyn. Nat. Soc. 2019, 2019, 6342169. [Google Scholar] [CrossRef]
- Kouidere, A.; Labzai, A.; Ferjouchia, H.; Balatif, O.; Rachik, M. A new mathematical modeling with optimal control strategy for the dynamics of population of diabetics and its complications with effect of behavioral factors. J. Appl. Math. 2020, 2020, 1943410. [Google Scholar] [CrossRef]
- Ahourag, A.; El Moutaouakil, K.; Chellak, S.; Baizri, H.; Cheggour, M. Multi-criteria optimization for optimal nutrition of Moroccan diabetics. In Proceedings of the 2022 International Conference on Intelligent Systems and Computer Vision (ISCV), Fez, Morocco, 18–20 May 2022; pp. 1–6. [Google Scholar]
- El Moutaouakil, K.; Palade, V.; Safouan, S.; Charroud, A. FP-Conv-CM: Fuzzy probabilistic convolution C-means. Mathematics 2023, 11, 1931. [Google Scholar] [CrossRef]
- Bolduc, E.; Knee, G.C.; Gauger, E.M.; Leach, J. Projected gradient descent algorithms for quantum state tomography. npj Quantum Inf. 2017, 3, 44. [Google Scholar] [CrossRef]
- Auslender, A.; Teboulle, M. Lagrangian duality and related multiplier methods for variational inequality problems. SIAM J. Optim. 2000, 10, 1097–1115. [Google Scholar] [CrossRef]
- Föllmer, H.; Kabanov, Y.M. Optional decomposition and Lagrange multipliers. Financ. Stoch. 1997, 2, 69–81. [Google Scholar] [CrossRef]
- Rahman, Q.I.; Schmeisser, G. Characterization of the speed of convergence of the trapezoidal rule. Numer. Math. 1990, 57, 123–138. [Google Scholar] [CrossRef]
- Fleming, W.H.; Rishel, R.W. Deterministic and Stochastic Optimal Control; Springer: New York, NY, USA, 1975. [Google Scholar]
- Frigo, M.; Johnson, S.G. FFTW: An adaptive software architecture for the FFT. In Proceedings of the International Conference on Acoustics, Speech, Signal Processing, Seattle, WA, USA, 15 May 1998; Volume 3, pp. 1381–1384. [Google Scholar]
- Jawad, K.; Mahto, R.; Das, A.; Ahmed, S.U.; Aziz, R.M.; Kumar, P. Novel cuckoo search-based metaheuristic approach for deep learning prediction of depression. Appl. Sci. 2023, 13, 5322. [Google Scholar] [CrossRef]
- Ali, S.; Bhargava, A.; Saxena, A.; Kumar, P. A hybrid marine predator sine cosine algorithm for parameter selection of hybrid active power filter. Mathematics 2023, 11, 598. [Google Scholar] [CrossRef]
- Wang, Y.J.; Wang, G.G.; Tian, F.M.; Gong, D.W.; Pedrycz, W. Solving energy-efficient fuzzy hybrid flow-shop scheduling problem at a variable machine speed using an extended NSGA-II. Eng. Appl. Artif. Intell. 2023, 121, 105977. [Google Scholar] [CrossRef]
- Yazdinejad, A.; Dehghantanha, A.; Parizi, R.M.; Epiphaniou, G. An optimized fuzzy deep learning model for data classification based on NSGA-II. Neurocomputing 2023, 522, 116–128. [Google Scholar] [CrossRef]
- Rafati, N.; Hazbei, M.; Eicker, U. Louver configuration comparison in three Canadian cities utilizing NSGA-II. Build. Environ. 2023, 229, 109939. [Google Scholar] [CrossRef]
- Chen, H.; Feng, Z.; Liu, Y.; Chen, B.; Deng, T.; Qin, Y.; Xu, W. Multiobjective optimization of a 3D laser scanning scheme for engineering structures based on RF-NSGA-II. J. Constr. Eng. Manag. 2023, 149, 04022169. [Google Scholar] [CrossRef]
- Singh, M.K.; Choudhary, A.; Gulia, S.; Verma, A. Multi-objective NSGA-II optimization framework for UAV path planning in an UAV-assisted WSN. J. Supercomput. 2023, 79, 832–866. [Google Scholar] [CrossRef]
- Wang, D.; Wang, G.; Wang, H. Optimal lane change path planning based on the NSGA-II and TOPSIS algorithms. Appl. Sci. 2023, 13, 1149. [Google Scholar] [CrossRef]
- Nan, Y.; Zhang, H.; Zeng, Y.; Zheng, J.; Ge, Y. Faster and accurate green pepper detection using NSGA-II-based pruned YOLOv5l in the field environment. Comput. Electron. Agric. 2023, 205, 107563. [Google Scholar] [CrossRef]
- Li, S.; Zhou, H.; Xu, G. Research on optimal configuration of landscape storage in public buildings based on improved NSGA-II. Sustainability 2023, 15, 1460. [Google Scholar] [CrossRef]
- Wang, Z.; Shen, L.; Li, X.; Gao, L. An improved multi-objective firefly algorithm for energy-efficient hybrid flowshop rescheduling problem. J. Clean. Prod. 2023, 385, 135738. [Google Scholar] [CrossRef]
- Tiwari, A.; Chaturvedi, A. Automatic EEG channel selection for multiclass brain-computer interface classification using multiobjective improved firefly algorithm. Multimed. Tools Appl. 2023, 82, 5405–5433. [Google Scholar] [CrossRef]
- He, Y.; Peng, H.; Deng, C.; Dong, X.; Wu, Z.; Guo, Z. Reference point reconstruction-based firefly algorithm for irregular multi-objective optimization. Appl. Intell. 2023, 53, 962–983. [Google Scholar] [CrossRef]
- Ri, K.W.; Mun, K.H. Firefly algorithm hybridized with genetic algorithm for multi-objective integrated process planning and scheduling. Res. Sq. 2023. [Google Scholar] [CrossRef]
- Ahmadi, S.E.; Kazemi-Razi, S.M.; Marzband, M.; Ikpehai, A.; Abusorrah, A. Multi-objective stochastic techno-economic-environmental optimization of distribution networks with G2V and V2G systems. Electr. Power Syst. Res. 2023, 218, 109195. [Google Scholar] [CrossRef]
- Li, J.; Sun, G.; Wang, A.; Zheng, X.; Chen, Z.; Liang, S.; Liu, Y. Multi-objective sparse synthesis optimization of concentric circular antenna array via hybrid evolutionary computation approach. Expert Syst. Appl. 2023, 231, 120771. [Google Scholar] [CrossRef]
- Srinivasan, B.; Venkatesan, R.; Aljafari, B.; Kotecha, K.; Indragandhi, V.; Vairavasundaram, S. A novel multicriteria optimization technique for VLSI floorplanning based on hybridized firefly and ant colony systems. IEEE Access 2023, 11, 14677–14692. [Google Scholar] [CrossRef]
- Shou, S.; Luo, H.; Wang, X.; Li, Y.; Hu, J.; Su, L. Optimal configuration of power quality control device for new distribution network based on firefly algorithm. In Proceedings of the 2023 Panda Forum on Power and Energy (PandaFPE), Chengdu, China, 27–30 April 2023; pp. 872–876. [Google Scholar]
- Athisayam, A.; Kondal, M. Fault feature selection for the identification of compound gear-bearing faults using firefly algorithm. Int. J. Adv. Manuf. Technol. 2023, 125, 1777–1788. [Google Scholar] [CrossRef]
- El Moutaouakil, K.; Touhafi, A. A new recurrent neural network fuzzy mean square clustering method. In Proceedings of the 2020 5th International Conference on Cloud Computing and Artificial Intelligence: Technologies and Applications (CloudTech), Marrakesh, Morocco, 24–26 November 2020; pp. 1–5. [Google Scholar] [CrossRef]

| Option [12] | Configuration |
|---|---|
| Crossover operator | New_indiv = indiv1 + rand × atio × (indiv2 − indiv1) |
| Crossover ratio | 0.8 |
| Number of iterations | 60 |
| Mutation ratio | adaptive feasible |
| Option [13] | Configuration |
|---|---|
| Maximum number of iterations | 1000 |
| Swarm size | 25 |
| Light absorption coefficient | 1 |
| Attraction coefficient base value | 2 |
| Mutation coefficient | 0.2 |
| Mutation coefficient damping ratio | 0.98 |
| Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | ||
|---|---|---|---|---|---|
| Multi-objective vs. single-objective | u1 | 3% | 4% | 4% | 4% |
| u2 | 14% | 6% | 18% | 11% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Moutaouakil, K.; El Ouissari, A.; Palade, V.; Charroud, A.; Olaru, A.; Baïzri, H.; Chellak, S.; Cheggour, M. Multi-Objective Optimization for Controlling the Dynamics of the Diabetic Population. Mathematics 2023, 11, 2957. https://doi.org/10.3390/math11132957
El Moutaouakil K, El Ouissari A, Palade V, Charroud A, Olaru A, Baïzri H, Chellak S, Cheggour M. Multi-Objective Optimization for Controlling the Dynamics of the Diabetic Population. Mathematics. 2023; 11(13):2957. https://doi.org/10.3390/math11132957
Chicago/Turabian StyleEl Moutaouakil, Karim, Abdellatif El Ouissari, Vasile Palade, Anas Charroud, Adrian Olaru, Hicham Baïzri, Saliha Chellak, and Mouna Cheggour. 2023. "Multi-Objective Optimization for Controlling the Dynamics of the Diabetic Population" Mathematics 11, no. 13: 2957. https://doi.org/10.3390/math11132957
APA StyleEl Moutaouakil, K., El Ouissari, A., Palade, V., Charroud, A., Olaru, A., Baïzri, H., Chellak, S., & Cheggour, M. (2023). Multi-Objective Optimization for Controlling the Dynamics of the Diabetic Population. Mathematics, 11(13), 2957. https://doi.org/10.3390/math11132957








