An Extended-State Observer Based on Smooth Super-Twisting Sliding-Mode Controller for DC-DC Buck Converters
Abstract
1. Introduction
- (1)
- A pair of novel smooth functions is constructed to replace the sign function in conventional STA, and the stability of the optimized SSTA is demonstrated. Two sets of SSTESO are designed to estimate the matched and mismatched disturbance in a DC-DC buck converter system. Compared to the traditional ESO, the SSTESO not only accelerates the convergence of estimation error but also guarantees the accuracy of the disturbance estimate.
- (2)
- A smooth STSMC is proposed by adopting the SSTA to increase the dynamic response speed and further reduce chattering. The proposed SSTESO-based composite SSTSMC scheme is successfully applied to the DC-DC buck converter. Performance comparison experiments among the STSMC, SSTSMC, ESO-based SSTSMC, STESO-based SSTSMC, and SSTESO-based SSTSMC schemes are carried out in simulations that validate the superiority of the proposed control scheme.
2. Conventional STESO-Based STSM Controller Design
2.1. Modeling of a DC-DC Buck Converter
2.2. Conventional STESO-Based STSM Controller
3. SSTESO-Based Smooth STSMC Design
3.1. Design of SSTESO
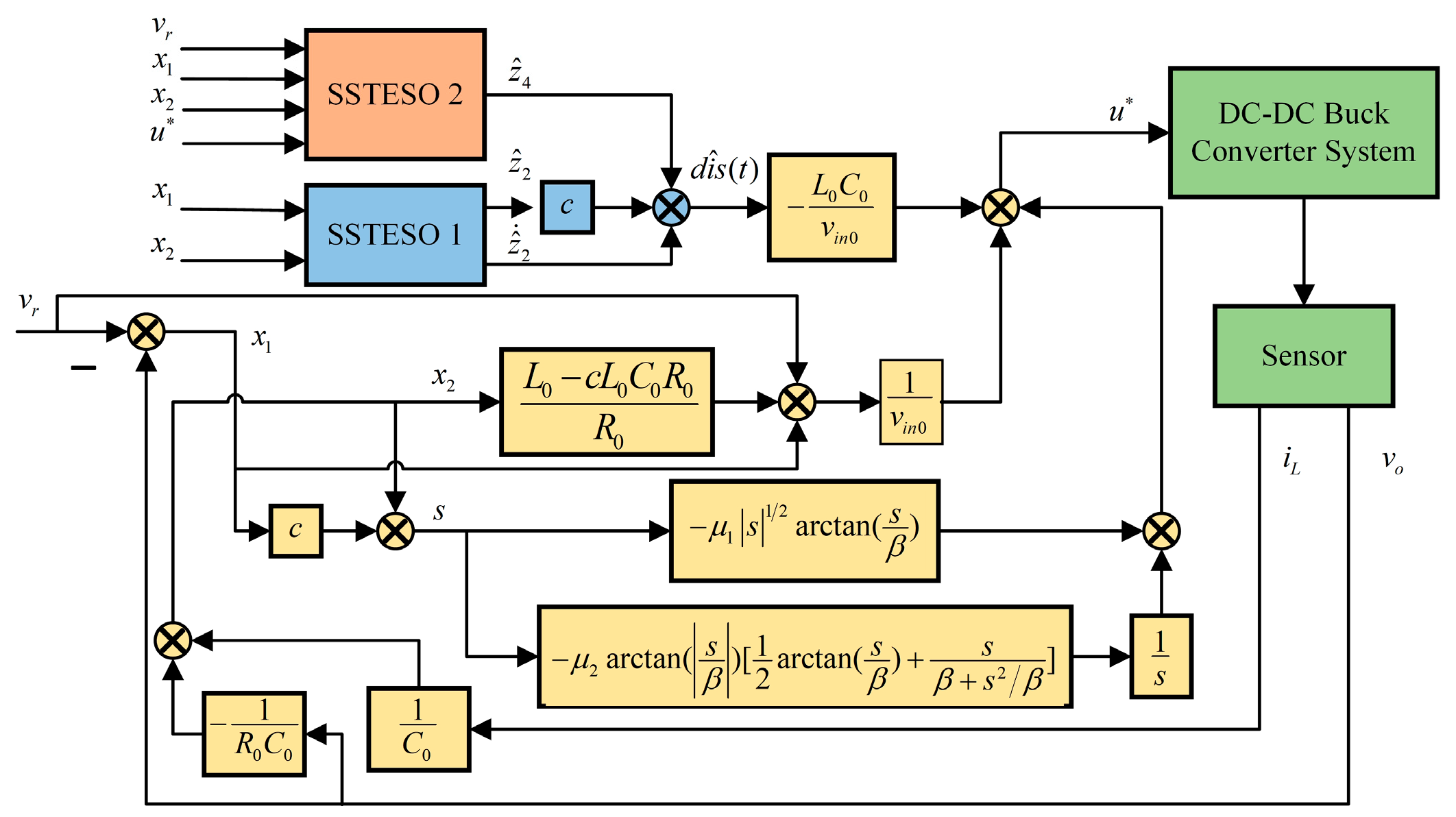
3.2. SSTESO-Based SSTSMC Design
4. Simulation Study
4.1. Controller Comparative Analysis
- (1)
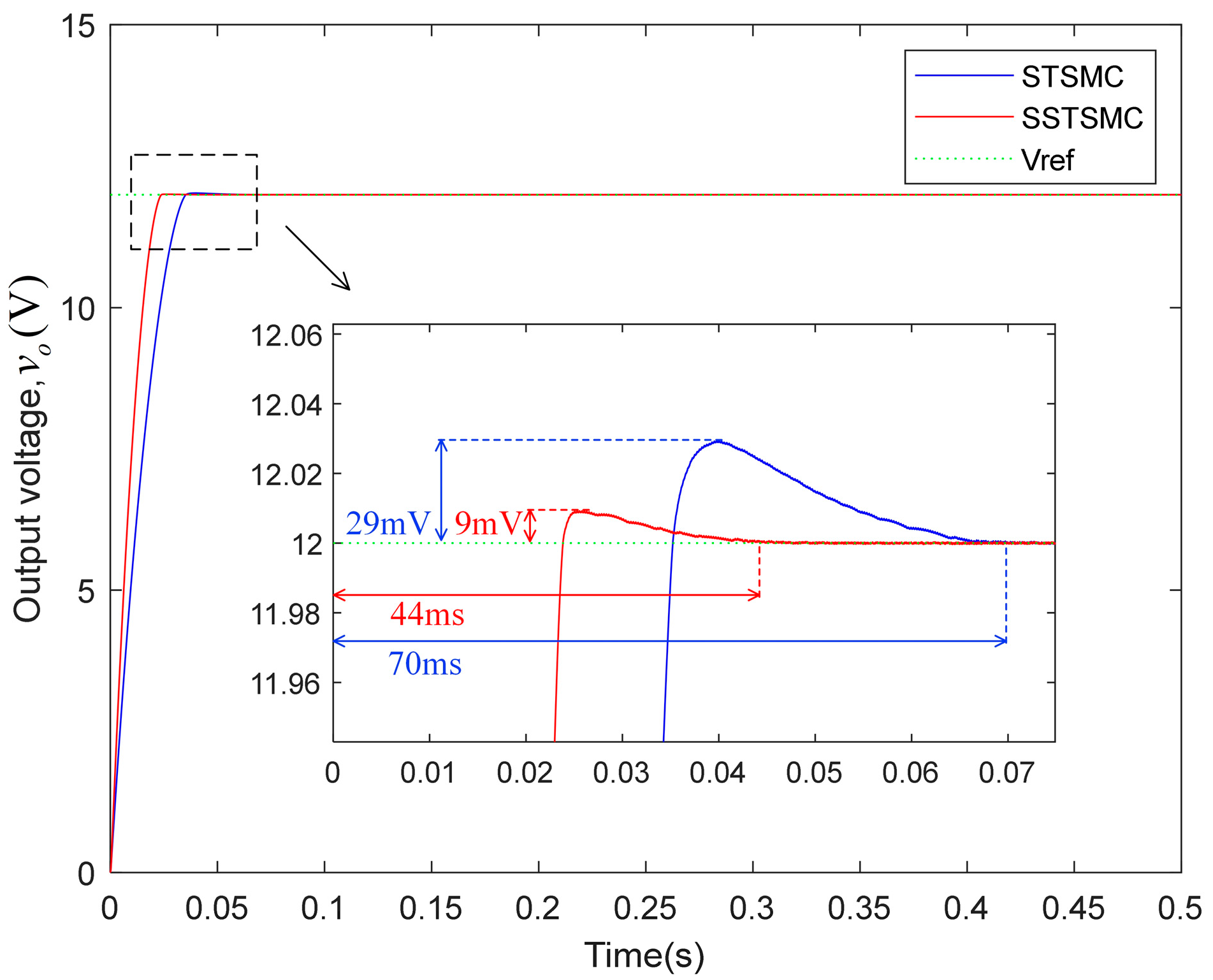
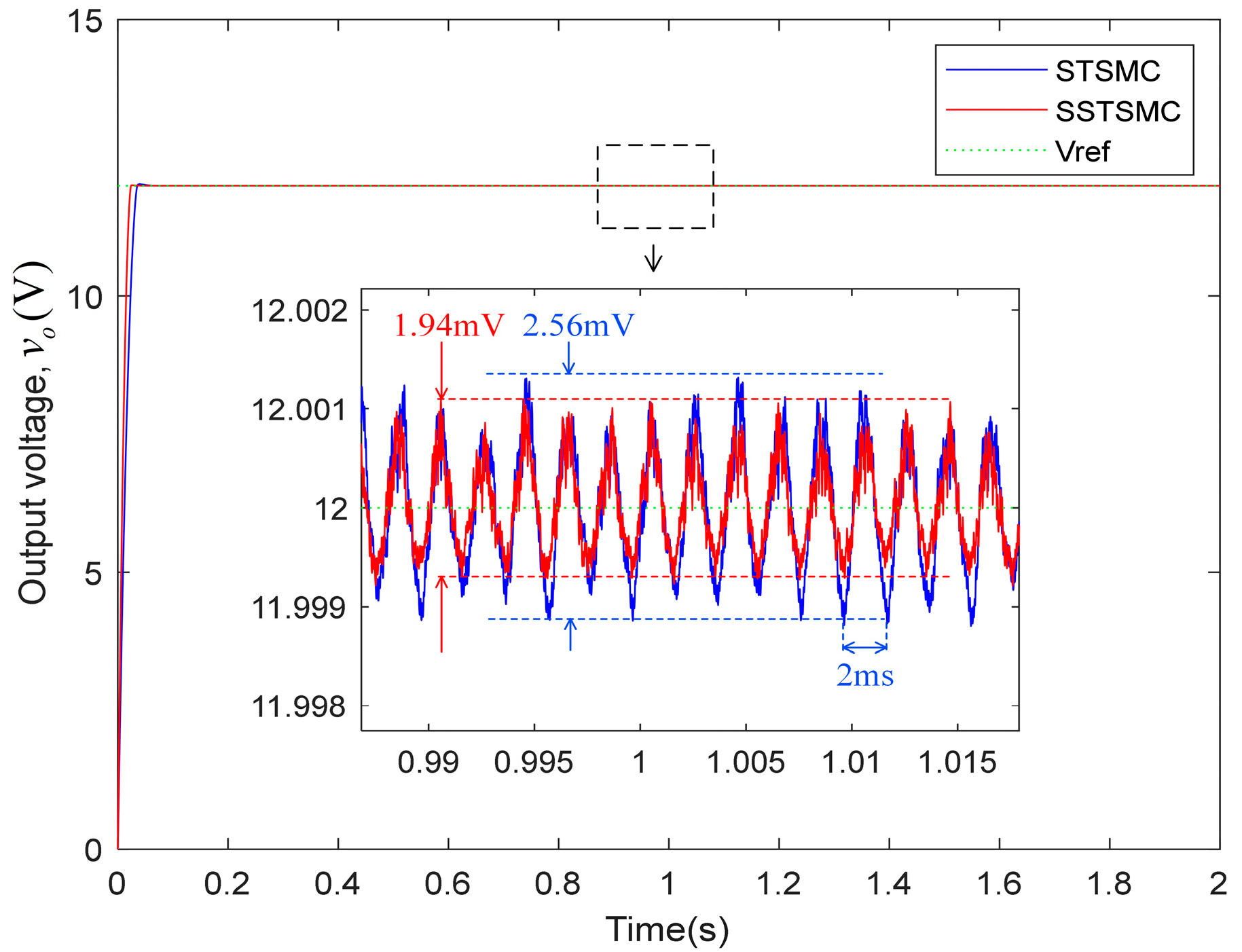
- Startup-Phase Analysis
- (2)
- Reference-Voltage Variations
- (3)
- Linear Load-Resistance Variations
- (4)
- Input-Voltage Variations
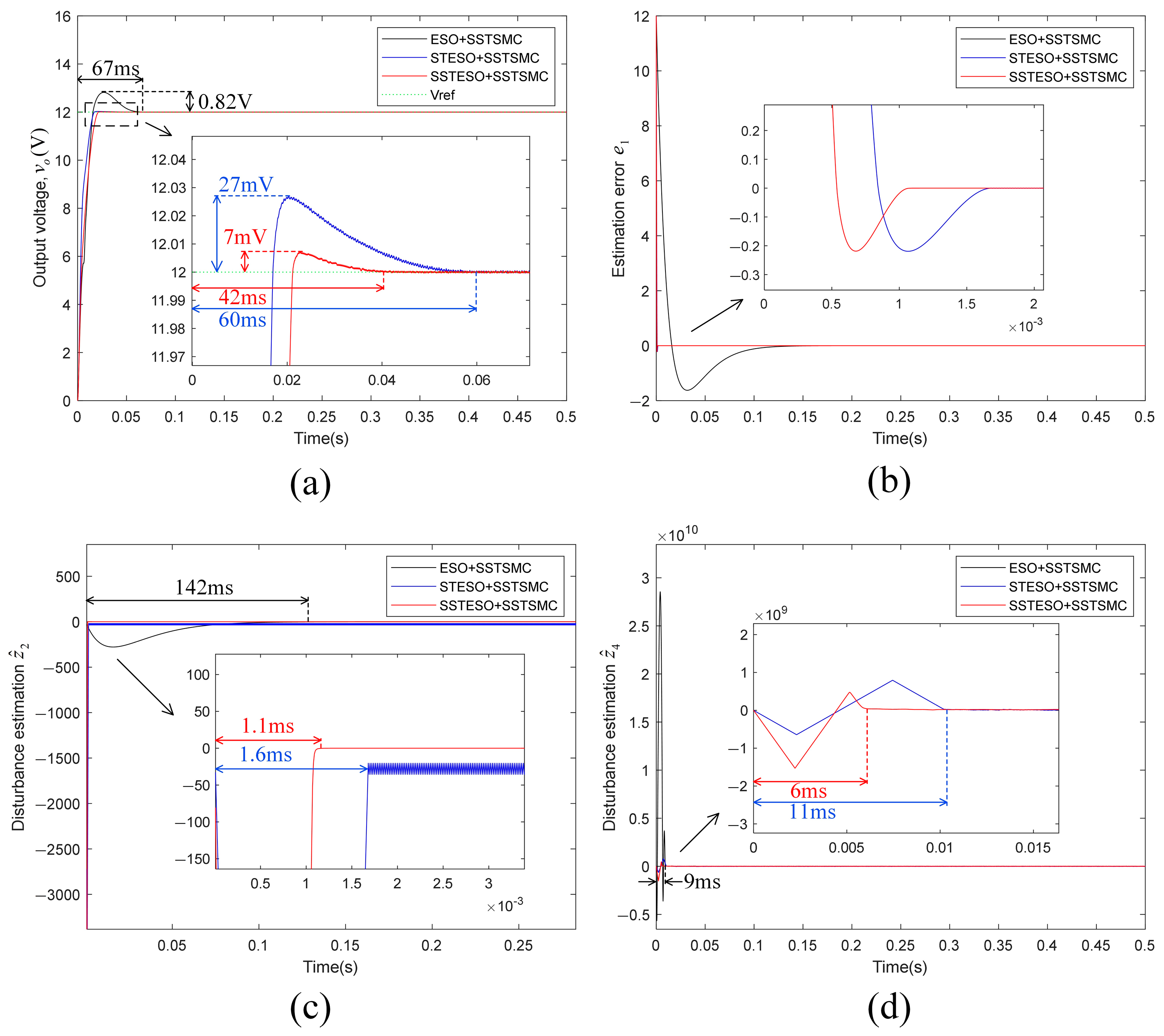
4.2. Extended-State Observer Comparative Analysis
- (1)
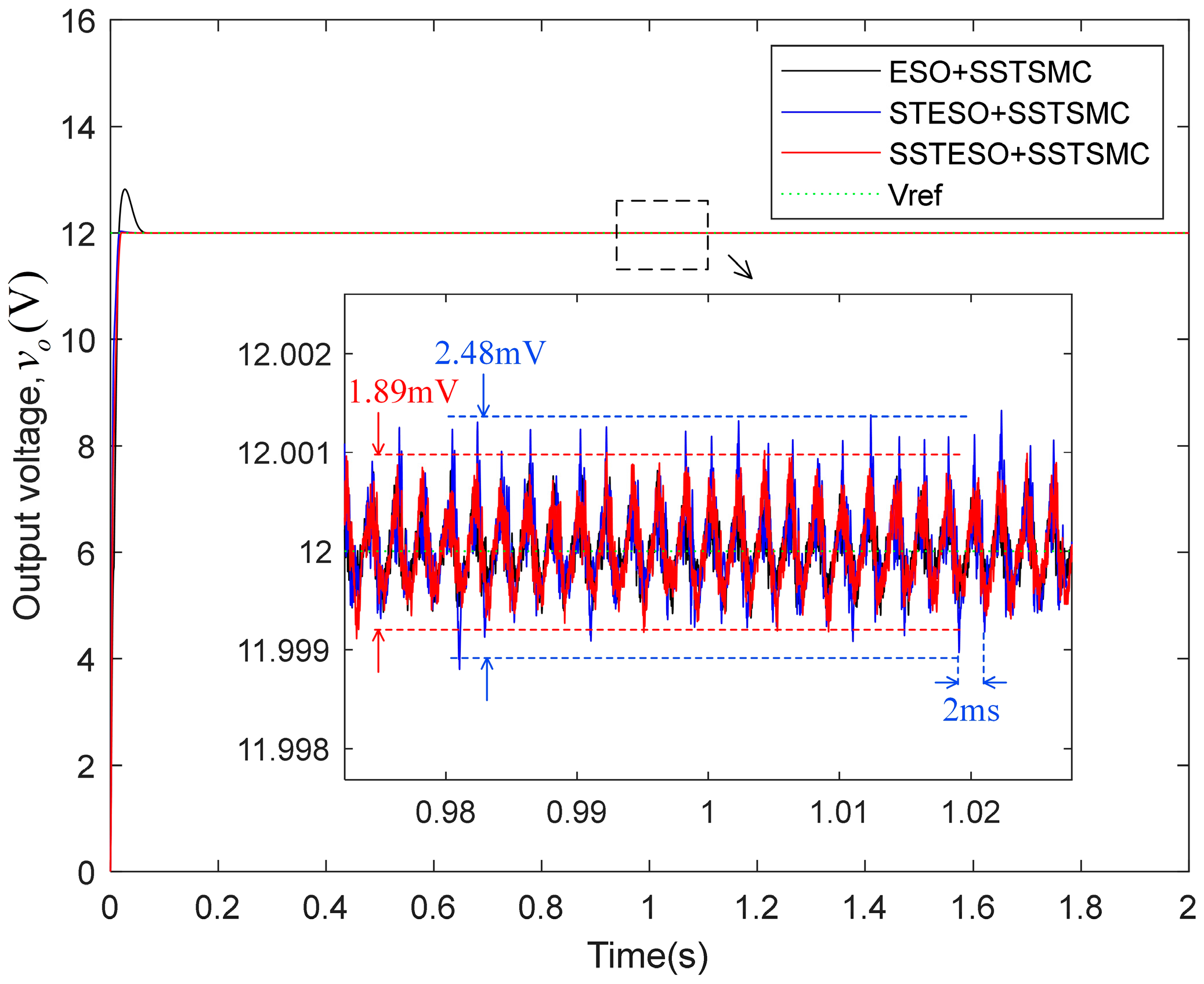
- Startup-Phase Analysis
- (2)
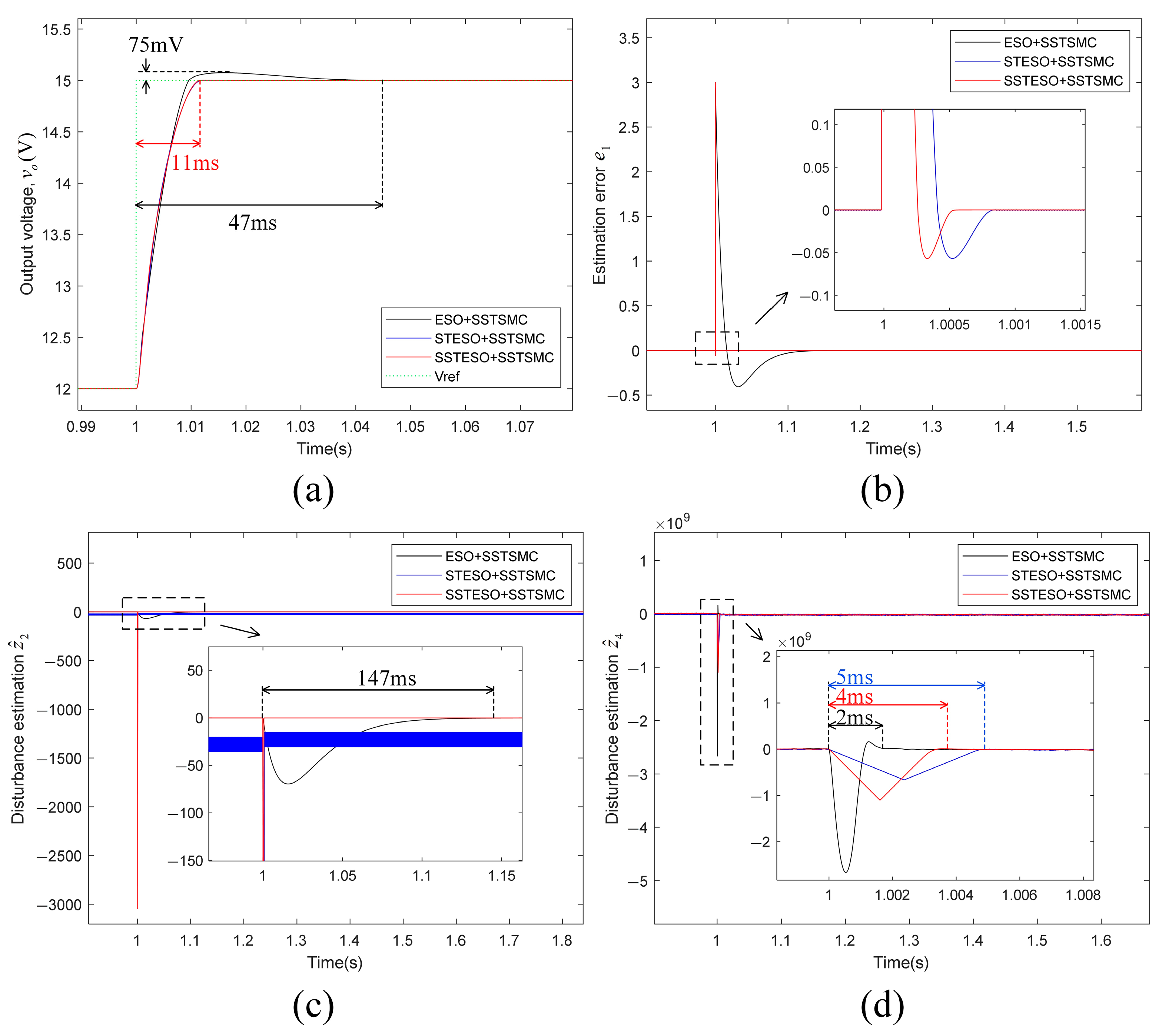
- Reference-Voltage Variations
- (3)
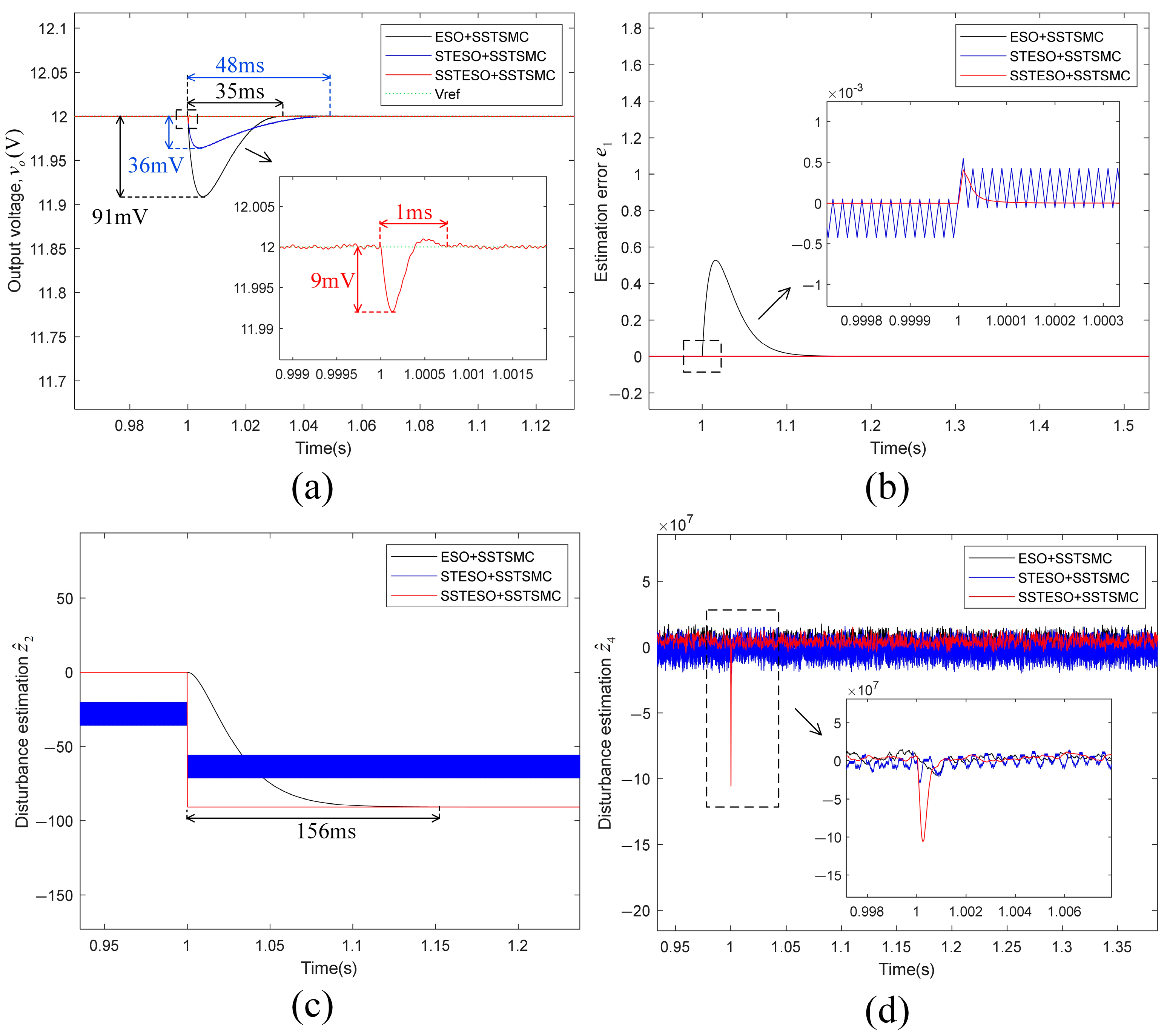
- Linear Load-Resistance Variations
- (4)
- Input-Voltage Variations
4.3. Detail Results Analysis and Summary
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sarikhani, A.; Allahverdinejad, B.; Hamzeh, M. A Nonisolated Buck–Boost DC–DC Converter with Continuous Input Current for Photovoltaic Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 804–811. [Google Scholar] [CrossRef]
- Vinnikov, D.; Chub, A.; Kosenko, R.; Zakis, J.; Liivik, E. Comparison of Performance of Phase-Shift and Asymmetrical Pulsewidth Modulation Techniques for the Novel Galvanically Isolated Buck–Boost DC–DC Converter for Photovoltaic Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 624–637. [Google Scholar] [CrossRef]
- Zapata, J.W.; Kouro, S.; Carrasco, G.; Renaudineau, H.; Meynard, T.A. Analysis of Partial Power DC–DC Converters for Two-Stage Photovoltaic Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 591–603. [Google Scholar] [CrossRef]
- Ramirez-Murillo, H.; Restrepo, C.; Konjedic, T.; Calvente, J.; Romero, A.; Baier, C.R.; Giral, R. An Efficiency Comparison of Fuel-Cell Hybrid Systems Based on the Versatile Buck–Boost Converter. IEEE Trans. Power Electron. 2018, 33, 1237–1246. [Google Scholar] [CrossRef]
- Wu, H.; Sun, K.; Chen, L.; Zhu, L.; Xing, Y. High Step-Up/Step-Down Soft-Switching Bidirectional DC–DC Converter with Coupled-Inductor and Voltage Matching Control for Energy Storage Systems. IEEE Trans. Ind. Electron. 2016, 63, 2892–2903. [Google Scholar] [CrossRef]
- Gobbato, C.; Kohler, S.; Souza, I.; Denardin, G.; Lopes, J. Integrated Topology of DC–DC Converter for LED Street Lighting System Based on Modular Drivers. IEEE Trans. Ind. Appl. 2018, 54, 3881–3889. [Google Scholar] [CrossRef]
- Hong, W.; Lee, M. A 7.4-MHz Tri-Mode DC-DC Buck Converter with Load Current Prediction Scheme and Seamless Mode Transition for IoT Applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 4544–4555. [Google Scholar] [CrossRef]
- Kim, S.-Y.; Hwang, K.C.; Yang, Y.; Lee, K.-Y.; Park, Y.-J.; Ali, I.; Nga, T.T.K.; Ryu, H.-C.; Khan, Z.H.N.; Park, S.-M.; et al. Design of a High Efficiency DC–DC Buck Converter with Two-Step Digital PWM and Low Power Self-Tracking Zero Current Detector for IoT Applications. IEEE Trans. Power Electron. 2018, 33, 1428–1439. [Google Scholar] [CrossRef]
- Zhao, M.; Li, M.; Song, S.; Hu, Y.; Yao, Y.; Bai, X.; Hu, R.; Wu, X.; Tan, Z. An Ultra-Low Quiescent Current Tri-Mode DC-DC Buck Converter with 92.1% Peak Efficiency for IoT Applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 428–439. [Google Scholar] [CrossRef]
- Bi, K.; Lv, H.; Chen, L.; Li, J.; Zhu, Y.; Huang, W.; Fan, Q. A Model Predictive Controlled Bidirectional Four Quadrant Flying Capacitor DC/DC Converter Applied in Energy Storage System. IEEE Trans. Power Electron. 2022, 37, 7705–7717. [Google Scholar] [CrossRef]
- Chen, J.; Chen, Y.; Tong, L.; Peng, L.; Kang, Y. A Backpropagation Neural Network-Based Explicit Model Predictive Control for DC–DC Converters with High Switching Frequency. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2124–2142. [Google Scholar] [CrossRef]
- Liu, P.-J.; Chien, L.-H. A High-Efficiency Integrated Multimode Battery Charger with an Adaptive Supply Voltage Control Scheme. IEEE Trans. Power Electron. 2018, 33, 6869–6876. [Google Scholar] [CrossRef]
- Wu, J.; Lu, Y. Decoupling and Optimal Control of Multilevel Buck DC–DC Converters with Inverse System Theory. IEEE Trans. Ind. Electron. 2020, 67, 7861–7870. [Google Scholar] [CrossRef]
- Ding, S.; Zheng, W.X.; Sun, J.; Wang, J. Second-Order Sliding-Mode Controller Design and Its Implementation for Buck Converters. IEEE Trans. Ind. Inform. 2018, 14, 1990–2000. [Google Scholar] [CrossRef]
- Komurcugil, H.; Biricik, S.; Guler, N. Indirect Sliding Mode Control for DC–DC SEPIC Converters. IEEE Trans. Ind. Inform. 2020, 16, 4099–4108. [Google Scholar] [CrossRef]
- Lin, X.; Liu, J.; Liu, F.; Liu, Z.; Gao, Y.; Sun, G. Fractional-Order Sliding Mode Approach of Buck Converters with Mismatched Disturbances. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 3890–3900. [Google Scholar] [CrossRef]
- Jin, H.; Zhao, X. Approach Angle-Based Saturation Function of Modified Complementary Sliding Mode Control for PMLSM. IEEE Access 2019, 7, 126014–126024. [Google Scholar] [CrossRef]
- Rakhtala, S.M.; Casavola, A. Real-Time Voltage Control Based on a Cascaded Super Twisting Algorithm Structure for DC–DC Converters. IEEE Trans. Ind. Electron. 2022, 69, 633–641. [Google Scholar] [CrossRef]
- Linares-Flores, J.; Juarez-Abad, J.A.J.; Hernandez-Mendez, A.; Castro-Heredia, O.; Guerrero-Castellanos, J.F.; Heredia-Barba, R.R.; Curiel-Olivares, G. Sliding Mode Control Based on Linear Extended State Observer for DC-to-DC Buck–Boost Power Converter System with Mismatched Disturbances. IEEE Trans. Ind. Appl. 2022, 58, 940–950. [Google Scholar] [CrossRef]
- Zhuo, S.; Gaillard, A.; Xu, L.; Bai, H.; Paire, D.; Gao, F. Enhanced Robust Control of a DC–DC Converter for Fuel Cell Application Based on High-Order Extended State Observer. IEEE Trans. Transp. Electrif. 2020, 6, 278–287. [Google Scholar] [CrossRef]
- Zhuo, S.; Gaillard, A.; Xu, L.; Paire, D.; Gao, F. Extended State Observer-Based Control of DC–DC Converters for Fuel Cell Application. IEEE Trans. Power Electron. 2020, 35, 9923–9932. [Google Scholar] [CrossRef]
- Lakomy, K.; Madonski, R.; Dai, B.; Yang, J.; Kicki, P.; Ansari, M.; Li, S. Active Disturbance Rejection Control Design with Suppression of Sensor Noise Effects in Application to DC–DC Buck Power Converter. IEEE Trans. Ind. Electron. 2022, 69, 816–824. [Google Scholar] [CrossRef]
- Yang, J.; Cui, H.; Li, S.; Zolotas, A. Optimized Active Disturbance Rejection Control for DC-DC Buck Converters with Uncertainties Using a Reduced-Order GPI Observer. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 832–841. [Google Scholar] [CrossRef]
- Hou, Q.; Ding, S. Finite-Time Extended State Observer-Based Super-Twisting Sliding Mode Controller for PMSM Drives with Inertia Identification. IEEE Trans. Transp. Electrif. 2022, 8, 1918–1929. [Google Scholar] [CrossRef]
- Zhao, L.; Zheng, C.; Wang, Y.; Liu, B. A Finite-Time Control for a Pneumatic Cylinder Servo System Based on a Super-Twisting Extended State Observer. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 1164–1173. [Google Scholar] [CrossRef]
- Fei, J.; Zhang, L.; Zhuo, J.; Fang, Y. Wavelet Fuzzy Neural Super-Twisting Sliding Mode Harmonic Control of Active Power Filter. IEEE Trans. Fuzzy Syst. 2023, 1–12. [Google Scholar] [CrossRef]
- Fei, J.; Wang, Z.; Pan, Q. Self-Constructing Fuzzy Neural Fractional-Order Sliding Mode Control of Active Power Filter. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Fei, J.; Wang, Z.; Fang, Y. Self-Evolving Chebyshev Fuzzy Neural Fractional-Order Sliding Mode Control for Active Power Filter. IEEE Trans. Ind. Inform. 2022, 19, 2729–2739. [Google Scholar] [CrossRef]
- Tong, S.; Sun, K.; Sui, S. Observer-Based Adaptive Fuzzy Decentralized Optimal Control Design for Strict-Feedback Nonlinear Large-Scale Systems. IEEE Trans. Fuzzy Syst. 2018, 26, 569–584. [Google Scholar] [CrossRef]
- Fei, J.; Chen, Y.; Liu, L.; Fang, Y. Fuzzy Multiple Hidden Layer Recurrent Neural Control of Nonlinear System Using Terminal Sliding-Mode Controller. IEEE Trans. Cybern. 2022, 52, 9519–9534. [Google Scholar] [CrossRef]
- Fei, J.; Wang, H.; Fang, Y. Novel Neural Network Fractional-order Sliding Mode Control with Application to Active Power Filter. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 3508–3518. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Tong, S. Fuzzy Adaptive Optimized Leader-Following Formation Control for Second-Order Stochastic Multiagent Systems. IEEE Trans. Ind. Inform. 2022, 18, 6026–6037. [Google Scholar] [CrossRef]
- Fei, J.; Liu, L. Real-Time Nonlinear Model Predictive Control of Active Power Filter Using Self-Feedback Recurrent Fuzzy Neural Network Estimator. IEEE Trans. Ind. Electron. 2022, 69, 8366–8376. [Google Scholar] [CrossRef]
- Fei, J.; Wang, Z.; Liang, X.; Feng, Z.; Xue, Y. Adaptive Fractional Sliding Mode Control of Micro gyroscope System Using Double Loop Recurrent Fuzzy Neural Network Structure. IEEE Trans. Fuzzy Syst. 2022, 30, 1712–1721. [Google Scholar] [CrossRef]
- Zhou, R.; Fu, C.; Tan, W. Implementation of Linear Controllers via Active Disturbance Rejection Control Structure. IEEE Trans. Ind. Electron. 2021, 68, 6217–6226. [Google Scholar] [CrossRef]
- Levant, A. Robust exact differentiation via sliding mode technique. Automatica 1998, 34, 379–384. [Google Scholar] [CrossRef]




| Description | Parameter | Value | Units |
|---|---|---|---|
| Inductor | H | ||
| Capacitor | F | ||
| Load resistance | |||
| Input voltage | 25 | V | |
| Reference voltage | V |
| Controllers | Parameters and Values |
|---|---|
| STSMC | , , |
| SSTSMC | , , , |
| ESO+SSTSMC | , , , , , , , |
| STESO+SSTSMC | , , , , , , , , , |
| SSTESO+SSTSMC | , , , , , , , , , , , |
| Simulation | Controller | ||
|---|---|---|---|
| (1) | STSMC | 29 | 70 |
| SSTSMC | 9 | 44 | |
| ESO+SSTSMC | 820 | 67 | |
| STESO+SSTSMC | 27 | 60 | |
| SSTESO+SSTSMC | 7 | 42 | |
| (2) | STSMC | - | 19 |
| SSTSMC | - | 12 | |
| ESO+SSTSMC | 75 | 47 | |
| STESO+SSTSMC | - | 11 | |
| SSTESO+SSTSMC | - | 11 | |
| (3) | STSMC | 210 | 98 |
| SSTSMC | 100 | 78 | |
| ESO+SSTSMC | 91 | 35 | |
| STESO+SSTSMC | 36 | 48 | |
| SSTESO+SSTSMC | 9 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, D.; Fang, Y.; Fei, J. An Extended-State Observer Based on Smooth Super-Twisting Sliding-Mode Controller for DC-DC Buck Converters. Mathematics 2023, 11, 2835. https://doi.org/10.3390/math11132835
Jiang D, Fang Y, Fei J. An Extended-State Observer Based on Smooth Super-Twisting Sliding-Mode Controller for DC-DC Buck Converters. Mathematics. 2023; 11(13):2835. https://doi.org/10.3390/math11132835
Chicago/Turabian StyleJiang, Dian, Yunmei Fang, and Juntao Fei. 2023. "An Extended-State Observer Based on Smooth Super-Twisting Sliding-Mode Controller for DC-DC Buck Converters" Mathematics 11, no. 13: 2835. https://doi.org/10.3390/math11132835
APA StyleJiang, D., Fang, Y., & Fei, J. (2023). An Extended-State Observer Based on Smooth Super-Twisting Sliding-Mode Controller for DC-DC Buck Converters. Mathematics, 11(13), 2835. https://doi.org/10.3390/math11132835







