Sparse Support Tensor Machine with Scaled Kernel Functions
Abstract
1. Introduction
- Sparse-kernelized STM model: Taking the sparsity of support tensors into consideration, the sparse-kernelized STM model is proposed, which can flexibly govern the number of support tensors through sparsity constraints. Moreover, the Gaussian RBF kernel in combination with tensor decomposition was utilized to handle nonlinearly separable tensor data.
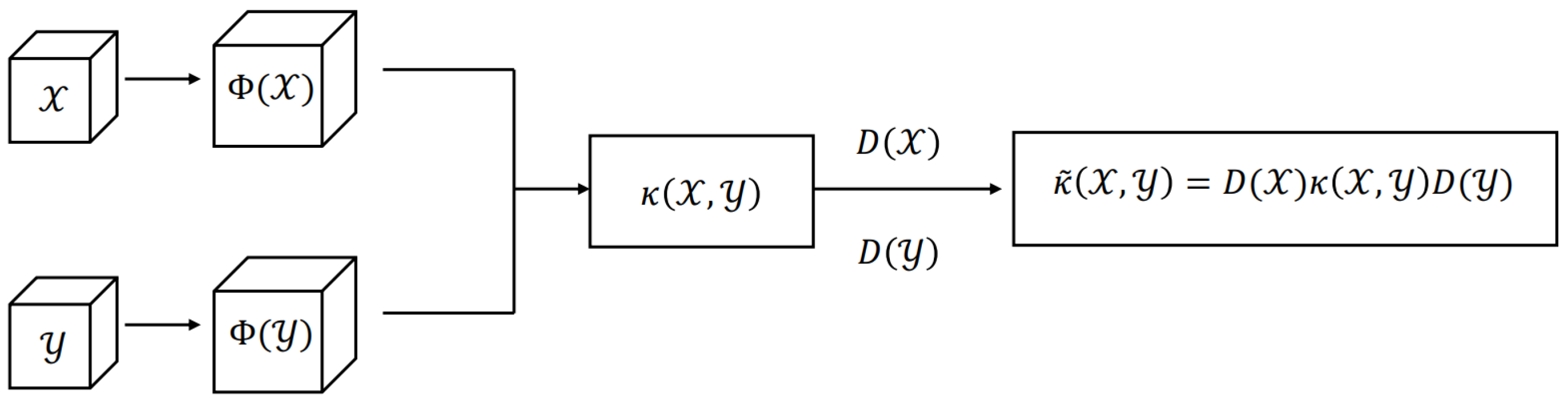
- Scaled kernel function: To alleviate the local risk caused by the constant kernel width, we modified the kernel through conformal transformation by exploiting the structure of Riemannian geometry induced by the kernel function.
- Two-stage method: The scaling kernel function can be realized via a two-stage training process. In the first stage, we obtained prior information on support tensors by utilizing a primal kernel. Then, the scaled kernel was used to obtain the final classifier in the second stage. Leveraging the sparse structure, we applied the subspace Newton method to solve the optimization problems in both stages.
2. Related Works
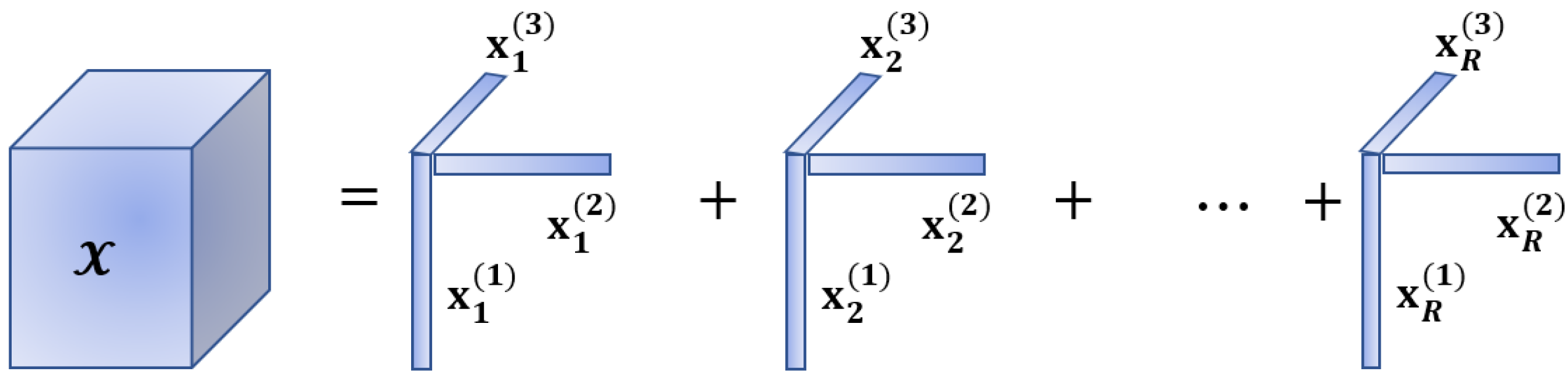
3. Tensor Basics
4. Sparse STM with Scaled Kernels
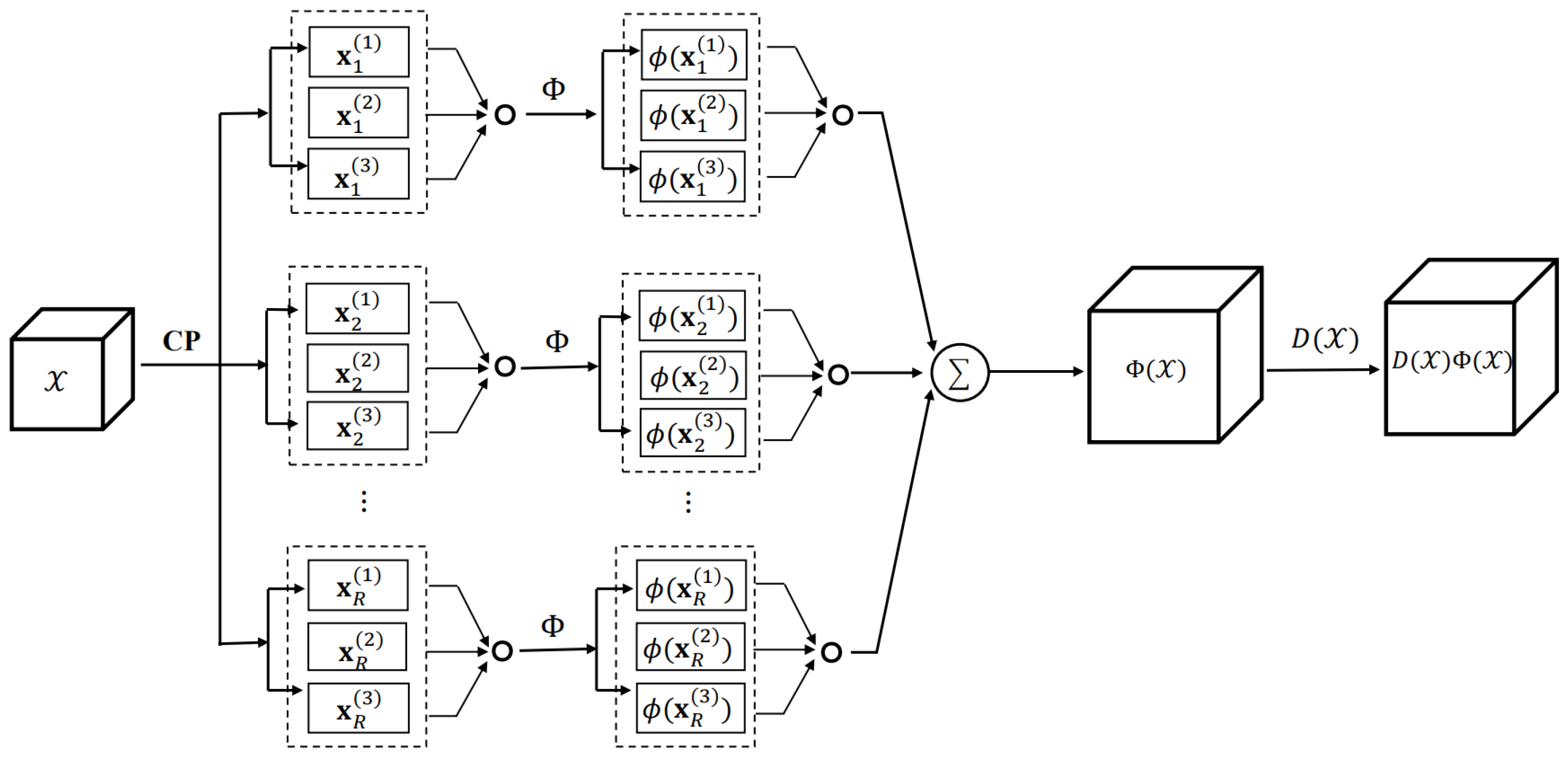
4.1. The Proposed Sparse STM Model
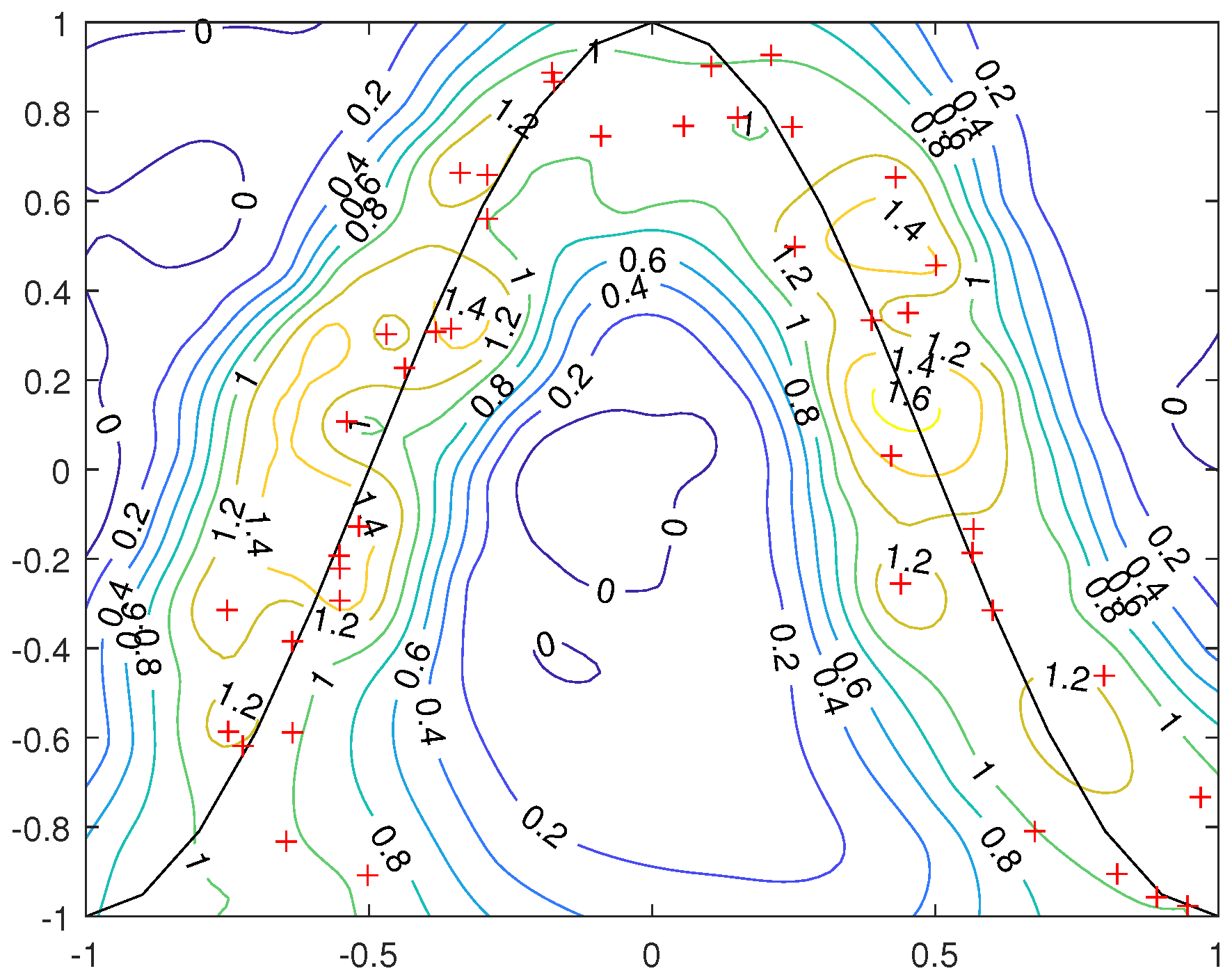
4.2. Scaling Tensor Kernel Functions
4.3. The Proposed NKSTM Approach
| Algorithm 1 (re-NKSTM) NKSTM with the rescaling kernel. |
| Input: Training dataset , parameters , the CP rank R. |
| Output: The solution . |
| Step 1: Initialize , pick , and ; |
| Step 2: Compute by NSSVM with the tensorial RBF kernel ; |
| Step 3: If the stopping criterion is satisfied, then go to Step 4; otherwise, set and go to Step 2; |
| Step 4: Compute the modified kernel by (11) to rescale the primal kernel ; |
| Step 5: Compute by NSSVM with the tensorial RBF kernel ; |
| Step 6: If the stopping criterion is satisfied, then stop; otherwise, set and go to Step 5. |
- The main term involved in computing is , which has a complexity of about since , and computing the inverse of requires at most ;
- To pick , we need to compute and pick out the k largest elements of . The complexity of computing the former is and the latter is .
| Algorithm 2 (NKSTM) Newton-kernelized STM. |
| Input: Training dataset , the parameters , the CP rank R. |
| Output: The solution . |
| Step 1: Initialize , pick , and ; |
| Step 2: Compute by NSSVM with the tensorial RBF kernel; |
| Step 3: If the stopping criterion is satisfied, then stop; otherwise, set and go to Step 2. |
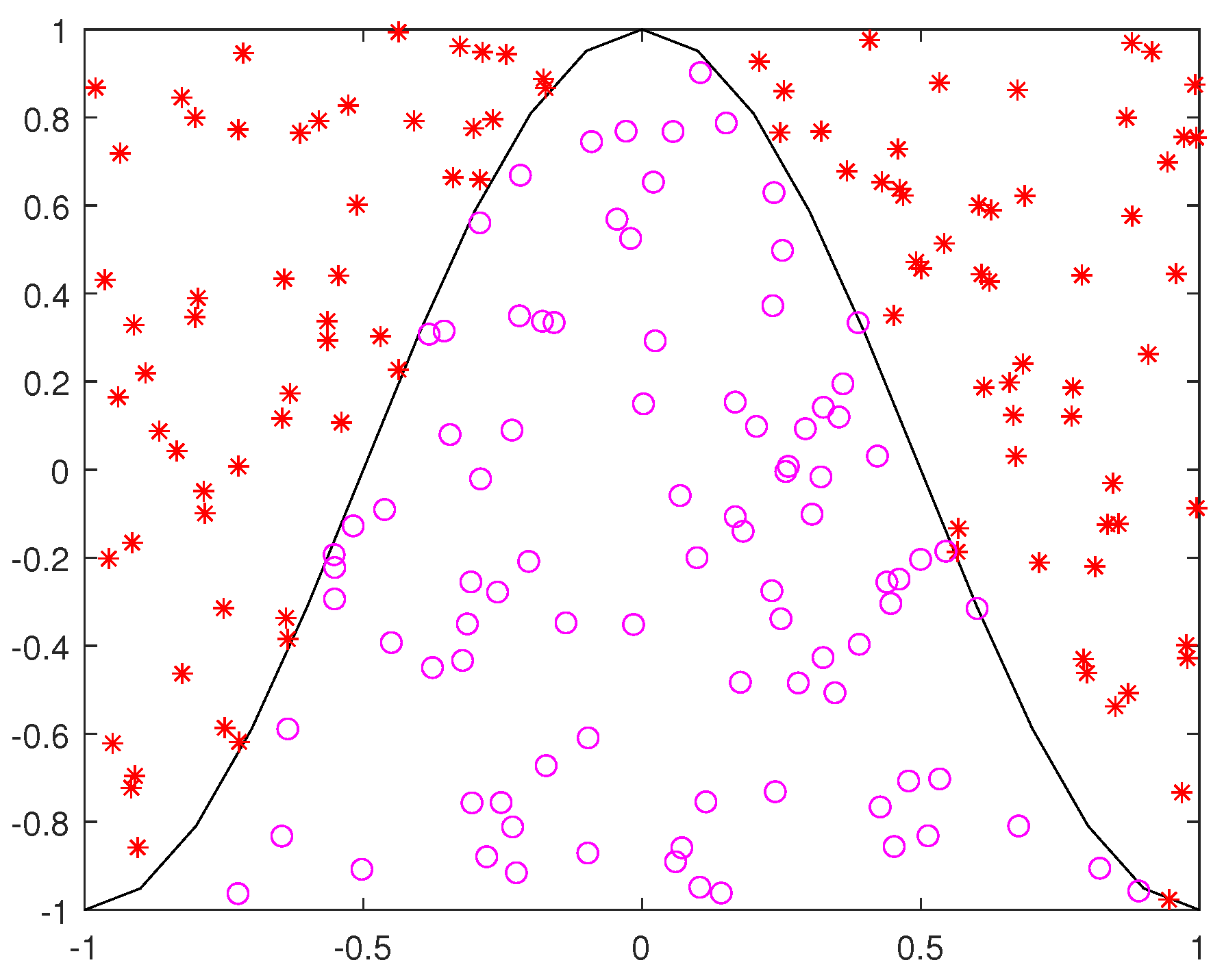
5. Numerical Experiments
5.1. Benchmark Methods
- LIBSVM: SVM with hinge loss was implemented by Lin et al. [47], which is one of the most popular classification methods based on vector space. In this paper, we consider the SVM with a Gaussian kernel.
- NSSVM-RBF: NSSVM based on vector space was developed by Zhou [35] for data reduction, which is a linearly kernelized SVM optimization problem with sparsity constraints. We consider the Gaussian RBF kernel for nonlinearly separable data.
- DuSK: He et al. [24] proposed a dual structure-preserving kernel based on CP decomposition for supervised tensor learning to boost tensor classification performances. In the experiment, we chose the Gaussian RBF kernel.
- TT-MMK: Kour et al. [27] introduced a tensor train multi-way multi-level kernel (TT-MMK), which converts the available TT decomposition into the CP decomposition for kernelized classification. The Gaussian RBF kernel was adopted in the article.
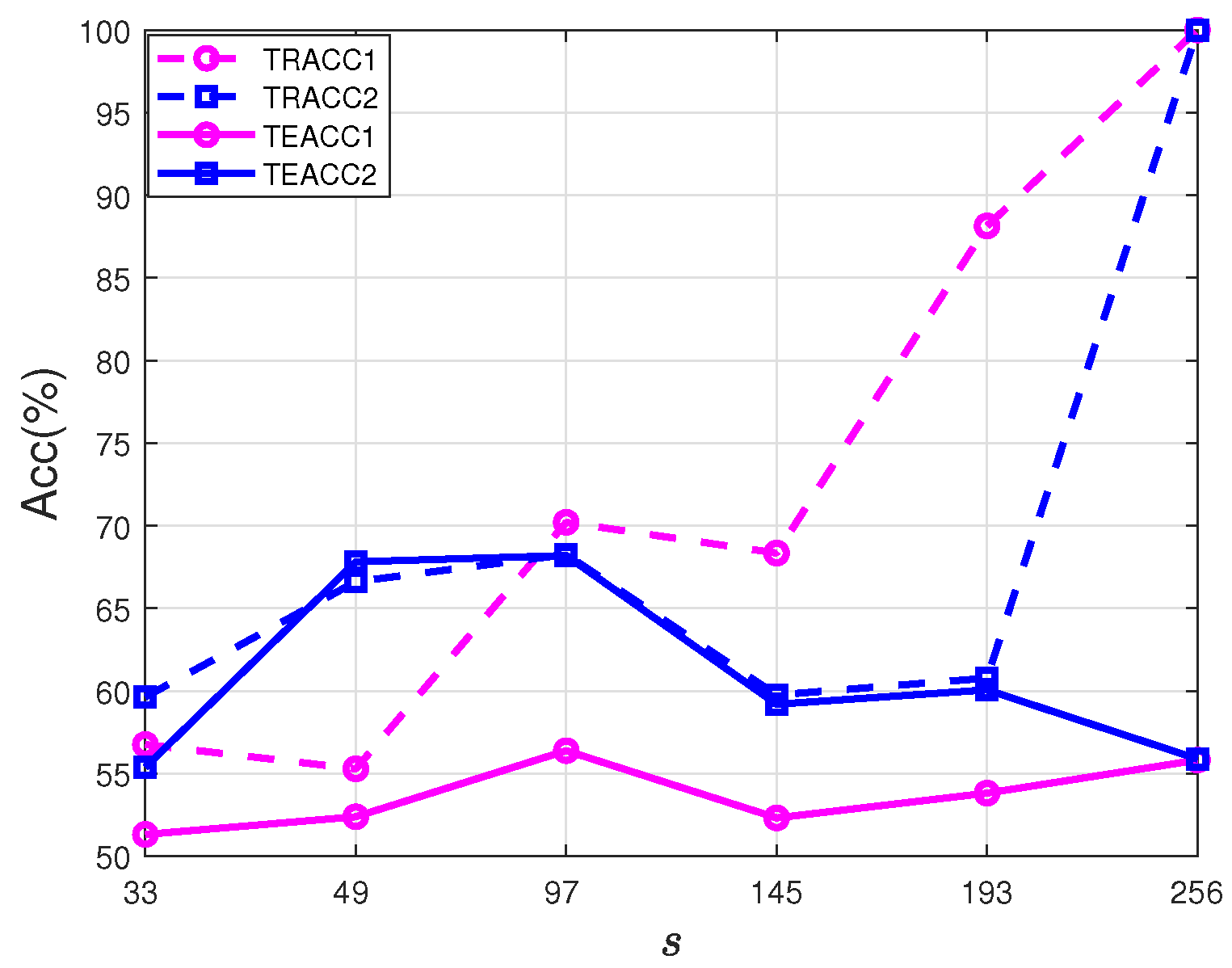
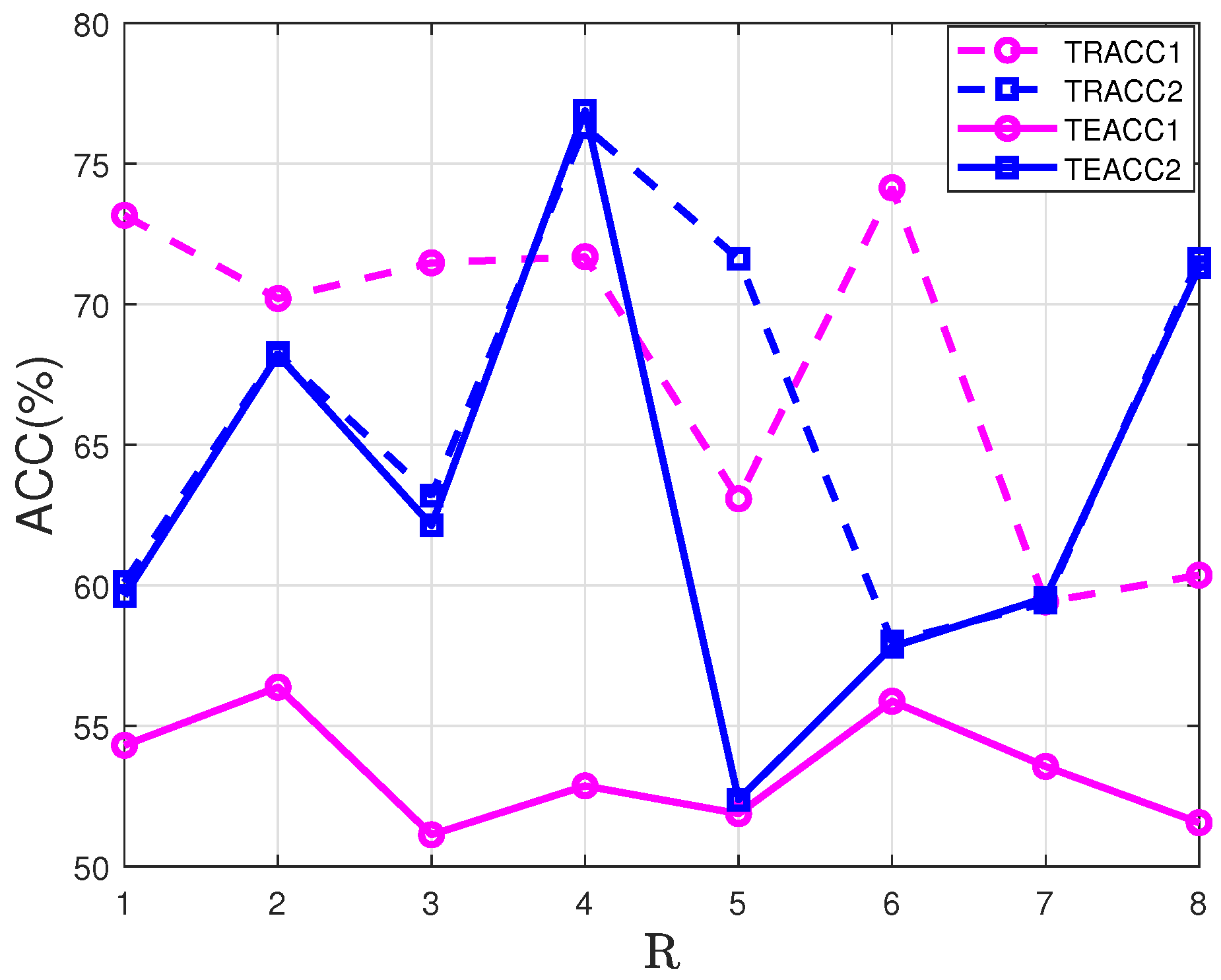
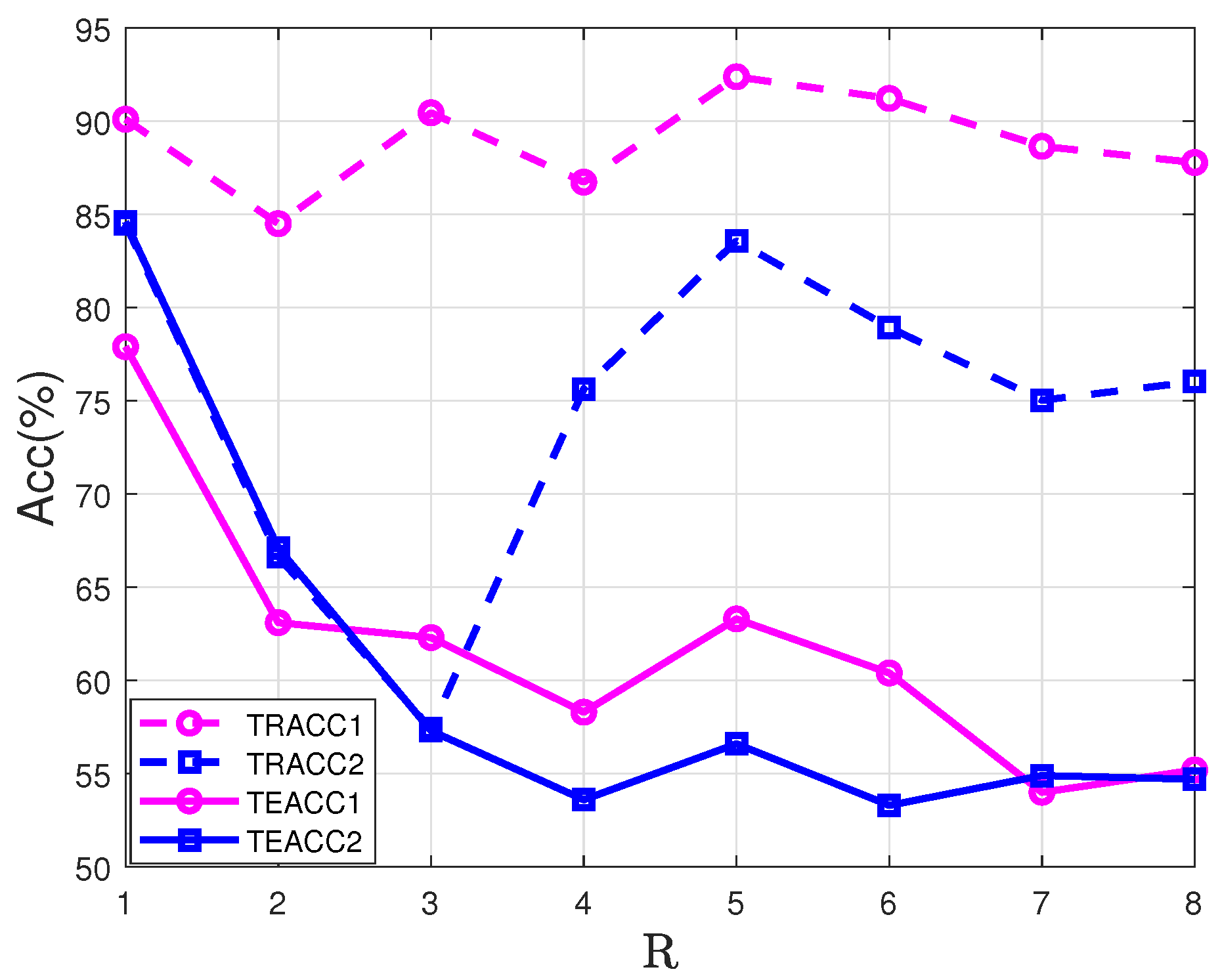
5.2. StarPlus fMRI Dataset
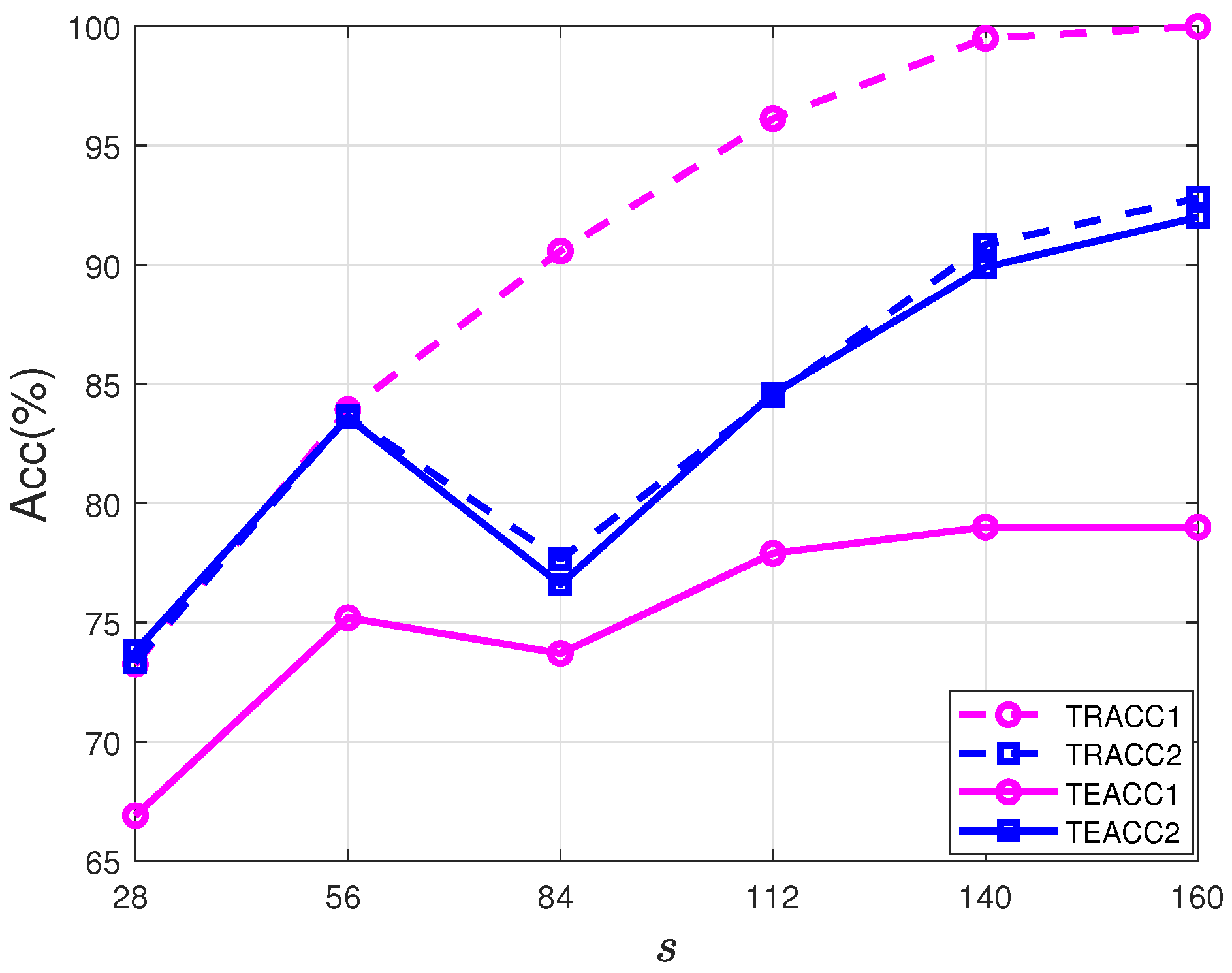
5.3. CIFAR-10 Dataset
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Zhu, C.; Long, Z.; Liu, Y. Tensor regression. Found. Trends Mach. Learn. 2021, 14, 379–565. [Google Scholar] [CrossRef]
- Kolda, T.; Bader, B. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Xing, Y.; Wang, M.; Yang, S.; Zhang, K. Pansharpening with multiscale geometric support tensor machine. IEEE Geosci. Remote Sens. Lett. 2018, 56, 2503–2517. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Tao, D.; Huang, X. A multifeature tensor for remote-sensing target recognition. IEEE Geosci. Remote Sens. Lett. 2011, 8, 374–378. [Google Scholar] [CrossRef]
- Zhou, B.; Song, B.; Hassan, M.; Alamri, A. Multilinear rank support tensor machine for crowd density estimation. Eng. Appl. Artif. Intel. 2018, 72, 382–392. [Google Scholar] [CrossRef]
- Zhao, Z.; Chow, T. Maximum margin multisurface support tensor machines with application to image classification and segmentation. Expert Syst. Appl. 2012, 39, 849–860. [Google Scholar]
- He, Z.; Shao, H.; Cheng, J.; Zhao, X.; Yang, Y. Support tensor machine with dynamic penalty factors and its application to the fault diagnosis of rotating machinery with unbalanced data. Mech. Syst. Signal Process. 2020, 141, 106441. [Google Scholar] [CrossRef]
- Hu, C.; He, S.; Wang, Y. A classification method to detect faults in a rotating machinery based on kernelled support tensor machine and multilinear principal component analysis. Appl. Intell. 2021, 51, 2609–2621. [Google Scholar] [CrossRef]
- Tao, D.; Li, X.; Hu, W.; Maybank, S.; Wu, X. Supervised tensor learning. In Proceedings of the Fifth IEEE International Conference on Data Mining, Houston, TX, USA, 27–30 November 2005; pp. 450–457. [Google Scholar]
- Tao, D.; Li, X.; Wu, X.; Hu, W.; Maybank, S. Supervised tensor learning. Knowl. Inf. Syst. 2007, 13, 1–42. [Google Scholar] [CrossRef]
- Kotsia, I.; Patras, I. Support tucker machines. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), IEEE, Colorado Springs, CO, USA, 20–25 June 2011; pp. 633–640. [Google Scholar]
- Khemchandani, R.; Karpatne, A.; Chandra, S. Proximal support tensor machines. Int. J. Mach. Learn. Cyber. 2013, 4, 703–712. [Google Scholar] [CrossRef]
- Chen, C.; Batselier, K.; Ko, C.Y.; Wong, N. A support tensor train machine. In Proceedings of the 2019 International Joint Conference on Neural Networks, Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar]
- Sun, T.; Sun, X. New results on classification modeling of noisy tensor datasets: A fuzzy support tensor machine dual model. IEEE Trans. Syst. Man Cybern. 2021, 99, 1–13. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, K.; Zhong, P. One-class support tensor machine. Knowl.-Based Syst. 2016, 96, 14–28. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, X.; Wang, Y. Twin support tensor machines for MC detection. J. Electron. 2009, 26, 318–325. [Google Scholar] [CrossRef]
- Shi, H.; Zhao, X.; Zhen, L.; Jing, L. Twin bounded support tensor machine for classification. Int. J. Pattern Recogn. 2016, 30, 1650002.1–1650002.20. [Google Scholar] [CrossRef]
- Rastogi, R.; Sharma, S. Ternary tree based-structural twin support tensor machine for clustering. Pattern Anal. Appl. 2021, 24, 61–74. [Google Scholar] [CrossRef]
- Yan, S.; Xu, D.; Yang, Q.; Zhang, L.; Tang, X.; Zhang, H. Multilinear discriminant analysis for face recognition. IEEE Trans. Image Process. 2007, 16, 212–220. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Plataniotis, K.; Venetsanopoulos, A. MPCA: Multilinear principal component analysis of tensor objects. IEEE Trans. Neural Netw. 2008, 19, 18–39. [Google Scholar] [PubMed]
- Kotsia, I.; Guo, W.; Patras, I. Higher rank support tensor machines for visual recognition. Pattern Recognit. 2012, 45, 4192–4203. [Google Scholar] [CrossRef]
- Yang, B. Research and Application of Machine Learning Algorithm Based Tensor Representation; China Agricultural University: Beijing, China, 2017. [Google Scholar]
- Rubinov, M.; Knock, S.; Stam, C.; Micheloyannis, S.; Harris, A.; Williams, L.; Breakspear, M. Small-world properties of nonlinear brain activity in schizophrenia. Hum. Brain Mapp. 2009, 30, 403–416. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Kong, X.; Yu, P.; Ragin, A.; Hao, Z.; Yang, X. DuSK: A dual structure-preserving kernel for supervised tensor learning with applications to neuroimages. In Proceedings of the 2014 SIAM International Conference on Data Mining SIAM, Philadelphia, PA, USA, 24–26 April 2014; pp. 127–135. [Google Scholar]
- He, L.; Lu, C.; Ma, G.; Wang, S.; Shen, L.; Yu, P.; Ragin, A. Kernelized support tensor machines. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 1442–1451. [Google Scholar]
- Chen, C.; Batselier, K.; Yu, W.; Wong, N. Kernelized support tensor train machines. Pattern Recognit. 2022, 122, 108337. [Google Scholar] [CrossRef]
- Kour, K.; Dolgov, S.; Stoll, M.; Benner, P. Efficient structure-preserving support tensor train machine. J. Mach. Learn. Res. 2023, 24, 1–22. [Google Scholar]
- Deng, X.; Shi, Y.; Yao, D.; Tang, X.; Mi, C.; Xiao, J.; Zhang, X. A kernelized support tensor-ring machine for high-dimensional data classification. In Proceedings of the International Conference on Electronic Information Technology and Smart Agriculture (ICEITSA), IEEE, Huaihua, China, 10–12 December 2021; pp. 159–165. [Google Scholar]
- Scholkopf, B.; Burges, C.; Smola, A. Advances in Kernel Methods; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Amari, S.; Wu, S. Improving support vector machine classifiers by modifying kernel functions. Neural Netw. 1999, 12, 783–789. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Amari, S. Conformal transformation of kernel functions: A data-dependent way to improve support vector machine classifiers. Neural Process. Lett. 2001, 25, 59–67. [Google Scholar]
- Williams, P.; Li, S.; Feng, J.; Wu, S. Scaling the kernel function to improve performance of the support vector machine. In International Symposium on Neural Networks; Springer: Berlin/Heidelberg, Germany, 2005; pp. 831–836. [Google Scholar]
- Williams, P.; Wu, S.; Feng, J. Improving the performance of the support vector machine: Two geometrical scaling methods. StudFuzz 2005, 177, 205–218. [Google Scholar]
- Chang, Q.; Chen, Q.; Wang, X. Scaling Gaussian RBF kernel width to improve SVM classification. In Proceedings of the International Conference on Neural Networks and Brain, Beijing, China, 13–15 October 2005. [Google Scholar]
- Zhou, S. Sparse SVM for sufficient data reduction. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 5560–5571. [Google Scholar] [CrossRef]
- Wang, S.; Luo, Z. Low rank support tensor machine based on L0/1 soft-margin loss function. Oper. Res. Trans. 2021, 25, 160–172. (In Chinese) [Google Scholar]
- Lian, H. Learning rate for convex support tensor machines. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3755–3760. [Google Scholar] [CrossRef]
- Shu, T.; Yang, Z.X. Support tensor machine based on nuclear norm of tensor. J. Neijiang Norm. Univ. 2017, 32, 34–39. (In Chinese) [Google Scholar]
- He, L.F.; Lu, C.T.; Ding, H.; Wang, S.; Shen, L.L.; Yu, P.; Ragin, A.B. Multi-way multi-level kernel modeling for neuroimaging classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 356–364. [Google Scholar]
- Hao, Z.; He, L.; Chen, B.; Yang, X. A linear support higher-order tensor machine for classification. IEEE Trans. Image Process. 2013, 22, 2911–2920. [Google Scholar] [PubMed]
- Qi, L.; Luo, Z. Tensor Analysis: Spectral Theory and Special Tensors; SIAM Press: Philadelphia, PA, USA, 2017. [Google Scholar]
- Nion, D.; Lathauwer, L. An enhanced line search scheme for complex-valued tensor decompositions. Application in DS-CDMA. Signal Process. 2008, 21, 749–755. [Google Scholar] [CrossRef]
- Steinwart, I.; Christmann, A. Support Vector Machines; Springer: New York, NY, USA, 2008. [Google Scholar]
- Zhao, L.; Mammadov, M.J.; Yearwood, J. From convex to nonconvex: A loss function analysis for binary classification. In Proceedings of the IEEE International Conference on Data Mining Workshops, Sydney, NSW, Australia, 13 December 2010; pp. 1281–1288. [Google Scholar]
- Wang, Q.; Ma, Y.; Zhao, K.; Tian, Y. A comprehensive survey of loss functions in machine learning. Ann. Data. Sci. 2022, 9, 187–212. [Google Scholar] [CrossRef]
- Wang, H.; Xiu, N. Analysis of loss functions in support vector machines. Adv. Math. 2021, 50, 801–828. (In Chinese) [Google Scholar]
- Chang, C.; Lin, C. LIBSVM: A library for support vector machines. ACM Trans. Intel. Syst. Tec. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; Technical Report; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]



| Kernel (Scaled) | Loss | LRD | SST | DR | |
|---|---|---|---|---|---|
| Tao et al. [10] | × (×) | hinge | CP | × | ✓ |
| Kotsia et al. [11] | × (×) | hinge | Tucker | × | ✓ |
| Kotsia et al. [21] | × (×) | hinge | CP | × | ✓ |
| Yang et al. [22] | × (×) | hinge | × | × | × |
| Chen et al. [13] | × (×) | hinge | TT | × | ✓ |
| Shu et al. [38] | ×(×) | hinge | × | × | × |
| Wang et al. [36] | × (×) | 0/1 loss | × | × | × |
| Hao et al. [40] | linear(×) | hinge | CP | × | ✓ |
| He et al. [24] | RBF(×) | hinge | CP | × | ✓ |
| He et al. [25] | RBF(×) | hinge | CP | × | ✓ |
| Chen et al. [26] | RBF(×) | hinge | TT | × | ✓ |
| Kour et al. [27] | RBF(×) | hinge | TT | × | ✓ |
| Deng et al. [28] | RBF (×) | hinge | TR | × | ✓ |
| Our work | RBF (✓) | piecewise quadratic smooth loss | CP | × | × |
| re-NKSTM | NKSTM | LIBSVM | NSSVM-RBF | DuSK | TT-MMK |
|---|---|---|---|---|---|
| 76.88 | 52.87 | 50.00 | 50.00 | 56.37 | 57.44 |
| Class Pair | re-NKSTM | NKSTM | LIBSVM | NSSVM-RBF | DuSK | TT-MMK |
|---|---|---|---|---|---|---|
| ‘bird, deer’ | 75.40 | 67.50 | 62.50 | 60.70 | 73.00 | 73.40 |
| ‘deer, horse’ | 88.30 | 66.10 | 54.70 | 71.10 | 70.30 | 71.20 |
| ‘bird, horse’ | 90.00 | 69.40 | 71.10 | 72.90 | 73.20 | 76.10 |
| ‘truck, ship’ | 82.90 | 75.30 | 76.40 | 75.80 | 78.40 | 78.20 |
| ‘automobile, ship’ | 83.30 | 74.40 | 60.30 | 77.70 | 78.30 | 77.30 |
| ‘automobile, cat’ | 84.60 | 77.90 | 65.80 | 77.10 | 79.10 | 79.50 |
| ‘automobile, horse’ | 79.20 | 75.00 | 72.50 | 78.60 | 76.40 | 75.90 |
| ‘air, ship’ | 73.10 | 65.90 | 65.10 | 69.80 | 68.70 | 71.50 |
| ‘automobile, truck’ | 87.10 | 69.00 | 58.10 | 71.90 | 73.10 | 72.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Luo, Z. Sparse Support Tensor Machine with Scaled Kernel Functions. Mathematics 2023, 11, 2829. https://doi.org/10.3390/math11132829
Wang S, Luo Z. Sparse Support Tensor Machine with Scaled Kernel Functions. Mathematics. 2023; 11(13):2829. https://doi.org/10.3390/math11132829
Chicago/Turabian StyleWang, Shuangyue, and Ziyan Luo. 2023. "Sparse Support Tensor Machine with Scaled Kernel Functions" Mathematics 11, no. 13: 2829. https://doi.org/10.3390/math11132829
APA StyleWang, S., & Luo, Z. (2023). Sparse Support Tensor Machine with Scaled Kernel Functions. Mathematics, 11(13), 2829. https://doi.org/10.3390/math11132829




