On Incidence-Dependent Management Strategies against an SEIRS Epidemic: Extinction of the Epidemic Using Allee Effect
Abstract
1. Introduction
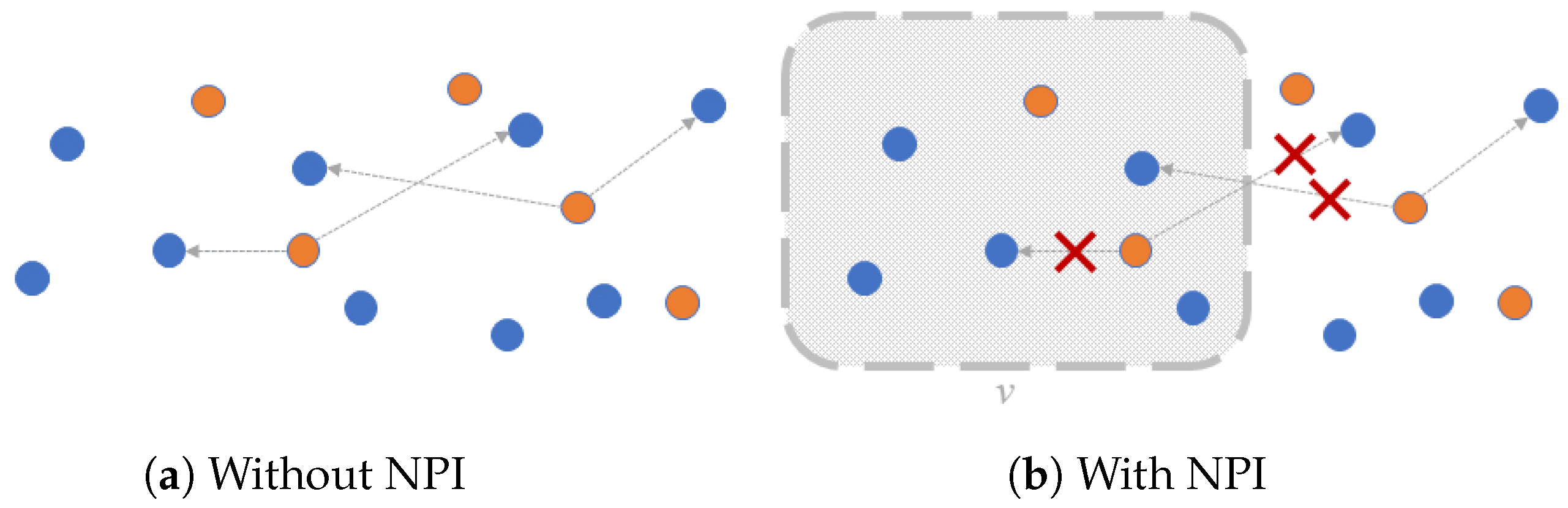
2. An SEIRS Model with NPI Depending on the Number of Infected People
2.1. Disease-Free Equilibria
2.2. Endemic Equilibria
2.3. Stability Analysis
2.3.1. Local Stability of the DFE
2.3.2. Local Stability for an Endemic Equilibrium
2.4. Numerical Simulations
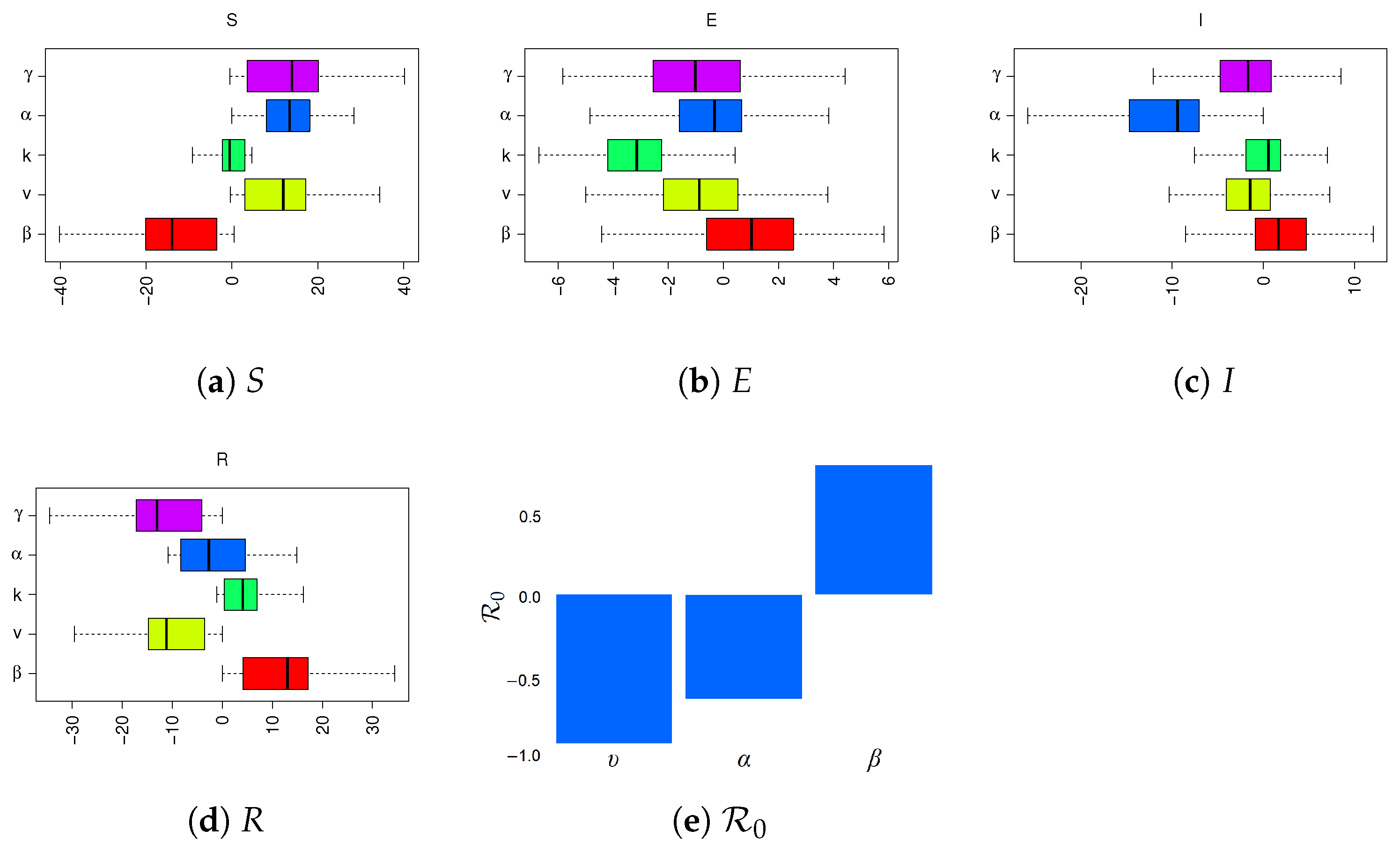
2.5. Sensitivity Analysis
3. Application to the COVID-19 Epidemic
3.1. Background of the COVID-19 Pandemic
3.2. Dynamics without Protection Measures: Parameters Estimation Based on COVID-19
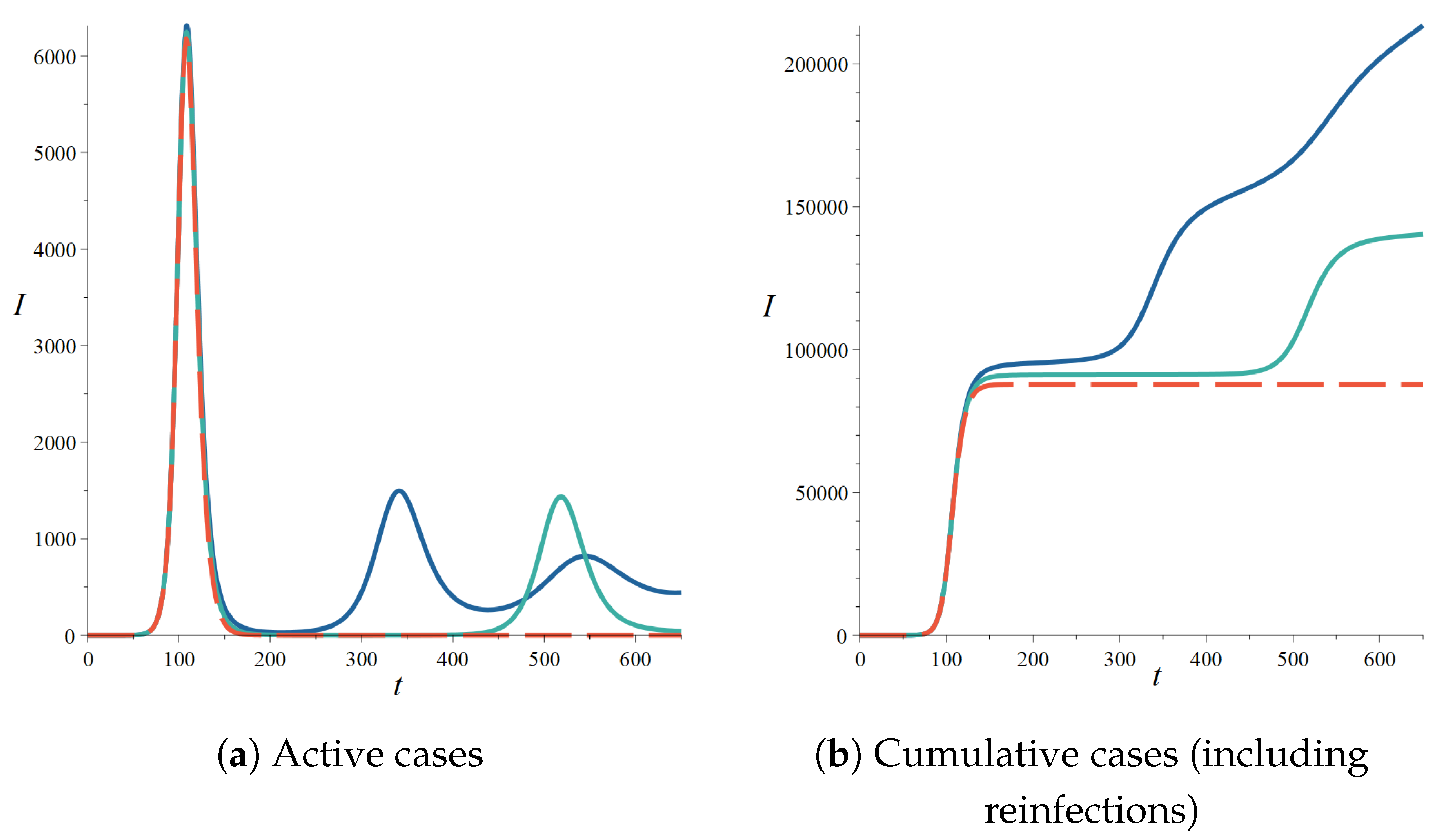
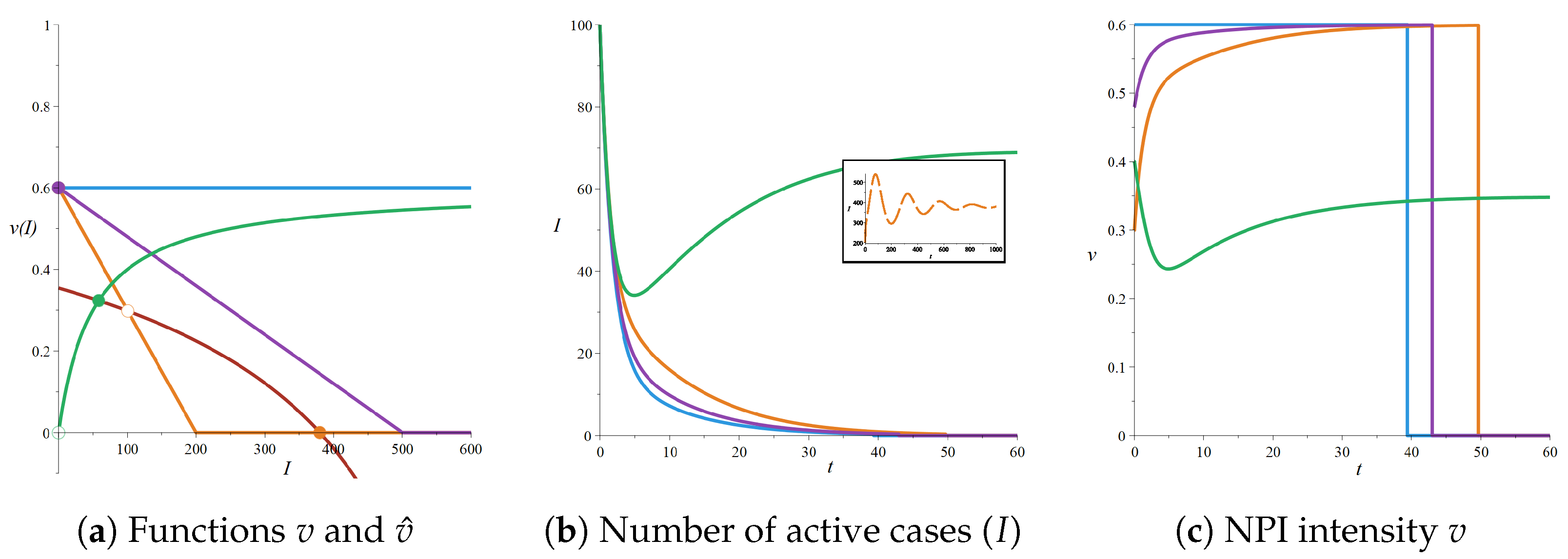
4. Possible Strategies against an Epidemic with Reinfection
4.1. Strategy 1: Constant Control
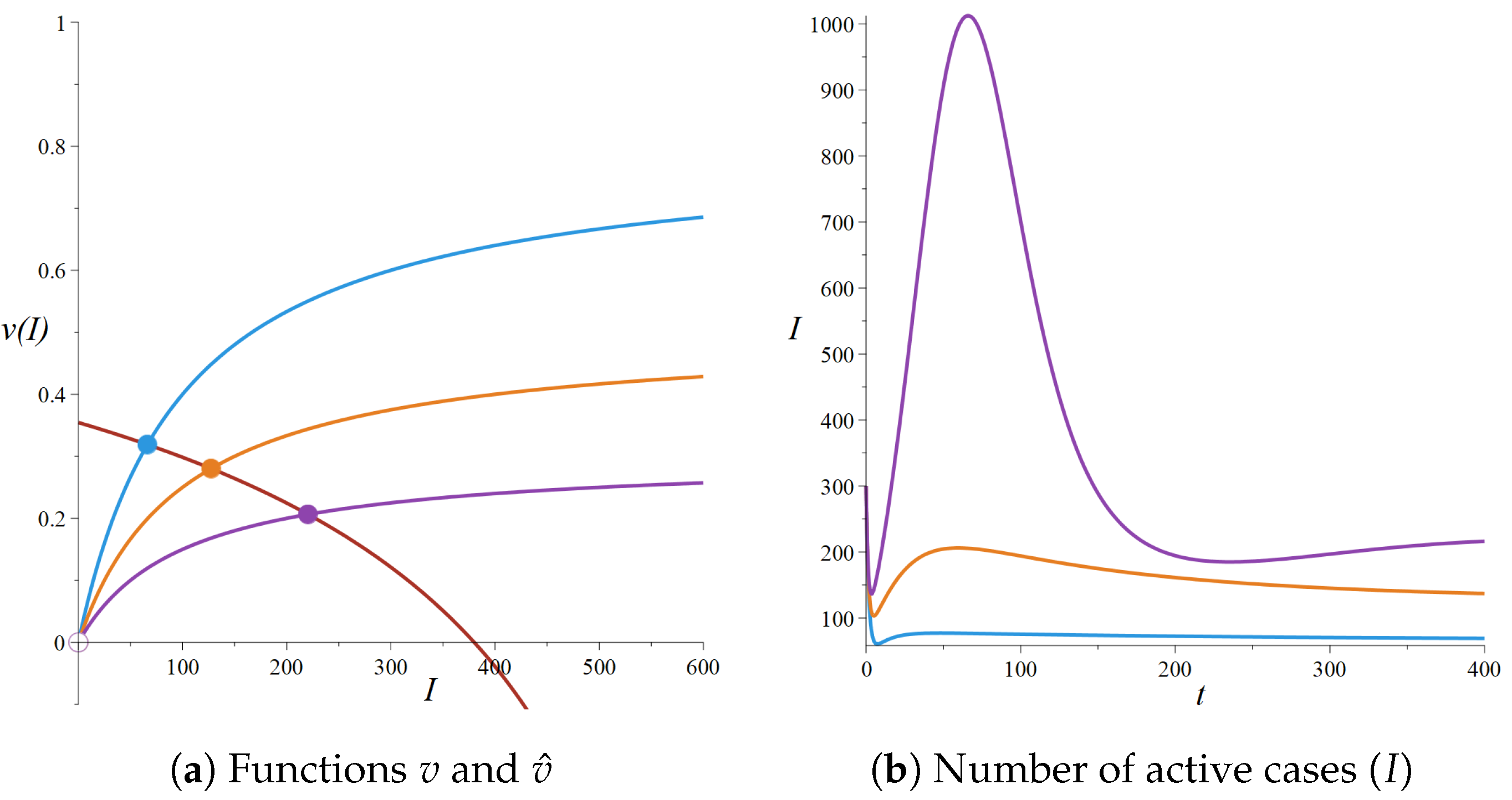
4.2. Strategy 2: NPI Intensity Increasing with the Number of Cases
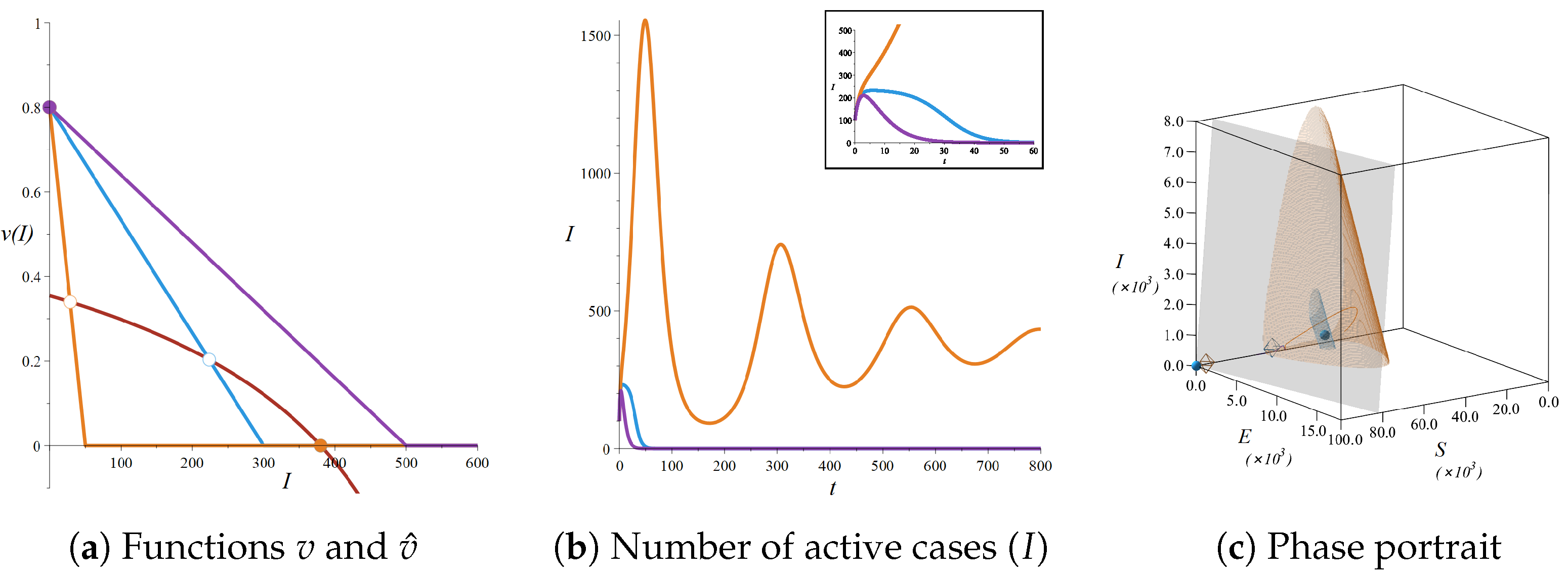
4.3. Strategy 3: Seek to Extinguish the Epidemic
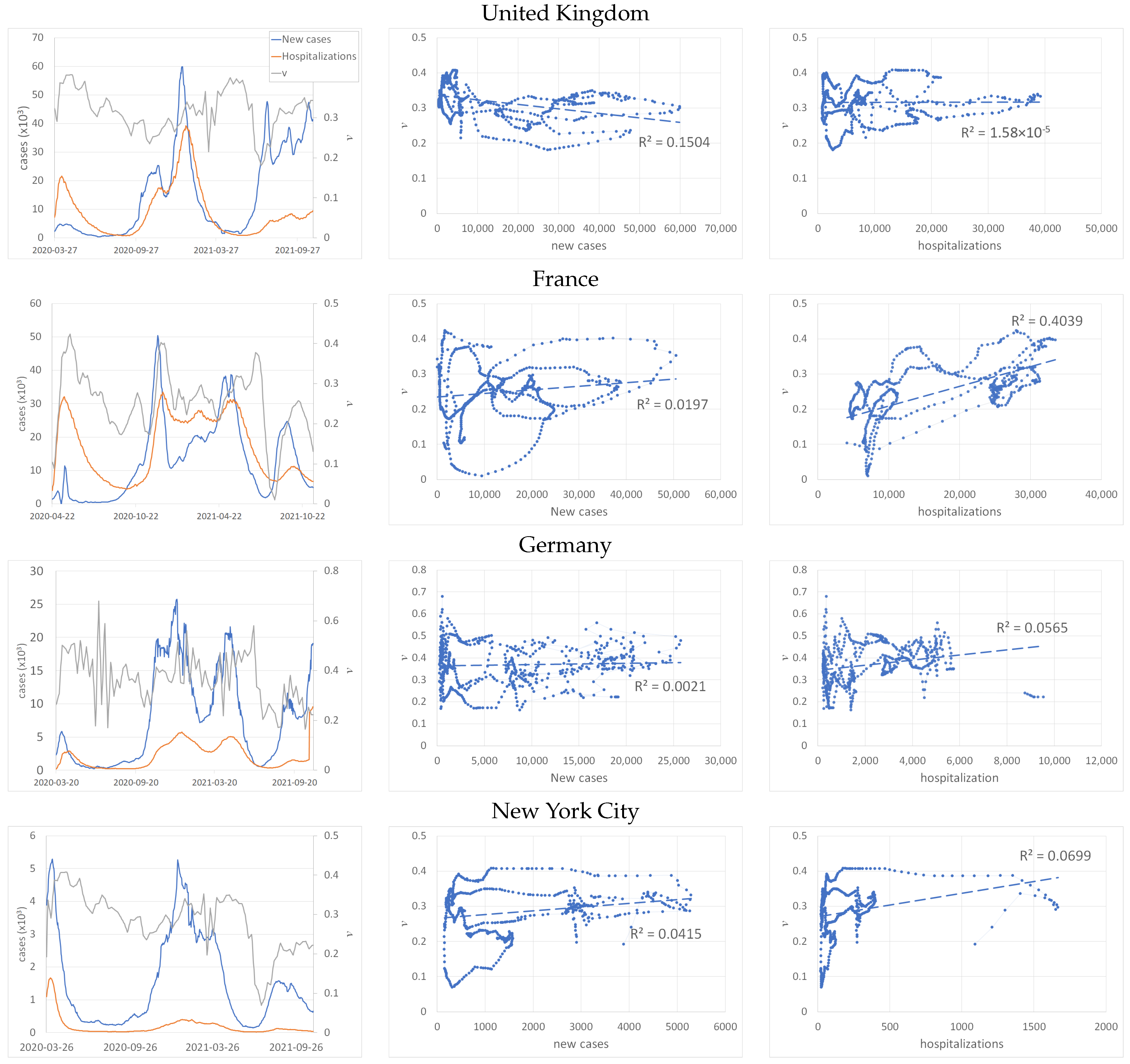
5. Case of the COVID-19 Pandemic: Estimation of NPI Intensities and Identification of the Strategies Chosen by Several Countries
6. Comparison and Discussion of the Effects of Various NPI Strategies on the Dynamics of the Epidemic
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NPIs | Non-Pharmaceutical Interventions |
Appendix A. Mathematical Properties of the Model
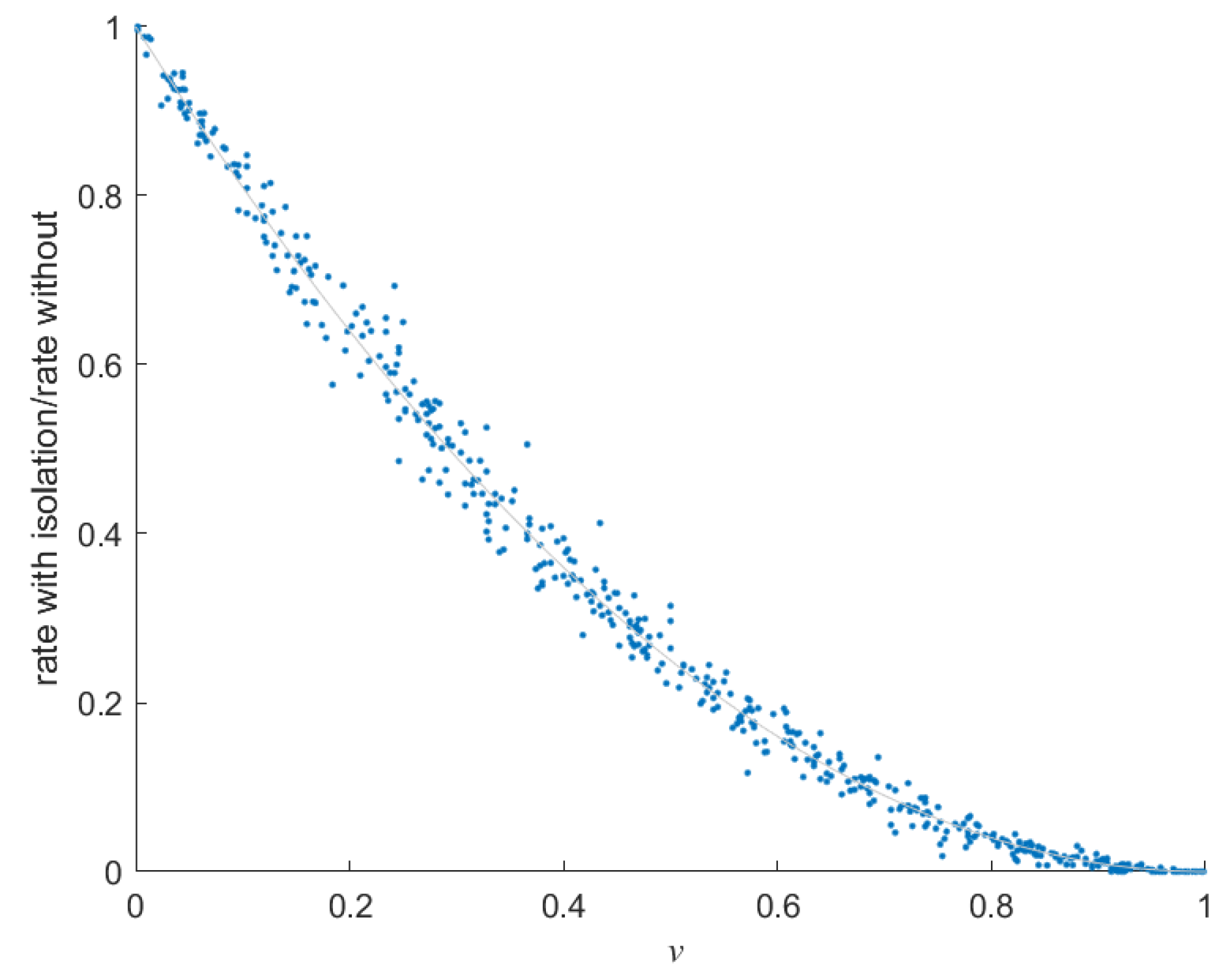
Appendix B. More Details on the Infection Rate Formula
Appendix B.1. Detailed Calculation of the Infection Rate Formula
Appendix B.2. Simulation of Infectious Contacts
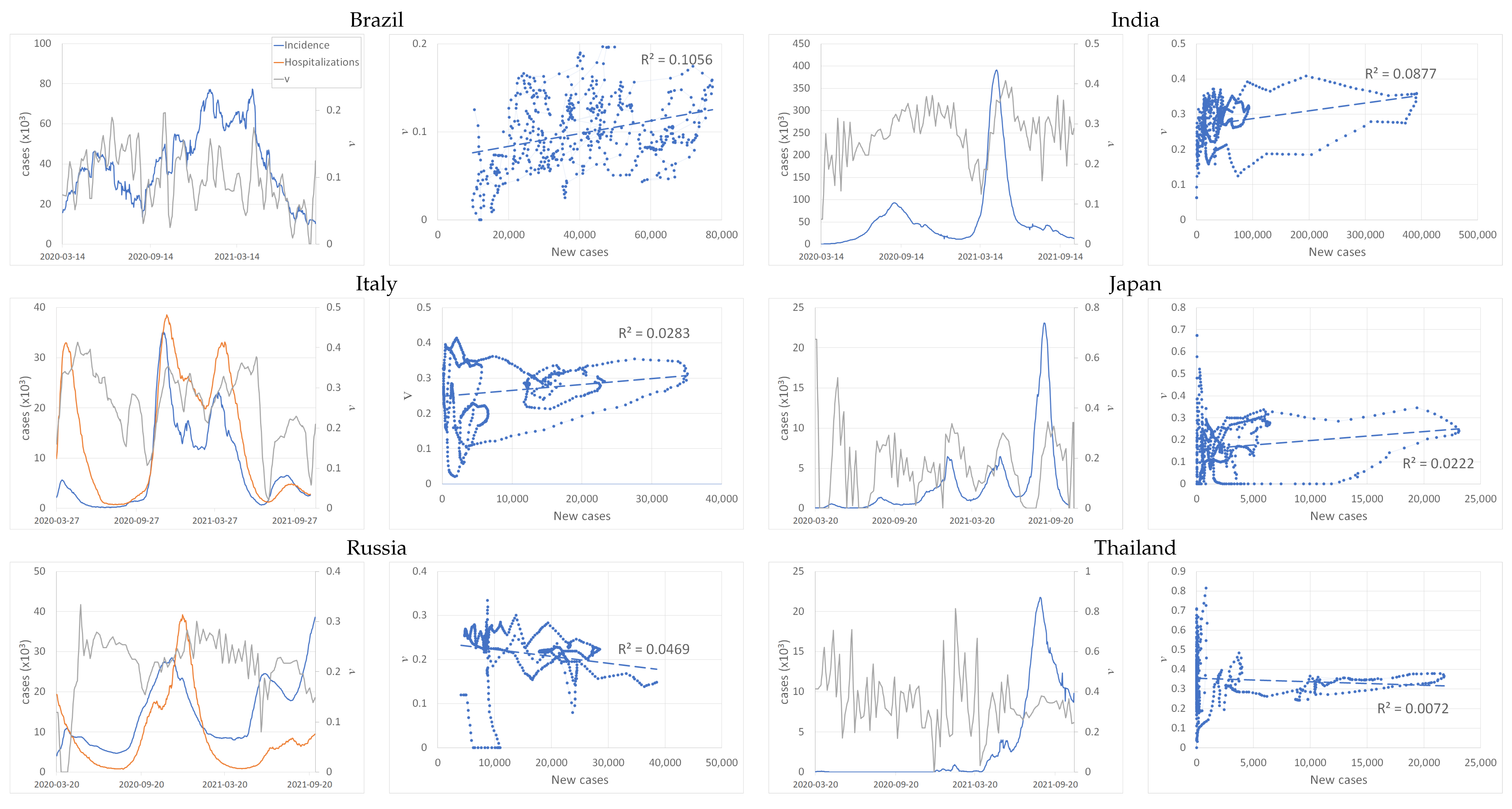
Appendix C. Illustration for Several Other Countries
References
- Allee, W.C.; Bowen, E.S. Studies in animal aggregations: Mass protection against colloidal silver among goldfishes. J. Exp. Zool. 1932, 61, 185–207. [Google Scholar] [CrossRef]
- Odum, E.P.; Barrett, G.W. Fundamentals of Ecology; Saunders Philadelphia: Philadelphia, PA, USA, 1971. [Google Scholar]
- Courchamp, F.; Berec, L.; Gascoigne, J. Allee Effects in Ecology and Conservation; OUP Oxford: Singapore, 2008. [Google Scholar]
- Holden, M.H.; McDonald-Madden, E. High prices for rare species can drive large populations extinct: The anthropogenic Allee effect revisited. J. Theor. Biol. 2017, 429, 170–180. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Gu, Z.; Xia, S.; Shi, B.; Zhou, X.N.; Shi, Y.; Liu, J. What are the underlying transmission patterns of COVID-19 outbreak? An age-specific social contact characterization. EClinicalMedicine 2020, 22, 100354. [Google Scholar] [CrossRef]
- Xia, S.; Liu, J.; Cheung, W. Identifying the relative priorities of subpopulations for containing infectious disease spread. PLoS ONE 2013, 8, e65271. [Google Scholar] [CrossRef] [PubMed]
- Perkins, T.A.; Paz-Soldan, V.A.; Stoddard, S.T.; Morrison, A.C.; Forshey, B.M.; Long, K.C.; Halsey, E.S.; Kochel, T.J.; Elder, J.P.; Kitron, U.; et al. Calling in sick: Impacts of fever on intra-urban human mobility. Proc. R. Soc. B Biol. Sci. 2016, 283, 20160390. [Google Scholar] [CrossRef] [PubMed]
- Auger, P.; Moussaoui, A. On the Threshold of Release of Confinement in an Epidemic SEIR Model Taking into Account the Protective Effect of Mask. Bull. Math. Biol. 2021, 83, 25. [Google Scholar] [CrossRef] [PubMed]
- Howard, J.; Huang, A.; Li, Z.; Tufekci, Z.; Zdimal, V.; van der Westhuizen, H.M.; von Delft, A.; Price, A.; Fridman, L.; Tang, L.H.; et al. An evidence review of face masks against COVID-19. Proc. Natl. Acad. Sci. USA 2021, 118, e2014564118. [Google Scholar] [CrossRef] [PubMed]
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Fehlberg, E. Klassische Runge-Kutta-Formeln vierter und niedrigerer Ordnung mit Schrittweiten-Kontrolle und ihre Anwendung auf Wärmeleitungsprobleme. Computing 1970, 6, 61–71. [Google Scholar] [CrossRef]
- Shokri, A.; Mehdizadeh Khalsaraei, M.; Molayi, M. Nonstandard Dynamically Consistent Numerical Methods for MSEIR Model. J. Appl. Comput. Mech. 2022, 8, 196–205. [Google Scholar] [CrossRef]
- Khalsaraei, M.M.; Shokri, A.; Ramos, H.; Heydari, S. A positive and elementary stable nonstandard explicit scheme for a mathematical model of the influenza disease. Math. Comput. Simul. 2021, 182, 397–410. [Google Scholar] [CrossRef]
- Kamrujjaman, M.; Mahmud, M.S.; Ahmed, S.; Qayum, M.O.; Alam, M.M.; Hassan, M.N.; Islam, M.R.; Nipa, K.F.; Bulut, U. SARS-CoV-2 and Rohingya Refugee Camp, Bangladesh: Uncertainty and How the Government Took Over the Situation. Biology 2021, 10, 124. [Google Scholar] [CrossRef] [PubMed]
- Bauch, C.; d’Onofrio, A.; Manfredi, P. Behavioral Epidemiology of Infectious Diseases: An Overview. In Modeling the Interplay between Human Behavior and the Spread of Infectious Diseases; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; pp. 1–19. [Google Scholar] [CrossRef]
- Manfredi, P.; D’Onofrio, A. Modeling the Interplay between Human Behavior and the Spread of Infectious Diseases; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Feng, Z.; Cramm, J.M.; Nieboer, A.P. Associations of Social Cohesion and Socioeconomic Status with Health Behaviours among Middle-Aged and Older Chinese People. Int. J. Environ. Res. Public Health 2021, 18, 4894. [Google Scholar] [CrossRef]
- Centers for Disease Control. 2021. Available online: https://www.cdc.gov/nhsn/covid19/report-patient-impact.html (accessed on 1 March 2023).
- Trentini, F.; Marziano, V.; Guzzetta, G.; Tirani, M.; Cereda, D.; Poletti, P.; Piccarreta, R.; Barone, A.; Preziosi, G.; Arduini, F.; et al. Pressure on the Health-Care System and Intensive Care Utilization During the COVID-19 Outbreak in the Lombardy Region of Italy: A Retrospective Observational Study in 43,538 Hospitalized Patients. Am. J. Epidemiol. 2021, 191, 137–146. [Google Scholar] [CrossRef] [PubMed]
- Antonini, C.; Calandrini, S.; Stracci, F.; Dario, C.; Bianconi, F. Mathematical Modeling and Robustness Analysis to Unravel COVID-19 Transmission Dynamics: The Italy Case. Biology 2020, 9, 394. [Google Scholar] [CrossRef]
- Ota, M. Will we see protection or reinfection in COVID-19? Nat. Rev. Immunol. 2020, 20, 351. [Google Scholar] [CrossRef]
- Stokel-Walker, C. What we know about COVID-19 reinfection so far. BMJ 2021, 372, n99. [Google Scholar] [CrossRef]
- Ward, H.; Cooke, G.; Atchison, C.; Whitaker, M.; Elliott, J.; Moshe, M.; Brown, J.C.; Flower, B.; Daunt, A.; Ainslie, K.; et al. Declining prevalence of antibody positivity to SARS-CoV-2: A community study of 365,000 adults. Lancet Reg. Health-Eur. 2021, 4, 100098. [Google Scholar] [CrossRef]
- Callaway, E. Fast-spreading COVID variant can elude immune responses. Nature 2021, 589, 500–501. [Google Scholar] [CrossRef]
- Tillett, R.L.; Sevinsky, J.R.; Hartley, P.D.; Kerwin, H.; Crawford, N.; Gorzalski, A.; Laverdure, C.; Verma, S.C.; Rossetto, C.C.; Jackson, D.; et al. Genomic evidence for reinfection with SARS-CoV-2: A case study. Lancet Infect. Dis. 2021, 21, 52–58. [Google Scholar] [CrossRef]
- Adam, D. MODELLING THE PANDEMIC The simulations driving the world’s response to COVID-19. Nature 2020, 580, 316–318. [Google Scholar] [CrossRef] [PubMed]
- Kissler, S.M.; Tedijanto, C.; Goldstein, E.; Grad, Y.H.; Lipsitch, M. Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period. Science 2020, 368, 860–868. [Google Scholar] [CrossRef] [PubMed]
- Bacaër, N. Un modèle mathématique des débuts de l’épidémie de coronavirus en France. Math. Model. Nat. Phenom. 2020, 15, 29. [Google Scholar] [CrossRef]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. Understanding unreported cases in the COVID-19 epidemic outbreak in Wuhan, China, and the importance of major public health interventions. Biology 2020, 9, 50. [Google Scholar] [CrossRef]
- Sun, H.; Qiu, Y.; Yan, H.; Huang, Y.; Zhu, Y.; Gu, J.; Chen, S.X. Tracking Reproductivity of COVID-19 Epidemic in China with Varying Coefficient SIR Model. J. Data Sci. 2022, 18, 455–472. [Google Scholar] [CrossRef]
- Kuniya, T. Prediction of the epidemic peak of coronavirus disease in Japan, 2020. J. Clin. Med. 2020, 9, 789. [Google Scholar] [CrossRef]
- Moussaoui, A.; Auger, P. Prediction of confinement effects on the number of COVID-19 outbreak in Algeria. Math. Model. Nat. Phenom. 2020, 15, 37. [Google Scholar] [CrossRef]
- Moussaoui, A.; Zerga, E.H. Transmission dynamics of COVID-19 in Algeria: The impact of physical distancing and face masks. Aims Public Health 2020, 7, 816. [Google Scholar] [CrossRef]
- Kucharski, A.J.; Klepac, P.; Conlan, A.J.; Kissler, S.M.; Tang, M.L.; Fry, H.; Gog, J.R.; Edmunds, W.J.; Emery, J.C.; Medley, G.; et al. Effectiveness of isolation, testing, contact tracing, and physical distancing on reducing transmission of SARS-CoV-2 in different settings: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 1151–1160. [Google Scholar] [CrossRef]
- Tuite, A.R.; Fisman, D.N.; Greer, A.L. Mathematical modelling of COVID-19 transmission and mitigation strategies in the population of Ontario, Canada. Cmaj 2020, 192, E497–E505. [Google Scholar] [CrossRef]
- Malkov, E. Simulation of coronavirus disease 2019 (COVID-19) scenarios with possibility of reinfection. Chaos Solitons Fractals 2020, 139, 110296. [Google Scholar] [CrossRef]
- Batistela, C.M.; Correa, D.P.; Bueno, Á.M.; Piqueira, J.R.C. SIRSi compartmental model for COVID-19 pandemic with immunity loss. Chaos Solitons Fractals 2021, 142, 110388. [Google Scholar] [CrossRef]
- Costa, A.O.C.; de Carvalho Aragão Neto, H.; Lopes Nunes, A.P.; Dias de Castro, R.; Nóbrega de Almeida, R. COVID-19: Is reinfection possible? EXCLI J. 2021, 20, 522–536. [Google Scholar] [CrossRef]
- Cai, L.; Liu, J.; Chen, Y. Dynamics of an Age-Structured HIV Model with Super-Infection. Appl. Comput. Math. Int. J. 2021, 20, 257–276. [Google Scholar]
- Sheehan, M.M.; Reddy, A.J.; Rothberg, M.B. Reinfection Rates Among Patients Who Previously Tested Positive for Coronavirus Disease 2019: A Retrospective Cohort Study. Clin. Infect. Dis. Off. Publ. Infect. Dis. Soc. Am. 2021, 73, 1882–1886. [Google Scholar] [CrossRef] [PubMed]
- Hanrath, A.T.; Payne, B.A.I.; Duncan, C.J.A. Prior SARS-CoV-2 infection is associated with protection against symptomatic reinfection. J. Infect. 2021, 82, e29–e30. [Google Scholar] [CrossRef] [PubMed]
- Sabino, E.C.E.A. Resurgence of COVID-19 in Manaus, Brazil, despite high seroprevalence. Lancet 2021, 397, 452–455. [Google Scholar] [CrossRef]
- Goddard, A.F.; Patel, M. SARS-CoV-2 variants and ending the COVID-19 pandemic. Lancet 2021, 397, 952–954. [Google Scholar]
- Hoffmann, M.; Krüger, N.; Schulz, S.; Cossmann, A.; Rocha, C.; Kempf, A.; Nehlmeier, I.; Graichen, L.; Moldenhauer, A.S.; Winkler, M.S.; et al. The Omicron variant is highly resistant against antibody-mediated neutralization: Implications for control of the COVID-19 pandemic. Cell 2022, 185, 447–456.e11. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, N. Report 49: Growth and Immune Escape of the Omicron SARS-CoV-2 Variant of Concern in England; Technical Report; Imperial College London: London, UK, 2021. [Google Scholar] [CrossRef]
- Santé Publique France. 2021. Available online: https://www.santepubliquefrance.fr/dossiers/coronavirus-covid-19/coronavirus-chiffres-cles-et-evolution-de-\la-covid-19-en-france-et-dans-le-monde/articles/covid-19-tableau-de-bord\-del-epidemie-en-chiffres (accessed on 26 October 2022).
- Ma, Q.; Liu, J.; Liu, Q.; Kang, L.; Liu, R.; Jing, W.; Wu, Y.; Liu, M. Global Percentage of Asymptomatic SARS-CoV-2 Infections Among the Tested Population and Individuals With Confirmed COVID-19 Diagnosis: A Systematic Review and Meta-analysis. JAMA Netw. Open 2021, 4, e2137257. [Google Scholar] [CrossRef]
- Johansson, M.A.; Quandelacy, T.M.; Kada, S.; Prasad, P.V.; Steele, M.; Brooks, J.T.; Slayton, R.B.; Biggerstaff, M.; Butler, J.C. SARS-CoV-2 Transmission From People Without COVID-19 Symptoms. JAMA Netw. Open 2021, 4, e2035057. [Google Scholar] [CrossRef]
- Bender, J.K.; Brandl, M.; Höhle, M.; Buchholz, U.; Zeitlmann, N. Analysis of Asymptomatic and Presymptomatic Transmission in SARS-CoV-2 Outbreak, Germany, 2020. Emerg. Infect. Dis. 2021, 27, 1159–1163. [Google Scholar] [CrossRef]
- Luo, L.; Liu, D.; Liao, X.; Wu, X.; Jing, Q.; Zheng, J.; Liu, F.; Yang, S.; Bi, H.; Li, Z.; et al. Contact settings and risk for transmission in 3410 close contacts of patients with COVID-19 in Guangzhou, China: A prospective cohort study. Ann. Intern. Med. 2020, 173, 879–887. [Google Scholar] [CrossRef]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Volume 61: Texts in Applied Mathematics; Springer: Boston, MA, USA, 2015. [Google Scholar] [CrossRef]
- He, X.; Lau, E.H.; Wu, P.; Deng, X.; Wang, J.; Hao, X.; Lau, Y.C.; Wong, J.Y.; Guan, Y.; Tan, X.; et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med. 2020, 26, 672–675. [Google Scholar] [CrossRef]
- Walsh, K.A.; Spillane, S.; Comber, L.; Cardwell, K.; Harrington, P.; Connell, J.; Teljeur, C.; Broderick, N.; Gascun, C.F.D.; Smith, S.M.; et al. The duration of infectiousness of individuals infected with SARS-CoV-2. J. Infect. 2020, 81, 847–856. [Google Scholar] [CrossRef] [PubMed]
- Lauer, S.A.; Grantz, K.H.; Bi, Q.; Jones, F.K.; Zheng, Q.; Meredith, H.R.; Azman, A.S.; Reich, N.G.; Lessler, J. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: Estimation and application. Ann. Intern. Med. 2020, 172, 577–582. [Google Scholar] [CrossRef]
- Hilton, J.; Keeling, M.J. Estimation of country-level basic reproductive ratios for novel Coronavirus (SARS-CoV-2/COVID-19) using synthetic contact matrices. PLoS Comput. Biol. 2020, 16, e1008031. [Google Scholar] [CrossRef] [PubMed]
- Ke, R.; Romero-Severson, E.; Sanche, S.; Hengartner, N. Estimating the reproductive number R0 of SARS-CoV-2 in the United States and eight European countries and implications for vaccination. J. Theor. Biol. 2021, 517, 110621. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, N.M.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunubá, Z.; Cuomo-Dannenburg, G.; et al. Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. Imperial College COVID-19 Response Team. Imp. Coll. COVID-19 Response Team 2020, 20, 77482. [Google Scholar]
- Hoffart, A.; Johnson, S.U.; Ebrahimi, O.V. Loneliness and Social Distancing During the COVID-19 Pandemic: Risk Factors and Associations With Psychopathology. Front. Psychiatry 2020, 11, 589127. [Google Scholar] [CrossRef]
- Lüdecke, D.; von dem Knesebeck, O. Decline in Mental Health in the Beginning of the COVID-19 Outbreak Among European Older Adults—Associations With Social Factors, Infection Rates, and Government Response. Front. Public Health 2022, 10, 844560. [Google Scholar] [CrossRef] [PubMed]
- Arino, J.; Van Den Driessche, P. The basic reproduction number in a multi-city compartmental epidemic model. In Positive Systems; Springer: Berlin/Heidelberg, Germany, 2003; pp. 135–142. [Google Scholar]
- Arino, J.; Van den Driessche, P. Disease spread in metapopulations. Fields Inst. Commun. 2006, 48, 1–13. [Google Scholar]


| Parameter | Interpretation |
|---|---|
| infection rate | |
| k | transfer rate from exposed to infected. is the average incubation duration. |
| is the average time spent in the infectious state. | |
| transfer rate from recovered to susceptible. is the average time before | |
| losing immunity. | |
| v | intensity of NPI, measured as the equivalent proportion of the population |
| in isolation. |
| Strategy 1 | Strategy 2 | Strategy 3 | |
|---|---|---|---|
| Effectiveness | high | low | high |
| Intensity | highest | medium | high |
| Duration | short | very long | short |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen-Huu, T.; Auger, P.; Moussaoui, A. On Incidence-Dependent Management Strategies against an SEIRS Epidemic: Extinction of the Epidemic Using Allee Effect. Mathematics 2023, 11, 2822. https://doi.org/10.3390/math11132822
Nguyen-Huu T, Auger P, Moussaoui A. On Incidence-Dependent Management Strategies against an SEIRS Epidemic: Extinction of the Epidemic Using Allee Effect. Mathematics. 2023; 11(13):2822. https://doi.org/10.3390/math11132822
Chicago/Turabian StyleNguyen-Huu, Tri, Pierre Auger, and Ali Moussaoui. 2023. "On Incidence-Dependent Management Strategies against an SEIRS Epidemic: Extinction of the Epidemic Using Allee Effect" Mathematics 11, no. 13: 2822. https://doi.org/10.3390/math11132822
APA StyleNguyen-Huu, T., Auger, P., & Moussaoui, A. (2023). On Incidence-Dependent Management Strategies against an SEIRS Epidemic: Extinction of the Epidemic Using Allee Effect. Mathematics, 11(13), 2822. https://doi.org/10.3390/math11132822







