Abstract
We investigated two different approaches, which can be used to extend the standard quantum statistical mechanics. One is based on fractional calculus, and the other considers the extension of the concept of entropy, i.e., the Tsallis statistics. We reviewed and discussed some of the main properties of these approaches and used the thermal Green function formalism to perform the developments, simultaneously allowing us to analyze each case’s dynamics and thermodynamics aspects. In particular, the results allow us to understand how the extensions change the behavior of some quantities, particularly fluctuations related to the system.
MSC:
82B03; 82B05; 82B10
1. Introduction
Statistical mechanics is one of the most intriguing fields of physics, where dynamics and probability are used for analyzing the behavior of systems in connection with thermodynamics. The foundations of this field resulted from intense discussions between adherents of different points of view, with the ideas first formulated by Boltzmann as a crucial starting point [1,2,3,4]. It has been successfully applied in many systems [5,6], allowing us to obtain a suitable description. On the other hand, the existence of many different phenomena, such as self-gravitating systems [7], turbulent systems [8], quantum systems with long-range interactions [9], non-Markovian systems [10,11], and anomalous diffusion [12], among others, which are characterized, for example, by fractal and multifractal aspects [13], has motivated the extension of the approach used in these contexts to obtain a suitable description. One of the possibilities for facing systems with unusual properties, such as long-range interactions, fractal and or multifractal aspects, was proposed in Ref. [14]. It considers the following extension for the Boltzmann–Gibbs entropy, namely Tsallis entropy,
where the parameter q can be connected to different aspects of the system [15]. Equation (1) recovers the standard Boltzmann–Gibbs entropy for , i.e., , where is the Boltzmann constant. Other entropies have also been considered to extend the standard approach, such as the Renyi entropy [16,17] and the Kaniadakis entropy [18,19]. The approach based on Equation (1) has been applied in different scenarios such as relativistic gas [20], Bose–Einstein condensation [21,22], seismology [23], and high energy multiparticle production [24]. Simultaneously with these developments, fractional calculus has been advanced in different fields as a powerful approach to incorporating different aspects of the system with extensions of the differential operators to a noninteger order. It has been applied in several scenarios, such as anomalous diffusion [25,26,27], anomalous charge transport in semiconductor [28], chaos [29], magnetic resonance imaging [30,31,32,33,34], and electrical impedance [35,36]. The fractional approach has also been used in thermodynamics [37,38,39] and/or in statistical mechanics [40,41,42]. In the first case, it extended the differential operator in the thermodynamic relations to a noninteger order fractional operator. In this context, ideal gas and gas with a weak interaction were analyzed and compared with experimental data [39]. Fractional calculus has also been used to extend statistical mechanics through fundamental equations such as the Liouville equation [43], with the possibility of applications in different scenarios, including long-range interactions and fractal and multifractal aspects, among others.
Here, we analyzed the quantum statistical mechanics in these approaches by focusing on fractional calculus and Tsallis formalism by extending and revisiting some results in the literature [44,45,46]. These results allow us to understand how the dynamic aspects and statistical weight changes the behavior of the thermodynamic quantities, particularly fluctuations related to the system.
2. Generalized Statistical Mechanics
Let us start our analysis of two possibilities for extending statistical mechanics, firstly by considering the case related to the fractional operators. Next, we considered the Tsallis formalism, which has been developed from the extension of the concept of entropy. After these developments, we analyzed the mixing between the fractional approach and a general entropy, which has the Tsallis entropy as a particular case. We focused on the quantum statistics for these cases and used the formalism employed in Ref. [47] regarding the thermal Green function method, which allowed us to evidence the differences among these cases.
2.1. Fractional Dynamics and Statistical Mechanics
We shall consider the following effective Hamiltonian:
where and are second quantized operators, is an effective constant, is a distribution,
is the quantum Riesz operator [26,27], is a nonlocal term, and the last term is the interaction between the components of the system. The extension of the kinetic energy to fractional operators also incorporates a nonlocal behavior and recovers the usual one for . It is also important to mention that the nonlocal term is such that , to preserve the interpretations concerning as in the standard case in terms of the field operator. In addition, this Hamiltonian extends the one discussed in Refs. [44,45] with the presence of the fractional derivative in the space of distributed order and the nonlocal term. It should be stressed that Equation (2) can also be considered a phenomenological approach, where the parameters are adjusted to capture the behavior exhibited by the experimental data. In this sense, different systems may interact differently and require different parameter values. The Heisenberg equation yields for the following equation of motion:
Equation (4) is a Schrödinger-like equation with a nonlocal term and a fractional derivative applied to the spatial variable instead of the usual differential operators applied to the spatial variable. This equation in a first quantized perspective, without the interaction term, was analyzed in several scenarios [45,48,49]. In particular, the solution for the free case (i.e., absence of external fields and without interaction) reminds us of the Lévy distribution. By using the Fourier transform, we can simplify Equation (4) to
From this equation, we can observe that the presence of the fractional derivative changes the exponent of the momentum, and the solution in the absence of interaction potentials is given by
for the case . Equation (6) for formally reminds the Fourier transform of the Lévy distributions, which are characterized by a power law in the asymptotic behavior in the representation. This feature can be related to extending the Brownian trajectories in the path integral formalism to the Lévy ones, which implies fractional differential operators [40].
Now, let us analyze the quantum statistics from the above scenario. To perform this analysis, we used the thermal Green function technique, which may be directly related to the dynamical aspects of the and allowed us to obtain several physical quantities, such as the density of particles, specific heat, and other thermodynamical quantities. Following Ref. [47], we defined the one-particle Green function as follows:
where the thermodynamic averages, , were evaluated by taking the grand canonical ensemble into account, i.e.,
is the Dyson time-ordering operator and 1, and correspond to the variables and , respectively. From this equation, we can define the correlation functions:
where > and < represent the Green function to , and . The upper (lower) sign corresponds to the bosonic (fermionic) case. From Equations (7) and (9), it is possible to show that by using the cyclic invariance of the trace . This result shows that the above Green function satisfies the same periodic boundary condition of the non-fractional case [47], in contrast to the one [46,50,51] formulated within the Tsallis formalism [52]. Similarly to what is performed in the usual case, we may introduce the spectral function, , defined as follows:
with
and
The form of the previous equations for the Green thermal functions results from the translational and rotational invariance of the Hamiltonian considered here for the absence of external potential. By using Equation (9) and the boundary condition obtained above, we can express and as follows:
i.e., in terms of the spectral function, with . It is worth mentioning that is directly connected with the Fermi–Dirac or Bose–Einstein distribution. In this manner, the dynamic aspects are connected with the spectral function, which will give the dispersion of the energy related to the interaction term. The equation of motion satisfied by the Green function defined in Equation (7) is given by
It can be obtained by using the Heisenberg equation, where is given by
To obtain a solution for Equation (14), we may consistently approximate Equation (15) in accordance with the propagator interpretation of . The first approximation to be considered for Equation (15) to obtain information from Equation (14) is the Hartree approximation, . The second is the Hartree–Fock approximation given by . Other approximations consider the collision process connected to the interaction potential. These approximations have a direct influence on the behavior of the spectral function. The two first cases are formally given in terms of the delta Dirac function, i.e., the energy is localized. For the other cases characterized by collision terms, the behavior is not localized and can be related to a power-law distribution.
By using the previous results, we may relate with the average of the particle density with momentum and energy , i.e.,
Equation (16) allows us to obtain the pressure for this system by using the equation . Another useful result that may be obtained in this framework concerns the grand canonical potential, . By incorporating a coupling constant, , in front of the interaction energy, we have
in the absence of external potential, where
and is the volume where the system is defined. This result differs from the one presented in Refs. [44,45]. In Equation (18), we have the presence of a term connected with the nonlocal term in the Hamiltonian and the fact that the kinetic energy has a distribution of the moments.
Now, we consider the free particle case in this context in the Hartree approximation with the presence of the nonlocal term. Equation (14) can be written as follows:
We can also simplify Equation (19) by approximating the interaction term with a constant, i.e.,
for a translationally invariant system with and . By using the previous result and the equation
where , it is possible to obtain from Equation (19) the following result:
with the spectral function in this approximation being given by
Equation (23) allows us to obtain the number of particles in terms of the chemical potential , or vice versa, and the internal energy as follows:
and
These equations allow us to show that, in the limit of low density (), the pressure can be found. It is given by , which is essentially the van der Waals equation without the volume exclusion effect. This feature suggests that the presence of a fractional derivative in Equation (2) does not change the thermodynamic relations, as expected. The changes are expected in the quantities directly connected with the effect of the dynamics, such as in the low-temperature limit, in which the dynamic effects are pronounced. At this point, we can mention the developments performed in Refs. [37,38,39], where the thermodynamics relations were extended by incorporating fractional differential operators.
Figure 1 shows the behavior of the internal energy and the specific heat in the low-temperature limit for the Bose–Einstein distribution in the case . It shows that the fractional term present in the Hamiltonian has a pronounced effect on the low-temperature limit. This point is evidence that energy fluctuations are governed by the fractional terms in this limit when present in the system. It is worth mentioning that several systems present the behavior for the specific heat in this limit, such as two-dimensional Kagome antiferromagnet, [53], and amorphous and crystalline particles at low temperatures [45]. In the limit of high temperatures, we recovered the standard behavior for the specific heat as shown in Figure 1.
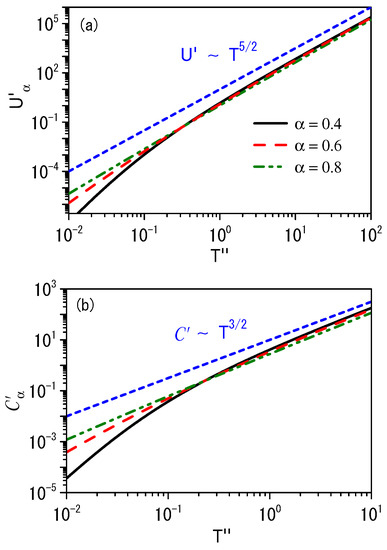
Figure 1.
Behavior of the internal energy (see (a)) and the specific heat (see (b)) for the Bose–Einstein distribution by taking into account, where and . This choice combines the usual and fractional kinetic energies and shows that the fractional one has a pronounced effect on the asymptotic limit of low temperature. We considered, for simplicity, and .
Another case that has an unusual behavior in low temperatures is liquid Helium [54] as shown in Figure 2. The behavior in this limit for the specific heat is as discussed in Ref. [54], which is the one obtained with the formalism presented in this section for the Bose–Einstein distribution. From a phenomenological point of view, the fractional approach captures the complex behavior of the interactions present in this system, which deserves a careful analysis.
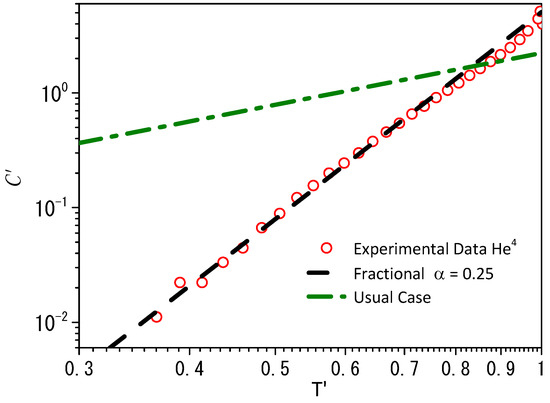
Figure 2.
This figure shows the behavior of the model for an ideal Bose–Einstein distribution with and the experimental data obtained from Ref. [55] for the specific heat of liquid Helium. The following relations are valid: and , similar to what was performed in Ref. [55].
2.2. Tsallis Approach and Thermal Green Functions
Let us start our discussion about quantum statistics in the context of Tsallis formalism. It will review and follow the developments performed in Ref. [50] in terms of the thermal Green function formalism.
The main difference to previous development concerns the statistical approach used, which is based on the Tsallis entropy [15], i.e.,
instead of the usual entropy. Applying the maximum principle of entropy, we can obtain the density matrix by taking into account the normalized constraints [14],
and the usual normalization of the density matrix . It is given by
where
and with . Here, is the normalized temperature and and are the Lagrange multipliers associated with the normalized q-expectation values. Two self-consistency conditions follow from Equation (29): and . By using the previous results, the expression for a general normalized q-expectation value is then
From Equation (30), , can be deduced. Equation (30) can also be written as follows:
where
In the previous equations of this section, we considered the Hamiltonian given by Equation (2) with and , which corresponds to the standard form of the Hamiltonian with an interaction term. In this approach to statistical mechanics, we revisited some of the developments performed in the previous section. The one-particle Green function is then with the normalized q-average as follows [50]:
The previous equation recovers the standard case for , i.e., . By using the integral contour representation employed in Refs. [46,51],
with and , where the contour C starts from on the real axis, encircles the origin once counterclockwise and returns to , Equation (34) is expressed in terms of the Green function with :
where
with . One particle’s standard result for the Green function is recovered for . As before, we can introduce correlation functions [46,50]
The spectral weight function in frequency space by taking the Fourier transform concerning time differences, , can be introduced as before. We assumed a translational invariance in time at this stage. We can thus express and in terms of these in the following way [46,50]:
and
The spectral function weight is a given system property not dependent on the ensemble as in the previous case. The results appear to be similar to those in the previous section with the modifications noted here. Using the Fourier representations of the step functions involved in the time-ordered Green function in Equation (36), an important result can be deduced [50]:
For a uniform system, we can take Fourier transforms concerning as in the previous section and express the one-particle momentum distribution function in terms of the spectral weight function of the N-particle system as follows:
The chemical potential is determined by the following expression:
It is worth mentioning that the spectral function in this context is determined by the thermal Green function, which emerges from the following equation:
which is similar to the one presented before. However, the simple form of the boundary condition cannot be applied due to the structure of the statistical distribution, which is a power law instead of an exponential. For the free particle case, it is possible to show that as in the previous case. This result for the free particle case implies that the internal energy is given by
It is also possible to consider the Hartree approximation for Equation (44), with similar results for the spectral function. In fact, for the Hartree approximation, i.e., , it is possible to show that the dynamics equation for the Green function is given by:
Equation (46) may be simplified by using similar assumptions to those used for Equation (19) and allow us to obtain , where . Note that considering collision terms implies using boundary conditions that will lead us to cumbersome calculations [56,57]. Thus, obtaining the corrections due to the collision terms is harder than the previous one in this context. Figure 3 illustrates the behavior of the specific heat for the formalism presented in this section. We observe that the behavior in the low and high temperatures is similar to that in the standard case. The difference is for intermediate temperatures, i.e., temperatures nearly , for the values of q considered in this figure.
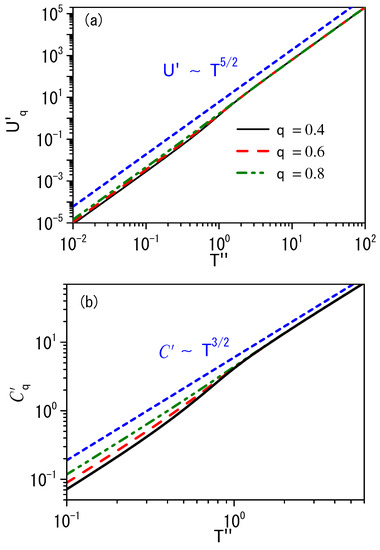
Figure 3.
Behavior of the internal energy (see (a)) and the specific heat (see (b)) for the Bose–Einstein distribution by taking the free particle case into account, where and . We consider, for simplicity, .
2.3. Fractional-Generalized Entropy and Thermal Green Functions
Now, we consider the fractional approach in the context of thermostatistics obtained from a generalized entropy, which can be related to the Tsallis entropy. For this, we considered the entropy [58], , which can be related to the Tsallis and Renyi entropies. Applying the maximum entropy principle, we can obtain the density matrix by considering the normalized constraints defined in the previous section, respectively. It is given by:
where , with
In this context, the normalized temperature is represented by , instead of , presented in the previous section. The parameters and are the Lagrange multipliers associated with the normalized q-expectation values as before. Similar to the previous section, we may consider the following form for the q-expectation values:
where
and
In this approach to statistical mechanics, the one-particle Green function is given by:
which is formally equal to the one presented in the previous section. In fact, Equation (52) has the same formal aspect of Equation (34). However, the q-average is given by Equation (49), obtained from the distribution given by Equation (47), which has a different dependence on the Lagrange parameter . We may also use the integral contour representation employed in the previous section to obtain
where, in this case, . In terms of the definitions presented in this section for the expectation values and the thermal Green function, we can express and as follows:
and
These results are formally equal to the previous ones for the Tsallis case and can also be expressed in terms of the spectral function . The spectral function in this context is determined by the thermal Green functions, which emerge from the following equation:
which has a fractional spatial derivative of distributed order in the kinetic term and the presence of a nonlocal term. For the free particle case, it is possible to show that
This result allows us to show that the internal energy for this case is given by
and the mean value for the number of particles is
Figure 4 shows the trend of the specific heat for the previous cases and the mixing of the two cases obtained with the approach presented in this section. It is possible to verify that the fractional kinetic term, i.e., , has a pronounced effect on the limit of small and high temperatures. We observe the effect of for intermediate temperature as in Figure 3b.
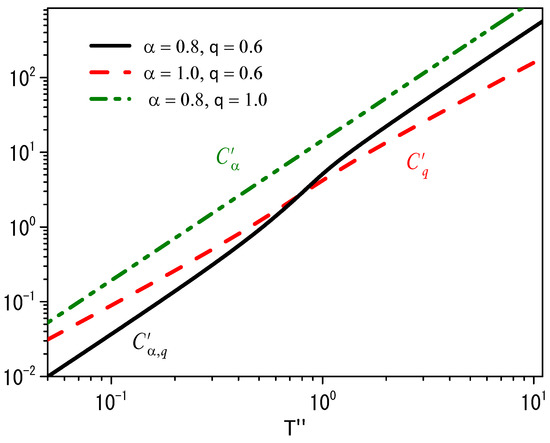
Figure 4.
Trend of the specific heat for the Bose–Einstein distribution by taking the free particle case into account with and , where and . We consider, for simplicity, .
3. Discussions and Conclusions
We investigated two different extensions of the quantum statistical approach. The first one considers an effective Hamiltonian in terms of the fractional derivative in the space of distributed order with a nonlocal term. The second one considers the extension of the concept of entropy to a non-additive case, allowing us to obtain power-law distributions for the statistical weight instead of the Boltzmann–Gibbs distributions characterized by exponential behavior. These approaches were investigated using the thermal Green functions, which allowed us to work in a unified way with the Bose–Einstein and Fermi–Dirac distributions and establish some differences between the formalisms. In this case, we obtained the behavior with the temperature for internal energy and the specific heat for both extensions of the quantum statistics. The behavior for each case was illustrated in Figure 1 and Figure 3. We observed for the first case that, depending on the choice of the fractional parameter in the distributed fractional space derivative, the behavior in the low-temperature limit is different from usual when . In the limit of high temperatures, the usual behavior is recovered. This feature reflects the mixing of the usual and the fractional differential operators connected to the different forms of the kinetic term. In particular, we considered this feature to fit the specific heat of from the phenomenological point of view (see Figure 2). For the case worked out in Section 2.2, we observed that the behavior for intermediate temperatures is different from usual for the free particle case. In the other limits, we see the same behavior as the temperature changes. These results have shown that different approaches present different behaviors. Choosing these or other extensions, such as the one presented in Section 2.3, which extends the results presented in Section 2.1 and Section 2.2 (see, Figure 4), requires a careful system analysis to choose the suitable approach. We hope that the results presented here can be helpful in the discussion of systems with nonstandard behavior and statistical approaches.
Author Contributions
Conceptualization, E.K.L., L.R.E. and L.R.d.S.; methodology, E.K.L., L.R.E. and L.R.d.S.; formal analysis, E.K.L., L.R.E. and L.R.d.S.; investigation, E.K.L., L.R.E. and L.R.d.S.; writing—original draft preparation, E.K.L., L.R.E. and L.R.d.S.; writing—review and editing, E.K.L., L.R.E. and L.R.d.S. All authors have read and agreed to the published version of the manuscript.
Funding
E.K.L. acknowledges the support of the CNPq (Grant No. 301715/2022-0).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Uffink, J. Boltzmann’s Work in Statistical Physics. In The Stanford Encyclopedia of Philosophy, Summer 2022 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2022. [Google Scholar]
- Goldstein, S. Boltzmann’s approach to statistical mechanics. In Chance in Physics: Foundations and Perspectives; Springer: Berlin/Heidelberg, Germany, 2001; pp. 39–54. [Google Scholar]
- Klein, M.J. The development of Boltzmann’s statistical ideas. In Proceedings of the The Boltzmann Equation: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 1973; pp. 53–106. [Google Scholar]
- Lebowitz, J.L. Statistical mechanics: A selective review of two central issues. Rev. Mod Phys. 1999, 71, S346. [Google Scholar] [CrossRef]
- Pathria, R.K. Statistical Mechanics; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Huang, K. Statistical Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Ourabah, K. Quasiequilibrium self-gravitating systems. Phys. Rev. D 2020, 102, 043017. [Google Scholar] [CrossRef]
- Jung, S.; Swinney, H.L. Velocity difference statistics in turbulence. Phys. Rev. E 2005, 72, 026304. [Google Scholar] [CrossRef] [PubMed]
- Defenu, N.; Donner, T.; Macrí, T.; Pagano, G.; Ruffo, S.; Trombettoni, A. Long-range interacting quantum systems. arXiv 2021, arXiv:2109.01063. [Google Scholar]
- Xiong, H.N.; Lo, P.Y.; Zhang, W.M.; Nori, F.; Feng, D.H. Non-Markovian dynamics impact on the foundations of statistical mechanics. arXiv 2013, arXiv:1311.1282. [Google Scholar]
- Speck, T.; Seifert, U. The Jarzynski relation, fluctuation theorems, and stochastic thermodynamics for non-Markovian processes. J. Stat. Mech: Theory Exp. 2007, 2007, L09002. [Google Scholar] [CrossRef]
- Pękalski, A.; Sznajd-Weron, K. Anomalous Diffusion: From Basics to Applications; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Klages, R. Microscopic Chaos, Fractals and Transport in Nonequilibrium Statistical Mechanics; World Scientific: Singapore, 2007. [Google Scholar]
- Tsallis, C.; Mendes, R.S.; Plastino, A.R. The role of constraints within generalized nonextensive statistics. Phys. A 1998, 261, 534–554. [Google Scholar] [CrossRef]
- Abe, S.; Okamoto, Y. Nonextensive Statistical Mechanics and Its Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; Volume 560. [Google Scholar]
- Lenzi, E.K.; Mendes, R.S.; da Silva, L.R. Statistical mechanics based on Renyi entropy. Phys. A 2000, 280, 337–345. [Google Scholar] [CrossRef]
- Glushak, P.A.; Markiv, B.B.; Tokarchuk, M.V. Zubarev’s nonequilibrium statistical operator method in the generalized statistics of multiparticle systems. Theor. Math. Phys. 2018, 194, 57–73. [Google Scholar] [CrossRef]
- Kaniadakis, G.; Lissia, M.; Scarfone, A.M. Two-parameter deformations of logarithm, exponential, and entropy: A consistent framework for generalized statistical mechanics. Phys. Rev. E 2005, 71, 046128. [Google Scholar] [CrossRef]
- Kaniadakis, G. Maximum entropy principle and power-law tailed distributions. Eur. Phys. J. B 2009, 70, 3–13. [Google Scholar] [CrossRef]
- Curado, E.M.F.; Cedeño, C.E.; Soares, I.D.; Tsallis, C. Relativistic gas: Lorentz-invariant distribution for the velocities. Chaos 2022, 32, 103110. [Google Scholar] [CrossRef]
- Megías, E.; Timóteo, V.S.; Gammal, A.; Deppman, A. Bose–Einstein condensation and non-extensive statistics for finite systems. Phys. A 2022, 585, 126440. [Google Scholar] [CrossRef]
- Rovenchak, A.; Krynytskyi, Y. Ideal Bose gas in steep one-dimensional traps. Low Temp. Phys. 2022, 48, 20–25. [Google Scholar] [CrossRef]
- Sigalotti, L.D.G.; Ramírez-Rojas, A.; Vargas, C.A. Tsallis q-Statistics in Seismology. Entropy 2023, 25, 408. [Google Scholar] [CrossRef]
- Wilk, G.; Włodarczyk, Z. Some Non-Obvious Consequences of Non-Extensiveness of Entropy. Entropy 2023, 25, 474. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Evangelista, L.R.; Lenzi, E.K. Fractional Diffusion Equations and Anomalous Diffusion; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Evangelista, L.R.; Lenzi, E.K. An Introduction to Anomalous Diffusion and Relaxation; Springer Nature: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Uchaikin, V.V.; Sibatov, R. Fractional Kinetics in Solids: Anomalous Charge Transport in Semiconductors, Dielectrics, and Nanosystems; World Scientific: Singapore, 2013. [Google Scholar]
- Zaslavsky, G.M. Chaos, fractional kinetics, and anomalous transport. Phys. Rep. 2002, 371, 461–580. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Ribeiro, H.V.; Lenzi, M.K.; Evangelista, L.R.; Magin, R.L. Fractional diffusion with geometric constraints: Application to signal decay in magnetic resonance imaging (MRI). Mathematics 2022, 10, 389. [Google Scholar] [CrossRef]
- Magin, R.L.; Karaman, M.M.; Hall, M.G.; Zhu, W.; Zhou, X.J. Capturing complexity of the diffusion-weighted MR signal decay. Magn. Reson. Imaging 2019, 56, 110–118. [Google Scholar] [CrossRef] [PubMed]
- Magin, R.L. Models of diffusion signal decay in magnetic resonance imaging: Capturing complexity. Concept. Magn. Reson. A 2016, 45, e21401. [Google Scholar] [CrossRef]
- Magin, R.L.; Hall, M.G.; Karaman, M.M.; Vegh, V. Fractional calculus models of magnetic resonance phenomena: Relaxation and diffusion. Crit. Rev. Biomed. Eng. 2020, 48, 285–326. [Google Scholar] [CrossRef]
- Magin, R.L.; Karani, H.; Wang, S.; Liang, Y. Fractional order complexity model of the diffusion signal decay in MRI. Mathematics 2019, 7, 348. [Google Scholar] [CrossRef]
- Barbero, G.; Evangelista, L.R.; Lenzi, E.K. Time-fractional approach to the electrochemical impedance: The Displacement current. J. Electroanal. Chem. 2022, 920, 116588. [Google Scholar] [CrossRef]
- Bisquert, J.; Compte, A. Theory of the electrochemical impedance of anomalous diffusion. J. Electroanal. Chem. 2001, 499, 112–120. [Google Scholar] [CrossRef]
- Meilanov, R.P.; Magomedov, R.A. Thermodynamics in fractional calculus. J. Eng. Phys. Thermophy. 2014, 87, 1521–1531. [Google Scholar] [CrossRef]
- Magomedov, R.A.; Meilanov, R.R.; Meilanov, R.P.; Akhmedov, E.N.; Beybalaev, V.D.; Aliverdiev, A.A. To the fractal equation of state. Proc. J. Phys. Conf. Ser. 2017, 891, 012331. [Google Scholar] [CrossRef]
- Magomedov, R.A.; Meilanov, R.P.; Akhmedov, E.N.; Aliverdiev, A.A. Calculation of multicomponent compound properties using generalization of thermodynamics in derivatives of fractional order. Proc. J. Phys. Conf. Ser. 2016, 774, 012025. [Google Scholar] [CrossRef]
- Laskin, N. Fractional quantum mechanics. Phys. Rev. E 2000, 62, 3135. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional statistical mechanics. Chaos 2006, 16, 033108. [Google Scholar] [CrossRef]
- Korichi, Z.; Meftah, M.T. Statistical mechanics based on fractional classical and quantum mechanics. J. Math. Phys. 2014, 55, 033302. [Google Scholar] [CrossRef]
- Tarasov, V.E. Nonlocal statistical mechanics: General fractional Liouville equations and their solutions. Phys. A 2023, 609, 128366. [Google Scholar] [CrossRef]
- Lenzi, E.K.; de Oliveira, B.F.; Astrath, N.G.C.; Malacarne, L.C.; Mendes, R.S.; Baesso, M.L.; Evangelista, L.R. Fractional approach, quantum statistics, and non-crystalline solids at very low temperatures. Eur. Phys. J. B 2008, 62, 155–158. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Astrath, N.G.C.; Rossato, R.; Evangelista, L.R. Nonlocal effects on the thermal behavior of non-crystalline solids. Braz. J. Phys. 2009, 39, 507–510. [Google Scholar] [CrossRef]
- Rajagopal, A.K.; Mendes, R.S.; Lenzi, E.K. Quantum statistical mechanics for nonextensive systems: Prediction for possible experimental tests. Phys. Rev. Lett. 1998, 80, 3907. [Google Scholar] [CrossRef]
- Kadanoff, L.P.; Baym, G. Quantum Statistical Mechanics; CRC Press: Boca Raton, FL, USA, 1963. [Google Scholar]
- Sandev, T.; Petreska, I.; Lenzi, E.K. Time-dependent Schrödinger-like equation with nonlocal term. J. Math. Phys. 2014, 55, 092105. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Evangelista, L.R.; Zola, R.S.; Petreska, I.; Sandev, T. Fractional Schrödinger equation and anomalous relaxation: Nonlocal terms and delta potentials. Mod. Phys. Lett. A 2021, 36, 2140004. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Mendes, R.S.; Rajagopal, A.K. Green functions based on Tsallis nonextensive statistical mechanics: Normalized q-expectation value formulation. Phys. A 2000, 286, 503–517. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Mendes, R.S.; Rajagopal, A.K. Quantum statistical mechanics for nonextensive systems. Phys. Rev. E 1999, 59, 1398. [Google Scholar] [CrossRef]
- Tsallis, C. Probabilistic and Stochastic Dynamical Foundations of Nonextensive Statistical Mechanics. In Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: Berlin/Heidelberg, Germany, 2023; pp. 139–227. [Google Scholar]
- Wei, Y.; Ma, X.; Feng, Z.; Zhang, Y.; Zhang, L.; Yang, H.; Qi, Y.; Meng, Z.Y.; Wang, Y.C.; Shi, Y.; et al. Nonlocal effects of low-energy excitations in quantum-spin-liquid candidate Cu3Zn(OH)6FBr. Chin. Phys. Lett. 2021, 38, 097501. [Google Scholar] [CrossRef]
- Kramers, H.C.; Wasscher, J.D.; Gorter, C.J. The specific heat of liquid helium between 0.25 and 1.9° K. Physica 1952, 18, 329–338. [Google Scholar] [CrossRef]
- Rovenchak, A. Ideal Bose-gas in nonadditive statistics. Low Temp. Phys. 2018, 44, 1025–1031. [Google Scholar] [CrossRef]
- Biró, T.S.; Shen, K.M.; Zhang, B.W. Non-extensive quantum statistics with particle–hole symmetry. Phys. A 2015, 428, 410–415. [Google Scholar] [CrossRef]
- Rahaman, M.; Bhattacharyya, T.; Alam, J. Thermal field theory of the Tsallis statistics. arXiv 2019, arXiv:1906.02893. [Google Scholar]
- Lenzi, E.K.; Lenzi, M.K.; Belich, H.; Lucena, L.S. Specific heat in the nonextensive statistics: Effective temperature and Lagrange parameter β. Phys. Lett. A 2002, 292, 315–319, Erratum in Phys. Lett. A 2002, 299, 318. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).