Abstract
This paper introduces an improved sequential convex programming algorithm using adaptive non-uniform discretization for the hypersonic entry problem. In order to ensure real-time performance, an inverse-free precise discretization based on first-order hold discretization is adopted to obtain a high-accuracy solution with fewer temporal nodes, which would lead to constraint violation between the temporal nodes due to the sparse time grid. To deal with this limitation, an adaptive non-uniform discretization is developed, which provides a search direction for purposeful clustering of discrete points by adding penalty terms in the problem construction process. Numerical results show that the proposed method has fast convergence with high accuracy while all the path constraints are satisfied over the time horizon, thus giving potential to real-time trajectory planning.
Keywords:
hypersonic entry; real-time trajectory planning; sequential convex programming; adaptive non-uniform discretization; feasibility guarantee MSC:
90C25; 49M25
1. Introduction
With the increasing demand for spacecraft autonomy, not only the accuracy and optimality of the result trajectory but also the stability and efficiency of the solving algorithm are of crucial importance for real-time guidance. For the hypersonic entry problem, trajectory optimization is a popular method due to its extensive application prospect, yet it is still very challenging because of the highly nonlinear and complicated dynamics and constraints involved [1,2,3,4,5].
For the trajectory optimization problem, the existing methods can be classified as indirect methods and direct methods [6]. Based on Pontryagin’s maximum principle [7], indirect methods derive the necessary conditions of optimality and solve a two-point boundary value problem (TPBVP) to obtain the result trajectory [8,9]. Due to the inherent nonlinearity in dynamics of the hypersonic entry problem, the solution of TPBVP presents significant challenges and falls short of real-time requirements [10]. Despite theoretical guarantees on the optimality of the solution, practical considerations limit its feasibility. The direct methods convert the original problem into an approximated finite parameter optimization problem and use a nonlinear programming (NLP) algorithm to solve it [11,12,13]. Although NLP-based methods have been successful in many applications, the time-consuming solution process and the lack of convergence guarantee are major challenges [10]. Furthermore, an appropriate initial guess should be selected to achieve a high-quality solution, especially for the hypersonic entry problem.
In recent years, the application of convex optimization in trajectory optimization has shown great potential in many problem, including powered descent guidance [14] and spacecraft rendezvous and proximity operations [15]. If a problem can be formulated in a convex form, it can be solved in polynomial time with a strong convergence guarantee while obtaining the global optimal solution [16,17]. There are many state-of-the-art solvers based on the interior-point method (IPM) [18], such as GUROBI [19], MOSEK [20], and ECOS [21], to solve convex optimization problems efficiently. However, the majority of the trajectory optimization problems are non-convex. To deal with the nonlinearity in dynamics and constraints, the sequential convex programming (SCP) technique is developed to solve a sequence of convex subproblems to approximate the original problem [22]. The sub-problems are formulated by linearization about a reference trajectory and subsequently solved via iterative refinement of the reference trajectory until convergence of the solution is achieved. In order to ensure the convex approximation is accurate, a trust region is imposed to make sure that the solution is not far from the reference trajectory. There are both hard and soft methods to address the trust region [23,24]. Recently, this SCP technique has been applied to hypersonic re-entry problems and has shown its effectiveness to obtain high-accuracy solutions. Liu formulated the entry problem as a second-order cone programming (SOCP) problem and applies the successive convexification method to solve it [25]. Wang and Grant proposed an improved SCP algorithm and introduced a new control input for the entry problem [26,27]. Wang and Cui developed a rapid trajectory optimization algorithm with the pseudospectral method [28]. However, multiple hundreds of temporal nodes are usually required to maintain the accuracy due to the nonlinearity of the hypersonic entry problem and the long flight duration. Achieving a balance between real-time performance and accuracy represents a significant challenge, as reducing the number of discrete points may result in a loss of precision.
To deal with this issue, Kamath and Açıkmeşe et al. [29,30,31] propose an inverse-free precise discretization based on first-order hold (FOH) discretization. Considering the consistency of the original non-convex dynamics with the reference trajectory and addition of the stitching condition, this discretization would guarantee high accuracy with few temporal nodes and has been effectively applied to various problems, including powered descent guidance [29], multi-phase rocket landing [30], and hypersonic entry guidance [31]. In [31], the amount of the temporal nodes is only 40 to achieve the commensurate accuracy in [27], which necessitated an excess of 200 nodes. Nevertheless, for uniform discretization, a reduced number of temporal nodes would generate a sparse time grid, which may lead to constraint violation between the temporal nodes since the constraints are only imposed at discrete points in the SCP subproblems, resulting in a new issue. In [30], an non-uniform discretization with additional time interval dilation variables is introduced in multi-phase rocket landing to adaptively decide the turning points of different phases. A similar idea is extended to the hypersonic entry problem and the penalized trust region (PTR) algorithm, a soft trust region method, is used to construct the SCP process [31]. However, the resulting trajectory would still experience constraint violation. In addition, in our experiment for the hypersonic entry problem, both hard and soft trust region methods with additional time interval variables showed worse convergence compared with those with uniform discretization. One of the reasons is that the dynamics are time-sensitive, and the other is that an effective search direction should be given to achieve a purposeful distribution of discrete points.
In this paper, we propose a novel adaptive non-uniform discretization method to handle the above issues.
- An inverse-free precise discretization is adopted to obtain high accuracy with few temporal nodes for real-time performance.
- An adaptive non-uniform discretizaiton is proposed to construct the SCP subproblem with additional penalty terms. This would give the solver a search direction to cluster the temporal nodes more purposefully and the propagated trajectory would satisfy all the path constraints as a result, which is the main contribution of this paper.
- The validity of proposed method is substantiated through a numerical experiment compared with other SCP methods.
This paper is organized as follows. Section 2 presents the model of the hypersonic entry trajectory optimization problem including the dynamics and constraints. Section 3 introduces the adaptive non-uniform discretization and constructs the SCP subproblem and iteration process. Simulation and results analysis are shown in Section 4. The conclusions are summarized in Section 5.
2. Problem Formulation
In this section, we consider a typical entry trajectory problem for an unpowered hypersonic vehicle with multiple path constraints.
2.1. 3-DoF Entry Dynamics
The dimensionless dynamic equations over a spherical, rotating Earth can be modeled as follows. More details can be referred to in [27].
where the state vectors are , representing the orbital radius, longitude, latitude, relative velocity, flight path angle, and heading angle, respectively. The Earth rotation-dependent terms, , and the lift and drag accelerations, , in (1) are shown below.
where is the Earth self-rotation rate, is the atmospheric density depending on the altitude h, , m is the reference area and mass of the vehicle, and are the aerodynamic lift and drag coefficients related to Mach number and the attack angle .
As in [27], the control variable is restricted to bank angle . The attack angle is pre-specified as a function of Mach number, as described in Section 4. All the variables are dimensionless and the dimensionless factors are shown in Table 1, where km and m/s2 represent the Earth’s radius and the acceleration of gravity, respectively.

Table 1.
The dimensionless factors’ values.
2.2. State, Control, and Path Constraints
The inital and terminal conditions are
The control bounds and control rate constraints are given as follows:
where and are the bounds of the bank angle and its rate, respectively.
Three typical path constraints, including heat rate, dynamic pressure, and normal load, are considered:
In this paper, no-fly zone constraints are considered as well, which are defined as cylinder zones with center , radius , and infinite altitude. Thus, the no-fly zone constraints are expressed as
2.3. Nonconvex Optimal Control Problem
The maximum terminal velocity hypersonic entry trajectory optimization problems with fixed flight time are considered in this paper, which is the same as [27]. The nonconvex optimal control problem is shown in Problem 1.
Problem 1.
3. Improved SCP Method with Adaptive Non-Uniform Discretization
In this section, we introduce the improved SCP algorithm using adaptive non-uniform discretization for the hypersonic entry problem. In the interest of completeness, we provide a brief introduction to the non-uniform scheme and precise discretization technique, both of which, as in [31], are utilized in the proposed method. Further details will be presented subsequently. In order to seek an appropriate search direction and achieve a purposeful distribution of temporal nodes, additional penalty terms with respect to the nonlinear term of path constraints and the distance term from the trajectory to the no-fly zone center are considered in the SCP subproblem construction.
3.1. Time Interval Dilation
To introduce the non-uniform discretization, we consider the original nonlinear dynamics in the sub-interval ,
where , and define an affine map to normalize the orginal time interval (may not be equal) to a fixed interval, :
where is the length of the th time interval and can be referred to as the time interval dilation [30]. So far, the dynamics Equation (8) can be rewritten with respect to the normalized time :
By treating as additional decision variables, the solver is allowed to decide the adaptive time grids rather than a uniform temporal grid.
What is more, some exact constraints should be added in practical implementation to ensure physical meaning:
to ensure the time order and adjacent temporal nodes are not far away, and
to ensure the fixed flight time.
3.2. Convexification and Discretization
A convex approximation of the dynamic (10) can be obtained by the first-order Tylor expansion about a reference trajectory . The approximate equation is a linear time-varing (LTV) system as follows:
where are the Jacobians of the dynamics with state control and time dilation, respectively.
For discretization, a precise inverse-free discretization technique based on first-order hold (FOH) is adopted [29,30,31]. In the FOH case, the control input signal is considered as a piecewise affine function; thus, the control variables are only defined at the discrete time nodes and the control signal in the sub-interval can be parameterized as follows:
where and as given in (9). Thus, The LTV dynamics (13) can be easily rewritten with respect to the deviations from the reference trajectory.
where denotes the reference quantity, denotes the deviations from the reference trajectory, i.e., and , and the coefficient matrixes are the same as (14). It can be considered that the reference trajectory in the sub-interval is in accordance with the original dynamics (10), rather than the convex approximation (13), like the typical FOH discretization in [32].
According to the knowledge of the linear system [33], the unique solution of (16) for and is
where
where is called the state transition matrix (STM) with the following properties: , , and .
In order to eliminate the inversion operation to avoid numerical problems, the in (18) have the closer forms, as shown in Thereom 1, which is not proven in [29,30,31].
Theorem 1.
Proof.
Choosing the as an example, then taking the derivative and invoking the chain rule yields
For simplicity, we define and as 0 and 1, respectively, which denote that t is in the sub-interval . Then evaluating the LTV system (13) at , we obtain
Since the reference trajectory may not satisfy the original dynamics (1) in the sub-interval , Equation (22) would give trajectory segments, which makes a discontinuity occur in the temporal time nodes . The stitching condition is introduced to obtain a continuous trajectory over the time horizon, as shown in Figure 1.
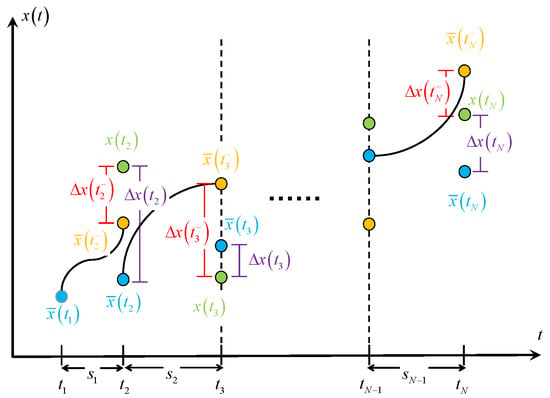
Figure 1.
The discontinuity in the temporal nodes and the stitching condition, as in [31].
As a result, the discretized dynamics in terms of the deviations are as follows:
where , and , which denotes the integration of the original dynamic in from the reference trajectory.
Thus the discretized dynamics with respect to absolute variables are recovered from Equation (23):
With the idea of consistency of the original dynamics of the reference trajectory in sub-intervals and the addition of the stitching condition, the accuracy of the solution would be improved even over a sparse time grid.
3.3. Additional Penalty Terms in SCP Subproblem
In our experiments for the non-uniform scheme, it is observed that regardless of a hard trust region method with additional fixed constraints or a soft trust region method by augmenting the objective function with penalty terms, the method may not converge or converge very slowly, while the resulting propagated trajectory may violate the path constraints between temporal nodes as well.
As mentioned above, one reason is that an effective search direction should be given. Inspired by the PTR algorithm [24], we augment the objective function with additional penalty terms with respect to the nonlinear term of path constraints and the distance term of the no-fly zone, which would give a more purposeful direction to distribute the temporal nodes. As the path constraints exhibit high levels of nonlinearity, the logarithm transformation is used to mitigate this issue.
3.3.1. Log-Tranforms of Path Constraints
Consider the typical path constraints (5) of the hypersonic entry problem: heat rate, dynamic pressure, and normal load. Since the Tylor expansion of the original path constraints (5) would obtain complicated nonlinear terms, we take the logarithm transformation of both sides of (5):
Due to the monotonicity of logarithmic transformations, Equation (25) is equivalent to (5), while the transformed constraints are linear to orbital radius r and only nonlinear to velocity V. Thus, the Tylor expansion of the transformed constraints has a simpler nonlinear term than that of the original constraints.
Consider the second-order Tylor series expansion of :
Then we replace in (25) with the primary term as the linearization of the transformed constraints and augment the objective function with the nonlinear term , since the quadratic term is convex. With the variable time-step scheme and additional nonlinear penalty term, this would give the optimizer a target or direction to incentivize the temporal nodes to cluster around the highly nonlinear region.
3.3.2. Distance Penalty Term of No-Fly Zone
The propagated trajectory between temporal nodes could be within the no-fly zone because of the sparse time interval, as shown in Figure 2. In order to address the above issue, prior work is to set a dense time grid around the no-fly zone in advance. Instead of that, our method can allow discrete points to adaptively cluster around the no-fly zone during iteration, which would take full advantage of the non-uniform scheme.
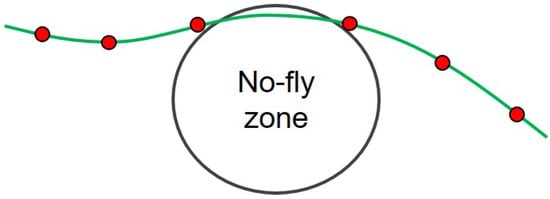
Figure 2.
The propagated trajectory within the no-fly zone.
The nonlinear no-fly zone constraints (6) can be linearized with first-order Tylor expansion:
where .
We penalize the distance from the trajectory to the center of the no-fly zone in the objective function, which would give the solver a search direction with physical significance. With the linear no-fly zone constraints (27), the discrete points would tend to cluster around the no-fly zone and disperse beyond it.
Note that the penalty term of the no-fly zone should be restricted to several temporal nodes to prevent all nodes from gathering around the no-fly zone.
3.4. Discrete Convex Subproblem and Iteration Algorithm
After the appeal discussion, we summarize the discrete convex sub-problem as shown in Problem 2. The control difference is regarded as the control rate constraint because of the FOH approximation of control. A hard trust region on time dilation is enforced in constraints, while the objective function is augmented with trust region terms of state and control, and two additional penalty terms: the nonlinear term of path constraints and distance penalty term of the no-fly zone. The trust term of time dilation can be omitted since the penalty terms of path constraints and the no-fly zone have shown a good iterative performance in our experiment. Thus, the SCP iteration process is given in Algorithm 1 as follows:
| Algorithm 1: Improved SCP algorithm with adaptive non-uniform discretization |
 |
4. Numerical Results
In this section, the effectiveness of the proposed method is verified compared with a different SCP algorithm, as shown in Table 2. Two cases are considered to focus on distinct instances of constraint violation. Case 1 does not include the no-fly zone constraint and focuses on potential violations of path constraints as the number of discrete points decreases. With an additional no-fly zone constraint, Case 2 focuses on the phenomenon that the propagated trajectory may pass through the no-fly zone.

Table 2.
Comparative SCP methods.
The reference area and the mass of the vehicle are m2 and kg. The aerodynamic coefficients depend on the attack angle (in degrees), while the angle-of-attack profile depends on the vehicle’s velocity:
The remaining simulation parameters are shown in Table 3, which is the same as [27].

Table 3.
Parameters for entry problem.
The subproblem is constructed in YALMIP [34], a MATLAB modeling toolbox, and solved by ECOS [21], an open-source convex optimization solver. All of the numerical simulations are running on a personal desktop with an Intel Core i9 3.1 GHz processor.
The initial reference is the trajectory obtained by integrating the original dynamics (1) with the given initial control, as in [27]. The convergence condition is selected as and , where and are the solution of the subproblem.
4.1. Iterative Performance
Comparisons of the state and control profiles for Case 1 and Case 2 are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. The account of temporal nodes for the proposed method are as follows. SCP1 and SCP2 are each 40, in which case the constraint violation is observed, and SCP3 is 300 in order to maintain the same accuracy as the above methods.
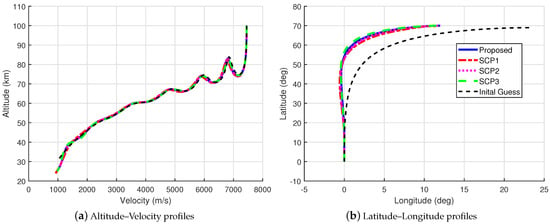
Figure 3.
Comparisons of the altitude–velocity and latitude–longitude profiles for Case 1.
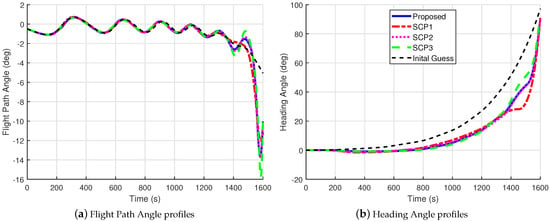
Figure 4.
Comparisons of the flight path angle and heading angle profiles for Case 1.
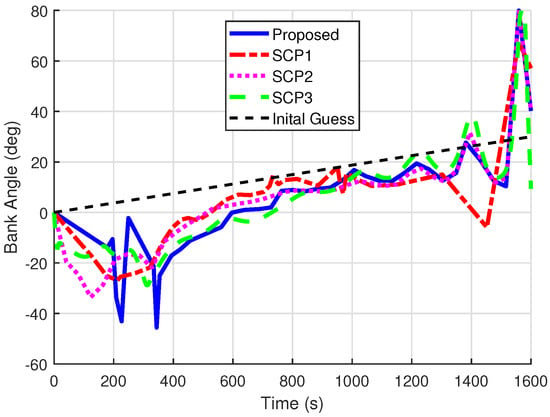
Figure 5.
Comparisons of the control profile for Case 1.
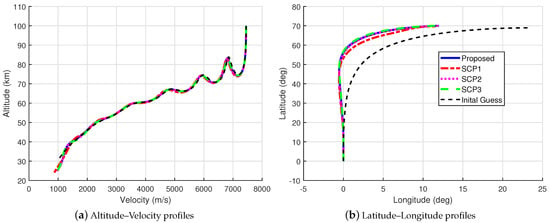
Figure 6.
Comparisons of the altitude–velocity and latitude-longitude profiles for Case 2.
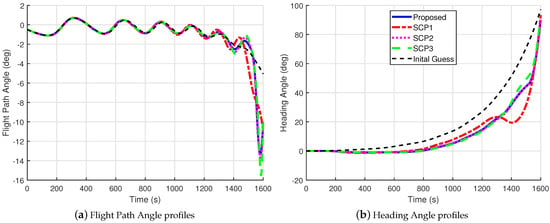
Figure 7.
Comparisons of the flight path angle and heading angle profiles for Case 2.
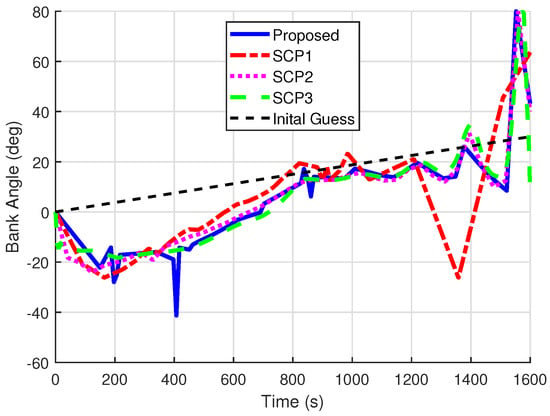
Figure 8.
Comparisons of the control profile for Case 2.
It can be seen that the solutions of the proposed method are similar to those from SCP2 and SCP3. Note that the solutions of SCP1 are quite different due to its poor convergence. As shown in Figure 5 and Figure 8, one shortcoming of the proposed method is that the control jitter in the segments where points cluster is obvious because of the dense time grid around those points.
The iterative performance of the proposed method and comparative methods is shown in Figure 9. The iteration number of the proposed method is less than the comparative methods. Note that the comparative methods would require more iterations to meet the convergence condition when the objective function is near the optimal value, while the proposed method required fewer iterations, demonstrating its fast convergence. What is more, for the non-uniform scheme, SCP1 with light penalty weighting in reached the maximum number of iterations, while that with heavy weighting would show negligible alterations for the distribution of temporal nodes; thus, the addition of time interval dilation is not necessary in this case.
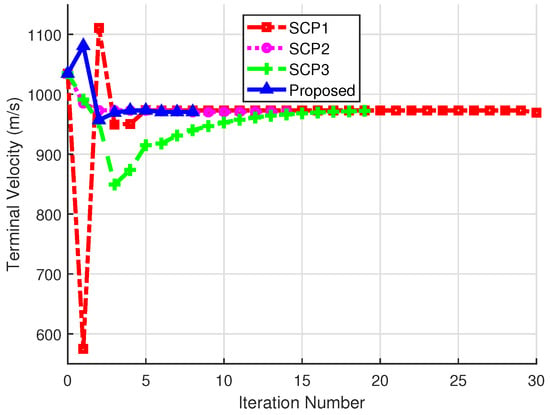
Figure 9.
The terminal velocity in each iteration.
For the non-uniform scheme, the discrete point distribution and the change of time dilation, , with iterations are shown in Figure 10. It can be observed that there is no obvious clustering rule for SCP1, while the position of discrete points always changes with the number of iterations. In contrast, the discrete points of the proposed method would cluster after a few iterations. In addition, the results of time interval change with iterations show that the proposed method has stable convergence performance, since the change between two adjacent iterations decreases progressively, which means the result trajectory would become increasingly similar.
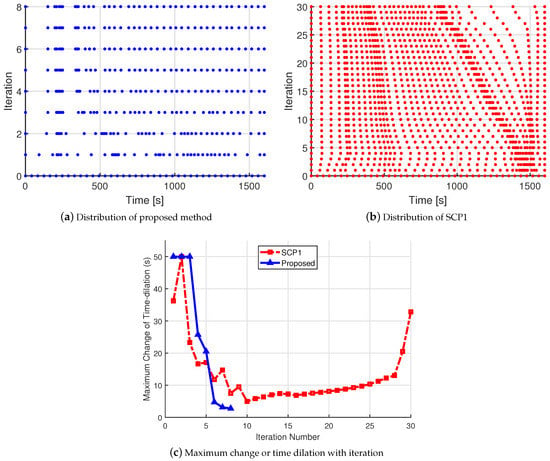
Figure 10.
Discrete point distribution and time dilation change with iteration.
In order to guarantee that the result trajectory of the SCP process is feasible to meet the original dynamics, the residual error between the optimized results and the trajectory obtained by integrating the original dynamics is measured. The residual error results for Case 1 and Case 2 are shown in Table 4 and Table 5, averaged over 50 simulation runs.

Table 4.
Residual error with different temporal nodes for Case 1.

Table 5.
Residual error for entry problem for Case 2.
It can be observed that for SCP2 and SCP3, the precise discretization can guarantee commensurate accuracy with fewer temporal nodes, while more than 200 nodes are needed to achieve the same result in [27], which demonstrates the effectiveness of the precise discretization. Note that, with the non-uniform scheme, SCP1 showed worse convergence performance and low accuracy as mentioned above, which means that the feasibility of the result trajectory is not guaranteed. In contrast, the proposed method overcomes the shortcomings, maintains the advantage of the precise discretization, and shows better convergence performance, as shown in Table 4 and Table 5.
4.2. Constraint Satisfaction Performance
As mentioned above, for the uniform precise discretization, the propagated trajectory may violate the path constraints between temporal nodes due to the sparse time grid. This phenomenon was observed to occur when the account of temporal nodes decreased to 40. Thus, we choose the case of 40 nodes for presentation. The path constraints of the proposed method for Case 1 are shown in Figure 11 and contrasted with SCP1 and SCP2.
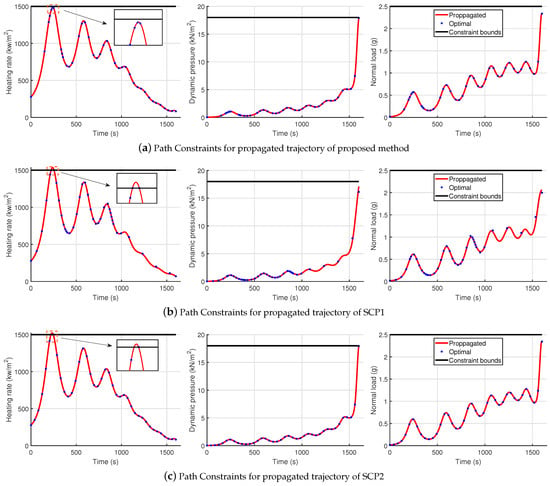
Figure 11.
Path constraints of propagated trajectories for Case 1.
It can be observed that the heat load would touch the boundary during the initial state of flight. The constraint violations occur for the propagated trajectory of SCP1 and SPC2 due to the sparse time grid. In contrast, the propagated trajectory of the proposed method satisfies the path constraints over the time horizon. In addition, the discrete points would cluster around the peak value of heat load, as shown in Figure 11.
Furthermore, the same phenomenon may occur for the no-fly zone constraints as well. Case 2 focuses on the no-fly zone constraint violation, and the numerical results are shown in Figure 12. In this case, all the path constraints were satisfied for all methods in our experiments. It can be observed that the propagated trajectories of SCP1 and SCP2 both pass through the no-fly zone. Note that, for the non-uniform scheme, the discrete points of SCP1 do not cluster around the no-fly zone. The 3D trajectory of tbe proposed method is shown in Figure 12b; the points in red are set to cluster around the no-fly zone. The propagated trajectory of the proposed method skimmed over the no-fly zone, while the time interval between adjacent red points is the minimum set in (11), which indicated that the point distribution of the proposed method is better than SCP2.
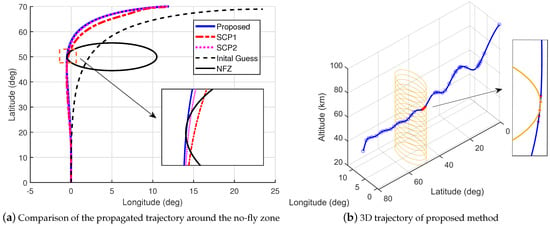
Figure 12.
The propagated trajectory for Case 2.
5. Conclusions
This paper proposes an improved SCP algorithm for the hypersonic entry problem using a novel adaptive non-uniform discretization. The proposed method has advantages in performance of path constraint satisfaction and convergence. Firstly, the proposed method employs an inverse-free precise discretization to ensure high accuracy and real-time performance. Then, an adaptive non-uniform scheme is developed to distribute discrete points adaptively by adding additional penalty terms in the SCP subproblem, which would guarantee constraint satisfaction. Finally, numerical results show that the proposed method achieves a fast convergence while maintaining high accuracy with few temporal nodes. More importantly, the discrete points of the proposed method would cluster around the segment where the constraints may be violated, and the propagated trajectory satisfies all the path constraints over the time horizon even for a small number of discrete points.
Future work will focus on the following points: (1) Due to the non-uniform scheme, a similar idea can extend to the hypersonic entry problem with the waypoint constraint and other problems; (2) The simulation will be carried out on an embedded platform to verify the effectiveness of the proposed method for a limited-power environment; (3) High-performance solvers are considered to further improve the solving speed, such as the proportional integral projected gradient method [35], a first-order method for the conic convex problem.
Author Contributions
Methodology, J.M.; Validation, J.W.; Writing—original draft preparation, J.M.; Writing—review and editing, J.W., Q.Z. and H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Basic and Applied Basic Research Project of Guangzhou Municipal Science and Technology Bureau, grant number 202201011187.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lu, P. Entry guidance and trajectory control for reusable launch vehicle. J. Guid. Control Dyn. 1997, 20, 143–149. [Google Scholar] [CrossRef]
- Shen, Z.; Lu, P. Onboard generation of three-dimensional constrained entry trajectories. J. Guid. Control Dyn. 2003, 26, 111–121. [Google Scholar] [CrossRef]
- Lu, P. Entry guidance: A unified method. J. Guid. Control Dyn. 2014, 37, 713–728. [Google Scholar] [CrossRef]
- Jorris, T.R.; Cobb, R.G. Three-dimensional trajectory optimization satisfying waypoint and no-fly zone constraints. J. Guid. Control Dyn. 2009, 32, 551–572. [Google Scholar] [CrossRef]
- Grant, M.J.; Braun, R.D. Rapid indirect trajectory optimization for conceptual design of hypersonic missions. J. Spacecr. Rocket. 2015, 52, 177–182. [Google Scholar] [CrossRef]
- Betts, J.T. Survey of numerical methods for trajectory optimization. J. Guid. Control Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef]
- Pontryagin, L.S. Mathematical Theory of Optimal Processes; CRC Press: Boca Raton, FL, USA, 1987. [Google Scholar]
- Pan, B.; Lu, P.; Pan, X.; Ma, Y. Double-homotopy method for solving optimal control problems. J. Guid. Control Dyn. 2016, 39, 1706–1720. [Google Scholar] [CrossRef]
- Zheng, Y.; Cui, H.; Ai, Y. Indirect trajectory optimization for mars entry with maximum terminal altitude. J. Spacecr. Rocket. 2017, 54, 1068–1080. [Google Scholar] [CrossRef]
- Ben-Asher, J.Z. Optimal Control Theory with Aerospace Applications; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2010. [Google Scholar]
- Fahroo, F.; Ross, I.M. Direct trajectory optimization by a Chebyshev pseudospectral method. J. Guid. Control Dyn. 2002, 25, 160–166. [Google Scholar] [CrossRef]
- Kameswaran, S.; Biegler, L.T. Convergence rates for direct transcription of optimal control problems using collocation at Radau points. Comput. Optim. Appl. 2008, 41, 81–126. [Google Scholar] [CrossRef]
- Garg, D.; Patterson, M.; Hager, W.W.; Rao, A.V.; Benson, D.A.; Huntington, G.T. A unified framework for the numerical solution of optimal control problems using pseudospectral methods. Automatica 2010, 46, 1843–1851. [Google Scholar] [CrossRef]
- Acikmese, B.; Ploen, S.R. Convex programming approach to powered descent guidance for mars landing. J. Guid. Control Dyn. 2007, 30, 1353–1366. [Google Scholar] [CrossRef]
- Lu, P.; Liu, X. Autonomous trajectory planning for rendezvous and proximity operations by conic optimization. J. Guid. Control Dyn. 2013, 36, 375–389. [Google Scholar] [CrossRef]
- Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Liu, X.; Lu, P.; Pan, B. Survey of convex optimization for aerospace applications. Astrodynamics 2017, 1, 23–40. [Google Scholar] [CrossRef]
- Wright, S.J. Primal-Dual Interior-Point Methods; SIAM: Philadelphia, PA, USA, 1997. [Google Scholar]
- Gurobi Optimization, Ltd. Gurobi Optimizer Reference Manual. 2021. Available online: https://www.gurobi.com/documentation/current/refman/index.html (accessed on 22 May 2023).
- ApS, M. Mosek optimization toolbox for matlab. User’s Guide Ref. Manual Version 2019, 4, 1. [Google Scholar]
- Domahidi, A.; Chu, E.; Boyd, S. ECOS: An SOCP solver for embedded systems. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 3071–3076. [Google Scholar]
- Mao, Y.; Szmuk, M.; Xu, X.; Açikmese, B. Successive convexification: A superlinearly convergent algorithm for non-convex optimal control problems. arXiv 2018, arXiv:1804.06539. [Google Scholar]
- Szmuk, M.; Acikmese, B.; Berning, A.W. Successive convexification for fuel-optimal powered landing with aerodynamic drag and non-convex constraints. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, San Diego, CA, USA, 4–8 January 2016; p. 0378. [Google Scholar]
- Malyuta, D.; Reynolds, T.P.; Szmuk, M.; Lew, T.; Bonalli, R.; Pavone, M.; Acikmese, B. Convex optimization for trajectory generation. arXiv 2021, arXiv:2106.09125. [Google Scholar]
- Liu, X.; Shen, Z.; Lu, P. Entry trajectory optimization by second-order cone programming. J. Guid. Control Dyn. 2016, 39, 227–241. [Google Scholar] [CrossRef]
- Wang, Z.; Grant, M.J. Constrained trajectory optimization for planetary entry via sequential convex programming. J. Guid. Control Dyn. 2017, 40, 2603–2615. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, Y. Improved sequential convex programming algorithms for entry trajectory optimization. J. Spacecr. Rocket. 2020, 57, 1373–1386. [Google Scholar] [CrossRef]
- Wang, J.; Cui, N.; Wei, C. Rapid trajectory optimization for hypersonic entry using a pseudospectral-convex algorithm. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 5227–5238. [Google Scholar] [CrossRef]
- Kamath, A.G.; Elango, P.; Kim, T.; Mceowen, S.; Yu, Y.; Carson, J.M.; Mesbahi, M.; Acikmese, B. Customized real-time first-order methods for onboard dual quaternion-based 6-DoF powered-descent guidance. In Proceedings of the AIAA SCITECH 2023 Forum, Orlando, FL, USA, 8–12 January 2023; p. 2003. [Google Scholar]
- Kamath, A.G.; Elango, P.; Yu, Y.; Mceowen, S.; Carson, J.M., III; Açıkmeşe, B. Real-Time Sequential Conic Optimization for Multi-Phase Rocket Landing Guidance. arXiv 2022, arXiv:2212.00375. [Google Scholar]
- Mceowen, S.; Kamath, A.G.; Elango, P.; Kim, T.; Buckner, S.C.; Acikmese, B. High-Accuracy 3-DoF Hypersonic Reentry Guidance via Sequential Convex Programming. In Proceedings of the AIAA SCITECH 2023 Forum, San Diego, CA, USA, 8–12 January 2023; p. 0300. [Google Scholar]
- Reynolds, T.P. Computational Guidance and Control for Aerospace Systems; University of Washington: Seattle, WA, USA, 2020. [Google Scholar]
- Antsaklis, P.J.; Michel, A.N. Linear Systems; Springer: Berlin/Heidelberg, Germany, 1997; Volume 8. [Google Scholar]
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No. 04CH37508), Taipei, Taiwan, 2–4 September 2004; pp. 284–289. [Google Scholar]
- Yu, Y.; Elango, P.; Topcu, U.; Açıkmeşe, B. Proportional–integral projected gradient method for conic optimization. Automatica 2022, 142, 110359. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).