1. Introduction
Singularly Perturbed Problems (SPPs) are widespread in nature. SPPs often occur in different applied fields such as control systems or fluid dynamics, among others [
1,
2,
3]. In particular, systems of Singularly Perturbed Partial Differential Equations (SPPDEs) frequently arise in the modeling of heat and mass transfer processes whenever the diffusion coefficients and the thermal conductivity are very small [
4]. In [
2,
3], some mathematical models are developed for generators and their controls in control systems using singular perturbation techniques. The models are based on a system of
n SPPs, whose first
m equations (with
) have the higher order derivatives affected by a small parameter
. It is well-known that classical numerical methods are not satisfactory for SPPs because of the multiscale behavior of the solutions [
1]. A similar type of non-SPPs has a wide range of real-time applications, for instance, the calcium distribution in nerve cells is a dynamical system that is a generalized two-dimensional space-time reaction-diffusion model [
5,
6].
Many unconventional numerical methods can be found in the literature to solve various types of SPPs [
7,
8,
9,
10,
11]. A numerical method composed of the backward Euler method together with the HODIE (High Order via Differential Identity Expansion) scheme, classical central difference scheme, and a Shishkin mesh has appeared recently in [
12] for a system of SPPDEs of Convection–diffusion (CD) type in which all the higher order spatial derivatives are multiplied by a parameter
. In [
13], a numerical method which is a combination of the backward Euler scheme, the upwind finite difference scheme, and a nonuniform mesh based on a monitor function is devised for the aforementioned system with two equations in which the higher order spatial derivatives are multiplied by different perturbation parameters. For this same system, a numerical method consisting of the backward Euler method, a hybrid scheme, and a Shishkin mesh is developed in [
14] with higher order convergence in space.
A scheme based on standard finite difference operators and the condensing mesh technique is designed in [
15] to solve a system of two SPPDEs of Reaction–diffusion (RD) type in which all the higher order spatial derivatives are multiplied by a parameter
. The aforementioned system in which the higher order spatial derivatives are multiplied by different parameters is solved by a numerical method in [
16], which consists of two additive schemes using a Shishkin mesh and a standard central difference operator. This problem is extended to a general system in [
17] and solved by a numerical method composed of classical finite difference operators and appropriate layer-adapted meshes. For this same type of system with two equations, the convergence in both time and space is improved in [
18] through a numerical method which consists of the Crank–Nicolson method, the classical central difference scheme, and a Shishkin mesh. The aforementioned problem is extended to a general system in [
19] in which only the higher order convergence in space is maintained through a numerical method composed of classical finite difference operators and a Shishkin mesh. For the same system, the higher order convergence in time is achieved with the Crank–Nicolson method in [
20].
In [
21], a first-order scheme for a system of two singularly perturbed RD equations was presented, where only the second derivative of the first equation was multiplied by a small perturbation parameter. For this system, a higher order convergent scheme was developed in [
22]. The article [
23] deals with the construction of a numerical method for a general system of
n singularly perturbed RD equations in which only the first
equations are multiplied by different perturbation parameters. Inspired by [
21] and [
23], a numerical method is devised in [
24] for a similar system of SPPDEs with more assumptions. Motivated by [
2,
3,
15,
24], in this work, a system of
n SPPDEs of RD type is considered in which only the first
m equations (with
) are multiplied by
.
The structure of the paper is as follows. In
Section 2, we state the problem to be solved. The existence, uniqueness, and stability properties of the continuous solution are presented in
Section 3. In addition, the decomposition of the solution (into regular and singular components) and bounds on its derivatives are established.
Section 4 contains the design of a finite difference scheme using a piecewise uniform Shishkin mesh to solve the discrete problem, which provides a robust numerical approximation to the solution. In
Section 5, the error analysis of the numerical solution based on barrier function techniques is derived, which sets up the theoretical results. A numerical example is given in
Section 6 to conform the applicability and expected rate of accuracy of the present method with the parameter-uniform maximum pointwise error, parameter-uniform error constant, and parameter-uniform rate of convergence in the tables and graphs, which validate the major findings of the paper.
2. Continuous Problem
Let consider the singularly perturbed time-dependent RD system
where
, with
and
For
, we use the notations
. We note that
and
E are square matrices of dimension
n with
, where
appears
m times (
), being
It is assumed that for all
the elements
of
satisfy
and
for some constant
. In operator form, the system (
1) and (2) is written as follows:
with
given by
where
I is used to denote the identity matrix.
Taking
in (
1) and (2), the reduced problem is obtained, which is given for
by
for
,
, with
on
.
In general,
on
for
. Hence, the components
for
of the solution
of (
1) and (2) exhibit boundary layers near
and
, whereas the components
for
exhibit no layer throughout the domain.
In this paper, we adopt the following notations. For any continuous vector function on and , and for any mesh function and Throughout this article, and denote positive constants, which are independent of and the discretization parameters N and
3. Analytical Results
Some of the analytical properties, maximum principles, stability results, and derivative bounds of the exact solution (
1) and (2) and its regular and singular components are estimated. The derivative bounds are necessary for the numerical analysis that is derived thoroughly in this section. The existence of the solution
of (
1) and (2) is stated in Theorem 1 without proof. For more details, the reader is referred to [
25].
Theorem 1. Assume the components of B and are sufficiently smooth functions, , and the following compatibility conditions are satisfied at the corners and of Γ:and Then, there exists a solution of (1) and (2) such that where is the space of Hölder continuous functions with .
Lemma 1 (Maximum Principle)
. Let us assume that condition (4) holds and is any function in the domain of such that on Γ and on Ω. Then, it is on Proof. Let
be such that
. The result follows immediately if
Suppose
Then,
and
Let
We have that
Using (
4), we obtain
, which is a contradiction. Thus,
, and the lemma is proven. □
Lemma 2 (Stability Result)
. Let us assume that condition (4) holds and is any function in the domain of We find that for and , it holds that Proof. Let
Define
, where
. Then,
on
and using (
4),
on
Hence, from Lemma 1,
on
which proves the result. □
Lemma 3. Let us assume that conditions (3), (4), (6)–(10) hold. In this case, for , , , and , we get Proof. The bound on
follows from Lemma 2. Differentiating the
equation in (
1) partially with respect to
t once and rearranging the terms, we obtain
Then, the bound on
follows by using Lemma 2. The bound on
can be derived in the same way. For each
consider a neighborhood
such that
Then, by using the mean value theorem with
, we find that for
, it is
and thus,
Now, consider the relation
Using the bounds of
and
the bound of
follows from (
12). The bound on
follows by using a similar procedure considering the interval
where
Further, the bounds of the mixed derivatives can also be derived by using this same technique. From (
1), we obtain
The bounds on
follow from (
14). Differentiating (
14) with respect to
x once and using the bounds of
B and
the bound on
follow. In addition, differentiating (
14) with respect to
x twice and using the bounds of
,
,
and
the bound on
follows. □
Now, we decompose
into two parts
and
such that
with
, where
is the solution of the reduced problem (
5),
is the solution of
and the component
is the solution of
We can decompose the component further as and such that , where on on on and on on on .
Lemma 4. Let us assume that conditions (3), (4), (6)–(10) hold. In this case, for , , and , we have Proof. From (
5), it is not hard to see that for
and
, it holds that
From (
15) and the above bounds, it is clear that
is the solution of a problem similar to (
1) and (2). Hence, the estimates in Lemma 3 hold for the components of
and their derivatives after replacing
by
and appropriate derivatives. Thus, the bounds of
and its derivatives follow from those of
and their derivatives. □
The layer functions
associated with the solution
of (
1) and (2) are defined for all
by
Lemma 5. Let us assume that conditions (3), (4), (6)–(10) hold. In this case, for , , we have that Analogous results hold for and their derivatives with x replaced by
Proof. Define the functions
,
and
,
. Then,
on
for proper choices of
and
Now, for
, we get
Using (
4), we find that
on
By using Lemma 1 with
, the bounds of
and
follow. Now, we derive the bounds on
and
Define the functions
,
and
,
. Differentiate the equation
partially with respect to
t once and rearrange the terms to get
Using Lemmas 3 and 4, we obtain that
. Thus, the bounds of
and
follow from using Lemma 1 applied to the functions
. From Lemmas 3 and 4, we get
It is not hard to verify that
and
≤
and
Using the above estimates in (
17), it can be obtained that
Now, define the functions
,
and
,
. Using Lemma 1 with the functions
, the bounds of
and
follow. Using the mean value theorem with
and similar arguments to those used to get a bound of
, we deduce that
Since
and
the bounds on
follow from (
20). Using a similar procedure, the bounds on
can be derived. The bounds on
follow from the equation
Differentiating the equation
once and twice partially with respect to
x and using the above bounds, the bounds on
and
can be readily obtained. □
4. Discretization of the Domain and Discretized Problem
In this section, a finite difference scheme using a piecewise uniform Shishkin mesh with a well-suited transition parameter for the SPPDE (
1) and (2) is considered (see [
1] and references therein). A rectangular mesh
with
mesh regions is now constructed on the domain
The rectangular mesh
consists of a piecewise uniform Shishkin mesh on the spatial domain
and a uniform mesh on the temporal domain
. Let
,
,
,
,
,
and
. On the spatial domain
, a piecewise uniform Shishkin mesh
with
N mesh intervals is constructed using a transition parameter
as follows. Thus, we split the interval [0,1] as
where the parameter
is a function of
,
and
N, given by
Each of the sub-intervals
and
is divided into
subintervals using appropriate uniform mesh points, whereas
is divided into
sub-intervals using also appropriate uniform mesh points. On the temporal domain
a uniform mesh
with
M mesh intervals is placed. The discrete problem corresponding to (
1) and (2) is
Here,
and such that and
In operator form, the problem (
21) is written as follows:
Thus, the operator is defined by
Lemma 6. [Discrete Maximum Principle] Let us assume that condition (4) holds and is any mesh function such that on and, on . Then, it holds that on Proof. Take
for which
. The result follows immediately if
Suppose
Then
∉
,
and
Let
Now, we have
Using (
4), we get
which is a contradiction. Thus,
≥ 0, and the lemma is proven. □
Lemma 7 (Discrete Stability Result)
. Let us assume that condition (4) holds and is any mesh function. Then, for and , we have that Proof. Let
Define
±
, where
Then
on
and using (
4) we find that
≥
on
Hence, from Lemma 6, we have
on
, which proves the result. □
5. Error Analysis
This section gives an error bound of the solution provided by the present method. We began by considering the decomposition of the solution of the discrete problem (
21). This is similar to the continuous case. The solution
of the problem (
21) can be decomposed into
and
such that
, where
is the solution of
and
is the solution of
It is noted that for any smooth function
, we have
and
where,
and
Theorem 2. Let and be the components of , and let and be the components of . Then, for all and , it holds that Proof. From the defining equation for
and (
23), we have
and from (
16) and (
24), we have
Note that for all
Since
, for any choice of the parameter
from (
25), (26), and (
30), for
and
, we have
and
Then, using Lemma 4, (
28) follows from (
32) and (
33) for
. Now, we estimate the error in
From (
31), we obtain
Here, we consider that the argument depends on whether
or
If
, then
, and it follows
in this case. Using (
25), (26), and (
34), for
and
, we get
and
Later, using Lemma 5, for
, we get
Now, assume
. Let us prove the results on the domains
and
separately. The spatial mesh spacing on both intervals
and
is
Using (
25), (26) and (
34) for both
and
and Lemma 5, for
, we get
Finally, consider the interval
Here, the spatial mesh spacing is
≤
From (
25), (26), (
34) and using Lemma 5, for
and
, we have
and
From (
25), (
27), (
34) and using Lemma 5, for
and
, we obtain
and
It is not difficult to get
Now, we proceed with the proof by considering two instances:
and
. In the first instance, using Lemma 5 and (
41) in (
37) and (
38), for
, we get
Consider the second choice
In this case, using Lemma 5 and (
41) in (
39) and (
40), for
, we have
Using similar arguments, we can estimate the error in By combining the error estimates for and (29) holds in all cases for . □
Theorem 3. Let us denote by the solution of (1) and (2) and by the solution of (21). Then, for all and , we have Proof. Note that for all
and
,
Using Theorem 2 with (
43), one can obtain
Therefore, by using Lemma 7 with (
44), for all
and
, we obtain the desired error bound, which is given by
This completes the proof. □
The obtained error bound provides the parameter uniform estimate as the constant C is independent of the perturbation parameter . Furthermore, the numerical solution converges to the continuous solution almost linearly.
6. Numerical Illustrations
In this section, we consider a trial problem to investigate the effectiveness of the present method. The notations
, and
correspond to the parameter-uniform maximum pointwise errors, the parameter-uniform error constants, and the parameter-uniform rates of convergence, respectively. Let
be an approximation of the true solution
on the mesh
, where
M and
N are the number of mesh points on each direction. We take
for the time-direction, and
for the space-direction. The exact solution for the considered test problem is not available, so for a finite set of values of the perturbation parameter
, the parameter-uniform maximum errors are obtained as
From these values, one can obtain the parameter-uniform rate of convergence using
and the parameter-uniform error constant given by
Example 1. Consider the following system of parabolic equation for with on on and on It is to be noted that the above problem satisfies conditions (
3) and (
4) and all the compatibility conditions (
6)–(
10). For different values of
the values of
, and
in the variable
x with a uniform mesh consist of 10 mesh intervals for the variable
t given in
Table 1, and for different values of
the values of
, and
in the variable
t with a piecewise uniform Shishkin mesh consist of 128 mesh intervals for the variable
x given in
Table 2. From
Table 1 and
Table 2, it can be observed that the errors are independent of the singular perturbation parameter
and decrease as the numbers of mesh points
M and
N increase. Surface plots of the maximum error of the solution of the above test problem are presented in
Figure 1 and
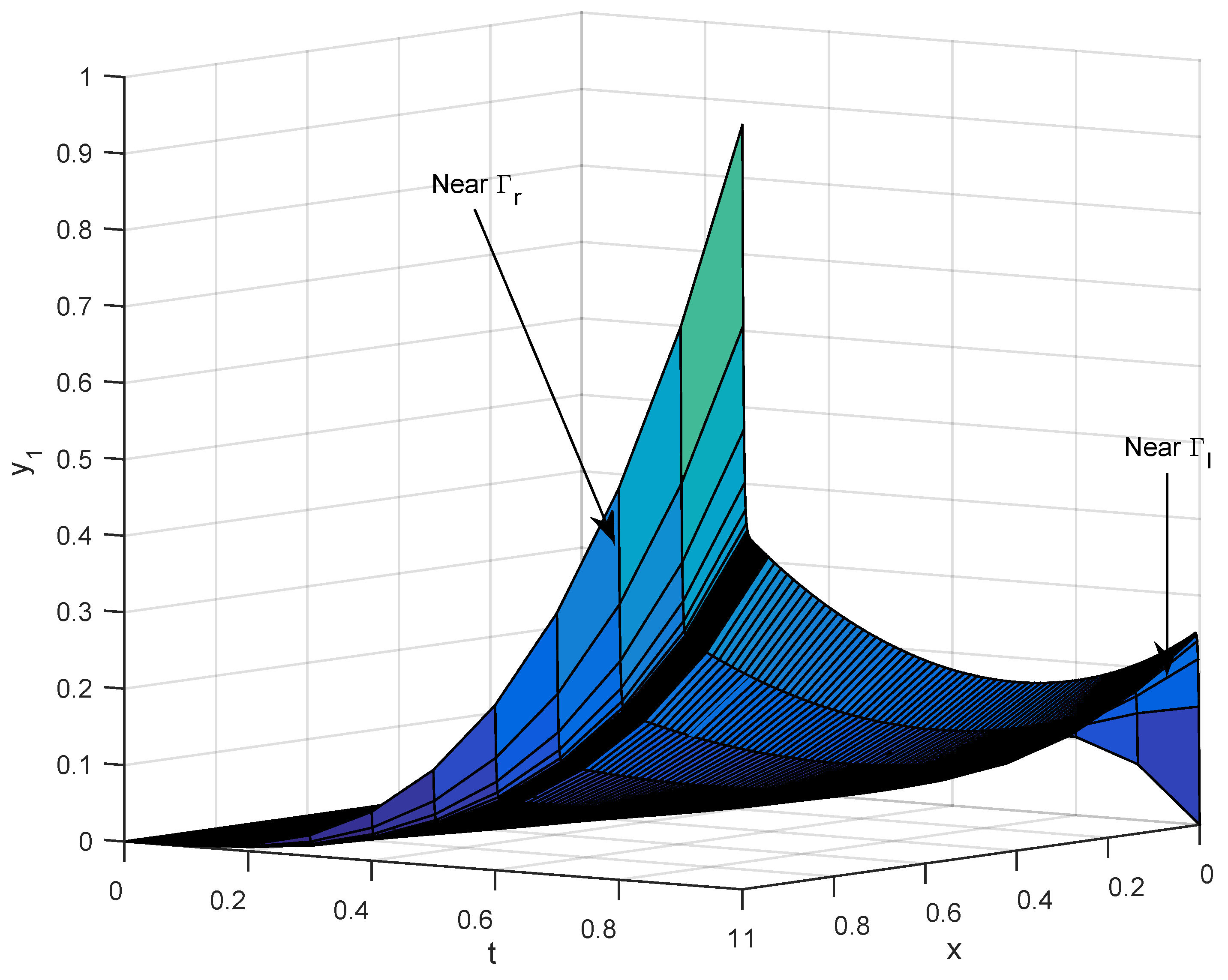
Figure 2. For
, and
Figure 1 shows the numerical solution of the component
of the solution
. It is observed that the component
changes rapidly near
and
(boundary layers) due to the presence of the perturbation parameter.
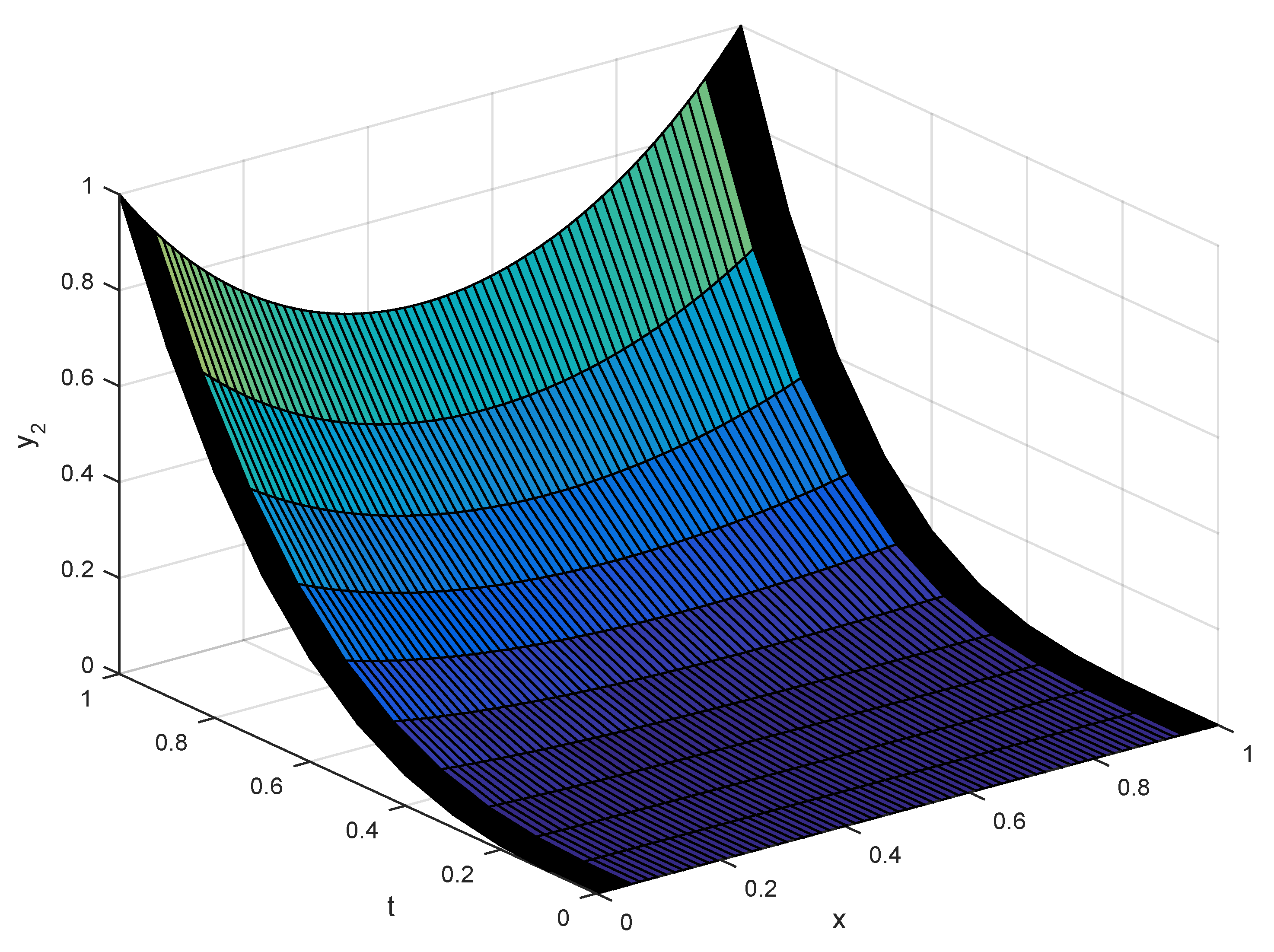
Figure 2 shows the numerical solution of the component
, but it varies smoothly throughout the domain. Furthermore,
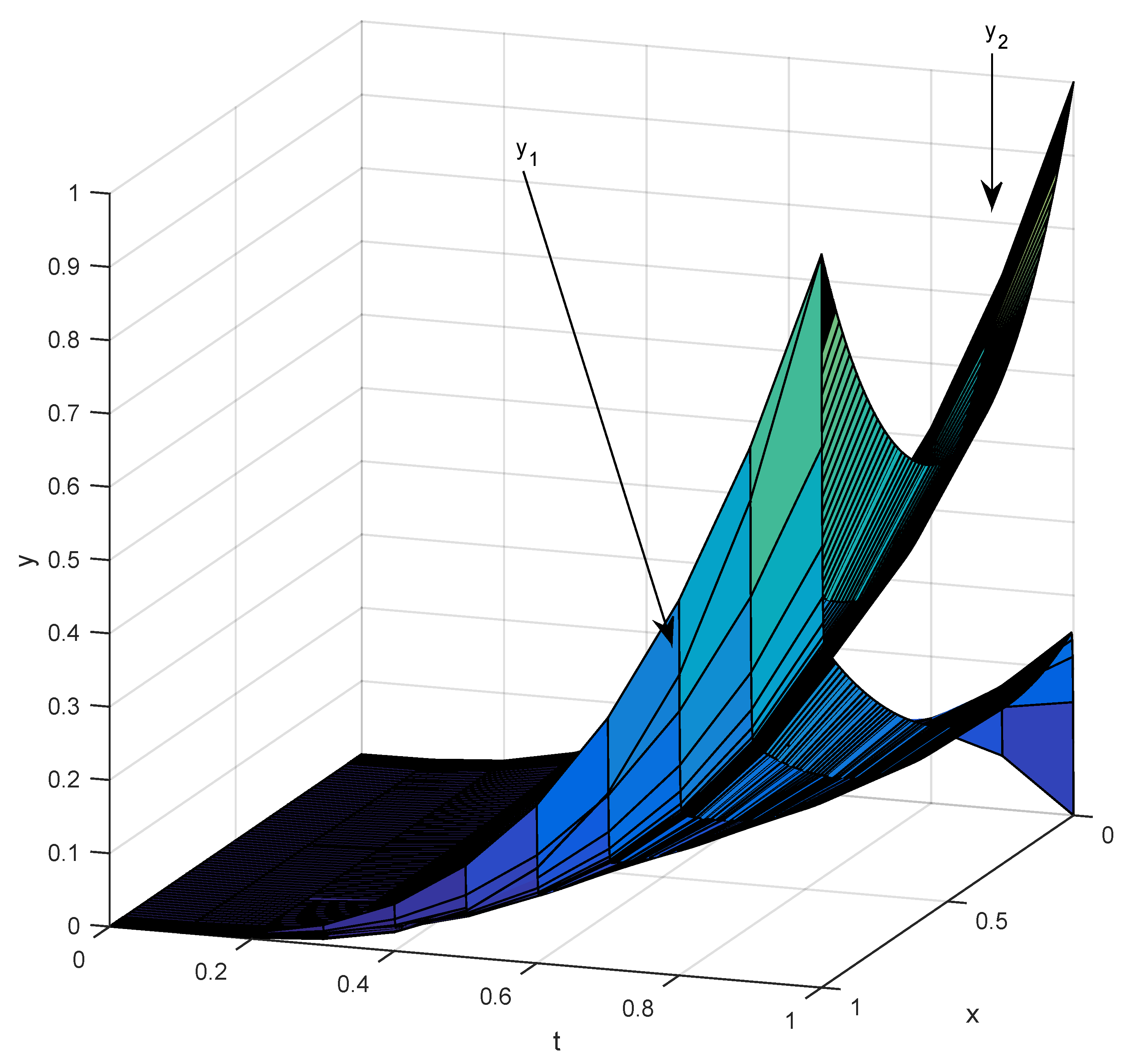
Figure 3 shows the numerical solution of
for the errors given in
Figure 4 and
Figure 5, which clearly indicate that the error bound is
, as expected.