Matrix Factorization Techniques in Machine Learning, Signal Processing, and Statistics
Abstract
1. Introduction
2. Compressed Sensing
2.1. Signal Model
2.2. RIP, ERC, and MIP
2.2.1. RIP
2.2.2. ERC
2.2.3. MIP
2.3. Sparse Recovery
2.4. Iterative Hard Thresholding
2.5. Orthogonal Matching Pursuit
2.6. LASSO
2.7. Other Sparse Algorithms
2.8. Restricted Isometry Property for Signal Recovery Methods
2.9. Related Topics
3. Dictionary Learning
3.1. Problem Formulation
3.2. Dictionary Learning Methods
4. Matrix Completion
4.1. Nuclear Norm Minimization
4.2. Matrix Factorization-Based Methods
Matrix Completion with Side Information
4.3. Theoretical Guarantees on the Exact Matrix Completion
4.4. Discrete Matrix Completion
5. Low-Rank Representation
6. Nonnegative Matrix Factorization
6.1. Multiplicative Update Algorithm
6.2. Alternating Nonnegative Least Squares
6.3. Other NMF Methods
6.3.1. Sparse NMF
6.3.2. Projective NMF
6.3.3. Graph-Regularized NMF
6.3.4. Weighted NMF
6.3.5. Bayesian NMF
6.3.6. Supervised or Semi-Supervised NMF
6.3.7. NMF for Mixed-Sign Data
6.3.8. Deep NMF
6.3.9. NMF for BSS
6.3.10. Online NMF
6.3.11. Coordinate Descent for NMF
6.3.12. Robust NMF
6.4. NMF for Clustering
6.5. Concept Factorization
7. Symmetric Positive Semi-Definite Matrix Approximation
8. CX Decomposition and CUR Decomposition
9. Conclusions
9.1. Optimization by Metaheuristics or Neurodynamics
9.2. A Few Topics for Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qiu, J.; Wang, H.; Lu, J.; Zhang, B.; Du, K.-L. Neural network implementations for PCA and its extensions. ISRN Artif. Intell. 2012, 2012, 847305. [Google Scholar] [CrossRef][Green Version]
- Du, K.-L.; Swamy, M.N.S. Neural Networks in a Softcomputing Framework; Springer: London, UK, 2006. [Google Scholar]
- Du, K.-L. Clustering: A Neural Network Approach. Neural Netw. 2010, 23, 89–107. [Google Scholar] [CrossRef]
- Du, K.-L.; Swamy, M.N.S. Neural Networks and Statistical Learning; Springer: London, UK, 2019. [Google Scholar]
- Gleichman, S.; Eldar, Y.C. Blind compressed sensing. IEEE Trans. Inf. Theory 2011, 57, 6958–6975. [Google Scholar] [CrossRef]
- Ravishankar, S.; Bresler, Y. Efficient blind compressed sensing using sparsifying transforms with convergence guarantees and application to magnetic resonance imaging. SIAM J. Imag. Sci. 2015, 8, 2519–2557. [Google Scholar] [CrossRef]
- Wu, Y.; Chi, Y.; Calderbank, R. Compressive blind source separation. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 89–92. [Google Scholar]
- Ding, C.H.; He, X.; Simon, H.D. On the equivalence of nonnegative matrix factorization and spectral clustering. In Proceedings of the SIAM International Conference on Data Mining, Newport Beach, CA, USA, 21–23 April 2005; pp. 606–610. [Google Scholar]
- Bengio, Y. Learning deep architectures for AI. Found. Trends Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- Olshausen, B.A.; Field, D.J. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature 1996, 381, 607–609. [Google Scholar] [CrossRef]
- Zhu, M.; Rozell, C.J. Visual nonclassical receptive field effects emerge from sparse coding in a dynamical system. PLoS Comput. Biol. 2013, 9, e1003191. [Google Scholar] [CrossRef]
- Unser, M.; Fageot, J.; Gupta, H. Representer theorems for sparsity-promoting ℓ1 regularization. IEEE Trans. Inf. Theory 2016, 62, 5167–5180. [Google Scholar] [CrossRef]
- Du, K.-L.; Leung, C.-S.; Mow, W.H.; Swamy, M.N.S. Perceptron: Learning, Generalization, Model Selection, Fault Tolerance, and Role in the Deep Learning Era. Mathematics 2022, 10, 4730. [Google Scholar] [CrossRef]
- Candes, E.J. Compressive sampling. In Proceedings of the International Congress of Mathematicians, Madrid, Spain, 22–30 August 2006; Volume 3, pp. 1433–1452. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Romero, D.; Ariananda, D.D.; Tian, Z.; Leus, G. Compressive covariance sensing: Structure-based compressive sensing beyond sparsity. IEEE Signal Process. Mag. 2016, 33, 78–93. [Google Scholar] [CrossRef]
- Candes, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2011, 58, 1–37. [Google Scholar] [CrossRef]
- Zhou, T.; Tao, D. GoDec: Randomized low-rank & sparse matrix decomposition in noisy case. In Proceedings of the 28th International Conference on Machine Learning, Bellevue, WA, USA, 28 June–2 July 2011; pp. 33–40. [Google Scholar]
- Guo, K.; Liu, L.; Xu, X.; Xu, D.; Tao, D. Godec+: Fast and robust low-rank matrix decomposition based on maximum correntropy. IEEE Trans. Neural Networks Learn. Syst. 2018, 29, 2323–2336. [Google Scholar] [CrossRef]
- Nguyen, L.T.; Kim, J.; Shim, B. Low-rank matrix completion: A contemporary survey. IEEE Access 2019, 7, 94215–94237. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by nonnegative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
- Hosoda, K.; Watanabe, M.; Wersing, H.; Korner, E.; Tsujino, H.; Tamura, H.; Fujita, I. A model for learning topographically organized parts-based representations of objects in visual cortex: Topographic nonnegative matrix factorization. Neural Comput. 2009, 21, 2605–2633. [Google Scholar] [CrossRef] [PubMed]
- Paatero, P.; Tapper, U. Positive matrix factorization: A nonnegative factor model with optimal utilization of error estimates of data values. Environmetrics 1994, 5, 111–126. [Google Scholar] [CrossRef]
- Berry, M.W.; Browne, M.; Langville, A.N.; Pauca, V.P.; Plemmons, R.J. Algorithms and applications for approximate nonnegative matrix factorization. Comput. Stat. Data Anal. 2007, 52, 155–173. [Google Scholar] [CrossRef]
- Sajda, P.; Du, S.; Brown, T.R.; Stoyanova, R.; Shungu, D.C.; Mao, X.; Parra, L.C. Nonnegative matrix factorization for rapid recovery of constituent spectra in magnetic resonance chemical shift imaging of the brain. IEEE Trans. Med. Imaging 2004, 23, 1453–1465. [Google Scholar] [CrossRef] [PubMed]
- Ding, C.; Li, T.; Peng, W.; Park, H. Orthogonal nonnegative matrix tri-factorizations for clustering. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’06), Philadelphia, PA, USA, 20–23 August 2006; pp. 126–135. [Google Scholar]
- Deerwester, S.C.; Dumais, S.T.; Landauer, T.K.; Furnas, G.W.; Harshman, R.A. Indexing by latent semantic analysis. J. Am. Soc. Inf. Sci. 1990, 416, 391–407. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. Decoding by linear programming. IEEE Trans. Inf. Theory 2005, 51, 4203–4215. [Google Scholar] [CrossRef]
- Donoho, D.L.; Maleki, A.; Montanari, A. Message-passing algorithms for compressed sensing. Proc. Natl. Acad. Sci. USA 2009, 106, 18914–18919. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Baraniuk, R.G.; Cevher, V.; Duarte, M.F.; Hegde, C. Model-based compressive sensing. IEEE Trans. Inf. Theory 2010, 56, 1982–2001. [Google Scholar] [CrossRef]
- Candes, E.J.; Plan, Y. A probabilistic and RIPless theory of compressed sensing. IEEE Trans. Inf. Theory 2011, 57, 7235–7254. [Google Scholar] [CrossRef]
- Misra, S.; Parrilo, P.A. Weighted l1-minimization for generalized non-uniform sparse model. IEEE Trans. Inf. Theory 2015, 61, 4424–4439. [Google Scholar] [CrossRef]
- Jalali, S.; Poor, H.V. Universal compressed sensing for almost lossless recovery. IEEE Trans. Inf. Theory 2017, 63, 2933–2953. [Google Scholar] [CrossRef]
- Tropp, J.A. Greed is good: Algorithmic results for sparse approximation. IEEE Trans. Inf. Theory 2004, 50, 2231–2242. [Google Scholar] [CrossRef]
- DeVore, R.A. Deterministic constructions of compressed sensing matrices. J. Complex. 2007, 23, 918–925. [Google Scholar] [CrossRef]
- Calderbank, R.; Howard, S.; Jafarpour, S. Construction of a large class of deterministic sensing matrices that satisfy a statistical isometry property. IEEE J. Sel. Top. Signal Process. 2010, 4, 358–374. [Google Scholar] [CrossRef]
- Dai, W.; Milenkovic, O. Weighted superimposed codes and constrained integer compressed sensing. IEEE Trans. Inf. Theory 2009, 55, 2215–2229. [Google Scholar] [CrossRef]
- Candes, E.J. The restricted isometry property and its implications for compressed sensing. Comptes Rendus Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]
- Weed, J. Approximately certifying the restricted isometry property is hard. IEEE Trans. Inf. Theory 2018, 64, 5488–5497. [Google Scholar] [CrossRef]
- Bandeira, A.S.; Fickus, M.; Mixon, D.G.; Wong, P. The road to deterministic matrices with the restricted isometry property. J. Fourier Anal. Appl. 2013, 19, 1123–1149. [Google Scholar] [CrossRef]
- Baraniuk, R.; Davenport, M.; DeVore, R.; Wakin, M. A simple proof of the restricted isometry property for random matrices. Constr. Approx. 2008, 28, 253–263. [Google Scholar] [CrossRef]
- Haviv, I.; Regev, O. The restricted isometry property of subsampled Fourier matrices. In Proceedings of the 27th Annual ACM-SIAM Symposium on Discrete Algorithms, Arlington, TX, USA, 10–12 January 2016; pp. 288–297. [Google Scholar]
- Donoho, D.L. For most large underdetermined systems of linear equations the minimal l1-norm solution is also the sparsest solution. Commun. Pure Appl. Math. 2006, 59, 797–829. [Google Scholar] [CrossRef]
- Ba, K.D.; Indyk, P.; Price, E.; Woodruff, D.P. Lower bounds for sparse recovery. In Proceedings of the 21st Annual ACM-SIAM Symp. Discrete Algorithms (SODA), Austin, TX, USA, 17–19 January 2010; pp. 1190–1197. [Google Scholar]
- Kashin, B.S.; Temlyakov, V.N. A remark on compressed sensing. Math. Notes 2007, 82, 748–755. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.K.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 2006, 59, 1207–1223. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. Near-optimal signal recovery from random projections: Universal encoding strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Barg, A.; Mazumdar, A.; Wang, R. Restricted isometry property of random subdictionaries. IEEE Trans. Inf. Theory 2015, 61, 4440–4450. [Google Scholar] [CrossRef]
- Allen-Zhu, Z.; Gelashvili, R.; Razenshteyn, I. Restricted isometry property for general p-norms. IEEE Trans. Inf. Theory 2016, 62, 5839–5854. [Google Scholar] [CrossRef]
- Soussen, C.; Gribonval, R.; Idier, J.; Herzet, C. Joint k-step analysis of orthogonal matching pursuit and orthogonal least squares. IEEE Trans. Inf. Theory 2013, 59, 3158–3174. [Google Scholar] [CrossRef]
- Kharratzadeh, M.; Sharifnassab, A.; Babaie-Zadeh, M. Invariancy of sparse recovery algorithms. IEEE Trans. Inf. Theory 2017, 63, 3333–3347. [Google Scholar] [CrossRef]
- Donoho, D.L.; Huo, X. Uncertainty principles and ideal atomic decomposition. IEEE Trans. Inf. Theory 2001, 47, 2845–2862. [Google Scholar] [CrossRef]
- Elad, M.; Bruckstein, A.M. A generalized uncertainty principle and sparse representation in pairs of RN bases. IEEE Trans. Inf. Theory 2002, 48, 2558–2567. [Google Scholar] [CrossRef]
- Donoho, D.L.; Elad, M. Optimally sparse representation in general (nonorthogonal) dictionaries via ℓ1 minimization. Proc. Nat. Acad. Sci. USA 2003, 100, 2197–2202. [Google Scholar] [CrossRef] [PubMed]
- Gribonval, R.; Nielsen, M. Sparse representations in unions of bases. IEEE Trans. Inf. Theory 2003, 49, 3320–3325. [Google Scholar] [CrossRef]
- Cai, T.; Wang, L.; Xu, G. Stable recovery of sparse signals and an oracle inequality. IEEE Trans. Inf. Theory 2010, 56, 3516–3522. [Google Scholar] [CrossRef]
- Cai, T.T.; Wang, L. Orthogonal matching pursuit for sparse signal recovery with noise. IEEE Trans. Inf. Theory 2011, 57, 4680–4688. [Google Scholar] [CrossRef]
- Nikolova, M. Description of the minimizers of least squares regularized with l0-norm. Uniqueness of the global minimizer. SIAM J. Imaging Sci. 2013, 6, 904–937. [Google Scholar] [CrossRef]
- Natarajan, B.K. Sparse approximate solutions to linear systems. SIAM J. Comput. 1995, 24, 227–234. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM J. Sci. Comput. 1998, 20, 33–61. [Google Scholar] [CrossRef]
- Lin, D.; Pitler, E.; Foster, D.P.; Ungar, L.H. In defense of l0. In Proceedings of the ICML/UAI/COLT Workshop on Sparse Optimization and Variable Selection, Helsinki, Finland, 9–12 July 2008. [Google Scholar]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Zhang, C.H. Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 2010, 38, 894–942. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Xu, W.; Tang, A. On the performance of sparse recovery via ℓp-minimization (0≤p≤1). IEEE Trans. Inf. Theory 2011, 57, 7255–7278. [Google Scholar] [CrossRef]
- Mallat, S.G.; Zhang, Z. Matching pursuits with timefrequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Los Alamitos, CA, USA, 3–6 November 1993; Volume 1, pp. 40–44. [Google Scholar]
- Rebollo-Neira, L.; Lowe, D. Optimized orthogonal matching pursuit approach. IEEE Signal Process. Lett. 2002, 9, 137–140. [Google Scholar] [CrossRef]
- Dai, W.; Milenkovic, O. Subspace pursuit for compressive sensing signal reconstruction. IEEE Trans. Inf. Theory 2009, 55, 2230–2249. [Google Scholar] [CrossRef]
- Needell, D.; Tropp, J.A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 2009, 26, 301–321. [Google Scholar] [CrossRef]
- Blumensath, T.; Davies, M.E. Iterative thresholding for sparse approximations. J. Fourier Anal. Appl. 2008, 14, 629–654. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef]
- Huebner, E.; Tichatschke, R. Relaxed proximal point algorithms for variational inequalities with multi-valued operators. Optim. Methods Softw. 2008, 23, 847–877. [Google Scholar] [CrossRef]
- Nesterov, Y. Gradient methods for minimizing composite functions. Math. Program. 2013, 140, 125–161. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted l1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Malioutov, D.M.; Cetin, M.; Willsky, A.S. Homotopy continuation for sparse signal representation. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Philadelphia, PA, USA, 18–23 March 2005; pp. 733–736. [Google Scholar]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef]
- Chartrand, R. Exact reconstruction of sparse signals via nonconvex minimization. IEEE Signal Process. Lett. 2007, 14, 707–710. [Google Scholar] [CrossRef]
- Cherfaoui, F.; Emiya, V.; Ralaivola, L.; Anthoine, S. Recovery and convergence rate of the Frank-Wolfe algorithm for the m-EXACT-SPARSE problem. IEEE Trans. Inf. Theory 2019, 65, 7407–7414. [Google Scholar] [CrossRef]
- Gribonval, R.; Vandergheynst, P. On the exponential convergence of matching pursuits in quasi-incoherent dictionaries. IEEE Trans. Inf. Theory 2006, 52, 255–261. [Google Scholar] [CrossRef]
- Foucart, S. Hard thresholding pursuit: An algorithm for compressive sensing. SIAM J. Numer. Anal. 2011, 49, 2543–2563. [Google Scholar] [CrossRef]
- Langford, J.; Li, L.; Zhang, T. Sparse online learning via truncated gradient. J. Mach. Learn. Res. 2009, 10, 777–801. [Google Scholar]
- Chen, L.; Gu, Y. The convergence guarantees of a non-convex approach for sparse recovery. IEEE Trans. Signal Process. 2014, 62, 3754–3767. [Google Scholar] [CrossRef]
- Chartrand, R.; Yin, W. Iteratively reweighted algorithms for compressive sensing. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Las Vegas, NV, USA, 30 March–4 April 2008; pp. 3869–3872. [Google Scholar]
- Xu, Z.; Chang, X.; Xu, F.; Zhang, H. L1/2 regularization: A thresholding representation theory and a fast solver. IEEE Trans. Neural Networks Learn. Syst. 2012, 23, 1013–1027. [Google Scholar]
- Marjanovic, G.; Solo, V. On lq optimization and matrix completion. IEEE Trans. Signal Process. 2012, 60, 5714–5724. [Google Scholar] [CrossRef]
- Chi, Y.; Scharf, L.L.; Pezeshki, A.; Calderbank, A.R. Sensitivity to basis mismatch in compressed sensing. IEEE Trans. Signal Process. 2011, 59, 2182–2195. [Google Scholar] [CrossRef]
- Li, X. Compressed sensing and matrix completion with constant proportion of corruptions. Constr. Approx. 2013, 37, 73–99. [Google Scholar] [CrossRef]
- Candes, E.J.; Fernandez-Granda, C. Towards a mathematical theory of super-resolution. Commun. Pure Appl. Math. 2014, 67, 906–956. [Google Scholar] [CrossRef]
- Tzagkarakis, G.; Nolan, J.P.; Tsakalides, P. Compressive sensing using symmetric alpha-stable distributions for robust sparse signal reconstruction. IEEE Trans. Signal Process. 2019, 67, 808–820. [Google Scholar] [CrossRef]
- Mohimani, H.; B-Zadeh, M.; Jutten, C. A fast approach for overcomplete sparse decomposition based on smoothed ℓ0 norm. IEEE Trans. Signal Process. 2009, 57, 289–301. [Google Scholar] [CrossRef]
- Gorodnitsky, I.F.; Rao, B.D. Sparse signal reconstruction from limited data using FOCUSS: A re-weighted minimum norm algorithm. IEEE Trans. Signal Process. 1997, 45, 600–616. [Google Scholar] [CrossRef]
- van den Berg, E.; Friedlander, M.P. Probing the Pareto frontier for basis pursuit solutions. SIAM J. Sci. Comput. 2008, 31, 890–912. [Google Scholar] [CrossRef]
- Blumensath, T.; Davies, M.E. Iterative hard thresholding for compressed sensing. Appl. Comput. Harmon. Anal. 2009, 27, 265–274. [Google Scholar] [CrossRef]
- Blumensath, T.; Davies, M.E. Normalized iterative hard thresholding: Guaranteed stability and performance. IEEE J. Sel. Top. Signal Process. 2010, 4, 298–309. [Google Scholar] [CrossRef]
- Blumensath, T. Compressed sensing with nonlinear observations and related nonlinear optimization problems. IEEE Trans. Inf. Theory 2013, 59, 3466–3474. [Google Scholar] [CrossRef]
- Cartis, C.; Thompson, A. A new and improved quantitative recovery analysis for iterative hard thresholding algorithms in compressed sensing. IEEE Trans. Inf. Theory 2015, 61, 2019–2042. [Google Scholar] [CrossRef]
- Gurel, N.M.; Kara, K.; Stojanov, A.; Smith, T.M.; Lemmin, T.; Alistarh, D.; Puschel, M.; Zhang, C. Compressive sensing using iterative hard thresholding with low precision data representation: Theory and applications. IEEE Trans. Signal Process. 2020, 68, 4268–4282. [Google Scholar] [CrossRef]
- Daubechies, I.; Defrise, M.; De Mol, C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. 2004, 57, 1413–1457. [Google Scholar] [CrossRef]
- Dong, Z.; Zhu, W. Homotopy methods based on l0-norm for compressed sensing. IEEE Trans. Neural Networks Learn. Syst. 2018, 29, 1132–1146. [Google Scholar] [CrossRef]
- Yuan, X.-T.; Li, P.; Zhang, T. Exact recovery of hard thresholding pursuit. Adv. Neural Inf. Process. Syst. 2016, 29, 3558–3566. [Google Scholar]
- Yuan, X.-T.; Li, P.; Zhang, T. Gradient hard thresholding pursuit. J. Mach. Learn. Res. 2018, 18, 1–43. [Google Scholar]
- Tropp, J.A.; Wright, S.J. Computational methods for sparse solution of linear inverse problems. Proc. IEEE 2010, 98, 948–958. [Google Scholar] [CrossRef]
- Shen, J.; Li, P. A tight bound of hard thresholding. J. Mach. Learn. Res. 2018, 18, 1–42. [Google Scholar]
- Yuan, X.-T.; Liu, B.; Wang, L.; Liu, Q.; Metaxas, D.N. Dual iterative hard thresholding. J. Mach. Learn. Res. 2020, 21, 1–50. [Google Scholar]
- Nguyen, N.H.; Chin, S.; Tran, T. A Unified Iterative Greedy Algorithm for Sparsity Constrained Optimization. 2013. Available online: https://sites.google.com/site/namnguyenjhu/gradMP.pdf (accessed on 1 March 2020).
- Nguyen, N.; Needell, D.; Woolf, T. Linear convergence of stochastic iterative greedy algorithms with sparse constraints. IEEE Trans. Inf. Theory 2017, 63, 6869–6895. [Google Scholar] [CrossRef]
- Axiotis, K.; Sviridenko, M. Sparse convex optimization via adaptively regularized hard thresholding. J. Mach. Learn. Res. 2021, 22, 1–47. [Google Scholar]
- Meng, N.; Zhao, Y.-B. Newton-step-based hard thresholding algorithms for sparse signal recovery. IEEE Trans. Signal Process. 2020, 68, 6594–6606. [Google Scholar] [CrossRef]
- Ravazzi, C.; Fosson, S.M.; Magli, E. Distributed iterative thresholding for ℓ0/ℓ1-regularized linear inverse problems. IEEE Trans. Inf. Theory 2015, 61, 2081–2100. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Donoho, D.L.; Tsaig, Y.; Drori, I.; Starck, J.-L. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit. IEEE Trans. Inf. Theory 2012, 58, 1094–1121. [Google Scholar] [CrossRef]
- Needell, D.; Vershynin, R. Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit. IEEE J. Sel. Top. Signal Process. 2010, 4, 310–316. [Google Scholar] [CrossRef]
- Wang, J.; Kwon, S.; Shim, B. Generalized orthogonal matching pursuit. IEEE Trans. Signal Process. 2012, 60, 6202–6216. [Google Scholar] [CrossRef]
- Liu, E.; Temlyakov, V.N. The orthogonal super greedy algorithm and applications in compressed sensing. IEEE Trans. Inf. Theory 2012, 58, 2040–2047. [Google Scholar] [CrossRef]
- Kwon, S.; Wang, J.; Shim, B. Multipath matching pursuit. IEEE Trans. Inf. Theory 2014, 60, 2986–3001. [Google Scholar] [CrossRef]
- Wang, J.; Li, P. Recovery of sparse signals using multiple orthogonal least squares. IEEE Trans. Signal Process. 2017, 65, 2049–2062. [Google Scholar] [CrossRef]
- Lu, L.; Xu, W.; Wang, Y.; Tian, Z. Recovery conditions of sparse signals using orthogonal least squares-type algorithms. IEEE Trans. Signal Process. 2022, 70, 4727–4741. [Google Scholar] [CrossRef]
- Kim, J.; Wang, J.; Nguyen, L.T.; Shim, B. Joint sparse recovery using signal space matching pursuit. IEEE Trans. Inf. Theory 2020, 66, 5072–5096. [Google Scholar] [CrossRef]
- Jain, P.; Tewari, A.; Dhillon, I.S. Orthogonal matching pursuit with replacement. Adv. Neural Inf. Process. Syst. 2011, 24, 1215–1223. [Google Scholar]
- Jain, P.; Tewari, A.; Dhillon, I.S. Partial hard thresholding. IEEE TRansactions Inf. Theory 2017, 63, 3029–3038. [Google Scholar] [CrossRef]
- Eldar, Y.C.; Kuppinger, P.; Bolcskei, H. Block-sparse signals: Uncertainty relations and efficient recovery. IEEE Trans. Signal Process. 2010, 58, 3042–3054. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Chakraborty, M. A two stage generalized block orthogonal matching pursuit (TSGBOMP) algorithm. IEEE Trans. Signal Process. 2021, 69, 5846–5858. [Google Scholar] [CrossRef]
- Rauhut, H. Stability results for random sampling of sparse trigonometric polynomials. IEEE Trans. Inf. Theory 2008, 54, 5661–5670. [Google Scholar] [CrossRef]
- Davenport, M.A.; Wakin, M.B. Analysis of orthogonal matching pursuit using the restricted isometry property. IEEE Trans. Inf. Theory 2010, 56, 4395–4401. [Google Scholar] [CrossRef]
- Mo, Q.; Yi, S. A remark on the restricted isometry property in orthogonal matching pursuit. IEEE Trans. Inf. Theory 2012, 58, 3654–3656. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso: A retrospective. J. R. Stat. Soc. Ser. B 2011, 73, 273–282. [Google Scholar] [CrossRef]
- Jaggi, M. An equivalence between the Lasso and support vector machines. In Regularization, Optimization, Kernels, and Support Vector Machines; Suykens, J.A.K., Signoretto, M., Argyriou, A., Eds.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2014; Chapter 1; pp. 1–26. [Google Scholar]
- Lee, M.; Shen, H.; Huang, J.Z.; Marron, J.S. Biclustering via sparse singular value decomposition. Biometrics 2010, 66, 1087–1095. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Tewari, A. Stochastic methods for l1-regularized loss minimization. J. Mach. Learn. Res. 2011, 12, 1865–1892. [Google Scholar]
- Lederer, J.; Vogt, M. Estimating the Lasso’s Effective Noise. J. Mach. Learn. Res. 2021, 22, 1–32. [Google Scholar]
- Chretien, S.; Darses, S. Sparse recovery with unknown variance: A LASSO-type approach. IEEE Trans. Inf. Theory 2014, 60, 3970–3988. [Google Scholar] [CrossRef]
- Roth, V. The generalized Lasso. IEEE Trans. Neural Netw. 2004, 15, 16–28. [Google Scholar] [CrossRef]
- Li, F.; Yang, Y.; Xing, E. FromLasso regression to feature vector machine. In Advances in Neural Information Processing Systems; Weiss, Y., Scholkopf., B., Platt, J., Eds.; MIT Press: Cambridge, MA, USA, 2006; Volume 18, pp. 779–786. [Google Scholar]
- Frandi, E.; Nanculef, R.; Lodi, S.; Sartori, C.; Suykens, J.A.K. Fast and scalable Lasso via stochastic Frank-Wolfe methods with a convergence guarantee. Mach. Learn. 2016, 104, 195–221. [Google Scholar] [CrossRef]
- Xu, H.; Mannor, S.; Caramanis, C. Sparse algorithms are not stable: A no-free-lunch theorem. In Proceedings of the IEEE 46th Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 23–26 September 2008; pp. 1299–1303. [Google Scholar]
- Homrighausen, D.; McDonald, D.J. Leave-one-out cross-validation is risk consistent for lasso. Mach. Learn. 2014, 97, 65–78. [Google Scholar] [CrossRef]
- Xu, H.; Caramanis, C.; Mannor, S. Robust regression and Lasso. IEEE Trans. Inf. Theory 2010, 56, 3561–3574. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Z.J.; McKeown, M.J. Asymptotic analysis of robust LASSOs in the presence of noise with large variance. IEEE Trans. Inf. Theory 2010, 56, 5131–5149. [Google Scholar] [CrossRef]
- Yuan, M.; Lin, Y. Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. B 2006, 68, 49–67. [Google Scholar] [CrossRef]
- Bunea, F.; Lederer, J.; She, Y. The group square-root Lasso: Theoretical properties and fast algorithms. IEEE Trans. Inf. Theory 2014, 60, 1313–1325. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2009. [Google Scholar]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Genovese, C.R.; Jin, J.; Wasserman, L.; Yao, Z. A comparison of the lasso and marginal regression. J. Mach. Learn. Res. 2012, 13, 2107–2143. [Google Scholar]
- Jolliffe, I.T.; Trendafilov, N.T.; Uddin, M. A modified principal component technique based on the LASSO. J. Comput. Graph. Stat. 2003, 12, 531–547. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Rotation of ill-defined principal components. Appl. Stat. 1989, 38, 139–147. [Google Scholar] [CrossRef]
- Cadima, J.; Jolliffe, I.T. Loading and correlations in the interpretation of principle compenents. Appl. Stat. 1995, 22, 203–214. [Google Scholar] [CrossRef]
- Lu, Z.; Zhang, Y. An augmented Lagrangian approach for sparse principal component analysis. Math. Program. 2012, 135, 149–193. [Google Scholar] [CrossRef]
- Moghaddam, B.; Weiss, Y.; Avidan, S. Spectral bounds for sparse PCA: Exact and greedy algorithms. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2006; Volume 18, pp. 915–922. [Google Scholar]
- d’Aspremont, A.; Bach, F.; El Ghaoui, L. Optimal solutions for sparse principal component analysis. J. Mach. Learn. Res. 2008, 9, 1269–1294. [Google Scholar]
- Shen, H.; Huang, J.Z. Sparse principal component analysis via regularized low rank matrix approximation. J. Multivar. Anal. 2008, 99, 1015–1034. [Google Scholar] [CrossRef]
- Journee, M.; Nesterov, Y.; Richtarik, P.; Sepulchre, R. Generalized power method for sparse principal component analysis. J. Mach. Learn. Res. 2010, 11, 517–553. [Google Scholar]
- Yuan, X.-T.; Zhang, T. Truncated power method for sparse eigenvalue problems. J. Mach. Learn. Res. 2013, 14, 899–925. [Google Scholar]
- Ma, Z. Sparse principal component analysis and iterative thresholding. Ann. Stat. 2013, 41, 772–801. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T.; Tibshirani, R. Sparse principal component analysis. J. Comput. Graph. Stat. 2006, 15, 265–286. [Google Scholar] [CrossRef]
- d’Aspremont, A.; El Ghaoui, L.; Jordan, M.I.; Lanckriet, G.R.G. A direct formulation for sparse PCA using semidefinite programming. SIAM Rev. 2007, 49, 434–448. [Google Scholar] [CrossRef]
- Zhang, Y.; El Ghaoui, L. Large-scale sparse principal component analysis with application to text data. In Advances in Neural Information Processing Systems; Curran & Associates Inc.: Red Hook, NY, USA, 2011; Volume 24, pp. 532–539. [Google Scholar]
- Jankov, J.; van de Geer, S. De-biased sparse PCA: Inference for eigenstructure of large covariance matrices. IEEE Trans. Inf. Theory 2021, 67, 2507–2527. [Google Scholar] [CrossRef]
- Chen, Y.; Gu, Y.; Hero, A.O., III. Sparse LMS for system identification. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009. [Google Scholar]
- Babadi, B.; Kalouptsidis, N.; Tarokh, V. SPARLS: The sparse RLS algorithm. IEEE Trans. Signal Process. 2010, 58, 4013–4025. [Google Scholar] [CrossRef]
- Yang, D.; Ma, Z.; Buja, A. A sparse singular value decomposition method for high-dimensional data. Journal of Computational and Graphical Statistics 2014, 23–942. [Google Scholar] [CrossRef]
- Witten, D.M.; Tibshirani, R.; Hastie, T. A penalized matrix decomposition, with applications to sparse principal components and canonical correlation analysis. Biostatistics 2009, 10, 515–534. [Google Scholar] [CrossRef] [PubMed]
- Mazumder, R.; Hastie, T.; Tibshirani, R. Spectral regularization algorithms for learning large incomplete matrices. J. Mach. Learn. Res. 2010, 11, 2287–2322. [Google Scholar] [PubMed]
- Engelhardt, B.E.; Stephens, M. Analysis of population structure: A unifying framework and novel methods based on sparse factor analysis. PLoS Genet. 2010, 6, e1001117. [Google Scholar] [CrossRef] [PubMed]
- Knowles, D.; Ghahramani, Z. Nonparametric Bayesian sparse factor. Ann. Appl. Stat. 2011, 5, 1534–1552. [Google Scholar] [CrossRef]
- Wang, W.; Stephens, M. Empirical Bayes matrix factorization. J. Mach. Learn. Res. 2021, 22, 1–40. [Google Scholar]
- Mo, Q.; Li, S. New bounds on the restricted isometry constant δ2k. Appl. Comput. Harmon. Anal. 2011, 31, 460–468. [Google Scholar] [CrossRef]
- Foucart, S.; Lai, M.-J. Sparsest solutions of underdetermined linear systems via lq-minimization for 0<q≤1. Appl. Comput. Harmon. Anal. 2009, 26, 395–407. [Google Scholar]
- Cai, T.T.; Wang, L.; Xu, G. New bounds for restricted isometry constants. IEEE Trans. Inf. Theory 2010, 56, 4388–4394. [Google Scholar] [CrossRef]
- Needell, D.; Vershynin, R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit. Found. Comput. Math. 2009, 9, 317–334. [Google Scholar] [CrossRef]
- Foucart, S.; Rauhut, H. A mathematical introduction to compressive sensing. Bull. Am. Math. Soc. 2017, 54, 151–165. [Google Scholar]
- Chang, L.-H.; Wu, J.-Y. Compressive-domain interference cancellation via orthogonal projection: How small the restricted isometry constant of the effective sensing matrix can be? In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 1–4 April 2012; pp. 256–261. [Google Scholar]
- Huang, S.; Zhu, J. Recovery of sparse signals using OMP and its variants: Convergence analysis based on RIP. Inverse Probl. 2011, 27, 035003. [Google Scholar] [CrossRef]
- Wu, R.; Chen, D.-R. The improved bounds of restricted isometry constant for recovery via ℓp-minimization. IEEE Trans. Inf. Theory 2013, 59, 6142–6147. [Google Scholar]
- Chang, L.-H.; Wu, J.-Y. An improved RIP-based performance Guarantee for sparse signal recovery via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2014, 60, 5702–5715. [Google Scholar] [CrossRef]
- Mo, Q. A Sharp Restricted Isometry Constant Bound of Orthogonal Matching Pursuit. 2015. Available online: https://arxiv.org/pdf/1501.01708.pdf (accessed on 1 March 2023).
- Wen, J.; Zhou, Z.; Wang, J.; Tang, X.; Mo, Q. A sharp condition for exact support recovery with orthogonal matching pursuit. IEEE Trans. Signal Process. 2017, 65, 1370–1382. [Google Scholar] [CrossRef]
- Wen, J.; Wang, J.; Zhang, Q. Nearly optimal bounds for orthogonal least squares. IEEE Trans. Signal Process. 2017, 65, 5347–5356. [Google Scholar] [CrossRef]
- Zhang, T. Sparse recovery with orthogonal matching pursuit under RIP. IEEE Trans. Inf. Theory 2011, 57, 6215–6221. [Google Scholar] [CrossRef]
- Livshitz, E.D.; Temlyakov, V.N. Sparse approximation and recovery by greedy algorithms. IEEE Trans. Inf. Theory 2014, 60, 3989–4000. [Google Scholar] [CrossRef]
- Cai, T.T.; Zhang, A. Sparse representation of a polytope and recovery of sparse signals and low-rank matrices. IEEE Trans. Inf. Theory 2014, 60, 122–132. [Google Scholar] [CrossRef]
- Zhang, R.; Li, S. A Proof of conjecture on restricted isometry property constants δtk (0<t<43). IEEE Trans. Inf. Theory 2018, 64, 1699–1705. [Google Scholar]
- Li, H.; Wang, J.; Yuan, X. On the fundamental limit of multipath matching pursuit. IEEE J. Sel. Top. Signal Process. 2018, 12, 916–927. [Google Scholar] [CrossRef]
- Giryes, R.; Elad, M. RIP-based near-oracle performance guarantees for SP, CoSaMP, and IHT. IEEE Trans. Signal Process. 2012, 60, 1465–1568. [Google Scholar] [CrossRef]
- Wen, J.; Zhou, Z.; Liu, Z.; Lai, M.-J.; Tang, X. Sharp sufficient conditions for stable recovery of block sparse signals by block orthogonal matching pursuit. Appl. Comput. Harmon. Anal. 2019, 47, 948–974. [Google Scholar] [CrossRef]
- Wu, R.; Huang, W.; Chen, D.-R. The exact support recovery of sparse signals with noise via orthogonal matching pursuit. IEEE Signal Process. Lett. 2013, 20, 403–406. [Google Scholar] [CrossRef]
- Zhang, R.; Li, S. Optimal RIP bounds for sparse signals recovery via ℓp minimization. Appl. Comput. Harmon. Anal. 2019, 47, 566–584. [Google Scholar] [CrossRef]
- Gribonval, R.; Nielsen, M. Highly sparse representations from dictionaries are unique and independent of the sparseness measure. Appl. Comput. Harmon. Anal. 2007, 22, 335–355. [Google Scholar] [CrossRef]
- Foucart, S.; Rauhut, H. A Mathematical Introduction to Compressive Sensing; Birkhauser: Cambridge, MA, USA, 2013. [Google Scholar]
- Peng, J.; Yue, S.; Li, H. NP/CMP equivalence: A phenomenon hidden among sparsity models l0 minimization and lp minimization for information processing. IEEE Trans. Inf. Theory 2015, 61, 4028–4033. [Google Scholar] [CrossRef]
- Wang, C.; Yue, S.; Peng, J. When is P such that l0-minimization equals to lp-minimization. arXiv 2015, arXiv:1511.07628. [Google Scholar]
- Boufounos, P.T.; Baraniuk, R.G. 1-bit compressive sensing. In Proceedings of the 42nd Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 19–21 March 2008; pp. 16–21. [Google Scholar]
- Gopi, S.; Netrapalli, P.; Jain, P.; Nori, A. One-bit compressed sensing: Provable support and vector recovery. In Proceedings of the 30th International Conference on Machine Learning (ICML), Atlanta, GA, USA, 16–21 June 2013; pp. 154–162. [Google Scholar]
- Plan, Y.; Vershynin, R. One-bit compressed sensing by linear programming. Commun. Pure Appl. Math. 2013, 66, 1275–1297. [Google Scholar] [CrossRef]
- Plan, Y.; Vershynin, R. Robust 1-bit compressed sensing and sparse logistic regression: A convex programming approach. IEEE Trans. Inf. Theory 2013, 59, 482–494. [Google Scholar] [CrossRef]
- Jacques, L.; Laska, J.N.; Boufounos, P.T.; Baraniuk, R.G. Robust 1-bit compressive sensing via binary stable embeddings of sparse vectors. IEEE Trans. Inf. Theory 2013, 59, 2082–2102. [Google Scholar] [CrossRef]
- Sun, J.Z.; Goyal, V.K. Optimal quantization of random measurements in compressed sensing. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Seoul, Republic of Korea, 28 June–3 July 2009; pp. 6–10. [Google Scholar]
- Baraniuk, R.G.; Foucart, S.; Needell, D.; Plan, Y.; Wootters, M. Exponential Decay of Reconstruction Error From Binary Measurements of Sparse Signals. IEEE Trans. Inf. Theory 2017, 63, 3368–3385. [Google Scholar] [CrossRef]
- Aissa-El-Bey, A.; Pastor, D.; Sbai, S.M.A.; Fadlallah, Y. Sparsity-based recovery of finite alphabet solutions to underdetermined linear systems. IEEE Trans. Inf. Theory 2015, 61, 2008–2018. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Spielman, D.; Wang, H.; Wright, J. Exact recovery of sparsely-used dictionaries. In Proceedings of the JMLR: Workshop and Conference Proceedings of the 25th Annual Conference on Learning Theory, Edinburgh, UK, 26 June–1 July 2012; Volume 23, pp. 37.1–37.18.
- Luh, K.; Vu, V. Dictionary learning with few samples and matrix concentration. IEEE Trans. Inf. Theory 2016, 62, 1516–1527. [Google Scholar] [CrossRef]
- Adamczak, R. A Note on the sample complexity of the Er-SpUD algorithm by Spielman, Wang and Wright for exact recovery of sparsely used dictionaries. J. Mach. Learn. Res. 2016, 17, 1–18. [Google Scholar]
- Olshausen, B.A.; Field, D.J. Sparse coding with an overcomplete basis set: A strategy employed by V1? Vis. Res. 1997, 37, 3311–3325. [Google Scholar] [CrossRef]
- Hoyer, P. Non-negative sparse coding. In Proceedings of the 12th IEEE Workshop on Neural Networks for Signal Processing, Martigny, Switzerland, 6 September 2002; pp. 557–565. [Google Scholar]
- Kim, H.; Park, H. Nonnegative matrix factorization based on alternating nonnegativity constrained least squares and active set method. SIAM J. Matrix Anal. Appl. 2008, 30, 713–730. [Google Scholar] [CrossRef]
- Kreutz-Delgado, K.; Murray, J.F.; Rao, B.D.; Engan, K.; Lee, T.-W.; Sejnowski, T.J. Dictionary learning algorithms for sparse representation. Neural Comput. 2003, 15, 349–396. [Google Scholar] [CrossRef]
- Jenatton, R.; Mairal, J.; Obozinski, G.; Bach, F. Proximal methods for hierarchical sparse coding. J. Mach. Learn. Res. 2011, 12, 2297–2334. [Google Scholar]
- Tibshirani, R.; Saunders, M.; Rosset, S.; Zhu, J.; Knight, K. Sparsity and smoothness via the fused lasso. J. R. Stat. Soc. Ser. B 2005, 67, 91–108. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J. Task-driven dictionary learning. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 791–804. [Google Scholar] [CrossRef]
- Attouch, H.; Bolte, J.; Redont, P.; Soubeyran, A. Proximal alternating minimization and projection methods for nonconvex problems: An approach based on the Kurdyka-Lojasiewicz inequality. Math. Oper. Res. 2010, 35, 438–457. [Google Scholar] [CrossRef]
- Bolte, J.; Sabach, S.; Teboulle, M. Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math. Program. 2014, 146, 459–494. [Google Scholar] [CrossRef]
- Bao, C.; Ji, H.; Quan, Y.; Shen, Z. Dictionary learning for sparse coding: Algorithms and convergence analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1356–1369. [Google Scholar] [CrossRef] [PubMed]
- Sivalingam, R.; Boley, D.; Morellas, V.; Papanikolopoulos, N. Tensor dictionary learning for positive definite matrices. IEEE Trans. Image Process. 2015, 24, 4592–4601. [Google Scholar] [CrossRef] [PubMed]
- Studer, C.; Kuppinger, P.; Pope, G.; Bolcskei, H. Recovery of Sparsely Corrupted Signals. IEEE Trans. Inf. Theory 2012, 58, 3115–3130. [Google Scholar] [CrossRef]
- Zarmehi, N.; Marvasti, F. Removal of sparse noise from sparse signals. Signal Process. 2019, 158, 91–99. [Google Scholar] [CrossRef]
- Exarchakis, G.; Lucke, J. Discrete sparse coding. Neural Comput. 2017, 29, 2979–3013. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wu, S.; Yu, B. Unique sharp local minimum in ℓ1-minimization complete dictionary learning. J. Mach. Learn. Res. 2020, 21, 1–52. [Google Scholar]
- Jung, A.; Eldar, Y.C.; Gortz, N. On the minimax risk of dictionary learning. IEEE Trans. Inf. Theory 2016, 62, 1501–1515. [Google Scholar] [CrossRef]
- Candes, E.; Eldar, Y.; Needell, D.; Randall, P. Compressed sensing with coherent and redundant dictionaries. Appl. Comput. Harmon. Anal. 2011, 31, 59–73. [Google Scholar] [CrossRef]
- Blumensath, T. Sampling and reconstructing signals from a union of linear subspaces. IEEE Trans. Inf. Theory 2011, 57, 4660–4671. [Google Scholar] [CrossRef]
- Davenport, M.A.; Needell, D.; Wakin, M.B. Signal space CoSaMP for sparse recovery with redundant dictionaries. IEEE Trans. Inf. Theory 2013, 59, 6820–6829. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G. Online learning for matrix factorization and sparse coding. J. Mach. Learn. Res. 2010, 11, 19–60. [Google Scholar]
- Lyu, H.; Needell, D.; Balzano, L. Online matrix factorization for Markovian data and applications to Network Dictionary Learning. J. Mach. Learn. Res. 2020, 21, 1–49. [Google Scholar]
- Elvira, C.; Chainais, P.; Dobigeon, N. Bayesian antisparse coding. IEEE Trans. Signal Process. 2017, 65, 1660–1672. [Google Scholar] [CrossRef]
- Liu, G.; Lin, Z.; Yu, Y. Robust subspace segmentation by low-rank representation. In Proceedings of the 25th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 663–670. [Google Scholar]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust recovery of subspace structures by low-rank representation. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 171–184. [Google Scholar] [CrossRef]
- Candes, E.J.; Recht, B. Exact matrix completion via convex optimization. Found. Comput. Math. 2009, 9, 717–772. [Google Scholar] [CrossRef]
- Fazel, M. Matrix Rank Minimization with Applications. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2002. [Google Scholar]
- Recht, B.; Fazel, M.; Parrilo, P.A. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Rev. 2010, 52, 471–501. [Google Scholar] [CrossRef]
- Foygel, R.; Srebro, N. Concentration-based guarantees for low-rank matrix reconstruction. JMLR Workshop Conf. Proc. 2011, 19, 315–339. [Google Scholar]
- Chen, Y.; Bhojanapalli, S.; Sanghavi, S.; Ward, R. Completing any low-rank matrix, provably. J. Mach. Learn. Res. 2015, 16, 2999–3034. [Google Scholar]
- Bhojanapalli, S.; Jain, P. Universal matrix completion. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 1881–1889. [Google Scholar]
- Toh, K.-C.; Yun, S. An accelerated proximal gradient algorithm for nuclear norm regularized least squares problems. Pac. J. Optim. 2010, 6, 615–640. [Google Scholar]
- Chen, C.; He, B.; Yuan, X. Matrix completion via an alternating direction method. IMA J. Numer. Anal. 2012, 32, 227–245. [Google Scholar] [CrossRef]
- Srebro, N.; Rennie, J.D.M.; Jaakkola, T.S. Maximum-margin matrix factorization. Adv. Neural Inf. Process. Syst. 2004, 17, 1329–1336. [Google Scholar]
- Lin, Z.; Ganesh, A.; Wright, J.; Wu, L.; Chen, M.; Ma, Y. Fast Convex Optimization Algorithms for Exact Recovery of a Corrupted Low-Rank Matrix; Technical Report UILU-ENG-09-2214; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2009. [Google Scholar]
- Lin, Z.; Chen, M.; Wu, L.; Ma, Y. The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices; Technical Report UILU-ENG-09-2215; Department of Electrical and Computer Engineering, University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2009. [Google Scholar]
- Keshavan, R.H.; Montanari, A.; Oh, S. Matrix completion from a few entries. IEEE Trans. Inf. Theory 2010, 56, 2980–2998. [Google Scholar] [CrossRef]
- Cai, J.-F.; Candes, E.J.; Shen, Z. A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Ke, Q.; Kanade, T. Robust L1 norm factorization in the presence of outliers and missing data by alternative convex programming. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–26 June 2005; pp. 739–746. [Google Scholar]
- Eriksson, A.; van den Hengel, A. Efficient computation of robust weighted low-rank matrix approximations using the L1 norm. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1681–1690. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.; Zhang, R. Matrix completion via non-convex relaxation and adaptive correlation learning. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 1981–1991. [Google Scholar] [CrossRef]
- Recht, B. A simpler approach to matrix completion. J. Mach. Learn. Res. 2011, 12, 3413–3430. [Google Scholar]
- Candes, E.J.; Plan, Y. Matrix completion with noise. Proc. IEEE 2010, 98, 925–936. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. The power of convex relaxation: Near-optimal matrix completion. IEEE Trans. Inf. Theory 2010, 56, 2053–2080. [Google Scholar] [CrossRef]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Zhou, Y.; Wilkinson, D.; Schreiber, R.; Pan, R. Large-scale parallel collaborative filtering for the netix prize. In Proceedings of the 4th International Conference on Algorithmic Aspects in Information and Management, Shanghai, China, 23–25 June 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 337–348. [Google Scholar]
- Pitaval, R.-A.; Dai, W.; Tirkkonen, O. Convergence of gradient descent for low-rank matrix approximation. IEEE Trans. Inf. Theory 2015, 61, 4451–4457. [Google Scholar] [CrossRef]
- Wright, J.; Ganesh, A.; Rao, S.; Peng, Y.; Ma, Y. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization. Adv. Neural Inf. Process. Syst. 2009, 22, 2080–2088. [Google Scholar]
- Hou, K.; Zhou, Z.; So, A.M.-C.; Luo, Z.-Q. On the linear convergence of the proximal gradient method for trace norm regularization. Adv. Neural Inf. Process. Syst. 2013, 26, 710–718. [Google Scholar]
- Gemulla, R.; Nijkamp, E.; Haas, P.J.; Sismanis, Y. Large-scale matrix factorization with distributed stochastic gradient descent. In Proceedings of the 17th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 21–24 August 2011; pp. 69–77. [Google Scholar]
- Recht, B.; Re, C. Parallel stochastic gradient algorithms for largescale matrix completion. Math. Program. Comput. 2013, 5, 201–226. [Google Scholar] [CrossRef]
- Pilaszy, I.; Zibriczky, D.; Tikk, D. Fast ALS-based matrix factorization for explicit and implicit feedback datasets. In Proceedings of the 4th ACM Conference on Recommender Systems, Barcelona, Spain, 26–30 September 2010; pp. 71–78. [Google Scholar]
- Yu, H.-F.; Hsieh, C.-J.; Si, S.; Dhillon, I. Scalable coordinate descent approaches to parallel matrix factorization for recommender systems. In Proceedings of the IEEE 12th International Conference on Data Mining, Brussels, Belgium, 10–13 December 2012; pp. 765–774. [Google Scholar]
- Ji, S.; Ye, J. An accelerated gradient method for trace norm minimization. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada; 2009; pp. 457–464. [Google Scholar]
- Liu, Y.; Jiao, L.C.; Shang, F.; Yin, F.; Liu, F. An efficient matrix bi-factorization alternative optimization method for low-rank matrix recovery and completion. Neural Netw. 2013, 48, 8–18. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Zhang, D.; Ye, J.; Li, X.; He, X. Fast and accurate matrix completion via truncated nuclear norm regularization. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2117–2130. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.; Feng, X.; Wang, W.; Zhang, L. Generalized Unitarily Invariant Gauge Regularization for Fast Low-Rank Matrix Recovery. IEEE Trans. Neural Networks Learn. Syst. 2021, 32, 1627–1641. [Google Scholar] [CrossRef] [PubMed]
- Srebro, N.; Shraibman, A. Rank, trace-norm and max-norm. In Proceedings of the 18th Annual Conference on Learning Theory (COLT), Bertinoro, Italy, 27–30 June 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 545–560. [Google Scholar]
- Rennie, J.D.M.; Srebro, N. Fast maximum margin matrix factorization for collaborative prediction. In Proceedings of the 22nd International Conference of Machine Learning, Bonn, Germany, 7–11 August 2005; pp. 713–719. [Google Scholar]
- Takacs, G.; Pilaszy, I.; Nemeth, B.; Tikk, D. Scalable collaborative filtering approaches for large recommender systems. J. Mach. Learn. Res. 2009, 10, 623–656. [Google Scholar]
- Hastie, T.; Mazumder, R.; Lee, J.D.; Zadeh, R. Matrix completion and low-rank SVD via fast alternating least squares. J. Mach. Learn. Res. 2015, 16, 3367–3402. [Google Scholar]
- Mackey, L.; Talwalkar, A.; Jordan, M.I. Distributed matrix completion and robust factorization. J. Mach. Learn. Res. 2015, 16, 913–960. [Google Scholar]
- Kim, E.; Lee, M.; Choi, C.-H.; Kwak, N.; Oh, S. Efficient l1-norm-based low-rank matrix approximations for large-scale problems using alternating rectified gradient method. IEEE Trans. Neural Networks Learn. Syst. 2015, 26, 237–251. [Google Scholar]
- Mishra, B.; Apuroop, K.A.; Sepulchre, R. A Riemannian geometry for low-rank matrix completion. arXiv 2012, arXiv:1211.1550. [Google Scholar]
- Tong, T.; Ma, C.; Chi, Y. Accelerating ill-conditioned low-rank matrix estimation via scaled gradient descent. J. Mach. Learn. Res. 2021, 22, 1–63. [Google Scholar]
- Haldar, J.P.; Hernando, D. Rank-constrained solutions to linear matrix equations using power-factorization. IEEE Signal Process. Lett. 2009, 16, 584–587. [Google Scholar] [CrossRef]
- Jain, P.; Dhillon, I.S. Provable inductive matrix completion. arXiv 2013, arXiv:1306.0626. [Google Scholar]
- Lee, K.; Wu, Y.; Bresler, Y. Near-optimal compressed sensing of a class of sparse low-rank matrices via sparse power factorization. IEEE Trans. Inf. Theory 2018, 64, 1666–1698. [Google Scholar] [CrossRef]
- Qin, X.; Blomstedt, P.; Leppaaho, E.; Parviainen, P.; Kaski, S. Distributed Bayesian matrix factorization with limited communication. Mach. Learn. 2019, 108, 1805–1830. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, C.; Zhang, J. Bayesian deep matrix factorization network for multiple images denoising. Neural Netw. 2020, 123, 420–428. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Xie, H.-B.; Fan, X.; Xu, R.Y.D.; Van Huffel, S.; Mengersen, K. Kernelized sparse Bayesian matrix factorization. IEEE Trans. Neural Networks Learn. Syst. 2021, 32, 391–404. [Google Scholar] [CrossRef] [PubMed]
- Hu, E.-L.; Kwok, J.T. Low-rank matrix learning using biconvex surrogate minimization. IEEE Trans. Neural Networks Learn. Syst. 2019, 30, 3517–3527. [Google Scholar] [CrossRef] [PubMed]
- Khalitov, R.; Yu, T.; Cheng, L.; Yang, Z. Sparse factorization of square matrices with application to neural attention modeling. Neural Netw. 2022, 152, 160–168. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Jin, R.; Zhou, Z.-H. Speedup matrix completion with side information: Application to multi-label learning. Adv. Neural Inf. Process. Syst. 2013, 26, 2301–2309. [Google Scholar]
- Chiang, K.-Y.; Hsieh, C.-J.; Dhillon, I.S. Matrix completion with noisy side information. Adv. Neural Inf. Process. Syst. 2015, 28, 3447–3455. [Google Scholar]
- Shah, V.; Rao, N.; Ding, W. Matrix factorization with side and higher order information. stat 2017, 1050, 4. [Google Scholar]
- Si, S.; Chiang, K.-Y.; Hsieh, C.-J.; Rao, N.; Dhillon, I.S. Goal-directed inductive matrix completion. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1165–1174. [Google Scholar]
- Eftekhari, A.; Yang, D.; Wakin, M.B. Weighted matrix completion and recovery with prior subspace information. IEEE Trans. Inf. Theory 2018, 64, 4044–4071. [Google Scholar] [CrossRef]
- Bertsimas, D.; Li, M.L. Fast exact matrix completion: A unified optimization framework for matrix completion. J. Mach. Learn. Res. 2020, 21, 1–43. [Google Scholar]
- Lu, J.; Liang, G.; Sun, J.; Bi, J. A sparse interactive model for matrix completion with side information. Adv. Neural Inf. Process. Syst. 2016, 29, 4071–4079. [Google Scholar]
- Chen, Y. Incoherence-optimal matrix completion. IEEE Trans. Inf. Theory 2015, 61, 2909–2923. [Google Scholar] [CrossRef]
- Jain, P.; Netrapalli, P.; Sanghavi, S. Low-rank matrix completion using alternating minimization. In Proceedings of the 45th Annual ACM Symposium on Theory of Computing, Palo Alto, CA, USA, 1–4 June 2013; pp. 665–674. [Google Scholar]
- Chandrasekaran, V.; Sanghavi, S.; Parrilo, P.A.; Willsky, A.S. Rank-sparsity incoherence for matrix decomposition. SIAM J. Optim. 2011, 21, 572–596. [Google Scholar] [CrossRef]
- Chen, Y.; Jalali, A.; Sanghavi, S.; Caramanis, C. Low-rank matrix recovery from errors and erasures. IEEE Trans. Inf. Theory 2013, 59, 4324–4337. [Google Scholar] [CrossRef][Green Version]
- Negahban, S.; Wainwright, M.J. Restricted strong convexity and weighted matrix completion: Optimal bounds with noise. J. Mach. Learn. Res. 2012, 13, 1665–1697. [Google Scholar]
- Candes, E.J.; Plan, Y. Tight oracle inequalities for low-rank matrix recovery from a minimal number of noisy random measurements. IEEE Trans. Inf. Theory 2011, 57, 2342–2359. [Google Scholar] [CrossRef]
- Gross, D. Recovering low-rank matrices from few coefficients in any basis. IEEE Trans. Inf. Theory 2011, 57, 1548–1566. [Google Scholar] [CrossRef]
- Krishnamurthy, A.; Singh, A. Low-rank matrix and tensor completion via adaptive sampling. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2013; Volume 26, pp. 836–844. [Google Scholar]
- Krishnamurthy, A.; Singh, A. On the power of adaptivity in matrix completion and approximation. arXiv 2014, arXiv:1407.3619. [Google Scholar]
- Sun, R.; Luo, Z.-Q. Guaranteed matrix completion via non-convex factorization. IEEE Trans. Inf. Theory 2016, 62, 6535–6579. [Google Scholar] [CrossRef]
- Malloy, M.L.; Nowak, R.D. Near-optimal adaptive compressed sensing. IEEE Trans. Inf. Theory 2014, 60, 4001–4012. [Google Scholar] [CrossRef]
- Ding, L.; Chen, Y. Leave-one-out approach for matrix completion: Primal and dual analysis. IEEE Trans. Inf. Theory 2020, 66, 7274–7301. [Google Scholar] [CrossRef]
- Chen, Y.; Chi, Y. Robust spectral compressed sensing via structured matrix completion. IEEE Trans. Inf. Theory 2014, 60, 6576–6601. [Google Scholar] [CrossRef]
- Shamir, O.; Shalev-Shwartz, S. Matrix completion with the trace norm: Learning, bounding, and transducing. J. Mach. Learn. Res. 2014, 15, 3401–3423. [Google Scholar]
- Chatterjee, S. A deterministic theory of low rank matrix completion. IEEE Trans. Inf. Theory 2020, 66, 8046–8055. [Google Scholar] [CrossRef]
- Jin, H.; Ma, Y.; Jiang, F. Matrix completion with covariate information and informative missingness. J. Mach. Learn. Res. 2022, 23, 1–62. [Google Scholar]
- Oymak, S.; Jalali, A.; Fazel, M.; Eldar, Y.C.; Hassibi, B. Simultaneously structured models with application to sparse and low-rank matrices. IEEE Trans. Inf. Theory 2015, 61, 2886–2908. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, H.; Caramanis, C.; Sanghavi, S. Matrix completion with column manipulation: Near-optimal sample-robustness-rank tradeoffs. IEEE Trans. Inf. Theory 2016, 62, 503–526. [Google Scholar] [CrossRef]
- Cai, T.; Zhou, W.-X. A max-norm constrained minimization approach to 1-bit matrix completion. J. Mach. Learn. Res. 2013, 14, 3619–3647. [Google Scholar]
- Davenport, M.A.; Plan, Y.; van den Berg, E.; Wootters, M. 1-bit matrix completion. Inf. Inference 2014, 3, 189–223. [Google Scholar] [CrossRef]
- Bhaskar, S.A. Probabilistic low-rank matrix completion from quantized measurements. J. Mach. Learn. Res. 2016, 17, 1–34. [Google Scholar]
- Salakhutdinov, R.; Srebro, N. Collaborative filtering in a non-uniform world: Learning with the weighted trace norm. In Advances in Neural Information Processing Systems; LaFerty, J., Williams, C.K.I., Shawe-Taylor, J., Zemel, R.S., Culotta, A., Eds.; MIT Press: Cambridge, MA, USA, 2010; Volume 23, pp. 2056–2064. [Google Scholar]
- Foygel, R.; Shamir, O.; Srebro, N.; Salakhutdinov, R. Learning with the weighted trace-norm under arbitrary sampling distributions. Adv. Neural Inf. Process. Syst. 2011, 24, 2133–2141. [Google Scholar]
- Lafond, J.; Klopp, O.; Moulines, E.; Salmon, J. Probabilistic low-rank matrix completion on finite alphabets. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2014; Volume 27, pp. 1727–1735. [Google Scholar]
- Cao, Y.; Xie, Y. Categorical matrix completion. In Proceedings of the IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Cancun, Mexico, 13–16 December 2015; pp. 369–372. [Google Scholar]
- Elhamifar, E.; Vidal, R. Sparse subspace clustering: Algorithm, theory, and applications. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2765–2781. [Google Scholar] [CrossRef]
- Yin, M.; Cai, S.; Gao, J. Robust face recognition via double low-rank matrix recovery for feature extraction. In Proceedings of the IEEE International Conference on Image Processing, Melbourne, Australia, 15–18 September 2013; pp. 3770–3774. [Google Scholar]
- Bahmani, S.; Romberg, J. Near-optimal estimation of simultaneously sparse and low-rank matrices from nested linear measurements. Inf. Inference 2016, 5, 331–351. [Google Scholar] [CrossRef]
- Wong, R.K.W.; Lee, T.C.M. Matrix completion with noisy entries and outliers. J. Mach. Learn. Res. 2017, 18, 1–25. [Google Scholar]
- Mi, J.-X.; Zhang, Y.-N.; Lai, Z.; Li, W.; Zhou, L.; Zhong, F. Principal component analysis based on nuclear norm minimization. Neural Netw. 2019, 118, 1–16. [Google Scholar] [CrossRef]
- Pokala, P.K.; Hemadri, R.V.; Seelamantula, C.S. Iteratively reweighted minimax-concave penalty minimization for accurate low-rank plus sparse matrix decomposition. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 8992–9010. [Google Scholar] [CrossRef]
- Baes, M.; Herrera, C.; Neufeld, A.; Ruyssen, P. Low-rank plus sparse decomposition of covariance matrices using neural network parametrization. IEEE Trans. Neural Networks Learn. Syst. 2023, 34, 171–185. [Google Scholar] [CrossRef] [PubMed]
- Tenenbaum, J.B.; de Silva, V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Yan, S.; Hu, Y.; Niyogi, P.; Zhang, H.J. Face recognition using Laplacianfaces. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 328–340. [Google Scholar]
- He, X.; Cai, D.; Yan, S.; Zhang, H.-J. Neighborhood preserving embedding. In Proceedings of the 10th IEEE International Conference on Computer Vision, Beijing, China, 17–20 October 2005; pp. 1208–1213. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef]
- Yin, M.; Gao, J.; Lin, Z. Laplacian regularized low-rank representation and its applications. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 504–517. [Google Scholar] [CrossRef]
- Hsu, D.; Kakade, S.M.; Zhang, T. Robust matrix decomposition with sparse corruptions. IEEE Trans. Inf. Theory 2011, 57, 7221–7234. [Google Scholar] [CrossRef]
- Donoho, D.; Stodden, V. When does nonnegative matrix factorization give a correct decomposition into parts? In Advances in Neural Information Processing Systems; MIT Press: Vancouver, BC, Canada; Cambridge, MA, USA, 2003; Volume 16, pp. 1141–1148. [Google Scholar]
- Gillis, N. Sparse and unique nonnegative matrix factorization through data preprocessing. J. Mach. Learn. Res. 2012, 13, 3349–3386. [Google Scholar]
- Vavasis, S.A. On the complexity of nonnegative matrix factorization. SIAM J. Optim. 2009, 20, 1364–1377. [Google Scholar] [CrossRef]
- Gillis, N.; Luce, R. Robust near-separable nonnegative matrix factorization using linear optimization. J. Mach. Learn. Res. 2014, 15, 1249–1280. [Google Scholar]
- Pan, J.; Gillis, N. Generalized separable nonnegative matrix factorization. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 1546–1561. [Google Scholar] [CrossRef]
- Pascual-Montano, A.; Carazo, J.M.; Kochi, K.; Lehmann, D.; Pascual-Marqui, R.D. Nonsmooth nonnegative matrix factorization (nsNMF). EEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 403–415. [Google Scholar] [CrossRef] [PubMed]
- Kompass, R. A generalized divergence measure for nonnegative matrix factorization. Neural Comput. 2007, 19, 780–791. [Google Scholar] [CrossRef]
- Dhillon, I.S.; Sra, S. Generalized nonnegative matrix approximations with Bregman divergences. Adv. Neural Inf. Process. Syst. 2006, 18, 283–290. [Google Scholar]
- Cichocki, A.; Zdunek, R. Multilayer nonnegative matrix factorization using projected gradient approaches. Int. J. Neural Syst. 2007, 17, 431–446. [Google Scholar] [CrossRef] [PubMed]
- Zdunek, R.; Cichocki, A. Fast nonnegative matrix factorization algorithms using projected gradient approaches for large-scale problems. Comput. Intell. Neurosci. 2008, 2008, 939567. [Google Scholar] [CrossRef]
- Cichocki, A.; Zdunek, R.; Amari, S. New algorithms for non-negative matrix factorization in applications to blind source separation. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Toulouse, France, 14–19 May 2006; Volume 5, pp. 621–624. [Google Scholar]
- Zhang, J.; Wei, L.; Feng, X.; Ma, Z.; Wang, Y. Pattern expression nonnegative matrix factorization: Algorithm and applications to blind source separation. Comput. Intell. Neurosci. 2008, 2008, 168769. [Google Scholar] [CrossRef]
- Yokota, T.; Zdunek, R.; Cichocki, A.; Yamashita, Y. Smooth nonnegative matrix and tensor factorizations for robust multi-way data analysis. Signal Process. 2015, 113, 234–249. [Google Scholar] [CrossRef]
- Keprt, A.; Snasel, V. Binary factor analysis with genetic algorithms. In Proceedings of the 4th IEEE International Workshop on Soft Computing as Transdisciplinary Science and Technology (WSTST), AINSC, Muroran, Japan, 25–27 May 2005; Volume 29, pp. 1259–1268. [Google Scholar]
- Lin, C.-J. On the convergence of multiplicative update algorithms for non-negative matrix factorization. IEEE Trans. Neural Netw. 2007, 18, 1589–1596. [Google Scholar]
- Li, L.-X.; Wu, L.; Zhang, H.-S.; Wu, F.-X. A fast algorithm for nonnegative matrix factorization and its convergence. IEEE Trans. Neural Networks Learn. Syst. 2014, 25, 1855–1863. [Google Scholar] [CrossRef]
- Liu, H.; Li, X.; Zheng, X. Solving non-negative matrix factorization by alternating least squares with a modified strategy. Data Min. Knowl. Discov. 2013, 26, 435–451. [Google Scholar] [CrossRef]
- Lin, C.-J. Projected gradients for non-negative matrix factorization. Neural Comput. 2007, 19, 2756–2779. [Google Scholar] [CrossRef] [PubMed]
- Zdunek, R.; Cichocki, A. Nonnegative matrix factorization with constrained second-order optimization. Signal Process. 2007, 87, 1904–1916. [Google Scholar] [CrossRef]
- Cichocki, A.; Anh-Huy, P. Fast local algorithms for large scale nonnegative matrix and tensor factorizations. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2009, 92, 708–721. [Google Scholar] [CrossRef]
- Kim, D.; Sra, S.; Dhillon, I.S. Fast projection-based methods for the least squares nonnegative matrix approximation problem. Stat. Anal. Data Min. 2008, 1, 38–51. [Google Scholar] [CrossRef]
- Hoyer, P.O. Nonnegative matrix factorization with sparseness constraints. J. Mach. Learn. Res. 2004, 5, 1457–1469. [Google Scholar]
- Laurberg, H.; Christensen, M.G.; Plumbley, M.D.; Hansen, L.K.; Jensen, S.H. Theorems on positive data: On the uniqueness of NMF. Comput. Intell. Neurosci. 2008, 2008, 764206. [Google Scholar] [CrossRef]
- Peharz, R.; Pernkopf, F. Sparse nonnegative matrix factorization with l0-constraints. Neurocomputing 2012, 80, 38–46. [Google Scholar] [CrossRef]
- Zhou, G.; Xie, S.; Yang, Z.; Yang, J.-M.; He, Z. Minimum-volume-constrained nonnegative matrix factorization: Enhanced ability of learning parts. IEEE Trans. Neural Netw. 2011, 22, 1626–1637. [Google Scholar] [CrossRef]
- Liu, T.; Gong, M.; Tao, D. Large-cone nonnegative matrix factorization. IEEE Trans. Neural Networks Learn. Syst. 2017, 28, 2129–2142. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Laaksonen, J. Multiplicative updates for non-negative projections. Neurocomputing 2007, 71, 363–373. [Google Scholar] [CrossRef]
- Yang, Z.; Oja, E. Linear and nonlinear projective nonnegative matrix factorization. IEEE Trans. Neural Netw. 2010, 21, 734–749. [Google Scholar] [CrossRef] [PubMed]
- Zafeiriou, S.; Petrou, M. Nonlinear non-negative component analysis algorithms. IEEE Trans. Image Process. 2010, 19, 1050–1066. [Google Scholar] [CrossRef] [PubMed]
- Cai, D.; He, X.; Han, J.; Huang, T.S. Graph regularized nonnegative matrix factorization for data representation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1548–1560. [Google Scholar]
- Yang, S.; Yi, Z.; Ye, M.; He, X. Convergence analysis of graph regularized non-negative matrix factorization. IEEE Trans. Knowl. Data Eng. 2014, 26, 2151–2165. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, K. Low-rank matrix approximation with manifold regularization. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1717–1729. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Yang, X.; Guan, N.; Yi, X. Online graph regularized non-negative matrix factorization for large-scale datasets. Neurocomputing 2016, 204, 162–171. [Google Scholar] [CrossRef]
- Ahmed, I.; Hu, X.B.; Acharya, M.P.; Ding, Y. Neighborhood structure assisted non-negative matrix factorization and its application in unsupervised point-wise anomaly detection. J. Mach. Learn. Res. 2021, 22, 1–32. [Google Scholar]
- Chen, M.; Gong, M.; Li, X. Feature weighted non-negative matrix factorization. IEEE Trans. Cybern. 2023, 53, 1093–1105. [Google Scholar] [CrossRef]
- Wei, J.; Tong, C.; Wu, B.; He, Q.; Qi, S.; Yao, Y.; Teng, Y. An entropy weighted nonnegative matrix factorization algorithm for feature representation. IEEE Trans. Neural Netw. Learn. Syst. 2022. [Google Scholar] [CrossRef]
- Hayashi, N. Variational approximation error in non-negative matrix factorization. Neural Netw. 2020, 126, 65–75. [Google Scholar] [CrossRef]
- Devarajan, K. A statistical framework for non-negative matrix factorization based on generalized dual divergence. Neural Netw. 2021, 140, 309–324. [Google Scholar] [CrossRef]
- Zafeiriou, S.; Tefas, A.; Buciu, I.; Pitas, I. Exploiting discriminant information in nonnegative matrix factorization with application to frontal face verification. IEEE Trans. Neural Netw. 2006, 17, 683–695. [Google Scholar] [CrossRef]
- Wang, J.J.-Y.; Gao, X. Max–min distance nonnegative matrix factorization. Neural Netw. 2015, 61, 75–84. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Lee, H.; Yoo, J.; Choi, S. Semi-supervised nonnegative matrix factorization. IEEE Signal Process. Lett. 2010, 17, 4–7. [Google Scholar]
- Liu, H.; Wu, Z.; Li, X.; Cai, D.; Huang, T.S. Constrained nonnegative matrix factorization for image representation. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1299–1311. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Li, T.; Zhang, C. Semi-supervised clustering via matrix factorization. In Proceedings of the SIAM International Conference on Data Mining, Atlanta, GA, USA, 24–26 April 2008; pp. 1–12. [Google Scholar]
- Chen, Y.; Rege, M.; Dong, M.; Hua, J. Non-negative matrix factorization for semi-supervised data clustering. Knowl. Inf. Syst. 2008, 17, 355–379. [Google Scholar] [CrossRef]
- Ding, C.; Li, T.; Jordan, M.I. Convex and semi-nonnegative matrix factorizations. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 45–55. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.-S.; Zeng, Q.; Pan, B. A survey of deep nonnegative matrix factorization. Neural Netw. 2022, 491, 305–320. [Google Scholar] [CrossRef]
- Yang, S.; Yi, Z. Convergence analysis of non-negative matrix factorization for BSS algorithm. Neural Process. Lett. 2010, 31, 45–64. [Google Scholar] [CrossRef]
- Guan, N.; Tao, D.; Luo, Z.; Yuan, B. Online nonnegative matrix factorization with robust stochastic approximation. IEEE Trans. Neural Networks Learn. Syst. 2012, 23, 1087–1099. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Lu, H. On-line learning parts-based representation via incremental orthogonal projective non-negative matrix factorization. Signal Process. 2013, 93, 1608–1623. [Google Scholar] [CrossRef]
- Zhao, R.; Tan, V.Y.F. Online nonnegative matrix factorization with outliers. IEEE Trans. Signal Process. 2017, 65, 555–570. [Google Scholar] [CrossRef]
- Hsieh, C.-J.; Dhillon, I.S. Fast coordinate descent methods with variable selection for non-negative matrix factorization. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; 2011; pp. 1064–1072. [Google Scholar]
- Li, L.; Lebanon, G.; Park, H. Fast Bregman divergence NMF using Taylor expansion and coordinate descent. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 307–315. [Google Scholar]
- Kimura, K.; Kudo, M.; Tanaka, Y. A column-wise update algorithm for nonnegative matrix factorization in Bregman divergence with an orthogonal constraint. Mach. Learn. 2016, 103, 285–306. [Google Scholar] [CrossRef]
- Kong, D.; Ding, C.; Huang, H. Robust nonnegative matrix factorization using l2,1-norm. In Proceedings of the 20th ACM International Conference on Information and Knowledge Management, Glasgow, UK, 24–28 October 2011; pp. 673–682. [Google Scholar]
- Guan, N.; Liu, T.; Zhang, Y.; Tao, D.; Davis, L.S. Truncated Cauchy non-negative matrix factorization. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 246–259. [Google Scholar] [CrossRef]
- Wu, X.; Kumar, V.; Quinlan, J.R.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef]
- Mirzal, A. A convergent algorithm for orthogonal nonnegative matrix factorization. J. Comput. Appl. Math. 2014, 260, 149–166. [Google Scholar] [CrossRef]
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J. Clustering with Bregman divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Zhang, X.; Zong, L.; Liu, X.; Luo, J. Constrained clustering with nonnegative matrix factorization. IEEE Trans. Neural Networks Learn. Syst. 2016, 27, 1514–1526. [Google Scholar] [CrossRef]
- Blumensath, T. Directional clustering through matrix factorization. IEEE Trans. Neural Networks Learn. Syst. 2016, 27, 2095–2107. [Google Scholar] [CrossRef]
- Kuang, D.; Ding, C.; Park, H. Symmetric nonnegative matrix factorization for graph clustering. In Proceedings of the 12th SIAM International Conference on Data Mining, Anaheim, CA, USA, 26–28 April 2012; pp. 106–117. [Google Scholar]
- He, Z.; Xie, S.; Zdunek, R.; Zhou, G.; Cichocki, A. Symmetric nonnegative matrix factorization: Algorithms and applications to probabilistic clustering. IEEE Trans. Neural Netw. 2011, 22, 2117–2131. [Google Scholar] [PubMed]
- Hou, L.; Chu, D.; Liao, L.-Z. A Progressive hierarchical alternating least squares method for symmetric nonnegative matrix factorization. IEEE Trans. Pattern Anal. Mach. Intell. 2022. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhu, Z.; Li, Q.; Liu, K. A provable splitting approach for symmetric nonnegative matrix factorization. IEEE Trans. Knowl. Data Eng. 2023, 35, 2206–2219. [Google Scholar] [CrossRef]
- Qin, Y.; Feng, G.; Ren, Y.; Zhang, X. Block-diagonal guided symmetric nonnegative matrix factorization. IEEE Trans. Knowl. Data Eng. 2023, 35, 2313–2325. [Google Scholar] [CrossRef]
- Xu, W.; Gong, Y. Document clustering by concept factorization. In Proceedings of the 27th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Sheffield, UK, 25–29 July 2004; pp. 202–209. [Google Scholar]
- He, Y.; Lu, H.; Huang, L.; Xie, S. Pairwise constrained concept factorization for data representation. Neural Netw. 2014, 52, 1–17. [Google Scholar] [CrossRef]
- Cai, D.; He, X.; Han, J. Locally consistent concept factorization for document clustering. IEEE Trans. Knowl. Data Eng. 2011, 23, 902–913. [Google Scholar] [CrossRef]
- Williams, C.; Seeger, M. Using the Nystrom method to speedup kernel machines. In Advances in Neural Information Processing Systems; Leen, T., Dietterich, T., Tresp, V., Eds.; MIT Press: Cambridge, MA, USA, 2001; Volume 13, pp. 682–690. [Google Scholar]
- Drineas, P.; Mahoney, M.W. On the Nystrom method for approximating a gram matrix for improved kernel-based learning. J. Mach. Learn. Res. 2005, 6, 2153–2175. [Google Scholar]
- Gittens, A.; Mahoney, M.W. Revisiting the Nystrom method for improved largescale machine learning. J. Mach. Learn. Res. 2016, 17, 3977–4041. [Google Scholar]
- Boutsidis, C.; Woodruff, D.P. Optimal CUR matrix decompositions. SIAM Journal on Computing 2017, 46–589. [Google Scholar] [CrossRef]
- Halko, N.; Martinsson, P.G.; Tropp, J.A. Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions. SIAM Rev. 2011, 53, 217–288. [Google Scholar] [CrossRef]
- Li, M.; Bi, W.; Kwok, J.T.; Lu, B.-L. Large-scale Nystrom kernel matrix approximation using randomized SVD. IEEE Trans. Neural Networks Learn. Syst. 2015, 26, 152–164. [Google Scholar]
- Wang, S.; Zhang, Z.; Zhang, T. Towards more efficient SPSD matrix approximation and CUR matrix decomposition. J. Mach. Learn. Res. 2016, 17, 1–49. [Google Scholar]
- Drineas, P.; Mahoney, M.W.; Muthukrishnan, S. Relative-error CUR matrix decompositions. SIAM J. Matrix Anal. Appl. 2008, 30, 844–881. [Google Scholar] [CrossRef]
- Drineas, P.; Mahoney, M.W.; Muthukrishnan, S. Subspace sampling and relative-error matrix approximation: Column-based methods. In Proceedings of the 10th Annual International Workshop on Randomization and Computation (RANDOM), LNCS, Barcelona, Spain, 28–30 August 2006; Volume 4110, pp. 316–326. [Google Scholar]
- Li, X.; Pang, Y. Deterministic column-based matrix decomposition. IEEE Trans. Knowl. Data Eng. 2010, 22, 145–149. [Google Scholar] [CrossRef]
- Mahoney, M.W.; Drineas, P. CUR matrix decompositions for improved data analysis. Proc. Natl. Acad. Sci. 2009, 106, 697–702. [Google Scholar] [CrossRef]
- Aldroubi, A.; Sekmen, A.; Koku, A.B.; Cakmak, A.F. Similarity matrix framework for data from union of subspaces. Appl. Comput. Harmon. Anal. 2018, 45, 425–435. [Google Scholar] [CrossRef]
- Drineas, P.; Kannan, R.; Mahoney, M.W. Fast Monte Carlo algorithms for matrices. III: Computing a compressed approximate matrix decomposition. SIAM J. Comput. 2006, 36, 184–206. [Google Scholar] [CrossRef]
- Voronin, S.; Martinsson, P.-G. Efficient algorithms for CUR and interpolative matrix decompositions. Adv. Comput. Math. 2017, 43, 495–516. [Google Scholar] [CrossRef]
- Cai, H.; Hamm, K.; Huang, L.; Li, J.; Wang, T. Rapid robust principal component analysis: CUR accelerated inexact low rank estimation. IEEE Signal Process. Lett. 2021, 28, 116–120. [Google Scholar] [CrossRef]
- Cai, H.; Hamm, K.; Huang, L.; Needell, D. Robust CUR decomposition: Theory and imaging applications. arXiv 2021, arXiv:2101.05231. [Google Scholar] [CrossRef]
- Goreinov, S.A.; Tyrtyshnikov, E.E.; Zamarashkin, N.L. A theory of pseudoskeleton approximations. Linear Algebra Its Appl. 1997, 261, 1–21. [Google Scholar] [CrossRef]
- Chiu, J.; Demanet, L. Sublinear randomized algorithms for skeleton decompositions. SIAM J. Matrix Anal. Appl. 2013, 34, 1361–1383. [Google Scholar] [CrossRef]
- Hamm, K.; Huang, L. Stability of sampling for CUR decompositions. Found. Data Sci. 2020, 2, 83–99. [Google Scholar] [CrossRef]
- Drineas, P.; Magdon-Ismail, M.; Mahoney, M.W.; Woodruff, D.P. Fast approximation of matrix coherence and statistical leverage. J. Mach. Learn. Res. 2012, 13, 3441–3472. [Google Scholar]
- Wang, S.; Zhang, Z. Improving CUR matrix decomposition and the Nystrom approximation via adaptive sampling. J. Mach. Learn. Res. 2013, 14, 2729–2769. [Google Scholar]
- Zhang, B.; Wu, Y.; Lu, J.; Du, K.-L. Evolutionary computation and its applications in neural and fuzzy systems. Appl. Comput. Intell. Soft Comput. 2011, 2011, 938240. [Google Scholar] [CrossRef]
- Du, K.-L.; Swamy, M.N.S. Search and Optimization by Metaheuristics; Springer: New York, NY, USA, 2016. [Google Scholar]
- Che, H.; Wang, J.; Cichocki, A. Sparse signal reconstruction via collaborative neurodynamic optimization. Neural Netw. 2022, 154, 255–269. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, J.; Kwong, S. Boolean matrix factorization based on collaborative neurodynamic optimization with Boltzmann machines. Neural Netw. 2022, 153, 142–151. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; He, X.; Huang, T.; Huang, J.; Li, P. A smoothing neural network for minimization ℓ1-ℓp in sparse signal reconstruction with measurement noises. Neural Netw. 2020, 122, 40–53. [Google Scholar] [CrossRef]
- Wei, Z.; Li, Q.; Wei, J.; Bian, W. Neural network for a class of sparse optimization with L0-regularization. Neural Netw. 2022, 151, 211–221. [Google Scholar] [CrossRef]
- Wang, H.; Feng, R.; Leung, C.-S.; Chan, H.P.; Constantinides, A.G. A Lagrange programming neural network approach with an ℓ0-norm sparsity measurement for sparse recovery and its circuit realization. Mathematics 2022, 10, 4801. [Google Scholar] [CrossRef]
- Li, X.; Wang, J.; Kwong, S. A discrete-time neurodynamic approach to sparsity-constrained nonnegative matrix factorization. Neural Comput. 2020, 32, 1531–1562. [Google Scholar] [CrossRef]
- Fan, J.; Chow, T.W.S. Non-linear matrix completion. Pattern Recognit. 2018, 77, 378–394. [Google Scholar] [CrossRef]
- Tsakiris, M.C. Low-rank matrix completion theory via Pluucker coordinates. IEEE Trans. Pattern Anal. Mach. Intell. 2023. [Google Scholar] [CrossRef]
- Burnwal, S.P.; Vidyasagar, M. Deterministic completion of rectangular matrices using asymmetric Ramanujan graphs: Exact and stable recovery. IEEE Trans. Signal Process. 2020, 68, 3834–3848. [Google Scholar] [CrossRef]
- Liu, G.; Liu, Q.; Yuan, X.-T.; Wang, M. Matrix completion with deterministic sampling: Theories and methods. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 549–566. [Google Scholar] [CrossRef] [PubMed]
- Boufounos, P.T. Sparse signal reconstruction from phase-only measurements. In Proceedings of the 10th International Conference on Sampling Theory and Applications (SampTA 2013), Bremen, Germany, 1–5 July 2013; pp. 256–259. [Google Scholar]
- Jacques, L.; Feuillen, T. The importance of phase in complex compressive sensing. IEEE Ttrans Inf. Theory 2021, 67, 4150–4161. [Google Scholar] [CrossRef]
- Wen, J.; Zhang, R.; Yu, W. Signal-dependent performance analysis of orthogonal matching pursuit for exact sparse recovery. IEEE Trans. Signal Process. 2020, 68, 5031–5046. [Google Scholar] [CrossRef]
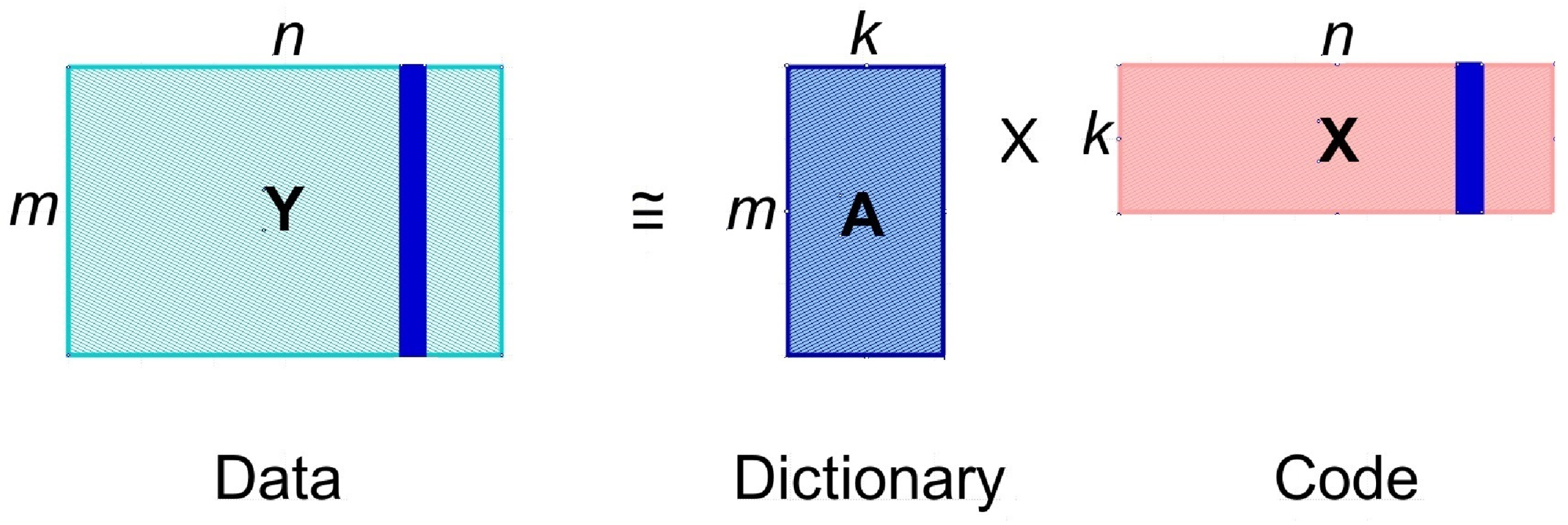
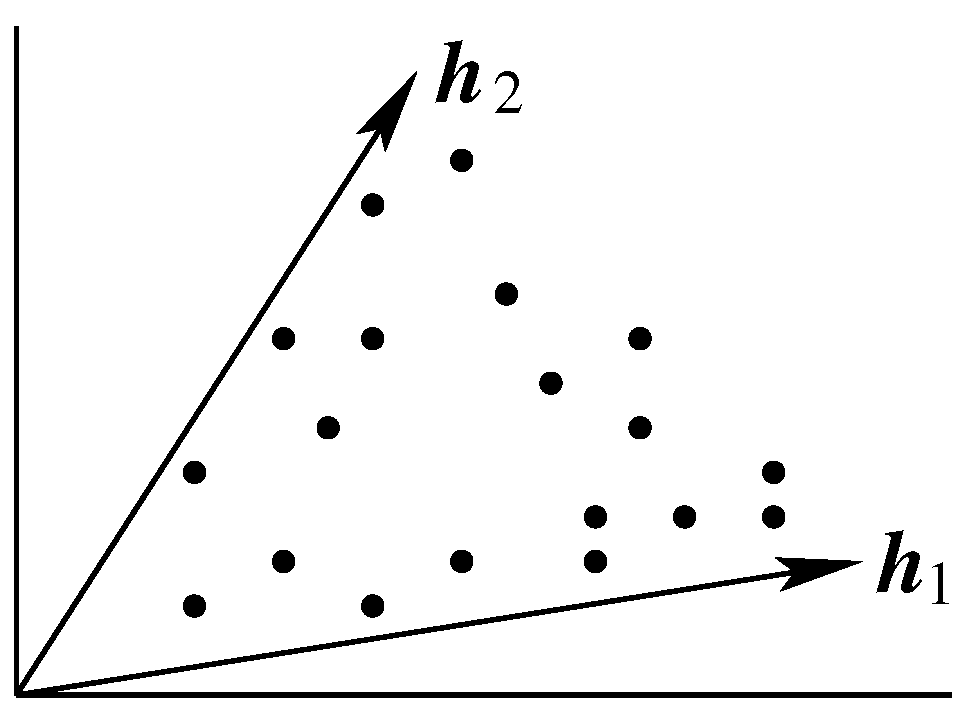
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, K.-L.; Swamy, M.N.S.; Wang, Z.-Q.; Mow, W.H. Matrix Factorization Techniques in Machine Learning, Signal Processing, and Statistics. Mathematics 2023, 11, 2674. https://doi.org/10.3390/math11122674
Du K-L, Swamy MNS, Wang Z-Q, Mow WH. Matrix Factorization Techniques in Machine Learning, Signal Processing, and Statistics. Mathematics. 2023; 11(12):2674. https://doi.org/10.3390/math11122674
Chicago/Turabian StyleDu, Ke-Lin, M. N. S. Swamy, Zhang-Quan Wang, and Wai Ho Mow. 2023. "Matrix Factorization Techniques in Machine Learning, Signal Processing, and Statistics" Mathematics 11, no. 12: 2674. https://doi.org/10.3390/math11122674
APA StyleDu, K.-L., Swamy, M. N. S., Wang, Z.-Q., & Mow, W. H. (2023). Matrix Factorization Techniques in Machine Learning, Signal Processing, and Statistics. Mathematics, 11(12), 2674. https://doi.org/10.3390/math11122674







