Abstract
A digital twin is a simulator of a physical system, which is built upon a series of models and computer programs with real-time data (from sensors or devices). Digital twins are used in various industries, such as manufacturing, healthcare, and transportation, to understand complex physical systems and make informed decisions. However, predictions and optimizations with digital twins can be time-consuming due to the high computational requirements and complexity of the underlying computer programs. This poses significant challenges in making well-informed and timely decisions using digital twins. This paper proposes a novel methodology, called the “digital triplet”, to facilitate real-time prediction and decision-making. A digital triplet is an efficient representation of a digital twin, constructed using statistical models and effective experimental designs. It offers two noteworthy advantages. Firstly, by leveraging modern statistical models, a digital triplet can effectively capture and represent the complexities of a digital twin, resulting in accurate predictions and reliable decision-making. Secondly, a digital triplet adopts a sequential design and modeling approach, allowing real-time updates in conjunction with its corresponding digital twin. We conduct comprehensive simulation studies to explore the application of various statistical models and designs in constructing a digital triplet. It is shown that Gaussian process regression coupled with sequential MaxPro designs exhibits superior performance compared to other modeling and design techniques in accurately constructing the digital triplet.
MSC:
62L05; 62P30
1. Introduction
1.1. Digital Twin
The complexity of a physical system can make it difficult to fully comprehend its behavior, predict its responses accurately, and identify optimal strategies for operation or control. A digital twin is a computer-based simulator built by integrating real-world data and theoretical foundations to represent a complex physical system. It enables a better understanding of the physical system and allows for monitoring, analysis, and optimization of the system. Digital twins have recently received a great deal of attention in many disciplines, particularly in manufacturing, healthcare, aerospace and defense, energy and utilities, and agriculture [1,2,3,4,5,6,7]. The Gartner company (2020) recognized the digital twin as an emerging technology that will continue to advance over the next many years.
Digital twins are a powerful tool for improving efficiency, productivity, and safety, as well as reducing downtime and maintenance costs, and enabling better decision-making in these areas. A digital twin typically consists of a physical object system, sensors, modeling and simulation, data analysis, artificial intelligence, network connectivity between the physical system and digital twin, and visualization. These components work together to develop a digital twin that can be used for various purposes. To implement a digital twin, one first identifies the physical system. The data collected from the sensors are used to develop a virtual model of the physical system, including its geometry, behavior, and other relevant characteristics. Intelligent analytic tools are utilized to analyze the data, and a virtual model is utilized to estimate the behavior and performance of the physical system. The digital twin enables users to make better decisions and optimize the physical system in a cost-effective and sustainable way. Despite the many benefits of digital twins, they also face several challenges, such as data quality, privacy and security of data, development and maintenance costs, model complexity, and others. Addressing these challenges will be crucial to fully realize the potential of digital twins in various industries.
1.2. Current Research on Digital Twin Modeling
Ref. [8] emphasized the importance of incorporating multiple modeling aspects in the development of effective digital twin models. These aspects include model construction, model assembly, model fusion, model verification, model modification, and model management. Model construction, for example, involves integration of knowledge from various disciplines to build a basic digital twin model (e.g., a unit-level digital twin model for a specific application field). By assembling elementary digital twin models in the spatial dimension, more complex digital twin models can be developed. The process of model construction involves various techniques, such as geometric model construction [9], physical model construction [10], behavioral model construction, and rule model construction [11].
In the context of digital twin modeling, geometric model construction involves creating models that represent the physical entity’s geometric appearance and topological information. Point cloud and building information modeling are among the commonly used techniques in the literature [9,12]. On the other hand, physical model construction involves using mathematical approximations to develop models for materials, loads, constraints, and mechanical properties. For instance, Ref. [10] reviewed digital twin models for fluid-dynamic behavior in electrohydraulic servo valves and evaluated their precision. Behavioral modeling incorporates dynamic functional behaviors by analyzing the motion evolution in time and space through kinematic and dynamic analysis [12], describing each behavior of a physical entity using differential equations [13]. Rule modeling extracts and represents rules from historical data, operational logic, and expertise, enabling digital twin models to perform decision-making, evaluation, and optimization. Machine learning is an effective technology that continually enhances and extends the performance of digital twin models by restructuring existing knowledge structures, taking various forms, each with distinct features. For example, Markov Chain Monte Carlo is capable of dynamic modeling, and Gaussian processes are gradually being applied to digital twin modeling as a powerful tool to improve the efficiency, safety, and sustainability of physical systems in a wide range of industries [11].
1.3. Digital Twins and Computer Experiments
Computer experiments involve using a computer program to model a system. While computer experiments and digital twins share some similarities, they share distinct concepts with different characteristics. Digital twins are built to enable users to monitor and optimize physical systems and make better decisions in a cost-effective and sustainable way, while computer experiments often refer to optimizing a specific aspect of a physical system and further testing its response. In terms of the inputs, digital twins provide real-time feedback, allowing engineers and researchers to adjust and optimize performance promptly, while computer experiments may require additional analysis to interpret results. For the outputs, the former always involves multiple processes (responses) while the latter tends to only one response. Digital twins consider the entire system, while computer experiments often focus on a specific aspect of the physical system. In summary, computer experiments and digital twins serve different purposes, use different data sources, and are applied in different industries.
A digital twin can be viewed as a combination of computer experiments. However, for geometric, physical, and behavioral models [13], more complex mathematical approximations or equations are often required, which can be difficult to solve in a short amount of time. For instance, in [13], each behavior of a physical entity was described by differential equations. Complex computer models are typically used to solve these equations. Evaluating a single output may take several hours or even days due to the large number of inputs and the complicated system. To overcome the high computational costs, computer experiments aim to find an approximate model that is much simpler than the true (but complicated) model by simulating the behavior of the process on a computer [14]. The distinct nature of computer experiments poses a unique challenge, which requires a special design for the experiment. Motivated by this, we propose a new concept—the digital triplet—which is the counterpart twin of the digital twin. The goal of the digital triplet is to rapidly and efficiently learn and estimate the digital twin, allowing it to avoid complex computations from mathematical equations and provide rapid feedback to the physical system, as shown in Figure 1. The digital triplet is a time-saving and efficient method for describing the digital twin. Many popular models, such as machine learning algorithms used in the construction of rule modeling in digital twins, can be used for its construction. More details on models for constructing the digital triplet are provided in Section 2.
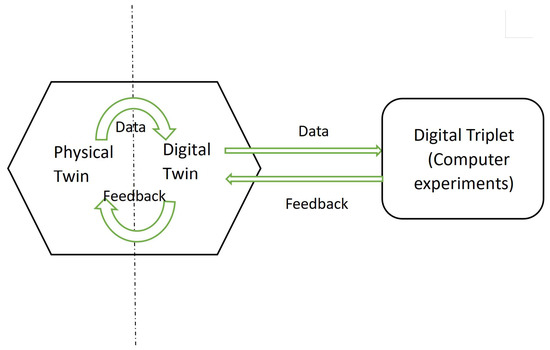
Figure 1.
Digital triplets to quickly and efficiently study digital twins.
The data collection step is crucial in the development of a digital triplet as it provides essential information for constructing an accurate model. However, the real-time data from a digital twin makes the commonly used method of data collection (single designs) inappropriate for creating a digital triplet. There is no established guideline for identifying effective designs that can accommodate real-time data in digital twins. This is an issue that warrants further investigation. This is, indeed, the necessity of a digital triplet.
1.4. Sequential Designs
A recommended approach for constructing a digital triplet that accommodates real-time data in a digital twin is to use a sequential (multiple-stage) design. Sequential designs are particularly useful in complex systems, where a structured approach is required to ensure all specifications are met, and they have been widely adopted in engineering, product development, and other fields [15,16]. With each stage building upon the results from the previous one, a sequential design offers a cost-effective and practical solution for constructing a digital triplet compared to single-stage designs.
Guidance for identifying the most promising predictive models and effective sequential designs is proposed. In general, Gaussian process regression is a widely used method for constructing a digital triplet due to its ability to model complex relationships. Space-filling designs, particularly sequential MaxPro designs, are commonly used and effective in Gaussian process regression to construct a digital triplet. Here, we provide numerical simulations involving five different models: linear model, second-order model, Gaussian process, artificial neural network, and automated machine learning,; six different designs: central composite design, D-optimal design, random design, maximin distance design, MaxPro design, and “hetGP” design; and six test functions to compare different designs and models in constructing a digital triplet. Simulation results generally support the use of Gaussian process regression and MaxPro designs for constructing the digital triplet. It is shown that the digital triplet can efficiently represent the digital twin and, consequently, provide rapid feedback to the physical system.
The paper is organized as follows: Section 2 presents some statistical and machine learning models that can be used for creating a digital triplet. Section 3 introduces sequential designs suitable for collecting the training data. Section 4 provides simulation studies to guide the selection of suitable designs and models. The numerical results indicate that the use of Gaussian process regression and sequential MaxPro designs perform well in constructing a digital triplet. It is also shown that a digital triplet can efficiently represent a digital twin to understand the physical system. Section 5 provides the conclusion and discussion.
2. Models for Digital Triplet
The proposed procedure for learning a digital twin involves collecting data points from the digital twin and then training a digital triplet on the collected data. The digital triplet can be likened to the response surface methodology (Box and Wilson, 1951 [17]) for sequentially learning a response surface and surrogate modeling for engineering problems. A range of statistical and machine learning models can be employed for this purpose, with the specific choice depending on the complexity and characteristics of the digital twin being modeled. In this section, we will introduce several models, such as linear regression, support vector machine, random forest, artificial neural network, Gaussian process regression, and automated machine learning. The performance of selected models in learning a digital twin will be evaluated in Section 4 and Section 5.
Linear regression [14] is a straightforward model that can be employed to learn a digital twin of a linear system. Given a response variable y and k input variables , a first-order linear model takes the following form, with coefficients , estimated via least-squares estimation:
When curvature and interactions between input variables are potentially present, a second-order model can be used:
In model (2), represents the intercept, through represent the coefficients for the linear terms of the input variables, through represent the coefficients for the quadratic terms, and through represent the coefficients for the interaction terms. These coefficients can also be estimated using least-squares estimation.
Support vector machine is a supervised machine learning algorithm used for classification and regression tasks [18,19]. The algorithm aims to identify a hyperplane in the data space that produces the largest minimum distance between training data from different classes, known as the maximum margin hyperplane. This hyperplane is defined by the vectors (data points) closest to the margin. Support vector machine has several advantages, including increased class separation, reduced expected prediction error, the ability to handle high-dimensional data, and the ability to perform both linear- and nonlinear-based analyses. Numerous studies have demonstrated the excellent performance of support vector machines in a wide range of real-world learning problems, making it one of the most effective and versatile classifiers available.
The classification and regression tree was proposed by [20] as a decision tree algorithm for classification and regression tasks. It recursively partitions the data to develop a tree-like structure that is easily interpretable and computationally efficient. This algorithm has broad applicability and can produce accurate predictions with minimal computational resources. To further improve its performance, Ref. [21] introduced random forest, which combines multiple decision trees. Each tree is trained on a random subset of the data and a subset of features is randomly selected at each node. The predictions of each tree are then combined, with the most common prediction selected as the final result. This approach of combining many weak or weakly-correlated classifiers has been shown to be effective in achieving high prediction accuracy.
The artificial neural network was first introduced by [22,23], taking inspiration from the way learning strengthens connections between neurons in the brain. Artificial neural networks are commonly represented as a diagram of nodes in different layers that are connected by weighted links. To enable greater modeling flexibility, at least one hidden layer is typically present between the input and output layers. The transformation between layers is represented by approximation models, with the simplest being a linear model. Although the connections between nodes can enable feedback to previous layers, the typical artificial neural network for model approximation is feedforward with one hidden layer. Considering a neural network as an illustration (specifically, with a single hidden layer consisting of four neurons), the commonly employed activation function for the jth hidden neuron is defined as follows:
where represents the parameters to be estimated, is a fixed value, and signifies the ith input value . Here, , and is the output from the jth hidden neuron . Artificial neural networks can accommodate complex, non-linear relationships between inputs and outputs, making them well-suited for tasks such as image and speech recognition. Artificial neural networks are a powerful and versatile tool that can be used to solve a wide range of machine learning problems.
Gaussian process regression is a powerful class of machine learning algorithms ([24]) and is commonly used in computer experiments for surrogate modeling, Bayesian optimization, and image processing. The key idea is to assume that the response follows a Gaussian process:
where for are the collected data, is the mean response, and is a stationary Gaussian process with zero mean and covariance function :
for some decreasing function . The correlation decays as a function of the distance between inputs and is typically defined by a kernel function. Commonly used kernel functions include the Gaussian kernel, exponential kernel, and Matérn kernel, among others (see, for example, [24]). The prediction for a new run is given by the posterior mean given the collected data, and the variance of the prediction is the posterior variance. Gaussian process regression not only predicts the response but also provides uncertainty quantification for the predicted values. As a result, it has been proven to be an effective tool for active learning, where the goal is to sequentially design new inputs for a given system.
Automated machine learning, proposed by [25], employs artificial intelligence and machine learning algorithms to automate the process of building, training, and optimizing machine learning models. This algorithm is particularly useful for non-experts in the field, as it is easy to implement and can automate many of the manual and time-consuming tasks involved in building machine learning models. Furthermore, automated machine learning can improve the accuracy of machine learning models by automating the process of selecting the best model and hyperparameters, leading to better performance and more accurate predictions.
3. Sequential Experimental Designs for Digital Triplet
Good training data are essential to ensure that the learned digital triplet accurately represents the behavior of the digital twin. Experimental design strategies play a crucial role in collecting high-quality training data that cover a wide range of conditions of input variables. Different methods of experimental design, such as optimal design, response surface design, Latin hypercube sampling, and space-filling designs, can be used to select input combinations effectively. By using these methods, one can obtain a set of input combinations that are representative of the digital twin and provide an accurate representation of its behavior. However, when the number of experimental runs is limited, a one-stage design may not be efficient to cover all input combinations. In such cases, a sequential design strategy may be more effective to improve the accuracy of a digital triplet. In this section, we discuss several commonly used experimental designs and sequential plans that can be used for learning digital twins.
When the true model is known or almost known, optimal design can be used to select the most informative input combinations to minimize estimation uncertainty and maximize the accuracy of the learned digital twin. The goal of optimal design is to choose input combinations that are most informative for learning the digital twin while minimizing the total number of experimental runs. Several criteria are available for finding optimal designs, such as D-optimality, A-optimality, and G-optimality. The D-optimality criterion maximizes the determinant of the information matrix, the A-optimality criterion minimizes the average variance of estimated model parameters, and the G-optimality criterion minimizes the maximum variance of the predicted value. Software such as the R package “OptimalDesign (1.0.1)” is available to obtain optimal designs. However, when the true model is not known and the assumed model is misspecified, optimal designs may not perform well and could result in biased or inefficient estimates of the parameters. When using optimal designs sequentially, we can specify the desired sample size for each stage and then determine the optimal design for that stage based on some optimality criterion.
Response surface design was first introduced by [17] for sequential optimization using first- and second-order linear regression. Initially, a first-order model is used to approximate the behavior of a system, i.e., the digital twin to be learned. As the system approaches the optimum, a second-order model is then employed to find the optimum with higher accuracy. This approach is commonly used in experimental design and optimization to efficiently identify the optimal settings of input variables, particularly when the relationship between the inputs and response variable is complex and nonlinear. Commonly used response surface designs include the central composite design [17], which comprises three parts: (i) a factorial or fractional factorial design that allows the estimation of a first-order linear model, (ii) a set of center points which are used to estimate the pure error variance and check for curvature in the response surface, and (iii) a set of axial points which are used to establish a second-order model and identify the optimum. In the context of sequentially creating a digital triplet for a digital twin, a central composite design with the desired sample size can be used in each stage.
Space-filling designs are a type of experimental design that aims to ensure that the input space is evenly sampled and explored. These designs are particularly useful when the true underlying model is not known or when the model is very complex. These designs aim to distribute design points as uniformly as possible across the input space and have gained widespread use in the field of computer experiments [14]. Popular space-filling designs include Latin hypercube design [26], maximum entropy design [27], maximin distance design [28], and maximum projection design [29]. A Latin hypercube design divides the range of each input into equally sized intervals and samples each interval exactly once. A maximum entropy design maximizes the Shannon entropy of the experimental data. A maximin distance design maximizes the separation distance between design points. A maximum projection design maximizes the space-filling property in every projected dimension. When using such designs in a sequential manner for creating a digital triplet, we first use a space-filling design in the first stage to ensure that we cover the input space to the best extent and then add design points in the second stage to improve the coverage of the input space. This can help us improve the accuracy and predictive capability of the trained digital triplet. Commonly used software for generating sequential space-filling designs include the R packages “FSSF” [30] and “MaxPro” [31].
Additionally, the digital triplet can be iteratively refined through sequential experiments by using a first-stage design to fit a model, such as a Gaussian process regression, and updating the model to better represent the digital twin. For Gaussian process regression, [32] proposed a sequential learning algorithm that uses a look-ahead-based mean-squared prediction error (MSPE) criterion. The algorithm selects the next design point that leads to the minimum integrated MSPE over the entire input space, based on the current estimated model. This approach helps to select design points that improve the accuracy of the digital triplet over the entire input space, rather than just at specific points. The R package “hetGP” can be used to obtain such a sequential design for Gaussian process regression.
4. Simulation Studies
The simulations given here involve five different models and six different designs to learn six test functions. The five models include the linear model (1), second-order model (2), Gaussian process regression (4), artificial neural network (5), and automated machine learning (listed in Table 1). The software used to perform these models is listed in the second column of Table 1. For simplicity, we only consider two-stage experiments. The six different designs include central composite design (with ), D-optimal design, random design, maximin distance design, MaxPro design, and “hetGP” design in the first stage, as well as their sequential designs in the second stage (as listed in Table 2).

Table 1.
Models and theirs software.

Table 2.
Experimental designs.
We use a combination of each design and each model to predict the (unknown) test functions. Such a process is replicated 500 times. In each replication, the design points of the sequential central composite design, sequential D-optimal design, sequential maximin distance design, and sequential MaxPro design remain fixed, while the design points of random designs are randomly selected. The hetGP design is independently constructed using the R package “hetGP”. We consider all models in Table 1 and designs in Table 2. The hGP design can only be constructed in Gaussian process regression so this design does not cooperate with other models in our simulations. In addition, the D-optimal design relies on the model. For the linear model and the second-order model, the theoretically optimal designs can be found in the R package “OptimalDesign”. For all other models in Table 1, the research on their optimal designs is still in the preliminary stage so we use the D-optimal design under the second-order model as a substitute for these optimal designs. In each case, we assume a standard deviation of . The testing data consist of all full grid points, where s is the number of levels in each dimension. To evaluate the performance of models, RMSE (defined below) is a commonly used criterion, which is a statistical measure of the difference between a predicted value and its corresponding true value:
where is the predicted value obtained via the fitting model, is observation i from the test function, and n is the number of samples. A lower RMSE value indicates a better fit between the predicted and actual values, implying a better model performance. Note that and in RMSE are evaluated with respect to testing data only. The average RMSE values of different combinations of designs and models for establishing a digital triplet are to be compared.
4.1. Two-Dimensional Cases
Three widely used (two-dimensional) test functions are used to investigate the goodness of design and model, namely, the McCormick function, Ackley function, and Rastrigin function. Their respective analytic expressions and domains are displayed in Table 3. We set to obtain = 10,000 full grid points within the domain of each test function. In the first stage, the number of design points is 12, while in the second stage, it is 84. We also conduct an example with 42 design points in the first stage. For brevity, we will not elaborate on this example any further in this paper. The design points and their sequential designs are displayed in Figure 2 for McCormick function, as an illustration. For the central composite design, the first stage involves a two-level full factorial design with four axial points and four center points. In the second stage, we introduce an additional nine replicates for each point from the first stage, excluding the center points. For the D-optimal design, we initially construct a 12-run optimal design and subsequently add another 72-run optimal design in the second stage. Similarly, the random design can be constructed in both stages. For the maximin distance design, we start with a 12-run design in the first stage, followed by sequentially adding 72 additional points based on the points from the first stage. The MaxPro design is constructed in the same manner. For hetGP design, it selects the next design point that leads to the minimum integrated MSPE over the entire input space, based on the current estimated model. This approach helps to select design points that improve the accuracy of the digital triplet over the entire input space, rather than just at specific points. The designs for sequential central composite, sequential D-optimal, sequential maximin distance, and sequential MaxPro designs are fixed across all replications. However, the sequential random and hGP designs may vary between replications, and we simply show a single random replication as an example. For each sequential design, the design points in the first stage are labeled as ∗, while the additional points in the second stage are labeled as •. All points labeled with either ∗ or • constitute the design in the second stage. The size of each label is directly proportional to the frequency of the corresponding point.

Table 3.
Three two-dimensional test functions.
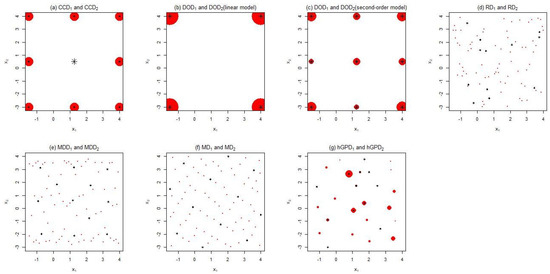
Figure 2.
Plot of each design for McCormick function (∗ and • represent the design points in the first stage and the additional points in the second stage. The size of each label is directly proportional to the frequency of the corresponding point).
For each test function, we evaluate the average RMSE from 500 replicates for all combinations of the designs and models. We then plot these average RMSE values in both stages in Figure 3. Compared with the Ackley function, the other two test functions have larger scales of ranges so they often lead to larger average RMSE values. In terms of real-time property, the digital twin often gives more importance to the latest stage. In the second stage, the additional points result in a decrease in the RMSE for each case. For all designs, the decrease in RMSE is most significant for GP model, particularly for the McCormick function. The linear model often leads to a smaller decrease in RMSE, since it is not an appropriate model for the test function.
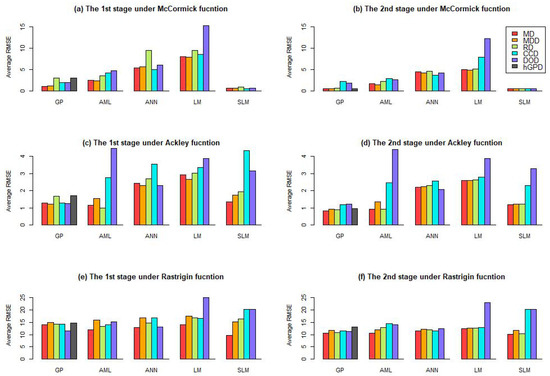
Figure 3.
The average RMSE among different designs under each model. (All subfigures share the same legend. In the legend, the label “MD” represents MD in the first stage and MD in the second stage. Other labels have similar representative meanings).
Figure 3 illustrates that the second-order model and Gaussian process model outperform other models, particularly the Gaussian process model. The second-order model performs well on the McCormick function as it can be approximated by the second-order model. However, for the other two test functions, the second-order model is not a good approximation, particularly when paired with its optimal design, as shown in Figure 3c–f. The models with maximum average RMSE under different designs are linear models. The linear model is unable to approximate the nonlinear behavior of all test functions effectively. It implies that the optimal design leads to a poorer predictive ability of the linear and second-order models under model misspecification. Therefore, we recommend using the Gaussian process model at each stage. In terms of design, the best designs with minimum average RMSE are the sequential MaxPro design, especially for Ackley and Rastrigin functions, particularly in the second stage. For McCormick functions on each stage, the best designs with minimum average RMSE are sequential maximin distance designs. The best designs with minimum average RMSE are the sequential MaxPro design, especially for Ackley and Rastrigin functions. Therefore, we recommend using space-filling sequential designs, particularly sequential MaxPro design, to estimate complex unknown relationships.
Extending to heteroscedastic digital twins, we assume for illustration purposes, where is the variable with the domain [0, 1], resulting from a linear transformation on . To model a distribution of responses over a domain of variables, one needs to take into account both response mean and variance. A Gaussian process is an appropriate choice for this purpose. Figure 4 displays boxplots of 500 replicates of RMSE for each design under the GP model. Figure 4 indicates that, for each test function and design, the fluctuation in RMSE in the second stage significantly decreases compared to that in the first stage. Moreover, the average RMSE decreases in the second stage for all cases. The sequential MaxPro design, maximin distance design, and hGP design have similar average RMSE values for McCormick and Ackley functions. The three designs have smaller average RMSE values than all other designs. Moreover, the hGP design has the smallest RMSE in each stage for the Ackley function and in the second stage for the McCormick function, while the sequential MaxPro design has the smallest RMSE in the first stage. For the Rastrigin function, the sequential MaxPro design has a significantly smaller RMSE than other designs in the second stage. Overall, the hGP design and sequential MaxPro design are the best choices under the RMSE criterion. However, when there was a large fluctuation in for the Rastrigin function, the hGP design had a significant fluctuation in RMSE. This is due to the fact that optimizing the global optima (minimum or maximum) of an unknown function is a time-consuming and challenging problem, resulting in the unstable performance of “hetGP”.
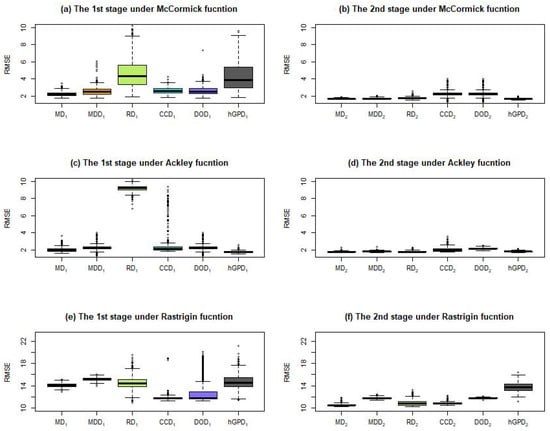
Figure 4.
The boxplot of RMSE for each design under Gaussian process for heteroscedastic digital twin.
In summary, Gaussian process regression is most appropriate to construct a digital triplet. Sequential space-filling designs, particularly sequential MaxPro designs, are most effective in Gaussian process regression to approximate digital twins. For stochastic digital twins, especially for heteroscedastic cases, hGP designs have been theoretically and numerically proven to be effective for Gaussian processes. However, our simulations show that the performance of the hGP design is unstable. They may be an appropriate design for constructing stochastic Gaussian processes if the current technologies used for constructing hGP designs can be enhanced.
4.2. Six-Dimensional Cases
In this subsection, we consider a larger dimension. The six-dimensional cases include the OTL circuit function, the Borehole function, and the Robot arm function. Their analytic expressions and domains are listed in Table 4. Let , so that testing data have = 15,625 full grid points in the domain of each test function. Let the number of points in the first stage be 26 and that in the second stage be 104. We also conduct an example with 52 design points in the first stage. For brevity, we will not elaborate on this example any further in this paper. The average RMSE among different designs for each model in both two stages and the average RMSE among different models for each design in both two stages are plotted in Figure 5. For the second-order model, the number of all parameters is 28, so each design in the first stage is unable to estimate test function by this model. Thus, there are no data on average RMSE for the second-order model in Figure 5.

Table 4.
Six-dimensional test functions.
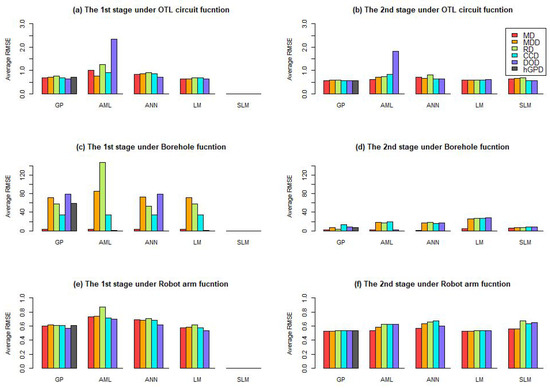
Figure 5.
The average RMSE among different designs under each model. (All subfigures share the same legend. In the legend, the label “MD” represents MD in the first stage and MD in the second stage. Other labels have similar representative meanings).
Compared with the Borehole function, the other two test functions have smaller scales of ranges so they often lead to smaller average RMSEs. For all designs, the decrease in RMSE under the Borehole function is most significant. In terms of design rank, Figure 5 shows that the best design (with minimum average RMSE) is the sequential MaxPro design, especially for Borehole and Robot arm functions. The best model (with minimum average RMSE) is the Gaussian process model. This is consistent with that of the two-dimensional cases, given in the previous subsection.
Extending to the heteroscedastic case, we keep the same error formulation used in Figure 4. Figure 6 displays all boxplots of RMSE of all 500 replicates for each design under the Gaussian process model. For the OTL circuit function, the D-optimal design has the smallest RMSE among all designs in the first stage, while the sequential MaxPro design has the smallest RMSE among all designs in the second stage. For the Borehole function, it is observed that the sequential MaxPro design has the smallest average RMSE in each stage. In the second stage, sequential maximin distance and sequential random designs have similar performances as that of sequential MaxPro design. For the Robot arm function, all designs have a similar RMSE in each stage. The optimal one is the hGP design in the first stage and the sequential MaxPro design in the second stage. Overall, the sequential MaxPro design is the best choice for heteroscedastic digital twins. However, for high-dimensional cases, the hGP design has significant fluctuations in RMSE.
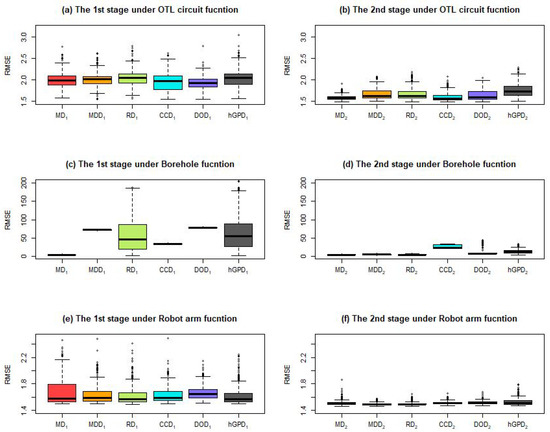
Figure 6.
The boxplot of RMSE for each design under Gaussian process for heteroscedastic digital twin.
4.3. Summary
In summary, Gaussian process regression is shown to be effective as a model to construct a digital triplet. Sequential space-filling designs, such as the sequential MaxPro design, are most efficient when coupled with Gaussian process regression to create a digital triplet.
For heteroscedastic digital twins, hGP designs may be unstable. They may be an appropriate design for constructing stochastic Gaussian processes if the current technologies used for constructing hGP designs can be enhanced. In addition, adding points one at a time in a serial manner would be slow and not aligned with modern, distributed advanced computing capabilities. Therefore, efficient construction of batch sequential MaxPro designs and batch hGP designs is also a topic worthy of future investigation.
5. Conclusions and Discussion
A physical system often requires costly and time-consuming experiments to study and optimize. To address this issue, the concept of digital twins has been introduced. This is a computer program that leverages real-world data to develop simulators to understand the physical system. However, mathematical equations used to model digital twins can be challenging to solve in an efficient manner. To overcome this limitation, we propose a concept called digital triplet, as an efficient counterpart of a digital twin. The digital triplet aims to represent the digital twin efficiently, thereby avoiding complex computations from mathematical equations and, thus, supporting a digital twin in understanding the physical system. Note that the digital triplet procedure proposed in this paper differs from the concept of digital triplet used in some of the literature [33,34], which refer to the application of artificial intelligence techniques to enhance the performance of digital twin systems. We emphasize the use of sequential experimental designs to learn about a digital twin system and construct a response surface using machine learning models as an alternative to the digital twin for fast prediction and decision-making.
A digital triplet is constructed by statistical models and efficient designs. It is able to accommodate any statistical model and sequential design. In the literature, various statistical models and sequential designs have been investigated. Since a digital twin can acquire real-time data and update itself promptly, it is crucial for a digital triplet to also update itself in real time based on observations from the digital twin. In this regard, a sequential design, specifically, a multi-stage design, is desirable. Simulation studies indicate that Gaussian process regression is shown to be appropriate as a model to construct a digital triplet. Sequential space-filling designs, such as the sequential MaxPro design, are most effective in Gaussian process regression to create a digital triplet. It is shown that the digital triplet can efficiently represent the digital twin to understand the physical system.
For heteroscedastic digital twins, our simulations show that the performance of the hGP design is unstable, even though it is an adaptive design. This may be an appropriate design for constructing stochastic Gaussian processes if the current technologies used for constructing hGP designs can be enhanced. In addition, adding points one at a time in a serial manner would be slow and not aligned with modern, distributed advanced computing capabilities. Therefore, efficient construction pf batch sequential MaxPro designs and batch hGP designs is also a topic worthy of future investigation.
Author Contributions
Methodology, X.Z., D.K.J.L. and L.W.; Software, X.Z.; Writing—original draft, X.Z.; Writing—review & editing, X.Z., D.K.J.L. and L.W. All authors have read and agreed to the published version of the manuscript.
Funding
Lin was supported by the National Science Foundation, via Grant DMS-18102925.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, X.; Wang, Z.; Hua, Q.; Shang, W.L.; Luo, Q.; Yu, K. AI-empowered speed extraction via port-like videos for vehicular trajectory analysis. IEEE Trans. Intell. Transp. Syst. 2023, 24, 4541–4552. [Google Scholar] [CrossRef]
- Dai, Y.; Zhang, Y. Adaptive digital twin for vehicular edge computing and networks. J. Commun. Inf. Netw. 2022, 7, 48–59. [Google Scholar] [CrossRef]
- Tao, F.; Qi, Q. Make more digital twins. Nature 2019, 573, 490–491. [Google Scholar] [CrossRef] [PubMed]
- Tao, F.; Zhang, H.; Liu, A.; Nee, A.Y.C. Digital Twin in Industry: State-of-the-Art. IEEE Trans. Ind. Inform. 2019, 15, 2405–2415. [Google Scholar] [CrossRef]
- Wagg, D.J.; Worden, K.; Barthorpe, R.J.; Gardner, P. Digital twins: State-of-the-aArt and future directions for modeling and simulation in egineering dynamics applications. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2020, 6, 030901. [Google Scholar] [CrossRef]
- Wright, L.; Davidson, S. How to tell the difference between a model and a digital twin. Adv. Model. Simul. Eng. Sci. 2020, 7, 1–13. [Google Scholar] [CrossRef]
- Zheng, Y.; Yang, S.; Cheng, H. An application framework of digital twin and its case study. J. Ambient. Intell. Humaniz. Comput. 2019, 10, 1141–1153. [Google Scholar] [CrossRef]
- Tao, F.; Xiao, B.; Qi, Q.L.; Cheng, J.F.; Ji, P. Digital twin modeling. J. Manuf. Syst. 2022, 64, 372–389. [Google Scholar] [CrossRef]
- Angjeliu, G.; Coronelli, D.; Cardani, G. Development of the simulation model for digital twin applications in historical masonry buildings: The integration between numerical and experimental reality. Comput. Struct. 2020, 238, 106282. [Google Scholar] [CrossRef]
- Berri, P.C.; Dalla Vedova, M.D.L. A review of simplified servovalve models for digital twins of electrohydraulic actuators. J. Phys. Conf. Ser. Appl. Phys. Simul. Comput. 2020, 1603, 23–25. [Google Scholar] [CrossRef]
- Chakraborty, S.L.; Adhikari, S. Machine learning based digital twin for dynamical systems with multiple time-scales. arXiv 2020, arXiv:2005.05862. [Google Scholar] [CrossRef]
- Liu, C.; Jiang, P.; Jiang, W. Web-based digital twin modeling and remote control of cyber-physical production systems. Robot. Comput.-Integr. Manuf. 2020, 64, 101956. [Google Scholar] [CrossRef]
- Tarkhov, D.A.; Malykhina, G.F. Neural network modeling methods for creating digital twins of real objects. J. Phys. Conf. Ser. 2019, 1236, 012056. [Google Scholar] [CrossRef]
- Fang, K.T.; Li, R.Z.; Sudjianto, A. Design and Modeling for Computer Experiments; Chapman and Hall/CRC: New York, NY, USA, 2005. [Google Scholar]
- Ranjan, P.; Bingham, D.; Michailidis, G. Sequential experiment design for contour estimation from complex computer codes. Technometrics 2008, 50, 527–541. [Google Scholar] [CrossRef]
- Williams, B.J.; Santner, T.J.; Notz, W.I. Sequential design of computer experiments to minimize integrated response functions. Stat. Sin. 2000, 10, 1133–1152. [Google Scholar]
- Box, G.E.P.; Wilson, K.B. On the experimental attainment of optimum conditions. J. R. Stat. Soc. Ser. B 1951, 13, 1–45. [Google Scholar] [CrossRef]
- Burges, C. A tutorial on support vector machines for pattern recognition. In Data Mining and Knowledge Discovery; Kluwer Academic Publishers: Boston, MA, USA, 1998. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Wadsworth: Belmont, CA, USA, 1984. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- White, H. Learning in neural networks: A statistical perspective. Neural Comput. 1989, 1, 425–464. [Google Scholar] [CrossRef]
- Lippmann, R.P. An introduction to computing with neural nets. IEEE ASSP Mag. 1987, 4, 4–22. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Thornton, C.; Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Auto-WEKA: Combined Selection and Hyperparameter Optimization of Classification Algorithms. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’13, Chicago, IL, USA, 11–14 August 2013; pp. 847–855. [Google Scholar]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. Comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 33, 239–245. [Google Scholar]
- Santner, T.J.; Williams, B.J.; Notz, W.I.; Williams, B.J. The Design and Analysis of Computer Experiments; Springer: New York, NY, USA, 2003. [Google Scholar]
- Johnson, M.E.; Moore, L.M.; Ylvisaker, D. Minimax and maximin distance design. J. Stat. Plan. Inference 1990, 26, 131–148. [Google Scholar] [CrossRef]
- Joseph, V.R.; Gul, E.; Ba, S. Maximum projection designs for computer experiments. Biometrika 2015, 102, 371–380. [Google Scholar] [CrossRef]
- Shang, B.Y.; Apley, D.W. Large-scale fully-sequential space-filling algorithms for computer experiments. J. Qual. Technol. 2019, 53, 173–196. [Google Scholar] [CrossRef]
- Ba, S.; Joseph, V.R. Maximum Projection Designs. R Package Version, 4.1-2. 2018. Available online: https://CRAN.R-project.org/package=MaxPro (accessed on 30 May 2023).
- Binois, M.; Huang, J.; Gramacy, R.B.; Ludkovski, M. Replication or exploration? Sequential design for stochastic simulation experiments. Technometrics 2019, 61, 7–23. [Google Scholar] [CrossRef]
- Gichane, M.M.; Byiringiro, J.B.; Chesang, A.K.; Nyaga, P.M.; Langat, R.K.; Smajic, H.; Kiiru, C.W. Digital triplet approach for real-time monitoring and control of an elevator security system. Designs 2020, 4, 9. [Google Scholar] [CrossRef]
- Umeda, Y.; Ota, J.; Kojima, F.; Saito, M.; Matsuzawa, H.; Sukekawa, T.; Takeuchi, A.; Makida, K.; Shirafuji, S. Development of an education program for digital manufacturing system engineers based on ‘Digital Triplet’ concept. Procedia Manuf. 2019, 31, 363–369. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).