Trapezoidal Interval Type-2 Fuzzy PIPRECIA-MARCOS Model for Management Efficiency of Traffic Flow on Observed Road Sections

Abstract

Road infrastructure management is an extremely important task of traffic engineering. For the purpose of efficient management, it is necessary to determine the efficiency of the traffic flow through PAE 85%, AADT and other exploitation parameters on the one hand, and the number of different types of traffic accidents on the other. In this paper, a novel TrIT2F (trapezoidal interval type-2 fuzzy) PIPRECIA (pivot pairwise relative criteria importance assessment)-TrIT2F MARCOS (measurement of alternatives and ranking according to compromise solution) was developed in order to, in a defined set of 14 road segments, identify the most efficient one for data related to light goods vehicles. Through this the aims and contributions of the study can be manifested. The evaluation was carried out on the basis of seven criteria with weights obtained using the TrIT2F PIPRECIA, while the final results were presented through the TrIT2F MARCOS method. To average part of the input data, the Dombi and Bonferroni operators have been applied. The final results of the applied TrIT2F PIPRECIA-TrIT2F MARCOS model show the following ranking of road segments, according to which Vrhovi–Šešlije M-I-103 with a gradient of −1.00 represents the best solution: A5 > A8 > A2 > A1 > A4 > A3 > A6 > A12 > A13 = A14 > A11 > A7 > A9 > A10. In addition, the validation of the obtained results was conducted by changing the values of the four most important criteria and changing the size of the decision matrix. Tests have shown great stability of the developed TrIT2F PIPRECIA-TrIT2F MARCOS model.

1. Introduction

The implementation efficiency of traffic requirements is the primary objective of a comprehensive process of development and exploitation of the road network. Capacity and level of service (LoS) analyses are some of the basic procedures in balancing demands (traffic flows) and supply (routes) [1,2,3]. Balancing supply and demand is a very complex and multidisciplinary optimization process with the main goal of determining rational project solutions—functionally and economically justified. The selection of indicators, i.e., criteria that can realistically show the effectiveness of conditions in the traffic flow, depends, on the one hand, on road elements, but also on the characteristics of the traffic flow [4,5].

The safe and smooth movement of vehicles on roads with the presence of continuous (optimal) speeds and the geometric conditions of roads, as well as other road conditions, become conflicting tasks, so a rational balancing between these two imperatives is important due to their contradictions. In order to achieve maximum efficiency and safety in traffic, it is necessary to reduce the number of access points, increase flow rates, establish the greatest possible traffic flow homogenization, manage traffic in order to obtain continuous movement of vehicles, reduce gradients, increase the radii of curves and the like. Due to the increase in the number of access points, the level of access control decreases, which results in lowering the level of traffic safety to an unacceptable level.

A heterogeneous traffic flow is composed of different classes of vehicles, and in order to evaluate the effect of different vehicle classes, the passenger car equivalent (PCE) is used [6,7]. With the increased percentage of participation of heavy and light goods vehicles, there is a decrease in the capacity of the road due to their dimensions and weaker performance compared to passenger vehicles. The heterogeneous structure of the traffic flow often leads to the emergence of potential conflicts in traffic (slow movements, nervousness of a driver behind a truck, wish to overtake, etc.), which can be the cause of accidents with material damage, injured persons or fatalities.

The aim of this paper is to determine the efficiency of a defined set of 14 segments of road infrastructure based on data collected on light goods vehicles. The evaluation criteria imply a combination of road exploitation parameters and consequent outputs. Based on these aims the following research question can be asked: can a formed MCDM model offer enough data for the sustainable management of road infrastructure, and can the obtained results help decisionmakers to improve the level of traffic safety?

The application of fuzzy concepts in MCDM models makes it possible to consider complexities and uncertainties in decisions [8]; that is one of the reasons to handle the MCDM model with TrIT2F. Additionally, such a model based on an expert’s assessment and quantification of the linguistic scale in quantitative data provided more precise decisions. The greatest contribution of this paper is the creation of a completely novel model consisting of two MCDM methods extended with trapezoidal interval type-2 fuzzy numbers. This model offers certain advantages and can be applied in other areas of decision making. Forming an extension of two MCDM methods (the first for determining the values of criteria and the second for ranking potential solutions) with TrIT2F represents an additional contribution because in this way we have offered a completely new model. Some integrated MCDM models applied different theories, and it is necessary to enable defuzzification to apply criteria weights in the ranking method, even though in our study that is not the case that represented advantages. Simply put, the obtained criteria weights can be applied in ranking methods without any additional operation.

This paper presents the assessment of the efficiency and safety of the traffic flow shown on the main sections of two-lane roads, whereby an adequate model for the assessment of efficiency, determined on 14 relevant road segments, was developed. Additionally, the ranking of all 14 road segments was performed using the TrIT2F PIPRECIA-TrIT2F MARCOS model. Section 2 contains a literature review and a tabular presentation of relevant research on evaluating the efficiency of roads, especially based on the examination of passenger car equivalents, as an indicator of traffic flow structure. The methods developed for this purpose are highlighted in Section 3, and the criteria and quantitative data necessary for the assessment of road segments using the linguistic scale for the TrIT2F MARCOS method are defined in Section 4. Section 5 provides the results and analysis of the TrIT2F PIPRECIA-TrIT2F MARCOS model, while Section 6 presents the validation tests.

2. Literature Review

Many studies have been conducted in order to understand the effect of different categories of traffic flow vehicles. Scientific papers based on the examination of PCE mainly referred to the assessment of PCE in relation to different categories of vehicles under different traffic and road conditions [9,10,11,12]. Using different methods for determining PCE values, differences in values were found for each of the applied methods [13,14]. Additionally, the highway capacity manual (HCM) recommends the use of PCE values, which are often criticized by researchers [15,16,17,18]. In order to determine the PCE value, speed indicators [16,19,20], time headway values [13,21,22], vehicle travel times [14,17] and the like are used. Certain studies base their results on the collection of data on microsimulation models [18,23]. Additionally, according to the research by Lu et al. [24] on highways, it has been proven that the PCE value increases by increasing the flow rate. As for motorcycles, Rongviriyapanich and Suppattrakul [25] derive PCE values near intersections and mid-block sections using time headway. They come to the conclusion that the PCE for motorcycles is constantly decreasing with a proportional increase in other vehicle categories. Reference [26] showed that analyzing the PCE for road capacity values, the capacity of the road with a central island is larger than that of the road with a double dotted line. Based on two measurement locations of expressways in Singapore [27], it was shown that differential speed limits for commercial vehicles resulted in significant differences in PCE values for traffic compositions. Additionally, taking into account only traffic compositions at pre-signalized intersections [28], PCE calibration values for given conditions were proposed. In addition, the equivalency factors for the same location vary significantly based on traffic speed [29]. By analyzing theoretical knowledge and their application on Indian roads [30] using eight methods, it has been shown that there is a great need to consider all possible modalities for determining PCE values as a function of influencing factors that can be adopted worldwide. An overview of the related studies is presented in Table 1.

Table 1. Overview of related studies.

Reference	Road Type	Vehicle Classes for PCE Determination	The Method Based on:	Research Approach	Conclusion
Muhammad [5]	Urban arterials (midblock)	9 vehicle classes	Time headway.	12 arterials in Karachi	Significant differences were found between the values of PCE factors from each method.
Dadi Vasavi Swetha [6]	National highway and urban roads	5 vehicle classes (HV, LCV, CAR, two wheeler and three wheeler)	Determining travel time and road width occupancy for different types of vehicles.	4 road types (national highway and urban roads)	High PCEs at low density consume high road capacity. Therefore, there is a good reason to include service lanes for slow vehicles to increase road capacity.
Bouhouras and Basbas, [13]	The main entry points to the area; the primary road arterial network	Commercial vehicles	Time headway on a survey marked line.	27 at-grade signalized intersections	The calculated values for the survey area (PCE = 2.18) are close to the recommended values for Greece (PCE = 2.00).
Pulugurtha & Jain [7]	Urban or rural roads	Trucks	Least square regression model based on the travel time of trucks.	Urban and rural area	The coefficients show that the average travel time of trucks is higher than the PC travel time.
Sarraj & Jadili, [14]	Urban roads	Buses and animal-driven carts	Time headways on a marked line.	Three main signalized intersections	The calculated values for the three intersections are (PCE = 2.00) for buses and (PCE = 1.67) for animal-driven carts.
De Luca & Dell’Acqua [8]	Two sections of a non-urban two-lane road	Small (L < 5), midsize (5 < L < 7), midsize (7 < L < 10), long vehicle 1 (10 < L < 15), long vehicle 2 (15 < L < 20), extra-long vehicle (L > 20)	Flow rate–speed–density relations as a function of HCM-2010 values.	Two-lane highways	PCE values vary significantly depending on vehicle flow rates, while they are almost unaffected by changes in speed values.
Juniardi & Efendi [9]	14 m wide Kartini street	Motorcycles	Vehicle travel time.	Four-lane one-way road	There is a difference between the PCE and the PCE value obtained from the Indonesian Highway Capacity Manual (MKJI) 1997.
Lu et al. [16]	Highway	Trucks	Headway model.	Two-lane two-way	The results show that traffic volumes on a two-lane highway in both directions have a significant impact on PCE values.
Zhou et al. [10]	I-80 Freeway	Truck compositions	VISSIM 9.0 simulation of traffic flows.	A freeway with two or three lanes per direction	PCE values in HCM-6 underestimate the values of truck impact on 4-lane freeway segments.
Li et al. [18]	Urban road	Buses, commercial vehicles, and passenger cars	The average time headway.	Two-lane urban secondary road	The capacity of the road with a central island is larger than that of the road with a double dotted line.
Ahlam & Al-zerjawi [11]	Rural and urban highway	Single-unit trucks and buses	Free-flow speeds.	Forty-two multilane rural and suburban highway segments	Based on the study results, the passenger car unit factor (PCU) for trucks and buses is 2.0.
R. Srinivasa Rao et al. [22]	All roads	All vehicles	Various.	All	There is a great need to consider all possible modalities for determining PCE values as a function of influencing factors that can be adopted worldwide.
Adnan [15]	Urban arterials	Cars/jeeps/vans/taxis motorcycles/scooters auto rickshaw, pickups, mini buses, large buses, trucks and trailers	Headway method.	12 different urban arterials of Karachi	Significant differences are found among the values of PCE factors from each method.
Yeung et al. [19]	Urban expressways	Motorcycles, PA, light goods vehicles and heavy goods vehicles	Multiple linear regression.	Two expressway locations in Singapore	Differential speed limits for commercial vehicles have resulted in differences in lane-wise traffic compositions.
Abhimanyu & Goliya [12]	Two-lane highways	Two wheelers, motorized, auto rickshaws, small/standard cars, big cars and vans, light commercial vehicles, two/three-axle trucks, multi-axle trucks, buses, tractors, tractor with trailers, cycles	By calculating the average speed of a vehicle type on the road with respect to a standard passenger vehicle.	Two-lane highways	It is found that the Chandra method is more accurate compared to the occupancy time method.
Sugiarto et al. [20]	Three pretimed signalized intersections	Motorcycle (MC), passenger car (PC), and motorized rickshaw (MR)	The extended car-following model	Signalized intersection	The calibration of PCEs was proposed by considering only vehicular compositions at pretimed signalized intersections.
Al-Obaedi [21]	Freeway segments	Heavy goods vehicles	Headway method	M25 and the M42 motorway	For the same location, the equivalency factors vary significantly based on traffic speed.

There is a large number of methods that can be applied to manage traffic flow efficiency. Many impedance-based methods have been developed to address this challenge. Using the impedance method, as well as a deep neural network, a new method for FL (fault location) is suggested, which can provide a unique answer [31]. Additionally, a type-3 fuzzy neural network is used to estimate the parameters of the backstepping control method and can be a useful tool for managing the efficiency of the traffic flow [32]. One potential solution is the application of the proportional–integral–derivative controller for managing traffic flows. The application of this method was used for adjusting the proportional–integral–derivative parameters through the model predictive control and generalized type-2 fuzzy-logic systems [33].

3. Methods

3.1. Basic Operations with TrIT2F Sets

Basic definitions and operations with TrIT2FS are shown below.

Definition 1 ([34,35]).

A TrIT2FS $\widetilde{\stackrel{~}{A}}$ derived from universal set X is as follows:

$$\tilde{A}( x )=[{\tilde{A}}^L( x ),{\tilde{A}}^U( x )]=((a_1^L,a_2^L,a_3^L,a_4^L;H_1({\tilde{A}}^L),H_2({\tilde{A}}^L)),(a_1^U,a_2^U,a_3^U,a_4^U;H_1({\tilde{A}}^U),H_2({\tilde{A}}^U))$$

where ${\tilde{A}}^L( x )$ and  ${\tilde{A}}^U( x )$ indicate the lower and the upper functions of $\widetilde{\stackrel{~}{A}}$, respectively,  ${a_1^L,a}_2^L,a_3^L,a_4^L,$ $a_1^U,a_2^U,a_3^U$ and  $a_4^U$ denote reference points, and  $H_1$ and  $H_2$ represent the membership degrees of the upper and lower functions of the TrIT2FS  $\widetilde{\stackrel{~}{A}}$. The characteristic functions of TrIT2FS also have the following properties:  $H_1({\tilde{A}}^L)\in \left[0,1\right],H_2({\tilde{A}}^L)\in \left[0,1\right],H_1({\tilde{A}}^U)\in \left[0,1\right]$ and  $H_2({\tilde{A}}^U)\in \left[0,1\right]$.

Definition 2 ([36]).

$${\tilde{A}}_1=[{\tilde{A}}_1^L,{\tilde{A}}_1^U]=((a_{11}^L,a_{12}^L,a_{13}^L,a_{14}^L;H_1({\tilde{A}}_1^L),H_2({\tilde{A}}_1^U)),(a_{11}^U,a_{12}^U,a_{13}^U,a_{14}^U;H_1({\tilde{A}}_1^U),H_2({\tilde{A}}_1^U))$$

and

$${\tilde{A}}_2=[{\tilde{A}}_2^L,{\tilde{A}}_2^U]=((a_{21}^L,a_{22}^L,a_{23}^L,a_{24}^L;H_1({\tilde{A}}_2^L),H_2({\tilde{A}}_2^U)),(a_{21}^U,a_{22}^U,a_{23}^U,a_{24}^U;H_1({\tilde{A}}_2^U),H_2({\tilde{A}}_2^U))$$

are two trapezoidal interval type-2 fuzzy numbers (TrIT2FN), and the fundamental mathematical operations of two TrIT2FNs,  ${\widetilde{\stackrel{~}{A}}}_1$ and  ${\widetilde{\stackrel{~}{A}}}_2$, are defined in Equations (1)–(7).

$$\begin{array}{l}{\tilde{A}}_1\oplus {\tilde{A}}_2=\left({\tilde{A}}_1^L,{\tilde{A}}_1^U\right)\oplus \left({\tilde{A}}_2^L,{\tilde{A}}_2^U\right)=(a_{11}^L+a_{21}^L,a_{12}^L+a_{22}^L,a_{13}^L+a_{23}^L,a_{14}^L+a_{24}^L;\min \left(H_1({\tilde{A}}_1^L),H_1({\tilde{A}}_2^U)\right),\\ \min \left(H_2({\tilde{A}}_1^L),H_2({\tilde{A}}_2^U)\right),(a_{11}^U+a_{21}^U,a_{12}^U+a_{22}^U,a_{13}^U+a_{23}^U,a_{14}^U+a_{24}^U;\min \left(H_1({\tilde{A}}_1^U),H_1({\tilde{A}}_2^U)\right),\min \left(H_2({\tilde{A}}_1^U),H_2({\tilde{A}}_2^U)\right)\end{array}$$

(1)

$${\widetilde{\stackrel{~}{A}}}_1\ominus {\widetilde{\stackrel{~}{A}}}_2=({\tilde{A}}_1^L,{\tilde{A}}_1^U)\ominus ({\tilde{A}}_2^L,{\tilde{A}}_2^U)=\left(\begin{array}{c}(a_{11}^L-a_{24}^L,a_{12}^L-a_{23}^L,a_{13}^L-a_{22}^L,a_{14}^L-a_{21}^L;\\ \min (H_1({\tilde{A}}_1^L),H_1({\tilde{A}}_2^L)),\min (H_2({\tilde{A}}_1^L),H_2({\tilde{A}}_2^L))\\ (a_{11}^U-a_{24}^U,a_{12}^U-a_{23}^U,a_{13}^U-a_{22}^U,a_{14}^U-a_{21}^U;\\ \min (H_1({\tilde{A}}_1^U),H_1({\tilde{A}}_2^U)),\min (H_2({\tilde{A}}_1^U),H_2({\tilde{A}}_2^U))\end{array}\right)$$

(2)

$${\widetilde{\stackrel{~}{A}}}_1\otimes {\widetilde{\stackrel{~}{A}}}_2=({\tilde{A}}_1^L,{\tilde{A}}_1^U)\otimes ({\tilde{A}}_2^L,{\tilde{A}}_2^U)=\left(\begin{array}{c}(a_{11}^L x a_{21}^L,a_{12}^L x a_{22}^L,a_{13}^L x a_{23}^L,a_{14}^L x a_{24}^L;\\ \min (H_1({\tilde{A}}_1^L),H_1({\tilde{A}}_2^L),\min (H_2({\tilde{A}}_1^L),H_2({\tilde{A}}_2^L))\\ (a_{11}^U x a_{21}^U,a_{12}^U x a_{22}^U,a_{13}^U x a_{23}^U,a_{14}^U x a_{24}^U;\\ \min (H_1({\tilde{A}}_1^U),H_1({\tilde{A}}_2^U),\min (H_2({\tilde{A}}_1^U),H_2({\tilde{A}}_2^U))\end{array}\right)$$

(3)

$${\widetilde{\stackrel{~}{A}}}_1\oslash {\widetilde{\stackrel{~}{A}}}_2=({\tilde{A}}_1^L,{\tilde{A}}_1^U)\oslash ({\tilde{A}}_2^L,{\tilde{A}}_2^U)=\left(\begin{array}{c}(a_{11}^L/a_{24}^L,a_{12}^L/a_{23}^L,a_{13}^L/a_{22}^L,a_{14}^L/a_{21}^L;\\ \min (H_1({\tilde{A}}_1^L),H_1({\tilde{A}}_2^L),\min (H_2({\tilde{A}}_1^L),H_2({\tilde{A}}_2^L),)\\ (a_{11}^U/a_{24}^U,a_{12}^U/a_{23}^U,a_{13}^U/a_{22}^U,a_{14}^U/a_{21}^U;\\ \min (H_1({\tilde{A}}_1^U),H_1({\tilde{A}}_2^U),\min (H_2({\tilde{A}}_1^U),H_2({\tilde{A}}_2^U))\end{array}\right)$$

(4)

$$\gamma {\widetilde{\stackrel{~}{A}}}_1=\gamma x ({\tilde{A}}_1^L,{\tilde{A}}_1^U)=\left(\begin{array}{c}(\gamma x a_{11}^L,\gamma x a_{12}^L,\gamma x a_{13}^L,\gamma x a_{14}^L;H_1({\tilde{A}}_1^L),H_2({\tilde{A}}_1^L)\\ (\gamma x a_{11}^U,\gamma x a_{12}^U,\gamma x a_{13}^U,\gamma x a_{14}^U;H_1({\tilde{A}}_1^U),H_2({\tilde{A}}_1^U)\end{array}\right),\gamma >0$$

(5)

$${({\widetilde{\stackrel{~}{A}}}_1)}^{\gamma }={({\tilde{A}}_1^L,{\tilde{A}}_1^U)}^{\gamma }=\left(\begin{array}{c}({{(a}_{11}^L)}^{\gamma },{{(a}_{12}^L)}^{\gamma },{{(a}_{13}^L)}^{\gamma },{{(a}_{14}^L)}^{\gamma };H_1({\tilde{A}}_1^L),H_2({\tilde{A}}_1^L)\\ ({{(a}_{11}^U)}^{\gamma },{{(a}_{12}^U)}^{\gamma },{{(a}_{13}^U)}^{\gamma },{{(a}_{14}^U)}^{\gamma };H_1({\tilde{A}}_1^U),H_2({\tilde{A}}_1^U)\end{array}\right)$$

(6)

Definition 3 ([37]).

Where $\widetilde{\stackrel{~}{A}}=[{\tilde{A}}^L(x),{\tilde{A}}^U(x)]((a_1^L,a_2^L,a_3^L,a_4^L;H_1({\tilde{A}}^L),H_2({\tilde{A}}^L))$,  ${{(a}_1^U,a}_2^U,a_3^U,a_4^U;H_1({\tilde{A}}^U),H_2({\tilde{A}}^U)))$ is a TrIT2FN, the defuzzified approach is as follows:

$$\begin{array}{c}D\mathrm{T}\mathrm{r}\mathrm{I}\mathrm{T}2\mathrm{F}\mathrm{N} (\widetilde{\stackrel{~}{A}}) \\ =(\begin{array}{c}\frac{\frac{(a_4^L-a_1^L)+(H_1({\tilde{A}}^L) x a_2^L-a_1^L)+(H_2({\tilde{A}}^L) x a_3^L-a_1^L)}{4}+a_1^L}{2}+\\ \frac{\frac{(a_4^U-a_1^U)+(H_1({\tilde{A}}^U) x a_2^U-a_1^U)+(H_2({\tilde{A}}^U) x a_3^U-a_1^U)}{4}+a_1^U}{2}\end{array})\end{array}$$

(7)

3.2. Preliminaries—Dombi Aggregator

The Dombi aggregator [38,39] is presented below (Equation (8)).

$$\begin{array}{l}\left({\wp }_j\right)=\frac{{\displaystyle {\sum }_{j=1}^n\left({\wp }_j\right)}}{1+\left({\displaystyle \sum _{j=1}^n{w}_j}\left(\frac{1-f\left({\wp }_j\right)}{f\left({\wp }_j\right)}\right)\right)}\\ f\left({\wp }_j\right)=\frac{{\wp }_j}{{\displaystyle \sum _{j=1}^n{\wp }_j}}\end{array}$$

(8)

w_j represents the weight of the decisionmaker or another component depending on what is being averaged.

3.3. Preliminaries—Bonferroni Aggregator

The Bonferroni aggregator [40,41,42] was used in this paper to average the number of traffic accidents (Equation (9)).

$${\alpha }_j={\left(\frac{1}{\epsilon (\epsilon -1)}{\displaystyle \sum _{\begin{array}{l}i,j=1\\ i\ne j\end{array}}^{\epsilon }{\alpha }_i^p\otimes {\alpha }_j^q}\right)}^{\frac{1}{p+q}}$$

(9)

where ε represents the number of years for traffic accidents, and p, q ≥ 0 are a set of non-negative numbers.

3.4. Trapezoidal Interval Type-2 Fuzzy PIPRECIA

In contrast to the fuzzy form with triangular numbers [43,44], in this developed version of the PIPRECIA method, there are certain differences that are manifested through the following.

Step 1. For the TrIT2F PIPRECIA method, it is necessary to sort criteria according to their expected importance, so the most important criterion is in the first place, and the last one is the least important.

Step 2. To determine the mutual importance of the criteria, it is necessary to use the scale in Table 2, which is different from to Fuzzy PIPRECIA, in which scales 0–1 and 1–2 are exclusively used, depending on the individual importance of criteria.

Table 2. Scale for determining the importance of criteria.

Linguistic Terms for Evaluating Criteria	TrIT2FNs
Extremely low importance (ELI)	(0, 0.1, 0.1, 0.2; 1, 1), (0, 0.1, 0.1, 0.15; 0.9, 0.9)
Very low importance (VLI)	(0.1, 0.2, 0.2, 0.3; 1, 1), (0.15, 0.2, 0.2, 0.25; 0.9, 0.9)
Low importance (LI)	(0.2, 0.3, 0.3, 0.4; 1, 1), (0.25, 0.3, 0.3, 0.35; 0.9, 0.9)
Medium low importance (MLI)	(0.3, 0.4, 0.4, 0.5; 1, 1), (0.35, 0.4, 0.4, 0.45; 0.9, 0.9)
Medium importance (MI)	(0.4, 0.5, 0.5, 0.6; 1, 1), (0.45, 0.5, 0.5, 0.55; 0.9, 0.9)
Medium high importance (MHI)	(0.5, 0.6, 0.6, 0.7; 1, 1), (0.55, 0.6, 0.6, 0.65; 0.9, 0.9)
High importance (HI)	(0.6, 0.7, 0.7, 0.8; 1, 1), (0.65, 0.7, 0.7, 0.75; 0.9, 0.9)
Very high importance (VHI)	(0.7, 0.8, 0.8, 0.9; 1, 1), (0.75, 0.8, 0.8, 0.85; 0.9, 0.9)
Extremely high importance (EHI)	(0.8, 0.9, 0.9, 1; 1, 1), (0.85, 0.90, 0.90, 1; 0.9, 0.9)

By assigning the linguistic labels in Table 2, a $\widetilde{{\tau }_j}$ matrix is obtained (Equation (10)).

$$\widetilde{{\tau }_j}=\left[\begin{array}{l}{\tau }_1\\ {\tau }_2\\ \cdots \\ {\tau }_n\end{array}\right]$$

(10)

in which ${\tau }_1$ indicates the most important criterion, and ${\tau }_n$ is the last criterion, which has the least importance. It is also important to note that ${\tau }_1$ has values $\left(1,1,1,1,1,1\right),\left(1,1,1,1,1,1\right)$.

Step 3. Determining the coefficient $\widetilde{{\varsigma }_j}$ (Equation (11)):

$$\widetilde{{\varsigma }_j}=\{\begin{array}{l}=\tilde{1}\hspace{1em}\hspace{1em}if\hspace{1em}j=1\\ 2-\widetilde{{\tau }_j}\hspace{1em}if\hspace{1em}j>1\end{array}\Rightarrow \widetilde{{\varsigma }_j}=\{\begin{array}{l}\left(1,1,1,1,1,1\right),\left(1,1,1,1,1,1\right)\\ 2-\widetilde{{\tau }_j}\end{array}$$

(11)

Step 4. Determining the fuzzy weight ${\tilde{\gamma }}_j$ (Equation (12)):

$$\widetilde{{\gamma }_j}=\{\begin{array}{l}=\tilde{1}\hspace{1em}\hspace{1em}if\hspace{1em}j=1\\ \frac{\widetilde{{\gamma }_{j-1}}}{\widetilde{{\varsigma }_j}}\hspace{1em}\hspace{0.17em}if\hspace{1em}j>1\end{array}\Rightarrow \widetilde{{\gamma }_j}=\{\begin{array}{l}\left(1,1,1,1,1,1\right),\left(1,1,1,1,1,1\right)\\ \frac{\widetilde{{\gamma }_{j-1}}}{\widetilde{{\varsigma }_j}}\end{array}$$

(12)

Step 5. Determining the relative weight of criterion $\widetilde{w_j}$ (Equation (13)):

$$\widetilde{w_j}=\frac{\widetilde{{\gamma }_j}}{{\displaystyle \sum _{j=1}^n\widetilde{{\gamma }_j}}}$$

(13)

In the following section, the inverse steps of the TrIT2F PIPRECIA method are presented.

Step 6. It is necessary to form a $\widetilde{{\tau }_j}\prime$ matrix (Equation (14)) in which the criteria are inversely arranged.

$$\widetilde{{\tau }_j}\prime =\left[\begin{array}{l}{\tau }_1\prime \\ {\tau }_2\prime \\ \cdots \\ {\tau }_n\prime \end{array}\right]$$

(14)

in which ${\tau }_1\prime$ denotes the least important criterion, and ${\tau }_n\prime$ is the last criterion, which is the most important. It is also significant to note that ${\tau }_n\prime$ has values $\left(1,1,1,1,1,1\right),\left(1,1,1,1,1,1\right)$.

Step 7. Determining the coefficient $\widetilde{{\varsigma }_j}\prime$ (Equation (15)):

$$\widetilde{{\varsigma }_j}\prime =\{\begin{array}{l}=\tilde{1}\hspace{1em}\hspace{1em}if\hspace{1em}j=n\\ 2-\widetilde{{\tau }_j}\prime \hspace{1em}if\hspace{1em}j>n\end{array}\Rightarrow \widetilde{{\varsigma }_j}=\{\begin{array}{l}\left(1,1,1,1,1,1\right),\left(1,1,1,1,1,1\right)\\ 2-\widetilde{{\tau }_j}\prime \end{array}$$

(15)

Step 8. Determining the fuzzy weight $\widetilde{{\gamma }_j}\prime$ (Equation (16)):

$$\widetilde{{\gamma }_j}\prime =\{\begin{array}{l}=\tilde{1}\hspace{1em}\hspace{1em}if\hspace{1em}j=n\\ \frac{\widetilde{{\gamma }_{j\prime -1}}}{\widetilde{{\varsigma }_j}\prime }\hspace{1em}\hspace{0.17em}if\hspace{1em}j>n\end{array}\Rightarrow \widetilde{{\gamma }_j}=\{\begin{array}{l}\left(1,1,1,1,1,1\right),\left(1,1,1,1,1,1\right)\\ \frac{\widetilde{{\gamma }_{j\prime -1}}}{\widetilde{{\varsigma }_j}\prime }\end{array}$$

(16)

Step 9. Determining the relative weight of the criterion $\widetilde{w_j}\prime$ (Equation (17)):

$$\widetilde{w_j}\prime =\frac{\widetilde{{\gamma }_j}\prime }{{\displaystyle \sum _{j=1}^n\widetilde{{\gamma }_j}}\prime }$$

(17)

Step 10. In order to obtain the final TrIT2F PIPRECIA weights, it is necessary to determine the arithmetic mean of $\widetilde{w_j}$ and $\widetilde{w_j}\prime$. Additionally, it is necessary to calculate the Spearman and Pearson correlation coefficients in order to determine correlations of ranks and weights between TrIT2F PIPRECIA and the inverse TrIT2F PIPRECIA method.

3.5. Trapezoidal Interval Type-2 Fuzzy MARCOS

The fuzzy MARCOS approach [45] has quickly become very popular and is perhaps one of the most frequently applied method in its different forms in various fields of research [46,47].

Step 1. Creation of initial TrIT2F matrix (Equation (18)) based on the evaluation of decision makers according to the linguistic estimates shown in Table 3.

$$\widetilde{{\beta }_{ij}}=\left[\begin{array}{cccc}{\tilde{\beta }}_{11}& {\tilde{\beta }}_{12}& ⋮& {\tilde{\beta }}_{1n}\\ {\tilde{\beta }}_{21}& {\tilde{\beta }}_{22}& ⋮& {\tilde{\beta }}_{2n}\\ \cdots & \cdots & \cdots & \cdots \\ {\tilde{\beta }}_{m1}& {\tilde{\beta }}_{m2}& ⋮& {\tilde{\beta }}_{mn}\end{array}\right]$$

(18)

Table 3. TrIT2FNs for evaluating alternatives.

Linguistic Terms for Evaluating Alternatives	TrIT2FNs
Extremely low (EL)	(0, 0, 0, 0.1; 1, 1), (0, 0, 0, 0.05; 0.9, 0.9)
Very low (VL)	(0, 0.1, 0.1, 0.3; 1, 1), (0.05, 0.1, 0.1, 0.2; 0.9, 0.9)
Low (L)	(0.1, 0.3, 0.3, 0.5; 1, 1), (0.2, 0.3, 0.3, 0.4; 0.9, 0.9)
Medium (M)	(0.3, 0.5, 0.5, 0.7; 1, 1), (0.4, 0.5, 0.5, 0.6; 0.9, 0.9)
High (H)	(0.5, 0.7, 0.7, 0.9; 1, 1), (0.6, 0.7, 0.7, 0.8; 0.9, 0.9)
Very high (VH)	(0.7, 0.9, 0.9, 1; 1, 1), (0.8, 0.9, 0.9, 0.95; 0.9, 0.9)
Extremely high (EH)	(0.9, 1, 1, 1; 1, 1), (0.95, 1, 1, 1; 0.9, 0.9)

Step 2. Defining an anti-ideal solution A(AI) (Equation (19)):

$$\tilde{A}\left(AI\right)=\underset{i}{\overset{}{\min }}{\tilde{\beta }}_{ij}\hspace{1em}if\hspace{0.17em}j\in \hspace{0.17em}B\hspace{1em}and\hspace{1em}\underset{i}{\max }{\tilde{\beta }}_{ij}\hspace{1em}if\hspace{0.17em}j\in C$$

(19)

and an ideal solution A(ID) (Equation (20)):

$$\tilde{A}\left(ID\right)=\underset{i}{\overset{}{\max }}{\tilde{\beta }}_{ij}\hspace{1em}if\hspace{0.17em}j\in \hspace{0.17em}B\hspace{1em}and\hspace{1em}\underset{i}{\min }{\tilde{\beta }}_{ij}\hspace{1em}if\hspace{0.17em}j\in C$$

(20)

Step 3. Performing the normalization of the previous TrIT2FNs matrix using Equations (21) and (22):

$$\begin{array}{l}{\tilde{n}}_{ij}=\left(n_{ij}^{l1},n_{ij}^{l2},n_{ij}^{l3},n_{ij}^{l4},n_{ij}^{\delta },n_{ij}^{\delta }\right),\left(n_{ij}^{u1},n_{ij}^{u2},n_{ij}^{u3},n_{ij}^{u4},n_{ij}^{\rho },n_{ij}^{\rho }\right)\\ =\left(\frac{{\beta }_{id}^{l1}}{{\beta }_{ij}^{l4}},\frac{{\beta }_{id}^{l2}}{{\beta }_{ij}^{l3}},\frac{{\beta }_{id}^{l3}}{{\beta }_{ij}^{l2}},\frac{{\beta }_{id}^{l4}}{{\beta }_{ij}^{l1}},n_{ij}^{\delta },n_{ij}^{\delta }\right),\left(\frac{{\beta }_{id}^{u1}}{{\beta }_{ij}^{u4}},\frac{{\beta }_{id}^{u2}}{{\beta }_{ij}^{u3}},\frac{{\beta }_{id}^{u3}}{{\beta }_{ij}^{u2}},\frac{{\beta }_{id}^{u4}}{{\beta }_{ij}^{u1}},n_{ij}^{\rho },n_{ij}^{\rho }\right)\hspace{1em}if\hspace{0.17em}j\in \hspace{0.17em}C\end{array}$$

(21)

$$\begin{array}{l}{\tilde{n}}_{ij}=\left(n_{ij}^{l1},n_{ij}^{l2},n_{ij}^{l3},n_{ij}^{l4},n_{ij}^{\delta },n_{ij}^{\delta }\right),\left(n_{ij}^{u1},n_{ij}^{u2},n_{ij}^{u3},n_{ij}^{u4},n_{ij}^{\rho },n_{ij}^{\rho }\right)\\ =\left(\frac{{\beta }_{ij}^{l1}}{{\beta }_{id}^{l4}},\frac{{\beta }_{ij}^{l2}}{{\beta }_{id}^{l3}},\frac{{\beta }_{ij}^{l3}}{{\beta }_{id}^{l2}},\frac{{\beta }_{ij}^{l4}}{{\beta }_{id}^{l1}},n_{ij}^{\delta },n_{ij}^{\delta }\right),\left(\frac{{\beta }_{ij}^{u1}}{{\beta }_{id}^{u4}},\frac{{\beta }_{ij}^{u2}}{{\beta }_{id}^{u3}},\frac{{\beta }_{ij}^{u3}}{{\beta }_{id}^{u2}},\frac{{\beta }_{ij}^{u4}}{{\beta }_{id}^{u1}},n_{ij}^{\rho },n_{ij}^{\rho }\right)\hspace{1em}if\hspace{0.17em}j\in \hspace{0.17em}B\end{array}$$

(22)

Step 4. Weighting the previous TrIT2FNs matrix (Equation (23)).

$$\begin{array}{l}{\tilde{v}}_{ij}=\left(v_{ij}^{l1},v_{ij}^{l2},v_{ij}^{l3},v_{ij}^{l4},v_{ij}^{\delta },v_{ij}^{\delta }\right),\left(v_{ij}^{u1},v_{ij}^{u2},v_{ij}^{u3},v_{ij}^{u4},v_{ij}^{\rho },v_{ij}^{\rho }\right)=\\ {\tilde{n}}_{ij}\otimes {\tilde{w}}_j=\left(n_{ij}^{l1}\times w_j^{l1},n_{ij}^{l2}\times w_j^{l2},n_{ij}^{l3}\times w_j^{l3},n_{ij}^{l4}\times w_j^{l4}\right),\left(n_{ij}^{u1}\times w_j^{u1},n_{ij}^{u2}\times w_j^{u2},n_{ij}^{u3}\times w_j^{u3},n_{ij}^{u4}\times w_j^{u4}\right)\end{array}$$

(23)

Step 5. Calculation of the S_i matrix (Equation (24)):

$${\tilde{S}}_i={\displaystyle \sum _{i=1}^n{\tilde{v}}_{ij}}$$

(24)

and defuzzification of these values using, for example, a centroid method.

Step 6. Calculation of the degree of usefulness K_i using Equations (25) and (26).

$$K_i{}^{-}=\frac{S_i}{S_{aai}}$$

(25)

$$K_i{}^{+}=\frac{S_i}{S_{id}}$$

(26)

Step 7. Determining the utility function $f(Ki)$.

Utility function according to the anti-ideal solution (Equation (27)):

$$f\left(K_i^{+}\right)=\frac{K_i^{-}}{K_i^{-}+K_i^{+}}$$

(27)

Utility function according to the ideal solution (Equation (28)):

$$f\left(K_i^{-}\right)=\frac{K_i^{+}}{K_i^{-}+K_i^{+}}$$

(28)

Step 8. Calculation of the final utility function (Equation (29)):

$$f\left(K_i\right)=\frac{K_i^{+}+K_i^{-}}{1+\frac{1-f\left(K_i^{+}\right)}{f\left(K_i^{+}\right)}+\frac{1-f\left(K_i^{-}\right)}{f\left(K_i^{-}\right)}};$$

(29)

Step 9. Ranking alternatives.

4. Problem Description and Model Formation

This section of the paper describes the problem and formation of the model for evaluating the traffic flow efficiency on the observed road sections. Parameters and collected data for light goods vehicles were taken into account. A total of six sections of two-lane roads have been considered and used to select measuring segments at 14 locations with different longitudinal gradients from −5.52% to +7.45%, which represent alternatives in the multi-criteria model. All 14 alternatives were selected on the measuring sections of first-order main roads in Bosnia and Herzegovina. The 14 alternatives are part of the four selected routes on the main road network (M-I-103, M-I-105, M-I-106, M-I-108), as shown in Table 4.

Table 4. Choice of an alternative as a function of selecting a longitudinal gradient (rise/fall).

Alternative	Measuring Segments	Category and the Number of the Road	Longitudinal Gradient (%)
A1	Ivanjska–Šargovac	M-I-108	−5.52
A2	Vrhovi–Šešlije	M-I-103	−5.00
A3	Ivanjska–Šargovac	M-I-108	−2.98
A4	Ivanjska–Šargovac	M-I-108	−2.00
A5	Vrhovi–Šešlije	M-I-103	−1.00
A6	Rudanka–Doboj	M-I-105	±0.00
A7	Klašnice–Prnjavor	M-I-106	+1.00
A8	Klupe–Teslić	M-I-108	+2.07
A9	Klašnice–Prnjavor	M-I-106	+3.20
A10	Klašnice–Prnjavor	M-I-106	+4.00
A11	Vrhovi–Šešlije	M-I-103	+5.00
A12	Obodnik–Klupe	M-I-108	+6.03
A13	Obodnik–Klupe	M-I-108	+6.84
A14	Obodnik–Klupe	M-I-108	+7.45

Previously selected road segments used to assess the efficiency of traffic flow were evaluated on the basis of seven different criteria. C1-road gradient, C2-PCE85%, C3-AADT, C4-TA with fatalities, C5-TA with serious injuries, C6-TA with minor injuries, and C7-TA with material damage.

The values of the first criterion for all road segments are: −5.52, −5.00, −2.98, −2.00, −1.00, 0.00, 1.00, 2.0, 3.20, 4.00, 5.00, 6.03, 6.84, 7.45%. The equivalent values of the second criterion are as follows: 3.818, 3.818, 5.939, 5.091, 2.970, 7.636, 7.636, 6.788, 6.788, 9.333, 12.727, 12.727, 12.727, 12.727. Criteria C3–C7 need to be processed in terms of obtaining one parameter for each criterion, given that the data were collected for several years. So, AADT and different types of TA are considered.

By analyzing criterion C3, it can be seen that the conditions of vehicle movement in the traffic flow on most of the six road sections with the observed 14 measuring segments are defined by the conditions of free or normal traffic flow.

By analyzing the AADT of the given measuring segments, the AADT values per year continuously increase, but not more than 3% annually. A special eccentric value of AADT is on the Rudanka–Doboj section (A6), which is over 10,000 [veh/day]. For alternatives (measuring segments) A2, A5, A11 of the Vrhovi–Šešlije section and A12, A13, A14 of the Obodnik–Klupe section, the value of AADT does not exceed 5000 [veh/day] in the period from 2013 to 2017. These two sections have free traffic flow conditions, which are shown in Figure 1.

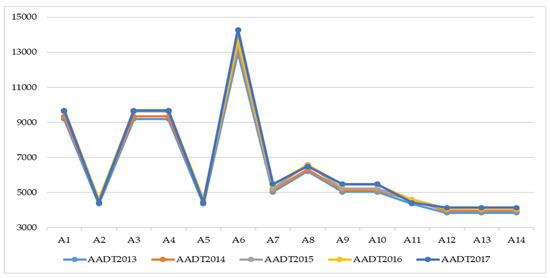
Figure 1. AADT in the period 2013–2017.

The final values of AADT, which is an integral part of the initial decision matrix, were obtained using the Dombi operator:

$$\begin{array}{l}\left({\wp }_1\right)=\frac{{\displaystyle {\sum }_{j=1}^n\left({\wp }_j\right)}}{1+\left({\displaystyle \sum _{j=1}^n{w}_j}\left(\frac{1-f\left({\wp }_j\right)}{f\left({\wp }_j\right)}\right)\right)}=\frac{47526}{1+\left(\frac{1}{5}\left(\frac{1-0.194}{0.194}\right)+\frac{1}{5}\left(\frac{1-0.197}{0.197}\right)+\frac{1}{5}\left(\frac{1-0.202}{0.202}\right)+\frac{1}{5}\left(\frac{1-0.204}{0.204}\right)+\frac{1}{5}\left(\frac{1-0.203}{0.203}\right)\right)}=9501\\ f\left({\wp }_1\right)=\frac{{\wp }_1}{{\displaystyle \sum _{j=1}^n{\wp }_j}}=\frac{9199}{9199+\hspace{0.17em}9342+\hspace{0.17em}9618+9699+\hspace{0.17em}9668}=\frac{9199}{47526}=0.194\end{array}$$

One of the criteria analyzed in Figure 2 in the period from 2016 to 2019 was the number of traffic accidents (with fatalities, minor and serious physical injuries, and material damage). The criterion has been taken from the database on traffic accidents, and it refers to all 14 selected alternatives (measuring road segments). Most accidents occur with material damage, and deviations by years were observed in the number of accidents with material damage in 2017 and the number of accidents with minor injuries in 2019. The highest number of fatalities in traffic accidents for the given alternatives was recorded in 2016 (29 fatalities), and the highest number of accidents with material damage on the given alternatives was recorded in 2017 (615 accidents). Individually, in 2019, the largest number of fatalities (four fatalities) occurred on the Ivanjska–Šargovac section (A1, A2, and A3).

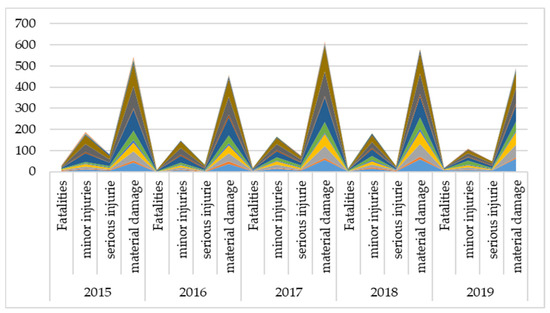
Figure 2. The number of traffic accidents in a five-year period.

An example of averaging these values is given below.

$$\begin{array}{l}B{M}^{p=1,q=1}=\left(3,0,1,1,4\right)={\varpi }_{Y_{1(1)}}^{}={\left(\frac{1}{5(5-1)}{\displaystyle \sum _{\begin{array}{l}i,j=1\\ i\ne j\end{array}}^5{\varpi }_{Y_{1(1)}i}^{}{\varpi }_{Y_{1(1)}j}^{}}\right)}^{\frac{1}{1+1}}=\\ {\left(0.050\left(3^1\cdot 0^1+3^1\cdot 1^1+3^1\cdot 1^1+3^1\cdot 4^1+0^1\cdot 3^1+0^1\cdot 1^1+0^1\cdot 1^1+0^1\cdot 4^1+\mathrm{\dots }+4^1\cdot 3^1+4^1\cdot 0^1+4^1\cdot 1^1+4^1\cdot 4^1\right)\right)}^{\frac{1}{1+1}}=1.643\end{array}$$

After collecting data, defining all elements of the MCDM model, and averaging a larger set of parameters for C3–C7, a quantitative decision matrix, shown in Table 5, was formed.

Table 5. Quantitative data for forming the decision matrix.

	Gradient (%)	PCE 85%	AADT	TA FAT.	TA SI	TA MI	TA MD
A1	−5.52	3.818	9501.006	1.643	3.082	11.743	51.181
A2	−5.00	3.818	4500.113	0.632	2.490	3.701	9.701
A3	−2.98	5.939	9501.006	1.643	3.082	11.743	51.181
A4	−2.00	5.091	9501.006	1.643	3.082	11.743	51.181
A5	−1.00	2.970	4500.113	0.632	2.490	3.701	9.701
A6	0.00	7.636	13,585.38	1.183	4.207	13.616	45.898
A7	1.00	7.636	5262.903	2.588	9.343	29.345	95.112
A8	2.07	6.788	6435.535	0.000	1.975	4.764	9.322
A9	3.20	6.788	5262.903	2.588	9.343	29.345	95.112
A10	4.00	9.333	5262.903	2.588	9.343	29.345	95.112
A11	5.00	12.727	4500.113	0.632	2.490	3.701	9.701
A12	6.03	12.727	4020.851	0.316	0.548	1.225	4.483
A13	6.84	12.727	4020.851	0.316	0.548	1.225	4.483
A14	7.45	12.727	4020.851	0.316	0.548	1.225	4.483

When it comes to the first criterion, the limit value refers to zero, that is, a horizontal ground or as little gradient as possible is desirable, so that road segments were evaluated according to this criterion. When it comes to the other criteria, estimates are modeled according to the desired minimum values, except for the AADT criterion, where higher values are desired.

Then, it is necessary to evaluate the alternatives using the linguistic scale shown in Table 3. By applying the consensus in which three decisionmakers participated, the estimates in Figure 3 were given. It is important to note that when evaluating the alternatives, the preferences of the criteria were considered, and within the TrIT2F MARCOS initial matrix, the criteria were modeled as beneficial.

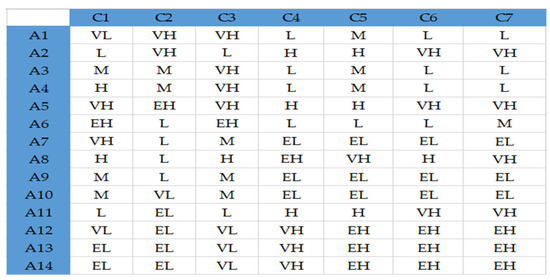
Figure 3. Evaluation of road segments using the linguistic scale for the TrIT2F MARCOS method.

5. Results and Analysis

In this section of the paper, the results are presented with reference to individual details of the calculation. First, the matrix is formed:

$$\widetilde{{\tau }_j}=\begin{array}{c}{C}_2\\ C_3\\ C_4\\ C_5\\ C_6\\ C_1\\ C_7\end{array}\left[\begin{array}{c}\left(1,1,1,1,1,1\right),\left(1,1,1,1,1,1\right)\\ \left(0.8,0.9,0.9,1,1,1\right),\left(0.85,0.9,0.9,1,0.9,0.9\right)\\ \left(0.8,0.9,0.9,1,1,1\right),\left(0.85,0.9,0.9,1,0.9,0.9\right)\\ \left(0.7,0.8,0.8,0.9,1,1\right),\left(0.75,0.8,0.8,0.85,0.9,0.9\right)\\ \left(0.6,0.7,0.7,0.8,1,1\right),\left(0.65,0.7,0.7,0.75,0.9,0.9\right)\\ \left(0.5,0.6,0.6,0.7,1,1\right),\left(0.55,0.6,0.6,0.65,0.9,0.9\right)\\ \left(0.4,0.5,0.5,0.6,1,1\right),\left(0.45,0.5,0.5,0.55,0.9,0.9\right)\end{array}\right]$$

Then, matrix $\widetilde{{\varsigma }_j}$

$$\widetilde{{\varsigma }_j}=\left[\begin{array}{c}\left(1,1,1,1,1,1\right),\left(1,1,1,1,1,1\right)\\ \left(1,1.1,1.1,1.2,1,1\right),\left(1,1.1,1.1,1.15,0.9,0.9\right)\\ \left(1,1.1,1.1,1.2,1,1\right),\left(1,1.1,1.1,1.15,0.9,0.9\right)\\ \left(1.1,\mathrm{1.2.1.2},1.3,1,1\right),\left(1.15,\mathrm{1.2.1.2},1.25,0.9,0.9\right)\\ \left(1.2,1.3,1.3,1.4,1,1\right),\left(1.25,1.3,1.3,1.35,0.9,0.9\right)\\ \left(1.3,1.4,1.4,1.5,1,1\right),\left(1.35,1.4,1.4,1.45,0.9,0.9\right)\\ \left(1.4,1.5,1.5,1.6,1,1\right),\left(1.45,1.5,1.5,1.55,0.9,0.9\right)\end{array}\right]$$

(30)

is obtained as follows

$$\widetilde{{\varsigma }_3}=\left(2-1,2-0.9,2-0.9,2-0.8,1,1\right)$$

After that, the matrix $\widetilde{{\gamma }_j}$ is computed

$$\widetilde{{\gamma }_j}=\left[\begin{array}{c}\left(1,1,1,1,1,1\right),\left(1,1,1,1,1,1\right)\\ \left(0.833,0.909,0.909,1,1,1\right),\left(0.87,0.909,0.909,1,0.9,0.9\right)\\ \left(0.694,0.826,0.826,1,1,1\right),\left(0.756,0.826,0.826,1,0.9,0.9\right)\\ \left(0.534,0.689,0.689,0.909,1,1\right),\left(0.605,0.689,0.689,0.87,0.9,0.9\right)\\ \left(0.382,0.530,0.530,0.758,1,1\right),\left(0.448,0.530,0.530,0.696,0.9,0.9\right)\\ \left(0.254,0.378,0.378,0.583,1,1\right),\left(0.309,0.378,0.378,0.515,0.9,0.9\right)\\ \left(0.159,0.252,0.252,0.416,1,1\right),\left(0.199,0.252,0.252,0.355,0.9,0.9\right)\end{array}\right]$$

in the following way:

$$\begin{array}{l}{\tilde{\gamma }}_3=\left(\frac{1}{1.2},\frac{1}{1.1},\frac{1}{1.1},\frac{1}{1},1,1\right),\left(\frac{1}{1.15},\frac{1}{1.1},\frac{1}{1.1},\frac{1}{1},0.9,0.9\right)\\ {\tilde{\gamma }}_4=\left(\frac{0.833}{1.2},\frac{0.826}{1.1},\frac{0.826}{1.1},\frac{1}{1},1,1\right),\left(\frac{0.87}{1.15},\frac{0.909}{1.1},\frac{0.909}{1.1},\frac{1}{1},0.9,0.9\right)\end{array}$$

The weights of criteria $\widetilde{w_j}$ are obtained by applying Equation (12), and they are as follows:

$$\begin{array}{l}{\tilde{w}}_2=\left(0.177,0.218,0.218,0.259,1,1\right),\left(0.184,0.218,0.218,0.239,0.9,0.9\right)\\ {\tilde{w}}_3=\left(0.147,0.198,0.198,0.259,1,1\right),\left(0.160,0.198,0.198,0.239,0.9,0.9\right)\\ {\tilde{w}}_4=\left(0.123,0.180,0.180,0.259,1,1\right),\left(0.139,0.180,0.180,0.239,0.9,0.9\right)\\ {\tilde{w}}_5=\left(0.094,0.150,0.150,0.236,1,1\right),\left(0.111,0.150,0.150,0.208,0.9,0.9\right)\\ {\tilde{w}}_6=\left(0.067,0.116,0.116,0.196,1,1\right),\left(0.082,0.116,0.116,0.166,0.9,0.9\right)\\ {\tilde{w}}_1=\left(0.045,0.083,0.083,0.151,1,1\right),\left(0.057,0.083,0.083,0.123,0.9,0.9\right)\\ {\tilde{w}}_7=\left(0.028,0.055,0.055,0.108,1,1\right),\left(0.037,0.055,0.055,0.085,0.9,0.9\right)\end{array}$$

By applying the inverse TrIT2F PIPRECIA step, the following values are obtained:

$$\begin{array}{l}{\tilde{w}}_2=\left(0.252,0.299,0.299,0.321,1,1\right),\left(0.272,0.299,0.299,0.321,0.9,0.9\right)\\ {\tilde{w}}_3=\left(0.176,0.199,0.199,0.222,1,1\right),\left(0.176,0.199,0.199,0.222,0.9,0.9\right)\\ {\tilde{w}}_4=\left(0.121,0.142,0.142,0.164,1,1\right),\left(0.121,0.142,0.142,0.164,0.9,0.9\right)\\ {\tilde{w}}_5=\left(0.090,0.110,0.110,0.131,1,1\right),\left(0.090,0.110,0.110,0.131,0.9,0.9\right)\\ {\tilde{w}}_6=\left(0.072,0.091,0.091,0.114,1,1\right),\left(0.072,0.091,0.091,0.114,0.9,0.9\right)\\ {\tilde{w}}_1=\left(0.062,0.083,0.083,0.114,1,1\right),\left(0.062,0.083,0.083,0.114,0.9,0.9\right)\\ {\tilde{w}}_7=\left(0.054,0.075,0.075,0.114,1,1\right),\left(0.054,0.075,0.075,0.114,0.9,0.9\right)\end{array}$$

After that, the final values are obtained using the TrIT2F PIPRECIA method, and they are shown in Table 6.

Table 6. Results of criteria importance obtained by applying the TrIT2F PIPRECIA method.

Criterion	Weights
C1	(0.046, 0.083, 0.083, 0.147, 1, 1)	(0.06, 0.083, 0.083, 0.119, 0.9, 0.9)
C2	(0.214, 0.259, 0.259, 0.301, 1, 1)	(0.228, 0.259, 0.259, 0.28, 0.9, 0.9)
C3	(0.152, 0.199, 0.199, 0.252, 1, 1)	(0.168, 0.199, 0.199, 0.23, 0.9, 0.9)
C4	(0.114, 0.161, 0.161, 0.224, 1, 1)	(0.13, 0.161, 0.161, 0.201, 0.9, 0.9)
C5	(0.085, 0.13, 0.13, 0.196, 1, 1)	(0.1, 0.13, 0.13, 0.17, 0.9, 0.9)
C6	(0.063, 0.103, 0.103, 0.17, 1, 1)	(0.077, 0.103, 0.103, 0.14, 0.9, 0.9)
C7	(0.034, 0.065, 0.065, 0.125, 1, 1)	(0.045, 0.065, 0.065, 0.1, 0.9, 0.9)

The most important criterion is PCE 85%, followed by AADT, and three types of traffic accidents (with fatalities and serious and minor injuries), while the two criteria that are least important are gradient and traffic accidents with material damage. After the first phase of the model in which the TrIT2F criterion weights were calculated, the evaluation of alternatives was started. First, the linguistic values shown in Figure 3 were transformed into TrIT2FNs to obtain the initial matrix shown in Table 7.

Table 7. The initial decision matrix after the transformation of linguistic values into numerical values.

	C1		…	C7
AAI	(0, 0, 0, 0, 1, 1)	(0, 0, 0, 0.05, 0.9, 0.9)	⁝	(0, 0, 0, 0, 1, 1)	(0, 0, 0, 0.05, 0.9, 0.9)
A1	(0, 0.1, 0.1, 0.3, 1, 1)	(0.05, 0.1, 0.1, 0.2, 0.9, 0.9)		(0.1, 0.3, 0.3, 0.5, 1, 1)	(0.2, 0.3, 0.3, 0.4, 0.9, 0.9)
A2	(0.1, 0.3, 0.3, 0.5, 1, 1)	(0.2, 0.3, 0.3, 0.4, 0.9, 0.9)		(0.7, 0.9, 0.9, 1, 1, 1)	(0.8, 0.9, 0.9, 0.95, 0.9, 0.9)
A3	(0.3, 0.5, 0.5, 0.7, 1, 1)	(0.4, 0.5, 0.5, 0.6, 0.9, 0.9)		(0.1, 0.3, 0.3, 0.5, 1, 1)	(0.2, 0.3, 0.3, 0.4, 0.9, 0.9)
A4	(0.5, 0.7, 0.7, 0.9, 1, 1)	(0.6, 0.7, 0.7, 0.8, 0.9, 0.9)		(0.1, 0.3, 0.3, 0.5, 1, 1)	(0.2, 0.3, 0.3, 0.4, 0.9, 0.9)
A5	(0.7, 0.9, 0.9, 1, 1, 1)	(0.8, 0.9, 0.9, 0.95, 0.9, 0.9)		(0.7, 0.9, 0.9, 1, 1, 1)	(0.8, 0.9, 0.9, 0.95, 0.9, 0.9)
A6	(0.9, 1, 1, 1, 1, 1)	(0.95, 1, 1, 1, 0.9, 0.9)		(0.3, 0.5, 0.5, 0.7, 1, 1)	(0.4, 0.5, 0.5, 0.6, 0.9, 0.9)
A7	(0.7, 0.9, 0.9, 1, 1, 1)	(0.8, 0.9, 0.9, 0.95, 0.9, 0.9)		(0, 0, 0, 0, 1, 1)	(0, 0, 0, 0.05, 0.9, 0.9)
A8	(0.5, 0.7, 0.7, 0.9, 1, 1)	(0.6, 0.7, 0.7, 0.8, 0.9, 0.9)		(0.7, 0.9, 0.9, 1, 1, 1)	(0.8, 0.9, 0.9, 0.95, 0.9, 0.9)
A9	(0.3, 0.5, 0.5, 0.7, 1, 1)	(0.4, 0.5, 0.5, 0.6, 0.9, 0.9)		(0, 0, 0, 0, 1, 1)	(0, 0, 0, 0.05, 0.9, 0.9)
A10	(0.3, 0.5, 0.5, 0.7, 1, 1)	(0.4, 0.5, 0.5, 0.6, 0.9, 0.9)		(0, 0, 0, 0, 1, 1)	(0, 0, 0, 0.05, 0.9, 0.9)
A11	(0.1, 0.3, 0.3, 0.5, 1, 1)	(0.2, 0.3, 0.3, 0.4, 0.9, 0.9)		(0.7, 0.9, 0.9, 1, 1, 1)	(0.8, 0.9, 0.9, 0.95, 0.9, 0.9)
A12	(0, 0.1, 0.1, 0.3, 1, 1)	(0.05, 0.1, 0.1, 0.2, 0.9, 0.9)		(0.9, 1, 1, 1, 1, 1)	(0.95, 1, 1, 1, 0.9, 0.9)
A13	(0, 0, 0, 0, 1, 1)	(0, 0, 0, 0.05, 0.9, 0.9)		(0.9, 1, 1, 1, 1, 1)	(0.95, 1, 1, 1, 0.9, 0.9)
A14	(0, 0, 0, 0, 1, 1)	(0, 0, 0, 0.05, 0.9, 0.9)		(0.9, 1, 1, 1, 1, 1)	(0.95, 1, 1, 1, 0.9, 0.9)
AI	(0.9, 1, 1, 1, 1, 1)	(0.95, 1, 1, 1, 0.9, 0.9)		(0.9, 1, 1, 1, 1, 1)	(0.95, 1, 1, 1, 0.9, 0.9)

The normalized TrIT2F MARCOS matrix shown in Table 8 is obtained as follows:

$${\tilde{n}}_{11}=\left(0,0.1,0.1,0.333,1,1\right),\left(0.05,0.1,0.1,0.211,0.9,0.9\right)=\left(\frac{0}{1},\frac{0.1}{1},\frac{0.1}{1},\frac{0.3}{0.9},1,1\right),\left(\frac{0.05}{1},\frac{0.1}{1},\frac{0.1}{1},\frac{0.2}{0.95},0.9,0.9\right)$$

Table 8. Normalized TrIT2F MARCOS matrix.

	C1		…	C7
AAI	(0, 0, 0, 0, 1, 1)	(0, 0, 0, 0.053, 0.9, 0.9)	⁝	(0, 0, 0, 0, 1, 1)	(0, 0, 0, 0.05, 0.9, 0.9)
A1	(0, 0.1, 0.1, 0.333, 1, 1)	(0.05, 0.1, 0.1, 0.211, 0.9, 0.9)		(0.1, 0.3, 0.3, 0.556, 1, 1)	(0.2, 0.3, 0.3, 0.4, 0.9, 0.9)
A2	(0.1, 0.3, 0.3, 0.556, 1, 1)	(0.2, 0.3, 0.3, 0.421, 0.9, 0.9)		(0.7, 0.9, 0.9, 1.111, 1, 1)	(0.8, 0.9, 0.9, 0.95, 0.9, 0.9)
A3	(0.3, 0.5, 0.5, 0.778, 1, 1)	(0.4, 0.5, 0.5, 0.632, 0.9, 0.9)		(0.1, 0.3, 0.3, 0.556, 1, 1)	(0.2, 0.3, 0.3, 0.4, 0.9, 0.9)
A4	(0.5, 0.7, 0.7, 1, 1, 1)	(0.6, 0.7, 0.7, 0.842, 0.9, 0.9)		(0.1, 0.3, 0.3, 0.556, 1, 1)	(0.2, 0.3, 0.3, 0.4, 0.9, 0.9)
A5	(0.7, 0.9, 0.9, 1.111, 1, 1)	(0.8, 0.9, 0.9, 1, 0.9, 0.9)		(0.7, 0.9, 0.9, 1.111, 1, 1)	(0.8, 0.9, 0.9, 0.95, 0.9, 0.9)
A6	(0.9, 1, 1, 1.111, 1, 1)	(0.95, 1, 1, 1.053, 0.9, 0.9)		(0.3, 0.5, 0.5, 0.778, 1, 1)	(0.4, 0.5, 0.5, 0.6, 0.9, 0.9)
A7	(0.7, 0.9, 0.9, 1.111, 1, 1)	(0.8, 0.9, 0.9, 1, 0.9, 0.9)		(0, 0, 0, 0, 1, 1)	(0, 0, 0, 0.05, 0.9, 0.9)
A8	(0.5, 0.7, 0.7, 1, 1, 1)	(0.6, 0.7, 0.7, 0.842, 0.9, 0.9)		(0.7, 0.9, 0.9, 1.111, 1, 1)	(0.8, 0.9, 0.9, 0.95, 0.9, 0.9)
A9	(0.3, 0.5, 0.5, 0.778, 1, 1)	(0.4, 0.5, 0.5, 0.632, 0.9, 0.9)		(0, 0, 0, 0, 1, 1)	(0, 0, 0, 0.05, 0.9, 0.9)
A10	(0.3, 0.5, 0.5, 0.778, 1, 1)	(0.4, 0.5, 0.5, 0.632, 0.9, 0.9)		(0, 0, 0, 0, 1, 1)	(0, 0, 0, 0.05, 0.9, 0.9)
A11	(0.1, 0.3, 0.3, 0.556, 1, 1)	(0.2, 0.3, 0.3, 0.421, 0.9, 0.9)		(0.7, 0.9, 0.9, 1.111, 1, 1)	(0.8, 0.9, 0.9, 0.95, 0.9, 0.9)
A12	(0, 0.1, 0.1, 0.333, 1, 1)	(0.05, 0.1, 0.1, 0.211, 0.9, 0.9)		(0.9, 1, 1, 1.111, 1, 1)	(0.95, 1, 1, 1, 0.9, 0.9)
A13	(0, 0, 0, 0, 1, 1)	(0, 0, 0, 0.053, 0.9, 0.9)		(0.9, 1, 1, 1.111, 1, 1)	(0.95, 1, 1, 1, 0.9, 0.9)
A14	(0, 0, 0, 0, 1, 1)	(0, 0, 0, 0.053, 0.9, 0.9)		(0.9, 1, 1, 1.111, 1, 1)	(0.95, 1, 1, 1, 0.9, 0.9)
Ideal	(0.9, 1, 1, 1.111, 1, 1)	(0.95, 1, 1, 1.053, 0.9, 0.9)		(0.9, 1, 1, 1.111, 1, 1)	(0.95, 1, 1, 1, 0.9, 0.9)

The normalized TrIT2F values are further multiplied by the weights of the criteria obtained by applying the TrIT2F PIPRECIA method, creating a weighted TrIT2F matrix, and the example of computation is as follows:

$$\begin{array}{l}{\tilde{v}}_{11}=\left(0,0.08,0.08,0.049,1,1\right),\left(0.03,0.08,0.08,0.025,0.9,0.9\right)=\\ \left(0\times 0.046,0.1\times 0.083,0.1\times 0.083,0.333\times 0.147,1,1\right),\left(0.05\times 0.06,0.1\times 0.083,0.1\times 0.083,0.211\times 0.119,0.9,0.9\right)\end{array}$$

Applying Equation (23), the Si matrix is calculated, and its example is given below:

$$\begin{array}{l}{\tilde{S}}_{aai}=\left(0,0.02,0.02,0.084,1,1\right),\left(0.008,0.02,0.02,0.101,0.9,0.9\right)\\ {\tilde{S}}_1=\left(0.303,0.584,0.584,1.104,1,1\right),\left(0.410,0.584,0.584,0.818,0.9,0.9\right)\\ {\tilde{S}}_2=\left(0.337,0.673,0.673,1.304,1,1\right),\left(0.464,0.673,0.673,0.960,0.9,0.9\right)\\ {\tilde{S}}_3=\left(0.231,0.514,0.514,1.069,1,1\right),\left(0.340,0.514,0.514,0.764,0.9,0.9\right)\\ {\tilde{S}}_4=\left(0.240,0.530,0.530,1.102,1,1\right),\left(0.352,0.530,0.530,0.789,0.9,0.9\right)\\ {\tilde{S}}_5=\left(0.499,0.868,0.868,1.525,1,1\right),\left(0.635,0.868,0.868,1.177,0.9,0.9\right)\\ {\tilde{S}}_6=\left(0.237,0.510,0.510,1.035,1,1\right),\left(0.341,0.510,0.510,0.754,0.9,0.9\right)\\ {\tilde{S}}_7=\left(0.100,0.251,0.251,0.526,1,1\right),\left(0.160,0.251,0.251,0.413,0.9,0.9\right)\\ {\tilde{S}}_8=\left(0.337,0.684,0.684,1.342,1,1\right),\left(0.469,0.684,0.684,0.992,0.9,0.9\right)\\ {\tilde{S}}_9=\left(0.081,0.218,0.218,0.477,1,1\right),\left(0.137,0.218,0.218,0.369,0.9,0.9\right)\\ {\tilde{S}}_{10}=\left(0.060,0.167,0.167,0.411,1,1\right),\left(0.102,0.167,0.167,0.310,0.9,0.9\right)\\ {\tilde{S}}_{11}=\left(0.187,0.440,0.440,0.969,1,1\right),\left(0.282,0.440,0.440,0.695,0.9,0.9\right)\\ {\tilde{S}}_{12}=\left(0.243,0.472,0.472,0.927,1,1\right),\left(0.327,0.472,0.472,0.669,0.9,0.9\right)\\ {\tilde{S}}_{13}=\left(0.243,0.464,0.464,0.878,1,1\right),\left(0.324,0.464,0.464,0.680,0.9,0.9\right)\\ {\tilde{S}}_{14}=\left(0.243,0.464,0.464,0.878,1,1\right),\left(0.324,0.464,0.464,0.680,0.9,0.9\right)\\ {\tilde{S}}_{ID}=\left(0.637,1.000,1.000,1.572,1,1\right),\left(0.768,1.000,1.000,1.283,0.9,0.9\right)\end{array}$$

Applying the other steps of the TrIT2F MARCOS method, the final rankings shown in Table 9 are obtained.

Table 9. Final results of the TrIT2F PIPRECIA-TrIT2F MARCOS model.

	Ki−	Ki+	fK−	fK+	Ki	Rank
A1	18.017	0.603	0.032	0.968	0.603	4
A2	20.870	0.699	0.032	0.968	0.698	3
A3	16.186	0.542	0.032	0.968	0.541	6
A4	16.712	0.560	0.032	0.968	0.559	5
A5	26.457	0.886	0.032	0.968	0.885	1
A6	15.992	0.535	0.032	0.968	0.535	7
A7	8.001	0.268	0.032	0.968	0.268	12
A8	21.307	0.713	0.032	0.968	0.713	2
A9	7.035	0.236	0.032	0.968	0.235	13
A10	5.641	0.189	0.032	0.968	0.189	14
A11	14.146	0.474	0.032	0.968	0.473	11
A12	14.814	0.496	0.032	0.968	0.495	8
A13	14.427	0.483	0.032	0.968	0.483	9
A14	14.427	0.483	0.032	0.968	0.483	9

Based on the extensive analysis done in the previous table, the listed alternatives (sections of the road) were ranked. The mentioned sections of the road (A1–A14) were considered in the longitudinal gradient range from −5.52% to +7.45%. The ranking was conducted according to the value of the Ki coefficient from the highest (highest value) to the lowest (lowest value) for all 14 alternatives. The final results of the applied TrIT2F PIPRECIA-TrIT2F MARCOS model show the following ranking of road segments, according to which Vrhovi–Šešlije M-I-103 with a gradient of −1.00 represents the best solution: A5 > A8 > A2 > A1 > A4 > A3 > A6 > A12 > A13 = A14 > A11 > A7 > A9 > A10. It is important to note that two segments, Obodnik–Klupe M-I-108 +6.84 and Obodnik–Klupe M-I-108 +7.45, share the same position, which primarily refers to the same input parameters, except for the longitudinal gradient when there are nuances in the differences.

6. Validation of Research Results and Discussion

In this section, the validation of the obtained results and the proposed TrIT2F PIPRE-CIA-TrIT2F MARCOS model was performed by changing the values of the criteria and changing the size of the decision matrix.

6.1. Sensitivity Analysis

In this section of the paper, changes in the values of the criteria were carried out, i.e., a simulation of new values through 40 scenarios. Every ten scenarios with the values of the four most important criteria (C2, C3, C4, and C5) changed in the range of 10–100%.

Therefore, in the last scenarios, S10, S20, S30 and S40, the values of the criteria C2, C3, C4, and C5 were reduced to zero, which practically means that they have been eliminated in these four scenarios. The values of all simulated criteria are presented in Figure 4.

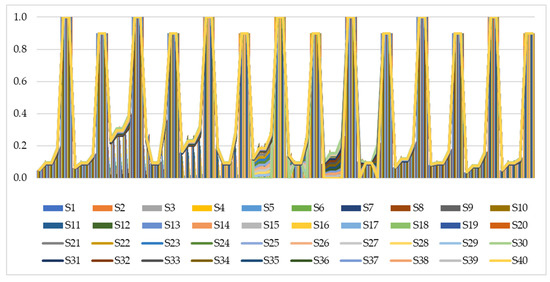
Figure 4. Simulation of values of criteria.

Figure 5 shows the results of the sensitivity analysis.

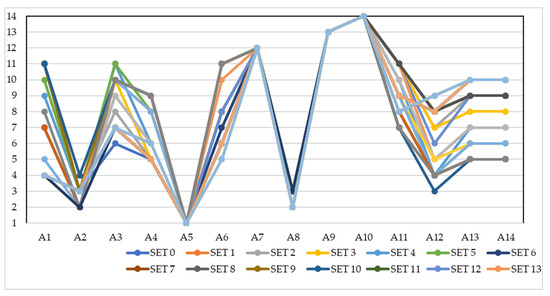
Figure 5. Results of the sensitivity analysis.

It is very important to note that the simulated values of the criteria, in which practically some criteria are eliminated, have a great influence on the final ranking of road infrastructure segments. In all scenarios, only four segments retain the initial ranking of the alternatives, namely A5, A7, A9 and A10, which are in the 1st, 12th, 13th, and 14th positions, respectively. It is an interesting situation that segments A13 and A14, which have the same compromise value in TrIT2F MARCOS, share the same position, which changes through the simulated scenarios. Therefore, the alternative A5 is always in the first place, regardless of the values of the criteria, while there is a large variation in the other alternatives. For example, by changing the significance of the most important criterion, C2, when its value decreases, the first alternative, A1, falls to lower positions (from 4th to even 11th place). The situation is similar with segments A3, A4 and A6, while decreasing the importance of the second criterion, the ranking of segments A11, A12, A13, and A14 increases.

6.2. The Influence of the Decision Matrix Size

The influence of the size of the decision matrix can often cause different results than those originally obtained. Therefore, in this paper, the stability of the TrIT2F PIPRECIA-TrIT2F MARCOS model was tested through 12 formed sets. In each set, the lowest-placed alternative is eliminated, with the fact that in the fourth set, two alternatives that share the same position, A13 and A14, are eliminated.

The results presented in Figure 6 show the values of the alternatives on the left and their rankings on the right. It can be concluded that changing the size of the initial decision matrix in the TrIT2F PIPRECIA-TrIT2F MARCOS model has no effect on rank changes.

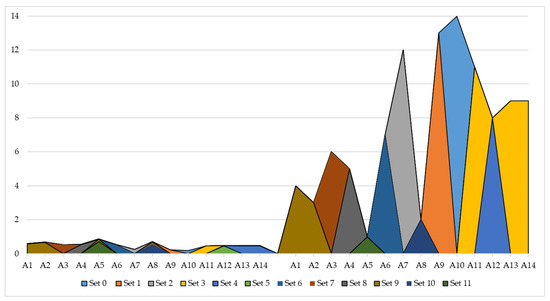
Figure 6. Results of the analysis of the influence of the decision matrix size.

The analysis of the impact of the road infrastructure on the efficiency of the traffic flow, in this case, can be compared to the assessment of the vulnerability of the road traffic system. Through this research, it can be concluded that the vulnerability of a network in different scenarios is analyzed from both the structural and functional perspectives, as also indicated in other studies [48,49]. The application of a similar methodology is shown in the ranking of qualitative and quantitative criteria of traffic safety and can be accepted as relevant in decision making [50,51]. Additionally, these studies can assist stakeholders in understanding the current state of transportation networks and planning future sustainability measures through the MCDM approach.

7. Conclusions

Constant monitoring of the road infrastructure and assessment of indicators of traffic flow efficiency and road exploitation have become an important parameter of road engineering management. In this paper, a set of 14 road segments was observed based on seven different parameters in order to determine the segments that have satisfactory traffic flow efficiency. For these purposes, a novel TrIT2F MCDM model has been developed, and it consists of the TrIT2F PIPRECIA method for determining the weights of criteria and the TrIT2F MARCOS method for evaluating and ranking alternatives. Forming extensions of two MCDM methods with TrIT2F, the first for determining criteria values and the second for alternative evaluation, is the main contribution of the paper. Additionally, this model can be applied to any other MCDM problem, so it has a large justification. In this way, scientific contributions have been ensured. At the same time, the set aims for the assessment of indicators of traffic flow efficiency and road exploitation to make the mentioned sections of the road sustainable have been achieved. The results of the newly developed model, which is the greatest contribution of this research, are: A5 > A8 > A2 > A1 > A4 > A3 > A6 > A12 > A13 = A14 > A11 > A7 > A9 > A10. These results should be the basis for road management institutions to make necessary changes and bring new rules for traffic flow on considered road sections, while also, of course, taking into account the type of considered vehicle. After that, the validation of the obtained results was carried out, which shows that the final results greatly depend on changing the importance of the criteria, while the size of the decision matrix has no influence, i.e., the results remain identical. Despite the mentioned advantages of the study, there are also some limitations. The limitations are as follows: the small length of road considered in the study through 14 road sections in comparison to the total length of the road, considering the data, and utilizing a model for only one type of vehicle (light goods vehicles) or a small number of decisionmakers.

Future research is related to the formation of a larger set of road infrastructure segments, and a larger set of evaluation criteria. Additionally, the application of this model is possible in other areas of traffic engineering or in other areas of research. Using other theories, such intuitionistic fuzzy sets [52] or quasirung orthopair fuzzy sets, can be one of the guidelines for the next research project.