Parameter Estimation for Nonlinear Diffusion Problems by the Constrained Homotopy Method
Abstract
1. Introduction
2. Mathematical Model
3. Parameter Estimation Framework
4. Inversion Method
4.1. Basic Iterative Method
4.2. Homotopy Method
4.3. Global Convergence of Homotopy Method
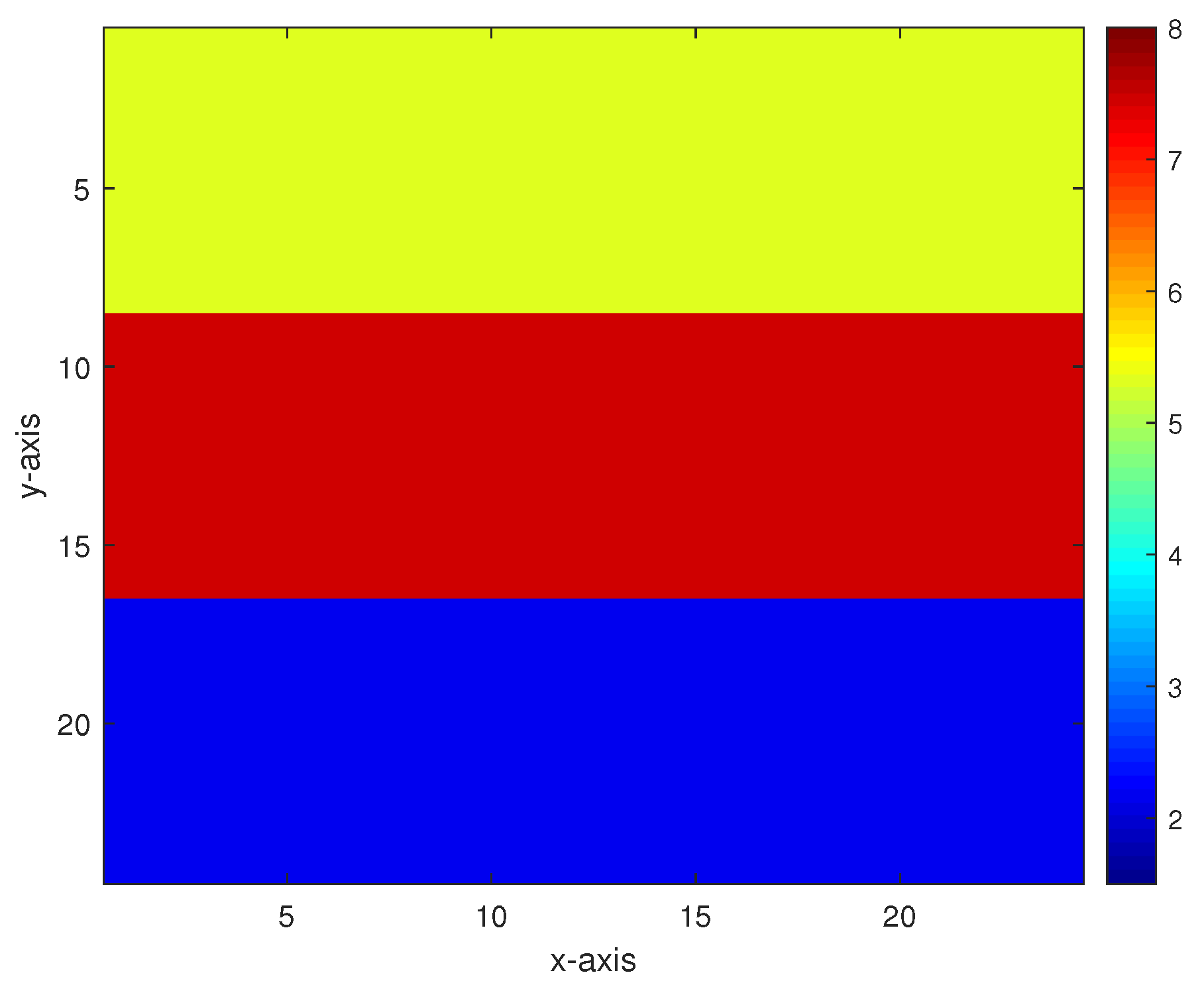
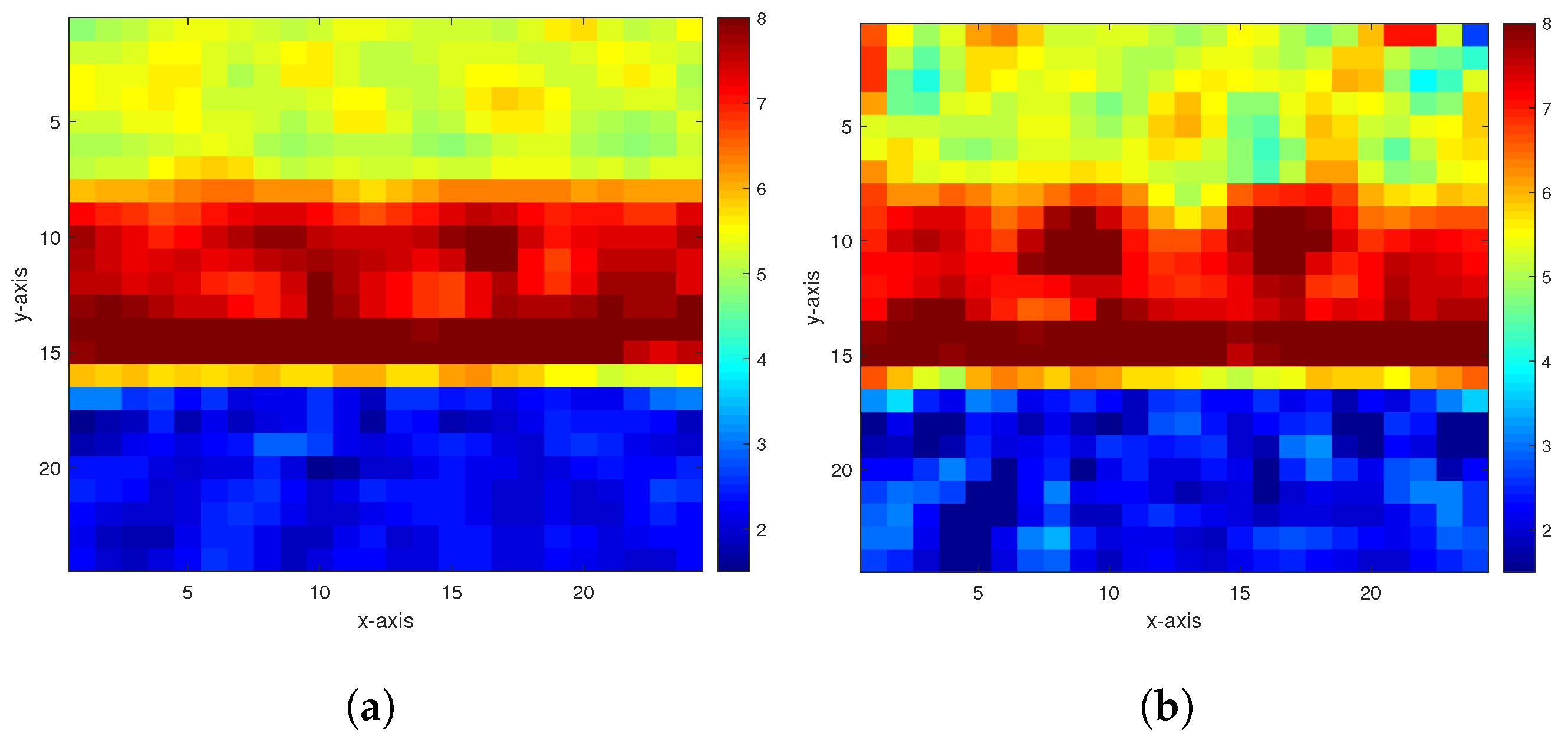
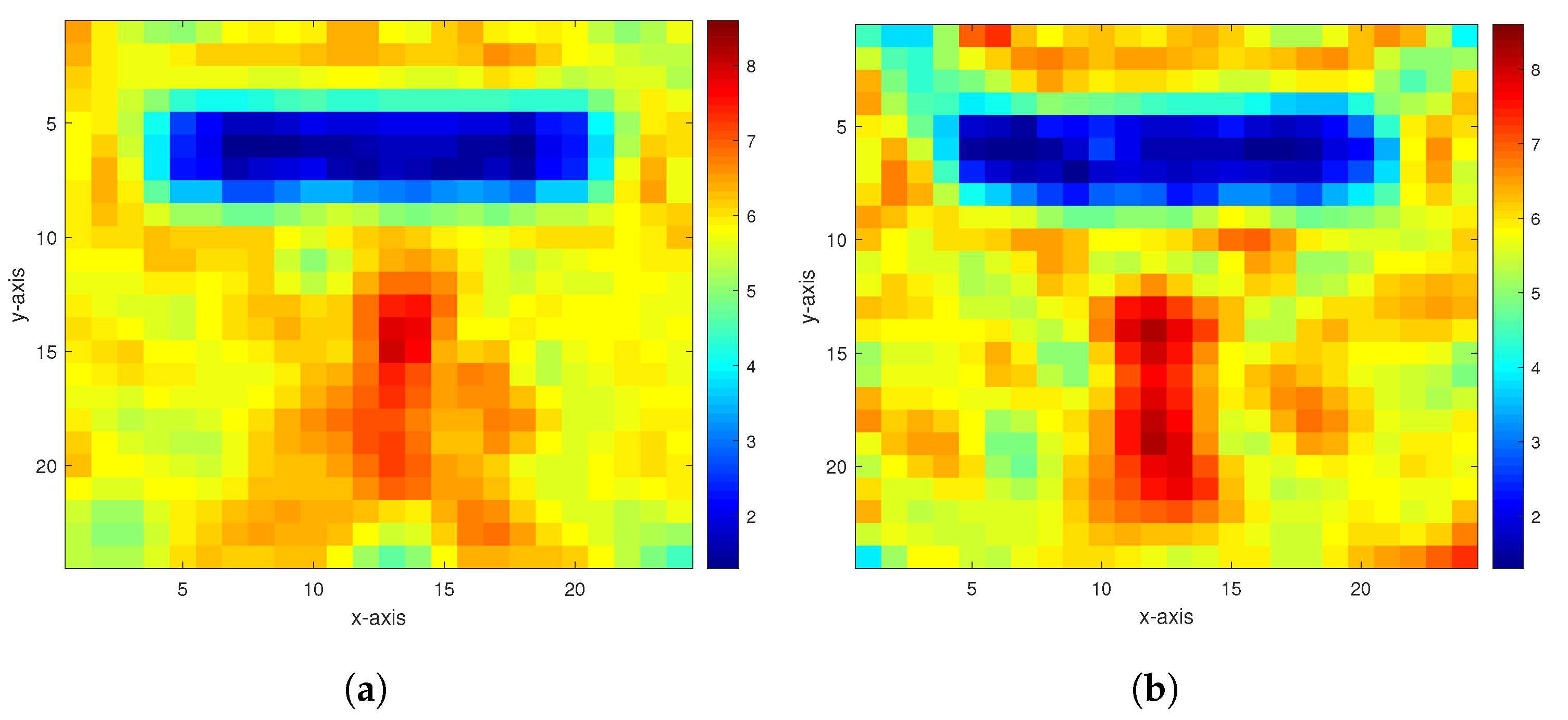
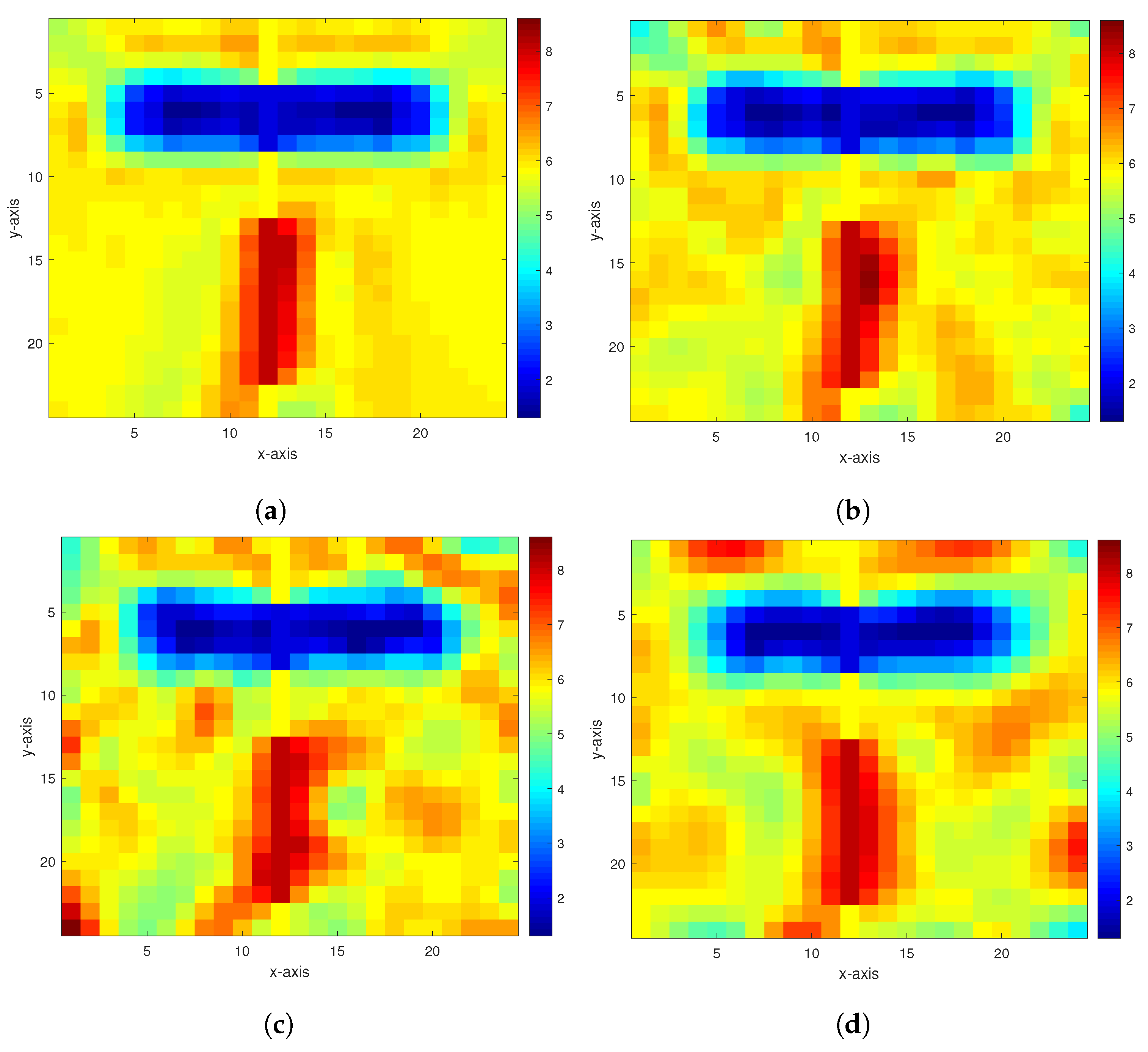
5. Numerical Experiments and Results
- (1)
- The constrained homotopy method has global convergence, fast convergence speed, and good stability;
- (2)
- Both the constrained homotopy method and the homotopy method have wider region of convergence than the constrained method;
- (3)
- The constrained homotopy method has a stronger noise suppression ability than the homotopy method.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nilssen, T.K.; Mannseth, T.; Tai, X.C. Permeability estimation with the augmented Lagrangian method for a nonlinear diffusion equation. Comput. Geosci. 2003, 7, 27–47. [Google Scholar] [CrossRef]
- Zeki, M.; Tinaztepe, R.; Tatar, S.; Ulusoy, S.; Al-Hajj, R. Determination of a nonlinear coefficient in a time-fractional diffusion equation. Fractal Fract. 2023, 7, 371. [Google Scholar] [CrossRef]
- Guerngar, N.; Nane, E.; Tinaztepe, R.; Ulusoy, S.; Van Wyk, H.W. Simultaneous inversion for the fractional exponents in the space-time fractional diffusion equation. Fract. Calc. Appl. Anal. 2021, 24, 818–847. [Google Scholar] [CrossRef]
- Brociek, R.; Wajda, A.; Słota, D. Inverse problem for a two-dimensional anomalous diffusion equation with a fractional derivative of the Riemann–Liouville type. Energies 2021, 14, 3082. [Google Scholar] [CrossRef]
- Brociek, R.; Wajda, A.; Słota, D. Comparison of heuristic algorithms in identification of parameters of anomalous diffusion model based on measurements from sensors. Sensors 2023, 23, 1722. [Google Scholar] [CrossRef]
- Brociek, R.; Chmielowska, A.; Słota, D. Parameter identification in the two-dimensional Riesz space fractional diffusion equation. Fractal Fract. 2020, 4, 39. [Google Scholar] [CrossRef]
- Mittal, G.; Giri, A.K. Convergence rates for iteratively regularized Gauss–Newton method subject to stability constraints. J. Comput. Appl. Math. 2022, 400, 113744. [Google Scholar] [CrossRef]
- Al-Mahdawi, H.K.I.; Alkattan, H.; Abotaleb, M.; Kadi, A.; El-kenawy, E.-S.M. Updating the Landweber iteration method for solving inverse problems. Mathematics 2022, 10, 2798. [Google Scholar] [CrossRef]
- Bergou, E.H.; Diouane, Y.; Kungurtsev, V. Convergence and complexity analysis of a Levenberg–Marquardt algorithm for inverse problems. J. Optim. Theory Appl. 2020, 185, 927–944. [Google Scholar] [CrossRef]
- Qian, E.; Grepl, M.; Veroy, K.; Willcox, K. A certified trust region reduced basis approach to PDE-constrained optimization. SIAM J. Sci. Comput. 2017, 39, S434–S460. [Google Scholar] [CrossRef]
- Li, H.; Schwab, J.; Antholzer, S.; Haltmeier, M. NETT: Solving inverse problems with deep neural networks. Inverse Probl. 2020, 36, 065005. [Google Scholar] [CrossRef]
- Bochud, N.; Vallet, Q.; Bala, Y.; Follet, H.; Minonzio, J.G.; Laugier, P. Genetic algorithms-based inversion of multimode guided waves for cortical bone characterization. Phys. Med. Biol. 2016, 61, 6953. [Google Scholar] [CrossRef]
- Tavares, R.S.; Sato, A.K.; Martins, T.C.; Lima, R.G.; Tsuzuki, M.S.G. GPU acceleration of absolute EIT image reconstruction using simulated annealing. Biomed. Signal Process. 2019, 52, 445–455. [Google Scholar] [CrossRef]
- Brociek, R.; Wajda, A.; Błasik, M.; Słota, D. An application of the homotopy analysis method for the time- or space-fractional heat equation. Fractal Fract. 2023, 7, 224. [Google Scholar] [CrossRef]
- Yasmin, H. Application of Aboodh homotopy perturbation transform method for fractional-order convection-reaction-diffusion equation within Caputo and Atangana-Baleanu operators. Symmetry 2023, 15, 453. [Google Scholar] [CrossRef]
- Yasmin, H.; Alshehry, A.S.; Saeed, A.M.; Shah, R.; Nonlaopon, K. Application of the q-homotopy analysis transform method to fractional-order Kolmogorov and Rosenau-Hyman models within the Atangana-Baleanu operator. Symmetry 2023, 15, 671. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Araghi, M.A.F.; Sidorov, D. Dynamical strategy on homotopy perturbation method for solving second kind integral equations using the CESTAC method. J. Comput. Appl. Math. 2022, 411, 114226. [Google Scholar] [CrossRef]
- Watson, L.T. Globally convergent homotopy methods: A tutorial. Appl. Math. Comput. 1989, 31, 369–396. [Google Scholar]
- Jegen, M.D.; Everett, M.E.; Schultz, A. Using homotopy to invert geophysical data. Geophysics 2001, 66, 1749–1760. [Google Scholar] [CrossRef]
- Ping, P.; Chu, R.; Zhang, Y.; Zeng, Q. A homotopy inversion method for Rayleigh wave dispersion data. J. Appl. Geophys. 2023, 209, 104914. [Google Scholar] [CrossRef]
- Ghanati, R.; Müller-Petke, M. A homotopy continuation inversion of geoelectrical sounding data. J. Appl. Geophys. 2021, 191, 104356. [Google Scholar] [CrossRef]
- Słota, D.; Chmielowska, A.; Brociek, R.; Szczygieł, M. Application of the homotopy method for fractional inverse Stefan problem. Energies 2020, 13, 5474. [Google Scholar] [CrossRef]
- Słota, D. Homotopy perturbation method for solving the two-phase inverse Stefan problem. Numer. Heat Transf. A-Appl. 2011, 59, 755–768. [Google Scholar] [CrossRef]
- Hetmaniok, E.; Słota, D.; Wituła, R.; Zielonka, A. Solution of the one-phase inverse Stefan problem by using the homotopy analysis method. Appl. Math. Model. 2015, 39, 6793–6805. [Google Scholar] [CrossRef]
- Hu, J.L.; Hirasawa, K.; Kumamaru, K. A homotopy approach to improving PEM identification of ARMAX models. Automatica 2001, 37, 1323–1334. [Google Scholar] [CrossRef]
- Zhang, W.; Tan, C.; Dong, F. Non-linear reconstruction for ERT inverse problem based on homotopy algorithm. IEEE Sens. J. 2023, 23, 10404–10412. [Google Scholar] [CrossRef]
- Biswal, U.; Chakraverty, S.; Ojha, B.K. Application of homotopy perturbation method in inverse analysis of Jeffery-Hamel flow problem. Eur. J. Mech. B Fluids 2021, 86, 107–112. [Google Scholar] [CrossRef]
- Hetmaniok, E.; Nowak, I.; Słota, D.; Wituła, R. Application of the homotopy perturbation method for the solution of inverse heat conduction problem. Int. Commun. Heat Mass 2012, 39, 30–35. [Google Scholar] [CrossRef]
- Hetmaniok, E.; Nowak, I.; Słota, D.; Wituła, R.; Zielonka, A. Solution of the inverse heat conduction problem with Neumann boundary condition by using the homotopy perturbation method. Therm. Sci. 2013, 17, 643–650. [Google Scholar] [CrossRef]
- Shakeri, F.; Dehghan, M. Inverse problem of diffusion equation by He’s homotopy perturbation method. Phys. Scr. 2007, 75, 551–556. [Google Scholar] [CrossRef]
- Liu, T. A multigrid-homotopy method for nonlinear inverse problems. Comput. Math. Appl. 2020, 79, 1706–1717. [Google Scholar] [CrossRef]
- Liu, T. A wavelet multiscale-homotopy method for the parameter identification problem of partial differential equations. Comput. Math. Appl. 2016, 71, 1519–1523. [Google Scholar] [CrossRef]
- Enting, I.G.; Pearman, G.I. Description of a one-dimensional carbon cycle model calibrated using techniques of constrained inversion. Tellus B 1987, 39, 459–476. [Google Scholar] [CrossRef]
- Rolon, L.; Mohaghegh, S.D.; Ameri, S.; Gaskari, R.; McDaniel, B. Using artificial neural networks to generate synthetic well logs. J. Nat. Gas Sci. Eng. 2009, 1, 118–133. [Google Scholar] [CrossRef]
- Atzberger, C.; Richter, K. Spatially constrained inversion of radiative transfer models for improved LAI mapping from future Sentinel-2 imagery. Remote Sens. Environ. 2012, 120, 208–218. [Google Scholar] [CrossRef]
- Siemon, B.; Auken, E.; Christiansen, A.V. Laterally constrained inversion of helicopter-borne frequency-domain electromagnetic data. J. Appl. Geophys. 2009, 67, 259–268. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, T.; Liu, S. Identification of space-dependent permeability in nonlinear diffusion equation from interior measurements using wavelet multiscale method. Inverse Probl. Sci. Eng. 2014, 22, 259–268. [Google Scholar] [CrossRef]
- Bakushinskii, A.B. The problem of the convergence of the iteratively regularized Gauss–Newton method. Comput. Math. Math. Phys. 1992, 32, 1503–1509. [Google Scholar]
- Bao, G.; Liu, J. Numerical solution of inverse scattering problems with multi-experimental limited aperture data. SIAM J. Sci. Comput. 2003, 25, 1102–1117. [Google Scholar] [CrossRef]


| Noise Level | Inversion Method | Relative Error | CPU Run Time (s) |
|---|---|---|---|
| 40 dB | Constrained homotopy method | 0.0835 | 228.9241 |
| Homotopy method | 0.0890 | 256.4925 | |
| Constrained method | No convergence | No convergence | |
| 30 dB | Constrained homotopy method | 0.0849 | 230.9774 |
| Homotopy method | 0.1062 | 257.6150 | |
| Constrained method | No convergence | No convergence | |
| 20 dB | Constrained homotopy method | 0.0921 | 259.9313 |
| Homotopy method | No convergence | No convergence | |
| Constrained method | No convergence | No convergence | |
| 10 dB | Constrained homotopy method | 0.1018 | 284.2159 |
| Homotopy method | No convergence | No convergence | |
| Constrained method | No convergence | No convergence |
| Noise Level | Inversion Method | Relative Error | CPU Run Time (s) |
|---|---|---|---|
| 40 dB | Constrained homotopy method | 0.0633 | 223.1658 |
| Homotopy method | 0.0799 | 224.1277 | |
| Constrained method | No convergence | No convergence | |
| 30 dB | Constrained homotopy method | 0.0674 | 224.3204 |
| Homotopy method | 0.0805 | 249.1969 | |
| Constrained method | No convergence | No convergence | |
| 20 dB | Constrained homotopy method | 0.0827 | 225.0038 |
| Homotopy method | No convergence | No convergence | |
| Constrained method | No convergence | No convergence | |
| 10 dB | Constrained homotopy method | 0.0871 | 251.2146 |
| Homotopy method | No convergence | No convergence | |
| Constrained method | No convergence | No convergence |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Ding, Z.; Yu, J.; Zhang, W. Parameter Estimation for Nonlinear Diffusion Problems by the Constrained Homotopy Method. Mathematics 2023, 11, 2642. https://doi.org/10.3390/math11122642
Liu T, Ding Z, Yu J, Zhang W. Parameter Estimation for Nonlinear Diffusion Problems by the Constrained Homotopy Method. Mathematics. 2023; 11(12):2642. https://doi.org/10.3390/math11122642
Chicago/Turabian StyleLiu, Tao, Zijian Ding, Jiayuan Yu, and Wenwen Zhang. 2023. "Parameter Estimation for Nonlinear Diffusion Problems by the Constrained Homotopy Method" Mathematics 11, no. 12: 2642. https://doi.org/10.3390/math11122642
APA StyleLiu, T., Ding, Z., Yu, J., & Zhang, W. (2023). Parameter Estimation for Nonlinear Diffusion Problems by the Constrained Homotopy Method. Mathematics, 11(12), 2642. https://doi.org/10.3390/math11122642










