An Improved Arithmetic Optimization Algorithm and Its Application to Determine the Parameters of Support Vector Machine
Abstract
:1. Introduction
2. Basic AOA
2.1. Math Optimizer Accelerated (MOA) Function
2.2. Global Exploration
2.3. Local Exploitation
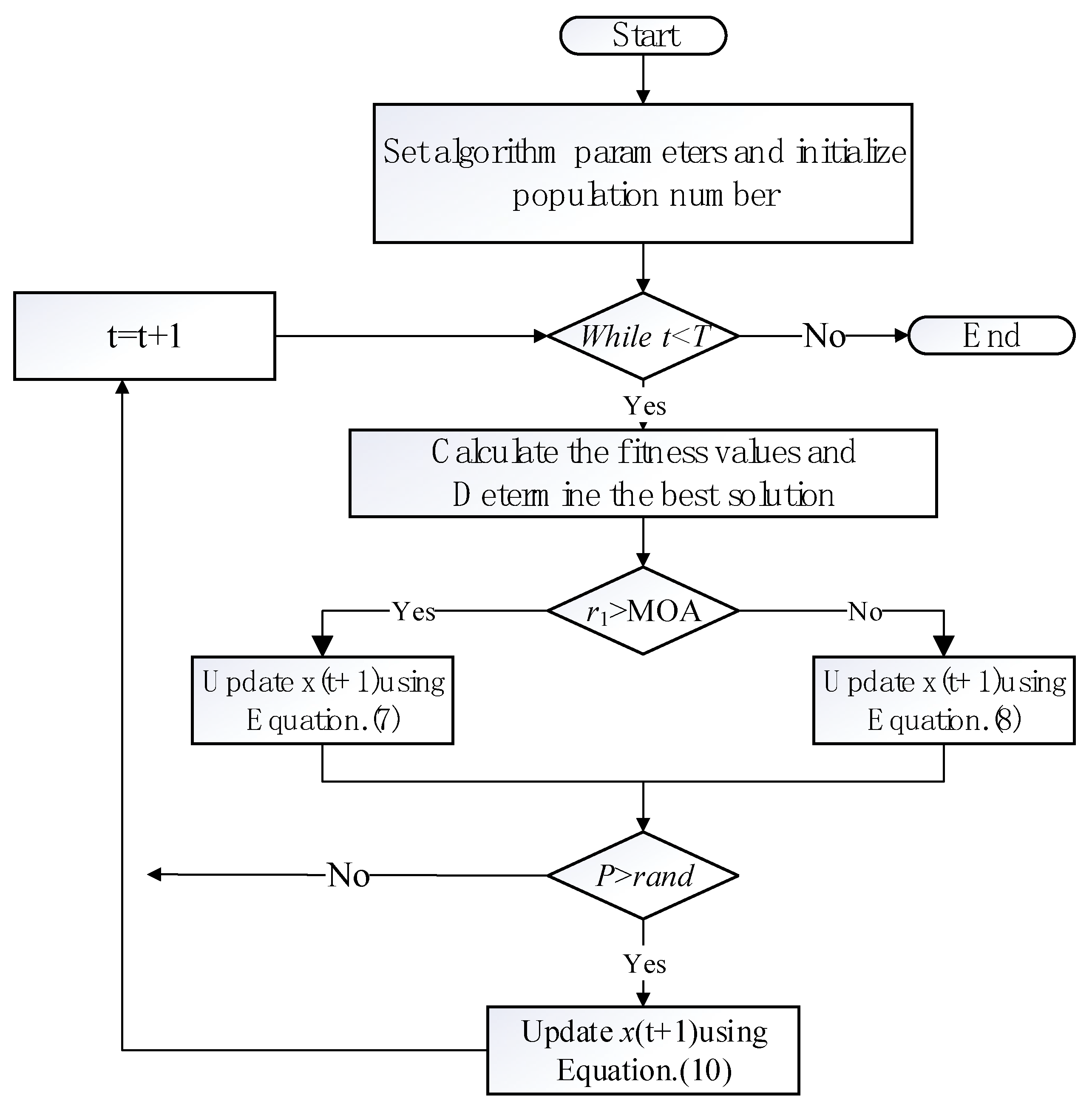
3. Our Proposed IAOA
3.1. Dynamic Inertia Weights
| Algorithm 1: AOA |
| 1.Set population size N, the maximum number of iterations T. 2.Set up the initial parameters t = 0, α, μ. 3.Initialize the positions of the individuals xi (i = 1, 2, …, N). 4.While (t < T) 5. Update the MOA using Equation (1) and the MOP using Equation (3). 6. Calculate the fitness values and Determine the best solution. 7. For i = 1, 2, …, N do 8. For j = 1, 2, …, Dim 9. Generate the random values between [0, 1] (r1, r2, r3). 10. If r1 > MOA 11. Update the position of x(t + 1) using Equation (2). 12. Else 13. Update the position of x(t + 1) using Equation (5) 14. End if 15. End for 16. End for 17. t = t + 1. 18.End while 19.Return the best solution (x) |
3.2. Dynamic Coefficient of Mutation and Triangular Mutation Strategy
| Algorithm 2: IAOA |
| 1.Set population size N, the maximum number of iterations T. 2.Set up the initial parameters t = 0, α, μ. 3.Initialize the positions of the individuals xi (i = 1, 2, …, N). 4.While (t < T) 5. Update the w(t) using Equation (6) 6. Update the MOA using Equation (1) and the MOP using Equation (3). 7. Calculate the fitness values and Determine the best solution. 8. For i = 1, 2, …, N do 9. For j = 1, 2, …, Dim 10. Generate the random values between [0, 1] (r1, r2, r3). 11. If r1 > MOA 12. Update the position of x(t + 1) using Equation (7). 13. Else 14. Update the position of x(t + 1) using Equation (8) 15. End if 16. Calculate the p using Equation (9) 17. if p > rand 18. Update the position of x(t + 1) using Equation (10). 19. end if 20. End for 21. End for 22. t = t + 1. 23.End while 24.Return the best solution(x) |
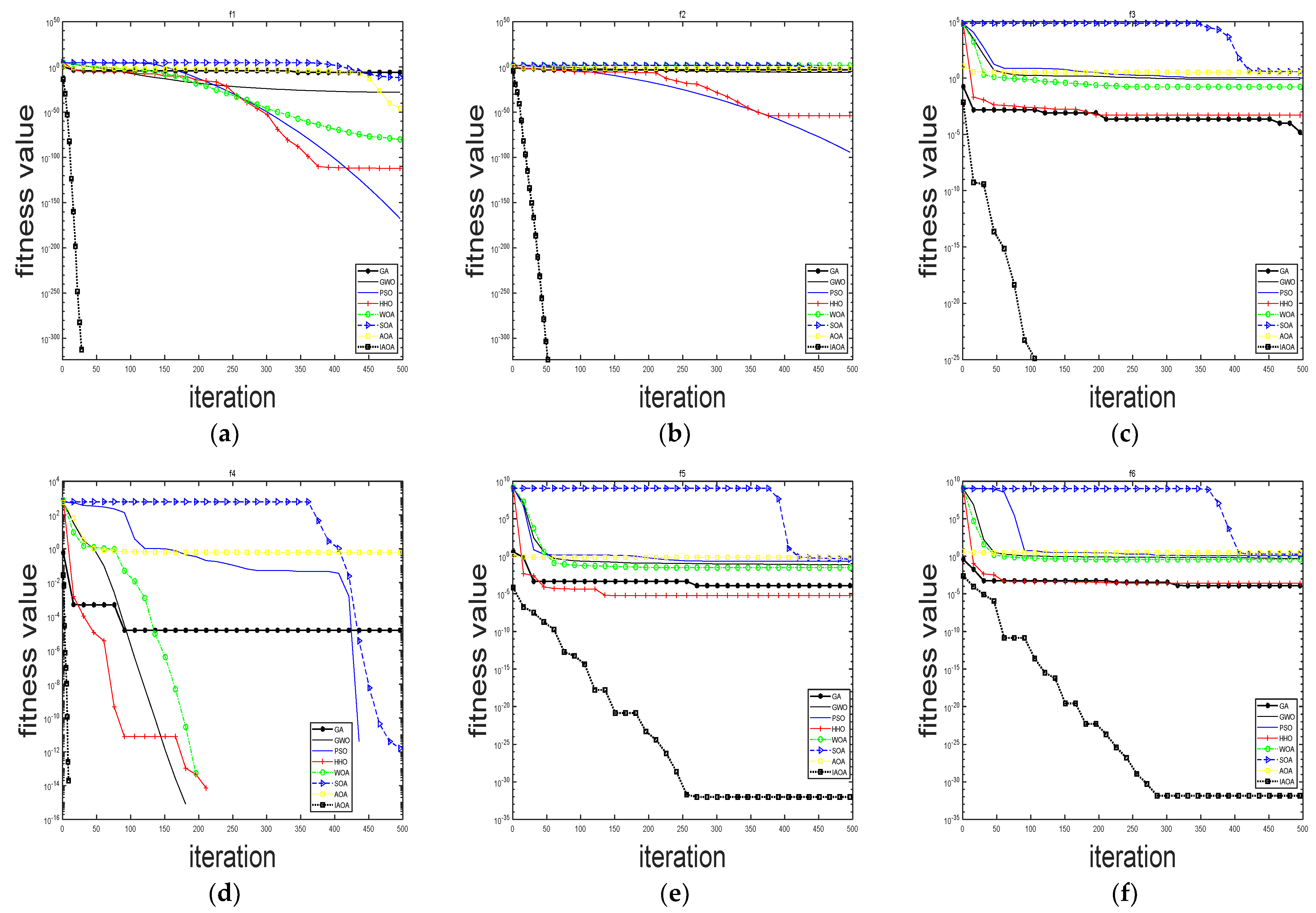
4. Benchmark Test Function Numerical Experiments and Results
4.1. Experimental Conditions
4.2. Benchmark Test Functions and Algorithm Parameters
4.3. Comparison and Analysis of Experimental Results
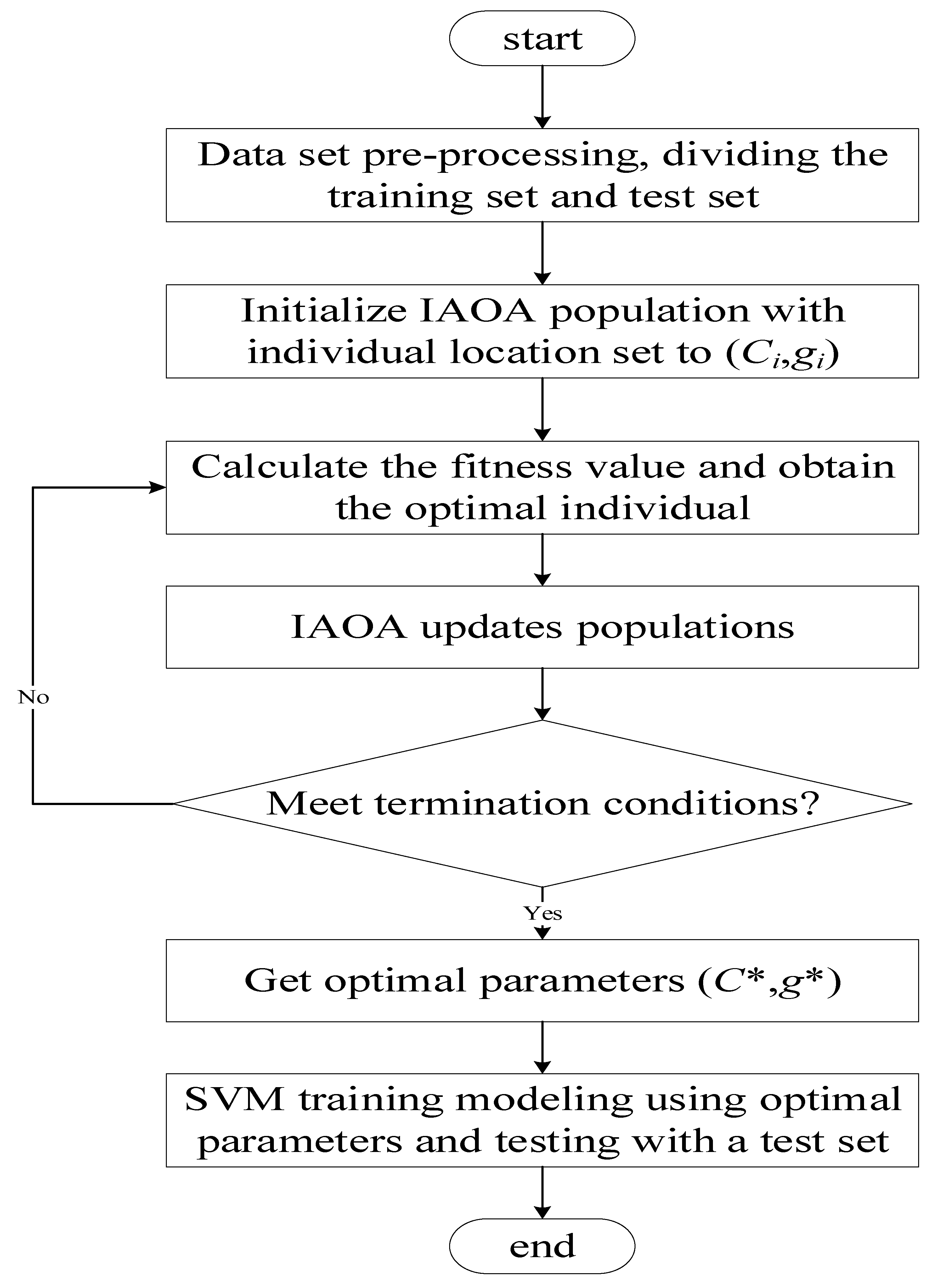
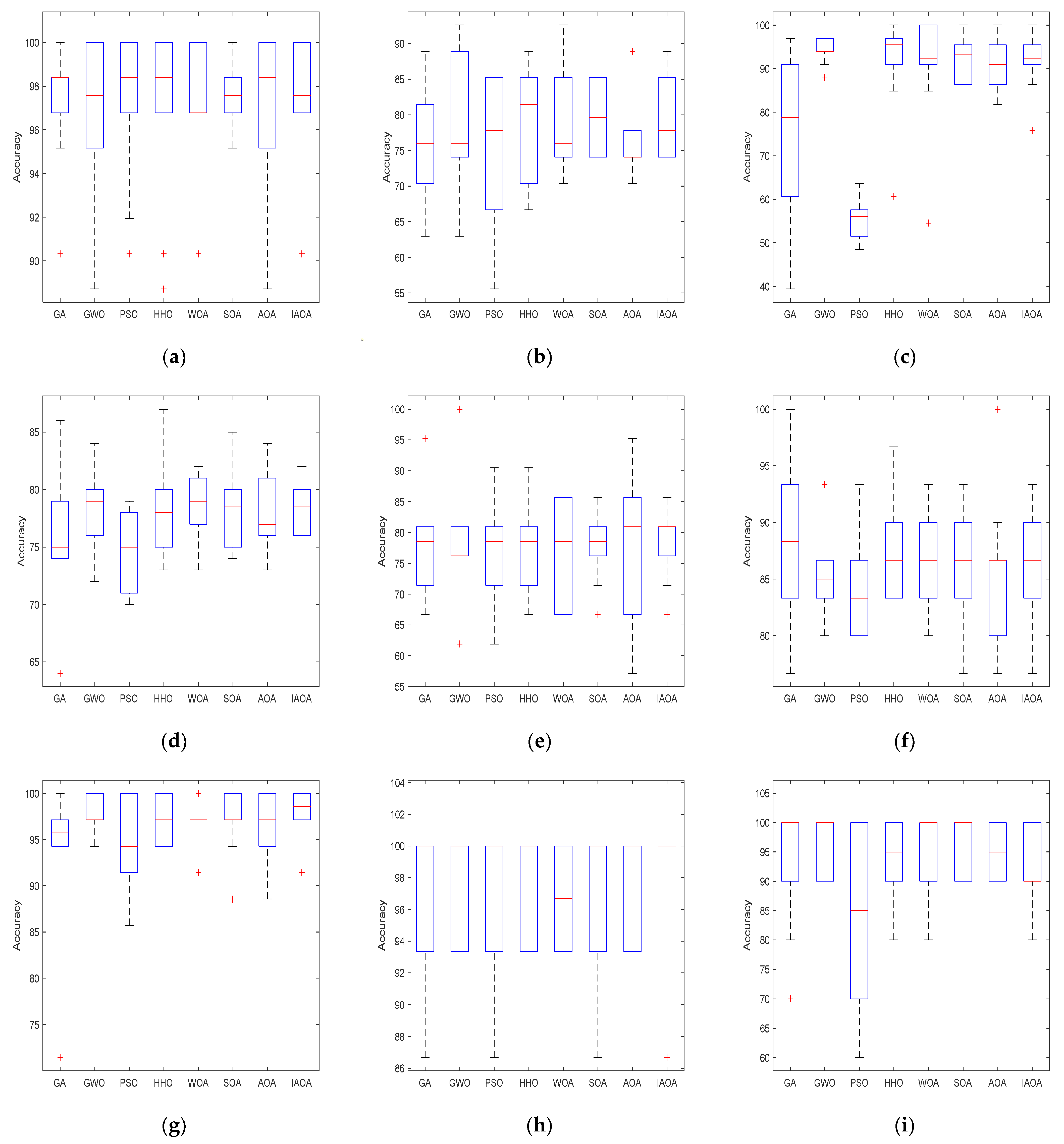
5. Support Vector Machine (SVM) Parameter Optimization
5.1. SVM Model and Classification Experimental Procedure
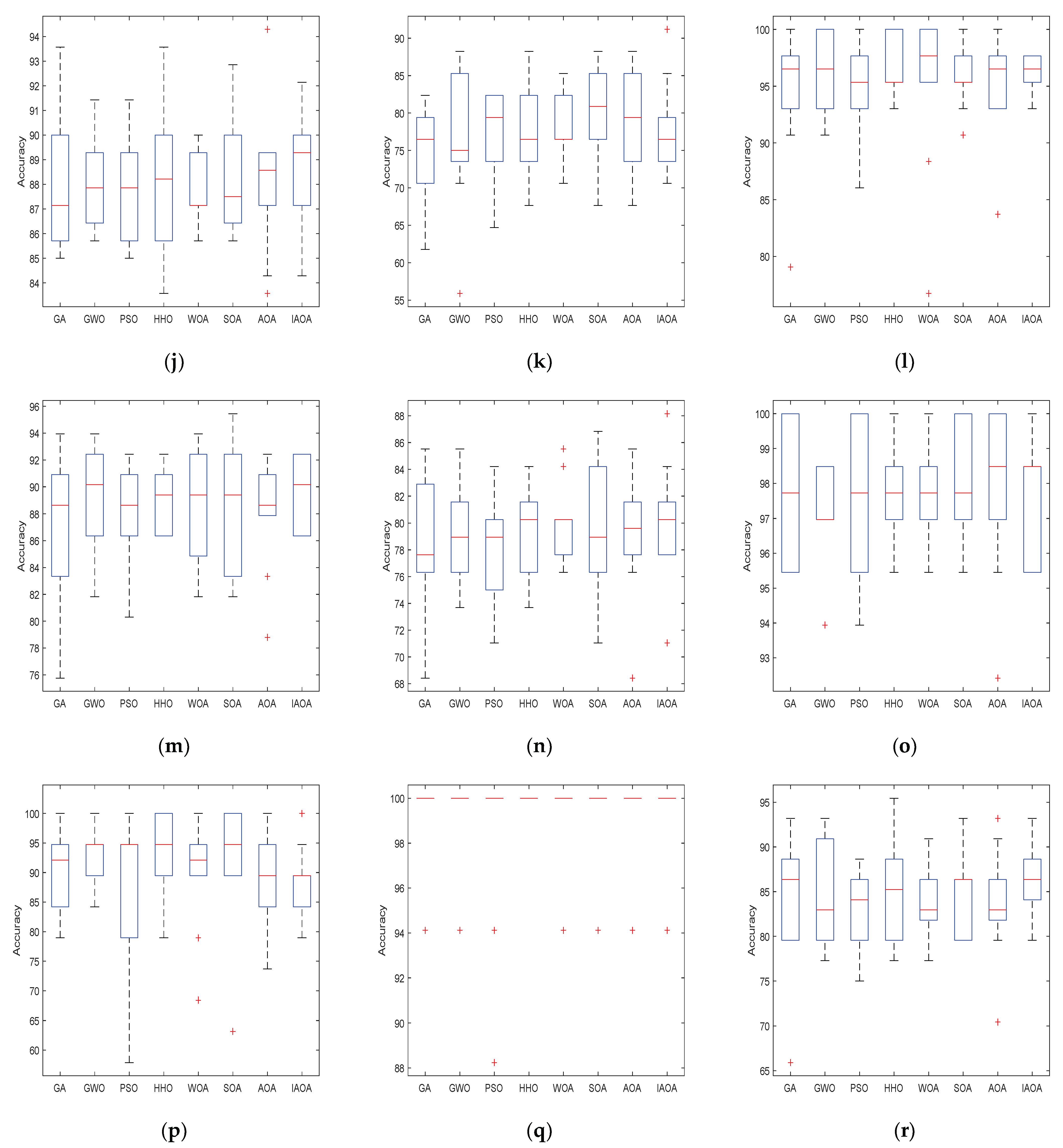
5.2. SVM Classification Test
5.3. Handwritten Number Recognition Based on SVM Parameter Optimization
Handwriting Numeral Recognition Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hussain, K.; Mohd Salleh, M.N.; Cheng, S.; Shi, Y. Metaheuristic Research: A Comprehensive Survey—Artificial Intelligence Review. Artif. Intell. Rev. 2019, 52, 2191–2233. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Hauschild, M.; Pelikan, M. An introduction and survey of estimation of distribution algorithms. Swarm Evol. Comput. 2011, 1, 111–128. [Google Scholar] [CrossRef]
- Adleman, L.M. Molecular computation of solutions to combinatorial problems. Science 1994, 266, 1021–1024. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, C. Gene expression programming: A new adaptive algorithm for solving problems. Complex Syst. 2001, 13, 87–129. [Google Scholar]
- Neri, F.; Cotta, C. Memetic algorithms and memetic computing optimization: A literature review. Swarm Evol. Comput. 2012, 2, 1–14. [Google Scholar] [CrossRef]
- Reynolds, R.G.; Peng, B. Cultural algorithms: Computational modeling of how cultures learn to solve problems: An engineering example. Cybern. Syst. Int. J. 2005, 36, 753–771. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Gandomi, A.H.; Yang, X.S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowl. Based Syst. 2019, 165, 169–196. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Future Gener. Comput. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Erol, O.K.; Eksin, I. A new optimization method: Big bang–big crunch. Adv. Eng. Softw. 2006, 37, 106–111. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Abedinpourshotorban, H.; Shamsuddin, S.M.; Beheshti, Z.; Jawawi, D.N. Electromagnetic field optimization: A physics-inspired metaheuristic optimization algorithm. Swarm Evol. Comput. 2016, 26, 8–22. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: An optimization method for continuous non-linear large scale problems. Inf. Sci. 2012, 183, 1–15. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Talatahari, S.; Azar, B.F.; Sheikholeslami, R.; Gandomi, A. Imperialist competitive algorithm combined with chaos for global optimization. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1312–1319. [Google Scholar] [CrossRef]
- Li, J.; Tan, Y. A comprehensive review of the fireworks algorithm. ACM Comput. Surv. CSUR 2019, 52, 1–28. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, R.; Yang, J.; Ding, K.; Li, Y.; Hu, J. Collective decision optimization algorithm: A new heuristic optimization method. Neurocomputing 2017, 221, 123–137. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A. A comprehensive survey of the Grasshopper optimization algorithm: Results, variants, and applications. Neural Comput. Appl. 2020, 32, 15533–15556. [Google Scholar] [CrossRef]
- Zhang, J.; Gong, D.; Zhang, Y. A niching PSO-based multi-robot cooperation method for localizing odor sources. Neurocomputing 2014, 123, 308–317. [Google Scholar] [CrossRef]
- Ma, D.; Ma, J.; Xu, P. An adaptive clustering protocol using niching particle swarm optimization for wireless sensor networks. Asian J. Control 2015, 17, 1435–1443. [Google Scholar] [CrossRef]
- Mehmood, S.; Cagnoni, S.; Mordonini, M.; Khan, S.A. An embedded architecture for real-time object detection in digital images based on niching particle swarm optimization. J. Real Time Image Process. 2015, 10, 75–89. [Google Scholar] [CrossRef]
- Gholami, M.; Alashti, R.A.; Fathi, A. Optimal design of a honeycomb core composite sandwich panel using evolutionary optimization algorithms. Compos. Struct. 2016, 139, 254–262. [Google Scholar] [CrossRef]
- Mafarja, M.; Aljarah, I.; Heidari, A.A.; Hammouri, A.I.; Faris, H.; Al-Zoubi, A.M.; Mirjalili, S. Evolutionary population dynamics and grasshopper optimization approaches for feature selection problems. Knowl. Based Syst. 2018, 145, 25–45. [Google Scholar] [CrossRef]
- Tharwat, A.; Houssein, E.H.; Ahmed, M.M.; Hassanien, A.E.; Gabel, T. MOGOA algorithm for constrained and unconstrained multi-objective optimization problems. Appl. Intell. 2018, 48, 2268–2283. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Khatir, S.; Tiachacht, S.; Le Thanh, C.; Ghandourah, E.; Mirjalili, S.; Wahab, M.A. An improved Artificial Neural Network using Arithmetic Optimization Algorithm for damage assessment in FGM composite plates. Compos. Struct. 2021, 273, 114287. [Google Scholar] [CrossRef]
- Deepa, N.; Chokkalingam, S.P. Optimization of VGG16 utilizing the Arithmetic Optimization Algorithm for early detection of Alzheimer’s disease. Biomed. Signal Process. Control 2022, 74, 103455. [Google Scholar] [CrossRef]
- Almalawi, A.; Khan, A.I.; Alsolami, F.; Alkhathlan, A.; Fahad, A.; Irshad, K.; Alfakeeh, A.S.; Qaiyum, S. Arithmetic optimization algorithm with deep learning enabled airborne particle-bound metals size prediction model. Chemosphere 2022, 303, 134960. [Google Scholar] [CrossRef]
- Ahmadi, B.; Younesi, S.; Ceylan, O.; Ozdemir, A. The Arithmetic Optimization Algorithm for Optimal Energy Resource Planning. In Proceedings of the 2021 56th International Universities Power Engineering Conference (UPEC), Middlesbrough, UK, 31 August 2021–3 September 2021; pp. 1–6. [Google Scholar]
- Bhat, S.J.; Santhosh, K.V. A localization and deployment model for wireless sensor networks using arithmetic optimization algorithm. Peer Peer Netw. Appl. 2022, 15, 1473–1485. [Google Scholar] [CrossRef]
- Kaveh, A.; Hamedani, K.B. Improved arithmetic optimization algorithm and its application to discrete structural optimization. Structures 2022, 35, 748–764. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E. Advanced arithmetic optimization algorithm for solving mechanical engineering design problems. PLoS ONE 2021, 16, e0255703. [Google Scholar] [CrossRef]
- Premkumar, M.; Jangir, P.; Kumar, B.S.; Sowmya, R.; Alhelou, H.H.; Abualigah, L.; Yildiz, A.R.; Mirjalili, S. A new arithmetic optimization algorithm for solving real-world multiobjective CEC-2021 constrained optimization problems: Diversity analysis and validations. IEEE Access 2021, 9, 84263–84295. [Google Scholar] [CrossRef]
- Zheng, R.; Jia, H.; Abualigah, L.; Liu, Q.; Wang, S. Deep ensemble of slime mold algorithm and arithmetic optimization algorithm for global optimization. Processes 2021, 9, 1774. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Sumari, P.; Gandomi, A. A novel evolutionary arithmetic optimization algorithm for multilevel thresholding segmentation of COVID-19 ct images. Processes 2021, 9, 1155. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Abualigah, L.; Ewees, A.A.; Al-Qaness, M.A.A.; Yousri, D.; Alshathri, S.; Elaziz, M.A. An electric fish-based arithmetic optimization algorithm for feature selection. Entropy 2021, 23, 1189. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.B.; Wang, W.F.; Xu, L.; Pan, J.S.; Chu, S.C. An Adaptive Parallel Arithmetic Optimization Algorithm for Robot Path Planning. Available online: https://www.hindawi.com/journals/jat/2021/3606895/ (accessed on 6 July 2022).
- Ewees, A.A.; Al-qaness, M.A.; Abualigah, L.; Oliva, D.; Algamal, Z.Y.; Anter, A.M.; Ibrahim, R.A.; Ghoniem, R.M.; Elaziz, M.A. Boosting arithmetic optimization algorithm with genetic algorithm operators for feature selection: Case study on cox proportional hazards model. Mathematics 2021, 9, 2321. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A. Improved multi-core arithmetic optimization algorithm-based ensemble mutation formultidisciplinary applications. J. Intell. Manuf. 2022, 1–42. [Google Scholar] [CrossRef]
- Khodadadi, N.; Snasel, V.; Mirjalili, S. Dynamic arithmetic optimization algorithm for truss optimization under natural frequency constraints. IEEE Access 2022, 10, 16188–16208. [Google Scholar] [CrossRef]
- Mahajan, S.; Abualigah, L.; Pandit, A.K.; Altalhi, M. Hybrid Aquila optimizer with arithmetic optimization algorithm for global optimization tasks. Soft Comput. 2022, 26, 4863–4881. [Google Scholar] [CrossRef]
- Li, X.-D.; Wang, J.-S.; Hao, W.-K.; Zhang, M.; Wang, M. Chaotic arithmetic optimization algorithm. Appl. Intell. 2022, 1–40. [Google Scholar] [CrossRef]
- Elaziz, M.A.; Abualigah, L.; Ibrahim, R.A.; Attiya, I. IoT Workflow Scheduling Using Intelligent Arithmetic Optimization Algorithm in Fog Computing. Comput. Intell. Neurosci. 2022, 2021, 9114113. Available online: https://www.hindawi.com/journals/cin/2021/9114113/ (accessed on 15 July 2022). [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Zhang, H.; Berg, A.C.; Maire, M.; Malik, J. SVM-KNN: Discriminative nearest neighbor classification for visual category recognition. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; pp. 2126–2136. [Google Scholar]
- Jerlin Rubini, L.; Perumal, E. Efficient classification of chronic kidney disease by using multi-kernel support vector machine and fruit fly optimization algorithm. Int. J. Imaging Syst. Technol. 2020, 30, 660–673. [Google Scholar] [CrossRef]
- Lin, G.Q.; Li, L.L.; Tseng, M.; Liu, H.-M.; Yuan, D.-D.; Tan, R.R. An improved moth-flame optimization algorithm for support vector machine prediction of photovoltaic power generation. J. Clean. Prod. 2020, 253, 119966. [Google Scholar] [CrossRef]
- Momin, J.; Xin-She, Y. A literature survey of benchmark functions for global optimization problems. J. Math. Model. Numer. Optim. 2013, 4, 150–194. [Google Scholar]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Fan, H.Y.; Lampinen, J. A trigonometric mutation operation to differential evolution. J. Glob. Optim. 2003, 27, 105–129. [Google Scholar] [CrossRef]
- Güraksın, G.E.; Haklı, H.; Uğuz, H. Support vector machines classification based on particle swarm optimization for bone age determination. Appl. Soft Comput. 2014, 24, 597–602. [Google Scholar] [CrossRef]
- Samadzadegan, F.; Soleymani, A.; Abbaspour, R.A. Evaluation of genetic algorithms for tuning SVM parameters in multi-class problems. In Proceedings of the 2010 11th International Symposium on Computational Intelligence and Informatics (CINTI), Budapest, Hungary, 18–20 November 2010; pp. 323–328. [Google Scholar]
- Bao, Y.; Hu, Z.; Xiong, T. A PSO and pattern search based memetic algorithm for SVMs parameters optimization. Neurocomputing 2013, 117, 98–106. [Google Scholar] [CrossRef]
- Eswaramoorthy, S.; Sivakumaran, N.; Sekaran, S. Grey Wolf Optimization Based Parameter Selection for Support Vector Machines. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2016, 35, 1513–1523. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Frank, A.; Asuncion, A. UCI Machine Learning Repository. 2010. Available online: http://archive.ics.uci.edu/ml (accessed on 15 July 2022).
- Bin, Z.; Yong, L.; Shao-Wei, X. Support vector machine and its application in handwritten numeral recognition. In Proceedings of the 15th International Conference on Pattern Recognition, Barcelona, Spain, 3–7 September 2000; pp. 720–723. [Google Scholar]


| Formula | Dim | Range | Fmin |
|---|---|---|---|
| 30/100/200 | [−100, 100] | 0 | |
| 30/100/200 | [−100, 100] | 0 | |
| 30/100/200 | [−100, 100] | 0 | |
| 30/100/200 | [−600, 600] | 0 | |
| 30/100/200 | [−50, 50] | 0 | |
| 30/100/200 | [−50, 50] | 0 |
| Algorithm | Parameter Setting |
|---|---|
| GA | Pm = 0.2, Pc = 0.6 |
| GWO | a linearly decreased from 2 to 0 |
| PSO | ω linearly decreased from 0.9 to 0.4, c1 = 2, c2 = 2 |
| HHO | q ∈ [0, 1]; r ∈ [0, 1]; E0 ∈ [−1, 1]; E1 ∈ [0, 2]; E ∈ [−2,2] |
| WOA | a linearly decreased from 2 to 0, r1 ∈ [0, 1], r2 ∈ [0, 1] |
| SOA | r1 ∈ [0, 1], r2 ∈ [0, 1] |
| AOA | r1 ∈ [0, 1], r2 ∈ [0, 1], r3 ∈ [0, 1], u = 0.5, α = 5 |
| IAOA | wbegin = 0.9, wend = 0.4, c ∈ [0.95, 1.05] |
| Function | Indext | Algorithms | |||||||
|---|---|---|---|---|---|---|---|---|---|
| GA | GWO | PSO | HHO | WOA | SOA | AOA | IAOA | ||
| f1 (Dim = 30) | Mean | 3.17 × 10−5 | 1.89 × 10−27 | 3.27 × 10−155 | 5.52 × 10−94 | 1.06 × 10−74 | 5.09 × 10−12 | 2.58 × 10−10 | 0.00 × 10+0 |
| Std | 7.39 × 10−5 | 3.54 × 10−27 | 1.79 × 10−154 | 3.01 × 10−93 | 3.19 × 10−74 | 7.42 × 10−12 | 1.41 × 10−9 | 0.00 × 10+0 | |
| Time | 0.1851 s | 0.3617 s | 0.1343 s | 0.1972 s | 0.1514 s | 0.2589 s | 0.1919 s | 0.2003 s | |
| f2 (Dim = 30) | Mean | 2.42 × 10−3 | 8.91 × 10−7 | 3.01 × 10−87 | 1.03 × 10−49 | 5.13 × 10+1 | 5.62 × 10−3 | 2.85 × 10−2 | 0.00 × 10+0 |
| Std | 3.20 × 10−3 | 5.89 × 10−7 | 1.65 × 10−86 | 3.51 × 10−49 | 2.89 × 10+1 | 1.24 × 10−2 | 1.86 × 10−2 | 0.00 × 10+0 | |
| Time | 0.0767 s | 0.3224 s | 0.1521 s | 0.2533 s | 0.1474 s | 0.2557 s | 0.2063 s | 0.2110 s | |
| f3 (Dim = 30) | Mean | 1.36 × 10−5 | 8.15 × 10−1 | 1.37 × 10+0 | 2.14 × 10−4 | 3.22 × 10−1 | 3.22 × 10+0 | 3.14 × 10+0 | 0.00 × 10+0 |
| Std | 2.50 × 10−5 | 3.99 × 10−1 | 2.85 × 10−1 | 2.93 × 10−4 | 1.82 × 10−1 | 5.18 × 10−1 | 2.40 × 10−1 | 0.00 × 10+0 | |
| Time | 0.0802 s | 0.3300 s | 0.1386 s | 0.3144 s | 0.1218 s | 0.2586 s | 0.1777 s | 0.1981 s | |
| f4 (Dim = 30) | Mean | 1.66 × 10−4 | 2.22 × 10−3 | 1.78 × 10−2 | 0.00 × 10+0 | 3.23 × 10−3 | 2.24 × 10−2 | 1.67 × 10−1 | 0.00 × 10+0 |
| Std | 2.76 × 10−4 | 5.94 × 10−3 | 6.37 × 10−2 | 0.00 × 10+0 | 1.77 × 10−2 | 2.88 × 10−2 | 1.41 × 10−1 | 0.00 × 10+0 | |
| Time | 0.0972 s | 0.1931 s | 0.1013 s | 0.2854 s | 0.1209 s | 0.1533 s | 0.1472 s | 0.1831 s | |
| f5 (Dim = 30) | Mean | 1.22 × 10−4 | 1.11 × 10−1 | 2.38 × 10−1 | 4.04 × 10−6 | 3.26 × 10−2 | 4.97 × 10−1 | 7.30 × 10−1 | 9.42 × 10−33 |
| Std | 2.40 × 10−4 | 6.52 × 10−2 | 3.82 × 10−2 | 6.63 × 10−6 | 2.31 × 10−2 | 1.14 × 10−1 | 3.37 × 10−2 | 2.78 × 10−48 | |
| Time | 0.1999 s | 0.4851 s | 0.3792 s | 0.9107 s | 0.3688 s | 0.4361 s | 0.4050 s | 0.6291 s | |
| f6 (Dim = 30) | Mean | 5.13 × 10−5 | 6.20 × 10−1 | 1.02 × 10+0 | 6.12 × 10−5 | 5.94 × 10−1 | 2.08 × 10+0 | 2.83 10+0 | 1.35 × 10−32 |
| Std | 1.00 × 10−4 | 2.39 × 10−1 | 2.05 × 10−1 | 8.38 × 10−5 | 3.00 × 10−1 | 2.46 × 10−1 | 1.08 × 10−1 | 5.57 × 10−48 | |
| time | 0.1896 s | 0.3792 s | 0.2763 s | 0.7032 s | 0.2942 s | 0.2982 s | 0.2891 s | 0.4713 s | |
| Function | Indext | Algorithms | |||||||
|---|---|---|---|---|---|---|---|---|---|
| GA | GWO | PSO | HHO | WOA | SOA | AOA | IAOA | ||
| f1 (Dim = 100) | Mean | 3.12 × 10−5 | 1.59 × 10−12 | 2.08 × 10−175 | 2.18 × 10−87 | 3.99 × 10−72 | 2.27 × 10−5 | 2.53 × 10−2 | 0.00 × 10+0 |
| Std | 6.05 × 10−5 | 9.86 × 10−13 | 0.00 × 10+0 | 8.44 × 10−87 | 1.54 × 10−71 | 3.07 × 10−5 | 1.01 × 10−2 | 0.00 × 10+0 | |
| f2 (Dim = 100) | Mean | 2.26 × 10−3 | 8.70 × 10−1 | 2.30 × 10−96 | 8.18 × 10−50 | 7.44 × 10+1 | 6.96 × 10+1 | 9.10 × 10−2 | 0.00 × 10−0 |
| Std | 2.27 × 10−3 | 8.54 × 10−1 | 2.85 × 10−98 | 2.56 × 10−49 | 2.23 × 10+1 | 1.53 × 10+1 | 1.50 × 10−2 | 0.00 × 10+0 | |
| f3 (Dim = 100) | Mean | 2.57 × 10−5 | 1.04 × 10+1 | 1.58 × 10+1 | 2.84 × 10−4 | 4.42 × 10+0 | 1.87 × 10+1 | 1.80 × 10+1 | 0.00 × 10+0 |
| Std | 4.65 × 10−5 | 9.39 × 10−1 | 8.71 × 10−1 | 4.84 × 10−4 | 9.99 × 10−1 | 4.70 × 10−1 | 6.91 × 10−1 | 0.00 × 10+0 | |
| f4 (Dim = 100) | Mean | 2.99 × 10−4 | 1.50 × 10−3 | 0.00 × 10+0 | 0.00 × 10+0 | 0.00 × 10+0 | 2.72 × 10−2 | 5.58 × 10+2 | 0.00 × 10+0 |
| Std | 4.54 × 10−4 | 5.83 × 10−3 | 0.00 × 10+0 | 0.00 × 10+0 | 0.00 × 10+0 | 5.54 × 10−2 | 7.89 × 10+1 | 0.00 × 10+0 | |
| f5 (Dim = 100) | Mean | 1.14 × 10−4 | 2.74 × 10−1 | 5.64 × 10−1 | 2.77 × 10−6 | 4.66 × 10−2 | 8.04 × 10−1 | 9.01 × 10−1 | 4.71 × 10−33 |
| Std | 1.89 × 10−4 | 7.50 × 10−2 | 7.12 × 10−2 | 3.86 × 10−6 | 1.58 × 10−2 | 8.75 × 10−2 | 2.63 × 10−2 | 7.08 × 10−49 | |
| f6 (Dim = 100) | Mean | 6.46 × 10−5 | 6.67 × 10+0 | 9.67 × 10+0 | 2.00 × 10−4 | 3.09 × 10+0 | 9.30 × 10+0 | 9.95 × 10+0 | 1.35 × 10−32 |
| Std | 1.81 × 10−4 | 4.60 × 10−1 | 2.81 × 10−1 | 3.43 × 10−4 | 8.95 × 10−1 | 2.77 × 10−1 | 7.06 × 10−2 | 2.83 × 10−48 | |
| f1 (Dim = 200) | Mean | 1.37 × 10−5 | 1.24 × 10−7 | 3.34 × 10−190 | 3.85 × 10−96 | 3.89 × 10−71 | 1.15 × 10−3 | 1.38 × 10−1 | 0.00 × 10+0 |
| Std | 1.91 × 10−5 | 6.41 × 10−8 | 0.00 × 10+0 | 1.28 × 10−95 | 1.32 × 10−70 | 1.01 × 10−3 | 1.82 × 10−2 | 0.00 × 10+0 | |
| f2 (Dim = 200) | Mean | 3.13 × 10−3 | 2.63 × 10+1 | 2.34 × 10−96 | 7.07 × 10−48 | 7.80 × 10+1 | 9.39 × 10+1 | 1.28 × 10−1 | 0.00 × 10+0 |
| Std | 3.17 × 10−3 | 5.71 × 10+0 | 1.13 × 10−98 | 1.96 × 10−47 | 1.91 × 10+1 | 2.45 × 10+0 | 1.27 × 10−2 | 0.00 × 10+0 | |
| f3 (Dim = 200) | Mean | 3.13 × 10−5 | 2.86 × 10+1 | 3.12 × 10+1 | 7.83 × 10−4 | 1.10 × 10+1 | 4.26 × 10+1 | 4.17 × 10+1 | 0.00 × 10+0 |
| Std | 1.03 × 10−4 | 1.93 × 10+0 | 6.88 × 10−1 | 1.21 × 10−3 | 4.03 × 10+0 | 8.86 × 10−1 | 7.20 × 10−1 | 0.00 × 10+0 | |
| f4 (Dim = 200) | Mean | 8.96 × 10−5 | 5.04 × 10−3 | 0.00 × 10+0 | 0.00 × 10+0 | 0.00 × 10+0 | 2.76 × 10−2 | 2.37 × 10+3 | 0.00 × 10+0 |
| Std | 1.60 × 10−4 | 1.33 × 10−2 | 0.00 × 10+0 | 0.00 × 10+0 | 0.00 × 10+0 | 5.48 × 10−2 | 4.92 × 10+2 | 0.00 × 10+0 | |
| f5 (Dim = 200) | Mean | 7.37 × 10−5 | 5.55 × 10−1 | 8.54 × 10−1 | 1.70 × 10−6 | 6.61 × 10−2 | 9.20 × 10−1 | 1.01 × 10+0 | 2.36 × 10−33 |
| Std | 1.57 × 10−4 | 7.86 × 10−2 | 3.57 × 10−2 | 2.34 × 10−6 | 2.88 × 10−2 | 5.59 × 10−2 | 1.16 × 10−2 | 3.54 × 10−49 | |
| f6 (Dim = 200) | Mean | 3.38 × 10−5 | 1.70 × 10+1 | 1.98 × 10+1 | 1.97 × 10−4 | 6.44 × 10+0 | 2.11 × 10+0 | 2.00 × 10+1 | 1.35 × 10−32 |
| Std | 6.18 × 10−5 | 7.08 × 10−1 | 7.96 × 10−2 | 3.49 × 10−4 | 2.16 × 10+0 | 1.58 × 10+0 | 1.78 × 10−2 | 2.83 × 10−48 | |
| Dataset | Features | Instances | Classes |
|---|---|---|---|
| Balance | 4 | 625 | 3 |
| Breast cancer | 9 | 277 | 2 |
| DNA | 180 | 2000 | 3 |
| German | 24 | 1000 | 2 |
| glass | 9 | 214 | 6 |
| Heart | 13 | 303 | 2 |
| Ionosphere | 34 | 351 | 2 |
| Iris | 4 | 150 | 3 |
| zoo | 16 | 101 | 7 |
| Letter | 16 | 5000 | 26 |
| Liver | 6 | 345 | 2 |
| Vote | 16 | 435 | 2 |
| Waveform | 21 | 5000 | 2 |
| Pima | 8 | 768 | 3 |
| Segment | 18 | 2310 | 7 |
| Sonar | 60 | 208 | 2 |
| Wine | 13 | 178 | 3 |
| Vehicle | 18 | 846 | 4 |
| Algorithm | GA | GWO | PSO | HHO | ||||
| Dataset | Avg ± std | Rank | Avg ± std | Rank | Avg ± std | Rank | Avg ± std | Rank |
| Balance | 97.10 ± 2.72 | 4 | 96.77 ± 3.72 | 8 | 97.10 ± 3.38 | 5 | 96.94 ± 4.06 | 7 |
| Breast cancer | 75.93 ± 7.86 | 7 | 78.52 ± 9.37 | 5 | 74.81 ± 9.85 | 8 | 78.52 ± 8.15 | 4 |
| DNA | 75.15 ± 19.58 | 7 | 93.94 ± 2.86 | 1 | 55.76 ± 4.56 | 8 | 91.21 ± 11.56 | 4 |
| German | 75.70 ± 5.50 | 7 | 78.60 + 3.60 | 1 | 74.60 ± 3.44 | 8 | 78.30 ± 4.14 | 5 |
| glass | 77.62 ± 8.11 | 4 | 77.14 ± 10.72 | 6 | 77.14 ± 7.71 | 7 | 77.62 ± 7.46 | 3 |
| Heart | 88.33 ± 7.24 | 1 | 85.33 ± 3.58 | 6 | 84.33 ± 4.73 | 8 | 87.67 ± 4.46 | 2 |
| Ionosphere | 93.71 ± 8.06 | 8 | 97.71 ± 2.25 | 2 | 94.57 ± 4.56 | 7 | 97.43 ± 2.5 | 3 |
| Iris | 97.33 ± 4.66 | 5 | 97.33 ± 3.44 | 3 | 96.67 ± 4.71 | 7 | 98.00 ± 3.22 | 2 |
| zoo | 93.00 ± 10.59 | 6 | 97.00 ± 4.83 | 1 | 85.00 ± 15.09 | 8 | 94.00 ± 6.99 | 4 |
| Letter | 88.21 ± 2.90 | 4 | 88.07 ± 1.78 | 6 | 87.93 ± 2.27 | 7 | 88.21 ± 3.30 | 5 |
| Liver | 75.00 ± 6.08 | 8 | 76.76 ± 9.85 | 7 | 76.76 ± 5.96 | 6 | 77.06 ± 6.47 | 5 |
| Vote | 94.65 ± 6.21 | 8 | 96.51 ± 3.51 | 2 | 94.65 ± 4.39 | 7 | 96.74 ± 2.50 | 1 |
| Waveform | 86.97 ± 5.35 | 8 | 89.39 ± 3.98 | 2 | 87.88 ± 3.71 | 7 | 89.09 ± 2.12 | 3 |
| Pima | 78.42 ± 5.27 | 7 | 79.21 ± 3.44 | 5 | 77.76 ± 3.94 | 8 | 79.34 ± 3.40 | 4 |
| Segment | 97.73 ± 1.92 | 5 | 97.27 ± 1.39 | 8 | 97.58 ± 2.49 | 6 | 97.73 ± 1.29 | 3 |
| Sonar | 90.53 ± 7.77 | 4 | 92.63 ± 5.66 | 2 | 87.37 ± 13.63 | 8 | 93.16 ± 7.04 | 1 |
| Wine | 98.82 ± 2.48 | 6 | 98.82 ± 2.48 | 7 | 98.24 ± 3.97 | 8 | 100.00 ± 0.00 | 1 |
| Vehicle | 84.09 ± 7.73 | 4 | 83.86 ± 5.91 | 5 | 83.41 ± 4.42 | 7 | 85.23 ± 5.59 | 2 |
| Algorithm | WOA | SOA | AOA | IAOA | ||||
| Dataset | Avg ± std | Rank | Avg ± std | Rank | Avg ± std | Rank | Avg ± std | Rank |
| Balance | 97.26 ± 2.85 | 3 | 97.42 ± 1.56 | 2 | 96.94 ± 3.60 | 6 | 97.58 ± 2.97 | 1 |
| Breast cancer | 79.26 ± 8.04 | 3 | 79.26 ± 5.00 | 2 | 77.41 ± 6.40 | 6 | 79.63 ± 6.11 | 1 |
| DNA | 90.30 ± 13.54 | 6 | 92.27 ± 4.82 | 2 | 90.91 ± 6.06 | 5 | 91.52 ± 6.71 | 3 |
| German | 78.50 ± 3.10 | 2 | 78.30 ± 3.27 | 4 | 77.70 ± 3.59 | 6 | 78.40 ± 2.41 | 3 |
| glass | 76.67 ± 8.23 | 8 | 77.62 ± 5.52 | 2 | 77.62 ± 12.10 | 5 | 78.10 ± 5.59 | 1 |
| Heart | 87.33 ± 4.39 | 3 | 86.33 ± 4.57 | 4 | 85.33 ± 6.70 | 7 | 86.00 ± 6.05 | 5 |
| Ionosphere | 96.57 ± 2.95 | 5 | 97.14 ± 3.56 | 4 | 96.57 ± 3.76 | 6 | 98.00 ± 2.71 | 1 |
| Iris | 96.67 ± 3.51 | 8 | 97.33 ± 4.66 | 6 | 97.33 ± 3.44 | 4 | 98.67 ± 4.22 | 1 |
| zoo | 94.00 ± 8.43 | 5 | 96.00 ± 5.16 | 2 | 95.00 ± 5.27 | 3 | 93.00 ± 6.75 | 7 |
| Letter | 87.71 ± 1.50 | 8 | 88.57 ± 2.69 | 2 | 88.57 ± 3.55 | 3 | 88.79 ± 2.23 | 1 |
| Liver | 78.24 ± 4.64 | 2 | 79.41 ± 7.07 | 1 | 78.24 ± 6.82 | 3 | 77.94 ± 6.39 | 4 |
| Vote | 95.12 ± 7.31 | 5 | 96.05 ± 2.91 | 4 | 94.88 ± 4.63 | 6 | 96.28 ± 1.63 | 3 |
| Waveform | 88.48 ± 4.30 | 5 | 88.79 ± 4.69 | 4 | 88.03 ± 4.19 | 6 | 89.55 ± 2.62 | 1 |
| Pima | 79.87 ± 3.10 | 2 | 79.47 ± 4.69 | 3 | 79.08 ± 4.74 | 6 | 80.13 ± 4.45 | 1 |
| Segment | 97.73 ± 1.64 | 4 | 98.03 ± 1.61 | 1 | 97.88 ± 2.39 | 2 | 97.42 ± 1.76 | 7 |
| Sonar | 90.00 ± 9.75 | 5 | 92.11 ± 10.89 | 3 | 88.42 ± 8.15 | 7 | 88.95 ± 5.79 | 6 |
| Wine | 99.41 ± 1.86 | 2 | 99.41 ± 1.86 | 3 | 99.41 ± 1.86 | 4 | 99.41 ± 1.86 | 5 |
| Vehicle | 83.64 ± 4.77 | 6 | 84.77 ± 4.55 | 3 | 83.41 ± 6.25 | 8 | 86.36 ± 4.15 | 1 |
| Parameters/Algorithms | GA | GWO | PSO | HHO | WOA | SOA | AOA | IAOA |
|---|---|---|---|---|---|---|---|---|
| C | 1.0054 | 4.7506 | 98.2224 | 1.5743 | 11.0905 | 1.00 × 10−6 | 36.1315 | 53.5288 |
| g | 0.0100 | 0.0001 | 7.7435 | 0.0052 | 3.92 × 10−4 | 1.00 × 10−6 | 1.81 × 10−4 | 0.0109 |
| Accuracy | 98.375 | 96.875 | 100 | 99.375 | 96.875 | 88.75 | 98.75 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, H.; Fu, X.; Zeng, Z.; Zhong, K.; Liu, S. An Improved Arithmetic Optimization Algorithm and Its Application to Determine the Parameters of Support Vector Machine. Mathematics 2022, 10, 2875. https://doi.org/10.3390/math10162875
Fang H, Fu X, Zeng Z, Zhong K, Liu S. An Improved Arithmetic Optimization Algorithm and Its Application to Determine the Parameters of Support Vector Machine. Mathematics. 2022; 10(16):2875. https://doi.org/10.3390/math10162875
Chicago/Turabian StyleFang, Heping, Xiaopeng Fu, Zhiyong Zeng, Kunhua Zhong, and Shuguang Liu. 2022. "An Improved Arithmetic Optimization Algorithm and Its Application to Determine the Parameters of Support Vector Machine" Mathematics 10, no. 16: 2875. https://doi.org/10.3390/math10162875
APA StyleFang, H., Fu, X., Zeng, Z., Zhong, K., & Liu, S. (2022). An Improved Arithmetic Optimization Algorithm and Its Application to Determine the Parameters of Support Vector Machine. Mathematics, 10(16), 2875. https://doi.org/10.3390/math10162875






