Performance Evaluation of Healthcare Supply Chain in Industry 4.0 with Linear Diophantine Fuzzy Sine-Trigonometric Aggregation Operations

Abstract

The concept of linear Diophantine fuzzy set (LDFS) theory with its control parameters is a strong model for machine learning and data-driven multi-criteria decision making (MCDM). The sine-trigonometric function (STF) has two significant features, periodicity and symmetry about the origin that are very useful tools for information analysis. Keeping in view the characteristics of both STF and LDFS theory, this article introduces the sine-trigonometric operations for linear Diophantine fuzzy numbers (LDFNs). These operational laws lay a foundation for developing new linear Diophantine fuzzy sine-trigonometric aggregation operators (LDFSTAOs). The integration of Industry 4.0 technology into healthcare has the potential to revolutionize patient care. One of the most challenging tasks is the selection of efficient suppliers for the healthcare supply chain (HSC). The traditional suppliers are not efficient in accordance with Industry 4.0, with particular uncertainties. A new MCDM framework is presented based on LDFSTAOs to examine the HSC performance in industry 4.0. A credibility test, sensitivity analysis and comparative analysis are performed to express the novelty, reliability, and efficiency of the proposed methodology.

1. Introduction

The healthcare supply chain (HSC) is a complex network of interrelated systems and operations that ensure the manufacturing, distribution, and delivery of pharmaceutical and other healthcare supplies. Manufacturers contribute significantly to the supply chain by producing drugs and healthcare medications. Distributors obtain huge quantities of medications and equipment from manufacturers and distribute them in appropriate locations. There are wholesalers who specialize in supplying only to hospitals, stores, or nursing homes. In addition to patients and their families, the HSC also includes officials, insurance companies, regulators of drug quality, and retail pharmacies. The international HSC has various built-in safety features to ensure that medical supplies are produced and distributed on time. An efficient supplier has the ability to anticipate and respond to emergent needs of healthcare medications.

The traditional HSC has to face a number of issues, including inaccurate records, lack of demand analysis, delayed supplies, high costs, and transitional difficulties to automation. Numerous global healthcare supply systems have recently been impacted by COVID-19, resulting in a shortage of healthcare medications and instruments. These challenges, as well as natural disasters, have compelled the global community to pursue technological advances in the field of healthcare systems. By combining the HSC with newly developed technologies with Industry 4.0 revolutions has enabled its digitalization. With the advent of cloud computation and large amounts of data, healthcare and technology have become intertwined. Manufacturing, logistics, and HSC management have already been customized as a result of the Internet of Things (IoT) and the automation of managerial processes. For instance, blockchain technology enables the combining of patients’ prescription and medical data from multiple sources into a single comprehensive set of updated facts. One of the potential benefits of this technology is that it is an inexpensive method that enables the user to quickly access the information without compromising its confidentiality. Blockchain technology is an autonomous method for ensuring the security of medical records. Some contemporary HSC trends in Industry 4.0 are shown in Figure 1.

A brief bibliometric analysis of supply chain (SC) and supplier selection (SS) in Industry 4.0 is given in

Table 1. Bibliometric analysis of SC and SS in Industry 4.0.

Researchers	Techniques	Applications
Xu [1]	Intuitionistic fuzzy CODAS method	Performance evaluation of blockchain industry
Yang et al. [2]	Bibliometric analysis	MCDM in shipping Industry 4.0
Krstic et al. [3]	COBRA method	Reverse logistics in Industry 4.0
Yavuz et al. [4]	HFS linguistic model	Evaluation of alternative-fuel vehicles
Farid and Riaz [5]	Prioritized interactive aggregation operators	Evaluation of efficient autonomous vehicles
Gružauskas et al. [6]	Optimization cost effective performance	Minimizing the trade-off with autonomous vehicles
Gerhátová et al. [7]	Bibliometric analysis	Implementation of Industry 4.0 railway transport
Qahtan et al. [8]	q-ROF rough sets model	Sustainable shipping transportation industry
Bravo and Vidal [9]	Optimization models	Freight transportation function in supply chain
Mondal and Roy [10]	ChIVT2PFS	sustainable supply chain management
Rong et al. [11]	cubic Fermatean fuzzy MARCOS	cold chain logistics distribution
Tansel [12]	Historical perspective	Industrial revolutions
ForouzeshNejad [13]	Hybrid MCDM	Supplier selection in Industry 4.0
Gao et al. [14]	VIKOR algorithm with q-RIVOF data	SSP of medical merchandise
He et al. [15]	Taxonomy approach under Pythagorean 2-tuple linguistic (P2TL) information	SS in medical equipment companies
Calik [16]	PFS-AHP and PFS-TOPSIS techniques	Green SS in the Industry 4.0
Wei et al. [17]	CoCoSo method based on SSAO and BWM for Fermatean fuzzy set (FFS)	Green SSP
Sharaf and Khalil [18]	TODIM approach for Spherical fuzzy information	Health and safety measurements
Sun and Cai [19]	GRA-TOPSIS for SVNS	Green SS
Saraji et al. [20]	Sustainable CRITIC-COPRAS framework for digital transformation	Handling challenges to Industry 4.0

.

HSC logistics in Industry 4.0 enables various smart features of business promotion with end-to-end (E2E) visibility, digitization, and undoubtedly supply chain operations, as well as tracking, control, and trustworthy logistics recognition.

The HSC in Industry 4.0 assists in delivering vital medical supplies to patients in an efficient and affordable way. It modernizes the healthcare industry by minimizing costs, enhancing quality of care, making accurate demand and supply projections, and automating processes. Organizations are presently employing technological advancements to build efficient routes for interaction and processes for collaboration to enhance the efficiency of their supply chains through improved information exchange. While businesses are continuously seeking methods to adjust to these new technologies, conventional supply chains must swiftly transform in order to successfully and efficiently incorporate the concepts of Industry 4.0 technologies to remain competitive in perpetually evolving and dynamic markets. Four revolutions of industries and logistics are briefly expressed in

Table 2. Four revolutions of industries and logistics.

Phases	Revolutions	Periods	Location	Approaches
1st	Mechanization	Late 18th–early 19th century	Industrial cities	Steam engines, mechanical production
2nd	Mass production	Late 19th–mid 20th century	Industrial regions	Electricity, division of labor
3rd	Automation	Second half 20th century	Global production networks	Electronics, Information technology
4th	Robotics, cloud computing	Early 21th century	Smart industries, smart technologies, connectivity, tracking, cost efficiency, smart cities, smart vehicles	Global value chains, supply chains, smart roads

.

The supplier selection problem (SSP) in the healthcare sector is a significant MCDM problem. SSP in pharmaceuticals, in particular, should be approached with caution because a poor choice might result in excessive expenses, inconvenient delays, and poor medical quality. This has a direct impact on the well-being of patients. Typically, environmental, economic, and social concerns are included in an SSP. Furthermore, 4.0 technologies are being used in the pharmaceutical industry. As a result, numerous researchers have now incorporated 4.0 technologies as a criterion for the SSP. Industry 4.0 technologies aid in the regulation of pharmaceutical manufacturing, demand and supply, quality, and cost-effectiveness. In a stochastic environment, various researchers have contributed to the SSP using different frameworks and methodologies.

The MCDM process involves the selection of the most suitable option among the available ones against specific criteria. However, uncertain data modeling and CRISP methods lead to vagueness and ambiguities in this process.To address these issues, Zadeh [21] initiated the concept of fuzzy sets (FSs), Pawlak [22] introduced rough sets (RSs), and Molodtsov [23] presented soft sets (SSs). All of these theories are independent generalizations of the CRISP set. FS theory has been further extended to many other theories such as intuitionistic fuzzy sets (IFSs) [24], Pythagorean fuzzy sets (PyFSs) [25,26], and q-rung orthopair fuzzy sets (q-ROFSs) [27]. These models are very useful tools to address uncertainties in machine learning and data-driven MCDM problems that are commonly experienced in real life. The q-ROF ARAS method [28] with entropy measures and prioritized complex spherical fuzzy [29] are new hybrid MCDM approaches. Score functions for q-ROFSs [30] and intuitionistic fuzzy hypersoft sets (IFHSSs) with similarity measures [31] provide new approaches for modeling uncertain information. Aggregation operators have been successfully utilized for the information aggregation process in MCDM problems [32,33,34].

LDFS theory was initially proposed by Riaz and Hashmi [35], and assigns a membership grade (MG), a non-membership grade (NMG), and control parameters (CPs) to each object. In this theory, a DM can freely choose these grades from [0, 1] in the MCDM process. The presence of CPs give a physical assessment of the objects in a best worst situation. CPs may be regarded as grades assigned to DM’s judgments. As a result, an LDFS aims to broaden the range of MG and NMG in MCDM/MADM process. The values of MG and NMG are $\mu ,\nu \in [0,1]$. Figure 2 provides a brief overview of the comparison between IFS, PyFS, q-ROFS, and LDFS.

Some recent contributions based on LDFS theory are expressed in

Table 3. Some recent contributions based on LDFS models.

Researchers	LDFS Models	Approaches and Applications
Mahmood et al. [36]	IVLDFS	Power Muirhead mean operators with decision making
Ali et al. [37]	Complex LDF uncertain linguistic	Heronian mean operators for MADM
Singh et al. [38]	LDF uncertain linguistic	Prospect theory with performance analysis
Gul and Aydogdu [39]	LDFS	An extension of TOPSIS
Kamaci [40]	Complex LDFS	CoSine similarity measures with MCDM applications
Kamaci [41]	LDF algebraic structures	Coding theory
Mohammad et al. [42]	LDFS theory	Extension of TOPSIS with MCDM
Hanif et al. [43]	LDF graphs and LDFS relations	Healthcare diagnosis
Ayub et al. [44]	LDF rough sets	LDFS relations with multi-stage MCDM
Jayakumar et al. [45]	Complex linear Diophantine fuzzy soft set	Finding a suitable spraying fertilizers solutions with agri-drone

.

Motivation and Highlights

The highlights and motivation are given as follows.

• Modeling uncertain information with LDFSs.
• Developing LDF sine-trigonometric aggregation operator for information analysis.
• The entropy method is utilized for computing weights of criteria.
• A robust MCDM framework is proposed based on LDFSTAOs.
• Performance analysis of healthcare suppliers with new MCDM method.
• Ranking index for feasible alternatives is determined with a score function to seek an optimal alternative.

The objectives, goals, and main contribution of the anticipated study are listed as follows.

1.

LDFS theory is an efficient approach to address uncertain problems in various fields.

2.

The symmetry about the origin and periodicity of sine-trigonometric function (STF) are two significant features that are useful for complying with the DMS expert opinion.

3.

This article introduces new sine-trigonometric operational laws for linear Diophantine fuzzy numbers (LDFNs) as well as linear Diophantine fuzzy sine-trigonometric aggregation operators (LDFSTAOs) are developed. Some functional characteristics of LDFSTAOs are also explored.

4.

Several important characteristics of AOs such as idempotency, boundedness, and monotonicity are also explored.

5.

The main objective is to establish a relationship between the aggregation operators and MCDM scenarios. The application of HSC in Industry 4.0 is developed to address the efficacy, comprehension, and purpose of the suggested aggregated operations.

6.

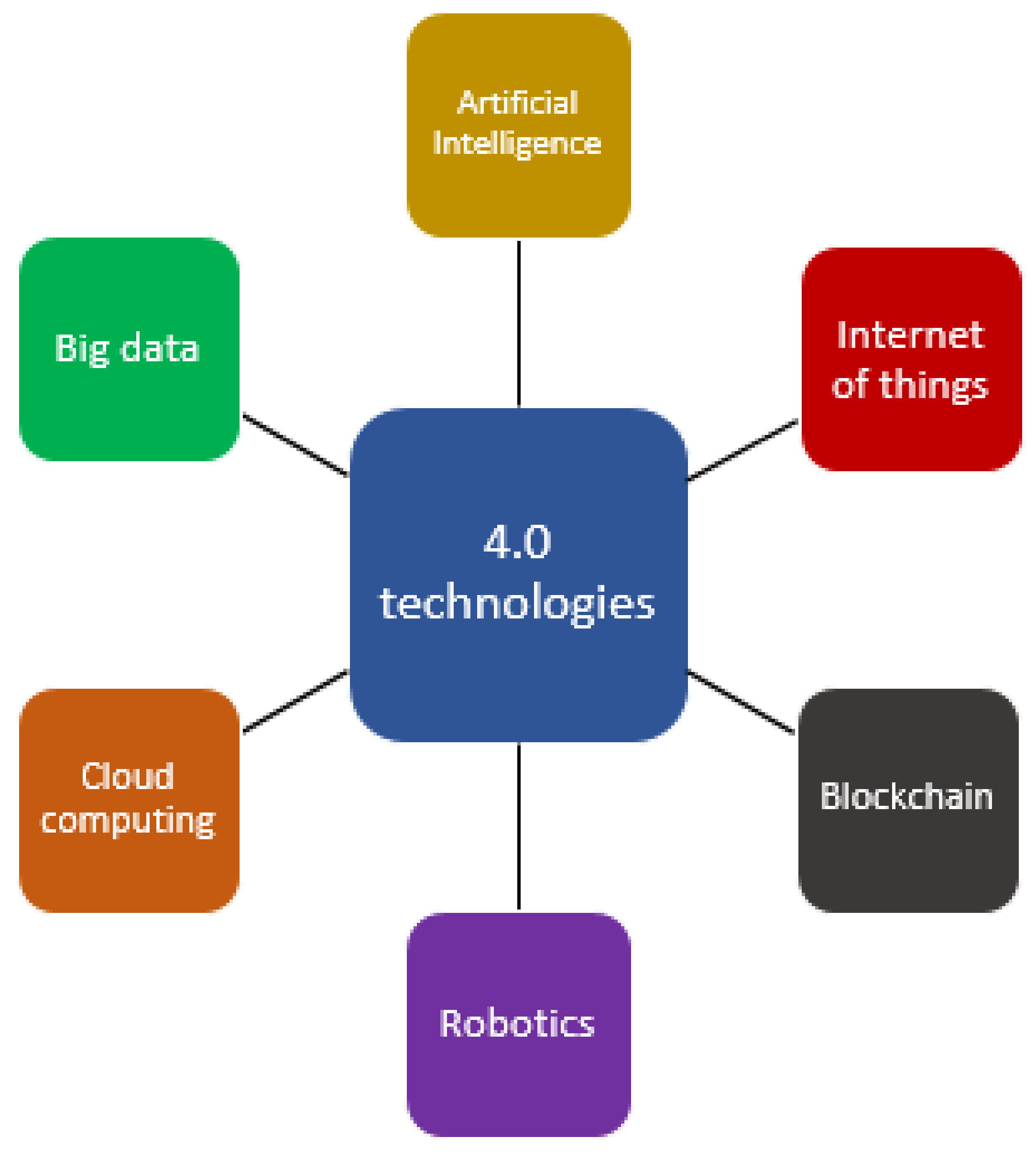
This study covers gaps in the literature and provides a broad domain for big data in fields such as healthcare, business, artificial intelligence, and machine learning in Industry 4.0. We can deal with challenges that contain any ambiguity and uncertainty. The conclusions drawn by applying the proposed operators and LDFSs to the MCDM framework will be more reliable and efficient.

This article is mainly composed into different sections as follows. Section 2 gives the fundamentals of the LDFSs, LDFNs, LDFS score function, LDFS accuracy function, and the fundamentals of LDFSs. Section 3 introduces the sine-trigonometric operational laws for LDFSs. Section 4 develops novel LDF sine-trigonometric averaging AOs. Section 5 introduces LDF sine-trigonometric geometric AOs. Section 6 discusses some important results of this study and indicates possible extension areas for future work.

2. Fundamental Concepts

In this section, we discuss some basic concepts that are essential for the current research work. We use the following notions and symbols in the remaining part of the manuscript.

Notions	Abbreviations	Symbols
Linear Diophantine fuzzy set	LDFS	L
Membership grade	MG	${\mu }_L$
Non-membership grade	NMG	${\nu }_L$
Control parameters	CPs	${\lambda }_L,{\eta }_L$
Score function	SF	$\mathsf{\Psi }$
Accuracy function	AF	$\mathsf{\Phi }$

Definition 1.

([35]). A LDFS L in X can be expressed as

$$L=\{(\ell ,\langle {\mu }_L(\ell ),{\nu }_L(\ell )\rangle ,\langle {\lambda }_L(\ell ),{\eta }_L(\ell )\rangle ):\ell \in L\}$$

where the values ${\mu }_L(\ell )$, ${\nu }_L(\ell )$, ${\lambda }_L(\ell )$, and ${\eta }_L(\ell )$ are taken from $[0,1]$, and these values represent the MG, NMG, and CPs of an element $\ell \in L$, respectively, such that

$$0\le {\lambda }_L(\ell )+{\eta }_L(\ell )\le 1,$$

$$0\le {\mu }_L(\ell ){\lambda }_L(\ell )+{\nu }_L(\ell ){\eta }_L(\ell )\le 1,$$

for every $\ell \in L$. The hesitancy grade (HG) can be calculated as

$${\hslash }_L(\ell ){\pi }_L(\ell )=1-({\mu }_L(\ell ){\lambda }_L(\ell )+{\nu }_L(\ell ){\eta }_L(\ell )),$$

where ${\hslash }_L$ are the CPs related to HG.

Definition 2.

([35]). A linear Diophantine fuzzy number (LDFN) is defined as

$$L=(\langle {\mu }_L,{\nu }_L\rangle ,\langle {\lambda }_L,{\eta }_L\rangle ),$$

where ${\mu }_L$, ${\nu }_L$, ${\lambda }_L$, ${\eta }_L\in [0,1]$ satisfy the following conditions

• $0\le {\lambda }_L+{\eta }_L\le 1$
• $0\le {\mu }_L{\lambda }_L+{\nu }_L{\eta }_L\le 1$

Definition 3.

([35]). Let $L_i=(\langle {\mu }_{L_i},{\nu }_{L_i}\rangle ,\langle {\lambda }_{L_i},{\eta }_{L_i}\rangle )$, $i=1,2$, and $\tau >0$. Then,

• $L_1⊞L_2=(\langle {\mu }_{L_1}+{\mu }_{L_2}-{\mu }_{L_1}{\mu }_{L_2},{\nu }_{L_1}{\nu }_{L_2}\rangle ,\langle {\lambda }_{L_1}+{\lambda }_{L_2}-{\lambda }_{L_1}{\lambda }_{L_2},{\eta }_{L_1}{\eta }_{L_2}\rangle )$,
• $L_1⊠L_2=(\langle {\mu }_{L_1}{\mu }_{L_2},{\nu }_{L_1}+{\nu }_{L_2}-{\nu }_{L_1}{\nu }_{L_2}\rangle ,\langle {\lambda }_{L_1}{\lambda }_{L_2},{\eta }_{L_1}+{\eta }_{L_2}-{\eta }_{L_1}{\eta }_{L_2}\rangle )$,
• $\tau L_1=(\langle 1-{(1-{\mu }_{L_1})}^{\tau },{\nu }_{L_1}^{\tau }\rangle ,\langle 1-{(1-{\lambda }_{L_1})}^{\tau },{\eta }_{L_1}^{\tau }\rangle )$,
• $L_1^{\tau }=(\langle {\mu }_{L_1}^{\tau },1-{(1-{\nu }_{L_1})}^{\tau }\rangle ,\langle {\lambda }_{L_1}^{\tau },1-{(1-{\eta }_{L_1})}^{\tau }\rangle )$.

Definition 4.

([35]). Let $L_i=(\langle {\mu }_{L_i},{\nu }_{L_i}\rangle ,\langle {\lambda }_{L_i},{\eta }_{L_i}\rangle )$, $i=1,2$. Then,

• $L_1^c=(\langle {\nu }_{L_1},{\mu }_{L_1}\rangle ,\langle {\eta }_{L_1},{\lambda }_{L_1}\rangle )$,
• $L_1⪯L_2$if${\mu }_{L_1}\le {\mu }_{L_2}$, ${\nu }_{L_1}\ge {\nu }_{L_2}$, ${\lambda }_{L_1}\le {\lambda }_{L_2}$and, ${\eta }_{L_1}\ge {\eta }_{L_2}$,
• $L_1=L_2$if${\mu }_{L_1}={\mu }_{L_2}$, ${\nu }_{L_1}={\nu }_{L_2}$, ${\lambda }_{L_1}={\lambda }_{L_2}$and, ${\eta }_{L_1}={\eta }_{L_2}$.

Definition 5.

([35]). The SF Ψ of an LDFN $L=(\langle {\mu }_L,{\nu }_L\rangle ,\langle {\lambda }_L,{\eta }_L\rangle )$ is defined as

$$\mathsf{\Psi }\left(L\right)=\frac{1}{2}[({\mu }_L-{\nu }_L)+({\lambda }_L-{\eta }_L)]$$

(1)

where $\mathsf{\Psi }\left(L\right)\in [-1,1]$.

Definition 6.

([35]). For an LDFN $L=(\langle {\mu }_L,{\nu }_L\rangle ,\langle {\lambda }_L,{\eta }_L\rangle )$, the AF Φ is computed as

$$\mathsf{\Phi }\left(L\right)=\frac{1}{2}\left[\left(\frac{{\mu }_L+{\nu }_L}{2}\right)+({\lambda }_L+{\eta }_L)\right]$$

(2)

where $\mathsf{\Phi }\left(L\right)\in [0,1]$.

Definition 7.

([35]). The SF and CF are used to compare two LDFNs as follows.

• If $\mathsf{\Psi }\left({\ell }_1\right)<\mathsf{\Psi }\left({\ell }_2\right)$, then ${\ell }_1<{\ell }_2$.
• If $\mathsf{\Psi }\left({\ell }_1\right)>\mathsf{\Psi }\left({\ell }_2\right)$, then ${\ell }_1>{\ell }_2$.
• If $\mathsf{\Psi }\left({\ell }_1\right)=\mathsf{\Psi }\left({\ell }_2\right)$, then ${\ell }_1<{\ell }_2$if $\mathsf{\Phi }\left({\ell }_1\right)<\mathsf{\Phi }\left({\ell }_2\right)$.
• If $\mathsf{\Psi }\left({\ell }_1\right)=\mathsf{\Psi }\left({\ell }_2\right)$, then ${\ell }_1>{\ell }_2$if $\mathsf{\Phi }\left({\ell }_1\right)>\mathsf{\Phi }\left({\ell }_2\right)$.
• If $\mathsf{\Psi }\left({\ell }_1\right)=\mathsf{\Psi }\left({\ell }_2\right)$, then ${\ell }_1={\ell }_2$if $\mathsf{\Phi }\left({\ell }_1\right)=\mathsf{\Phi }\left({\ell }_2\right)$.

Definition 8.

([46]). Let $L_i=(\langle {\mu }_{L_i},{\nu }_{L_i}\rangle ,\langle {\lambda }_{L_i},{\eta }_{L_i}\rangle )$, $i=1,2,...,r$, be a set of LDFNs and $\kappa =\{{\kappa }_1,{\kappa }_2,...,{\kappa }_r\}$ be the weight vector (WV) with ${\kappa }_i>0$ and ${\displaystyle \sum _{i=1}^r}{\kappa }_i=1$. Then, linear Diophantine fuzzy weighted averaging (LDFWA) operator is defined as

$$LDFWA(L_1,L_2,\dots ,L_r)=(\langle 1-{\displaystyle \prod _{i=1}^r}{(1-{\mu }_{L_i})}^{{\kappa }_i},{\displaystyle \prod _{i=1}^r}{\nu }_{L_i}^{{\kappa }_i}\rangle ,\langle 1-{\displaystyle \prod _{i=1}^r}{(1-{\lambda }_{L_i})}^{{\kappa }_i},{\displaystyle \prod _{i=1}^r}{\eta }_{L_i}^{{\kappa }_i}\rangle )$$

Definition 9.

([46]). Let $L_i=(\langle {\mu }_{L_i},{\nu }_{L_i}\rangle ,\langle {\lambda }_{L_i},{\eta }_{L_i}\rangle )$, $i=1,2,\dots ,r$, be a set of LDFNs and $\kappa =\{{\kappa }_1,{\kappa }_2,\dots ,{\kappa }_r\}$ be the WV with ${\kappa }_i>0$ and ${\displaystyle \sum _{i=1}^r}{\kappa }_i=1$. Then, linear Diophantine fuzzy weighted geometric (LDFWG) operator is defined as

$$LDFWG(L_1,L_2,\dots ,L_r)=(\langle {\displaystyle \prod _{i=1}^r}{\mu }_{L_i}^{{\kappa }_i},1-{\displaystyle \prod _{i=1}^r}{(1-{\nu }_{L_i})}^{{\kappa }_i}\rangle ,\langle {\displaystyle \prod _{i=1}^r}{\lambda }_{L_i}^{{\kappa }_i},1-{\displaystyle \prod _{i=1}^r}{(1-{\eta }_{L_i})}^{{\kappa }_i}\rangle )$$

3. Sine-Trigonometric Operational Laws for LDFNs

This section introduces the concept of sine-trigonometric operational laws for LDFNs.

Definition 10.

The sine-trigonometric operator on an LDFS

$$L=\{(\ell ,\langle {\mu }_L(\ell ),{\nu }_L(\ell )\rangle ,\langle {\lambda }_L(\ell ),{\eta }_L(\ell )\rangle ):\ell \in L\}$$

in X can be described as

$$sinL=\left(\begin{array}{c}(\ell ,〈sin\left(\frac{\pi }{2}{\mu }_L(\ell )\right),1-sin\left(\frac{\pi }{2}\left(1-{\nu }_L(\ell )\right)\right)〉,\\ 〈sin\left(\frac{\pi }{2}{\lambda }_L(\ell )\right),1-sin\left(\frac{\pi }{2}\left(1-{\eta }_L(\ell )\right)\right)〉):\ell \in X\end{array}\right)$$

(3)

The set $sinL$ is called sine-trigonometric-LDFS (ST-LDFS).

Theorem 1.

A ST-LDFS is an LDFS.

Proof. 

Let $L=\{(\ell ,\langle {\mu }_L(\ell ),{\nu }_L(\ell )\rangle ,\langle {\lambda }_L(\ell ),{\eta }_L(\ell )\rangle ):\ell \in L\}$ be an LDFS where ${\mu }_L(\ell )$, ${\nu }_L(\ell )$, ${\lambda }_L(\ell )$ and, ${\eta }_L(\ell )\in [0,1]$ with $0\le {\lambda }_L(\ell )+{\eta }_L(\ell )\le 1$ and $0\le {\mu }_L(\ell ){\lambda }_L(\ell )+{\nu }_L(\ell ){\eta }_L(\ell )\le 1$ for every $\ell \in X$. To prove that a ST-LDFS ($sinL$) is an LDFS, we need to show that $\forall \ell \in X$

i.

$sin\left(\frac{\pi }{2}{\mu }_L(\ell )\right),1-sin\left(\frac{\pi }{2}\left(1-{\nu }_L(\ell )\right)\right),sin\left(\frac{\pi }{2}{\lambda }_L(\ell )\right),1-sin\left(\frac{\pi }{2}\left(1-{\eta }_L(\ell )\right)\right)\in [0,1]$

ii.

$0\le sin\left(\frac{\pi }{2}{\lambda }_L(\ell )\right)+1-sin(\frac{\pi }{2}\left(1-{\eta }_L(\ell )\right)\le 1$

iii.

$0\le sin\left(\frac{\pi }{2}{\mu }_L(\ell )\right)sin\left(\frac{\pi }{2}{\lambda }_L(\ell )\right)+\left(1-sin\left(\frac{\pi }{2}\left(1-{\nu }_L(\ell )\right)\right)\right)(1-sin\left(\frac{\pi }{2}\left(1-{\eta }_L(\ell )\right)\right)\le 1$

Since $0\le {\mu }_L(\ell )\le 1$, so $0\le \frac{\pi }{2}{\mu }_L(\ell )\le \frac{\pi }{2}$ which gives $0\le sin\left(\frac{\pi }{2}{\mu }_L(\ell )\right)\le 1$ as sine is an increasing function in the first quadrant. Likewise, $0\le {\nu }_L(\ell )\le 1$, so $0\le \frac{\pi }{2}(1-{\nu }_L(\ell ))\le \frac{\pi }{2}$ which gives $0\le sin\left(\frac{\pi }{2}\left(1-{\nu }_L(\ell )\right)\right)\le 1$. In this way, we get $0\le 1-sin\left(\frac{\pi }{2}\left(1-{\nu }_L(\ell )\right)\right)\le 1$. Analogously, we can show that $0\le sin\left(\frac{\pi }{2}{\lambda }_L(\ell )\right)\le 1$ and $0\le 1-sin\left(\frac{\pi }{2}\left(1-{\eta }_L(\ell )\right)\right)\le 1$. Hence, the first condition is satisfied. Moreover, we know that for $t\in [0,\frac{\pi }{2}]$, $sint$ is an increasing function. Then, for $\frac{\pi }{2}{\lambda }_L(\ell ),\frac{\pi }{2}(1-{\eta }_L(\ell ))\in [0,\frac{\pi }{2}]$ and using $0\le \Re (\ell )+\Im (\ell )\le 1$, we obtain $\frac{\pi }{2}{\lambda }_L(\ell )\le \frac{\pi }{2}(1-{\eta }_L(\ell ))$. Now, $sin\left(\frac{\pi }{2}{\lambda }_L(\ell )\right)\le sin\left(\frac{\pi }{2}\left(1-{\eta }_L(\ell )\right)\right)$ which implies that $0\le sin\left(\frac{\pi }{2}{\lambda }_L(\ell )\right)+1-sin(\frac{\pi }{2}\left(1-{\eta }_L(\ell )\right)\le 1$. Hence, the second condition is satisfied.

Lastly, for $sin\left(\frac{\pi }{2}{\mu }_L(\ell )\right)\in [0,1]$ and $sin\left(\frac{\pi }{2}{\lambda }_L(\ell )\right)\in [0,1]$, we obtain

$sin\left(\frac{\pi }{2}{\mu }_L(\ell )\right)sin\left(\frac{\pi }{2}{\lambda }_L(\ell )\right)\in [0,1]$. Similarly, for $\left(1-sin\left(\frac{\pi }{2}\left(1-{\nu }_L(\ell )\right)\right)\right)\in [0,1]$ and $\left(1-sin\left(\frac{\pi }{2}\left(1-{\eta }_L(\ell )\right)\right)\right)\in [0,1]$, we have

$\left(1-sin\left(\frac{\pi }{2}\left(1-{\nu }_L(\ell )\right)\right)\right)\left(1-sin\left(\frac{\pi }{2}\left(1-{\eta }_L(\ell )\right)\right)\right)\in [0,1]$. Now, using the second condition, we have

$0\le sin\left(\frac{\pi }{2}{\mu }_L(\ell )\right)sin\left(\frac{\pi }{2}{\lambda }_L(\ell )\right)+\left(1-sin\left(\frac{\pi }{2}\left(1-{\nu }_L(\ell )\right)\right)\right)(1-sin\left(\frac{\pi }{2}\left(1-{\eta }_L(\ell )\right)\right)\le 1$.    □

Definition 11.

Let $L=(\langle {\mu }_L,{\nu }_L\rangle ,\langle {\lambda }_L,{\eta }_L\rangle )$ be an LDFN, then

$$sinL=\left(〈sin\left(\frac{\pi }{2}{\mu }_L\right),1-sin\left(\frac{\pi }{2}\left(1-{\nu }_L\right)\right)〉,〈sin\left(\frac{\pi }{2}{\lambda }_L\right),1-sin\left(\frac{\pi }{2}\left(1-{\eta }_L\right)\right)〉\right)$$

(4)

is called a ST-LDFN.

Definition 12.

Let $L_1=(\langle {\mu }_{L_1},{\nu }_{L_1}\rangle ,\langle {\lambda }_{L_1},{\eta }_{L_1}\rangle )$ and $L_2=(\langle {\mu }_{L_2},{\nu }_{L_2}\rangle ,\langle {\lambda }_{L_2},{\eta }_{L_2}\rangle )$ be two LDFNs, then STOLs for these LDFNs are presented as follows.

i.

$sin{L}_1⊞sin{L}_2=\left(\begin{array}{c}\langle 1-\left(1-sin\left(\frac{\pi }{2}{\mu }_{L_1}\right)\right)\left(1-sin\left(\frac{\pi }{2}{\mu }_{L_2}\right)\right),\\ \left(1-\left(sin\left(\frac{\pi }{2}(1-{\nu }_{L_1})\right)\right)\right)\left(1-\left(sin\left(\frac{\pi }{2}(1-{\nu }_{L_2})\right)\right)\right)\rangle ,\\ \langle 1-\left(1-sin\left(\frac{\pi }{2}{\lambda }_{L_1}\right)\right)\left(1-sin\left(\frac{\pi }{2}{\lambda }_{L_2}\right)\right),\\ \left(1-\left(sin\left(\frac{\pi }{2}(1-{\eta }_{L_1})\right)\right)\right)\left(1-\left(sin\left(\frac{\pi }{2}(1-{\eta }_{L_2})\right)\right)\right)\rangle \end{array}\right)$

ii.

$sin{L}_1⊠sin{L}_2=\left(\begin{array}{c}\langle sin\left(\frac{\pi }{2}{\mu }_{L_1}\right)sin\left(\frac{\pi }{2}{\mu }_{L_2}\right),\\ 1-\left(sin\left(\frac{\pi }{2}(1-{\nu }_{L_1})\right)\right)\left(sin\left(\frac{\pi }{2}(1-{\nu }_{L_2})\right)\right)\rangle ,\\ \langle sin\left(\frac{\pi }{2}{\lambda }_{L_1}\right)sin\left(\frac{\pi }{2}{\lambda }_{L_2}\right),\\ 1-\left(sin\left(\frac{\pi }{2}(1-{\eta }_{L_1})\right)\right)\left(sin\left(\frac{\pi }{2}(1-{\eta }_{L_2})\right)\right)\rangle \end{array}\right)$,

iii.

$\tau sin{L}_1=\left(\begin{array}{c}〈1-{\left(1-sin\left(\frac{\pi }{2}{\mu }_{L_1}\right)\right)}^{\tau },{\left(1-sin\left(\frac{\pi }{2}(1-{\nu }_{L_1})\right)\right)}^{\tau }〉,\\ 〈1-{\left(1-sin\left(\frac{\pi }{2}{\lambda }_{L_1}\right)\right)}^{\tau },{\left(1-sin\left(\frac{\pi }{2}(1-{\eta }_{L_1})\right)\right)}^{\tau }〉\end{array}\right)$; $\tau >0$,

iv.

${(sin{L}_1)}^{\tau }=\left(\begin{array}{c}〈{\left(sin\left(\frac{\pi }{2}{\mu }_{L_1}\right)\right)}^{\tau },1-{\left(sin\left(\frac{\pi }{2}(1-{\nu }_{L_1})\right)\right)}^{\tau }〉,\\ 〈{\left(sin\left(\frac{\pi }{2}{\lambda }_{L_1}\right)\right)}^{\tau },1-{\left(sin\left(\frac{\pi }{2}(1-{\eta }_{L_1})\right)\right)}^{\tau }〉\end{array}\right)$; $\tau >0$.

Theorem 2.

Let $L_1=(\langle {\mu }_{L_1},{\nu }_{L_1}\rangle ,\langle {\lambda }_{L_1},{\eta }_{L_1}\rangle )$, $L_2=(\langle {\mu }_{L_2},{\nu }_{L_2}\rangle ,\langle {\lambda }_{L_2},{\eta }_{L_2}\rangle )$ and $L_3=(\langle {\mu }_{L_3},{\nu }_{L_3}\rangle ,\langle {\lambda }_{L_3},{\eta }_{L_3}\rangle )$ be three LDFNs. Then,

i.

$sin{L}_1⊞sin{L}_2=sin{L}_2⊞sin{L}_1$

ii.

$sin{L}_1⊠sin{L}_2=sin{L}_2⊠sin{L}_1$

iii.

$(sin{L}_1⊞sin{L}_2)⊞sin{L}_3=sin{L}_1⊞(sin{L}_2⊞sin{L}_3)$

iv.

$(sin{L}_1⊠sin{L}_2)⊠sin{L}_3=sin{L}_1⊠(sin{L}_2⊠sin{L}_3)$

Proof. 

Straightforward.    □

Theorem 3.

For two LDFNs $L_1=(\langle {\mu }_{L_1},{\nu }_{L_1}\rangle ,\langle {\lambda }_{L_1},{\eta }_{L_1}\rangle )$ and $L_2=(\langle {\mu }_{L_2},{\nu }_{L_2}\rangle ,\langle {\lambda }_{L_2},{\eta }_{L_2}\rangle )$ and $\tau >0,{\tau }_1>0,{\tau }_2>0$, we have

i.

$\tau (sin{L}_1⊞sin{L}_2)=\tau sin{L}_1⊞\tau sin{L}_2$

ii.

${(sin{L}_1⊠sin{L}_2)}^{\tau }={(sin{L}_1)}^{\tau }⊠{(sin{L}_2)}^{\tau }$

iii.

${\tau }_{1}sin{L}_1⊞{\tau }_{2}sin{L}_1=({\tau }_1+{\tau }_2)sin{L}_1$

iv.

${(sin{L}_1)}^{{\tau }_1}⊠{(sin{L}_1)}^{{\tau }_2}={(sin{L}_1)}^{{\tau }_1+{\tau }_2}$

v.

${\left({(sin{L}_1)}^{{\tau }_1}\right)}^{{\tau }_2}={(sin{L}_1)}^{{\tau }_1{\tau }_2}$

Proof. 

It is sufficient to verify parts i and iv, and the rest can be validated in the same manner.

i.

For $\tau >0$, we have

$$\begin{array}{cc}\hfill \tau (sin{L}_1⊞sin{L}_2)& =\left(\begin{array}{cc}\langle 1-{\left(1-sin\left(\frac{\pi }{2}{\mu }_{L_1}\right)\right)}^{\tau }{\left(1-sin\left(\frac{\pi }{2}{\mu }_{L_2}\right)\right)}^{\tau },& \\ {\left(1-\left(sin\left(\frac{\pi }{2}(1-{\nu }_{L_1})\right)\right)\right)}^{\tau }{\left(1-\left(sin\left(\frac{\pi }{2}(1-{\nu }_{L_2})\right)\right)\right)}^{\tau }\rangle \\ \langle 1-{\left(1-sin\left(\frac{\pi }{2}{\lambda }_{L_1}\right)\right)}^{\tau }{\left(1-sin\left(\frac{\pi }{2}{\lambda }_{L_2}\right)\right)}^{\tau },& \\ {\left(1-\left(sin\left(\frac{\pi }{2}(1-{\eta }_{L_1})\right)\right)\right)}^{\tau }{\left(1-\left(sin\left(\frac{\pi }{2}(1-{\eta }_{L_2})\right)\right)\right)}^{\tau }\rangle \end{array}\right)\hfill \\ \hfill & =\left(\begin{array}{c}〈1-{\left(1-sin\left(\frac{\pi }{2}{\mu }_{L_1}\right)\right)}^{\tau },{\left(1-\left(sin\left(\frac{\pi }{2}(1-{\nu }_{L_1})\right)\right)\right)}^{\tau }〉,\\ 〈1-{\left(1-sin\left(\frac{\pi }{2}{\lambda }_{L_1}\right)\right)}^{\tau },{\left(1-\left(sin\left(\frac{\pi }{2}(1-{\eta }_{L_1})\right)\right)\right)}^{\tau }〉\end{array}\right)\hfill \\ & ⊞\left(\begin{array}{c}〈1-{\left(1-sin\left(\frac{\pi }{2}{\mu }_{L_2}\right)\right)}^{\tau },{\left(1-\left(sin\left(\frac{\pi }{2}(1-{\nu }_{L_2})\right)\right)\right)}^{\tau }〉,\\ 〈1-{\left(1-sin\left(\frac{\pi }{2}{\lambda }_{L_2}\right)\right)}^{\tau },{\left(1-\left(sin\left(\frac{\pi }{2}(1-{\eta }_{L_2})\right)\right)\right)}^{\tau }〉\end{array}\right)\hfill \\ \hfill & =\tau sin{L}_1⊞\tau sin{L}_2\hfill \end{array}$$

iv.

For ${\tau }_1,{\tau }_2>0$, we have

$$\begin{array}{cc}\hfill {\tau }_{1}sin{L}_1⊞{\tau }_{2}sin{L}_1& =\left(\begin{array}{c}〈1-{\left(1-sin\left(\frac{\pi }{2}{\mu }_{L_1}\right)\right)}^{{\tau }_1},{\left(1-\left(sin\left(\frac{\pi }{2}(1-{\nu }_{L_1})\right)\right)\right)}^{{\tau }_1}〉,\\ 〈1-{\left(1-sin\left(\frac{\pi }{2}{\lambda }_{L_1}\right)\right)}^{{\tau }_1},{\left(1-\left(sin\left(\frac{\pi }{2}(1-{\eta }_{L_1})\right)\right)\right)}^{{\tau }_1}〉\end{array}\right)\hfill \\ & ⊞\left(\begin{array}{c}〈1-{\left(1-sin\left(\frac{\pi }{2}{\mu }_{L_1}\right)\right)}^{{\tau }_2},{\left(1-\left(sin\left(\frac{\pi }{2}(1-{\nu }_{L_1})\right)\right)\right)}^{{\tau }_2}〉,\\ 〈1-{\left(1-sin\left(\frac{\pi }{2}{\lambda }_{L_1}\right)\right)}^{{\tau }_2},{\left(1-\left(sin\left(\frac{\pi }{2}(1-{\eta }_{L_1})\right)\right)\right)}^{{\tau }_2}〉\end{array}\right)\hfill \\ \hfill & =\left(\begin{array}{cc}\langle 1-{\left(1-sin\left(\frac{\pi }{2}{\mu }_{L_1}\right)\right)}^{{\tau }_1}{\left(1-sin\left(\frac{\pi }{2}{\mu }_{L_1}\right)\right)}^{{\tau }_2},& \\ {\left(1-\left(sin\left(\frac{\pi }{2}(1-{\nu }_{L_1})\right)\right)\right)}^{{\tau }_1}{\left(1-\left(sin\left(\frac{\pi }{2}(1-{\nu }_{L_1})\right)\right)\right)}^{{\tau }_2}\rangle ,\\ \langle 1-{\left(1-sin\left(\frac{\pi }{2}{\lambda }_{L_1}\right)\right)}^{{\tau }_1}{\left(1-sin\left(\frac{\pi }{2}{\lambda }_{L_1}\right)\right)}^{{\tau }_2},\\ {\left(1-\left(sin\left(\frac{\pi }{2}(1-{\eta }_{L_1})\right)\right)\right)}^{{\tau }_1}{\left(1-\left(sin\left(\frac{\pi }{2}(1-{\eta }_{L_1})\right)\right)\right)}^{{\tau }_2}\rangle \end{array}\right)\hfill \\ \hfill & =\left(\begin{array}{c}〈1-{\left(1-sin\left(\frac{\pi }{2}{\mu }_{L_1}\right)\right)}^{{\tau }_1+{\tau }_2},{\left(1-\left(sin\left(\frac{\pi }{2}(1-{\nu }_{L_1})\right)\right)\right)}^{{\tau }_1+{\tau }_2}〉,\\ 〈1-{\left(1-sin\left(\frac{\pi }{2}{\lambda }_{L_1}\right)\right)}^{{\tau }_1+{\tau }_2},{\left(1-\left(sin\left(\frac{\pi }{2}(1-{\eta }_{L_1})\right)\right)\right)}^{{\tau }_1+{\tau }_2}〉\end{array}\right)\hfill \\ \hfill & =({\tau }_1+{\tau }_2)sin{L}_1\hfill \end{array}$$

   □

Theorem 4.

If $L_1⪯L_2$, then $sin{L}_1⪯sin{L}_2$.

Proof. 

By Definition 4, $L_1⪯L_2$ if ${\mu }_{L_1}\le {\mu }_{L_2}$, ${\nu }_{L_1}\ge {\nu }_{L_2}$, ${\lambda }_{L_1}\le {\lambda }_{L_2}$ and, ${\eta }_{L_1}\ge {\eta }_{L_2}$. Then ${\mu }_{L_1}\le {\mu }_{L_2}$ for the interval $[0,\frac{\pi }{2}]$, and we obtain $sin\left(\frac{\pi }{2}{\mu }_{L_1}\right)\le sin\left(\frac{\pi }{2}{\mu }_{L_2}\right)$. Now, for ${\nu }_{L_1}\ge {\nu }_{L_2}$, we have $1-{\nu }_{L_1}\le 1-{\nu }_{L_2}$. Thus, $sin\left(\frac{\pi }{2}(1-{\nu }_{L_1})\right)\le sin\left(\frac{\pi }{2}(1-{\nu }_{L_2})\right)$ which implies that $1-sin\left(\frac{\pi }{2}(1-{\nu }_{L_1})\right)\ge 1-sin\left(\frac{\pi }{2}(1-{\nu }_{L_2})\right)$. Likewise, $sin\left(\frac{\pi }{2}{\lambda }_{L_1}\right)\le sin\left(\frac{\pi }{2}{\lambda }_{L_2}\right)$ and $1-sin\left(\frac{\pi }{2}(1-{\eta }_{L_1})\right)\ge 1-sin\left(\frac{\pi }{2}(1-{\eta }_{L_2})\right)$. Hence, by Definition 4, $sin{L}_1⪯sin{L}_2$.    □

4. Linear Diophantine Fuzzy Sine-Trigonometric Averaging Aggregation Operators

In this section, the concept of averaging AOs is proposed for LDF-STOLs. These operators are named as the LDFSTWA operator, LDFSTOWA operator, and LDFSTHWA operator. For the sake of convenience, we consider ${\mathsf{\Omega }}_i=sin\left(\frac{\pi }{2}{\mu }_{L_i}\right)$, ${\mho }_i=sin\left(\frac{\pi }{2}(1-{\nu }_{L_i})\right)$, ${▵}_i=sin\left(\frac{\pi }{2}{\lambda }_{L_i}\right)$, and ${\nabla }_i=sin\left(\frac{\pi }{2}(1-{\eta }_{L_i})\right)$, where $i=1,2,\dots ,r$.

4.1. LDFSTWA Operator

Definition 13.

Let Λ be a set of r distinct LDFNs. Then the LDFSTWA operator is a mapping LDFSTWA$:{\mathrm{\Lambda }}^r\to \mathrm{\Lambda }$ given as follows:

$$LDFSTWA(L_1,L_2,\dots ,L_r)={\hslash }_{1}sin{L}_1⊞{\hslash }_{2}sin{L}_2⊞\dots ⊞{\hslash }_{r}sin{L}_r$$

(5)

where $\hslash =\{{\hslash }_1,{\hslash }_2,\dots ,{\hslash }_r\}$ is the weight vector (WV) such that ${\hslash }_i>0$ and ${\displaystyle \sum _{i=1}^r}{\hslash }_i=1$. This mapping is termed as the "Linear Diophantine fuzzy sine-trigonometric weighted averaging (LDFSTWA) operator”.

Theorem 5.

Let $L_i=(\langle {\mu }_{L_i},{\nu }_{L_i}\rangle ,\langle {\lambda }_{L_i},{\eta }_{L_i}\rangle )$ be r LDFNs. Then, their combined value obtained by employing Equation (5) is an LDFN and is provided by

$$\begin{array}{c}\hfill LDFSTWA(L_1,L_2,\dots ,L_r)=\left(\begin{array}{c}〈1-{\displaystyle \prod _{i=1}^r}{\left(1-{\mathsf{\Omega }}_i\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^r}{\left(1-{\mho }_i\right)}^{{\hslash }_i}〉,\\ 〈1-{\displaystyle \prod _{i=1}^r}{\left(1-{▵}_i\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^r}{\left(1-{\nabla }_i\right)}^{{\hslash }_i}〉\end{array}\right)\end{array}$$

(6)

Proof. 

We proceed it with an induction on r. To begin, consider $r=2$. For this, we utilize the following two equations.

$${\hslash }_{1}sin{L}_1=\left(\begin{array}{c}〈1-{\left(1-{\mathsf{\Omega }}_1\right)}^{{\hslash }_1},{\left(1-{\mho }_1\right)}^{{\hslash }_1}〉,〈1-{\left(1-{▵}_1\right)}^{{\hslash }_1},{\left(1-{\nabla }_1\right)}^{{\hslash }_1}〉\end{array}\right)$$

$${\hslash }_{2}sin{L}_2=\left(\begin{array}{c}〈1-{\left(1-{\mathsf{\Omega }}_2\right)}^{{\hslash }_2},{\left(1-{\mho }_2\right)}^{{\hslash }_2}〉,〈1-{\left(1-{▵}_2\right)}^{{\hslash }_2},{\left(1-{\nabla }_2\right)}^{{\hslash }_2}〉\end{array}\right)$$

With the LDFSTWA operator, we obtain

$$\begin{array}{cc}\hfill LDFSTWA(L_1,L_2)=& {\hslash }_{1}sin{L}_1⊞{\hslash }_{2}sin{L}_2\hfill \\ \hfill =& \left(\begin{array}{c}〈1-{\left(1-{\mathsf{\Omega }}_1\right)}^{{\hslash }_1},{\left(1-{\mho }_1\right)}^{{\hslash }_1}〉,〈1-{\left(1-{▵}_1\right)}^{{\hslash }_1},{\left(1-{\nabla }_1\right)}^{{\hslash }_1}〉\end{array}\right)⊞\hfill \\ & \left(\begin{array}{c}〈1-{\left(1-{\mathsf{\Omega }}_2\right)}^{{\hslash }_2},{\left(1-{\mho }_2\right)}^{{\hslash }_2}〉,〈1-{\left(1-{▵}_2\right)}^{{\hslash }_2},{\left(1-{\nabla }_2\right)}^{{\hslash }_2}〉\end{array}\right)\hfill \\ \hfill =& \left(\begin{array}{c}〈1-{\left(1-{\mathsf{\Omega }}_1\right)}^{{\hslash }_1}{\left(1-{\mathsf{\Omega }}_2\right)}^{{\hslash }_2},{\left(1-{\mho }_1\right)}^{{\hslash }_1}{\left(1-{\mho }_2\right)}^{{\hslash }_2}〉,\\ 〈1-{\left(1-{▵}_1\right)}^{{\hslash }_1}{\left(1-{▵}_2\right)}^{{\hslash }_2},{\left(1-{\nabla }_1\right)}^{{\hslash }_1}{\left(1-{\nabla }_2\right)}^{{\hslash }_2}〉\end{array}\right)\hfill \\ \hfill =& \left(\begin{array}{c}〈1-{\displaystyle \prod _{i=1}^2}{\left(1-{\mathsf{\Omega }}_i\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^2}{\left(1-{\mho }_i\right)}^{{\hslash }_i}〉,〈1-{\displaystyle \prod _{i=1}^2}{\left(1-{▵}_i\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^2}{\left(1-{\nabla }_i\right)}^{{\hslash }_i}〉\end{array}\right)\hfill \end{array}$$

As a result, the theorem holds for $r=2$. Suppose the theorem holds for $r=k,k\in N$. That is,

$$\begin{array}{cc}\hfill LDFSTWA(L_1,L_2,\dots ,L_k)& ={\hslash }_{1}sin{L}_1⊞{\hslash }_{2}sin{L}_2⊞\dots ⊞{\hslash }_{k}sin{L}_k\hfill \\ \hfill & =\left(\begin{array}{c}〈1-{\displaystyle \prod _{i=1}^k}{\left(1-{\mathsf{\Omega }}_i\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^k}{\left(1-{\mho }_i\right)}^{{\hslash }_i}〉,〈1-{\displaystyle \prod _{i=1}^k}{\left(1-{▵}_i\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^k}{\left(1-{\nabla }_i\right)}^{{\hslash }_i}〉\end{array}\right)\hfill \end{array}$$

We show that the theorem holds true when $r=k+1$. Thus, we obtain

$$\begin{array}{cc}\hfill LDFSTWA(L_1,L_2,...,L_{k+1})& ={\hslash }_{1}sin{L}_1⊞{\hslash }_{2}sin{L}_2⊞\dots ⊞{\hslash }_{k}sin{L}_k⊞{\hslash }_{k+1}sin{L}_{k+1}\hfill \\ \hfill & =\left(\begin{array}{c}〈1-{\displaystyle \prod _{i=1}^k}{\left(1-{\mathsf{\Omega }}_i\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^k}{\left(1-{\mho }_i\right)}^{{\hslash }_i}〉,〈1-{\displaystyle \prod _{i=1}^k}{\left(1-{▵}_i\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^k}{\left(1-{\nabla }_i\right)}^{{\hslash }_i}〉\end{array}\right)⊞\hfill \\ & \left(\begin{array}{c}〈1-{\left(1-{\mathsf{\Omega }}_{k+1}\right)}^{{\hslash }_{k+1}},{\left(1-{\mho }_{k+1}\right)}^{{\hslash }_{k+1}}〉,〈1-{\left(1-{▵}_{k+1}\right)}^{{\hslash }_{k+1}},{\left(1-{\nabla }_{k+1}\right)}^{{\hslash }_{k+1}}〉\end{array}\right)\hfill \\ \hfill & =\left(\begin{array}{c}〈1-{\displaystyle \prod _{i=1}^{k+1}}{\left(1-{\mathsf{\Omega }}_i\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^{k+1}}{\left(1-{\mho }_i\right)}^{{\hslash }_i}〉,〈1-{\displaystyle \prod _{i=1}^{k+1}}{\left(1-{▵}_i\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^{k+1}}{\left(1-{\nabla }_i\right)}^{{\hslash }_i}〉\end{array}\right)\hfill \end{array}$$

It is true for $r=k+1$. This proves that the result is true $\forall n\in N$.    □

Example 1.

Let us contemplate three LDFNs as shown in 

Table 4. LDFNs.

$L_1$	$(\langle 0.813,0.916\rangle ,\langle 0.237,0.598\rangle )$
$L_2$	$(\langle 0.357,0.676\rangle ,\langle 0.357,0.468\rangle )$
$L_3$	$(\langle 0.779,0.868\rangle ,\langle 0.218,0.767\rangle )$

 and let $\hslash =\{0.297,0.378,0.325\}$ be their WV.

To calculate the aggregated value of these LDFNs, we first let  ${\mathsf{\Omega }}_i=sin\left(\frac{\pi }{2}{\mu }_{L_i}\right)$, ${\mho }_i=sin\left(\frac{\pi }{2}(1-{\nu }_{L_i})\right)$, ${▵}_i=sin\left(\frac{\pi }{2}{\lambda }_{L_i}\right)$, and ${\nabla }_i=sin\left(\frac{\pi }{2}(1-{\eta }_{L_i})\right)$, where $i=1,2,3$. These values are presented in 

Table 5. The values of ${\mathsf{\Omega }}_i$, ${\mho }_i$, ${▵}_i$, and ${\nabla }_i$ for $i=1,2,3$.

${\mathsf{\Omega }}_1$	$0.9572$	${\mho }_1$	$0.1316$	${▵}_1$	$0.3637$	${\nabla }_1$	$0.5903$
${\mathsf{\Omega }}_2$	$0.5318$	${\mho }_2$	$0.4872$	${▵}_2$	$0.5318$	${\nabla }_2$	$0.7417$
${\mathsf{\Omega }}_3$	$0.9403$	${\mho }_3$	$0.2059$	${▵}_3$	$0.3358$	${\nabla }_3$	$0.3579$

.

Now, we have  

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left(1-{\mathsf{\Omega }}_i\right)}^{{\hslash }_i}& ={\left(1-{\mathsf{\Omega }}_1\right)}^{{\hslash }_1}\times {\left(1-{\mathsf{\Omega }}_2\right)}^{{\hslash }_2}\times {\left(1-{\mathsf{\Omega }}_3\right)}^{{\hslash }_3}\hfill & \\ \hfill & ={\left(1-0.9572\right)}^{0.297}\times {\left(1-0.5318\right)}^{0.378}\times {\left(1-0.9403\right)}^{0.325}\hfill & \\ \hfill & =0.1178\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left(1-{\mho }_i\right)}^{{\hslash }_i}& ={\left(1-{\mho }_1\right)}^{{\hslash }_1}\times {\left(1-{\mho }_2\right)}^{{\hslash }_2}\times {\left(1-{\mho }_3\right)}^{{\hslash }_3}\hfill & \\ \hfill & ={\left(1-0.1316\right)}^{0.297}\times {\left(1-0.4872\right)}^{0.378}\times {\left(1-0.2059\right)}^{0.325}\hfill & \\ \hfill & =0.6912\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left(1-{▵}_i\right)}^{{\hslash }_i}& ={\left(1-{▵}_1\right)}^{{\hslash }_1}\times {\left(1-{▵}_2\right)}^{{\hslash }_2}\times {\left(1-{▵}_3\right)}^{{\hslash }_3}\hfill & \\ \hfill & ={\left(1-0.3637\right)}^{0.297}\times {\left(1-0.5318\right)}^{0.378}\times {\left(1-0.3358\right)}^{0.325}\hfill & \\ \hfill & =0.5746\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left(1-{\nabla }_i\right)}^{{\hslash }_i}& ={\left(1-{\nabla }_1\right)}^{{\hslash }_1}\times {\left(1-{\nabla }_2\right)}^{{\hslash }_2}\times {\left(1-{\nabla }_3\right)}^{{\hslash }_3}\hfill & \\ \hfill & ={\left(1-0.5903\right)}^{0.297}\times {\left(1-0.7417\right)}^{0.378}\times {\left(1-0.3579\right)}^{0.325}\hfill & \\ \hfill & =0.3982\hfill \end{array}$$

Now, using the above values, we compute the LDFSTWA operator as follows:

$$\begin{array}{ccc}\hfill LDFSTWA(L_1,L_2,L_3)& =\left(\begin{array}{c}〈1-{\displaystyle \prod _{i=1}^3}{\left(1-{\mathsf{\Omega }}_i\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^3}{\left(1-{\mho }_i\right)}^{{\hslash }_i}〉,\\ 〈1-{\displaystyle \prod _{i=1}^3}{\left(1-{▵}_i\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^3}{\left(1-{\nabla }_i\right)}^{{\hslash }_i}〉\end{array}\right)\hfill & \\ \hfill & =\left(\begin{array}{c}〈1-0.1178,0.6912〉,〈1-0.5746,0.3982〉\end{array}\right)\hfill & \\ \hfill & =\left(\begin{array}{c}〈0.8822,0.6912〉,〈0.4254,0.3982〉\end{array}\right)\hfill \end{array}$$

Theorem 6.

The properties of the LDFSTWA operator are as follows.

i. (Idempotency) If $L_i$, $i=1,2,\dots ,r$ are all equal, i.e., $L_i=L$, then

$$LDFSTWA(L_1,L_2,\dots ,L_r)=sinL.$$

ii. (Monotonicity) If $L_i$ and $L_i^{★}$ are two sets of LDFNs such that $L_i⪯L_i^{★}$, $\forall i=1,2,\dots ,r$, then

$$LDFSTWA(L_1,L_2,\dots ,L_r)⪯LDFSTWA(L_1^{★},L_2^{★},\dots ,L_r^{★}).$$

iii. (Boundedness) If $L_i$ be r LDFNs such that $L=(\langle \underset{i}{min}\left({\mu }_{L_i}\right),\underset{i}{max}({\nu }_{L_i})\rangle ,\langle \underset{i}{min}({\lambda }_{L_i}),$$\underset{i}{max}({\eta }_{L_i})\rangle )$ and $\overline{L}=(\langle \underset{i}{max}\left({\mu }_{L_i}\right),\underset{i}{min}({\nu }_{L_i})\rangle ,\langle \underset{i}{max}({\lambda }_{L_i}),\underset{i}{min}({\eta }_{L_i})\rangle )$, then

$$sin\underline{L}⪯LDFSTWA(L_1,L_2,\dots ,L_r)⪯sin\overline{L}.$$

Proof. 

i. Let $L_i=L=(\langle {\mu }_L,{\nu }_L\rangle ,\langle {\lambda }_L,{\eta }_L\rangle )$$\forall i=1,2,\dots ,r$. This shows that ${\mu }_{L_i}={\mu }_L$, ${\nu }_{L_i}={\nu }_L$, ${\lambda }_{L_i}={\lambda }_L$ and ${\eta }_{L_i}={\eta }_L$ for all $i=1,2,\dots ,r$. In this case, the terms ${\mathsf{\Omega }}_i$, ${\mho }_i$, ${▵}_i$ and ${\nabla }_i$ become ${\mathsf{\Omega }}_i=sin\left(\frac{\pi }{2}{\mu }_L\right)=\mathsf{\Omega }$, ${\mho }_i=sin\left(\frac{\pi }{2}(1-{\nu }_L)\right)=\mho$, ${▵}_i=sin\left(\frac{\pi }{2}{\lambda }_L\right)=▵$ and ${\nabla }_i=sin\left(\frac{\pi }{2}(1-{\eta }_L)\right)=\nabla$ Then, by using Equation (6), we have

$$\begin{array}{ccc}\hfill LDFSTWA(L_1,L_2,\dots ,L_r)& =\left(\begin{array}{c}〈1-{\displaystyle \prod _{i=1}^r}{\left(1-{\mathsf{\Omega }}_i\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^r}{\left(1-{\mho }_i\right)}^{{\hslash }_i}〉,\\ 〈1-{\displaystyle \prod _{i=1}^r}{\left(1-{▵}_i\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^r}{\left(1-{\nabla }_i\right)}^{{\hslash }_i}〉\end{array}\right)\hfill & \\ \hfill & =\left(\begin{array}{c}〈1-{\displaystyle \prod _{i=1}^r}{\left(1-\mathsf{\Omega }\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^r}{\left(1-\mho \right)}^{{\hslash }_i}〉,\\ 〈1-{\displaystyle \prod _{i=1}^r}{\left(1-▵\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^r}{\left(1-\nabla \right)}^{{\hslash }_i}〉\end{array}\right)\hfill & \\ \hfill & =\left(\begin{array}{c}〈1-{\left(1-\mathsf{\Omega }\right)}^{{\displaystyle \sum _{i=1}^r}{\hslash }_i},{\left(1-\mho \right)}^{{\displaystyle \sum _{i=1}^r}{\hslash }_i}〉,\\ 〈1-{\left(1-▵\right)}^{{\displaystyle \sum _{i=1}^r}{\hslash }_i},{\left(1-\nabla \right)}^{{\displaystyle \sum _{i=1}^r}{\hslash }_i}〉\end{array}\right)\hfill & \\ \hfill & =\left(\begin{array}{c}〈1-\left(1-\mathsf{\Omega }\right),\left(1-\mho \right)〉,〈1-\left(1-▵\right),\left(1-\nabla \right)〉\end{array}\right)\hfill & \\ \hfill & =\left(\begin{array}{c}〈\mathsf{\Omega },\left(1-\mho \right)〉,〈▵,\left(1-\nabla \right)〉\end{array}\right)\hfill & \\ \hfill & =sinL\hfill \end{array}$$

ii. Since $L_i⪯L_i^{★}$ so by Definition 4, ${\mu }_{L_i}\le {\mu }_{L_i^{★}}$, ${\nu }_{L_i}\ge {\nu }_{L_i^{★}}$, ${\lambda }_{L_i}\le {\lambda }_{L_i^{★}}$ and ${\eta }_{L_i}\ge {\eta }_{L_i^{★}}$, $\forall i=1,2,\dots ,r$. Assume that ${\mathsf{\Omega }}_i=sin\left(\frac{\pi }{2}{\mu }_{L_i}\right)$, ${\mho }_i=sin\left(\frac{\pi }{2}(1-{\nu }_{L_i})\right)$, ${▵}_i=sin\left(\frac{\pi }{2}{\lambda }_{L_i}\right)$ and ${\nabla }_i=sin\left(\frac{\pi }{2}(1-{\eta }_{L_i})\right)$ and ${\mathsf{\Omega }}_i^{★}=sin\left(\frac{\pi }{2}{\mu }_{L_i^{★}}\right)$, ${\mho }_i^{★}=sin\left(\frac{\pi }{2}(1-{\nu }_{L_i^{★}})\right)$, ${▵}_i^{★}=sin\left(\frac{\pi }{2}{\lambda }_{L_i^{★}}\right)$, and ${\nabla }_i^{★}=sin\left(\frac{\pi }{2}(1-{\eta }_{L_i^{★}})\right)$. Now, we obtain

$LDFSTWA(L_1,L_2,\dots ,L_r)=\left(\begin{array}{c}\langle 1-{\displaystyle \prod _{i=1}^r}{(1-{\mathsf{\Omega }}_i)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^r}{(1-{\mho }_i)}^{{\hslash }_i}\rangle ,\langle 1-{\displaystyle \prod _{i=1}^r}{(1-{▵}_i)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^r}{(1-{\nabla }_i)}^{{\hslash }_i}\rangle \end{array}\right)$ and LDFSTWA$(L_1^{★},L_2^{★},\dots ,L_r^{★})=\left(\begin{array}{c}\langle 1-{\displaystyle \prod _{i=1}^r}{(1-{\mathsf{\Omega }}_i^{★})}^{{\hslash }_i},{\displaystyle \prod _{i=1}^r}{(1-{\mho }_i^{★})}^{{\hslash }_i}\rangle ,\langle 1-{\displaystyle \prod _{i=1}^r}{(1-{▵}_i^{★})}^{{\hslash }_i},\prod _{i=1}^r{(1-{\nabla }_i^{★})}^{{\hslash }_i}\rangle \end{array}\right)$. Thus, we obtain

$${\mathsf{\Omega }}_i\le {\mathsf{\Omega }}_i^{★}$$

$$\Rightarrow 1-{\mathsf{\Omega }}_i\ge 1-{\mathsf{\Omega }}_i^{★}$$

$$\Rightarrow {\left(1-{\mathsf{\Omega }}_i\right)}^{{\hslash }_i}\ge {\left(1-{\mathsf{\Omega }}_i^{★}\right)}^{{\hslash }_i}$$

$$\Rightarrow {\displaystyle \prod _{i=1}^r}{\left(1-{\mathsf{\Omega }}_i\right)}^{{\hslash }_i}\ge {\displaystyle \prod _{i=1}^r}{\left(1-{\mathsf{\Omega }}_i^{★}\right)}^{{\hslash }_i}$$

$$\Rightarrow 1-{\displaystyle \prod _{i=1}^r}{\left(1-{\mathsf{\Omega }}_i\right)}^{{\hslash }_i}\le 1-{\displaystyle \prod _{i=1}^r}{\left(1-{\mathsf{\Omega }}_i^{★}\right)}^{{\hslash }_i}$$

Similarly,

$${\mho }_i\le {\mho }_i^{★}$$

$$\Rightarrow 1-{\mho }_i\ge 1-{\mho }_i^{★}$$

$$\Rightarrow {\left(1-{\mho }_i\right)}^{{\hslash }_i}\ge {\left(1-{\mho }_i^{★}\right)}^{{\hslash }_i}$$

$$\Rightarrow {\displaystyle \prod _{i=1}^r}{\left(1-{\mho }_i\right)}^{{\hslash }_i}\ge {\displaystyle \prod _{i=1}^r}{\left(1-{\mho }_i^{★}\right)}^{{\hslash }_i}$$

Likewise, one can prove that $1-{\displaystyle \prod _{i=1}^r}{\left(1-{▵}_i\right)}^{{\hslash }_i}\le 1-{\displaystyle \prod _{i=1}^r}{\left(1-{▵}_i^{★}\right)}^{{\hslash }_i}$ and ${\displaystyle \prod _{i=1}^r}{\left(1-{\nabla }_i\right)}^{{\hslash }_i}\ge {\displaystyle \prod _{i=1}^r}{\left(1-{\nabla }_i^{★}\right)}^{{\hslash }_i}$. Hence, by Definition 4, we get

$$LDFSTWA(L_1,L_2,\dots ,L_n)⪯LDFSTWA(L_1^{★},L_2^{★},\dots ,L_r^{★}).$$

iii. We eliminate it since it is identical to the preceding proof.    □

An LDFSTWA operator first assigns the weights to LDFNs and then finds their weighted aggregated value. Now we define another operator which first arranges the LDFNs in descending order and then assigns weights to their ordered positions. This operator is then used to aggregate the ordered weighted LDFNs. This operator is referred to as the LDFSTOWA operator.

4.2. LDFSTOWA Operator

Definition 14.

Let Λ be a set of r LDFNs, then the mapping LDFSTOWA $:{\mathrm{\Lambda }}^r\to \mathrm{\Lambda }$ is described as  

$$LDFSTOWA(L_1,L_2,\dots ,L_r)={\hslash }_{1}sin{L}_{\xi \left(1\right)}⊞{\hslash }_{2}sin{L}_{\xi \left(2\right)}⊞\dots ⊞{\hslash }_{r}sin{L}_{\xi \left(r\right)}$$

(7)

where $\left\{\xi \right(1),\xi (2),\dots ,\xi (r\left)\right\}$ is the family of $\{1,2,\dots ,r\}$ such that $L_{\xi (i-1)}\ge L_{\xi \left(i\right)}$, $\forall i=2,3,\dots ,r$ and $\hslash =\{{\hslash }_1,{\hslash }_2,\dots ,{\hslash }_r\}$ with ${\hslash }_i>0$ and ${\displaystyle \sum _{i=1}^r}{\hslash }_i=1$ is the WV associated with the ordered positions of the LDFNs. This mapping is termed as the “Linear Diophantine fuzzy sine-trigonometric ordered weighted averaging (LDFSTOWA) operator”.

Theorem 7.

Let $L_i=(\langle {\mu }_{L_i},{\nu }_{L_i}\rangle ,\langle {\lambda }_{L_i},{\eta }_{L_i}\rangle )$ be r LDFNs. Then, their combined value obtained by employing Equation (7) is an LDFN and is provided by

$$\begin{array}{c}\hfill LDFSTOWA(L_1,L_2,\dots ,L_r)=\left(\begin{array}{c}〈1-{\displaystyle \prod _{i=1}^r}{\left(1-{\mathsf{\Omega }}_{\xi \left(i\right)}\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^r}{\left(1-{\mho }_{\xi \left(i\right)}\right)}^{{\hslash }_i}〉,\\ 〈1-{\displaystyle \prod _{i=1}^r}{\left(1-{▵}_{\xi \left(i\right)}\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^r}{\left(1-{\nabla }_{\xi \left(i\right)}\right)}^{{\hslash }_i}〉\end{array}\right)\end{array}$$

(8)

Proof. 

Proof is straightforward.    □

Example 2.

Consider three LDFNs as shown in Table 4 and let $\hslash =\{0.297,0.378,0.325\}$ be their WV. To calculate the aggregated value of these LDFNs, we first calculate the score values of these LDFNs by using Equation (1) as follows.

$$\mathsf{\Psi }\left(L_1\right)=-0.232,\mathsf{\Psi }\left(L_2\right)=-0.215and\mathsf{\Psi }\left(L_3\right)=-0.319.$$

Rearranging the LDFNs, we obtain $L_2\succ L_1\succ L_3$. This gives

$$L_{\xi \left(1\right)}=L_2=(\langle 0.357,0.676\rangle ,\langle 0.357,0.468\rangle )$$

$$L_{\xi \left(2\right)}=L_1=(\langle 0.813,0.916\rangle ,\langle 0.237,0.598\rangle )$$

$$L_{\xi \left(3\right)}=L_3=(\langle 0.779,0.868\rangle ,\langle 0.218,0.767\rangle )$$

The values of ${\mathsf{\Omega }}_{\xi \left(i\right)}$, ${\mho }_{\xi \left(i\right)}$, ${▵}_{\xi \left(i\right)}$ and ${\nabla }_{\xi \left(i\right)}$ for $i=1,2,3$ are given in 

Table 6. The values of ${\mathsf{\Omega }}_{\xi \left(i\right)}$, ${\mho }_{\xi \left(i\right)}$, ${▵}_{\xi \left(i\right)}$, and ${\nabla }_{\xi \left(i\right)}$ for $i=1,2,3$.

${\mathsf{\Omega }}_{\xi \left(1\right)}$	$0.5318$	${\mho }_{\xi \left(1\right)}$	$0.4872$	${▵}_{\xi \left(1\right)}$	$0.5318$	${\nabla }_{\xi \left(1\right)}$	$0.7417$
${\mathsf{\Omega }}_{\xi \left(2\right)}$	$0.9572$	${\mho }_{\xi \left(2\right)}$	$0.1316$	${▵}_{\xi \left(2\right)}$	$0.3637$	${\nabla }_{\xi \left(2\right)}$	$0.5903$
${\mathsf{\Omega }}_{\xi \left(3\right)}$	$0.9403$	${\mho }_{\xi \left(3\right)}$	$0.2059$	${▵}_{\xi \left(3\right)}$	$0.3358$	${\nabla }_{\xi \left(3\right)}$	$0.3579$

.

Now, we obtain necessary computations as follows.

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left(1-{\mathsf{\Omega }}_{\xi \left(i\right)}\right)}^{{\hslash }_i}& ={\left(1-{\mathsf{\Omega }}_{\xi \left(1\right)}\right)}^{{\hslash }_1}\times {\left(1-{\mathsf{\Omega }}_{\xi \left(2\right)}\right)}^{{\hslash }_2}\times {\left(1-{\mathsf{\Omega }}_{\xi \left(3\right)}\right)}^{{\hslash }_3}\hfill & \\ \hfill & ={\left(1-0.5318\right)}^{0.297}\times {\left(1-0.9572\right)}^{0.378}\times {\left(1-0.9403\right)}^{0.325}\hfill & \\ \hfill & =0.0970\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left(1-{\mho }_{\xi \left(i\right)}\right)}^{{\hslash }_i}& ={\left(1-{\mho }_{\xi \left(1\right)}\right)}^{{\hslash }_1}\times {\left(1-{\mho }_{\xi \left(2\right)}\right)}^{{\hslash }_2}\times {\left(1-{\mho }_{\xi \left(3\right)}\right)}^{{\hslash }_3}\hfill & \\ \hfill & ={\left(1-0.4872\right)}^{0.297}\times {\left(1-0.1316\right)}^{0.378}\times {\left(1-0.2059\right)}^{0.325}\hfill & \\ \hfill & =0.7214\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left(1-{▵}_{\xi \left(i\right)}\right)}^{{\hslash }_i}& ={\left(1-{▵}_{\xi \left(1\right)}\right)}^{{\hslash }_1}\times {\left(1-{▵}_{\xi \left(2\right)}\right)}^{{\hslash }_2}\times {\left(1-{▵}_{\xi \left(3\right)}\right)}^{{\hslash }_3}\hfill & \\ \hfill & ={\left(1-0.5318\right)}^{0.297}\times {\left(1-0.3637\right)}^{0.378}\times {\left(1-0.3358\right)}^{0.325}\hfill & \\ \hfill & =0.5890\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left(1-{\nabla }_{\xi \left(i\right)}\right)}^{{\hslash }_i}& ={\left(1-{\nabla }_{\xi \left(1\right)}\right)}^{{\hslash }_1}\times {\left(1-{\nabla }_{\xi \left(2\right)}\right)}^{{\hslash }_2}\times {\left(1-{\nabla }_{\xi \left(3\right)}\right)}^{{\hslash }_3}\hfill & \\ \hfill & ={\left(1-0.7417\right)}^{0.297}\times {\left(1-0.5903\right)}^{0.378}\times {\left(1-0.3579\right)}^{0.325}\hfill & \\ \hfill & =0.4134\hfill \end{array}$$

Thus, we obtain further computations as follows.

$$\begin{array}{ccc}\hfill LDFSTOWA(L_1,L_2,L_3)& =\left(\begin{array}{c}〈1-{\displaystyle \prod _{i=1}^3}{\left(1-{\mathsf{\Omega }}_{\xi \left(i\right)}\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^3}{\left(1-{\mho }_{\xi \left(i\right)}\right)}^{{\hslash }_i}〉,\\ 〈1-{\displaystyle \prod _{i=1}^3}{\left(1-{▵}_{\xi \left(i\right)}\right)}^{{\hslash }_i},{\displaystyle \prod _{i=1}^3}{\left(1-{\nabla }_{\xi \left(i\right)}\right)}^{{\hslash }_i}〉\end{array}\right)\hfill & \\ \hfill & =\left(\begin{array}{c}〈1-0.0970,0.7214〉,〈1-0.5890,0.4134〉\end{array}\right)\hfill & \\ \hfill & =\left(\begin{array}{c}〈0.9030,0.7214〉,〈0.4110,0.4134〉\end{array}\right)\hfill \end{array}$$

Remark 1.

The LDFSTOWA operator holds some key characteristics such as idempotency, monotonicity, and boundedness.

We now present the LDFSTHWA operator, which is a generalization of both the LDFSTWA and the LDFSTOWA operators. This operator first weighs the LDFNs and then arranges them in descending order. Later on, it aggregates the ordered weighted positions of these weighted LDFNs.

4.3. LDFSTHWA Operator

Definition 15.

Let Λ be a set of r LDFNs, then the mapping LDFSTHWA $:{\Lambda }^r\to \Lambda$ with an associated WV $\lambda =\{{\lambda }_1,{\lambda }_2,,\dots ,{\lambda }_r\}$ with ${\lambda }_i>0$ and ${\displaystyle \sum _{i=1}^r}{\lambda }_i=1$ is defined as  

$$LDFSTHWA(L_1,L_2,\dots ,L_r)={\lambda }_{1}sin{\dot{L}}_{\xi \left(1\right)}⊞{\lambda }_{2}sin{\dot{L}}_{\xi \left(2\right)}⊞\dots ⊞{\lambda }_{r}sin{\dot{L}}_{\xi \left(r\right)}$$

(9)

where ${\dot{L}}_i=r{\hslash }_i{L}_i$ and $\left\{\xi \right(1),\xi (2),\dots ,\xi (r\left)\right\}$ is the family of $\{1,2,\dots ,r\}$ such that ${\dot{L}}_{\xi (i-1)}\ge {\dot{L}}_{\xi \left(i\right)}$, $\forall i=2,3,\dots ,r$. Here, $\hslash =\{{\hslash }_1,{\hslash }_2,\dots ,{\hslash }_r\}$ with ${\hslash }_i>0$ and ${\displaystyle \sum _{i=1}^r}{\hslash }_i=1$ is the WV of the LDFNs $L_i$. This mapping is termed as the “Linear Diophantine fuzzy sine-trigonometric hybrid weighted averaging (LDFSTHWA) operator”.

Theorem 8.

Let $L_i=(\langle {\mu }_{L_i},{\nu }_{L_i}\rangle ,\langle {\lambda }_{L_i},{\eta }_{L_i}\rangle )$ be r LDFNs. Then, their combined value obtained by employing Equation (9) is an LDFN and is provided by  

$$\begin{array}{c}\hfill LDFSTHWA(L_1,L_2,\dots ..,L_r)=\left(\begin{array}{c}〈1-{\displaystyle \prod _{i=1}^r}{\left(1-{\dot{\mathsf{\Omega }}}_{\xi \left(i\right)}\right)}^{{\lambda }_i},{\displaystyle \prod _{i=1}^r}{\left(1-{\dot{\mho }}_{\xi \left(i\right)}\right)}^{{\lambda }_i}〉,\\ 〈1-{\displaystyle \prod _{i=1}^r}{\left(1-{\dot{▵}}_{\xi \left(i\right)}\right)}^{{\lambda }_i},{\displaystyle \prod _{i=1}^r}{\left(1-{\dot{\nabla }}_{\xi \left(i\right)}\right)}^{{\lambda }_i}〉\end{array}\right)\end{array}$$

(10)

Proof. 

Straightforward.    □

Example 3.

Consider the three LDFNs shown in Table 4 and let $\hslash =\{0.297,0.378,0.325\}$ be their WV. Let $\lambda =\{0.313,0.286,0.401\}$ be the associated WV. Now,  

$${\dot{L}}_1=(\langle 0.6077,0.9590\rangle ,\langle 0.1257,0.7672\rangle )$$

$${\dot{L}}_2=(\langle 0.2494,0.7769\rangle ,\langle 0.2494,0.5994\rangle )$$

$${\dot{L}}_3=(\langle 0.6000,0.9278\rangle ,\langle 0.1245,0.8659\rangle )$$

The score values of these LDFNs by using Equation (1) as follows.  

$$\mathsf{\Psi }\left(L_1\right)=-0.4964,\mathsf{\Psi }\left(L_2\right)=-0.4388and\mathsf{\Psi }\left(L_3\right)=-0.5346.$$

Rearranging the LDFNs, we have ${\dot{L}}_2\succ {\dot{L}}_1\succ {\dot{L}}_3$. This gives  

$${\dot{L}}_{\xi \left(1\right)}={\dot{L}}_2=(\langle 0.2494,0.7769\rangle ,\langle 0.2494,0.5994\rangle )$$

$${\dot{L}}_{\xi \left(2\right)}={\dot{L}}_1=(\langle 0.6077,0.9590\rangle ,\langle 0.1257,0.7672\rangle )$$

$${\dot{L}}_{\xi \left(3\right)}={\dot{L}}_3=(\langle 0.6000,0.9278\rangle ,\langle 0.1245,0.8659\rangle )$$

The values of ${\dot{\mathsf{\Omega }}}_{\xi \left(i\right)}$, ${\dot{\mho }}_{\xi \left(i\right)}$, ${\dot{▵}}_{\xi \left(i\right)}$ and ${\dot{\nabla }}_{\xi \left(i\right)}$ for $i=1,2,3$ are given in 

Table 7. The values of ${\dot{\mathsf{\Omega }}}_{\xi \left(i\right)}$, ${\dot{\mho }}_{\xi \left(i\right)}$, ${\dot{▵}}_{\xi \left(i\right)}$ and ${\dot{\nabla }}_{\xi \left(i\right)}$ for $i=1,2,3$.

${\dot{\mathsf{\Omega }}}_{\xi \left(1\right)}$	$0.3818$	${\dot{\mho }}_{\xi \left(1\right)}$	$0.3433$	${\dot{▵}}_{\xi \left(1\right)}$	$0.3818$	${\dot{\nabla }}_{\xi \left(1\right)}$	$0.5885$
${\dot{\mathsf{\Omega }}}_{\xi \left(2\right)}$	$0.8161$	${\dot{\mho }}_{\xi \left(2\right)}$	$0.0644$	${\dot{▵}}_{\xi \left(2\right)}$	$0.1962$	${\dot{\nabla }}_{\xi \left(2\right)}$	$0.3576$
${\dot{\mathsf{\Omega }}}_{\xi \left(3\right)}$	$0.8090$	${\dot{\mho }}_{\xi \left(3\right)}$	$0.1132$	${\dot{▵}}_{\xi \left(3\right)}$	$0.1943$	${\dot{\nabla }}_{\xi \left(3\right)}$	$0.2091$

.

Now, we have the following computations.  

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left(1-{\dot{\mathsf{\Omega }}}_{\xi \left(i\right)}\right)}^{{\lambda }_i}& ={\left(1-{\dot{\mathsf{\Omega }}}_{\xi \left(1\right)}\right)}^{{\lambda }_1}\times {\left(1-{\dot{\mathsf{\Omega }}}_{\xi \left(2\right)}\right)}^{{\lambda }_2}\times {\left(1-{\dot{\mathsf{\Omega }}}_{\xi \left(3\right)}\right)}^{{\lambda }_3}\hfill & \\ \hfill & ={\left(1-0.3818\right)}^{0.313}\times {\left(1-0.8161\right)}^{0.286}\times {\left(1-0.8090\right)}^{0.401}\hfill & \\ \hfill & =0.2729\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left(1-{\dot{\mho }}_{\xi \left(i\right)}\right)}^{{\lambda }_i}& ={\left(1-{\dot{\mho }}_{\xi \left(1\right)}\right)}^{{\lambda }_1}\times {\left(1-{\dot{\mho }}_{\xi \left(2\right)}\right)}^{{\lambda }_2}\times {\left(1-{\dot{\mho }}_{\xi \left(3\right)}\right)}^{{\lambda }_3}\hfill & \\ \hfill & ={\left(1-0.3433\right)}^{0.313}\times {\left(1-0.0644\right)}^{0.286}\times {\left(1-0.1132\right)}^{0.401}\hfill & \\ \hfill & =0.8197\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left(1-{\dot{▵}}_{\xi \left(i\right)}\right)}^{{\lambda }_i}& ={\left(1-{\dot{▵}}_{\xi \left(1\right)}\right)}^{{\lambda }_1}\times {\left(1-{\dot{▵}}_{\xi \left(2\right)}\right)}^{{\lambda }_2}\times {\left(1-{\dot{▵}}_{\xi \left(3\right)}\right)}^{{\lambda }_3}\hfill & \\ \hfill & ={\left(1-0.3818\right)}^{0.313}\times {\left(1-0.1962\right)}^{0.286}\times {\left(1-0.1943\right)}^{0.401}\hfill & \\ \hfill & =0.7411\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left(1-{\dot{\nabla }}_{\xi \left(i\right)}\right)}^{{\lambda }_i}& ={\left(1-{\dot{\nabla }}_{\xi \left(1\right)}\right)}^{{\lambda }_1}\times {\left(1-{\dot{\nabla }}_{\xi \left(2\right)}\right)}^{{\lambda }_2}\times {\left(1-{\dot{\nabla }}_{\xi \left(3\right)}\right)}^{{\lambda }_3}\hfill & \\ \hfill & ={\left(1-0.5885\right)}^{0.313}\times {\left(1-0.3576\right)}^{0.286}\times {\left(1-0.2091\right)}^{0.401}\hfill & \\ \hfill & =0.6074\hfill \end{array}$$

Thus, we obtain essential computations as follows.

$$\begin{array}{ccc}\hfill LDFSTHWA(L_1,L_2,L_3)& =\left(\begin{array}{c}〈1-{\displaystyle \prod _{i=1}^3}{\left(1-{\dot{\mathsf{\Omega }}}_{\xi \left(i\right)}\right)}^{{\lambda }_i},{\displaystyle \prod _{i=1}^3}{\left(1-{\dot{\mho }}_{\xi \left(i\right)}\right)}^{{\lambda }_i}〉,\\ 〈1-{\displaystyle \prod _{i=1}^3}{\left(1-{\dot{▵}}_{\xi \left(i\right)}\right)}^{{\lambda }_i},{\displaystyle \prod _{i=1}^3}{\left(1-{\dot{\nabla }}_{\xi \left(i\right)}\right)}^{{\lambda }_i}〉\end{array}\right)\hfill & \\ \hfill & =\left(\begin{array}{c}〈1-0.2729,0.8197〉,〈1-0.7411,0.6074〉\end{array}\right)\hfill & \\ \hfill & =\left(\begin{array}{c}〈0.7271,0.8197〉,〈0.2589,0.6074〉\end{array}\right)\hfill \end{array}$$

Remark 2.

Note that

• If $\hslash =\{\frac{1}{r},\frac{1}{r},\dots ..,\frac{1}{r}\}$, then the LDFSTHWA operator reduces to the LDFSTOWA operator.
• If $\lambda =\{\frac{1}{r},\frac{1}{r},\dots ..,\frac{1}{r}\}$, then the LDFSTHWA operator reduces to the LDFSTWA operator.

5. Linear Diophantine Fuzzy Sine-Trigonometric Geometric Aggregation Operators

On the basis of LDF-STOLs, another family of AOs can be investigated, namely, geometric AOs. Now we introduce LDFSTWG operator, LDFSTOWG operator and LDFSTHWG operator.

5.1. LDFSTWG Operator

Definition 16.

For a set of r LDFNs, a mapping LDFSTWG$:{\mathsf{\Lambda }}^r\to \mathsf{\Lambda }$ is described as

$$LDFSTWG(L_1,L_2,\dots ,L_r)={(sin{L}_1)}^{{\hslash }_1}⊠{(sin{L}_2)}^{{\hslash }_2}⊠\dots ⊠{(sin{L}_r)}^{{\hslash }_r}$$

(11)

This mapping is termed as “Linear Diophantine fuzzy sine-trigonometric weighted geometric (LDFSTWG) operator”.

Theorem 9.

Let $L_i=(\langle {\mu }_{L_i},{\nu }_{L_i}\rangle ,\langle {\lambda }_{L_i},{\eta }_{L_i}\rangle )$ be r LDFNs. Then, their combined value obtained by employing Equation (11) is an LDFN and is provided by  

$$\begin{array}{c}\hfill LDFSTWG(L_1,L_2,\dots ,L_r)=\left(\begin{array}{c}〈{\displaystyle \prod _{i=1}^r}{\left({\mathsf{\Omega }}_i\right)}^{{\hslash }_i},1-{\displaystyle \prod _{i=1}^r}{\left({\mho }_i\right)}^{{\hslash }_i}〉,〈{\displaystyle \prod _{i=1}^r}{\left({▵}_i\right)}^{{\hslash }_i},1-{\displaystyle \prod _{i=1}^r}{\left({\nabla }_i\right)}^{{\hslash }_i}〉\end{array}\right)\end{array}$$

(12)

Example 4.

Consider the three LDFNs shown in Table 4 and let $\hslash =\{0.297,0.378,0.325\}$be their WV. The values of ${\mathsf{\Omega }}_i$, ${\mho }_i$, ${▵}_i$and${\nabla }_i$for$i=1,2,3$ were already calculated in Table 5. Now, we have  

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left({\mathsf{\Omega }}_i\right)}^{{\hslash }_i}& ={\left({\mathsf{\Omega }}_1\right)}^{{\hslash }_1}\times {\left({\mathsf{\Omega }}_2\right)}^{{\hslash }_2}\times {\left({\mathsf{\Omega }}_3\right)}^{{\hslash }_3}\hfill & \\ \hfill & ={\left(0.9572\right)}^{0.297}\times {\left(0.5318\right)}^{0.378}\times {\left(0.9403\right)}^{0.325}\hfill & \\ \hfill & =0.7621\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left({\mho }_i\right)}^{{\hslash }_i}& ={\left({\mho }_1\right)}^{{\hslash }_1}\times {\left({\mho }_2\right)}^{{\hslash }_2}\times {\left({\mho }_3\right)}^{{\hslash }_3}\hfill & \\ \hfill & ={\left(0.1316\right)}^{0.297}\times {\left(0.4872\right)}^{0.378}\times {\left(0.2059\right)}^{0.325}\hfill & \\ \hfill & =0.2496\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left({▵}_i\right)}^{{\hslash }_i}& ={\left({▵}_1\right)}^{{\hslash }_1}\times {\left({▵}_2\right)}^{{\hslash }_2}\times {\left({▵}_3\right)}^{{\hslash }_3}\hfill & \\ \hfill & ={\left(0.3637\right)}^{0.297}\times {\left(0.5318\right)}^{0.378}\times {\left(0.3358\right)}^{0.325}\hfill & \\ \hfill & =0.4091\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left({\nabla }_i\right)}^{{\hslash }_i}& ={\left({\nabla }_1\right)}^{{\hslash }_1}\times {\left({\nabla }_2\right)}^{{\hslash }_2}\times {\left({\nabla }_3\right)}^{{\hslash }_3}\hfill & \\ \hfill & ={\left(0.5903\right)}^{0.297}\times {\left(0.7417\right)}^{0.378}\times {\left(0.3579\right)}^{0.325}\hfill & \\ \hfill & =0.5469\hfill \end{array}$$

Now, we obtain the following values.

$$\begin{array}{ccc}\hfill LDFSTWG(L_1,L_2,L_3)& =\left(\begin{array}{c}〈{\displaystyle \prod _{i=1}^3}{\left({\mathsf{\Omega }}_i\right)}^{{\hslash }_i},1-{\displaystyle \prod _{i=1}^3}{\left({\mho }_i\right)}^{{\hslash }_i}〉,〈{\displaystyle \prod _{i=1}^3}{\left({▵}_i\right)}^{{\hslash }_i},1-{\displaystyle \prod _{i=1}^3}{\left({\nabla }_i\right)}^{{\hslash }_i}〉\end{array}\right)\hfill & \\ \hfill & =\left(\begin{array}{c}〈0.7621,1-0.2496〉,〈0.4091,1-0.5469〉\end{array}\right)\hfill & \\ \hfill & =\left(\begin{array}{c}〈0.7621,0.7504〉,〈0.4091,0.4531〉\end{array}\right)\hfill \end{array}$$

We observe that the properties of Theorem 6 hold for the LDFSTWG operator.

5.2. LDFSTOWG Operator

Definition 17.

For a set of r LDFNs, a mapping LDFSTOWG $:{\Lambda }^r\to \Lambda$is described as

$$LDFSTOWG(L_1,L_2,\dots ,L_r)={(sin{L}_{\xi \left(1\right)})}^{{\hslash }_1}⊠{(sin{L}_{\xi \left(2\right)})}^{{\hslash }_2}⊠\dots ⊠{(sin{L}_{\xi \left(r\right)})}^{{\hslash }_r}$$

(13)

where $\left\{\xi \right(1),\xi (2),\dots ,\xi (r\left)\right\}$ is the family of $\{1,2,\dots ,r\}$ such that $L_{\xi (i-1)}\ge L_{\xi \left(i\right)}$, $\forall i=2,3,\dots ,r$. This mapping is termed as the “Linear Diophantine fuzzy sine-trigonometric ordered weighted geometric (LDFSTOWG) operator”.

Theorem 10.

Let $L_i=(\langle {\mu }_{L_i},{\nu }_{L_i}\rangle ,\langle {\lambda }_{L_i},{\eta }_{L_i}\rangle )$ be r LDFNs. Then, their combined value obtained by employing Equation (11) is an LDFN, and is provided by

$$\begin{array}{c}\hfill LDFSTOWG(L_1,L_2,\dots ,L_r)=\left(\begin{array}{c}〈{\displaystyle \prod _{i=1}^r}{\left({\mathsf{\Omega }}_{\xi \left(i\right)}\right)}^{{\hslash }_i},1-{\displaystyle \prod _{i=1}^r}{\left({\mho }_{\xi \left(i\right)}\right)}^{{\hslash }_i}〉,\\ 〈{\displaystyle \prod _{i=1}^r}{\left({▵}_{\xi \left(i\right)}\right)}^{{\hslash }_i},1-{\displaystyle \prod _{i=1}^r}{\left({\nabla }_{\xi \left(i\right)}\right)}^{{\hslash }_i}〉\end{array}\right)\end{array}$$

(14)

Example 5.

Consider the three LDFNs shown in Table 4 and let $\hslash =\{0.297,0.378,0.325\}$ be their WV. The values of ${\mathsf{\Omega }}_{\xi \left(i\right)}$, ${\mho }_{\xi \left(i\right)}$, ${▵}_{\xi \left(i\right)}$ and ${\nabla }_{\xi \left(i\right)}$ for $i=1,2,3$ were calculated in Table 6. Now, we have  

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left({\mathsf{\Omega }}_{\xi \left(i\right)}\right)}^{{\hslash }_i}& ={\left({\mathsf{\Omega }}_{\xi \left(1\right)}\right)}^{{\hslash }_1}\times {\left({\mathsf{\Omega }}_{\xi \left(2\right)}\right)}^{{\hslash }_2}\times {\left({\mathsf{\Omega }}_{\xi \left(3\right)}\right)}^{{\hslash }_3}\hfill & \\ \hfill & ={\left(0.5318\right)}^{0.297}\times {\left(0.9572\right)}^{0.378}\times {\left(0.9403\right)}^{0.325}\hfill & \\ \hfill & =0.7992\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left({\mho }_{\xi \left(i\right)}\right)}^{{\hslash }_i}& ={\left({\mho }_{\xi \left(1\right)}\right)}^{{\hslash }_1}\times {\left({\mho }_{\xi \left(2\right)}\right)}^{{\hslash }_2}\times {\left({\mho }_{\xi \left(3\right)}\right)}^{{\hslash }_3}\hfill & \\ \hfill & ={\left(0.4872\right)}^{0.297}\times {\left(0.1316\right)}^{0.378}\times {\left(0.2059\right)}^{0.325}\hfill & \\ \hfill & =0.2245\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left({▵}_{\xi \left(i\right)}\right)}^{{\hslash }_i}& ={\left({▵}_{\xi \left(1\right)}\right)}^{{\hslash }_1}\times {\left({▵}_{\xi \left(2\right)}\right)}^{{\hslash }_2}\times {\left({▵}_{\xi \left(3\right)}\right)}^{{\hslash }_3}\hfill & \\ \hfill & ={\left(0.5318\right)}^{0.297}\times {\left(0.3637\right)}^{0.378}\times {\left(0.3358\right)}^{0.325}\hfill & \\ \hfill & =0.3967\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left({\nabla }_{\xi \left(i\right)}\right)}^{{\hslash }_i}& ={\left({\nabla }_{\xi \left(1\right)}\right)}^{{\hslash }_1}\times {\left({\nabla }_{\xi \left(2\right)}\right)}^{{\hslash }_2}\times {\left({\nabla }_{\xi \left(3\right)}\right)}^{{\hslash }_3}\hfill & \\ \hfill & ={\left(0.7417\right)}^{0.297}\times {\left(0.5903\right)}^{0.378}\times {\left(0.3579\right)}^{0.325}\hfill & \\ \hfill & =0.5369\hfill \end{array}$$

Thus, we obtain essential computations as follows.  

$$\begin{array}{ccc}\hfill LDFSTOWG(L_1,L_2,L_3)& =\left(\begin{array}{c}〈{\displaystyle \prod _{i=1}^3}{\left({\mathsf{\Omega }}_{\xi \left(i\right)}\right)}^{{\hslash }_i},1-{\displaystyle \prod _{i=1}^3}{\left({\mho }_{\xi \left(i\right)}\right)}^{{\hslash }_i}〉,〈{\displaystyle \prod _{i=1}^3}{\left({▵}_{\xi \left(i\right)}\right)}^{{\hslash }_i},1-{\displaystyle \prod _{i=1}^3}{\left({\nabla }_{\xi \left(i\right)}\right)}^{{\hslash }_i}〉\end{array}\right)\hfill & \\ \hfill & =\left(\begin{array}{c}〈0.7992,1-0.2245〉,〈0.3967,1-0.5369〉\end{array}\right)\hfill & \\ \hfill & =\left(\begin{array}{c}〈0.7992,0.7755〉,〈0.3967,0.4631〉\end{array}\right)\hfill \end{array}$$

Hence, the required conditions hold for LDFSTOWG operator.

5.3. LDFSTHWG Operator

Definition 18.

Let Λ be a set of r LDFNs, then mapping LDFSTHWG$:{\mathsf{\Lambda }}^r\to \mathsf{\Lambda }$ with an associated WV $\lambda =\{{\lambda }_1,{\lambda }_2,,\dots ,{\lambda }_r\}$ with ${\lambda }_i>0$ and ${\displaystyle \sum _{i=1}^r}{\lambda }_i=1$ is described as  

$$LDFSTHWG(L_1,L_2,\dots ,L_r)={(sin{\dot{L}}_{\xi \left(1\right)})}^{{\lambda }_1}⊠{(sin{\dot{L}}_{\xi \left(2\right)})}^{{\lambda }_2}⊠\dots ⊠{(sin{\dot{L}}_{\xi \left(r\right)})}^{{\lambda }_r}$$

(15)

where ${\dot{L}}_i={\left(L_i\right)}^{r{\hslash }_i}$ and $\left\{\xi \right(1),\xi (2),\dots ,\xi (r\left)\right\}$ is the family of $\{1,2,\dots ,r\}$ such that ${\dot{L}}_{\xi (i-1)}\ge {\dot{L}}_{\xi \left(i\right)}$, $\forall i=2,3,\dots ,r$. This mapping is termed as the“Linear Diophantine fuzzy sine-trigonometric hybrid weighted geometric (LDFSTHWG) operator”.

Theorem 11.

Let $L_i=(\langle {\mu }_{L_i},{\nu }_{L_i}\rangle ,\langle {\lambda }_{L_i},{\eta }_{L_i}\rangle )$ be r LDFNs. Then, their combined value obtained by employing Equation (15) is an LDFN and is provided by

$$\begin{array}{c}\hfill LDFSTHWG(L_1,L_2,\dots ,L_r)=\left(\begin{array}{c}〈{\displaystyle \prod _{i=1}^r}{\left({\dot{\mathsf{\Omega }}}_{\xi \left(i\right)}\right)}^{{\lambda }_i},1-{\displaystyle \prod _{i=1}^r}{\left({\dot{\mho }}_{\xi \left(i\right)}\right)}^{{\lambda }_i}〉,\\ 〈{\displaystyle \prod _{i=1}^r}{\left({\dot{▵}}_{\xi \left(i\right)}\right)}^{{\lambda }_i},1-{\displaystyle \prod _{i=1}^r}{\left({\dot{\nabla }}_{\xi \left(i\right)}\right)}^{{\lambda }_i}〉\end{array}\right)\end{array}$$

(16)

Example 6.

Consider the three LDFNs shown in Table 4 and let $\hslash =\{0.297,0.378,0.325\}$ be their WV. Let $\lambda =\{0.313,0.286,0.401\}$ be the associated WV. Now,

$${\dot{L}}_1=(\langle 0.9617,0.8359\rangle ,\langle 0.4061,0.3748\rangle )$$

$${\dot{L}}_2=(\langle 0.4887,0.5575\rangle ,\langle 0.4887,0.2874\rangle )$$

$${\dot{L}}_3=(\langle 0.9418,0.7858\rangle ,\langle 0.3451,0.6328\rangle )$$

The score values of these LDFNs by using Equation (1) are as follows.

$$\mathsf{\Psi }\left(L_1\right)=0.0786,\mathsf{\Psi }\left(L_2\right)=0.0662and\mathsf{\Psi }\left(L_3\right)=-0.0658.$$

Rearranging the LDFNs, we obtain${\dot{L}}_1\succ {\dot{L}}_2\succ {\dot{L}}_3$. This gives

$${\dot{L}}_{\xi \left(1\right)}={\dot{L}}_1=(\langle 0.9617,0.8359\rangle ,\langle 0.4061,0.3748\rangle )$$

$${\dot{L}}_{\xi \left(2\right)}={\dot{L}}_2=(\langle 0.4887,0.5575\rangle ,\langle 0.4887,0.2874\rangle )$$

$${\dot{L}}_{\xi \left(3\right)}={\dot{L}}_3=(\langle 0.9418,0.7858\rangle ,\langle 0.3451,0.6328\rangle )$$

The values of ${\dot{\mathsf{\Omega }}}_{\xi \left(i\right)}$, ${\dot{\mho }}_{\xi \left(i\right)}$, ${\dot{▵}}_{\xi \left(i\right)}$ and ${\dot{\nabla }}_{\xi \left(i\right)}$ for $i=1,2,3$ are given in 

Table 8. The values of ${\dot{\mathsf{\Omega }}}_{\xi \left(i\right)}$, ${\dot{\mho }}_{\xi \left(i\right)}$, ${\dot{▵}}_{\xi \left(i\right)}$, and ${\dot{\nabla }}_{\xi \left(i\right)}$ for $i=1,2,3$.

${\dot{\mathsf{\Omega }}}_{\xi \left(1\right)}$	$0.9982$	${\dot{\mho }}_{\xi \left(1\right)}$	$0.2549$	${\dot{▵}}_{\xi \left(1\right)}$	$0.5955$	${\dot{\nabla }}_{\xi \left(1\right)}$	$0.8316$
${\dot{\mathsf{\Omega }}}_{\xi \left(2\right)}$	$0.6944$	${\dot{\mho }}_{\xi \left(2\right)}$	$0.6404$	${\dot{▵}}_{\xi \left(2\right)}$	$0.6944$	${\dot{\nabla }}_{\xi \left(2\right)}$	$0.8998$
${\dot{\mathsf{\Omega }}}_{\xi \left(3\right)}$	$0.9958$	${\dot{\mho }}_{\xi \left(3\right)}$	$0.3302$	${\dot{▵}}_{\xi \left(3\right)}$	$0.5159$	${\dot{\nabla }}_{\xi \left(3\right)}$	$0.5453$

.

Thus, we have

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left({\dot{\mathsf{\Omega }}}_{\xi \left(i\right)}\right)}^{{\lambda }_i}& ={\left({\dot{\mathsf{\Omega }}}_{\xi \left(1\right)}\right)}^{{\lambda }_1}\times {\left({\dot{\mathsf{\Omega }}}_{\xi \left(2\right)}\right)}^{{\lambda }_2}\times {\left({\dot{\mathsf{\Omega }}}_{\xi \left(3\right)}\right)}^{{\lambda }_3}\hfill & \\ \hfill & ={\left(0.9982\right)}^{0.313}\times {\left(0.6944\right)}^{0.286}\times {\left(0.9958\right)}^{0.401}\hfill & \\ \hfill & =0.8989\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left({\dot{\mho }}_{\xi \left(i\right)}\right)}^{{\lambda }_i}& ={\left({\dot{\mho }}_{\xi \left(1\right)}\right)}^{{\lambda }_1}\times {\left({\dot{\mho }}_{\xi \left(2\right)}\right)}^{{\lambda }_2}\times {\left({\dot{\mho }}_{\xi \left(3\right)}\right)}^{{\lambda }_3}\hfill & \\ \hfill & ={\left(0.2549\right)}^{0.313}\times {\left(0.6404\right)}^{0.286}\times {\left(0.3302\right)}^{0.401}\hfill & \\ \hfill & =0.3680\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left({\dot{▵}}_{\xi \left(i\right)}\right)}^{{\lambda }_i}& ={\left({\dot{▵}}_{\xi \left(1\right)}\right)}^{{\lambda }_1}\times {\left({\dot{▵}}_{\xi \left(2\right)}\right)}^{{\lambda }_2}\times {\left({\dot{▵}}_{\xi \left(3\right)}\right)}^{{\lambda }_3}\hfill & \\ \hfill & ={\left(0.5955\right)}^{0.313}\times {\left(0.6944\right)}^{0.286}\times {\left(0.5159\right)}^{0.401}\hfill & \\ \hfill & =0.5874\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \prod _{i=1}^3}{\left({\dot{\nabla }}_{\xi \left(i\right)}\right)}^{{\lambda }_i}& ={\left({\dot{\nabla }}_{\xi \left(1\right)}\right)}^{{\lambda }_1}\times {\left({\dot{\nabla }}_{\xi \left(2\right)}\right)}^{{\lambda }_2}\times {\left({\dot{\nabla }}_{\xi \left(3\right)}\right)}^{{\lambda }_3}\hfill & \\ \hfill & ={\left(0.8316\right)}^{0.313}\times {\left(0.8998\right)}^{0.286}\times {\left(0.5453\right)}^{0.401}\hfill & \\ \hfill & =0.7181\hfill \end{array}$$

We obtain the value $LDFSTHWG(L_1,L_2,L_3)$ as follows.

$$\begin{array}{ccc}\hfill LDFSTHWG(L_1,L_2,L_3)& =\left(\begin{array}{c}〈{\displaystyle \prod _{i=1}^3}{\left({\dot{\mathsf{\Omega }}}_{\xi \left(i\right)}\right)}^{{\lambda }_i},1-{\displaystyle \prod _{i=1}^3}{\left({\dot{\mho }}_{\xi \left(i\right)}\right)}^{{\lambda }_i}〉,\\ 〈{\displaystyle \prod _{i=1}^3}{\left({\dot{▵}}_{\xi \left(i\right)}\right)}^{{\lambda }_i},1-{\displaystyle \prod _{i=1}^3}{\left({\dot{\nabla }}_{\xi \left(i\right)}\right)}^{{\lambda }_i}〉\end{array}\right)\hfill & \\ \hfill & =\left(\begin{array}{c}〈0.8989,1-0.3680〉,〈0.5874,1-0.7181〉\end{array}\right)\hfill & \\ \hfill & =\left(\begin{array}{c}〈0.8989,0.6320〉,〈0.5874,0.2819〉\end{array}\right)\hfill \end{array}$$

Remark 3.

Note that

• If $\hslash =\{\frac{1}{r},\frac{1}{r},\dots ,\frac{1}{r}\}$, then the LDFSTHWG operator reduces to the LDFSTOWG operator.
• If $\lambda =\{\frac{1}{r},\frac{1}{r},\dots ,\frac{1}{r}\}$, then the LDFSTHWG operator reduces to the LDFSTWG operator.

6. Multi-Criteria Decision Making

In this section, we construct Algorithm 1 to address the performance analysis of HSC suppliers by using LDFS and sine-trigonometric AOs.

Algorithm 1 (LDFS sine-trigonometric method)

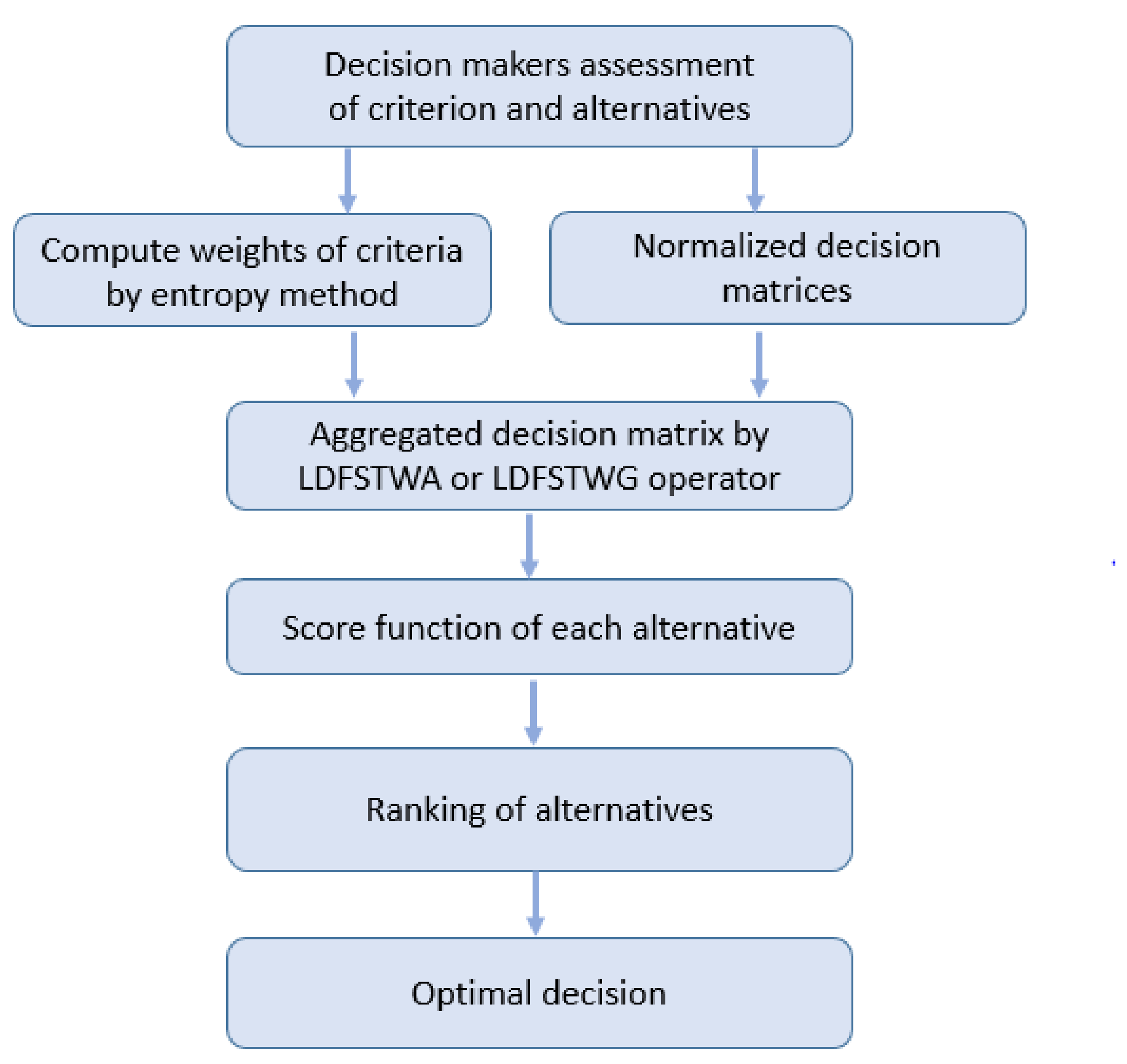
Let $X=\{X_i:i=1,2,\dots ,r\}$ be a set of objects/alternatives and $\complement =\{{\complement }_j:j=1,2,\dots ,s\}$ be a set of criterion. The decision-makers examine each alternative against each criteria and make their expert assessment in the form of LDFNs. This assessment is provided in terms of an LDF-DM. Let $\hslash =\{{\hslash }_1,{\hslash }_2,\dots ,{\hslash }_s\}$ be the unknown WV of the criteria. The proposed algorithm to examine the performance evaluation in HSC has the following steps. Step 1. Construct an LDF-DM $\aleph ={\left({ð}_{ij}\right)}_{r\times s}$ such that an entry ${ð}_{ij}$ reflects the evaluation of the alternative $X_i$ w.r.t the criterion ${\complement }_j$ in the form of an LDFN. Step 2. Obtain the normalized DM $⨿={\left({\delta }_{ij}\right)}_{r\times s}$ in the following way. $${\delta }_{ij}=\left\{\begin{array}{cc}(\langle {\mu }_{ij},{\nu }_{ij}\rangle ,\langle {\Re }_{ij},{\eta }_{ij}\rangle ),\hfill & \mathrm{For}\mathrm{benefit}\mathrm{type}\mathrm{criteria}\hfill \\ (\langle {\nu }_{ij},{\mu }_{ij}\rangle ,\langle {\eta }_{ij},{\Re }_{ij}\rangle ),\hfill & \mathrm{For}\mathrm{cost}\mathrm{type}\mathrm{criteria}\hfill \end{array}\right.$$ (17) Step 3. Calculate the weights of criteria by applying the entropy method. The entropy of the criteria ${\complement }_j$ is computed as follows. $${\eta }_j=\frac{1}{(\sqrt{2}-1)r}{\displaystyle \sum _{i=1}^r}\left[sin\left(\frac{\pi }{8}(2+{\mu }_{ij}-{\nu }_{ij}+{\Re }_{ij}-{\eta }_{ij})\right)+sin\left(\frac{\pi }{8}(2-{\mu }_{ij}+{\nu }_{ij}-{\Re }_{ij}+{\eta }_{ij})\right)-1\right]$$ (18) where $\frac{1}{(\sqrt{2}-1)r}$ is a constant with $0\le {\eta }_j\le 1$. The weights can now be calculated using the formula provided below. $${\hslash }_j=\frac{1-{\eta }_j}{s-{\displaystyle \sum _{j=1}^s}{\eta }_j}$$ (19) Step 4. Using the weights ${\hslash }_j$, combine the entries ${\delta }_{ij}$ to calculate the total value ${\alpha }_i$ of each alternative $X_i$ by employing the LDFSTWA or LDFSTWG operator. Step 5. Find the SF of ${\alpha }_i$, $i=1,2,\dots ,r$, by using Equation (1). Step 6. Arrange the objects/items to express ranking of ${\alpha }_i$’s. Step 7. Find the optimal object/item.

The flow chart of Algorithm is outlined in Figure 3 as follows.

6.1. Numerical Example

The pharmaceutical sector relies heavily on raw materials. They are the driving force behind pharmaceutical production. In pharmaceutics, there are two categories of raw materials: “active pharmaceutical ingredients (APIs) and excipients”. APIs are in charge of the medicine’s efficacy, whilst excipients add thickness and durability to the medication mix. When selecting raw material suppliers, pharmaceutical businesses must ensure that the qualities and profiles of the suppliers satisfy the industry’s defined supplier requirements. The traditional raw material SC presents numerous problems. Some of them are detailed briefly here.

• A superficial knowledge of the cold chain: Sometimes cold chain entities do not have precise knowledge about whereabouts, temperature, timing, and required moisture of raw materials.
• Forecasting demand precisely: One of the most difficult challenges for pharmaceutical supply chain experts is accurately anticipating demand so that all medicinal products are manufactured on time and delivered efficiently.
• Temperature fluctuations: Failures in temperature control produce various problems. For example, the COVID-19 vaccine from Pfizer must be kept between −70 °C and −60 °C. Any temperature changes can make the entire vaccine stock useless.
• Preserving pharmacological compliance: Regulatory business standards have become far more extensive and complex in recent years. Failure to comply can seriously harm finances, the goodwill of a business, and the lives of patients.

Given the limitations of SC, it is critical to incorporate Industry 4.0 into the raw materials of SSP for the pharma industry. The aforementioned issues can be addressed through the digitalization and automation of the HSC. This section focuses on presenting a numerical example to assist the pharmaceutical sector in identifying the best supplier in light of 4.0 digitalization. Consider a pharmaceutical manufacturing company seeking the best supplier for raw materials with the incorporation of 4.0 technologies. Let $\{X_1,X_2,X_3,X_4\}$ be four HSC suppliers of the raw materials in the pharmaceutical industry. Following a thorough assessment of the literature, the essential criteria were identified and reported in

Table 9. Criteria for performance evaluation of HSC supplier.

Criteria	Description	Type
Digitalization (${\complement }_1$)	Use of blockchain technology, big data and cloud computing	Benefit
Automation failure (${\complement }_2$)	Disruptions in IT systems, cyberattacks, spyware	Cost
Traceability (${\complement }_3$)	Use of IoT to determine the location of the materials	Benefit
Capacity (${\complement }_4$)	Ability to manufacture per day	Benefit
Delivery time (${\complement }_5$)	Time required to deliver the supplies	Cost
Cost (${\complement }_6$)	Cost which the supplier charges	Cost

.

The proposed methodology is utilized to find the best HSC supplier in Industry 4.0. In the performance evaluation problem, first we use an LDFSTWA operator.

Step 1. The DM’ assessment of criterion and alternatives in terms of the LDF DM is presented in

Table 10. LDF decision matrix.

	${\mathit{\complement }}_1$	${\complement }_2$	${\complement }_3$
$X_1$	$(\langle 0.517,0.329\rangle ,\langle 0.661,0.278\rangle )$	$(\langle 0.782,0.219\rangle ,\langle 0.677,0.322\rangle )$	$(\langle 0.456,0.568\rangle ,\langle 0.388,0.417\rangle )$
$X_2$	$(\langle 0.712,0.347\rangle ,\langle 0.444,0.455\rangle )$	$(\langle 0.456,0.515\rangle ,\langle 0.512,0.465\rangle )$	$(\langle 0.632,0.719\rangle ,\langle 0.501,0.321\rangle )$
$X_3$	$(\langle 0.317,0.456\rangle ,\langle 0.432,0.318\rangle )$	$(\langle 0.483,0.519\rangle ,\langle 0.618,0.311\rangle )$	$(\langle 0.529,0.631\rangle ,\langle 0.333,0.523\rangle )$
$X_4$	$(\langle 0.521,0.311\rangle ,\langle 0.487,0.288\rangle )$	$(\langle 0.687,0.348\rangle ,\langle 0.711,0.118\rangle )$	$(\langle 0.623,0.555\rangle ,\langle 0.474,0.507\rangle )$
	${\complement }_4$	${\complement }_5$	${\complement }_6$
$X_1$	$(\langle 0.812,0.267\rangle ,\langle 0.575,0.319\rangle )$	$(\langle 0.534,0.288\rangle ,\langle 0.433,0.387\rangle )$	$(\langle 0.678,0.474\rangle ,\langle 0.389,0.412\rangle )$
$X_2$	$(\langle 0.729,0.467\rangle ,\langle 0.386,0.498\rangle )$	$(\langle 0.321,0.478\rangle ,\langle 0.526,0.362\rangle )$	$(\langle 0.786,0.216\rangle ,\langle 0.427,0.519\rangle )$
$X_3$	$(\langle 0.646,0.227\rangle ,\langle 0.474,0.521\rangle )$	$(\langle 0.412,0.667\rangle ,\langle 0.332,0.529\rangle )$	$(\langle 0.517,0.348\rangle ,\langle 0.427,0.421\rangle )$
$X_4$	$(\langle 0.429,0.517\rangle ,\langle 0.328,0.487\rangle )$	$(\langle 0.712,0.482\rangle ,\langle 0.444,0.477\rangle )$	$(\langle 0.557,0.616\rangle ,\langle 0.317,0.502\rangle )$

.

Step 2. Since ${\complement }_2$, ${\complement }_5$, and ${\complement }_6$ are cost type criteria, we normalize the DM using Equation (17). The normalized LDF DM is displayed in

Table 11. Normalized LDF decision matrix.

	${\complement }_1$	${\complement }_2$	${\complement }_3$
$X_1$	$(\langle 0.517,0.329\rangle ,\langle 0.661,0.278\rangle )$	$(\langle 0.219,0.782\rangle ,\langle 0.322,0.677\rangle )$	$(\langle 0.456,0.568\rangle ,\langle 0.388,0.417\rangle )$
$X_2$	$(\langle 0.712,0.347\rangle ,\langle 0.444,0.455\rangle )$	$(\langle 0.515,0.456\rangle ,\langle 0.465,0.512\rangle )$	$(\langle 0.632,0.719\rangle ,\langle 0.501,0.321\rangle )$
$X_3$	$(\langle 0.317,0.456\rangle ,\langle 0.432,0.318\rangle )$	$(\langle 0.519,0.483\rangle ,\langle 0.311,0.618\rangle )$	$(\langle 0.529,0.631\rangle ,\langle 0.333,0.523\rangle )$
$X_4$	$(\langle 0.521,0.311\rangle ,\langle 0.487,0.288\rangle )$	$(\langle 0.348,0.687\rangle ,\langle 0.118,0.711\rangle )$	$(\langle 0.623,0.555\rangle ,\langle 0.474,0.507\rangle )$
	${\complement }_4$	${\complement }_5$	${\complement }_6$
$X_1$	$(\langle 0.812,0.267\rangle ,\langle 0.575,0.319\rangle )$	$(\langle 0.288,0.534\rangle ,\langle 0.387,0.433\rangle )$	$(\langle 0.474,0.678\rangle ,\langle 0.412,0.389\rangle )$
$X_2$	$(\langle 0.729,0.467\rangle ,\langle 0.386,0.498\rangle )$	$(\langle 0.478,0.321\rangle ,\langle 0.362,0.526\rangle )$	$(\langle 0.216,0.786\rangle ,\langle 0.519,0.427\rangle )$
$X_3$	$(\langle 0.646,0.227\rangle ,\langle 0.474,0.521\rangle )$	$(\langle 0.667,0.412\rangle ,\langle 0.529,0.332\rangle )$	$(\langle 0.348,0.517\rangle ,\langle 0.421,0.427\rangle )$
$X_4$	$(\langle 0.429,0.517\rangle ,\langle 0.328,0.487\rangle )$	$(\langle 0.482,0.712\rangle ,\langle 0.477,0.444\rangle )$	$(\langle 0.616,0.557\rangle ,\langle 0.502,0.317\rangle )$

.

Step 3. To compute the criteria weights, we determine their entropy using Equation (18). These values are ${\eta }_1=0.9594$, ${\eta }_2=0.8838$, ${\eta }_3=0.9924$, ${\eta }_4=0.9435$, ${\eta }_5=0.9784$, and ${\eta }_6=0.9769$. Now using Equation (19), we obtain the WV as $\hslash =\{0.1529,0.4375,0.0286,0.2127,$$0.0813,0.0870\}$.

Step 4. Using the WV and LDFSTWA operator, we compute the total value ${\alpha }_i$ of each alternative $X_i$ as given below.

$${\alpha }_1=(\langle 0.7052,0.3054\rangle ,\langle 0.6648,0.2430\rangle )$$

$${\alpha }_2=(\langle 0.7997,0.2421\rangle ,\langle 0.6427,0.2779\rangle )$$

$${\alpha }_3=(\langle 0.7374,0.1973\rangle ,\langle 0.5855,0.2837\rangle )$$

$${\alpha }_4=(\langle 0.6413,0.3604\rangle ,\langle 0.4762,0.2977\rangle )$$

Step 5. Applying Equation (1), we find the SVs of ${\alpha }_i$ as $\mathsf{\Psi }\left({\alpha }_1\right)=0.4108$, $\mathsf{\Psi }\left({\alpha }_2\right)=0.4612$, $\mathsf{\Psi }\left({\alpha }_3\right)=0.4210$, and $\mathsf{\Psi }\left({\alpha }_4\right)=0.2297$.

Step 6. Since $\mathsf{\Psi }\left({\alpha }_2\right)>\mathsf{\Psi }\left({\alpha }_3\right)>\mathsf{\Psi }\left({\alpha }_1\right)>\mathsf{\Psi }\left({\alpha }_4\right)$, the alternatives are ranked as

$$X_2\succ X_3\succ X_1\succ X_4.$$

Step 7. The required alternative is $X_2$.

In the performance evaluation problem, if we use the LDFSTWG operator for information fusion, the calculations are now provided.

Step 1. Using the WV and LDFSTWG operator, we obtain the total value ${\alpha }_i$ of each alternative $X_i$ as given below.

$${\alpha }_1=(\langle 0.5236,0.4659\rangle ,\langle 0.6085,0.3318\rangle )$$

$${\alpha }_2=(\langle 0.7338,0.2898\rangle ,\langle 0.6362,0.2830\rangle )$$

$${\alpha }_3=(\langle 0.6949,0.2330\rangle ,\langle 0.5645,0.3261\rangle )$$

$${\alpha }_4=(\langle 0.6142,0.4205\rangle ,\langle 0.3610,0.3870\rangle )$$

Step 2. Applying Equation (1), we find the SVs of ${\alpha }_i$ as $\mathsf{\Psi }\left({\alpha }_1\right)=0.1672$, $\mathsf{\Psi }\left({\alpha }_2\right)=0.3986$, $\mathsf{\Psi }\left({\alpha }_3\right)=0.3502$, and $\mathsf{\Psi }\left({\alpha }_4\right)=0.0838$.

Step 3. Since $\mathsf{\Psi }\left({\alpha }_2\right)>\mathsf{\Psi }\left({\alpha }_3\right)>\mathsf{\Psi }\left({\alpha }_1\right)>\mathsf{\Psi }\left({\alpha }_4\right)$, so the alternatives are ranked as $X_2\succ X_3\succ X_1\succ X_4$.

Step 4. The required alternative is $X_2$.

Figure 4 shows comparison of ranking of alternatives by using LDFSTWA, LDFSTWG, LDFWA, and LDFWG operators.

6.2. Credibility Test

Wang and Triantaphyllou [47] introduced three test criteria to assess the credibility of MCDM framework as follows.

• Criterion 1: For an MCDM technique to be credible, the best item must remain unaltered if a non-optimal item is replaced with a worse item, given that the criteria weights remain constant.
• Criterion 2: A reliable MCDM method possesses transitivity.
• Criterion 3: If we split an MCDM problem into sub-problems, the cumulative ranking of items derived by merging the sub-problem rankings must be the same as the original ranking.

Now we use these test criteria to examine the credibility of our proposed algorithm.

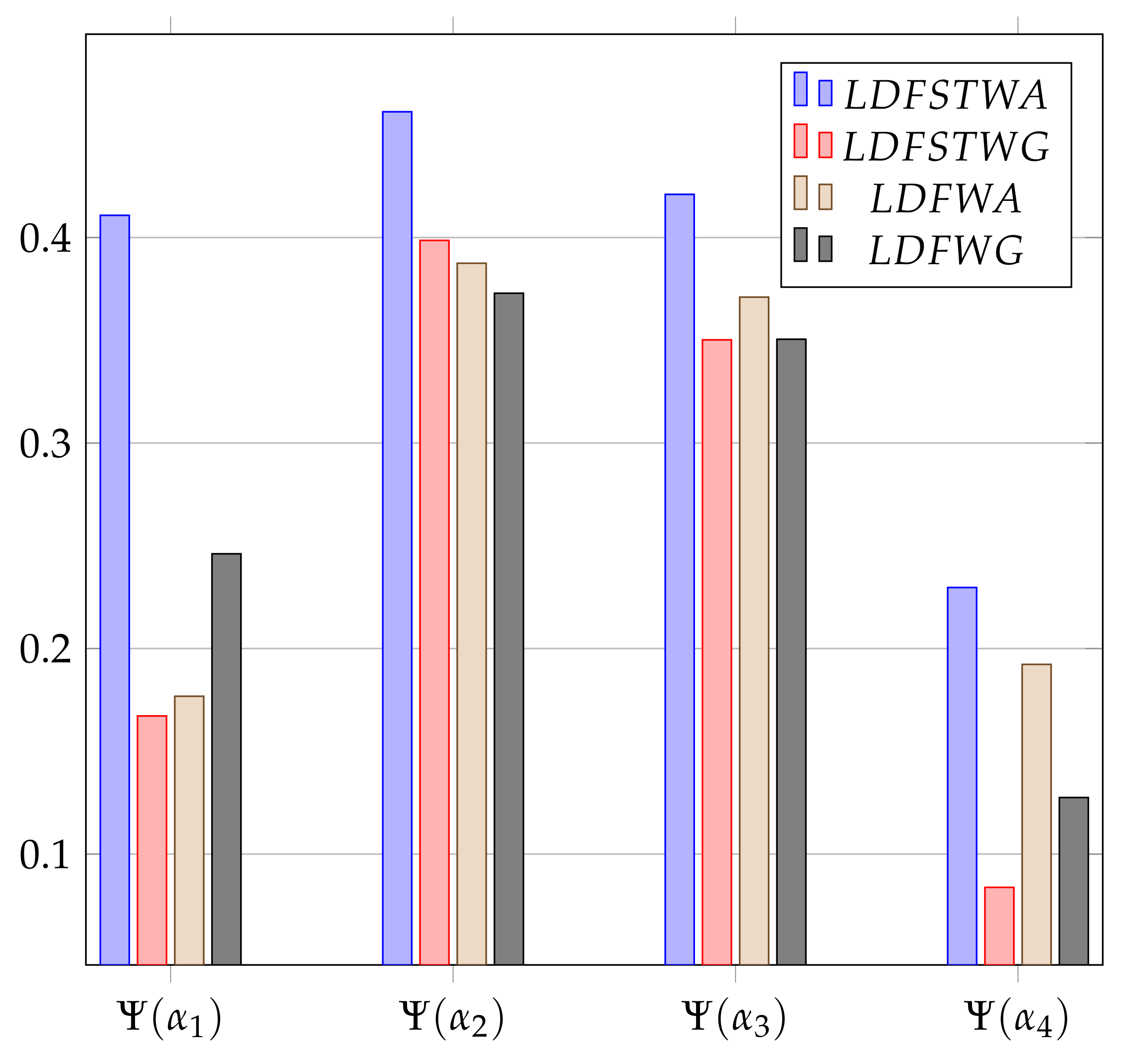
• Criterion 1: We replace alternative $X_4$ with a worse alternative $X_4^{\prime }$ in Table 10 and the amended LDF DM is shown in

  Table 12. Amended LDF decision matrix.

  	${\complement }_1$	${\complement }_2$	${\complement }_3$
  $X_1$	$(\langle 0.517,0.329\rangle ,\langle 0.661,0.278\rangle )$	$(\langle 0.782,0.219\rangle ,\langle 0.677,0.322\rangle )$	$(\langle 0.456,0.568\rangle ,\langle 0.388,0.417\rangle )$
  $X_2$	$(\langle 0.712,0.347\rangle ,\langle 0.444,0.455\rangle )$	$(\langle 0.456,0.515\rangle ,\langle 0.512,0.465\rangle )$	$(\langle 0.632,0.719\rangle ,\langle 0.501,0.321\rangle )$
  $X_3$	$(\langle 0.317,0.456\rangle ,\langle 0.432,0.318\rangle )$	$(\langle 0.483,0.519\rangle ,\langle 0.618,0.311\rangle )$	$(\langle 0.529,0.631\rangle ,\langle 0.333,0.523\rangle )$
  $X_4^{\prime }$	$(\langle 0.433,0.212\rangle ,\langle 0.214,0.127\rangle )$	$(\langle 0.319,0.537\rangle ,\langle 0.222,0.685\rangle )$	$(\langle 0.403,0.412\rangle ,\langle 0.521,0.496\rangle )$
  	${\complement }_4$	${\complement }_5$	${\complement }_6$
  $X_1$	$(\langle 0.812,0.267\rangle ,\langle 0.575,0.319\rangle )$	$(\langle 0.534,0.288\rangle ,\langle 0.433,0.387\rangle )$	$(\langle 0.678,0.474\rangle ,\langle 0.389,0.412\rangle )$
  $X_2$	$(\langle 0.729,0.467\rangle ,\langle 0.386,0.498\rangle )$	$(\langle 0.321,0.478\rangle ,\langle 0.526,0.362\rangle )$	$(\langle 0.786,0.216\rangle ,\langle 0.427,0.519\rangle )$
  $X_3$	$(\langle 0.646,0.227\rangle ,\langle 0.474,0.521\rangle )$	$(\langle 0.412,0.667\rangle ,\langle 0.332,0.529\rangle )$	$(\langle 0.517,0.348\rangle ,\langle 0.427,0.421\rangle )$
  $X_4$	$(\langle 0.410,0.531\rangle ,\langle 0.236,0.445\rangle )$	$(\langle 0.518,0.662\rangle ,\langle 0.406,0.384\rangle )$	$(\langle 0.759,0.678\rangle ,\langle 0.217,0.398\rangle )$

  .
  Now we apply the proposed algorithm using LDFSTWA operator. The score values are $\mathsf{\Psi }\left({\alpha }_1\right)=0.4108$, $\mathsf{\Psi }\left({\alpha }_2\right)=0.4612$, $\mathsf{\Psi }\left({\alpha }_3\right)=0.4210$, and $\mathsf{\Psi }\left({\alpha }_4^{\prime }\right)=0.2636$. As a result, the alternatives are sorted as follows: $X_2\succ X_3\succ X_1\succ X_4^{\prime }$. Hence, our proposed methodology meets criterion 1.
• Criterion 2 and 3: We split the problem into sub-problems $\{X_1,X_2\}$, $\{X_2,X_3\}$, $\{X_3,X_4\}$, and $\{X_4,X_1\}$. After applying the proposed technique to these sub-problems, we obtain $X_2\succ X_1$, $X_2\succ X_3$, $X_3\succ X_4$, and $X_1\succ X_4$. Now we obtain the cumulative ranking of these sub-problems as $X_2\succ X_3\succ X_1\succ X_4$ which is the same as the original ranking. Hence, our proposed methodology fulfills criterion 2 and 3.

6.3. Comparative Analysis

In this section, we compare the ranking of alternatives computed by the proposed MCDM with some existing approaches. The comparison of the LDFSTWA and LDFSWG operators is carried out with various operators including LDFWA, LDFWG, LDFEWA, LDFEWG, LDFEPWA, LDFEPWG, LDFPWA, LDFPWA, sinh-FOLDFWA, sinh-FOLDFWG, LDULGHWA, and LDULGHWG, and the ranking of alternatives is computed to demonstrate the efficiency of proposed AOs. The unanimous decision reveals that the optimal alternative remains same regardless of which AO is used. These findings are summarized in

Table 13. Comparison of different AOs.

Authors	AOs	Ranking	Optimal Object
Riaz  et al. [46]	LDFWA	$X_2\succ X_3\succ X_4\succ X_1$	$X_2$
	LDFWG	$X_2\succ X_3\succ X_1\succ X_4$	$X_4$
Iampan  et al. [48]	LDFEWA	$X_2\succ X_3\succ X_1\succ X_4$	$X_2$
	LDFEWG	$X_2\succ X_3\succ X_1\succ X_4$	$X_2$
Farid  et al. [49]	LDFEPWA	$X_2\succ X_1\succ X_4\succ X_3$	$X_2$
	LDFEPWG	$X_2\succ X_3\succ X_1\succ X_4$	$X_2$
Riaz  et al. [50]	LDFPWA	$X_2\succ X_3\succ X_4\succ X_1$	$X_2$
	LDFPWG	$X_2\succ X_3\succ X_4\succ X_1$	$X_2$
Naeem  et al. [51]	sinh-FOLDFWA	$X_2\succ X_3\succ X_4\succ X_1$	$X_2$
	sinh-FOLDFWG	$X_2\succ X_3\succ X_4\succ X_1$	$X_2$
Izatmand et al. [52]	LDULGHWA	$X_2\succ X_1\succ X_3\succ X_4$	$X_2$
	LDULGHWG	$X_2\succ X_1\succ X_3\succ X_4$	$X_2$
Proposed	LDFSTWA	$X_2\succ X_3\succ X_1\succ X_4$	$X_2$
	LDFSTWG	$X_2\succ X_3\succ X_1\succ X_4$	$X_2$

.

These findings demonstrate that the proposed MCDM technique is efficient and consistent for LDFS information. However, different techniques are used due to limitations and constraints of different fuzzy models to find the ranking of feasible alternatives. For example, Einstein t-corm and t-conorms are used for smooth information [48] while prioritized AO are used for linear prioritized relationships among the criteria [50] and LDFS-fairly averaging operator [53]. The proposed MCDM is based on sine-trigonometric function for efficient information aggregation and performance evaluation. Now we briefly discuss the advantages of the proposed MCDM framework.

6.3.1. Advantages of the Proposed Methodology

• The LDFS theory provides a robust approach for machine learning and modeling uncertain information in real-world problems. Other fuzzy theories have various strict constraints, while LDFS theory provides a freedom to constraints of DMs to choose MG and NMG in the performance evaluation process under multiple criteria.
• The sine function is significant for its characteristics of periodicity, smoothness, and symmetry about the origin. As a result, incorporating the sine-trigonometric function into the MCDM process gives an innovative approach for information analysis. Thus, we developed the LDF sine-trigonometric aggregation operator for information analysis.
• The entropy method is used to generate the criteria weights in the suggested technique. This distinguishes our strategy from others in which criteria weights are determined at random.
• The robust MCDM framework is proposed based on LDFSTAOs.
• A performance analysis of healthcare suppliers is carried out with the new MCDM method.
• The ranking index for feasible alternatives is determined with a score function to seek an optimal alternative.

6.3.2. Limitations of the Proposed Methodology

• The proposed AOs are not parameterized. When compared to a non-parameterized family of AOs, the presence of a parameter permits the decision-making process to broaden and produces more thorough results.
• The proposed methodology ignores the interconnections among the criterion. By taking this into account, the DMs may feel more confidence in their judgments.

7. Conclusions

Industry 4.0 technologies promise automation, digitization, and accuracy in the field of HSC. To take advantage of this emerging technology, this article explores the performance evaluation of an HSC supplier in view of Industry 4.0 based on LDFS information. The LDFS is a powerful fuzzy model to address uncertainties in MCDM challenges. It enlarges the space of MGs and NMGs by incorporating control parameters. This freedom of choice makes it more reliable. Owing to the usefulness of LDFS, we employed this fuzzy model in the research work. The sine function has some prominent characteristics: periodicity and symmetry about the origin.Therefore, sine-trigonometric operations have been introduced for the LDF context. Some intriguing characteristics of these operations have also been examined. We developed a variety of weighted averaging and geometric AOs using sine-trigonometric operations for LDFS information. Several features of these AOs have been explored. A new MCDM technique is developed to deal with uncertainties with the LDFS environment. The criteria weights in this technique are calculated using the entropy method. The goal of developing this strategy was to find the best HSC supplier. A numerical example is provided to depict the applicability of our proposed strategy. Additionally, we applied a credibility test to manifest the authenticity of our proposed technique. A comparative analysis is also presented to discuss the consistency and efficiency of the suggested MCDM framework.

In the future, we will extend LDFS theory towards Industry 5.0 advances for various fields including the supply chain, logistics, environmental sciences, healthcare, robotics, information retrieval systems, expert systems, machine learning, etc. The interconnection of the criteria is not taken into account in this study, thus we will include it in the future. We will develop new hybrid AOs such as LDF sine-trigonometric power AOs, LDF cosine-trigonometric AOs, LDF sine-trigonometric interaction AO, LDF sine-trigonometric normal AOs, and LDFS Schweizer–Sklar aggregation operators.