Dynamic Output Feedback Quantization Control of a Networked Control System with Dual-Channel Data Packet Loss
Abstract
:1. Introduction
2. Preliminaries
2.1. System Description
2.2. Quantization
2.3. Control Strategy and Closed-Loop System
2.4. Definitions and Lemma
3. Main Results
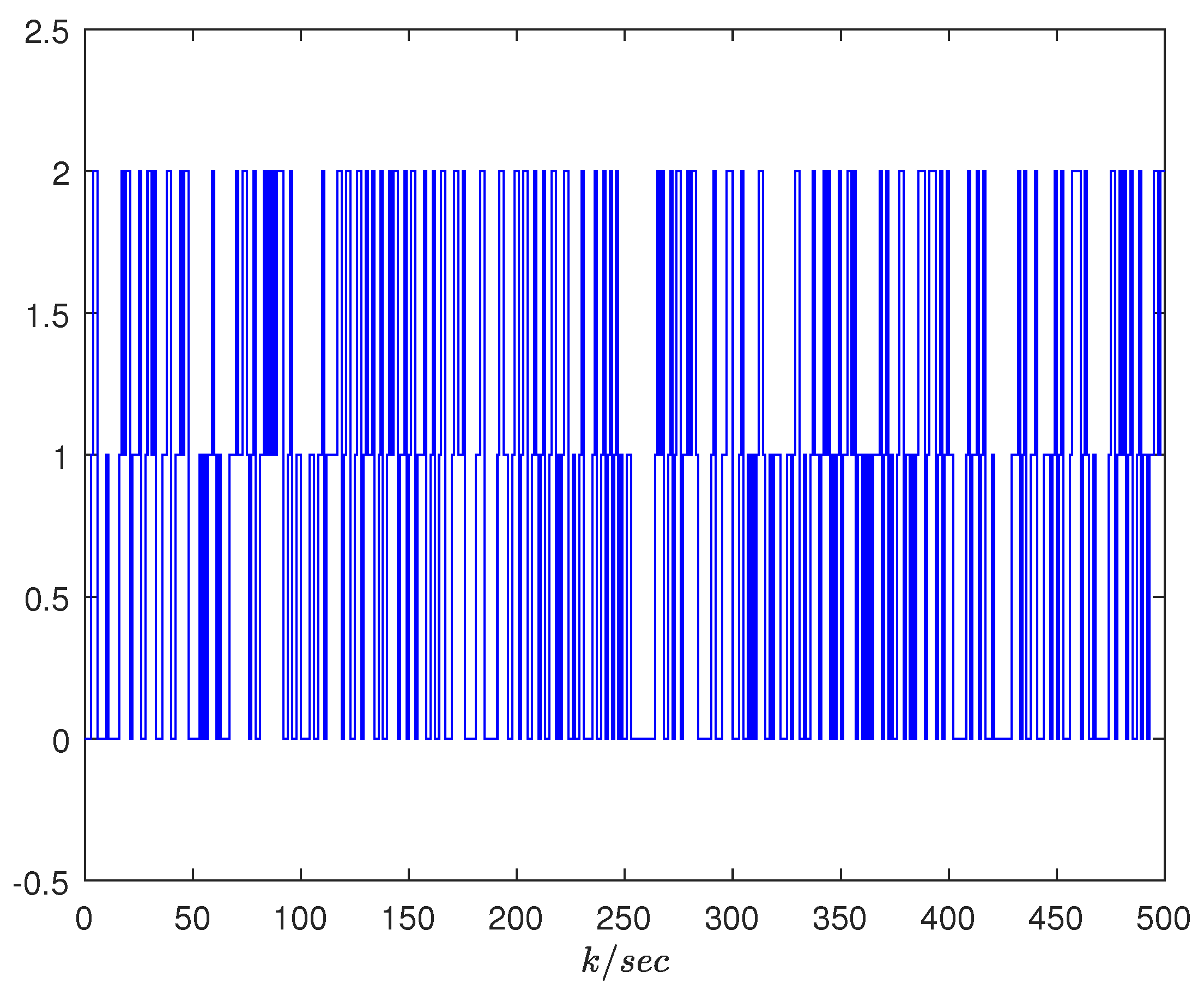
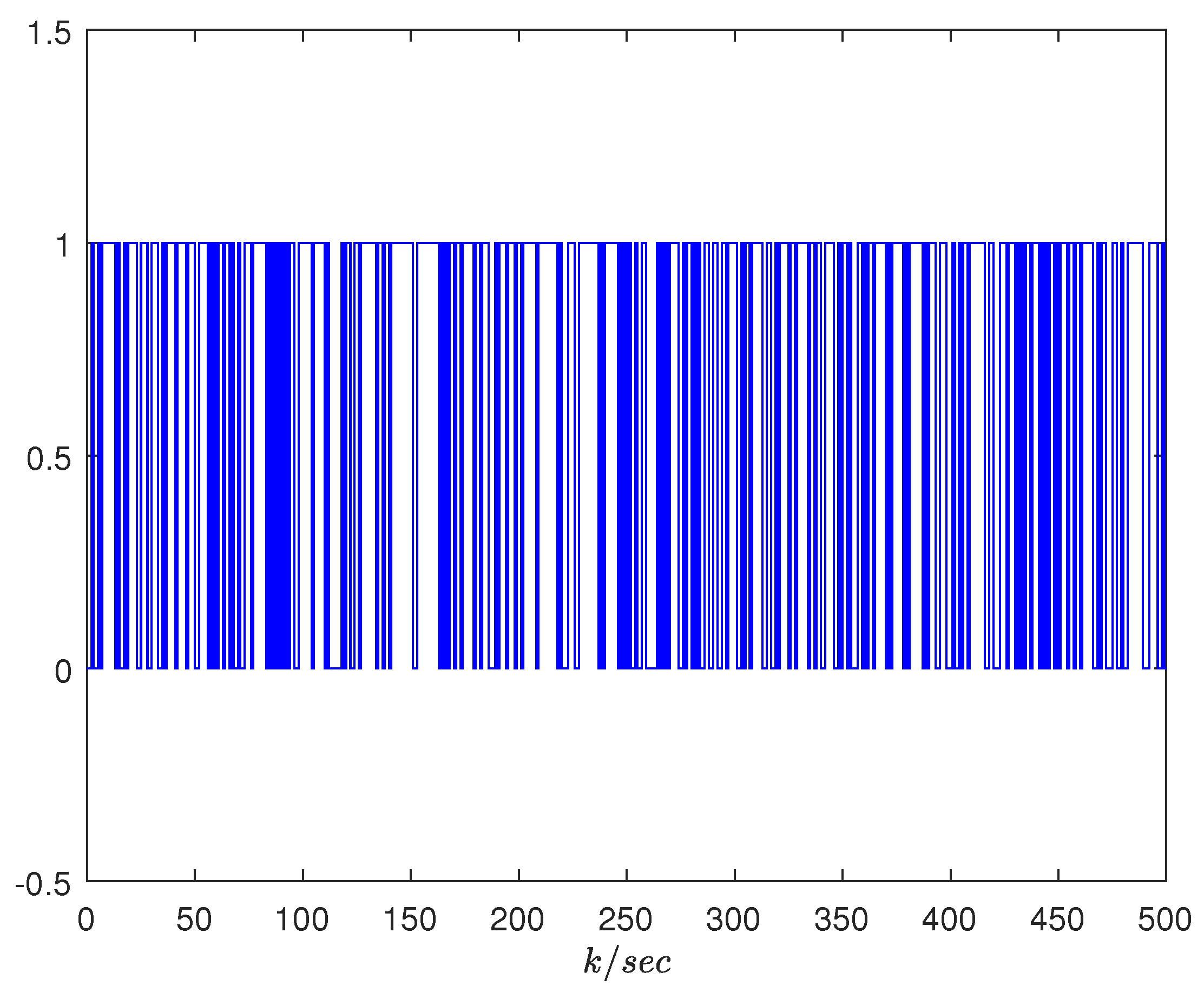
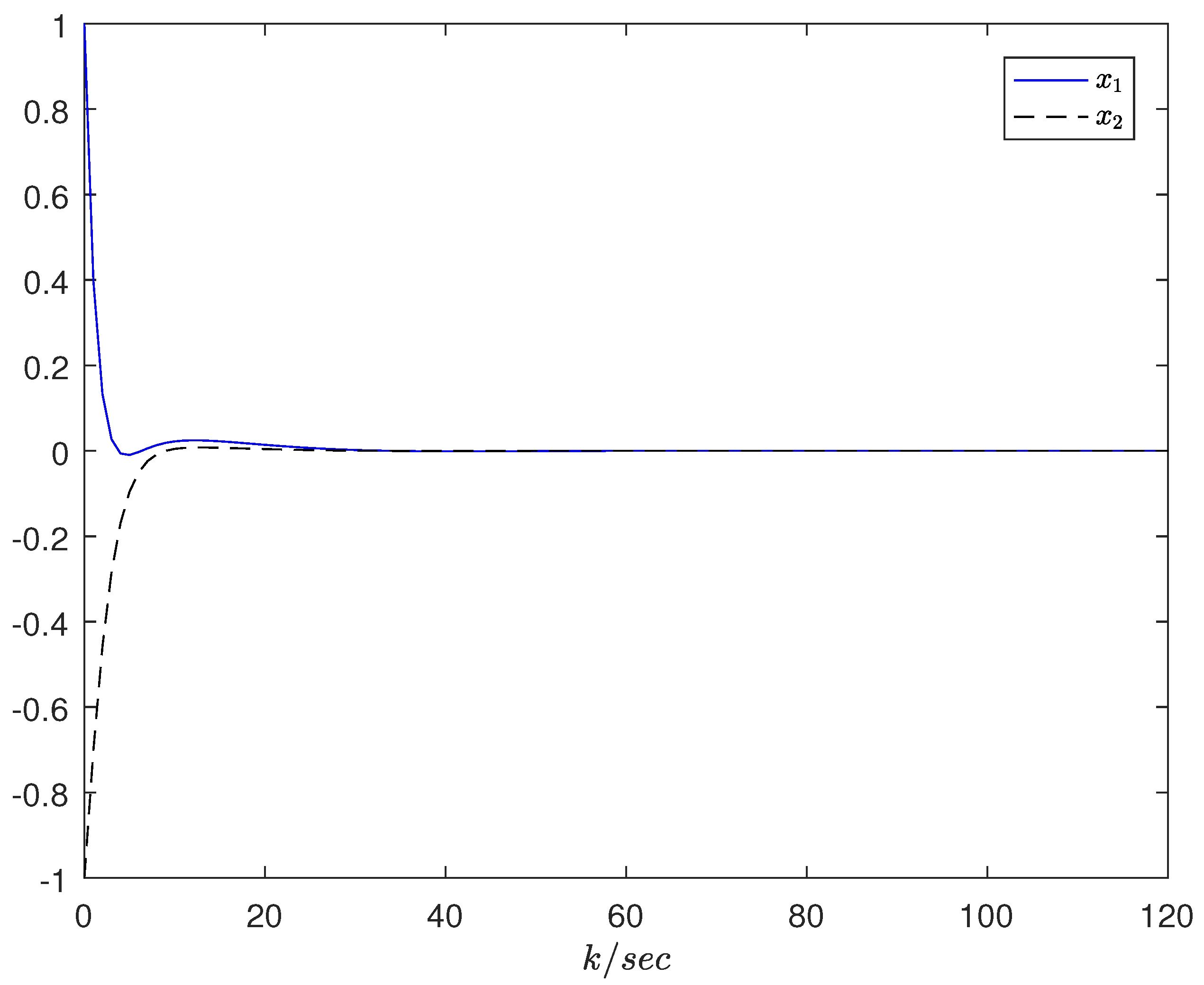
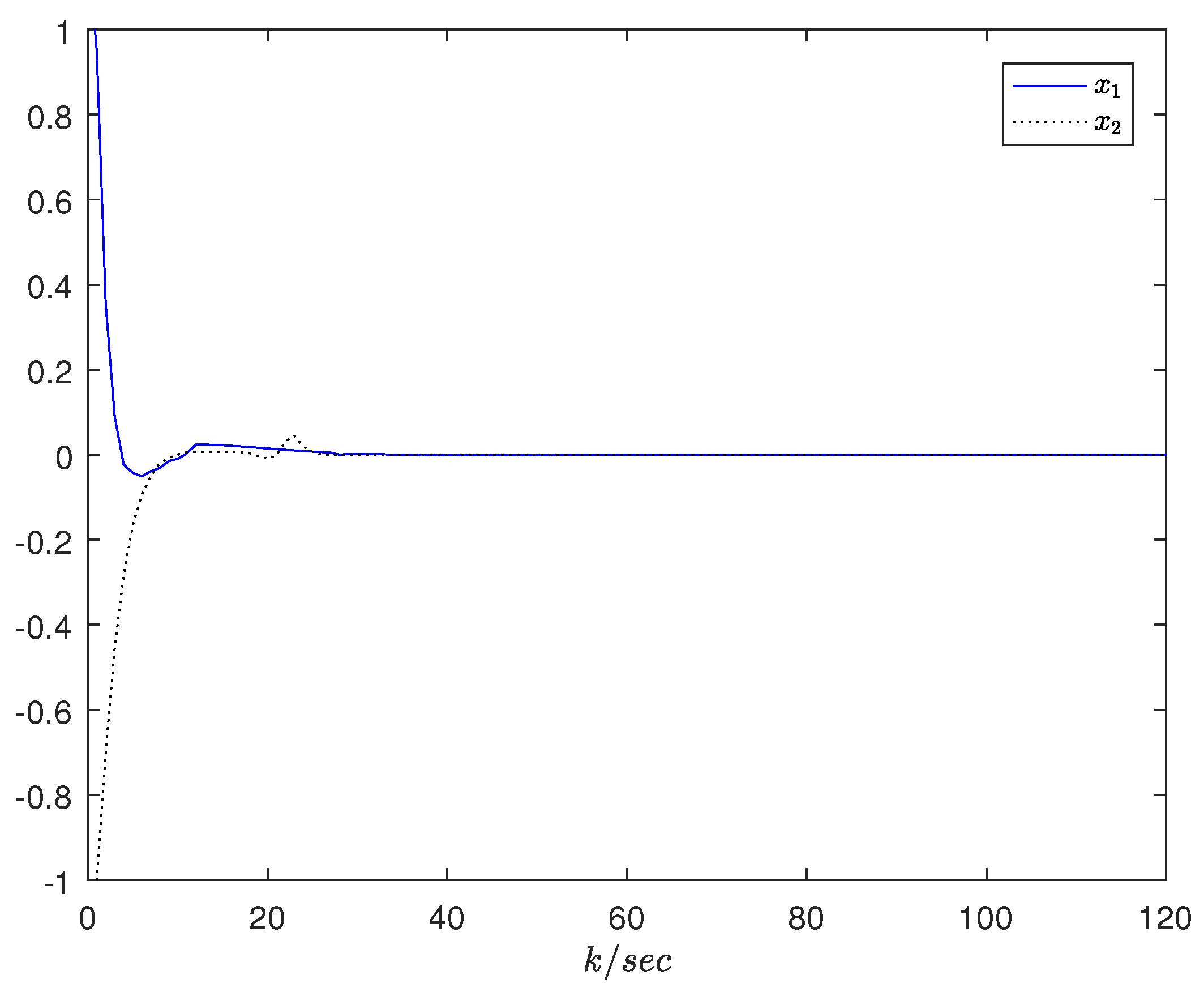
4. Examples
4.1. A Practical Example
4.2. A Numerical Example and Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NCSs | network control systems |
| MJS | Markov jump system |
| S/C | sensor-to-controller |
| C/A | controller-to-actuator |
| DOF | dynamic output feedback |
| TP | transition probability |
| SS | stochastically stable |
| LMI | linear matrix inequality |
References
- Walsh, G.; Ye, H.; Bushnell, L. Stability analysis of networked control systems. In Proceedings of the American Control Conference, San Diego, CA, USA, 2–4 June 1999; pp. 2876–2880. [Google Scholar]
- Mishra, S.; Pat, A.; Appasani, B.; Jha, A.; Kumar, M.; Pal, V.; Gautam, M. Event-triggered fractional-order PID control of fractional-order networked control system. Electr. Eng. 2021, 690, 205–216. [Google Scholar]
- Tian, Y.; Yan, H.; Zhang, H.; Cheng, J.; Shen, H. Asynchronous output feedback control of hidden semi-markov jump systems with random mode-dependent delays. IEEE Trans. Autom. Control 2022, 67, 4107–4114. [Google Scholar] [CrossRef]
- Hua, M.; Zheng, D.; Deng, F. Partially mode-dependent l2-l∞ filtering for discrete-time nonhomogeneous Markov jump systems with repeated scalar nonlinearities. Inf. Sci. 2018, 451–452, 223–239. [Google Scholar] [CrossRef]
- Boukas, E.K. H∞ control of discrete-time Markov jump systems with bounded transition probabilities. Optim. Control Appl. Meth. 2009, 30, 477–494. [Google Scholar] [CrossRef]
- Ma, H.; Jia, Y. H2 control of discrete-time periodic systems with Markovian jumps and multiplicative noise. Int. J. Control 2013, 86, 1837–1849. [Google Scholar] [CrossRef]
- Cheng, J.; Xie, L.; Park, J.H.; Yan, H. Protocol-based output-feedback control for semi-Markov jump systems. IEEE Trans. Autom. Control 2022, 67, 4346–4353. [Google Scholar] [CrossRef]
- Smith, S.; Seiler, P. Estimation with lossy measurements: Jump estimators for jump systems. IEEE Trans. Autom. Control 2015, 48, 2163–2171. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, L. Output feedback stabilization of networked control systems with packet dropouts. IEEE Trans. Autom. Control 2007, 52, 1705–1710. [Google Scholar] [CrossRef]
- Wu, J.; Chen, T. Design of networked control systems with packet dropouts. IEEE Trans. Autom. Control 2007, 52, 1314–1319. [Google Scholar] [CrossRef]
- Shi, Y.; Yu, B. Output feedback stabilization of networked control systems with random delays modeled by Markov chains. IEEE Trans. Autom. Control 2009, 54, 1668–1674. [Google Scholar]
- Shi, Y.; Yu, B. Robust mixed H2/H∞ control of networked control systems with random time delays in both forward and backward communication links. Automatica 2011, 47, 754–760. [Google Scholar] [CrossRef]
- Wu, D.; Wu, J.; Chen, S. Separation principle for a networked control systems with multiple-packet transmission. IET Control Theory Appl. 2011, 5, 507–513. [Google Scholar] [CrossRef]
- Aleksić, D.; Perić, Z.; Nikolić, J. Support region determination of the quasilogarithmic quantizer for Laplacian Source. Prz. Elektrotech. 2012, 88, 130–132. [Google Scholar]
- Tomić, S.; Perić, Z.; Tančić, M.; Nikolić, J. Backward adaptive and quasi-logarithmic quantizer for sub-band coding of audio. Inf. Technol. Control 2018, 47, 131–139. [Google Scholar]
- Kavikumar, R.; Kwon, O.-M.; Kaviarasan, B.; Sakthivel, R. Anti-disturbance control design for interval type-2 fuzzy stochastic systems with input quantization. IEEE Trans. Fuzzy Syst. 2022. [Google Scholar] [CrossRef]
- Wu, C.; Zhao, X. Quantized dynamic output feedback control and L2-gain analysis for a networked control systems: A hybrid approach. IEEE Trans. Netw. Sci. Eng. 2021, 8, 575–587. [Google Scholar] [CrossRef]
- Zhao, L.; Ma, X.; Wang, J. Networked predictive control for linear systems with quantizers by an event-driven strategy. J. Frankl. Inst. 2019, 356, 3245–3269. [Google Scholar] [CrossRef]
- Hua, M.; Qian, Y.; Deng, F.; Fei, J.; Cheng, P.; Chen, H. Filtering for discrete-time Takagi-Sugeno fuzzy nonhomogeneous Markov jump systems with quantization effects. IEEE Trans. Cybern. 2022, 52, 982–995. [Google Scholar] [CrossRef]
- Han, Q.; Liu, Y.; Yang, F. Optimal communication network-based H∞ quantized control with packet dropouts for a class of discrete-time neural networks with distributed time delay. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 426–434. [Google Scholar] [CrossRef]
- Zhang, M.; Shi, P.; Ma, L.; Cai, J.; Su, H. Network-based fuzzy control for nonlinear markov jump systems subject to quantization and dropout compensation. Fuzzy Sets Syst. 2019, 371, 96–109. [Google Scholar] [CrossRef]
- Yang, R.; Shi, P.; Liu, G.; Gao, H. Network-based feedback control for systems with mixed delays based on quantization and dropout compensation. Automatica 2011, 47, 2805–2809. [Google Scholar] [CrossRef]
- Sakthivel, R.; Kavikumar, R.; Mohammadzadeh, A.; Kwon, O.-M.; Kaviarasan, B. Fault estimation for mode-dependent IT2 fuzzy systems with quantized output signals. IEEE Trans. Fuzzy Syst. 2021, 29, 298–309. [Google Scholar] [CrossRef]
- Kalman, R. Nonlinear aspects of sampled-data control systems. Proc. Symp. Nonlinear Circuits Anal. 1956, 6, 273–313. [Google Scholar]
- Wu, B.; Liang, H.; Chang, X.; Zhao, X. Fuzzy H∞ output feedback control for nonlinear NCSs with quantization and stochastic communication protocol. IEEE Trans. Fuzzy Syst. 2021, 29, 2623–2634. [Google Scholar] [CrossRef]
- Yu, M.; Bai, S.; Yang, T.; Zhang, J. Quantized output feedback control of networked control systems with packet dropout. Int. J. Control Autom. Syst. 2018, 16, 2559–2568. [Google Scholar] [CrossRef]
- Wang, H.; Ga, R.; Zhang, Q.; Wen, S. Robust controller design for a networked control system with packet dropout and quantization error. In Proceedings of the 2015 International Conference on Advanced Mechatronic Systems (ICAMechS), Beijing, China, 22–24 August 2015; pp. 552–556. [Google Scholar]
- Ma, W.; Yang, Z. Non-fragile H∞ control for networked lipschitz nonlinear system subject to quantization and packet dropout. WIT Trans. Inf. Commun. Technol. 2014, 55, 629–638. [Google Scholar]
- Che, W.; Jin, X.; Ye, D. Quantized state-feedback H∞ control of networked control systems with Markov dropouts. In Proceedings of the 2012 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012; pp. 406–411. [Google Scholar]
- Okano, K.; Ishii, H. Stabilization of uncertain systems with finite data rates and markovian packet losses. IEEE Trans. Control Netw. Syst. 2014, 1, 298–307. [Google Scholar] [CrossRef]
- Wang, D.; Wang, J.; Wang, W. Output feedback control of networked control systems with packet dropouts in both channels. Inf. Sci. 2013, 221, 544–554. [Google Scholar] [CrossRef]
- Chen, H.; Gao, J.; Shi, T.; Lu, R. H∞ control for a networked control systems with time delay, data packet dropout and disorder. Neurocomputing 2016, 179, 211–218. [Google Scholar] [CrossRef]
- Mahmoud, M.S. Dynamic output feedback of networked control systems with partially known Markov chain packet dropouts. Optim. Control Appl. Methods 2015, 36, 29–44. [Google Scholar] [CrossRef]
- Perić, Z.; Nikolic, J. High-quality laplacian source quantisation using a combination of restricted and unrestricted logarithmic quantisers. IET Signal Process. 2012, 6, 633–640. [Google Scholar] [CrossRef]
- Kao, Y.; Xie, J.; Wang, C. Stabilization of singular Markovian jump systems with generally uncertain transition rates. IEEE Trans. Autom. Control 2014, 59, 2604–2610. [Google Scholar] [CrossRef]
- Dong, S.; Su, H.; Shi, P.; Lu, R.; Wu, Z. Filtering for discrete-time switched fuzzy systems with quantization. IEEE Trans. Fuzzy Syst. 2017, 25, 1616–1628. [Google Scholar] [CrossRef]
- Hua, M.; Bian, C.; Chen, J.; Fei, J. Quantized H∞ filtering for continuous-time nonhomogeneous Markov jump systems. Circ. Syst. Signal Process. 2020, 39, 3833–3857. [Google Scholar] [CrossRef]
- Boyd, S.; Ghaoui, L.E.; Feron, E.; Balakrishnan, V. Linear matrix inequalities in system and control theory. In SIAM Studies in Applied Mathematics; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Li, X.; Sun, S. H∞ control for networked stochastic non-linear systems with randomly occurring sensor saturations, multiple delays and packet dropouts. IET Control Theory Appl. 2017, 11, 2954–2963. [Google Scholar] [CrossRef]




| Theorem 4 | Literature [26] | |
|---|---|---|
| Performance index | 0.0901 | 0.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Hua, M.; Gao, M. Dynamic Output Feedback Quantization Control of a Networked Control System with Dual-Channel Data Packet Loss. Mathematics 2023, 11, 2544. https://doi.org/10.3390/math11112544
Zhang F, Hua M, Gao M. Dynamic Output Feedback Quantization Control of a Networked Control System with Dual-Channel Data Packet Loss. Mathematics. 2023; 11(11):2544. https://doi.org/10.3390/math11112544
Chicago/Turabian StyleZhang, Fan, Mingang Hua, and Mengyu Gao. 2023. "Dynamic Output Feedback Quantization Control of a Networked Control System with Dual-Channel Data Packet Loss" Mathematics 11, no. 11: 2544. https://doi.org/10.3390/math11112544
APA StyleZhang, F., Hua, M., & Gao, M. (2023). Dynamic Output Feedback Quantization Control of a Networked Control System with Dual-Channel Data Packet Loss. Mathematics, 11(11), 2544. https://doi.org/10.3390/math11112544






