Modeling and Heuristically Solving Group Train Operation Scheduling for Heavy-Haul Railway Transportation
Abstract
:1. Introduction
- Define and describe the grouping scheme (group order, number of unit trains within the group) and running process of group trains in detail.
- Propose a mathematical model and an algorithm for optimizing group train scheduling for heavy-haul special lines.
- Investigate the influence of the freight demand importance on scheduling optimization.
2. Related Work
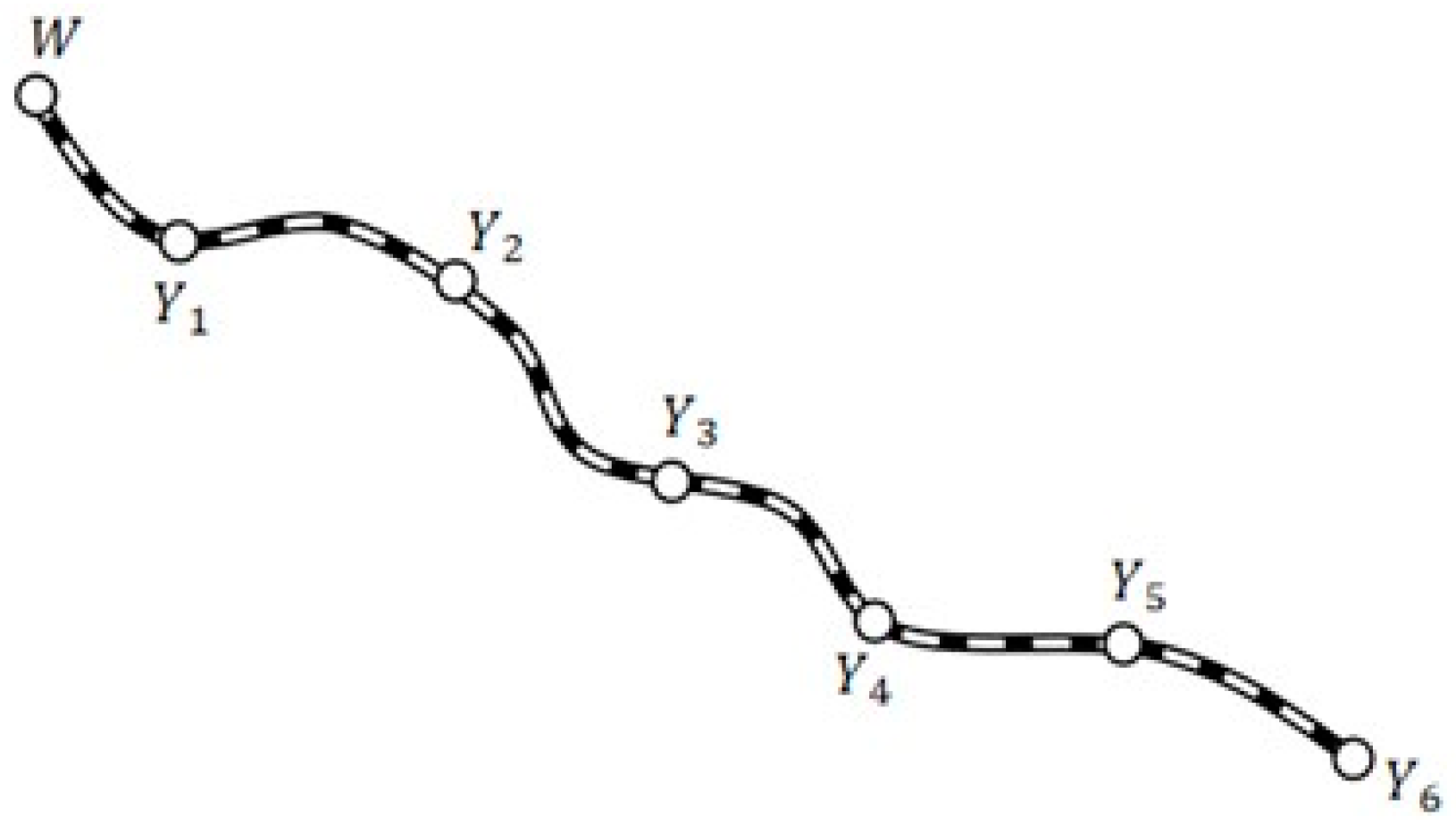
3. Problem Statement
4. Optimization Model
4.1. Model Assumptions
- (1)
- The cargo is of a single type along the line, and the quantity of cargo at the initial technical station is abundant;
- (2)
- The unit trains are sent in groups of the same weight with the same number in each group;
- (3)
- The average speed of a unit train within a group in the interval is constant.
- (4)
- The railway maintenance time is for daily maintenance, and the time is fixed.
4.2. Symbols and Variables
4.3. Mathematical Formulation
4.4. Constraints
5. Simulated Annealing Algorithm
5.1. Algorithm Framework
5.1.1. Generate Initial Solution
5.1.2. Energy Function
5.1.3. Generate Neighborhood Solutions
5.2. Steps of the Proposed Algorithm
6. Numerical Experiment
6.1. Case Description
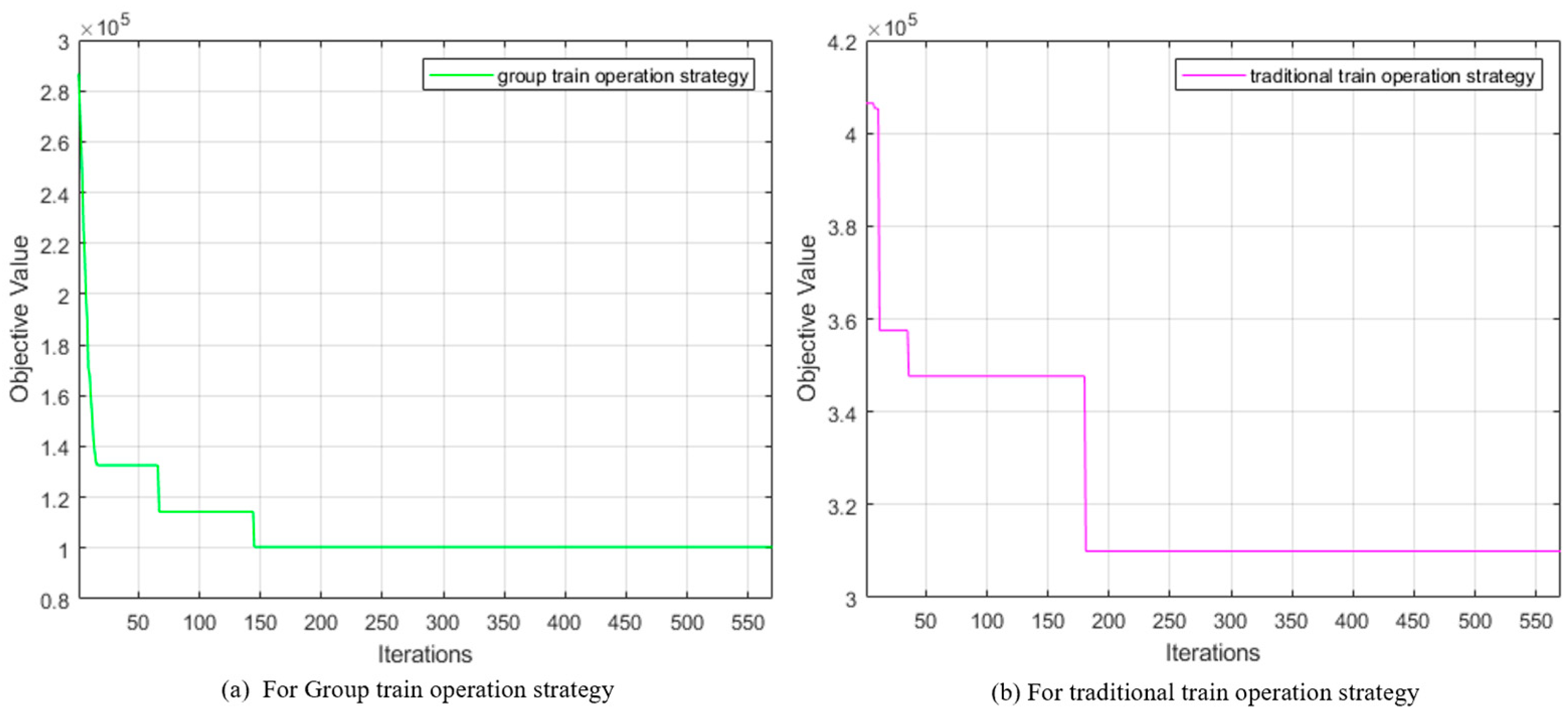
6.2. Solution Results
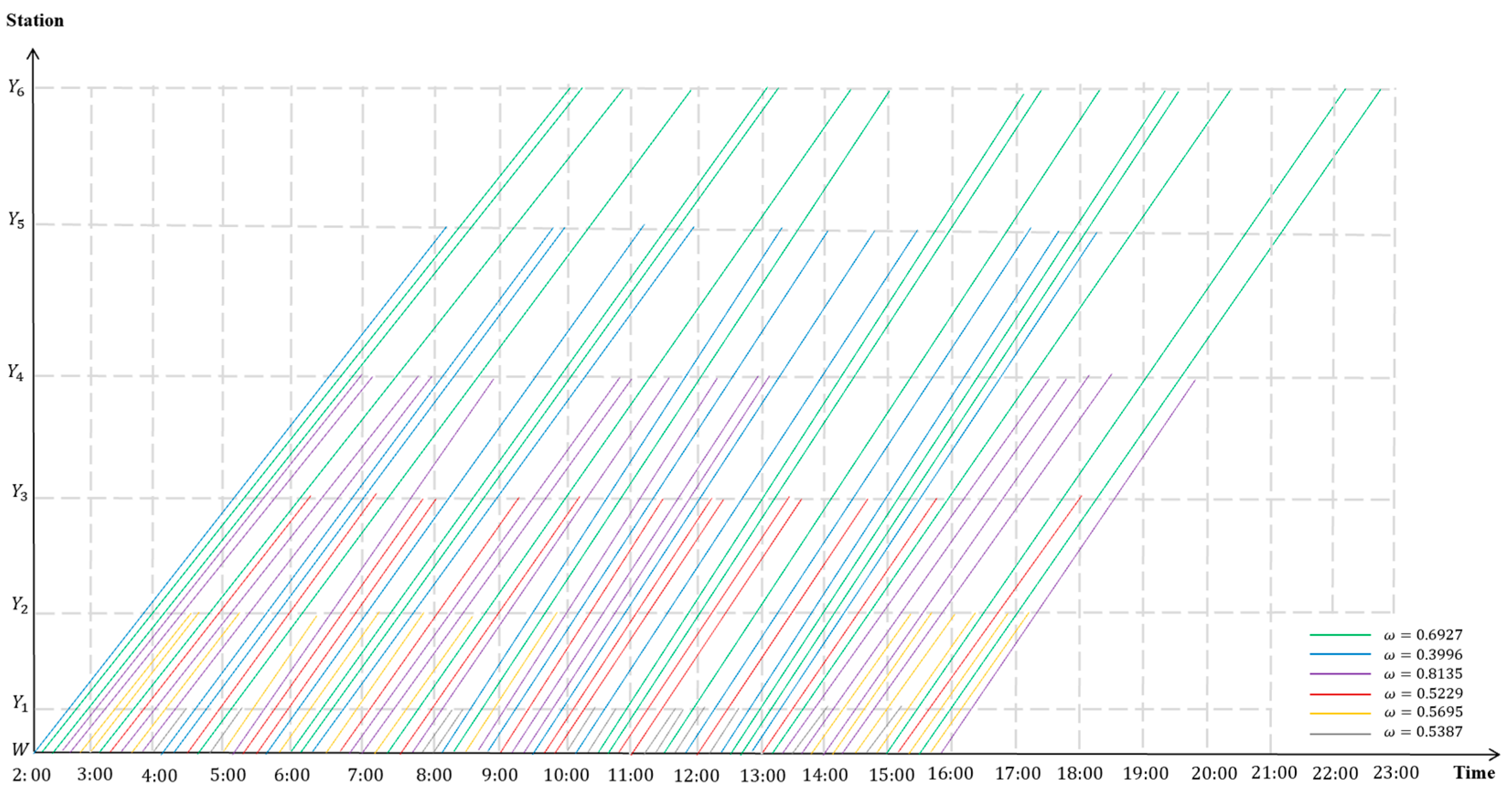
6.2.1. Group Train Operation Scheduling
6.2.2. Traditional Train Operation Scheduling
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, Y. Current Situation and Development of Railway Heavy-haul Transportation Technology System in China. China Railw. Sci. 2015, 36, 1–10. [Google Scholar]
- Ni, J.; Zhang, W.; Liu, N.; Zhang, D.; Zhao, B. Discussion on Demand Forecast and Development Countermeasures of Heavy-haul Railway Transportation during the 14th Five-Year Plan. Railw. Freight Transp. 2022, 40, 7–11+19. [Google Scholar]
- Chen, Y.; Cui, J. Research on Train Control System of Heavy-haul Railway Based on Virtual Grouping Technology. Railw. Stand. Des. 2022, 67, 1–6. [Google Scholar]
- Liu, L. Research and Prospect of Intelligent Control Technology for Virtually Coupled TrainFormation. Railw. Signal. Commun. Eng. 2020, 17, 1–9. [Google Scholar]
- The State Council. The Development Plan of Modern Comprehensive Transportation System in the 14th Five-Year Plan. Railw. Tech. Superv. 2022, 50, 9–23+27. [Google Scholar]
- Meo, C.D.; Vaio, M.D.; Flammini, F.; Nardone, R.; Santini, S.; Vittorini, V. ERTMS/ETCS Virtual Coupling: Proof of Concept and Numerical Analysis. IEEE Trans. Intell. Transp. Syst. 2020, 21, 2545–2556. [Google Scholar] [CrossRef]
- Pan, H.; Yang, L.; Liang, Z. Demand-oriented Integration Optimization of Train Timetabling and Rolling Stock Circulation Planning with Flexible Train Compositions: A Column-generation-based Approach. Eur. J. Oper. Res. 2023, 305, 184–206. [Google Scholar] [CrossRef]
- Wang, E.; Li, X.; Li, P.; Zhang, C.; Gao, Z. Joint optimization of train scheduling and routing in a coupled multi-resolution space–time railway network. Transp. Res. Part C Emerg. Technol. 2023, 147, 103994. [Google Scholar] [CrossRef]
- Jia, N.; Peng, Q.; Zhu, Y.; Jiang, Y.; Otto, A.N. A Bi-objective Optimization Model for the Last Train Timetabling Problem. J. Rail Transp. Plan. Manag. 2022, 23, 100333. [Google Scholar]
- Meng, L.; Zhou, X. An Integrated Train Service Plan Optimization Model with Variable Demand: A Team-based Scheduling Approach with Dual Cost Information in a Layered Network. Transp. Res. Part B Methodol. 2019, 125, 1–28. [Google Scholar] [CrossRef]
- Samà, M.; Pellegrini, P.; D’Ariano, A.; Rodriguez, J.; Pacciarelli, D. Ant colony optimization for the real-time train routing selection problem. Transp. Res. Part B Methodol. 2016, 85, 89–108. [Google Scholar] [CrossRef]
- Allafeepour, A.; Tavakoli, A.; Arvin, A. An optimization integrated approach for simultaneous allocation of railcars and locomotives for train formation based on a pre-designed time schedule. J. Rail Transp. Plan. Manag. 2023, 25, 100366. [Google Scholar] [CrossRef]
- Taslimi, B.; Sarijaloo, F.B.; Liu, H.; Pardalos, P.M. A Novel Mixed Integer Programming Model for Freight Train Travel Time Estimation. Eur. J. Oper. Res. 2022, 300, 676–688. [Google Scholar] [CrossRef]
- Xiao, J.; Lin, B.; Wang, J. Solving the Train Formation Plan Network Problem of the Single-block Train and Two-block Train using a Hybrid Algorithm of Genetic Algorithm and Tabu Search. Transp. Res. Part C Emerg. Technol. 2018, 86, 124–146. [Google Scholar] [CrossRef]
- Abuobidalla, O.; Chen, M.; Chauhan, S. A Matheuristic Method for Planning Railway Freight Transportation with Hazardous Materials. J. Rail Transp. Plan. Manag. 2019, 10, 46–61. [Google Scholar] [CrossRef]
- Bożejko, W.; Grymin, R.; Pempera, J. Scheduling and Routing Algorithms for Rail Freight Transportation. Procedia Eng. 2017, 178, 206–212. [Google Scholar] [CrossRef]
- Lidén, T.; Kalinowski, T.; Waterer, H. Resource Considerations for Integrated Planning of Railway Traffic and Maintenance Windows. J. Rail Transp. Plan. Manag. 2018, 8, 1–15. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, D.; Yin, Y. Integrated Optimization of Train Formation Plan and Rolling Stock Scheduling under Time-dependent Demand. Comput. Oper. Res. 2023, 150, 106049. [Google Scholar] [CrossRef]
- Zhang, C.; Qi, J.; Gao, Y.; Yang, L.; Gao, Z.; Meng, F. Integrated Optimization of Line Planning and Train Timetabling in Railway Corridors with Passengers’ Expected Departure Time Interval. Comput. Ind. Eng. 2021, 162, 107680. [Google Scholar] [CrossRef]
- Li, X.; Wang, D.; Li, K.; Gao, Z. A green train scheduling model and fuzzy multi-objective optimization algorithm. Appl. Math. Model. 2013, 37, 2063–2073. [Google Scholar] [CrossRef]
- Wei, R.; Jia, S.; Tong, R.; Zhang, S. Optimization of Train Planning for General Tree-Type Line. J. South China Univ. Technol. (Nat. Sci. Ed.) 2022, 50, 44–51+81. [Google Scholar]
- Schwerdfeger, S.; Otto, A.; Boysen, N. Rail platooning: Scheduling trains along a rail corridor with rapid-shunting facilities. Eur. J. Oper. Res. 2021, 294, 760–778. [Google Scholar] [CrossRef]
- Li, D.; Li, X.; Wang, J.; Li, Z. Train Operation Scheme of China-Laos Cross-Border Railway Corridor. Railw. Transp. Econ. 2022, 44, 1–8. [Google Scholar]
- Sahli, A.; Behiri, W.; Sana, B.; Chu, C. An Effective and Robust Genetic Algorithm for Urban Freight Transport Scheduling Using Passenger Rail Network. Comput. Ind. Eng. 2022, 173, 108645. [Google Scholar] [CrossRef]
- Xiao, J.; Pachl, J.; Lin, B.; Wang, J. Solving the Block-to-train Assignment Problem using the Heuristic Approach Based on the Genetic Algorithm and Tabu Search. Transp. Res. Part B Methodol. 2018, 108, 148–171. [Google Scholar] [CrossRef]
- Habiballahi, M.A.; Tamannaei, M.; Falsafain, H. Locomotive Assignment Problem with Consideration of Infrastructure and Freight Train Constraints: Mathematical Programming Model and Metaheuristic Solution Approaches. Comput. Ind. Eng. Part A 2022, 172, 108625. [Google Scholar] [CrossRef]
- Milenković, M.; Bojović, N.; Abramin, D. Railway Freight Wagon Fleet Size Optimization: A Real-world Application. J. Rail Transp. Plan. Manag. 2023, 26, 00373. [Google Scholar] [CrossRef]
- Abramov, A.; Podorozkina, A.; Bilenko, G.; Ivankova, L.; Okulova, M. Optimization of Freight Train Speeds on Railway Transport. Transp. Res. Procedia 2022, 61, 371–375. [Google Scholar] [CrossRef]
- Huang, W.; Shuai, B.; Xu, Y.; Zhang, S.; Mao, B. Railway Express Freight Train Service Sites Planning: A Two-stage Entropy-TOPSIS Approach. Transp. A Transp. Sci. 2019, 15, 807–823. [Google Scholar] [CrossRef]
- Li, Y. The Research on Heavy-Haul Transport Organization Plan of Existing Railway. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2012. [Google Scholar]
- Chen, W.; Chen, Z.; Ma, H.; Feng, F. An Optimization Model for Demand-Supply Matching in Daqin Heavy-Haul Railway Transportation. J. Railw. Sci. Eng. 2013, 10, 112–116. [Google Scholar]
- Yu, J. Research on Collaborative Optimization of The Construction Skylight and Train Operation Diagram of Busy Railway Main Lines. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2022. [Google Scholar]
- Yin, Q. Optimization of Locomotive Working for Freight Train on the Railway Sector. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2011. [Google Scholar]
- Ma, H. Research on Transport Demand and Supply Matching of Daqin Railway. Master’s Thesis, Central South University, Changsha, China, 2012. [Google Scholar]



| Symbol | Meaning |
|---|---|
| Set of network stations | |
| Number of stations, | |
| Initial technical station | |
| Station | |
| Set of network section numbers | |
| Number of railway sections, | |
| Number of operating group trains in a single day | |
| Number of groups, | |
| Number of heavy-haul trains within the group | |
| Number of trains, | |
| Set of freight demand numbers | |
| Number of freight demand, | |
| Freight demand importance | |
| Freight demand | |
| Cargo travel time of the group which has the same destination | |
| Cargo travel time of dispersed arriving train n in group m | |
| Departure time of train in group | |
| Arrival time of train in group | |
| Start time of maintenance time | |
| End time of maintenance time | |
| Latest arrival time at terminal station | |
| Length of the railway section | |
| Start and end points of the and segments | |
| Load of a unit train | |
| Number of locomotives to be pulled by a unit train | |
| Maximum number of locomotives on the network | |
| Departure interval of adjacent groups | |
| Departure interval of adjacent trains within the group | |
| Normal operating speed of the train section | |
| Decoupling running speed | |
| Actual supply of for freight demand | |
| Planned supply of for freight demand | |
| Transportation cost | |
| Total cargo travel time | |
| Departure cost of a train at the initial technical station | |
| Unit transportation cost | |
| Weighting coefficient of transportation cost | |
| Weighting coefficient of total cargo travel time |
| Variable | Meaning |
|---|---|
| A 0–1 decision variable which is 1 if station is the terminal station of freight demand Otherwise, it is 0. | |
| A 0–1 decision variable which is 1 if the freight demand of the whole group is . Otherwise, it is 0. | |
| A 0–1 decision variable which is 1 if the railway section belongs to the path of terminal station . Otherwise, it is 0. | |
| A 0–1 decision variable which is 1 if train in group belongs to freight demand . Otherwise, it is 0. |
| Station | Station Center | One-Day Freight Demand (in Ten Thousand Tons) | Latest Arrival Time | Station Level |
|---|---|---|---|---|
| DK0 + 00 | −42 | - | First-class | |
| DK16 + 00 | +6 | 18:00 | Third-class | |
| DK137 + 00 | +7 | 19:00 | Second-class | |
| DK267 + 00 | +7 | 20:00 | Second-class | |
| DK434 + 00 | +8 | 21:00 | First-class | |
| DK630 + 00 | +6 | 22:00 | Third-class | |
| DK811 + 00 | +8 | 23:00 | Second-class |
| Variable | Value |
|---|---|
| Normal operating speed of the train section (km∙h−1) | 100 |
| Decoupling running speed (km∙h−1) | 80 |
| Departure cost of the train at the initial technical station (CNY) | 5000 |
| Unit transportation cost (CNY) | 533 |
| Start time of maintenance | 24:00 |
| End time of maintenance | 02:00 (the next day) |
| Departure intervals of adjacent groups (minutes) | 18 |
| Departure intervals of adjacent in-group trains (minutes) | 6 |
| Departure intervals of adjacent traditional trains (minutes) | 10 |
| Weighting coefficient | 0.5, 0.5 |
| Freight Demand | ||||||
|---|---|---|---|---|---|---|
| Importance degree | 0.5387 | 0.5695 | 0.5229 | 0.8135 | 0.3996 | 0.6927 |
| Result | Value |
|---|---|
| Number of group trains | 11 |
| Number of trains within a group | 8 |
| Number of locomotives per unit | 88 |
| Total cargo travel time (hours) | 196.945 |
| Supply and demand matching difference in transportation cost (CNY) | 27,764 |
| Departure cost (CNY) | 55,000 |
| Result | Value |
|---|---|
| Number of group trains | 84 |
| Number of trains within a group | 1 |
| Number of locomotives per unit | 84 |
| Total cargo travel time (hours) | 333.28 |
| Supply and demand matching difference in transportation cost (CNY) | 0 |
| Departure cost (CNY) | 420,000 |
| Target | Group Train Operation Scheduling | Traditional Train Operation Scheduling |
|---|---|---|
| Target value | 100,470 | 309,984 |
| Transportation cost (CNY) | 82,764 | 420,000 |
| Supply and demand matching difference in transportation cost (CNY) | 27,764 | 0 |
| Departure cost (CNY) | 55,000 | 420,000 |
| The total cargo travel time (hours) | 196.945 | 333.280 |
| Freight Demand | Transport Path | Group Train Operation Scheduling | Traditional Train Operation Scheduling | Planned Supply | ||
|---|---|---|---|---|---|---|
| 7.5 | +1.5 | 6 | 0 | 6 | ||
| 7 | 0 | 7 | 0 | 7 | ||
| 7 | 0 | 7 | 0 | 7 | ||
| 8 | 0 | 8 | 0 | 8 | ||
| 6.5 | +0.5 | 6 | 0 | 6 | ||
| 8 | 0 | 8 | 0 | 8 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Zhuo, Q.; Zhang, L. Modeling and Heuristically Solving Group Train Operation Scheduling for Heavy-Haul Railway Transportation. Mathematics 2023, 11, 2489. https://doi.org/10.3390/math11112489
Chen W, Zhuo Q, Zhang L. Modeling and Heuristically Solving Group Train Operation Scheduling for Heavy-Haul Railway Transportation. Mathematics. 2023; 11(11):2489. https://doi.org/10.3390/math11112489
Chicago/Turabian StyleChen, Weiya, Qinyu Zhuo, and Lu Zhang. 2023. "Modeling and Heuristically Solving Group Train Operation Scheduling for Heavy-Haul Railway Transportation" Mathematics 11, no. 11: 2489. https://doi.org/10.3390/math11112489
APA StyleChen, W., Zhuo, Q., & Zhang, L. (2023). Modeling and Heuristically Solving Group Train Operation Scheduling for Heavy-Haul Railway Transportation. Mathematics, 11(11), 2489. https://doi.org/10.3390/math11112489







