Bursting Dynamics in a Singular Vector Field with Codimension Three Triple Zero Bifurcation
Abstract
1. Introduction
2. Mathematical Model
3. Bifurcation Analyses
3.1. Bifurcation Analysis on Plane for
3.2. Bifurcation Analysis on Plane for
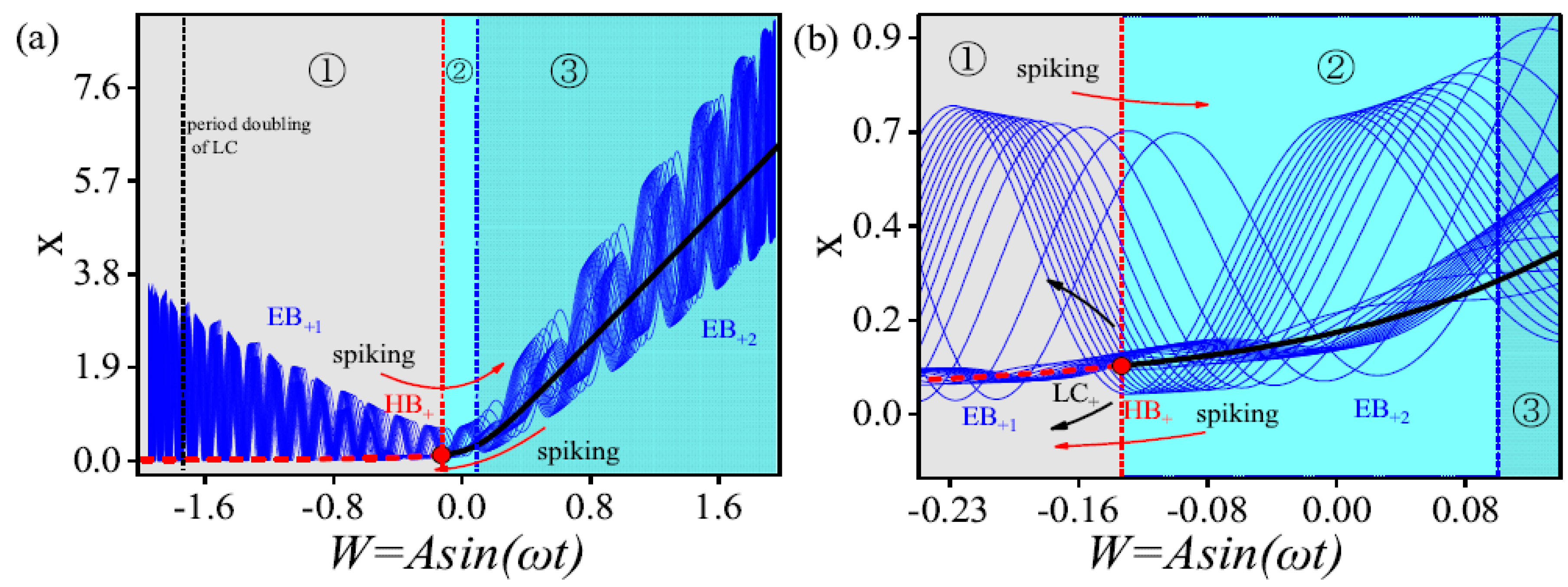
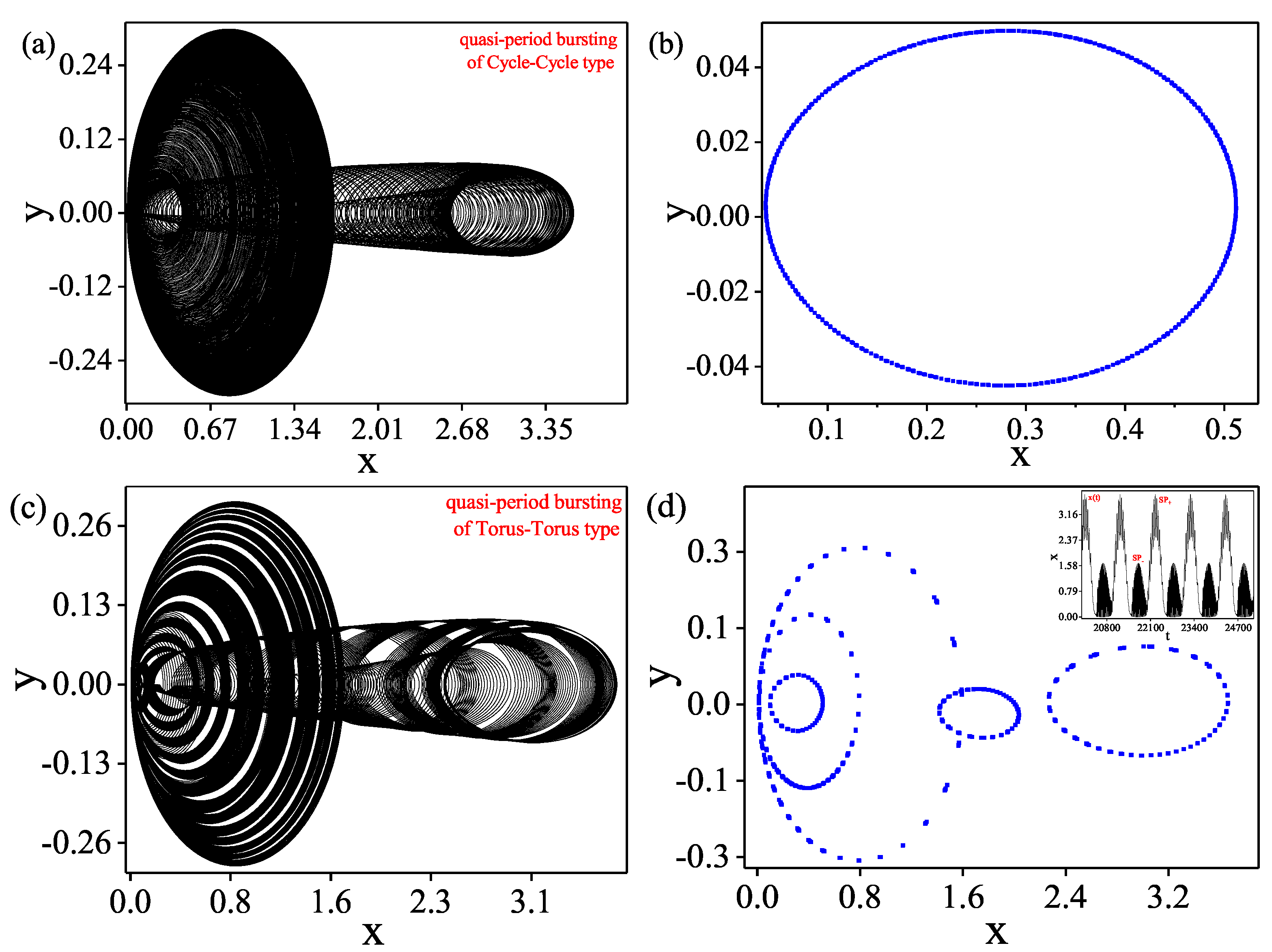
4. Evolution of Bursting Oscillations as Well as Their Mechanism
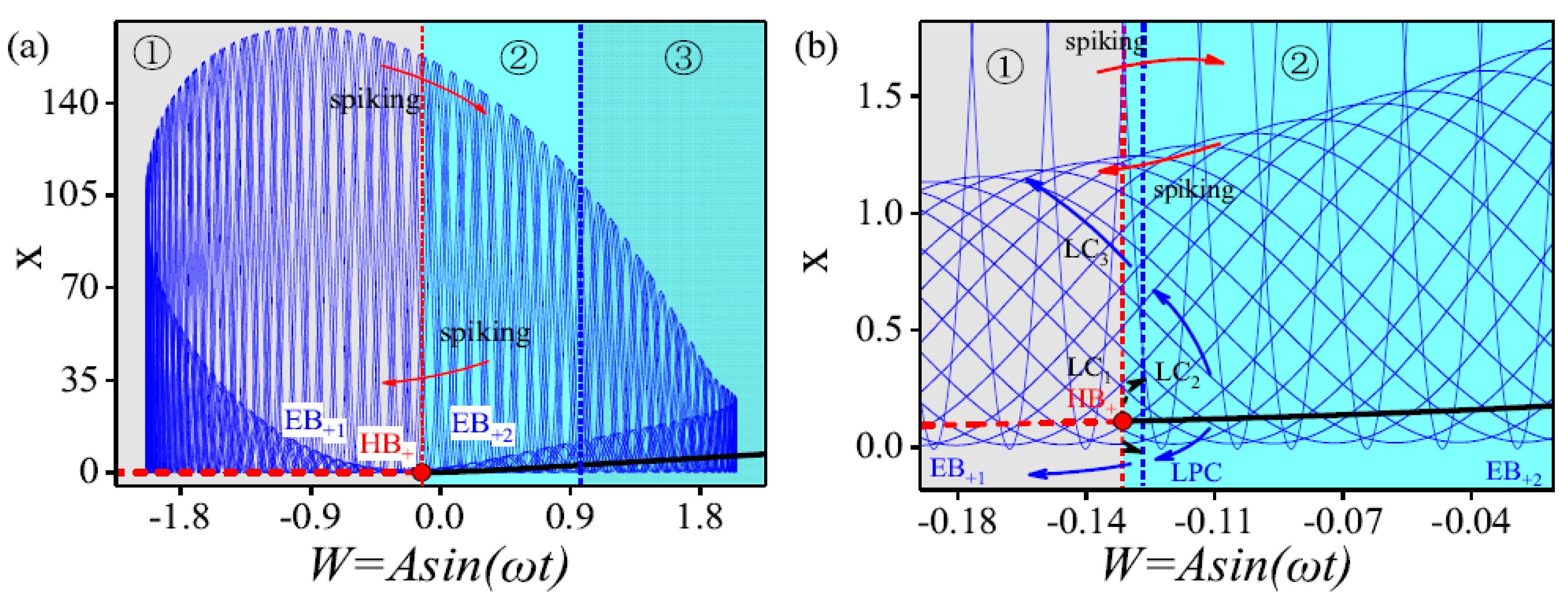
4.1. Bursting Oscillation for as Well as the Mechanism
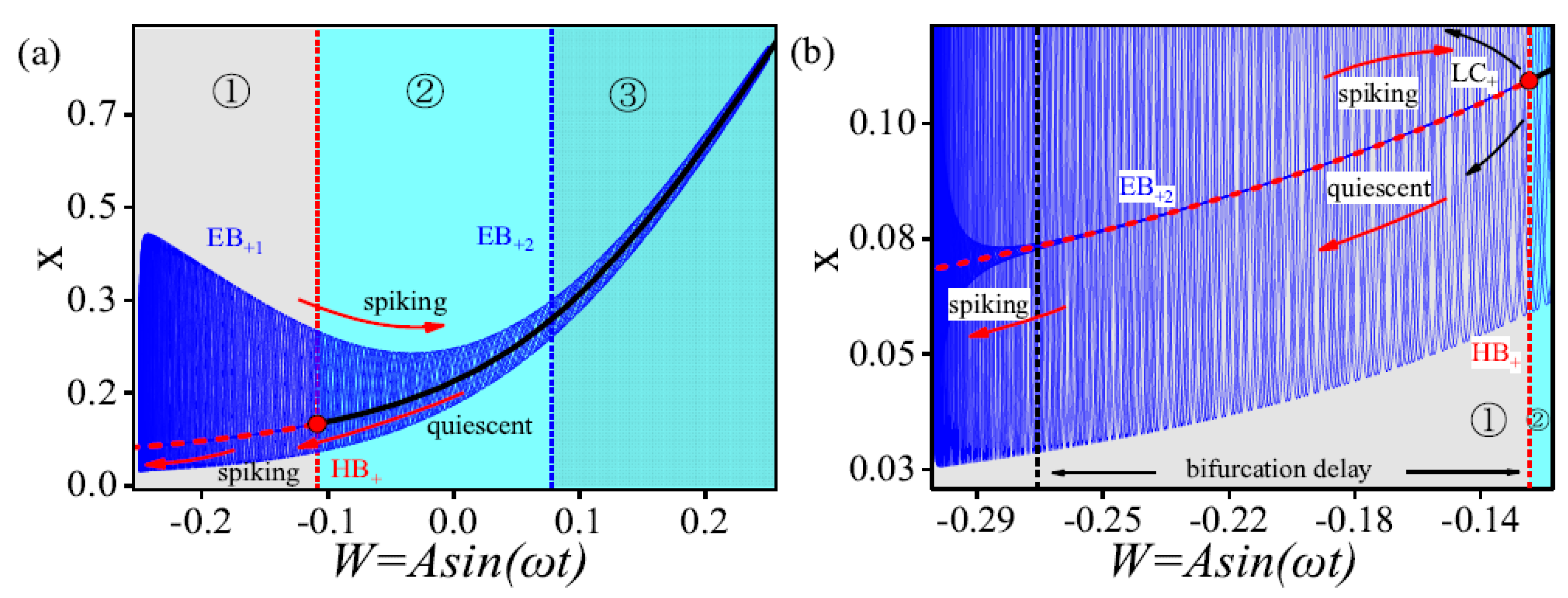
4.2. Bursting Oscillation for as Well as the Mechanism
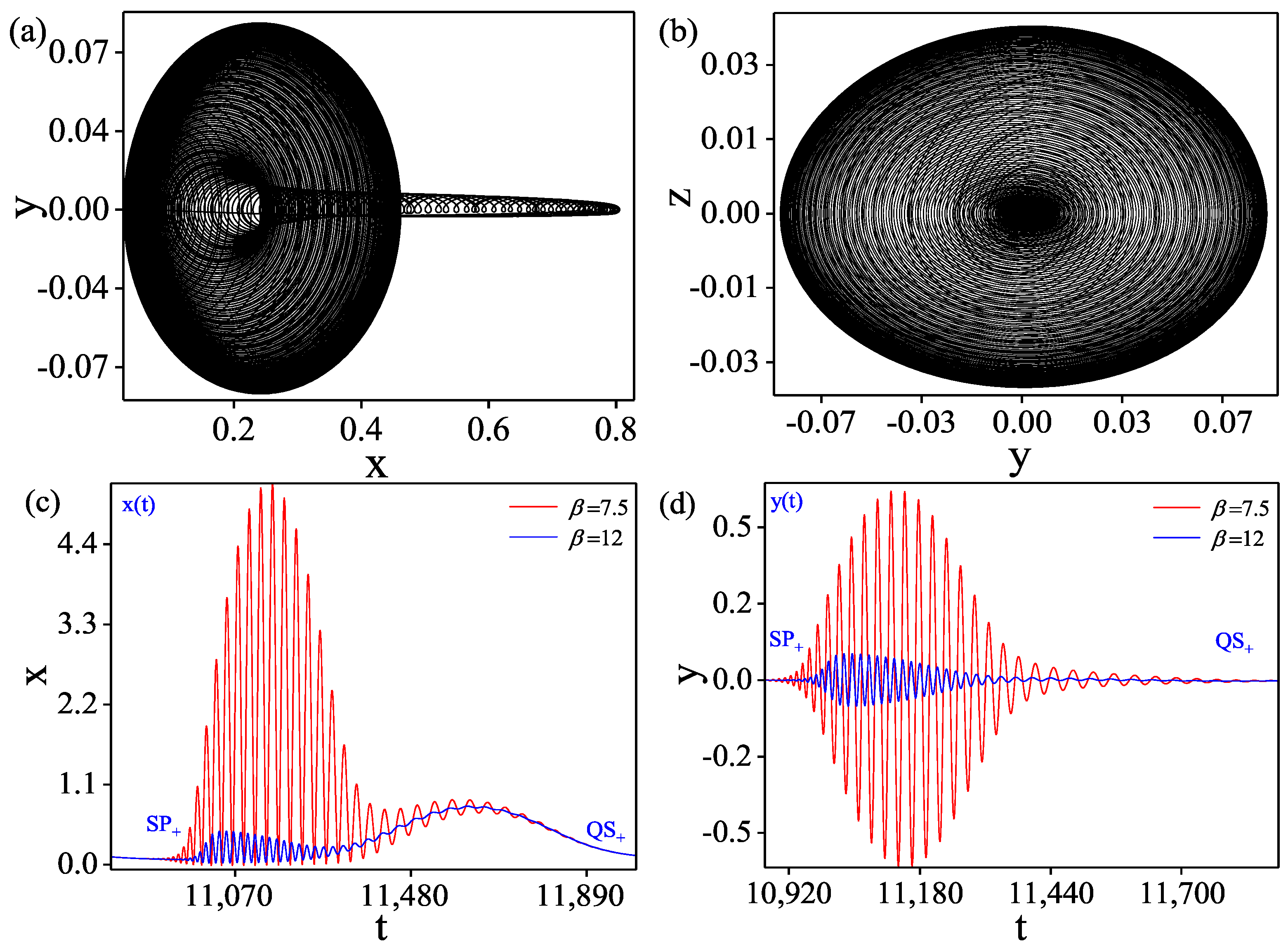
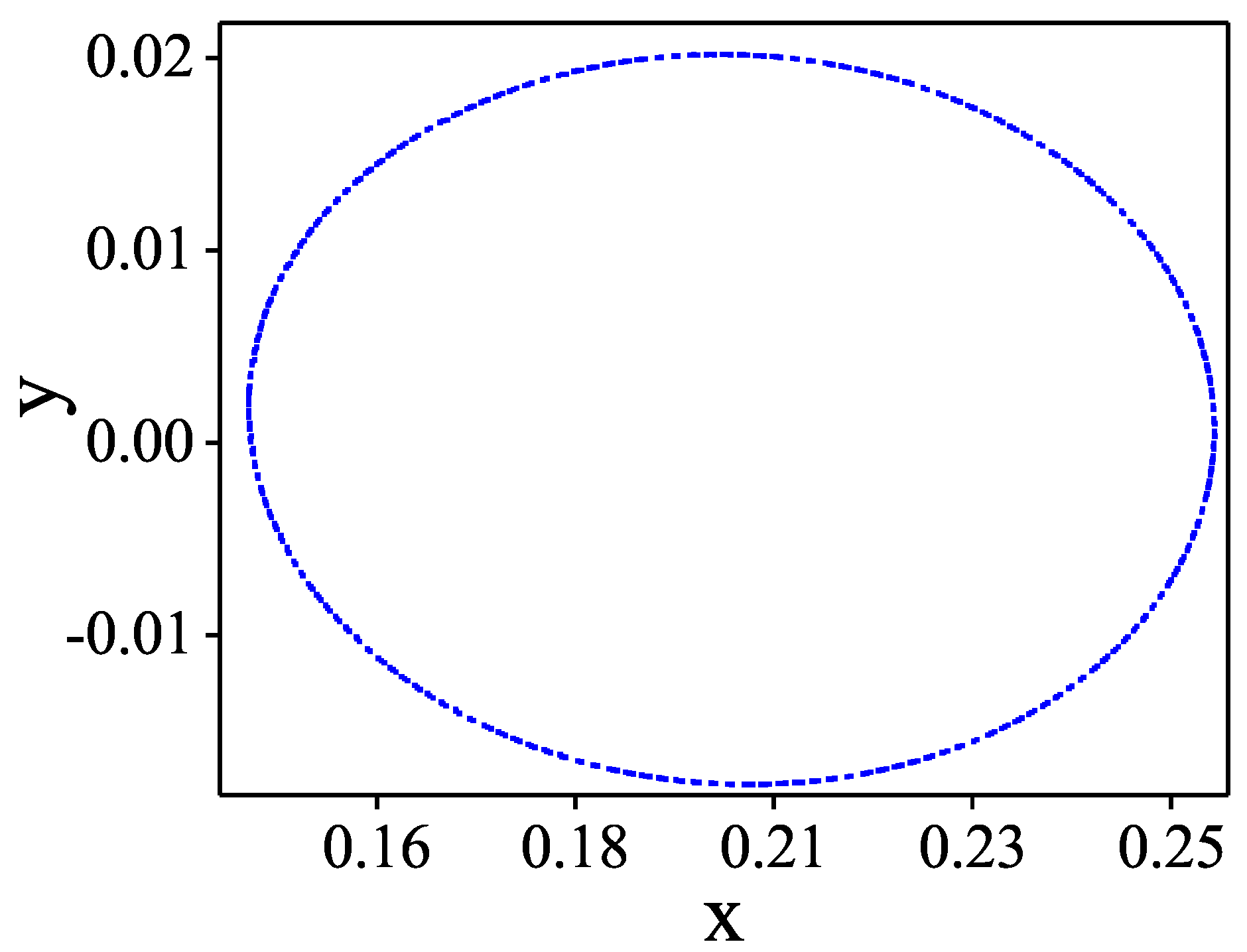
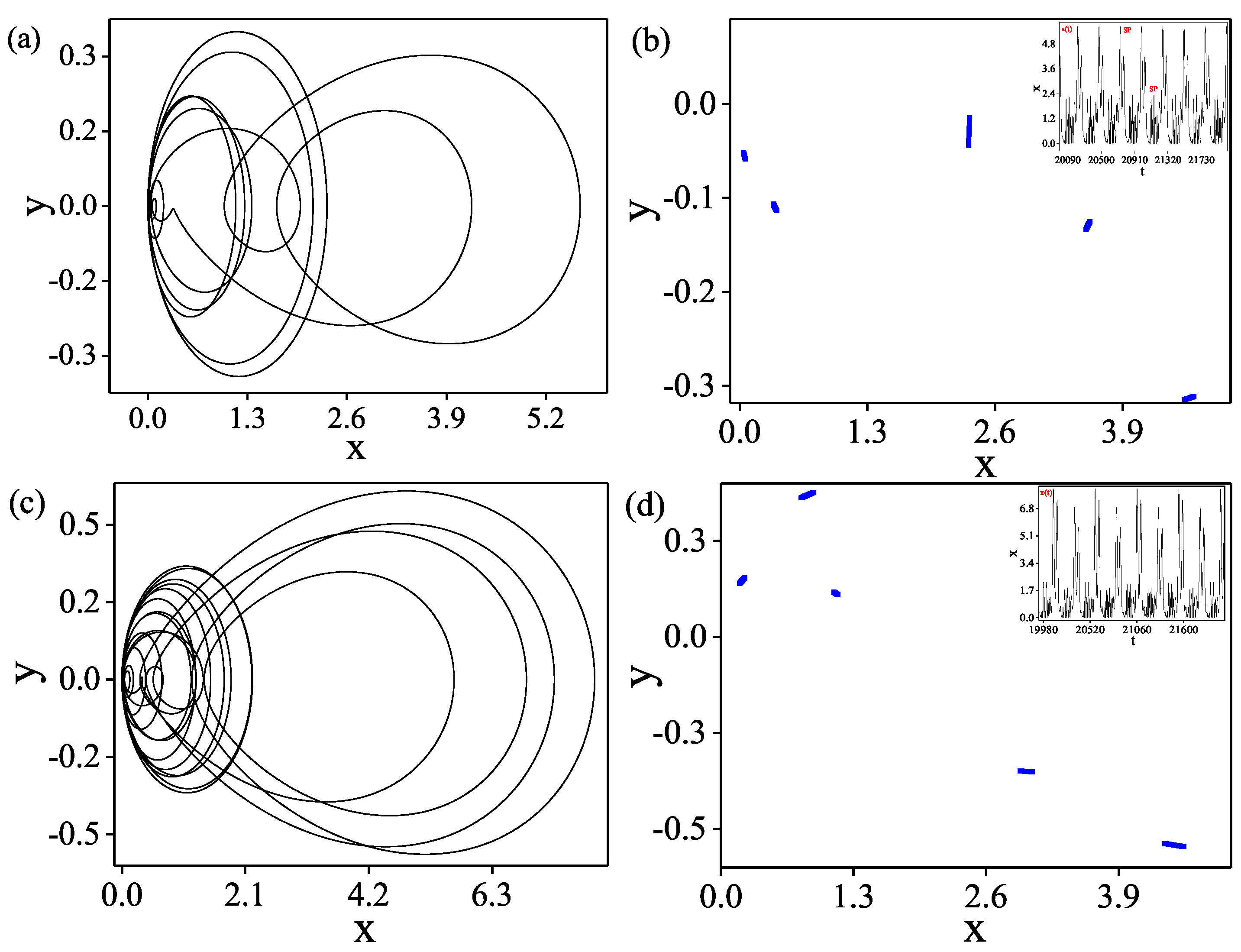
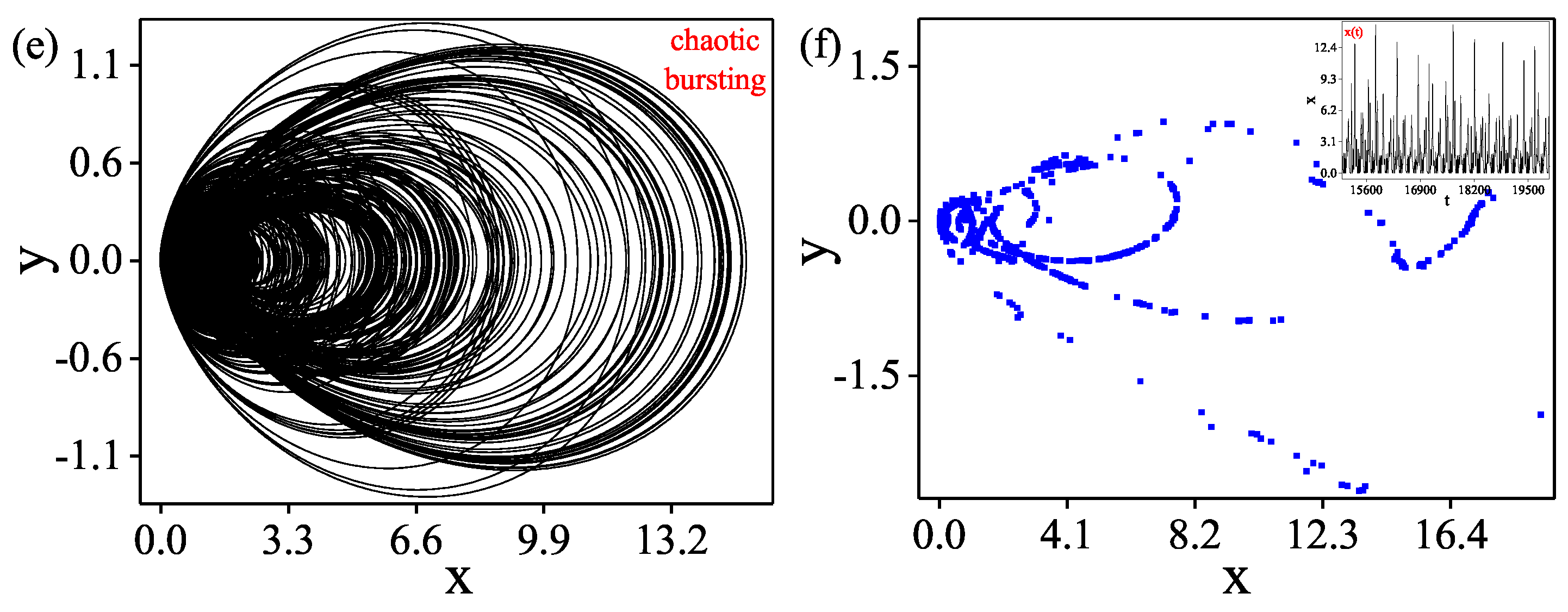
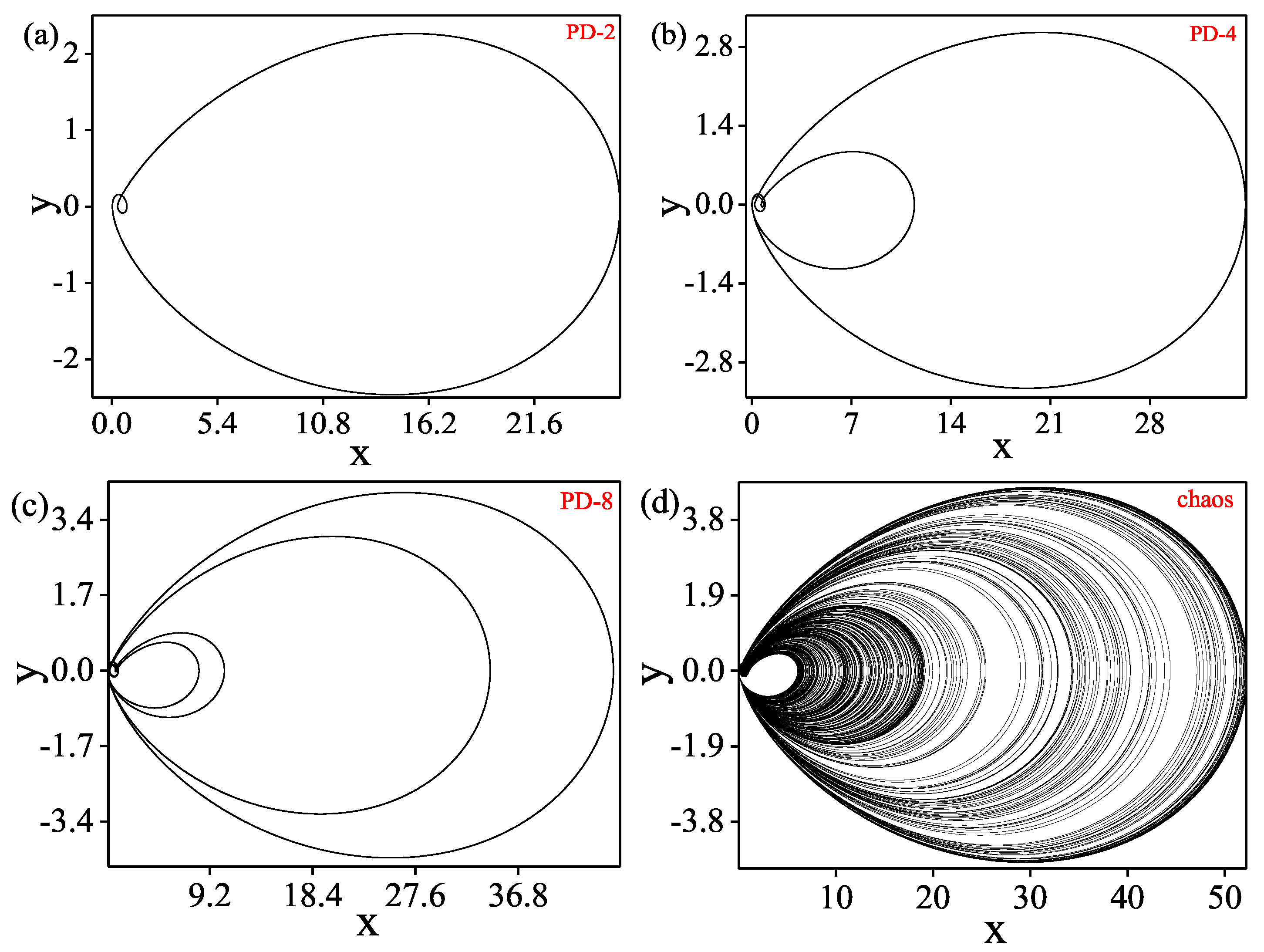
5. Evolution of Chaos
6. Conculusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Golubitsky, M.; Josic, K.; Kaper, T.J. An unfolding theory approach to bursting in fast-slow systems. In Global Analysis of Dynamical Systems, A Festschrift/Liber Amicorum Dedicated to Floris Takens for His 60th Birthday; Broer, H., Krauskopf, B., Vegter, G., Eds.; IOP Publishing: Bristol, UK, 2001; pp. 277–308. [Google Scholar] [CrossRef]
- Leimkuhler, B. An efficient multiple time-scale reversible integrator for the gravitational N-body problem. Appl. Numer. Math. 2002, 43, 175–190. [Google Scholar] [CrossRef]
- Fujimoto, K.; Kaneko, K. How fast elements can affect slow dynamics. Phys. D Nonlinear Phenom. 2003, 180, 1–16. [Google Scholar] [CrossRef][Green Version]
- Hou, L.; Chen, H.; Chen, Y.; Lu, K.; Liu, Z. Bifurcation and stability analysis of a nonlinear rotor system subjected to constant excitation and rub-impact. Mech. Syst. Signal Process. 2019, 125, 65–78. [Google Scholar] [CrossRef]
- Bonet, C.; Jeffrey, M.R.; Martín, P.; Olm, J.M. Novel slow–fast behaviour in an oscillator driven by a frequency-switching force. Commun. Nonlinear Sci. Numer. Simul. 2023, 118, 107032. [Google Scholar] [CrossRef]
- Bao, H.; Wang, N.; Bao, B.; Chen, M.; Jin, P.; Wang, G. Initial condition-dependent dynamics and transient period in memristor-based hypogenetic jerk system with four line equilibria. Commun. Nonlinear Sci. Numer. Simul. 2018, 57, 264–275. [Google Scholar] [CrossRef]
- Bi, Q.; Li, S.; Kurths, J.; Zhang, Z. The mechanism of bursting oscillations with different codimensional bifurcations and nonlinear structures. Nonlinear Dyn. 2016, 85, 993–1005. [Google Scholar] [CrossRef]
- Györgyi, L.; Field, R.J. A three-variable model of deterministic chaos in the Belousov–Zhabotinsky reaction. Nature 1992, 355, 808–810. [Google Scholar] [CrossRef]
- Vanag, V.K.; Zhabotinsky, A.M.; Epstein, I.R. Oscillatory clusters in the periodically illuminated, spatially extended Belousov-Zhabotinsky reaction. Phys. Rev. Lett. 2001, 86, 552. [Google Scholar] [CrossRef][Green Version]
- Huang, L.; Wu, G.; Zhang, Z.; Bi, Q. Fast–slow dynamics and bifurcation mechanism in a novel chaotic system. Int. J. Bifurc. Chaos 2019, 29, 1930028. [Google Scholar] [CrossRef]
- Wang, J. Active vibration control: Design towards performance limit. Mech. Syst. Signal Process. 2022, 171, 108926. [Google Scholar] [CrossRef]
- Dragan, V.; Stoica, A. Robust stabilization of two-time scale systems with respect to the normalized coprime factorization. Int. J. Control 2002, 75, 1–10. [Google Scholar] [CrossRef]
- Boussaada, I.; Morărescu, I.-C.; Niculescu, S. Inverted pendulum stabilization: Characterization of codimension-three triple zero bifurcation via multiple delayed proportional gains. Syst. Control Lett. 2015, 82, 1–9. [Google Scholar] [CrossRef][Green Version]
- Xue, M.; Gou, J.; Xia, Y.; Bi, Q. Computation of the normal form as well as the unfolding of the vector field with zero-zero-Hopf bifurcation at the origin. Math. Comput. Simul. 2021, 190, 377–397. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, X.; Bi, Q. Slow–Fast Behaviors and Their Mechanism in a Periodically Excited Dynamical System with Double Hopf Bifurcations. Int. J. Bifurc. Chaos 2021, 31, 2130022. [Google Scholar] [CrossRef]
- Mandadi, V.; Huseyin, K. Non-linear bifurcation analysis of non-gradient systems. Int. J. Non-Linear Mech. 1980, 15, 159–172. [Google Scholar] [CrossRef]
- Yu, P.; Huseyin, K. Bifurcations associated with a three-fold zero eigenvalue. Q. Appl. Math. 1988, 46, 193–216. [Google Scholar] [CrossRef][Green Version]
- Yu, P.; Huseyin, K. Bifurcations associated with a double zero of index two and a pair of purely imaginary eigenvalues. Int. J. Syst. Sci. 1988, 19, 1–21. [Google Scholar] [CrossRef]
- Bi, Q.; Yu, P. Computation of normal forms of differential equations associated with non-semisimple zero eigenvalues. Int. J. Bifurc. Chaos 1998, 8, 2279–2319. [Google Scholar] [CrossRef][Green Version]
- Freire, E.; Gamero, E.; Rodríguez-Luis, A.J.; Algaba, A. A note on the triple-zero linear degeneracy: Normal forms, dynamical and bifurcation behaviors of an unfolding. Int. J. Bifurc. Chaos 2002, 12, 2799–2820. [Google Scholar] [CrossRef]
- Algaba, A.; Domínguez-Moreno, M.C.; Merino, M.; Rodríguez-Luis, A.J. Takens–Bogdanov bifurcations of equilibria and periodic orbits in the Lorenz system. Commun. Nonlinear Sci. Numer. Simul. 2016, 30, 328–343. [Google Scholar] [CrossRef]
- Algaba, A.; Chung, K.-W.; Qin, B.-W.; Rodríguez-Luis, A.J. Computation of all the coefficients for the global connections in the Z2-symmetric Takens-Bogdanov normal forms. Commun. Nonlinear Sci. Numer. Simul. 2020, 81, 105012. [Google Scholar] [CrossRef]
- Duan, L.; Lu, Q.; Wang, Q. Two-parameter bifurcation analysis of firing activities in the Chay neuronal model. Neurocomputing 2008, 72, 341–351. [Google Scholar] [CrossRef]
- Duan, L.; Lu, Q.; Cheng, D. Bursting of Morris-Lecar neuronal model with current-feedback control. Sci. China Ser. E Technol. Sci. 2009, 52, 771–781. [Google Scholar] [CrossRef]
- Braun, F.; Mereu, A.C. Zero-Hopf bifurcation in a 3D jerk system. Nonlinear Anal. Real World Appl. 2021, 59, 103245. [Google Scholar] [CrossRef]
- Bao, H.; Ding, R.; Hua, M.; Wu, H.; Chen, B. Initial-condition effects on a two-memristor-based Jerk system. Mathematics 2022, 10, 411. [Google Scholar] [CrossRef]
- Saggio, M.L.; Spiegler, A.; Bernard, C.; Jirsa, V.K. Fast–slow bursters in the unfolding of a high codimension singularity and the ultra-slow transitions of classes. J. Math. Neurosci. 2017, 7, 7. [Google Scholar] [CrossRef][Green Version]
- Kuznetsov, Y.A. Elements of Applied Bifurcation Theory, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Sen, D.; Ghorai, S.; Banerjee, M.; Morozov, A. Bifurcation analysis of the predator–prey model with the Allee effect in the predator. J. Math. Biol. 2022, 84, 7. [Google Scholar] [CrossRef]
- Yang, R. Turing–Hopf bifurcation co-induced by cross-diffusion and delay in Schnakenberg system. Chaos Solitons Fractals 2022, 164, 112659. [Google Scholar] [CrossRef]
- Maleki, F.; Beheshti, B.; Hajihosseini, A.; Lamooki, G.R.R. The Bogdanov–Takens bifurcation analysis on a three dimensional recurrent neural network. Neurocomputing 2010, 73, 3066–3078. [Google Scholar] [CrossRef]
- Perko, L.M. A global analysis of the Bogdanov–Takens system. SIAM J. Appl. Math. 1992, 52, 1172–1192. [Google Scholar] [CrossRef]
- Baider, A.; Sanders, J.A. Further reduction of the Takens-Bogdanov normal form. J. Differ. Equ. 1992, 99, 205–244. [Google Scholar] [CrossRef][Green Version]
- Murdock, J. Asymptotic unfoldings of dynamical systems by normalizing beyond the normal form. J. Differ. Equ. 1998, 143, 151–190. [Google Scholar] [CrossRef][Green Version]
- Rinzel, J. Formal classification of bursting mechanisms in excitable systems. In Lecture Notes in Biomathematics; Teramoto, E., Yamaguti, M., Eds.; Springer: Berlin, Germany, 1987; pp. 267–281. [Google Scholar]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, W.; Li, S.; Chen, Z.; Bi, Q. Bursting Dynamics in a Singular Vector Field with Codimension Three Triple Zero Bifurcation. Mathematics 2023, 11, 2486. https://doi.org/10.3390/math11112486
Lyu W, Li S, Chen Z, Bi Q. Bursting Dynamics in a Singular Vector Field with Codimension Three Triple Zero Bifurcation. Mathematics. 2023; 11(11):2486. https://doi.org/10.3390/math11112486
Chicago/Turabian StyleLyu, Weipeng, Shaolong Li, Zhenyang Chen, and Qinsheng Bi. 2023. "Bursting Dynamics in a Singular Vector Field with Codimension Three Triple Zero Bifurcation" Mathematics 11, no. 11: 2486. https://doi.org/10.3390/math11112486
APA StyleLyu, W., Li, S., Chen, Z., & Bi, Q. (2023). Bursting Dynamics in a Singular Vector Field with Codimension Three Triple Zero Bifurcation. Mathematics, 11(11), 2486. https://doi.org/10.3390/math11112486





