On the Fractional-Order Complex Cosine Map: Fractal Analysis, Julia Set Control and Synchronization
Abstract
:1. Introduction
2. Mathematical Basics
3. The Discrete Fractional-Order Complex Cosine Map
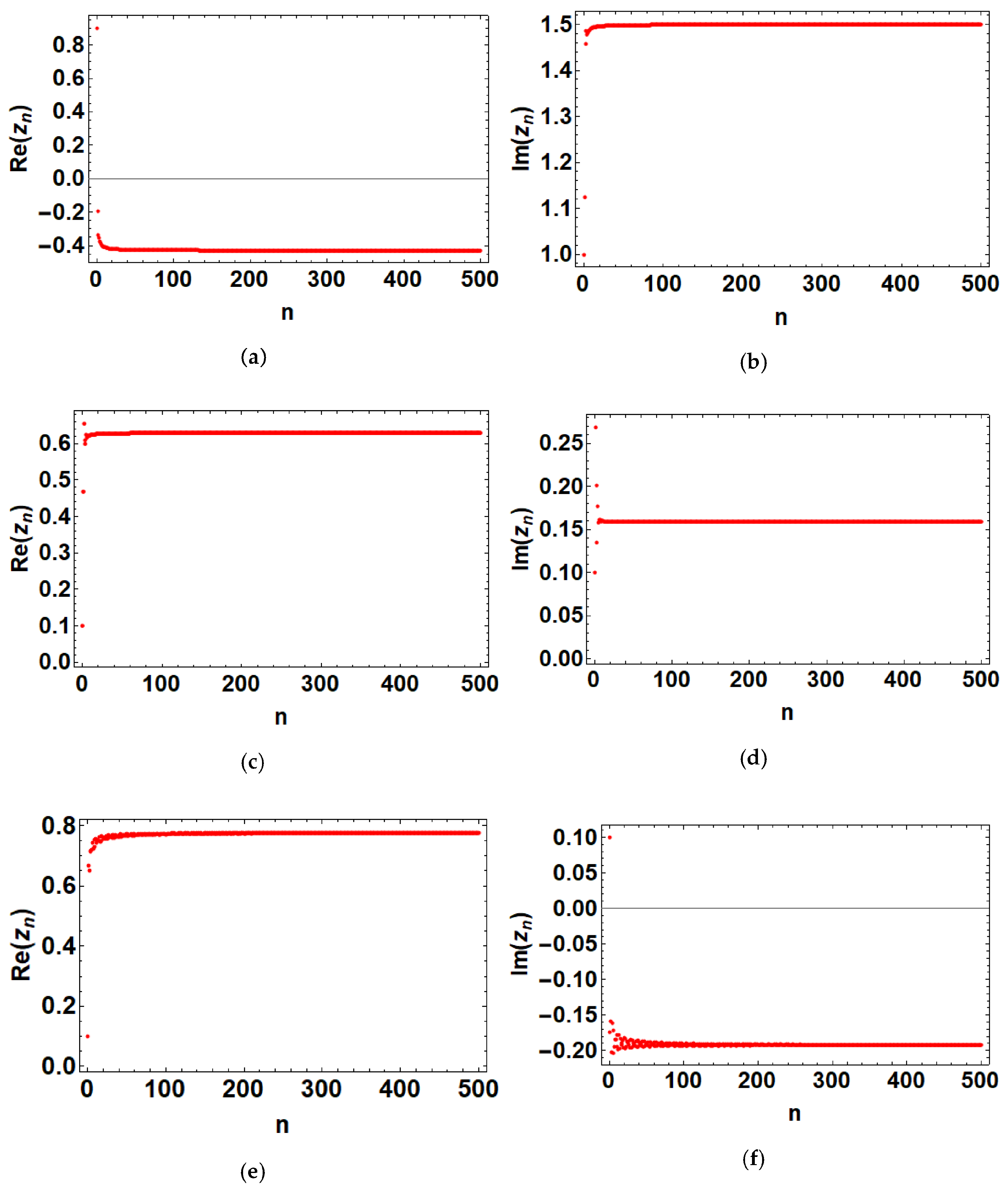
3.1. Stability Analysis of Fixed Points
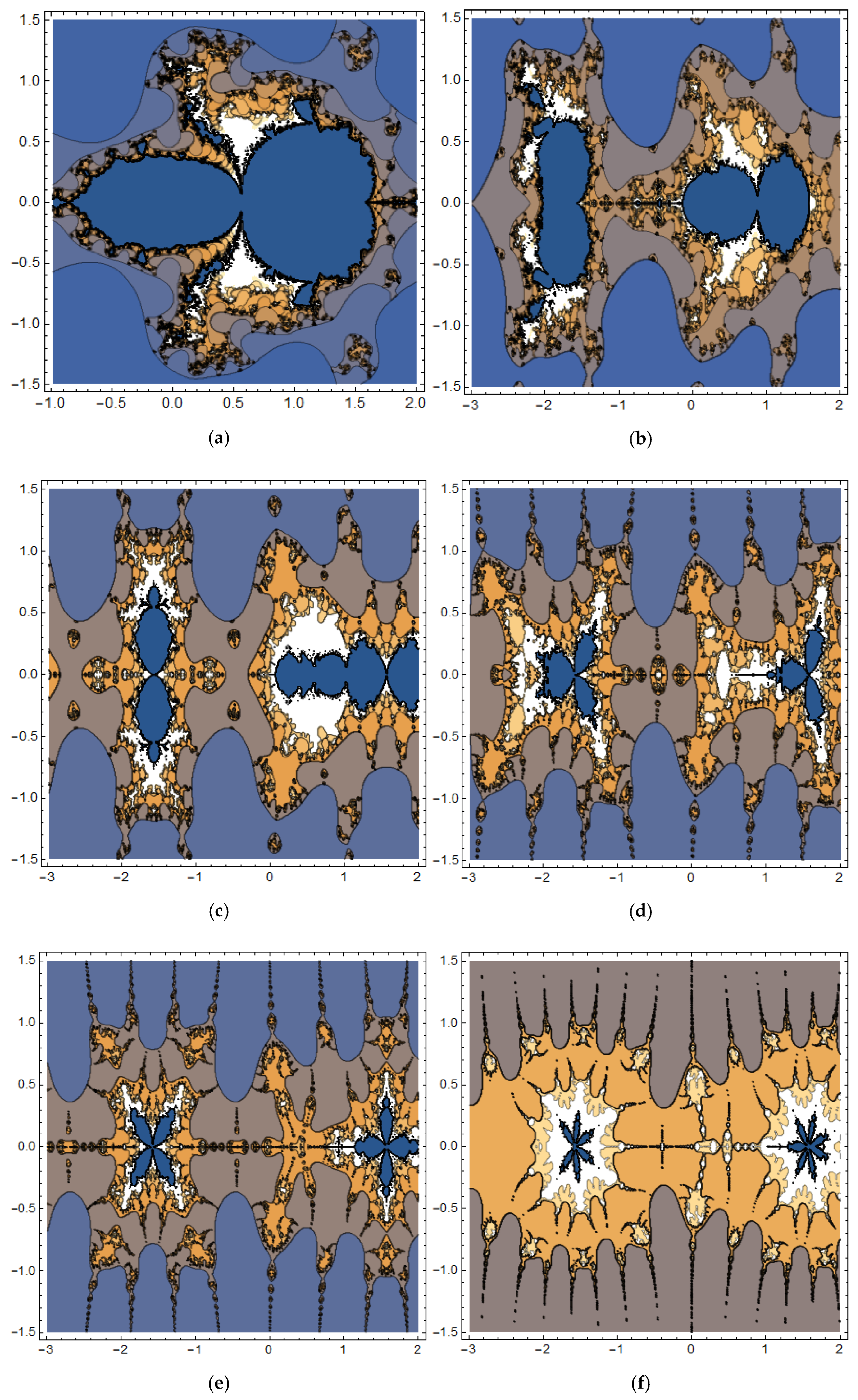
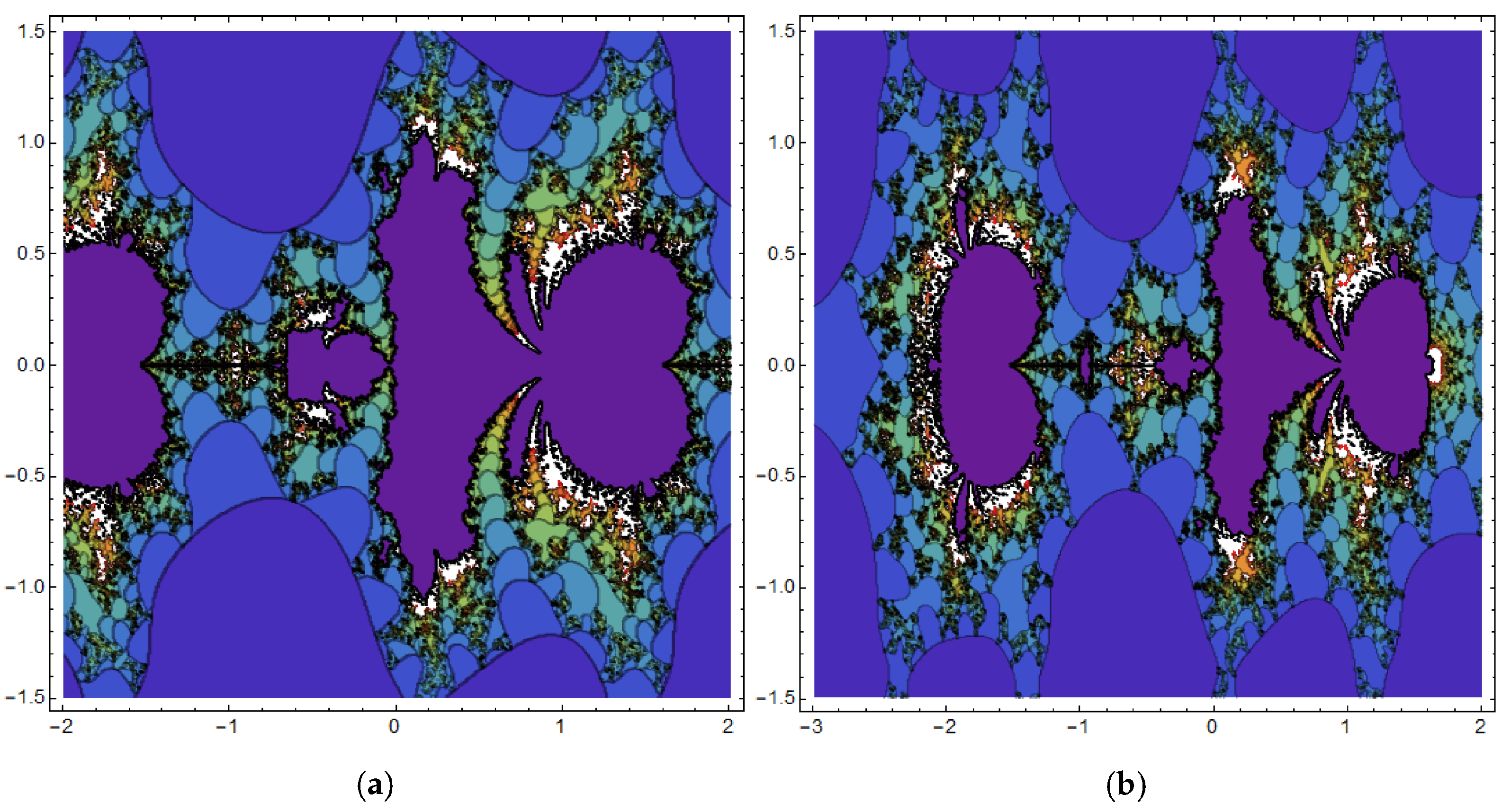
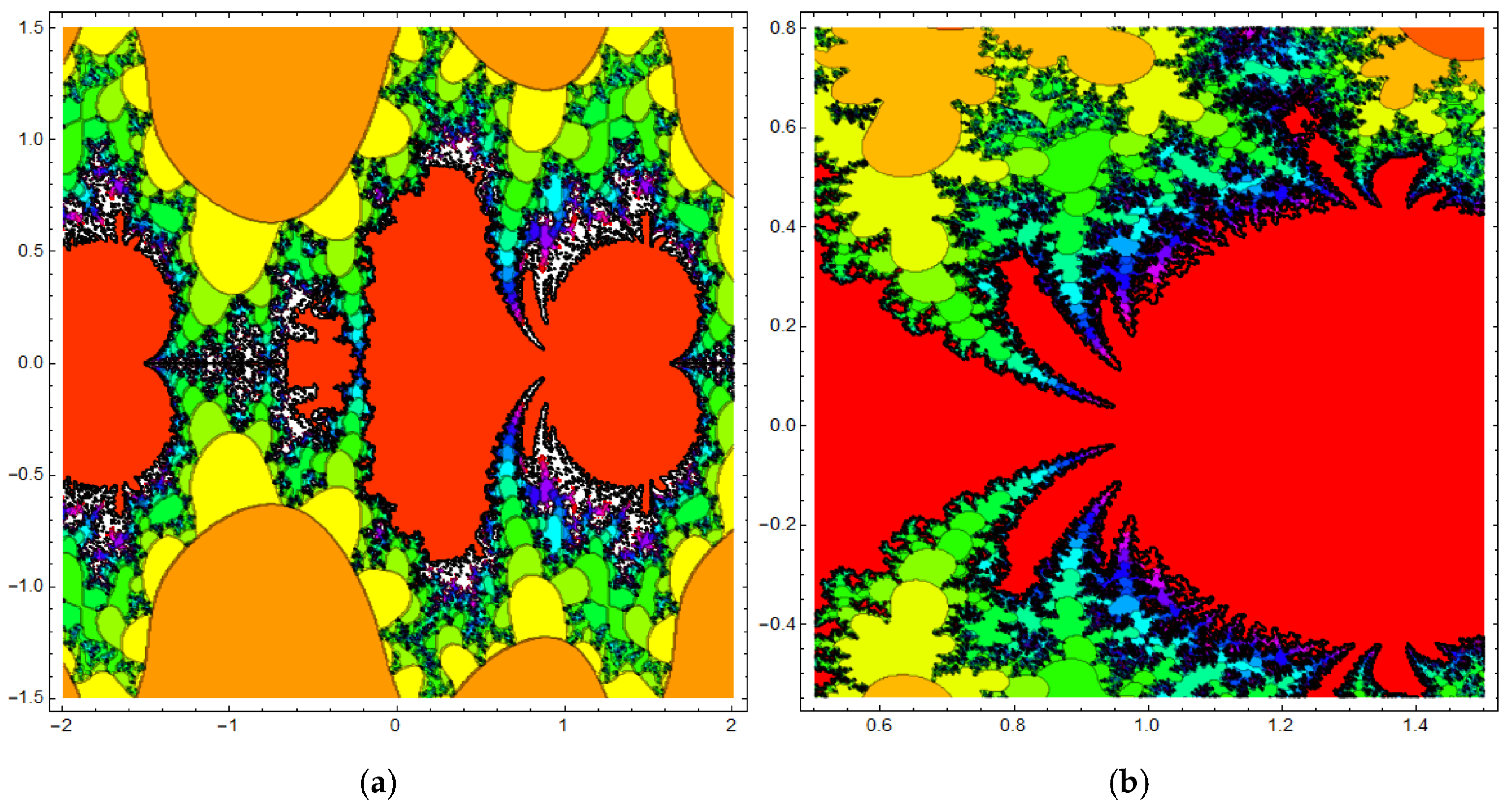
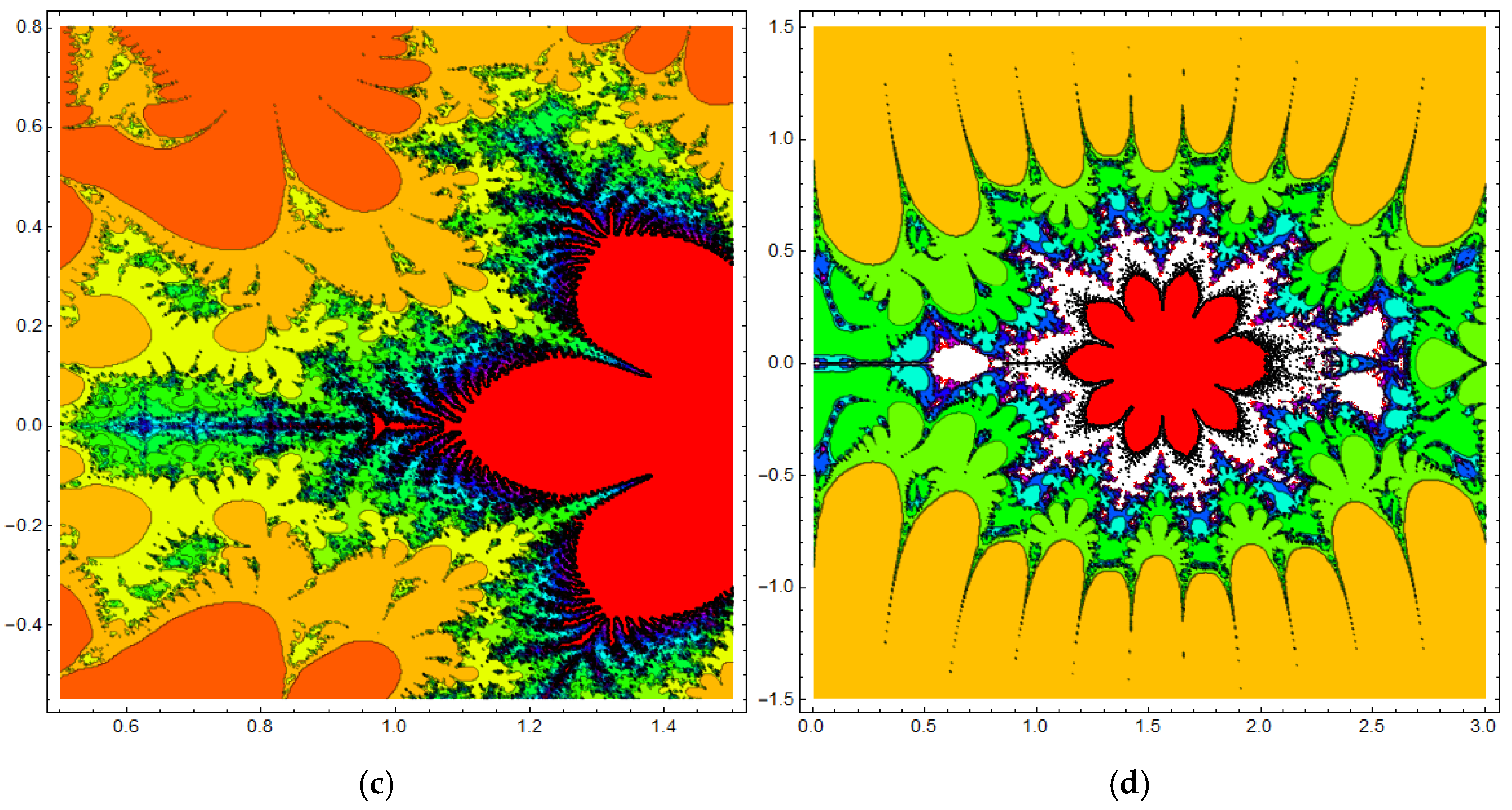
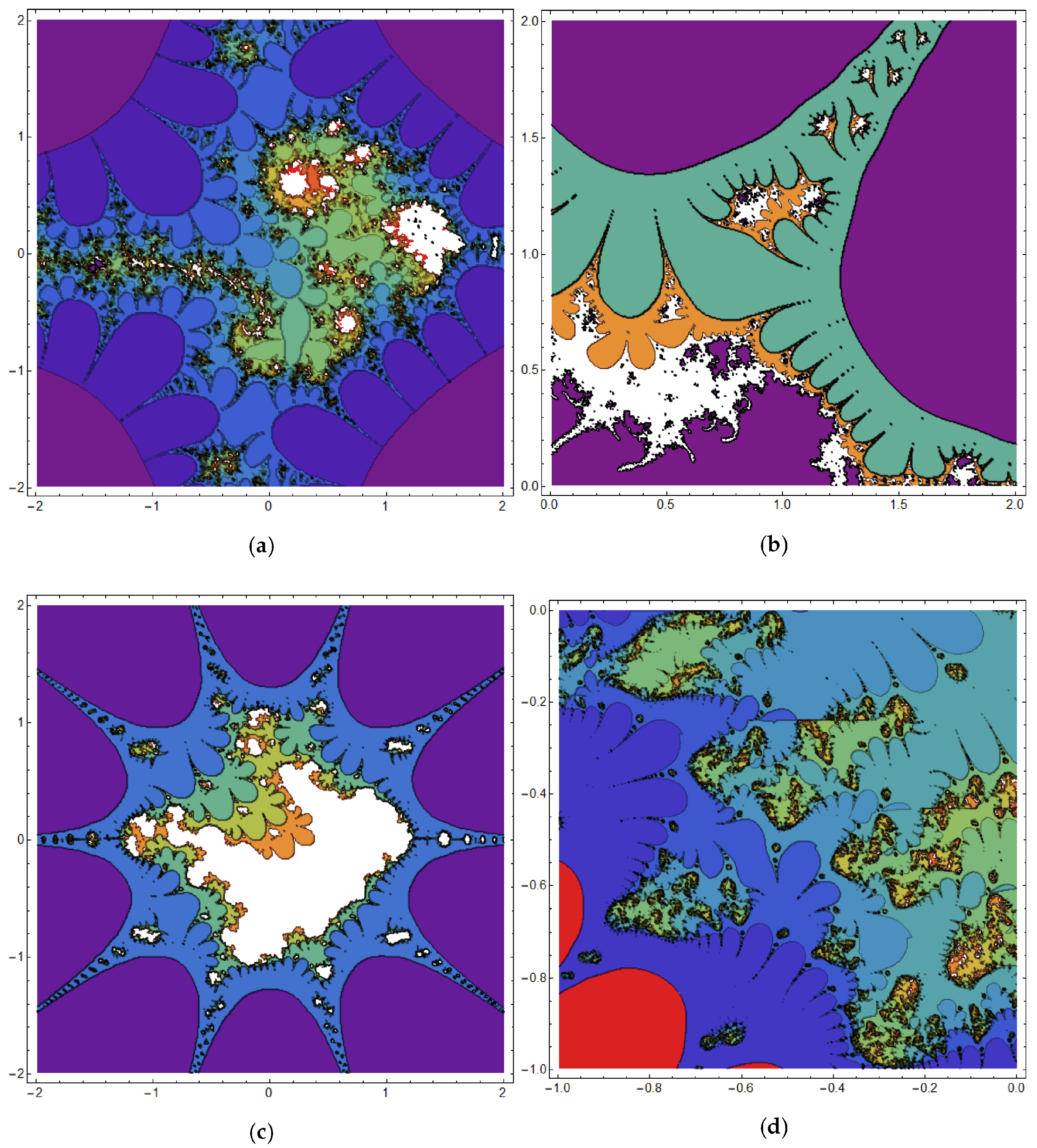
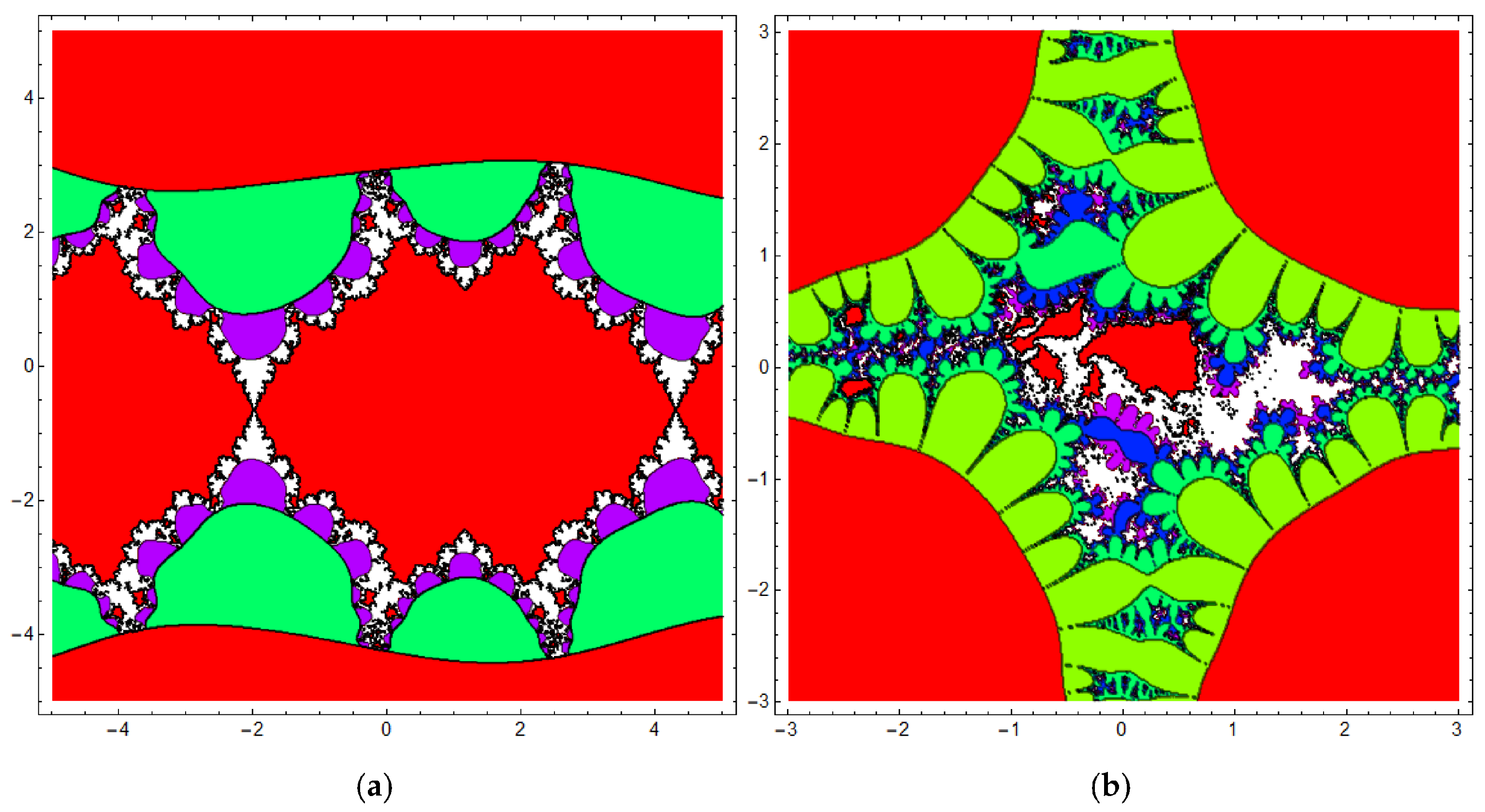
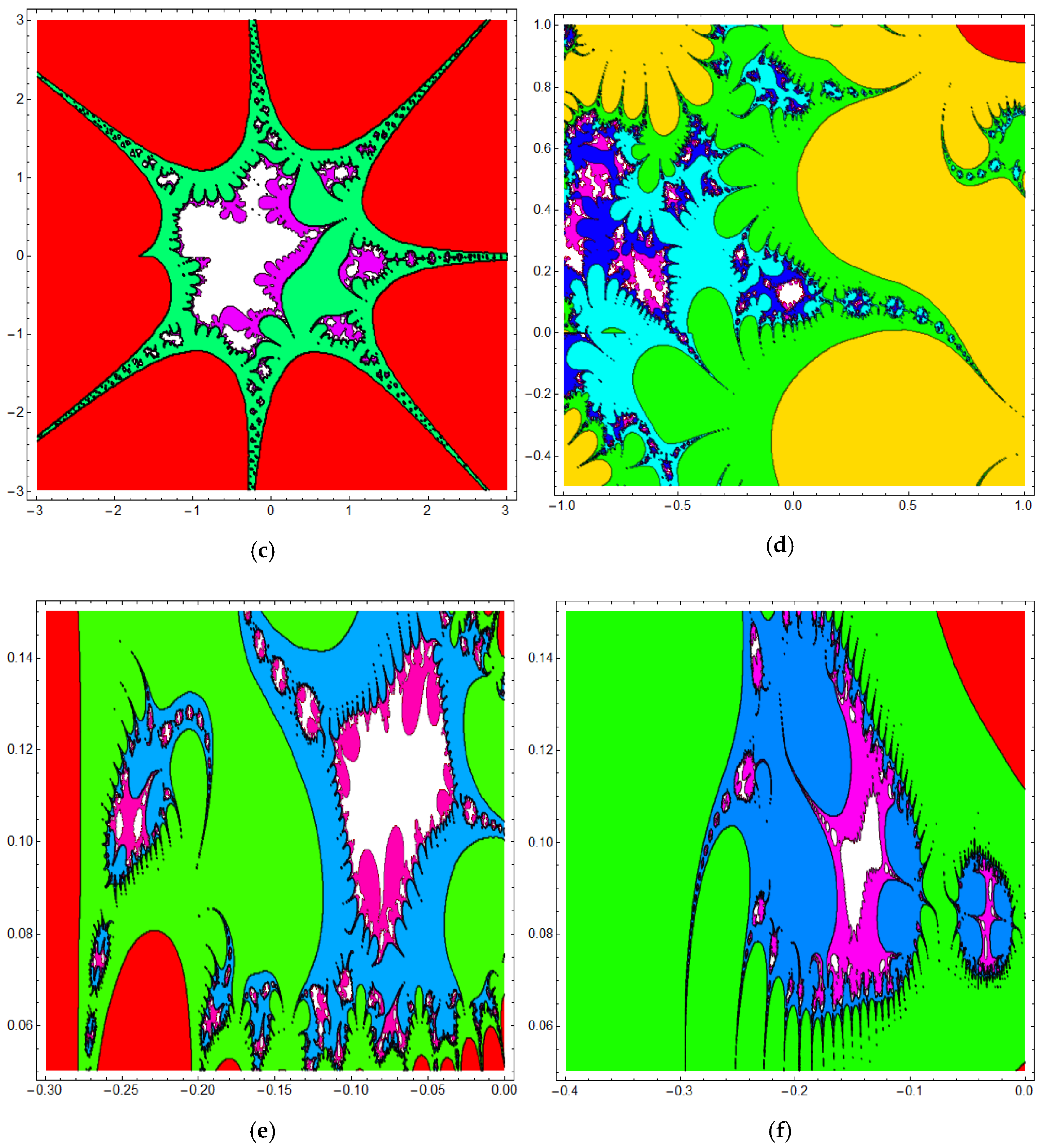
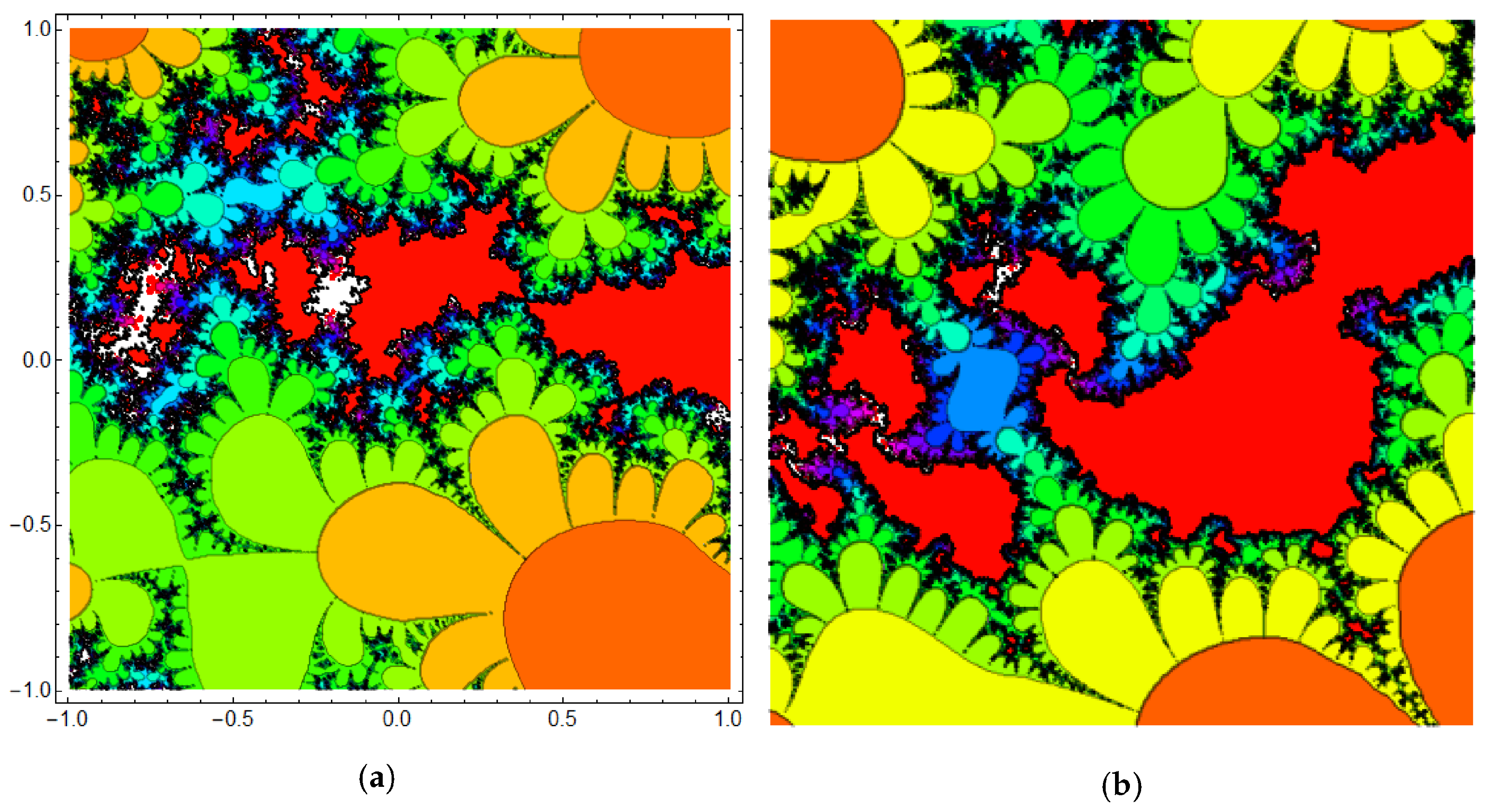
3.2. The Fractional Cosine Map Generates Fractal Sets
| Figure | Fractal Set | Parameters | Fractal Dimension |
|---|---|---|---|
| Figure 2 | Mandelbrot sets | different values of | |
| Figure 3 | Mandelbrot sets | different values of | |
| Figure 4 | Mandelbrot sets | different values of | |
| Figure 5 | Mandelbrot sets | different values of | |
| Figure 6 | Mandelbrot sets | different values of | |
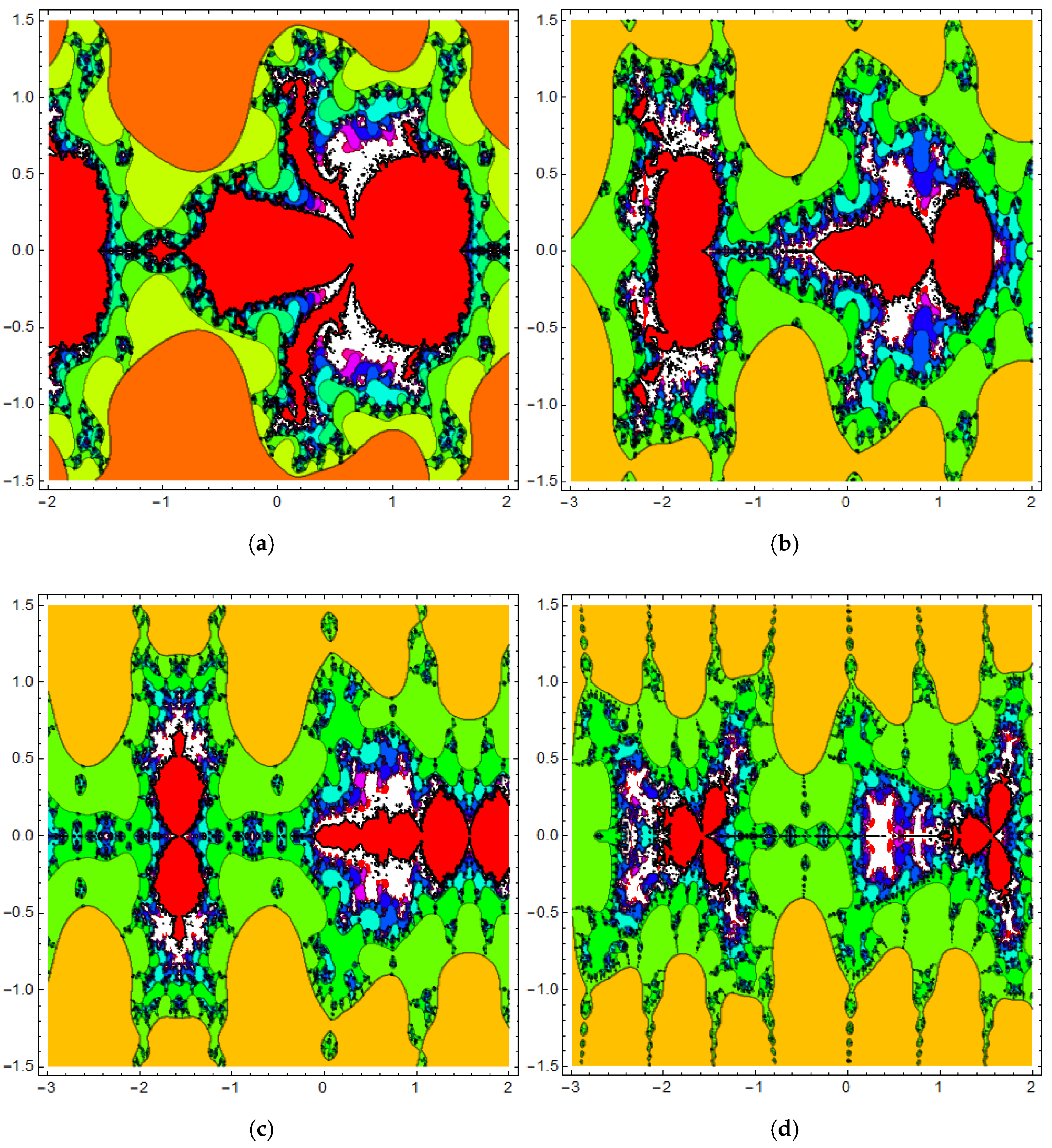
| Figure 7 | Julia sets | different values of p and | |
| Figure 8 | Julia sets | different values of p and | |
| Figure 9 | Julia sets | different values of p and |
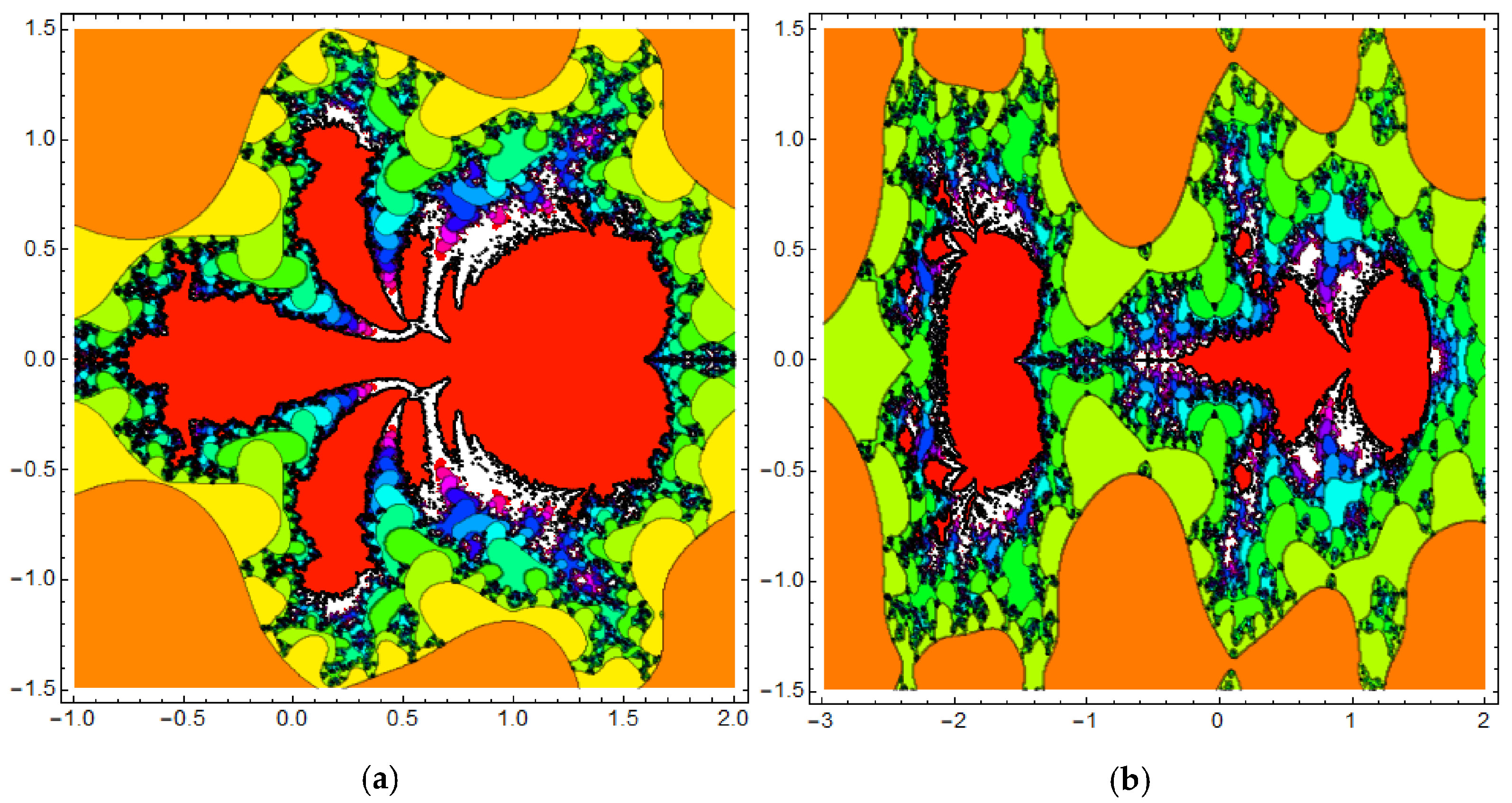
4. The Control and Synchronization of Julia Sets
4.1. Control of Julia Sets Generated by the Fractional Cosine Map
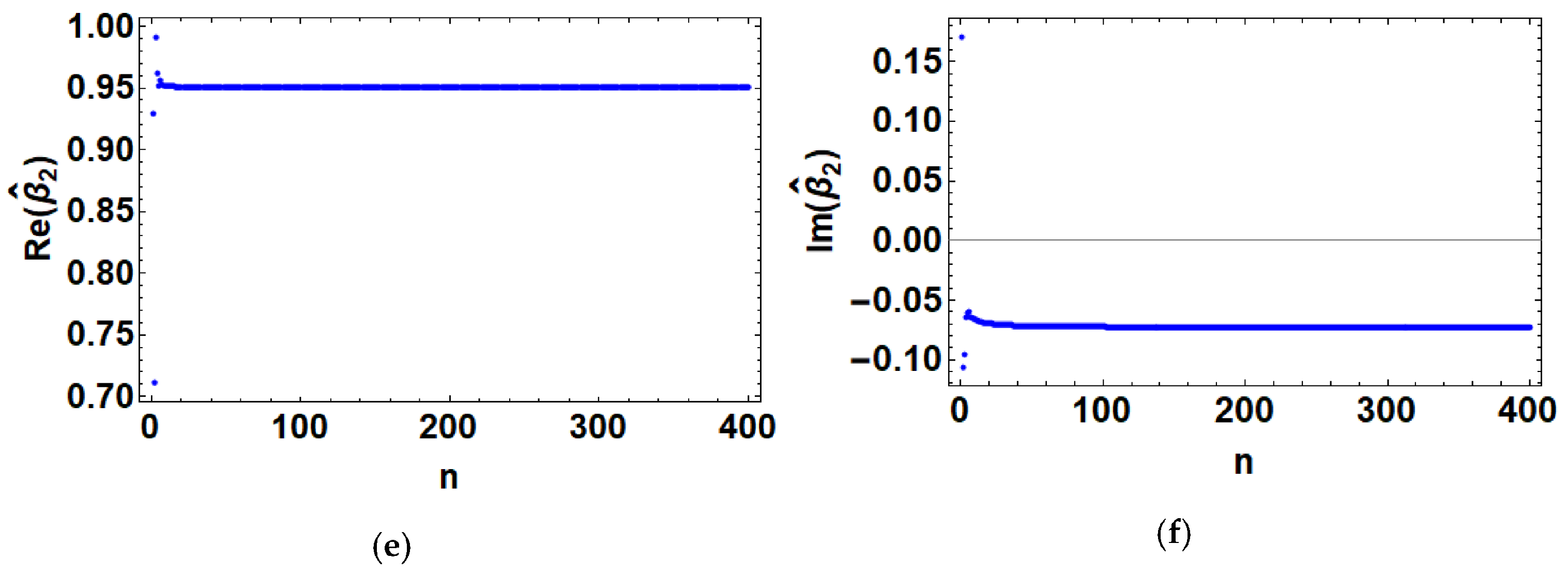
4.2. Synchronization of Julia Sets
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tu, P.N.V. Dynamical Systems—An Introduction with Applications in Economics and Biology; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos with Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Kuznetsov, Y.A. Elements of Applied Bifurcation Theory; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Kocarev, L.; Lian, S. Chaos-Based Cryptography; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Izhikevich, E.M. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Stavroulakis, P. Chaos Applications in Telecommunications; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Chen, G.; Yu, X. Chaos Control- Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Mandelbrot, B.B.; Evertsz, C.J.; Gutzwiller, M.C. Fractals and Chaos: The Mandelbrot Set and Beyond; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Peitgen, H.; Jurgens, H.; Saupe, D. Chaos and Fractals: New Frontiers in Science; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Wang, Y.; Shutang, L.; Li, H. Adaptive synchronization of Julia sets generated by Mittag-Leffler function. Commun. Nonlinear Sci. Numer. Simul. 2020, 83, 105115. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, S.; Li, H. On fractional difference logistic maps: Dynamic analysis and synchronous control. Nonlinear Dyn. 2020, 102, 579–588. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, S.; Wang, W. Fractal dimension analysis and control of Julia set generated by fractional Lotka–Volterra models. Commun. Nonlinear Sci. Numer. Simul. 2019, 72, 417–431. [Google Scholar] [CrossRef]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications; John Wiley and Sons Ltd.: Chichester, UK, 2014. [Google Scholar]
- Liu, S.T.; Zhang, Y.P.; Liu, C.A. Fractal Control and Its Applications; Springer Nature: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Jouini, L.; Ouannas, A.; Khennaoui, A.-A.; Wang, X.; Grassi, G.; Pham, V.-T. The fractional form of a new three-dimensional generalized Hénon map. Adv. Differ. Equ. 2019, 2019, 122. [Google Scholar] [CrossRef]
- Peng, Y.; He, S.; Sun, K. Chaos in the discrete memristor-based system with fractional-order difference. Results Phys. 2021, 24, 104106. [Google Scholar] [CrossRef]
- Edelman, M. Fractional Maps as Maps with Power-Law Memory. In Nonlinear Dynamics and Complexity; Springer: Berlin/Heidelberg, Germany, 2014; pp. 79–120. [Google Scholar]
- Edelman, M. Universality in systems with power-law memory and fractional dynamics. In Chaotic, Fractional, and Complex Dynamics: New Insights and Perspectives; Springer: Berlin/Heidelberg, Germany, 2018; pp. 147–171. [Google Scholar]
- Wang, C.; Ding, Q. A new two-dimensional map with hidden attractors. Entropy 2018, 20, 322. [Google Scholar] [CrossRef] [PubMed]
- Almatroud, A.O.; Khennaoui, A.-A.; Ouannas, A.; Pham, V.-T. Infinite line of equilibriums in a novel fractional map with coexisting infinitely many attractors and initial offset boosting. Int. J. Nonlinear Sci. Numer. Simul. 2021. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Momani, S.; Pham, V.T. The discrete fractional duffing system: Chaos, 0–1 test, C0 complexity, entropy, and control. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 083131. [Google Scholar] [CrossRef] [PubMed]
- Padron, J.P.; Perez, J.P.; Díaz, J.J.P.; Huerta, A.M. Time-Delay Synchronization and Anti-Synchronization of Variable-Order Fractional Discrete-Time Chen–Rossler Chaotic Systems Using Variable-Order Fractional Discrete-Time PID Control. Mathematics 2021, 9, 2149. [Google Scholar] [CrossRef]
- Talhaoui, M.Z.; Wang, X. A new fractional one dimensional chaotic map and its application in high-speed image encryption. Inf. Sci. 2020, 550, 13–26. [Google Scholar] [CrossRef]
- Elsonbaty, A.; Elsadany, A.; Kamal, F. On Discrete Fractional Complex Gaussian Map: Fractal Analysis, Julia Sets Control, and Encryption Application. Math. Probl. Eng. 2022, 2022, 8148831. [Google Scholar] [CrossRef]
- Askar, S.; Al-Khedhairi, A.; Elsonbaty, A.; Elsadany, A. Chaotic Discrete Fractional-Order Food Chain Model and Hybrid Image Encryption Scheme Application. Symmetry 2021, 13, 161. [Google Scholar] [CrossRef]
- Al-Khedhairi, A.; Elsonbaty, A.; Elsadany, A.A.; Hagras, E.A.A. Hybrid Cryptosystem Based on Pseudo Chaos of Novel Fractional Order Map and Elliptic Curves. IEEE Access 2020, 8, 57733–57748. [Google Scholar] [CrossRef]
- Pesin, Y.B.; Climenhaga, V. Lectures on Fractal Geometry and Dynamical Systems; American Mathematical Society: Providence, RI, USA, 2009. [Google Scholar]
- Brambila, F. Fractal Analysis—Applications in Physics, Engineering and Technology. Available online: https://www.intechopen.com/books/fractal-analysis-applications-in-physics-engineering-andtechnology (accessed on 28 October 2018).
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; Taylor and Francis: Abingdon, UK, 2018. [Google Scholar]
- Daftardar-Gejji, V. (Ed.) Fractional Calculus and Fractional Differential Equations; Springer: Singapore, 2019. [Google Scholar]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Radwan, A.G.; Khanday, F.A.; Said, L.A. (Eds) Fractional-Order Design: Devices, Circuits, and Systems; Academic Press: Cambridge, MA, USA, 2021. [Google Scholar]
- Ray, S.S.; Sahoo, S. Generalized Fractional Order Differential Equations Arising in Physical Models; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018. [Google Scholar]
- Das, S.; Pan, I. Fractional Order Signal Processing: Introductory Concepts and Applications; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Butera, S.; Di Paola, M. A physically based connection between fractional calculus and fractal geometry. Ann. Phys. 2014, 350, 146–158. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Wang, D.; Liu, S. A brief note on fractal dynamics of fractional Mandelbrot sets. Appl. Math. Comput. 2022, 432, 127353. [Google Scholar] [CrossRef]
- Danca, M.F.; Feckan, M. Mandelbrot set and Julia sets of fractional order. arXiv 2022, arXiv:2210.02037. [Google Scholar]
- Abdeljawad, T. On Riemann and Caputo fractional differences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar] [CrossRef]
- Čermák, J.; Győri, I.; Nechvátal, L. On explicit stability conditions for a linear fractional difference system. Fract. Calc. Appl. Anal. 2015, 18, 651. [Google Scholar] [CrossRef]
- Abu-Saris, R.; Al-Mdallal, Q. On the asymptotic stability of linear system of fractional-order difference equations. Fract. Calc. Appl. Anal. 2013, 16, 613–629. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elsadany, A.A.; Aldurayhim, A.; Agiza, H.N.; Elsonbaty, A. On the Fractional-Order Complex Cosine Map: Fractal Analysis, Julia Set Control and Synchronization. Mathematics 2023, 11, 727. https://doi.org/10.3390/math11030727
Elsadany AA, Aldurayhim A, Agiza HN, Elsonbaty A. On the Fractional-Order Complex Cosine Map: Fractal Analysis, Julia Set Control and Synchronization. Mathematics. 2023; 11(3):727. https://doi.org/10.3390/math11030727
Chicago/Turabian StyleElsadany, A. A., A. Aldurayhim, H. N. Agiza, and Amr Elsonbaty. 2023. "On the Fractional-Order Complex Cosine Map: Fractal Analysis, Julia Set Control and Synchronization" Mathematics 11, no. 3: 727. https://doi.org/10.3390/math11030727
APA StyleElsadany, A. A., Aldurayhim, A., Agiza, H. N., & Elsonbaty, A. (2023). On the Fractional-Order Complex Cosine Map: Fractal Analysis, Julia Set Control and Synchronization. Mathematics, 11(3), 727. https://doi.org/10.3390/math11030727







