Bayesian Estimations of Shannon Entropy and Rényi Entropy of Inverse Weibull Distribution
Abstract
:1. Introduction
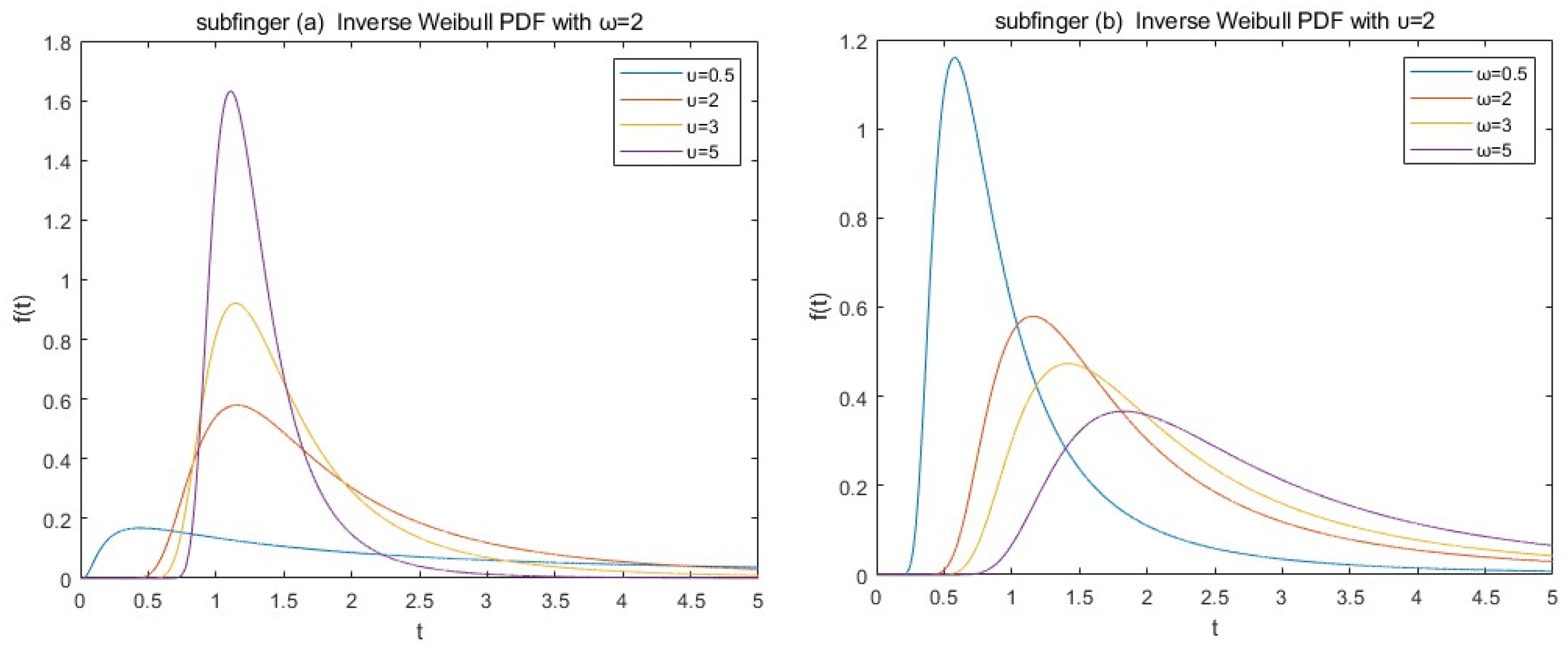
2. Preliminary Knowledge
- (i)
- The Shannon entropy of the IWD is shown in Equation (5):
- (ii)
- The Rényi entropy of the IWD is shown in Equation (6):where is the gamma function and is the Euler constant.
3. Maximum Likelihood Estimation
- (i)
- Give the accuracy , determine the interval , and verify .
- (ii)
- Find the midpoint of the interval and calculate .
- (iii)
- If , .
- (iv)
- If , ; if , .
- (v)
- If , is equal to or . If not, return to step (ii) to step (v).
4. Bayesian Estimation
4.1. Bayesian Estimation by Using Lindley Approximation under SE Loss Function
4.2. Bayesian Estimation by Using Lindley Approximation under SSE Loss Function
5. Monte Carlo Simulation
- (1)
- For Shannon entropy, the ML estimation performs better than the Bayesian estimation, while for Rényi entropy, the performance of ML estimation is similar to that of Bayesian estimation.
- (2)
- In Bayesian estimation, it is better to select the SE to estimate Shannon entropy. On the contrary, it is better to select the SSE to estimate Rényi entropy.
- (3)
- The sample size has a greater influence on Shannon entropy than on Rényi entropy. When the sample size increases gradually, the Bayesian estimation of Shannon entropy under SE is close to the ML estimation, but it has no obvious effect on Rényi entropy.
- (4)
- In Table 3, it can be noted that the coverage probability of ACIs is quite close to confidence levels.
6. Real Data Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics; University of California Press: Berkeley, CA, USA, 1970; Volume 4, pp. 547–561. [Google Scholar]
- Bulinski, A.; Dimitrov, D. Statistical Estimation of the Shannon Entropy. Acta Math. Sin. Engl. Ser. 2018, 35, 17–46. [Google Scholar] [CrossRef]
- Wolf, R. Information and entropies. Quantum Key Distrib. Introd. Exerc. 2021, 988, 53–89. [Google Scholar]
- Chacko, M.; Asha, P.S. Estimation of entropy for generalized exponential distribution based on record values. J. Indian Soc. Prob. St. 2019, 19, 79–96. [Google Scholar] [CrossRef]
- Liu, S.; Gui, W. Estimating the entropy for Lomax distribution based on generalized progressively hybrid censoring. Symmetry 2019, 11, 1219. [Google Scholar] [CrossRef]
- Shrahili, M.; El-Saeed, A.R.; Hassan, A.S.; Elbatal, I. Estimation of entropy for Log-Logistic distribution under progressive type II censoring. J. Nanomater. 2022, 3, 2739606. [Google Scholar] [CrossRef]
- Mahmoud, M.R.; Ahmad, M.A.M.; Mohamed, B.S.K. Estimating the entropy and residual entropy of a Lomax distribution under generalized type-II hybrid censoring. Math. Stat. 2021, 9, 780–791. [Google Scholar] [CrossRef]
- Hassan, O.; Mazen, N. Product of spacing estimation of entropy for inverse Weibull distribution under progressive type-II censored data with applications. J. Taibah Univ. Sci. 2022, 16, 259–269. [Google Scholar]
- Mavis, P.; Gayan, W.L.; Broderick, O.O. A New Class of Generalized Inverse Weibull Distribution with Applications. J. Appl. Math. Bioinform. 2014, 4, 17–35. [Google Scholar]
- Basheer, A.M. Alpha power inverse Weibull distribution with reliability application. J. Taibah Univ. Sci. 2019, 13, 423–432. [Google Scholar] [CrossRef]
- Valeriia, S.; Broderick, O.O. Weighted Inverse Weibull Distribution: Statistical Properties and Applications. Theor. Math. Appl. 2014, 4, 1–30. [Google Scholar]
- Keller, A.Z.; Kamath, A.R.R. Alternative reliability models for mechanical systems. In Proceedings of the 3rd International Conference on Reliability and Maintainability, Toulose, France, 16–21 October 1982. [Google Scholar]
- Abhijit, C.; Anindya, C. Use of the Fréchet distribution for UPV measurements in concrete. NDT E Int. 2012, 52, 122–128. [Google Scholar]
- Chiodo, E.; Falco, P.D.; Noia, L.P.D.; Mottola, F. Inverse loglogistic distribution for Extreme Wind Speed modeling: Genesis, identification and Bayes estimation. AIMS Energy 2018, 6, 926–948. [Google Scholar] [CrossRef]
- Langlands, A.; Pocock, S.J.; Kerr, G.R.; Gore, S.M. Long-term survival of patients with breast cancer: A study of the curability of the disease. BMJ 1979, 2, 1247–1251. [Google Scholar] [CrossRef]
- Ellah, A. Bayesian and non-Bayesian estimation of the inverse Weibull model based on generalized order statistics. Intell. Inf. Manag. 2012, 4, 23–31. [Google Scholar]
- Singh, S.K.; Singh, U.; Kumar, D. Bayesian estimation of parameters of inverse Weibull distribution. J. Appl. Stat. 2013, 40, 1597–1607. [Google Scholar] [CrossRef]
- Asuman, Y.; Mahmut, K. Reliability estimation and parameter estimation for inverse Weibull distribution under different loss functions. Kuwait J. Sci. 2022, 49, 2023051037. [Google Scholar]
- Sultan, K.S.; Alsadat, N.H.; Kundu, D. Bayesian and maximum likelihood estimations of the inverse Weibull parameters under progressive type-II censoring. J. Stat. Comput. Sim. 2014, 84, 2248–2265. [Google Scholar] [CrossRef]
- Amirzadi, A.; Jamkhaneh, E.B.; Deiri, E. A comparison of estimation methods for reliability function of inverse generalized Weibull distribution under new loss function. J. Stat. Comput. Sim. 2021, 91, 2595–2622. [Google Scholar] [CrossRef]
- Peng, X.; Yan, Z.Z. Bayesian estimation and prediction for the inverse Weibull distribution under general progressive censoring. Commun. Stat. Theory Methods 2016, 45, 621–635. [Google Scholar]
- Sindhu, T.N.; Feroze, N.; Aslam, M. Doubly censored data from two-component mixture of inverse Weibull distributions: Theory and Applications. J. Mod. Appl. Stat. Meth. 2016, 15, 322–349. [Google Scholar] [CrossRef]
- Mohammad, F.; Sana, S. Bayesian estimation and prediction for the inverse Weibull distribution based on lower record values. J. Stat. Appl. Probab. 2021, 10, 369–376. [Google Scholar]
- Faud, S. Al-Duais. Bayesian analysis of Record statistic from the inverse Weibull distribution under balanced loss function. Math. Probl. Eng. 2021, 2021, 6648462. [Google Scholar] [CrossRef]
- Li, C.P.; Hao, H.B. Reliability of a stress-strength model with inverse Weibull distribution. Int. J. Appl. Math. 2017, 47, 302–306. [Google Scholar]
- Ismail, A.; Al Tamimi, A. Optimum constant-stress partially accelerated life test plans using type-I censored data from the inverse Weibull distribution. Strength Mater. 2017, 49, 847–855. [Google Scholar] [CrossRef]
- Kang, S.B.; Han, J.T. The graphical method for goodness of fit test in the inverse Weibull distribution based on multiply type-II censored samples. SpringerPlus 2015, 4, 768. [Google Scholar] [CrossRef]
- Saboori, H.; Barmalzan, G.; Ayat, S.M. Generalized modified inverse Weibull distribution: Its properties and applications. Sankhya B 2020, 82, 247–269. [Google Scholar] [CrossRef]
- Liu, B.X.; Wang, C.J. Bayesian estimation of interval censored data with proportional hazards model under generalized exponential distribution. J. Appl. Stat. Manag. 2023, 42, 293–301. [Google Scholar]
- Ren, H.P. Bayesian estimation of parameter of Rayleigh distribution under symmetric entropy loss function. J. Jiangxi Univ. Sci. Technol. 2009, 31, 64–66. [Google Scholar]
- Mohammad, K.; Mina, A. Estimation of the Inverse Weibull Distribution Parameters under Type-I Hybrid Censoring. Austrian J. Stat. 2021, 50, 38–51. [Google Scholar]
- Algarni, A.; Elgarhy, M.; Almarashi, A.M.; Fayomi, A.; El-Saeed, A.R. Classical and Bayesian Estimation of the Inverse Weibull Distribution: Using Progressive Type-I Censoring Scheme. Adv. Civ. Eng. 2021, 2021, 5701529. [Google Scholar] [CrossRef]
- Zhou, J.H.; Luo, Y. Bayes information updating and multiperiod supply chain screening. Int. J. Prod. Econ. 2023, 256, 108750–108767. [Google Scholar] [CrossRef]
- Yulin, S.; Deniz, G.; Soung, C.L. Bayesian Over-the-Air Computation. IEEE J. Sel. Areas Commun. 2023, 41, 589–606. [Google Scholar]
- Taborsky, P.; Vermue, L.; Korzepa, M.; Morup, M. The Bayesian Cut. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 4111–4124. [Google Scholar] [CrossRef]
- Korup, O. Bayesian geomorphology. Earth Surf. Process Landf. 2021, 46, 151–172. [Google Scholar] [CrossRef]
- Ran, E.; Kfir, E.; Mu, X.S. Bayesian privacy. Theor. Econ. 2021, 16, 1557–1603. [Google Scholar]
- Luo, C.L.; Shen, L.J.; Xu, A.C. Modelling and estimation of system reliability under dynamic operating environments and lifetime ordering constraints. Reliab. Eng. Syst. Saf. 2022, 218, 108136–108145. [Google Scholar] [CrossRef]
- Peng, W.W.; Li, Y.F.; Yang, Y.J.; Mi, J.H.; Huang, H.Z. Bayesian Degradation Analysis with Inverse Gaussian Process Models Under Time-Varying Degradation Rates. IEEE Trans. Reliab. 2017, 66, 84–96. [Google Scholar] [CrossRef]
- František, B.; Frederik, A.; Julia, M.H. Informed Bayesian survival analysis. BMC Med. Res. Methodol. 2022, 22, 238–260. [Google Scholar]
- Liu, F.; Hu, X.G.; Bu, C.Y.; Yu, K. Fuzzy Bayesian Knowledge Tracing. IEEE Trans. Fuzzy Syst. 2022, 30, 2412–2425. [Google Scholar] [CrossRef]
- Zhuang, L.L.; Xu, A.C.; Wang, X.L. A prognostic driven predictive maintenance framework based on Bayesian deep learning. Reliab. Eng. Syst. Saf. 2023, 234, 109181–109192. [Google Scholar] [CrossRef]
- Xu, B.; Wang, D.H.; Wang, R.T. Estimator of scale parameter in a subclass of the exponential family under symmetric entropy loss. Northeast Math. J. 2008, 24, 447–457. [Google Scholar]
- Li, Q.; Wu, D. Bayesian analysis of Rayleigh distribution under progressive type-II censoring. J. Shanghai Polytech. Univ. 2019, 36, 114–117. [Google Scholar]
- Song, L.X.; Chen, Y.S.; Xu, J.M. Bayesian estimation of Pission distribution parameter under scale squared error loss function. J. Lanzhou Univ. Tech. 2008, 34, 152–154. [Google Scholar]
- Bjerkdal, T. Acquisition of resistance in guinea pigs infected with different doses of virulent tubercle bacilli. Am. J. Epidemiol. 1960, 72, 130–148. [Google Scholar] [CrossRef]
- Kundu, D.; Howlader, H. Bayesian inference and prediction of the inverse Weibull distribution for Type-II censored data. Comput. Stat. Data Anal. 2010, 54, 1547–1558. [Google Scholar] [CrossRef]
| Sample Size () | Estimate | MSE | ||||
|---|---|---|---|---|---|---|
| 10 | 1.0604 | 0.8259 | 0.8914 | 0.1903 | 0.3666 | 0.2065 |
| 20 | 1.1183 | 0.9631 | 0.9683 | 0.0863 | 0.1282 | 0.1186 |
| 30 | 1.1388 | 1.0301 | 1.0076 | 0.0558 | 0.0751 | 0.0766 |
| 40 | 1.1355 | 1.0526 | 1.0292 | 0.0445 | 0.0574 | 0.0592 |
| 50 | 1.1461 | 1.0788 | 1.0379 | 0.0323 | 0.0404 | 0.0472 |
| 60 | 1.1503 | 1.0938 | 1.0506 | 0.0287 | 0.0343 | 0.0399 |
| 70 | 1.1579 | 1.1093 | 1.0646 | 0.0244 | 0.0282 | 0.0334 |
| 80 | 1.1623 | 1.1196 | 1.0694 | 0.0197 | 0.0224 | 0.0284 |
| 90 | 1.1653 | 1.1272 | 1.0803 | 0.0171 | 0.0191 | 0.0256 |
| 100 | 1.1628 | 1.1284 | 1.0777 | 0.0161 | 0.0183 | 0.0244 |
| Sample Size () | Estimate | MSE | ||||
|---|---|---|---|---|---|---|
| 10 | 1.6681 | 1.7793 | 1.7682 | 0.0525 | 0.1075 | 0.0954 |
| 20 | 1.6056 | 1.6512 | 1.6587 | 0.0178 | 0.0218 | 0.0186 |
| 30 | 1.5999 | 1.6278 | 1.6229 | 0.0129 | 0.0136 | 0.0112 |
| 40 | 1.5903 | 1.6113 | 1.6082 | 0.0103 | 0.0103 | 0.0075 |
| 50 | 1.5829 | 1.5992 | 1.5972 | 0.0072 | 0.0071 | 0.0064 |
| 60 | 1.5809 | 1.5954 | 1.5896 | 0.0055 | 0.0057 | 0.0049 |
| 70 | 1.5765 | 1.5885 | 1.5878 | 0.0046 | 0.0046 | 0.0045 |
| 80 | 1.5781 | 1.5886 | 1.5857 | 0.0044 | 0.0041 | 0.0034 |
| 90 | 1.5752 | 1.5845 | 1.5779 | 0.0038 | 0.0038 | 0.0032 |
| 100 | 1.5731 | 1.5814 | 1.5775 | 0.0032 | 0.0032 | 0.0031 |
| Sample Size () | Shannon Entropy | Rényi Entropy | ||
|---|---|---|---|---|
| 10 | 0.9637 | 0.9752 | 0.9662 | 0.9791 |
| 20 | 0.9798 | 0.9894 | 0.9789 | 0.9884 |
| 30 | 0.9829 | 0.9916 | 0.9847 | 0.9930 |
| 40 | 0.9839 | 0.9941 | 0.9860 | 0.9953 |
| 50 | 0.9857 | 0.9946 | 0.9894 | 0.9957 |
| 60 | 0.9876 | 0.9947 | 0.9936 | 0.9954 |
| 70 | 0.9875 | 0.9947 | 0.9925 | 0.9965 |
| 80 | 0.9875 | 0.9940 | 0.9929 | 0.9972 |
| 90 | 0.9894 | 0.9955 | 0.9934 | 0.9966 |
| 100 | 0.9865 | 0.9950 | 0.9929 | 0.9971 |
| ML Estimates | Bayesian Estimates | ACIs | |||
|---|---|---|---|---|---|
| Under SE | Under SSE | ||||
| Shannon entropy | 5.6307 | 5.6998 | 4.8706 | (5.1858, 6.0757) | (5.1328, 6.1287) |
| Rényi entropy | 5.4129 | 4.7280 | 4.8706 | (5.1877, 5.6381) | (5.1609, 5.6649) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, H.; Hu, X. Bayesian Estimations of Shannon Entropy and Rényi Entropy of Inverse Weibull Distribution. Mathematics 2023, 11, 2483. https://doi.org/10.3390/math11112483
Ren H, Hu X. Bayesian Estimations of Shannon Entropy and Rényi Entropy of Inverse Weibull Distribution. Mathematics. 2023; 11(11):2483. https://doi.org/10.3390/math11112483
Chicago/Turabian StyleRen, Haiping, and Xue Hu. 2023. "Bayesian Estimations of Shannon Entropy and Rényi Entropy of Inverse Weibull Distribution" Mathematics 11, no. 11: 2483. https://doi.org/10.3390/math11112483
APA StyleRen, H., & Hu, X. (2023). Bayesian Estimations of Shannon Entropy and Rényi Entropy of Inverse Weibull Distribution. Mathematics, 11(11), 2483. https://doi.org/10.3390/math11112483





