Detection of Anomalies in Natural Complicated Data Structures Based on a Hybrid Approach

Abstract

A hybrid approach is proposed to detect anomalies in natural complicated data structures with high noise levels. The approach includes the application of an autoencoder neural network and singular spectrum analysis (SSA) with an adaptive anomaly detection algorithm (AADA) developed by the authors. The autoencoder is the quintessence of the representation learning algorithm, and it projects (selects) data features. Here, under-complete autoencoders are used. They are a product of the development of the principal component method and allow one to approximate complex nonlinear dependencies. Singular spectrum analysis decomposes data through the singular decomposition of matrix trajectories and makes it possible to detect the data structure in the noise. The AADA is based on the combination of wavelet transforms with threshold functions. Combinations of different constructions of wavelet transformation with threshold functions are widely applied to tasks relating to complex data processing. However, when the noise level is high and there is no complete knowledge of a useful signal, anomaly detection is not a trivial problem and requires a complex approach. This paper considers the use of adaptive threshold functions, the parameters of which are estimated on a probabilistic basis. Adaptive thresholds and a moving time window are introduced. The efficiency of the proposed method in detecting anomalies in neutron monitor data is illustrated. Neutron monitor data record cosmic ray intensities. We used neutron monitor data from ground stations. Anomalies in cosmic rays can create serious radiation hazards for people as well as for space and ground facilities. Thus, the diagnostics of anomalies in cosmic ray parameters is quite topical, and research is being carried out by teams from different countries. A comparison of the results for the autoencoder + AADA and SSA + AADA methods showed the higher efficiency of the autoencoder + AADA method. A more flexible NN apparatus provides better detection of short-period anomalies that have complicated structures. However, the combination of SSA and the AADA is efficient in the detection of long-term anomalies in cosmic rays that occur during strong magnetic storms. Thus, cosmic ray data analysis requires a more complex approach, including the use of the autoencoder and SSA with the AADA.

1. Introduction

In recent years, methods of data statistical modeling and analysis have been under intensive development in different spheres of human activity [1,2,3]. Forecasting and analysis methods aimed at the detection of anomalous natural phenomena are of special topicality in the field of environmental sciences [1,2,3,4]. The main problems in such tasks are the incomplete knowledge concerning useful signal structures, high noise levels, and the impossibility of suppressing noise completely. The requirements of high accuracy and real-time solutions make the method development more difficult. Strictly mathematical apparatuses are not effective enough, such that the application and development of heuristic approaches and methods are required.

Singular spectrum analysis (SSA) has been successfully applied in data analysis [5,6]. SSA allows for the investigation of data structures, the suppression of noise, and the detection of trends and periodicities [7,8,9,10]. For example, in [5], the authors used SSA together with support vector regression (LS-SVR) and a random forest (RF) to make precipitation forecasts. The investigations [5] showed that SSA-based data pre-processing made it possible to improve the performance of the LS-SVR and RF methods. The authors of [6] analyzed the compression of Earth geophysical data using SSA. Based on SSA, they succeeded in distinguishing six-month, twelve-month, and 10.6-year periods in the analyzed data. However, in cases where there is a complicated structure, linear approximation is not always effective, and the best results are obtained through the use of linear estimates [11]. The authors of [5] also noted this fact and plan to consider other ways of processing data, in particular, wavelet transformation.

Wavelets have a wide set of bases, making it possible to detect data that have complicated structures [11,12,13,14,15]. For example, algorithms of matching pursuit [14], such as using greedy algorithms, allow one to obtain quite accurate approximations, even in cases of incomplete data with relatively high levels of noise. In such cases, a signal is estimated by isolating coherent structures [11]. However, matching pursuit algorithms have very high computational complexity. If the energy of the signal is small relative to the energy of the noise, such estimates have very low thresholds [11], and the application of these algorithms does not allow one to obtain good results, as has been confirmed in investigations [16]. However, the flexibility of wavelet constructions makes it possible to combine these algorithms with different methods and adapt them to processed data. Complex hybrid approaches can be developed for complex data analysis using wavelet transforms. In [17], an F-filter [18] was applied together with wavelet transformation to detect low-amplitude periodicities. This allowed for the estimation of process changeability and the detection of hidden regularities in data within an interval under analysis.

In recent years, to approximate and analyze complex data, traditional statistical methods and modern heuristic tools, including elements of artificial intelligence and machine learning, have been combined more often [4,5,16,19]. Such combinations make it possible to improve the quality of data analysis procedures. Their efficiency is provided via the numerical realization of these methods. In this paper, we suggest a hybrid approach based on the combination of the developed adaptive anomaly detection algorithm (AADA) with an autoencoder neural network. It is known that if representative sampling is available, neural networks allow one to obtain approximations of acceptable accuracy when dealing with complex data. In this paper, we apply under-complete autoencoders, which have determinate bases (as a result of the development of the principal component method) that make it possible to approximate complex nonlinear dependencies. They have high adaptive capability and can significantly reduce noise levels [19]. The autoencoder is used in the paper to determine the characteristics of the data structures and to reduce noise. The further application of the AADA provides effective anomaly detection.

The AADA is based on the combination of wavelet transforms with threshold functions. In the AADA, we apply adaptive thresholds, which are estimated in a moving window based on the probabilistic approach. This algorithm is similar to the method described in [17]. It allows for the detection of the nonstationary features of different time–frequency structures.

The efficiency of the suggested approach is illustrated in the use of data taken from neutron monitors, which record cosmic ray (CR) intensity variations. Anomalies in cosmic rays can create hazards for people and space and ground facilities. Thus, the diagnostics of anomalies in cosmic ray parameters is very topical, and research is being carried out by teams from different countries [1,2,3,4].

Anomalies in CRs can have the form of sudden short-term increases relative to a characteristic level. Such features often occur before magnetic storms and are used as their predictors [20,21]. During strong magnetospheric storms, anomalies in CR data have a trend form with significant decreases (Forbush decreases [22]). Such anomalies may last for several days. In the background of significant anomalous decreases, short-term sudden peak-like changes, which have complex non-stationary spectra, can be observed. They indicate strong disturbances in the near-Earth space.

The complexity of CR data structures means that the application of classical methods and approaches is ineffective. For example, the application of the principal component method was attempted in [23] to investigate the combined effect of the solar activity level and the inclination of the neutral surface of the interplanetary magnetic field to galactic cosmic ray modulation in the heliosphere. The authors [23] obtained results that confirm theoretical conceptions and drift motions of cosmic rays in the heliosphere. However, the obtained results were not confirmed with the present theory due to the variation complexity of CRs. One of the most successful methods in this field is the station ring method [24]. This method is the most effective when data from high-latitude neutron monitors are used [24]. However, the conditions required for the implementation of the method cannot always be fulfilled due to the random distribution of stations over the globe and the significant impact of natural and man-made noises on the measurement results. It is also difficult to quantify the station ring method and, as a consequence, realize it numerically and estimate its accuracy.

Machine learning methods are also being developed to analyze CRs. For example, the authors of [25] suggest using graph neural networks to investigate the energy spectrum and content of CRs. This approach allows one to reduce time and computational efforts. However, at present, CR data analysis using this method is limited due to the configuration peculiarities of the applied detector [25]. In [26], a hybrid approach was proposed to filter artifacts in experiments focusing on the detection of cosmic rays. The authors [26] applied convolutional neural networks together with adaptive thresholds and Daubechies wavelets to reduce the number of false artifacts. The developed solution [26] made it possible to fully automate the analysis procedure. However, the constructed classifiers are limited in terms of annotator accuracy when recognizing if a hit is a signal or an artifact [26].

Due to the reasons mentioned above, the problem of CR data analysis and anomaly detection is topical and requires the application of a complex of methods and tools. This work continues these investigations [16,19]. The adaptive technique used for the estimation of thresholds in a wavelet space was described in detail in [16]. The authors of [19] showed the efficiency of the combination of wavelet transforms with the autoencoder network. In that paper, the approach was developed, and its efficiency for the near-real-time detection of CR complex-spectrum short-term anomalies, which precede magnetic storm commencement, was confirmed. The proposed method is also compared with the combination of SSA and the AADA. The application of SSA made it possible to detect a CR variation component that has a strong correlation with the geomagnetic activity Dst index [27]. These results confirm the theory [18] and show the importance of taking CRs into account in space weather forecasts.

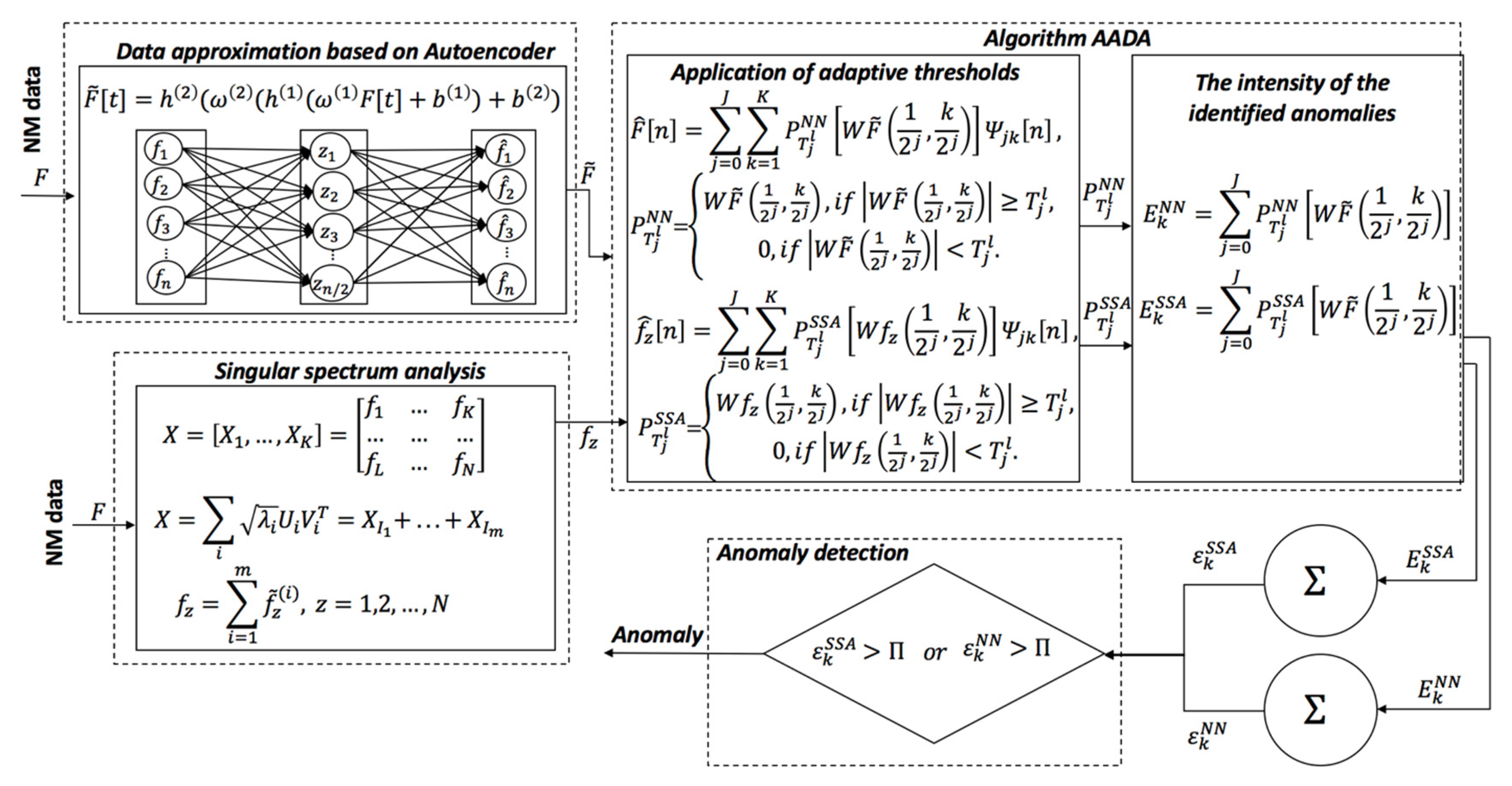
2. Description of the Applied Methods

2.1. Singular Spectrum Analysis

Based on singular spectrum analysis, the initial time series of F is transformed into a matrix followed by singular decomposition, grouping, and transition to time series components [8]. The algorithm used for the implementation of the method was suggested in [8] and is described below.

• Transformation of tshe initial one-dimensional series F into a trajectory matrix,

$$X=\left[X_1, \dots , X_K\right]=\left[\begin{array}{ccc}{f}_1& \dots & f_K\\ \dots & \dots & \dots \\ f_L& \dots & f_N\end{array}\right],$$

where $f_i$ is the initial series element, $L$ is the window length, and $N$ is the initial series length.

2.

Singular decomposition of the obtained trajectory matrix $X$.

Assume that $S=X{X}^T$, ${\lambda }_1,\dots ,{\lambda }_L$ are eigenvalues of $S$, taken in nonascending order (${\lambda }_1\ge \dots \ge {\lambda }_L\ge 0$), and $U_1,\dots ,U_L$ is the orthonormalized system of eigenvectors of the matrix $S$.

Assume that $d=\mathrm{rank} X=max\{i:{\lambda }_i>0\}$ (as a rule, in reality $d=L$) and $V_i=X^T{U}_i/{\lambda }_i\left(i=1,\dots ,d\right).$ In these notations, singular decomposition of the trajectory matrix $X$ can be written as follows:

$$X=X_1+\dots +X_d,$$

where the matrixes $X_i=\sqrt{{\lambda }_i}{U}_i{V}_i^T$ have the rank of 1 and are called elementary matrixes, $\sqrt{{\lambda }_i}$ are the singular numbers, which make up the singular spectrum and are the measure of data dispersion. $U_i$ is the left singular vector of the trajectory matrix $X$, and $V_i$ is the right singular vector of the trajectory matrix $X$.

Thus, the trajectory matrix $X$ can be represented in the following form:

$$X={\displaystyle \sum }_i\sqrt{{\lambda }_i}{U}_i{V}_i^T.$$

3.

The grouping of the set $d$ of elementary matrixes from item 2 on $m$ non-intersecting subsets $X_{I_i}$, $I_i\in${$I_1, \dots , I_m$}. Assume that $I_i=\left\{i_1,\dots ,i_p\right\}$, then the resulting matrix $X_{I_i}$, corresponding to group $I_i$, is determined as $X_{I_i}=X_{i_1}+\dots +X_{i_p}$.

Thus, the grouped singular decomposition of the trajectory matrix $X$ can be represented as follows:

$$X=X_{I_1}+\dots +X_{I_m}.$$

4.

Matrixes $X_{I_i}$ of the grouped decomposition are Hankelized (are averaged over anti-diagonals). Using the correspondence between the Hankel matrixes and the time series, the recovered series ${\tilde{F}}^{\left(k\right)}=\left({\tilde{f}}_1^{\left(k\right)}, \dots , {\tilde{f}}_N^{\left(k\right)}\right)$ are obtained. The initial series $F=(f_1, \dots , f_N)$ is decomposed into a sum $m$ of the recovered series, where each value of the initial series is equal to

$$f_i={\displaystyle \sum }_{k=1}^m{\tilde{f}}_i^{\left(k\right)},i=1,2,\dots ,N.$$

This decomposition is the main result of the SSA algorithm for time series analysis. This decomposition is meaningful if each of its components can be interpreted as either a trend, oscillation (periodicals), or noise.

2.2. Autoencoder Neural Network

The autoencoder is a feed-forward network trained without a teacher but by using the back-propagation method [28]. In the paper, we applied a two-layer autoencoder, where the initial one-dimensional series of $F$ was transformed according to the formula [28]

$$\tilde{F}=h^{\left(2\right)}\left(V^{\left(2\right)}(h^{\left(1\right)}\left(V^{\left(1\right)}F+b^{\left(1\right)}\right))+b^{\left(2\right)}\right),$$

where the superscript is (1), (2) is the layer number,$h^{\left(1\right)}\in {ℝ}^{d\times 1}$ is the non-linear activation function, $V^{\left(1\right)}\in {ℝ}^{d\times N}$ is the waight matrix, $F\in {ℝ}^{N\times 1}$ is the input vector, $N$ is the dimension of the input vector, $b^{\left(1\right)}\in {ℝ}^{d\times 1}$ is the displacement vector, $h^{\left(2\right)}\in {ℝ}^{N\times 1}$ is the linear activation function, $V^{\left(2\right)}\in {ℝ}^{N\times d}$ is the weight matrix, a $b^{\left(2\right)}\in {ℝ}^{N\times 1}$ is the displacement vector, and $ℝ$ are real numbers.

If we set the dimension of the network hidden layer to be smaller than the dimension of the input layer and use only linear activation functions, the network will realize the principal component method [28]. When increasing the number of hidden layers and introducing nonlinear activation functions, the network can approximate complex nonlinear relations in data.

The network architecture is illustrated in Figure 1.

In order to suppress noise, the dimension of the hidden layer architecture was set to be smaller than that of the output layer, ($d<N$).

2.3. Adaptive Anomaly Detection Algorithm

We proposed the AADA for the first time in [19]. The algorithm includes the following operations:

1.

Discrete time series $F\left[n\right]$ is represented in the form of the series [29,30]

$$F\left[n\right]={\displaystyle \sum }_{j=0}^J{\displaystyle \sum }_{k=1}^{K}WF\left(\frac{1}{2^j},\frac{k}{2^j}\right){\Psi }_{jk}\left[n\right],$$

where ${\Psi }_{jk}=2^{\frac{j}{2}}\Psi \left(2^{j}n-k\right)$ are the basic wavelets, $j,k\in N, WF\left(\frac{1}{2^j},\frac{k}{2^j}\right)=\langle F,{\Psi }_{jk}\rangle$ are the coefficients of function F decomposition into a series, $J$ is the largest scale of decomposition into a wavelet series, and $K$ is the series length.

2.

A threshold function is applied to wavelet coefficients of the time series $F\left[n\right]$ decomposition,

$$P_{T_j^l}\left[WF\left(\frac{1}{2^j},\frac{k}{2^j}\right)\right]=\left\{\begin{array}{c}WF\left(\frac{1}{2^j},\frac{k}{2^j}\right), if\left|WF\left(\frac{1}{2^j},\frac{k}{2^j}\right)\right|\ge T_j^l,\\ 0, if\left|WF\left(\frac{1}{2^j},\frac{k}{2^j}\right)\right|<T_j^l,\end{array}\right.$$

where $T_j^l=t_{1-\frac{\alpha }{2},l-1}{\widehat{\sigma }}_j^l$, $t_{\alpha ,N}$ are $\alpha$-quantiles of Student’s distribution [31], ${\widehat{\sigma }}_j^l$ is the coefficient root-mean-square deviation estimated in a moving window of the length $l$, ${\hat{\sigma }}_j^l=\sqrt{\frac{1}{l-1}{\sum }_{m=1}^l(WF\left(\frac{1}{2^j},\frac{k}{2^j}\right)-\overline{WF\left(\frac{1}{2^j},\frac{k}{2^j}\right)}{)}^2}$.

We obtain a representation of the series,

$$\widehat{F}\left[n\right]={\displaystyle \sum }_{j=0}^J{\displaystyle \sum }_{k=1}^K{P}_{T_j^l}\left[WF\left(\frac{1}{2^j},\frac{k}{2^j}\right)\right]{\Psi }_{jk}\left[n\right].$$

3.

For the detected anomalies, their intensities at the time instant $t=k$ can be estimated as follows:

$$E_k={\displaystyle \sum }_{j=0}^J{P}_{T_j^l}\left[WF\left(\frac{1}{2^j},\frac{k}{2^j}\right)\right],$$

which are positive in cases of function values anomalous increases and negative in cases of function values anomalous decreases.

2.4. Scheme of Method Realization

The proposed approach can be represented in the form of the scheme illustrated in Figure 2. The presence or absence of an anomaly in data is determined by the decision rule,

$$«\mathrm{There} \mathrm{is} \mathrm{an} \mathrm{anomaly} \mathrm{in} \mathrm{data} \mathrm{if} {\epsilon }_k^{NN}> \Pi \mathrm{or} {\epsilon }_k^{SSA}> \Pi »,$$

where ${\epsilon }_k^{NN}=\sum _{i=i-l}^{i+l}{E}_k^{NN}, {\epsilon }_k^{SSA}=\sum _{i=i-l}^{i+l}{E}_k^{SSA}$ are summary error vectors estimated in a moving time window of the length $l$ (in the paper, $l=5$), $E_k^{SSA}$ is the result of the application of SSA with the AADA (scheme), $E_k^{NN}$ is the result of the application of the autoencoder NN with the AADA (scheme), and $\Pi$ is the threshold value calculated empirically (based on posterior risk) separately for each station, taking into account the anisotropy of CRs and the characteristics of the recording instrumentation.

3. Data Processing Results

In the experiments, we used the minute data taken from the neutron monitor of a high-latitudinal station, Oulu [32] (www.nmdb.eu). Neutron monitor (NM) data reflect cosmic ray intensities (particle counts per minute (cpm)). Particle fluxes recorded by ground NM can be of galactic, solar, and Earth origin. Thus, based on ground NM, solar activity and the Earth’s seismic activity are investigated [33]. Neutron monitor data contain regular time variations, anomalous features, and natural and man-made noises [34]. Regular variations contain periodical variations, such as diurnal, 27-day, 11-year, and 22-year solar cycles. Anomalous features have different structures (Forbuch effects of different intensities and durations [22] and strong sudden ground proton increases (GLE-events)) occur in the data during disturbances in the near-Earth space. NM data structures at different stations differ due to anisotropy properties [24]. Weather conditions near a recording device (rain, snow, hail, wind, etc.) and instrumentation errors caused by readjustments also have a significant impact on NM data.

In the experiments, we applied a standard two-layer autoencoder architecture [28] (Figure 1). When constructing NN training sets, the data were selected on the basis of space weather factor analysis. The NN input vector dimension was $N=1440$ counts, which corresponds to a day (minute data). The NN hidden layer dimension was determined empirically and was taken to be $d=N/2$. To check the adequacy of the constructed NN, the Q-criterion was used [31]. The process of constructing the autoencoder network was described in detail for the problem of anomaly detection in CR data in [19].

Taking into account the diurnal variations, a window length of $L=1440$ counts (corresponds to a day) was used in the SSA method. Figure 3 illustrates the NM data over four different time intervals and the corresponding seven first components obtained on the basis of SSA (item 2 of the SSA algorithm). An analysis of Figure 3 shows that the initial NM data have a nonstationary structure and contain high noise levels. The detected components include a trend, periodical components, local features, and noise variations (Figure 3).

The matrixes grouping in the SSA algorithm (item 3 of the algorithm) was carried out by taking into account the eigenvalues (item 2 of the algorithm) and was based on the estimates of the confined dispersion fraction [28]. The graph of the first 30 eigenvalues is illustrated in Figure 4. The dashed line in Figure 4 separates the eigenvalues, which correspond to the components used in the analysis. The confined dispersion fraction was estimated using the following formula:

$$\frac{{\sigma }_1^2+{\sigma }_2^2\dots +{\sigma }_p^2}{{\sigma }_1^2+{\sigma }_2^2\dots +{\sigma }_p^2+\dots +{\sigma }_d^2}.$$

The results of the confined dispersion fraction estimates are shown in

Table 1. March 2023.

Component	Confined Dispersion Fraction
com1	0.8942
com1 + com2	0.9288
com1 + com2 + com3	0.9501
com1 + com2 + com3 + com4	0.9607
com1 + com2 + com3 + com4 + com5	0.9655
com1 + com2 + com3 + com4 + com5 + com6	0.9681
com1 + com2 + com3 + com4 + com5 + com6 + com7	0.9703

,

Table 2. April 2023.

Component	Confined Dispersion Fraction
com1	0.8262
com1 + com2	0.8934
com1 + com2 + com3	0.9247
com1 + com2 + com3 + com4	0.9353
com1 + com2 + com3 + com4 + com5	0.9395
com1 + com2 + com3 + com4 + com5 + com6	0.9427
com1 + com2 + com3 + com4 + com5 + com6 + com7	0.9458

,

Table 3. 27 October–4 November.

Component	Confined Dispersion Fraction
com1	0.7508
com1 + com2	0.8490
com1 + com2 + com3	0.9074
com1 + com2 + com3 + com4	0.9291
com1 + com2 + com3 + com4 + com5	0.9395
com1 + com2 + com3 + com4 + com5 + com6	0.9470
com1 + com2 + com3 + com4 + com5 + com6 + com7	0.9526

and

Table 4. March 2022.

Component	Confined Dispersion Fraction
com1	0.6269
com1 + com2	0.7581
com1 + com2 + com3	0.8307
com1 + com2 + com3 + com4	0.8649
com1 + com2 + com3 + com4 + com5	0.8835
com1 + com2 + com3 + com4 + com5 + com6	0.8964
com1 + com2 + com3 + com4 + com5 + com6 + com7	0.9049

. An analysis of Table 1, Table 2, Table 3 and Table 4 indicates that the first three components determine the greater fraction of the confined dispersion. The component with the 1st eigenvalue determines the trend, and the components with the 2nd and 3rd eigenvalues include diurnal periodicities in the CR data. The results obtained after the summation of these components are presented below.

In the SSA method, taking into account the presence of diurnal variations, a window length of $L=1440$ counts was used (corresponding to a day). The components were grouped, taking the eigenvalues into account. The plot of the eigenvalues for the first 30 components is shown in Figure 3. The dotted line in Figure 3 separates the eigenvalues, and these components were used in the analysis. The remaining components were taken as noise. Below are the results obtained by adding the components, corresponding to the 1st, 2nd, and 3rd eigenvalues. The component with the 1st eigenvalue determines the trend, and the components with the 2nd and 3rd eigenvalues include daily periodicities of the CR data.

Results of the Estimates of the Confined Dispersion Fraction

Figure 5 shows the results of the experiments during a strong magnetic storm, which occurred on 4 November 2022. To analyze the near-Earth space state, Figure 5a,b illustrates the data concerning the interplanetary magnetic field (IMF) Bz [35] component and geomagnetic activity Dst index [36], respectively.

Based on space weather data [35], the near-Earth space was calm on 29 October. From 30 October to 1 November, inhomogeneous accelerated fluxes from a coronal whole and a coronal mass ejections were recorded [35]. The disturbances in the near-Earth space were indicated by the increase in Bz fluctuation amplitude in the negative domain (decrease to Bz = −12 nT) (Figure 5a). The Dst index decrease on 1 November up to −36 nT (Figure 5a) denoted the anomalous increase in geomagnetic activity. According to the processed data (Figure 5d,e,g,h), low-intensity anomalies in the CR data were observed during that period. The results of the combinations of the autoencoder and SSA with the AADA are identical that confirms their reliability. The results also show the efficiency of both approaches in detecting low-intensity anomalies in the CR data.

According to the data [35], inhomogeneous accelerated fluxes from a coronal mass ejection were recorded on 3 and 4 November. They caused a strong magnetic storm occurrence at the end of the day on 3 November (at 20:00 UT). The strongest disturbances were observed on 4 November. The Dst index decreased to −105 nT (Figure 5b). The processing results (Figure 5d,e,g,h) show an anomalous increase in CR intensity before the storm and a significant decrease (Forbush decrease in high amplitude) during the strongest geomagnetic disturbances on 4 November. A comparison of the results of the different approaches (Figure 5d,e,g,h) illustrates the high efficiency of the autoencoder with the AADA (Figure 5g,h). The method allowed for the detection of the CR intensity anomalous increases, which occurred before the magnetic storm. The anomaly reached its maximum intensity on 3 November, 8 h before the storm. The results of the SSA and AADA combination (Figure 5d,e) also show positive anomaly occurrence during that period. However, due to the complicated nonlinear structure of the anomaly, the application of SSA turned out to be less effective. The result also points to the importance of taking into account the CR parameters for space weather forecasts.

Figure 6 shows the results of the application of the SSA + AADA method during a strong magnetic storm, which occurred on 23 March 2023. To analyze the near-Earth space state, Figure 6a,b illustrates the interplanetary magnetic field (MMF) Bz [35] component data and geomagnetic activity Dst index data [36], respectively.

Based on space weather data [35], an inhomogeneous flux from a coronal whole and a coronal mass ejection arrived on the first half of the day on 15 March. IMF Bz fluctuations increased and reached Bz = −17 nT in the negative domain (Figure 6a). At 20:00 UTC at the end of the day on 15 March, a geomagnetic disturbance was recorded [35]. The Dst index decreased to −38 nT at that time (Figure 6b). The near-Earth space state on 15 March was characterized as being weakly disturbed. The processing results (Figure 6d,e) show an anomalous decrease in CR intensity (Forbush decrease) several hours before the geomagnetic disturbance on 15 March. The anomaly reached its maximum intensity at 12:00 UTC on 16 March.

Further, an inhomogeneous accelerated flux from a coronal mass ejection arrived at 04:00 UTC on 23 March [35]. The GSM fluctuations were intensified (Figure 6a). At 11:00 UTC on 23 March, the geomagnetic storm commencement was recorded [35]. The Dst index value on 24 March decreased to Dst = −162 (Figure 6b). The processing results (Figure 6d,e) show an anomalous decrease in CR intensity (high-amplitude Forbush decrease) several hours before the geomagnetic storm on 23 March. The anomaly reached its maximum intensity at 14:00 UTC on 23 March.

Thus, the SSA + AADA method allowed for the detection of CR intensity anomalous decreases, which occurred several hours before the geomagnetic disturbances. The result also indicates the importance of taking into account the CR parameters for space weather forecasts.

Figure 7 shows the results of the experiments for the period 2–4 March 2023. According to space weather data [35], an inhomogeneous accelerated flux from a coronal whole and a coronal mass ejection arrived at 18:00 UTC on 2 March. At 23:00 UTC on 2 March, an anomalous increase in geomagnetic activity occurred (the Dst index decreased to −39 nT, Figure 7b). Based on the data [35], the magnetic storm commencement (marked by an orange vertical line) was recorded at 18:00 UTC on 2 March. The near-ground space state on 3 March was characterized as being unstable. A comparison of the results of the different methods (Figure 7d,e,g,h) shows the high efficiency of the autoencoder with the AADA combination (Figure 7g,h). The method allowed for the detection of the CR intensity anomalous increases, which occurred at the time of the geomagnetic disturbance commencement. The result of the SSA with the AADA combination (Figure 7d,e) turned out to be ineffective due to the complicated structure of the anomaly and the smoothing effect of the SSA method. The possibility of detecting low-amplitude anomalies through the use of an autoencoder with the AADA combination was studied in detail in [19]. Estimates showed the high sensitivity of that approach for short-period anomalies.

Figure 8 shows the results of the data processing for the period from 8 March 2022 to 28 March 2022 [32]. Figure 8a,b illustrates the IMF Bz component data and geomagnetic activity Dst index data, respectively. The orange vertical lines show the times of the geomagnetic disturbances. A red vertical line marks the moderate magnetic storm’s commencement.

According to space weather data [35], Bz component fluctuations increased and reached Bz = −10 nT (Figure 8a) on 11 March. The processing results (Figure 8d,e,g,h) show anomalous changes in the CR data during that period. At 23:00 UT at the end of the day on March 11, a weak magnetic storm was recorded [35]. During the storm on 12 March, the Dst index decreased to −51nT (Figure 8b). Based on the processed data (Figure 8d,e,g,h), an anomalous increase in CR intensity occurred during that period. It was clearly detected using the method based on the autoencoder and AADA combination. The next day, at 10:48 on 13 March, a moderate magnetic storm was recorded (minimum Dst = −85) [36]. According to the processed data (Figure 8d,e,g,h), the anomalous decrease in CR intensity (high-amplitude Forbush decrease) began at the time of the magnetic storm.

At the end of the period under analysis on 27 March, an inhomogeneous accelerated flux from a coronal whole and a coronal mass ejection arrived [35]. Bz component fluctuation amplitude increased (Bz = −11 nT, Figure 8a). Based on the data [35], an anomalous increase in geomagnetic activity was recorded at 06:00 UT on 27 March. According to the processed data (Figure 8d,e,g,h), an anomalous decrease in CR intensity (low-amplitude Forbush decrease) occurred 6 h before the geomagnetic disturbance.

We should note that the CR variation component, detected using SSA (Figure 8c), has a strong correlation with geomagnetic activity Dst index (Figure 8b) during the period under analysis. This correlation is the most clearly traced during the period that preceded and accompanied the moderate magnetic storm from 8 March 2022 to 23 March 2022. This result is of high applied significance and confirms the importance of taking into account the CR parameters for space weather forecasts. The result also shows the capability of SSA to suppress noises and detect CR variation components.

The results of the estimates of the suggested approach efficiency are presented in

Table 5. Estimate of the autoencoder + AADA method efficiency for different time window dimensions.

Period	Number of Geomagnetic Disturbances and Geomagnetic Storms	Wavelet Function	Moving Time Window Dimension	Result
2013–2015, 2019–2020	405	Coiflet 2	$l=720$	Detected: 64% Undetected: 36% False alarm: 32 events
			$l=1080$	Detected: 78% Undetected: 22% False alarm: 27 events
			$l=1440$	Detected: 87% Undetected: 13% False alarm: 27 events

,

Table 6. Estimate of the autoencoder + AADA method efficiency using different wavelet functions.

Period	Number of Geomagnetic Disturbances and Geomagnetic Storms	Moving Time Window Dimension	Wavelet Function	Results
2013–2015, 2019–2020	405	$l=1440$	Coiflet 1	Detected: 87% Undetected: 13% False alarm: 29 events
			Coiflet 2	Detected: 87% Undetected: 13% False alarm: 27 events
			Coiflet 3	Detected: 85% Undetected: 15% False alarm: 28 events
			Daubechies 1	Detected: 84% Undetected: 16% False alarm: 29 events
			Daubechies 2	Detected: 86% Undetected: 14% False alarm: 29 events

and

Table 7. Estimate of the SSA + AADA method efficiency (Coiflet 2 was used, time window length $l=1440$).

Period	Number of Geomagnetic Disturbances and Geomagnetic Storms	Results of SSA + AADA
2013–2015, 2019–2020	405	Detected: 84%
		Undetected: 16%
		False alarm: 35 events

. Table 5 shows the results of the autoencoder + AADA method when different time window dimensions $l$ (item 2 of Section 2.3) were used. Table 6 illustrates the results of this method when different wavelet functions were used. It follows from Table 5 and Table 6 that the best result was obtained for the time window $l=1440$ and Coiflet 2 wavelet function. The efficiency was ~87%. Table 7 presents the results of the SSA + AADA method. The percentage of anomaly detection by this method was ~84%.

Thus, based on the estimate results (Table 5, Table 6 and Table 7), the efficiency of the autoencoder + AADA method is higher than that of the SSA + AADA method. However, as shown above (Figure 6), the SSA + AADA method effectively detects the periods of long anomalous changes (from a day and longer) in CRs. Such anomalies are often observed during strong magnetic storms. The application of a more flexible NN apparatus enables the better detection of short-period anomalies (Figure 5, Figure 7 and Figure 8). Thus, a more complex approach is required to improve anomaly detection efficiency. A scheme of such an approach, including the use of SSA and the autoencoder with the AADA, is illustrated in Figure 2.

4. Conclusions

The work results confirmed the efficiency of the autoencoder and AADA combination in the analysis of CR data and the detection of anomalies. The complicated structure of CR data and high noise levels require the application of a complex of methods. The autoencoder makes it possible to approximate CR data time variations and suppress noise. The AADA can detect anomalies that have complicated structures and allows one to estimate their parameters. The algorithm’s adaptive capability and high detecting efficiency of wavelets lead to the possibility of detecting anomalies of different amplitude and duration in the presence of noise and the absence of priori data.

The comparison of the results of the autoencoder and SSA with the AADA combinations showed the higher efficiency of the autoencoder and AADA method. The anomaly detection by the method, based on the SSA and AADA combination, was ~84%. The anomaly detection when using this method, based on the autoencoder and AADA combination, was ~87%. Due to the complicatesd nonlinear structure of CR data, their approximation by the autoencoder provides high accuracy. However, the detailed analysis showed that the SSA and AADA method combination is effective when detecting CR long-term anomalies characteristic of strong magnetic storms. The application of a more flexible NN apparatus enables the better detection of short-period anomalies preceding magnetic storm commencement. The application of SSA turned out to be effective in detecting CR variation components when analyzing process dynamics. Thus, in order to improve the quality of CR data analysis, a more complex approach, including the use of SSA and the autoencoder with the AADA, is required.

The work results are of applied significance and confirm the importance of taking into account CR parameters for space weather forecasts. The strong correlation of CR variations with geomagnetic activity Dst index confirmed the theory [2] regarding the possibility of predicting magnetic storms based on CR flux data.