Finite-Time Super Twisting Disturbance Observer-Based Backstepping Control for Body-Flap Hypersonic Vehicle
Abstract
:1. Introduction
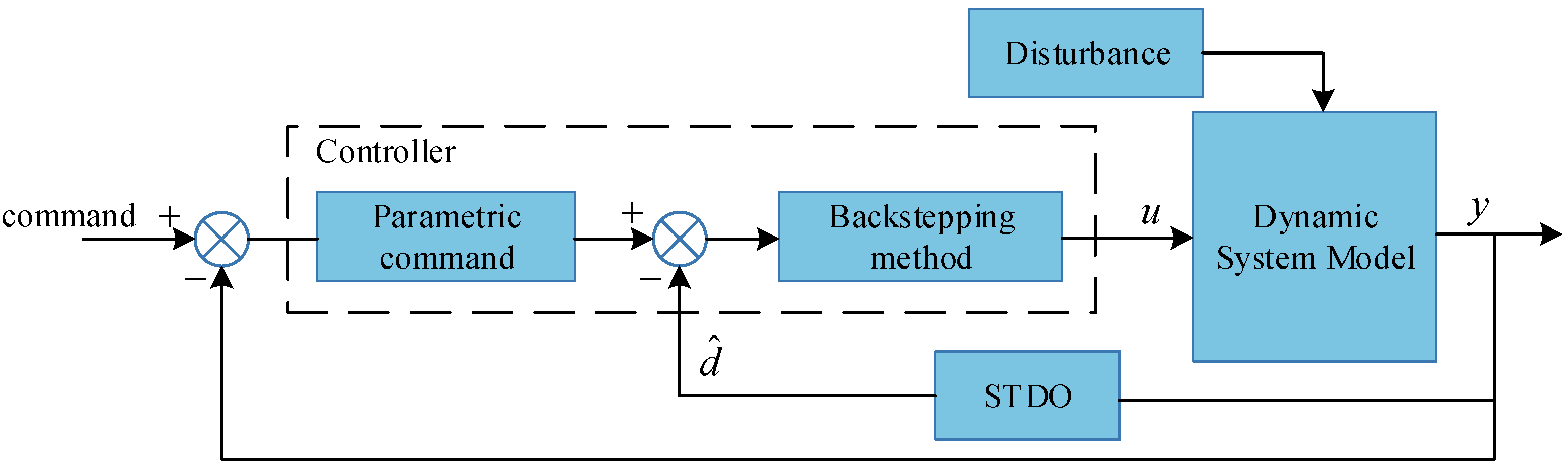
- The proposed STDO is employed for the lumped disturbances of a BFHSV, which has a smaller estimation error and smoother control variables than conventional super twisting approaches.
- The parametric command method can strengthen the states’ convergence speed of the backstepping control method. In addition, the “explosion of complexity” is avoided by introducing a second-order filter.
2. Problem Formulation
3. Super Twisting Algorithm Disturbance Observer Design
3.1. Observer Design
3.2. Stability Analysis
4. STDO-Based Improved Backstepping Controller Design
4.1. Improved Backstepping Controller Design
4.2. Stability Analysis
5. Simulation Results
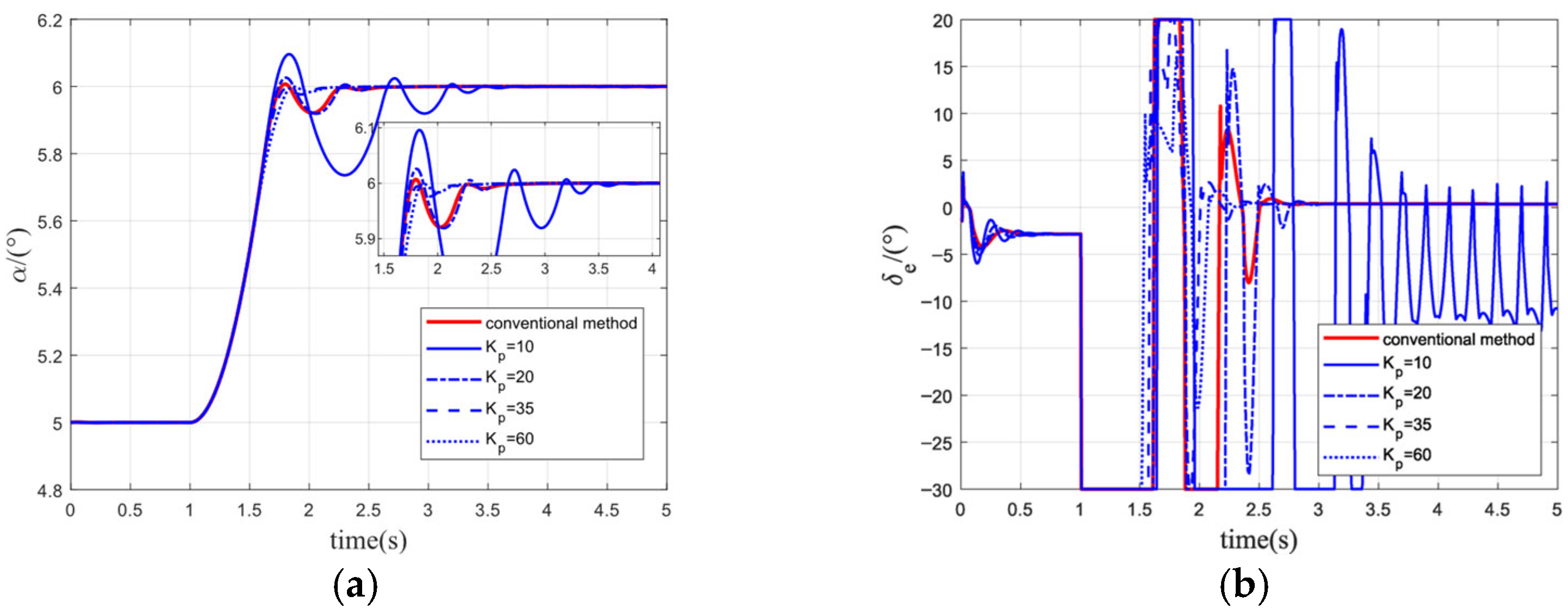
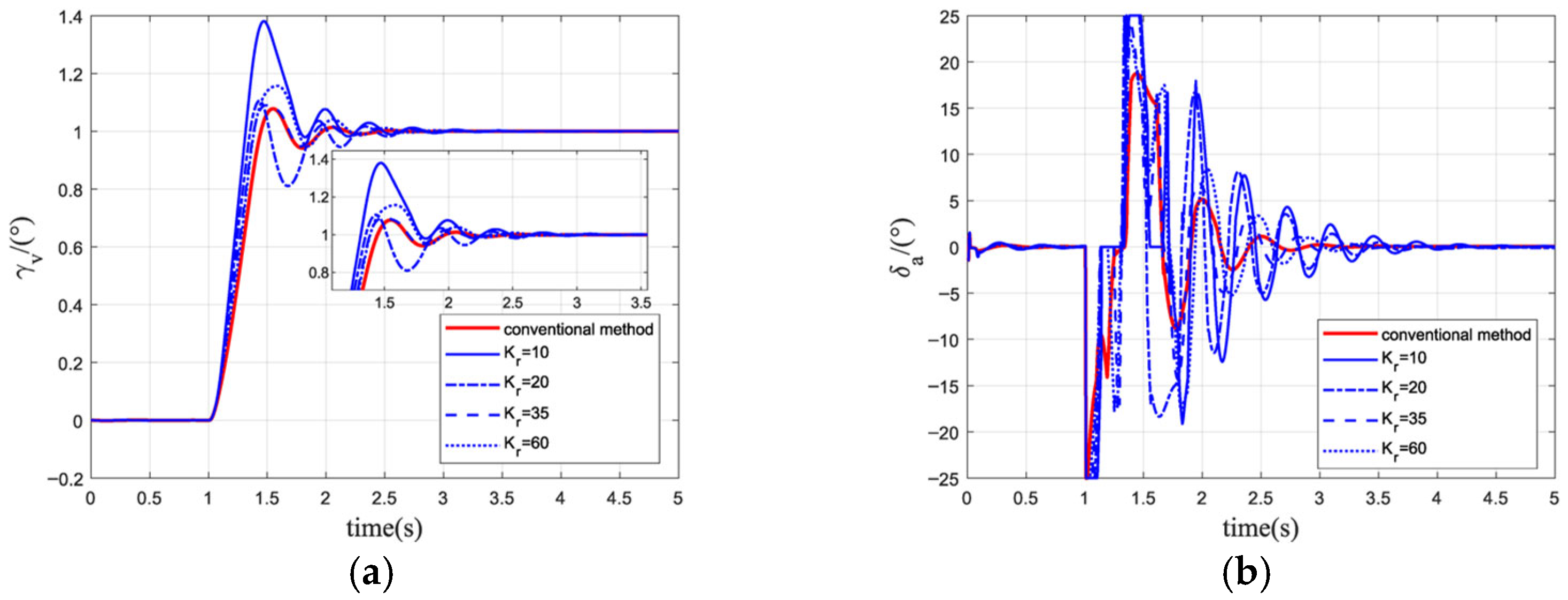
5.1. Simulation Analysis of The Parametric Command Method
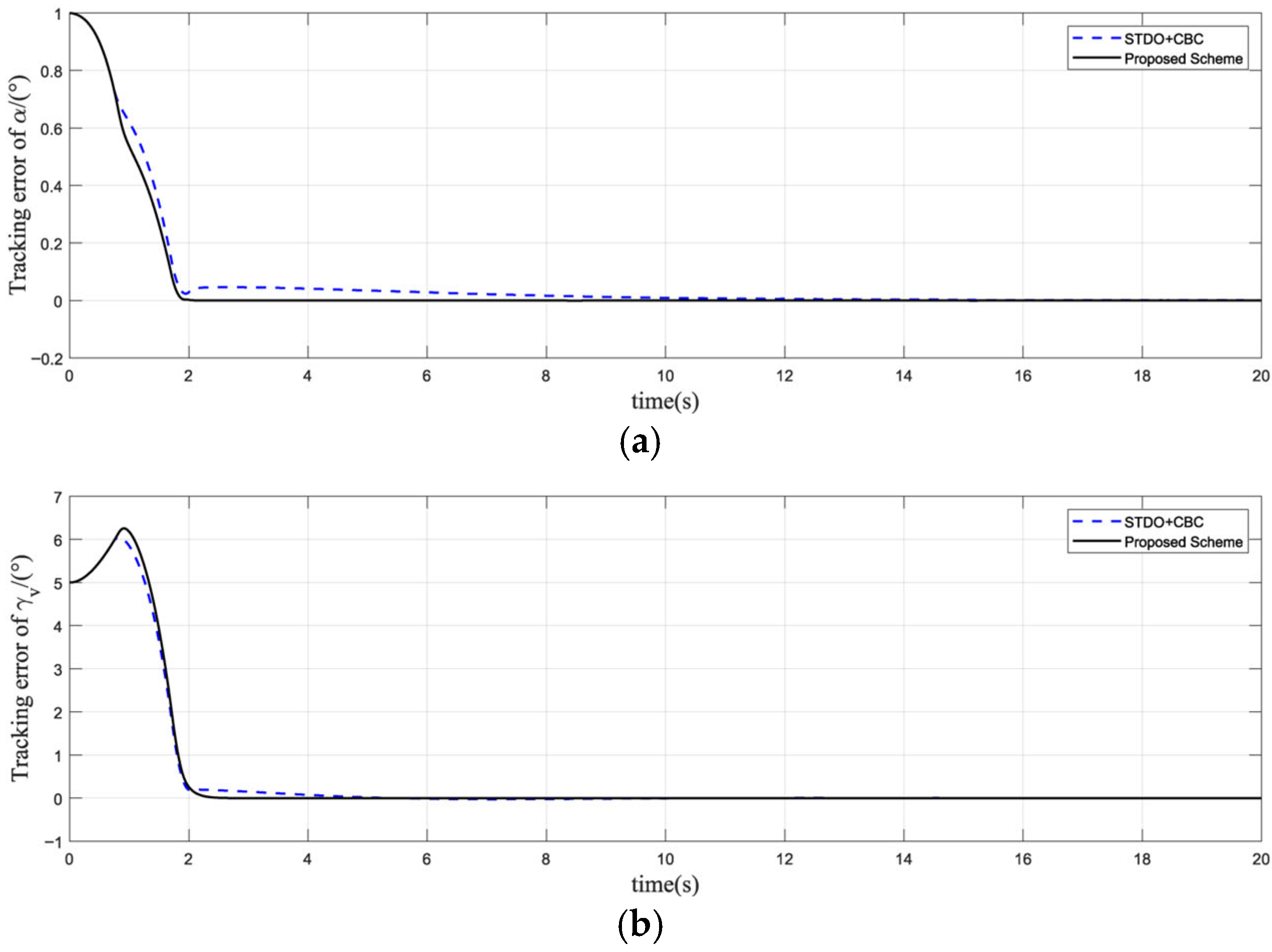
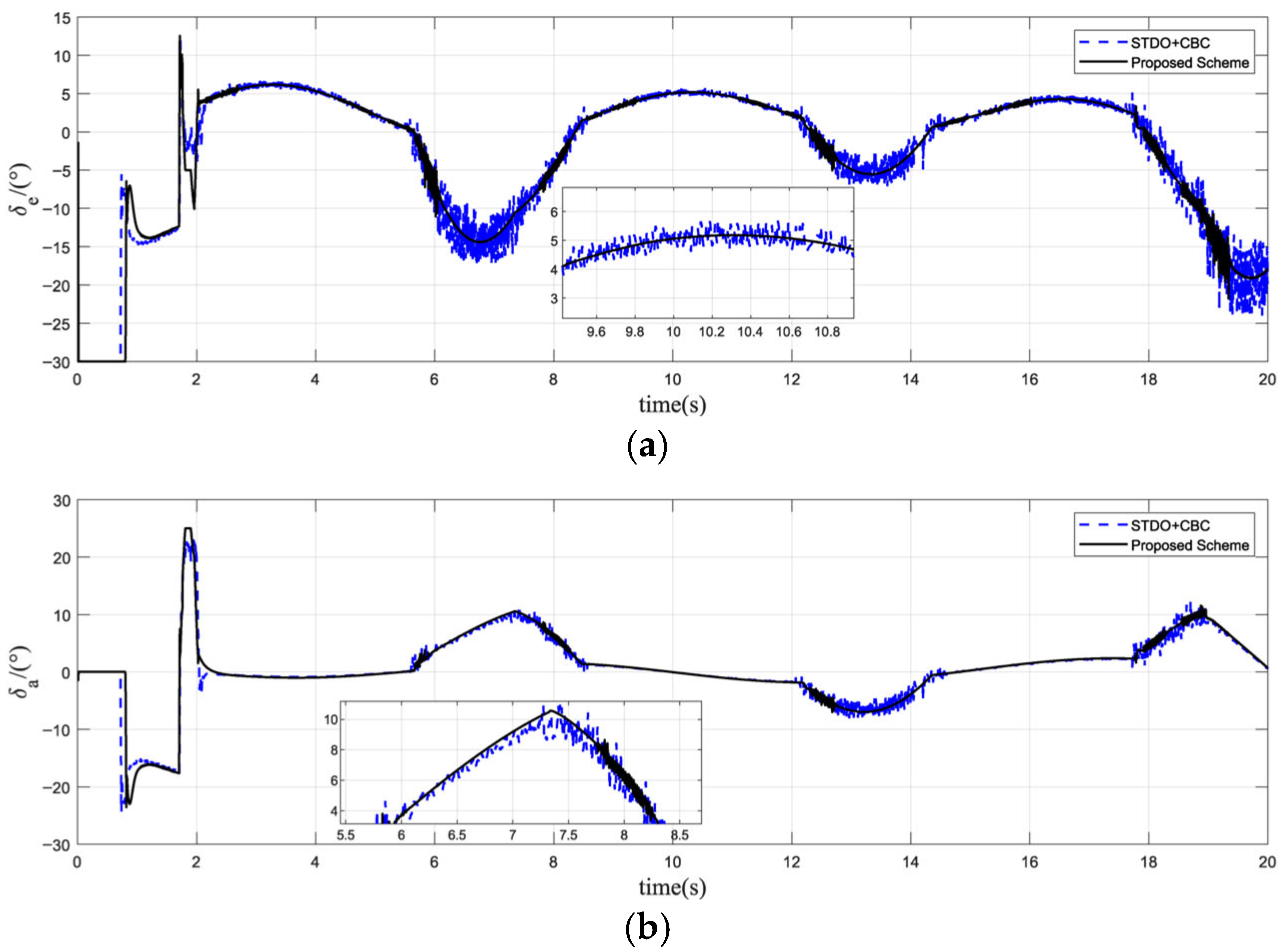
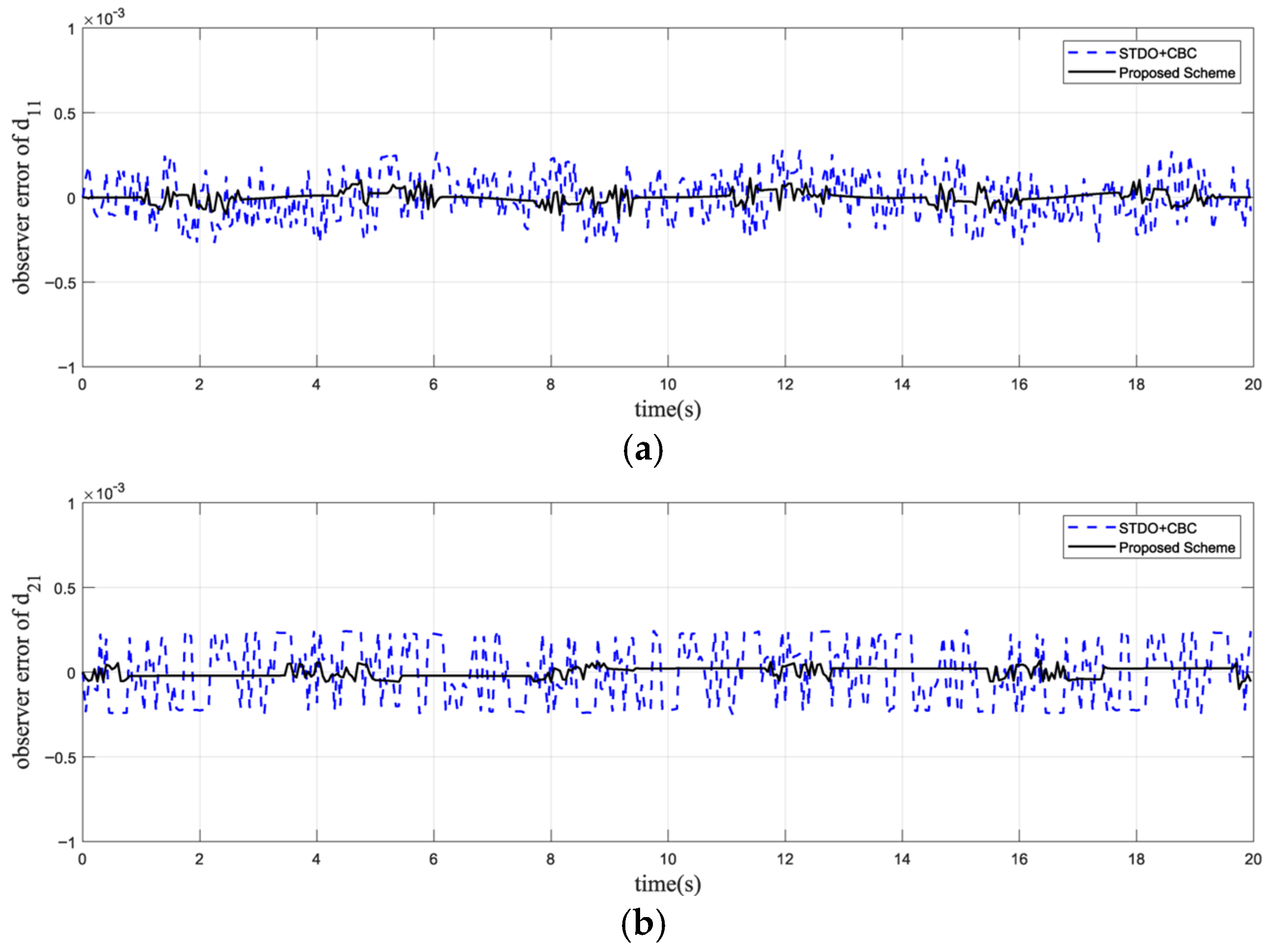
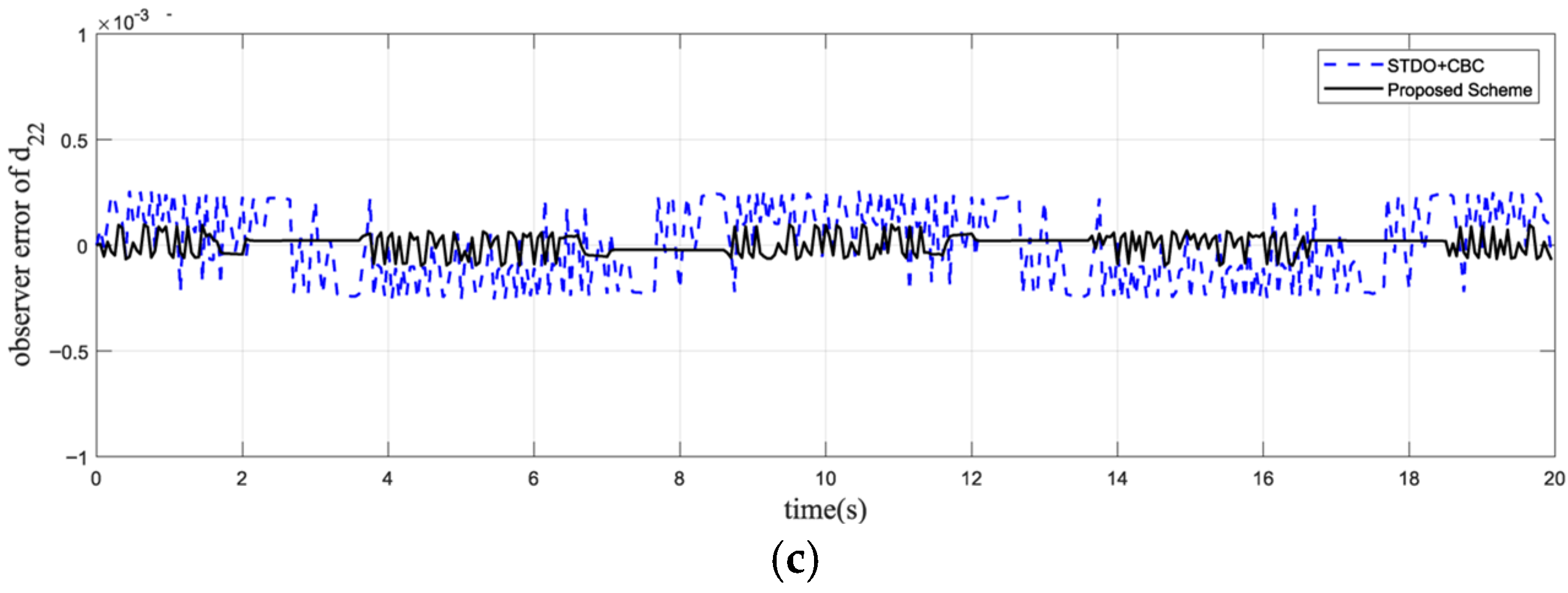
5.2. Simulation Analysis of The Proposed Control Scheme
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Walker, S.; Sherk, J.; Shell, D.; Schena, R.; Bergmann, J.; Gladbach, J. The DARPA/AF Falcon Program: The Hypersonic Technology Vehicle #2 (HTV-2) Flight Demonstration Phase. In Proceedings of the 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Dayton, OH, USA, 28 April 2008; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2008. [Google Scholar]
- Wright, D. Research Note to Hypersonic Boost-Glide Weapons by James M. Acton: Analysis of the Boost Phase of the HTV-2 Hypersonic Glider Tests. Sci. Glob. Secur. 2015, 23, 220–229. [Google Scholar] [CrossRef]
- Wang, F.; Wen, L.; Zhou, C.; Hua, C. Adaptive Preassigned-Time Controller Design for a Hypersonic Vehicle with Improved Performance and Uncertainties. ISA Trans. 2023, 132, 309–328. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Jiang, B.; Yang, H. Backstepping-Based Decentralized Fault-Tolerant Control of Hypersonic Vehicles in PDE-ODE Form. IEEE Trans. Autom. Control 2022, 67, 1210–1225. [Google Scholar] [CrossRef]
- Wang, G.; An, H.; Wang, Y.; Xia, H.; Ma, G. Intelligent Control of Air-Breathing Hypersonic Vehicles Subject to Path and Angle-of-Attack Constraints. Acta Astronaut. 2022, 198, 606–616. [Google Scholar] [CrossRef]
- Xu, B.; Shi, Z. An Overview on Flight Dynamics and Control Approaches for Hypersonic Vehicles. Sci. China Inf. Sci. 2015, 58, 1–19. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, X.; Bai, Y.; Cui, N. Global Smooth Sliding Mode Controller for Flexible Air-Breathing Hypersonic Vehicle with Actuator Faults. Aerosp. Sci. Technol. 2019, 92, 563–578. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Z.; An, J.; Zhou, X.; Hu, G.; Zhang, G.; Man, W. Adaptive Sliding Mode Control of Modular Self-Reconfigurable Spacecraft with Time-Delay Estimation. Def. Technol. 2022, 18, 2170–2180. [Google Scholar] [CrossRef]
- Yang, Z.; Mao, Q.; Dou, L.; Zong, Q.; Yang, J. Composite Design of Disturbance Observer and Reentry Attitude Controller: An Enhanced Finite-Time Technique for Aeroservoelastic Reusable Launch Vehicles. Int. J. Control Autom. Syst. 2022, 20, 2459–2473. [Google Scholar] [CrossRef]
- Jiang, S.; Tian, F.; Sun, S.; Liang, W. Integrated Guidance and Control of Guided Projectile with Multiple Constraints Based on Fuzzy Adaptive and Dynamic Surface. Def. Technol. 2020, 16, 1130–1141. [Google Scholar] [CrossRef]
- Zhang, C.; Ahn, C.K.; Wu, J.; He, W. Online-Learning Control with Weakened Saturation Response to Attitude Tracking: A Variable Learning Intensity Approach. Aerosp. Sci. Technol. 2021, 117, 106981. [Google Scholar] [CrossRef]
- Zhang, C.; Xiao, B.; Wu, J.; Li, B. On Low-Complexity Control Design to Spacecraft Attitude Stabilization: An Online-Learning Approach. Aerosp. Sci. Technol. 2021, 110, 106441. [Google Scholar] [CrossRef]
- Zhang, C.; Ahn, C.K.; Wu, J.; He, W.; Jiang, Y.; Liu, M. Robustification of Learning Observers to Uncertainty Identification via Time-Varying Learning Intensity. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 1292–1296. [Google Scholar] [CrossRef]
- Isidori, A. Nonlinear Control Systems II. In Communications and Control Engineering; Springer London: London, UK, 1999; ISBN 978-1-4471-1160-3. [Google Scholar]
- Ye, L.; Tian, B.; Liu, H.; Zong, Q.; Liang, B.; Yuan, B. Anti-Windup Robust Backstepping Control for an Underactuated Reusable Launch Vehicle. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1492–1502. [Google Scholar] [CrossRef]
- Wang, Z.; Bao, W.; Li, H. Second-Order Dynamic Sliding-Mode Control for Nonminimum Phase Underactuated Hypersonic Vehicles. IEEE Trans. Ind. Electron. 2017, 64, 3105–3112. [Google Scholar] [CrossRef]
- Moul, M.T.; Paulson, J.W. Dynamic Lateral Behavior of High-Performance Aircraft 1958. Available online: https://ntrs.nasa.gov/citations/19710069982 (accessed on 6 August 2013).
- Lei, R.-H.; Chen, L. Finite-Time Tracking Control and Vibration Suppression Based on the Concept of Virtual Control Force for Flexible Two-Link Space Robot. Def. Technol. 2021, 17, 874–883. [Google Scholar] [CrossRef]
- Wei, Y.; Deng, H.; Pan, Z.; Li, K.; Chen, H. Research on a Combinatorial Control Method for Coaxial Rotor Aircraft Based on Sliding Mode. Def. Technol. 2022, 18, 280–292. [Google Scholar] [CrossRef]
- Ji, P.; Min, F.; Zhang, F.; Ma, F. Tele-Aiming Control Design for Reconnaissance Robot Using a Strong Tracking Multi-Model Extended Super-Twisting Observer. IET Control Theory Appl. 2023, 17, 696–712. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Laghrouche, S.; Depernet, D.; N’Diaye, A.; Djerdir, A.; Cirrincione, M. Super-Twisting Sliding-Mode Observer-Based Model Reference Adaptive Speed Control for PMSM Drives. J. Frankl. Inst. 2023, 360, 985–1004. [Google Scholar] [CrossRef]
- Hu, X.; Guo, C.; Hu, C.; He, B. Sliding Mode Learning Control for T-S Fuzzy System and an Application to Hypersonic Flight Vehicle. Asian J. Control 2023, 25, 407–417. [Google Scholar] [CrossRef]
- Huang, S.; Jiang, J.; Li, O. Sliding Mode Backstepping Control for the Ascent Phase of Near-Space Hypersonic Vehicle Based on a Novel Triple Power Reaching Law. Aerospace 2022, 9, 755. [Google Scholar] [CrossRef]
- Ju, X.; Wei, C.; Xu, H.; Wang, F. Fractional-Order Sliding Mode Control with a Predefined-Time Observer for VTVL Reusable Launch Vehicles under Actuator Faults and Saturation Constraints. Isa Trans. 2022, 129, 55–72. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Hu, W.; Wei, C.; Xu, T. Nonlinear Disturbance Observer Based Adaptive Super-Twisting Sliding Mode Control for Generic Hypersonic Vehicles with Coupled Multisource Disturbances. Eur. J. Control 2021, 57, 253–262. [Google Scholar] [CrossRef]
- Gurumurthy, G.; Das, D.K. Terminal Sliding Mode Disturbance Observer Based Adaptive Super Twisting Sliding Mode Controller Design for a Class of Nonlinear Systems. Eur. J. Control 2021, 57, 232–241. [Google Scholar] [CrossRef]
- Snell, S.A.; Enns, D.F.; Garrard, W.L. Nonlinear Inversion Flight Control for a Supermaneuverable Aircraft. J. Guid. Control Dyn. 1992, 15, 976–984. [Google Scholar] [CrossRef]
- Wang, Z.; Li, H.; Bao, W. Body-flap attitude control method for lifting re-entry vehicle. J. Beijing Univ. Aeronaut. Astronaut. 2016, 42, 532–541. [Google Scholar] [CrossRef]
- Li, Z.; Zhai, J. Super-twisting Sliding Mode Trajectory Tracking Adaptive Control of Wheeled Mobile Robots with Disturbance Observer. Int. J. Robust Nonlinear Control 2022, 32, 9869–9881. [Google Scholar] [CrossRef]
- Mei, K.; Ding, S.; Yu, X. A Generalized Supertwisting Algorithm. IEEE Trans. Cybern. 2023, 53, 3951–3960. [Google Scholar] [CrossRef]
- Zhao, J.; Feng, D.; Cui, J.; Wang, X. Finite-Time Extended State Observer-Based Fixed-Time Attitude Control for Hypersonic Vehicles. Mathematics 2022, 10, 3162. [Google Scholar] [CrossRef]
- Li, C.-Y.; Jing, W.-X.; Gao, C.-S. Adaptive Backstepping-Based Flight Control System Using Integral Filters. Aerosp. Sci. Technol. 2009, 13, 105–113. [Google Scholar] [CrossRef]
- Zong, Q.; Dong, Q.; Wang, F.; Tian, B. Super Twisting Sliding Mode Control for a Flexible Air-Breathing Hypersonic Vehicle Based on Disturbance Observer. Sci. China Inf. Sci. 2015, 58, 1–15. [Google Scholar] [CrossRef]


| Parameters | Value | Parameters | Value |
|---|---|---|---|
| 1000 | 0.21 | ||
| 0.5 | −0.60 | ||
| 800 | −0.19 | ||
| 5000 | 0.02 | ||
| 5000 | −0.43 | ||
| 100 | −0.15 |
| Simulation Conditions | ts/s | ||||||
|---|---|---|---|---|---|---|---|
| α | |||||||
| Conventional Method | |||||||
| Parametric Command Method | 10 | ||||||
| 20 | |||||||
| 35 | |||||||
| 60 | |||||||
| Controllers | Parameters |
|---|---|
| STDO-BC | |
| STDO-CBC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Min, C.; Cui, J.; Li, F.; Feng, D.; Dai, P. Finite-Time Super Twisting Disturbance Observer-Based Backstepping Control for Body-Flap Hypersonic Vehicle. Mathematics 2023, 11, 2460. https://doi.org/10.3390/math11112460
Liu D, Min C, Cui J, Li F, Feng D, Dai P. Finite-Time Super Twisting Disturbance Observer-Based Backstepping Control for Body-Flap Hypersonic Vehicle. Mathematics. 2023; 11(11):2460. https://doi.org/10.3390/math11112460
Chicago/Turabian StyleLiu, Daiming, Changwan Min, Jiashan Cui, Fei Li, Dongzhu Feng, and Pei Dai. 2023. "Finite-Time Super Twisting Disturbance Observer-Based Backstepping Control for Body-Flap Hypersonic Vehicle" Mathematics 11, no. 11: 2460. https://doi.org/10.3390/math11112460
APA StyleLiu, D., Min, C., Cui, J., Li, F., Feng, D., & Dai, P. (2023). Finite-Time Super Twisting Disturbance Observer-Based Backstepping Control for Body-Flap Hypersonic Vehicle. Mathematics, 11(11), 2460. https://doi.org/10.3390/math11112460








