Bicluster Analysis of Heterogeneous Panel Data via M-Estimation

Abstract

This paper investigates the latent block structure in the heterogeneous panel data model. It is assumed that the regression coefficients have group structures across individuals and structural breaks over time, where change points can cause changes to the group structures and structural breaks can vary between subgroups. To recover the latent block structure, we propose a robust biclustering approach that utilizes M-estimation and concave fused penalties. An algorithm based on local quadratic approximation is developed to optimize the objective function, which is more compact and efficient than the ADMM algorithm. Moreover, we establish the oracle property of the penalized M-estimators and prove that the proposed estimator recovers the latent block structure with a probability approaching one. Finally, simulation studies on multiple datasets demonstrate the good finite sample performance of the proposed estimators.

1. Introduction

Panel data models can fully utilize both cross-sectional and time-series information, making them a popular tool in fields such as economics and finance. Traditional panel data models often assume that the regression coefficients are homogeneous across individuals and over periods, which is too rigid an assumption. In many real-world applications, heterogeneity in individual and/or time dimensions is often observed. For example, in precision medicine research, different subgroups of patients may respond differently to treatments, while in economics, events such as the 2009 European debt crisis led to varying debt-to-GDP ratios among European countries. Although these heterogeneous factors are unobserved and latent, modeling them will bring significant improvement to data analysis.

Numerous estimation methods have been developed for panel data models with heterogeneous coefficients, addressing two main sources of heterogeneity: individual and period. To account for heterogeneity across individuals, a commonly used assumption is that individuals can be classified into subgroups with identical coefficients within the same subgroup but different coefficients across subgroups. Penalty-based methods have been frequently used to cluster coefficients in the individual direction. Su et al. [1] propose C-Lasso, a modified version of Lasso, for subgroup identification and coefficient estimation. This method is based on a penalized objective function inspired by the fused Lasso method introduced by Tibshirani et al. [2]. Wang and Zhu [3] study high-dimensional panel data models using a concave fused penalty method for both subgroup identification and variable selection and proved the asymptotic properties of the proposed estimator under specific regularity conditions. To capture the heterogeneity that may exist over time, structural breaks are often assumed. Qian and Su [4] use a group fused Lasso method to estimate both the number of breaks and model parameters simultaneously. Furthermore, Qian and Su [5] employ an adaptive group fused Lasso approach that applies the shrinkage method to PLS and PGMM estimations. Their method can consistently determine the number of breaks and estimate the break dates with a probability approaching one.

However, these studies have two primary limitations. Firstly, they only account for heterogeneity in one dimension, which may be insufficient for modeling complex data prevalent in the era of big data. Secondly, their objective functions employ the least squares loss which can result in substantial estimation bias when the data distribution contains a heavy tail or outliers. Consequently, further research has been conducted to address these issues. Some researchers have focused on the two-dimensional heterogeneous panel data model, where the coefficients exhibit both subgroup structure and structural breaks. Okui and Wang [6] allow the number, timing, and size of structural breaks to vary across different subgroups and employ the K-means method and adaptive group fused Lasso method to identify the individual group structure and structural breaks, respectively. Lumsdaine et al. [7] study cases where the group structure of coefficients changes after the unknown structural break and develop a novel iterative algorithm to estimate the coefficients and recover the unknown structure. Additionally, some researchers have focused on robust estimation. For example, Zhang et al. [8] set the objective function as the sum of $L_1$ loss and concave pairwise fused penalty when studying the panel data model with an individual group structure and provide an easy-to-implement algorithm based on the idea of local linear approximation [9] to find local minima. Cheng et al. [10] further generalize the $L_1$ loss to a general loss function under the framework of M-estimation.

In this paper, we generalize the coefficient structure studied by [6,7] to a more general block structure. The regression coefficients with a block structure exhibit both an individual-group structure and temporal–structural breaks, where the individual-group structure can change at change points, and the temporal–structural breaks can vary across different groups. Furthermore, the regression coefficients are identical within the same sub-block, while they exhibit heterogeneity across different sub-blocks. This block structure is highly flexible and more general compared to the structures studied previously. Additionally, the homogeneous panel data model, the panel data model with a group structure, and the panel data model with structural breaks can all be viewed as special cases of the model being investigated in this study.

We propose a robust biclustering method based on M-estimation and double concave fused penalties for simultaneously recovering the unknown block structure and estimating the regression coefficients. The M-estimator exhibits robustness to heavy-tailed distributions and outliers, while the double concave fused penalty can automatically identify potential block structure. We develop an effective algorithm utilizing local quadratic approximation to optimize the objective function, which is computationally more efficient than the Alternating Direction Method of Multipliers (ADMM) [11] algorithm. Moreover, we establish the asymptotic convergence property of the oracle estimator and prove that the proposed estimator can recover the latent block structure with a probability approaching one. Simulation experiments on multiple datasets demonstrate that the estimator proposed in this paper has an excellent performance in finite sample situations. Additionally, models based on $L_1$ loss and $Huber$ loss functions can achieve more accurate results than those based on $L_2$ loss functions in the presence of heavy-tailed data distributions.

2. Materials and Methods

2.1. Model Setting

Given panel data observations $\{({\mathit{x}}_{it},y_{it}),i=1,\cdots ,N;t=1,\cdots ,T\}$, this paper explores a linear panel data model that accounts for the heterogeneity of intercept and slope coefficients across both the individual and time dimensions. The model is represented as follows,

$$y_{it}={\mu }_{it}+{\mathit{x}}_{it}^{\top }{\mathit{\zeta }}_{it}+{ϵ}_{it},i=1,\cdots ,N;t=1,\cdots T,$$

(1)

where $y_{it}\in \mathbb{R}$ is the response variable, and ${\mathit{x}}_{it}\in {\mathbb{R}}^{P-1}$ is the explanatory variable. The intercept term ${\mu }_{it}$ and the slope coefficient ${\mathit{\zeta }}_{it}\in {\mathbb{R}}^{P-1}$ can vary across both individual and time dimensions in the model. The random errors are assumed to be independent and identically distributed with a mean of 0 and a standard deviation of $\sigma$, and their distribution is denoted by f.

We assume that the observed data are collected from an unknown, $L^0$ different blocks, where the regression coefficients are homogeneous within the same block but heterogeneous across different blocks. It is worth noting that the group structure and structural breaks can be viewed as special cases of the block structure. Below, we provide the relevant notation to describe this block structure.

Let ${\mathit{\beta }}_{it}={({\mu }_{it},{\mathit{\eta }}_{it}^{\top })}^{\top }$ and ${\mathit{z}}_{it}={(1,{\mathit{x}}_{it}^{\top })}^{\top }$. Then, Equation (1) can be expressed as follows,

$$y_{it}={\mathit{z}}_{it}^{\top }{\mathit{\beta }}_{it}+{ϵ}_{it},i=1,\cdots ,N;t=1,\cdots ,T.$$

(2)

We denote the block structure as $\mathcal{B}=\{{\mathcal{B}}_1,\cdots ,{\mathcal{B}}_{L^0}\}$, where ${\mathcal{B}}_k$ represents the index set of samples belonging to the kth sub-block. If the ith individual’s observation at time t belongs to the kth sub-block, then $(i,t)\in {\mathcal{B}}_k$. Let ${\mathit{\alpha }}_1^0,\cdots ,{\mathit{\alpha }}_{L^0}^0$ denote the real regression coefficients corresponding to the $L^0$ sub-blocks, and let ${\mathit{\beta }}_{it}^0$ be the real value of ${\mathit{\beta }}_{it}$. Then, we have

$${\mathit{\beta }}_{it}^0=\left\{\begin{array}{ccc}\hfill {\mathit{\alpha }}_1^0,& & \mathrm{if}(i,t)\in {\mathcal{B}}_1,\hfill \\ \hfill {\mathit{\alpha }}_2^0,& & \mathrm{if}(i,t)\in {\mathcal{B}}_2,\hfill \\ \hfill \cdots & & \\ \hfill {\mathit{\alpha }}_{L^0}^0& & \mathrm{if}(i,t)\in {\mathcal{B}}_{L^0}.\hfill \end{array}\right.$$

(3)

In practical scenarios, the real block structure is often unknown. To recover the block structure described above, it is necessary to estimate the number of sub-blocks, the index sets of each block, and the block-specific coefficients.

2.2. Proposed Estimator

In this subsection, we propose a biclustering estimation method to automatically recover the block structure without specifying the number of blocks and provide robust estimates of regression coefficients via M-estimation and concave fused penalties. Let $\mathit{\beta }={({\mathit{\beta }}_{11}^{\top },{\mathit{\beta }}_{12}^{\top },\cdots ,{\mathit{\beta }}_{1T}^{\top },\cdots ,{\mathit{\beta }}_{N1}^{\top },{\mathit{\beta }}_{N2}^{\top },\cdots ,{\mathit{\beta }}_{NT}^{\top })}^{\top }$ denote the coefficients to be estimated. To recover the block structure under the fused sparse assumption, a natural idea is to shrink the coefficient differences $\left|\right|{\mathit{\beta }}_{\mathit{it}}-{\mathit{\beta }}_{j{t}^{{}^{\prime }}}\left|\right|$ between two samples $(i,t)$ and $(j,t^{{}^{\prime }})$ that belong to the same block ${\mathcal{B}}_l$ to zero. In the following, we present the objective function based on M-estimation and concave fused penalty as follows,

$$\begin{array}{cc}\hfill Q(\mathit{\beta };\lambda ,\gamma )& =\sum _{i=1}^N\sum _{t=1}^T\rho (y_{it}-{\mathit{z}}_{it}^{\top }{\mathit{\beta }}_{it})+\sum _{t=1}^T\sum _{i<j}{P}_{\lambda }\left(\right||{\mathit{\beta }}_{it}-{\mathit{\beta }}_{jt}\left|\right|)\hfill \\ & +\sum _{i=1}^N\sum _{t<t^{{}^{\prime }}}{P}_{\gamma }\left(\right||{\mathit{\beta }}_{it}-{\mathit{\beta }}_{i{t}^{{}^{\prime }}}\left|\right|),\hfill \end{array}$$

(4)

where the first term on the right-hand side is the regular loss function $\rho$ in the M-estimation literature. It satisfies several conditions, including being a continuous convex function on $\mathbb{R}$, almost everywhere differentiable except for a finite set of points, having a unique global minimum at 0, and $\rho \left(0\right)=0$. Commonly used loss functions such as least squares ($L_2$), absolute deviation ($L_1$), and Huber loss all satisfy these conditions. The second and third terms are two fused penalty terms designed to identify the individual-group structure and temporal–structure breaks.

Commonly used penalty terms include Lasso [12], Ridge [13], and Elastic net [14]. Ridge and Elastic net can shrink the fusion terms toward small values, but not exactly zero, which makes it challenging to cluster coefficients within the same block. Lasso, on the other hand, can shrink the fusion terms to exactly zero but has a tendency to introduce bias in the estimated coefficients. This bias can impact the accuracy of the parameter estimates and potentially lead to suboptimal results in recovering the latent block structure. To achieve both automatic recovery of the parameter structure and unbiased or nearly unbiased estimation of coefficients, concave fused penalty functions have been proposed, such as the smoothly clipped absolute deviation (SCAD) [15] and the minimax concave penalty (MCP) [16]. In this paper, following the approach of Wang and Zhu [3], Ma and Huang [17], Wang et al. [18], we use the SCAD penalty function with a tuning parameter $\lambda$,

$$P_{\lambda }\left(k\right)=\lambda {\int }_0^k{(1-x/\left(\lambda a\right))}_{+}dx,$$

(5)

and the MCP penalty function with a tuning parameter $\gamma$,

$$P_{\gamma }\left(k\right)=\gamma {\int }_0^{k}min\{1,(a-x/\gamma )/(a-1))\}dx,$$

(6)

where the fixed parameter a controls the concavity of the penalty function, and k represents pairwise differences in regression coefficients between individuals or periods. $P_{\lambda }\left(k\right)$ and $P_{\gamma }\left(k\right)$ can compress some pairwise difference values $\left|\right|{\mathit{\beta }}_{it}-{\mathit{\beta }}_{jt}\left|\right|$ and $\left|\right|{\mathit{\beta }}_{it}-{\mathit{\beta }}_{i{t}^{{}^{\prime }}}\left|\right|$ to zero, thereby recovering the block structure of the regression coefficients.

For a given $\lambda$ and $\gamma$, we define the proposed estimator as

$$\widehat{\mathit{\beta }}(\lambda ,\gamma )=\underset{\mathit{\beta }\in {\mathbb{R}}^{NTP}}{argmin}Q(\mathit{\beta };\lambda ,\gamma ).$$

(7)

In the following, we abbreviate $\widehat{\mathit{\beta }}(\lambda ,\gamma )$ as $\widehat{\mathit{\beta }}$ when there is no ambiguity. Although the penalty term in Equation (4) is concave and global minimum points are difficult to obtain, local minimum points can be obtained through iterative algorithms. Ma and Huang [17] and Wang et al. [18] apply the ADMM algorithm to solve the penalized optimization problem by transforming it into a Lagrangian-constrained optimization problem. However, the algorithm is computationally intensive and involves cumbersome steps. In this paper, we develop a novel algorithm based on local quadratic approximation [15] to solve Equation (4). In the next section, we provide a detailed derivation.

2.3. Proposed Algorithm

We propose a local quadratic approximation-based algorithm to solve Equation (7). The local quadratic approximation algorithm was introduced by Fan and Li [15]. Specifically, given a non-zero value $x_0$ as the initial value for the penalty function $P_{\lambda }\left(\right|x\left|\right)$, we can apply a first-order Taylor expansion on $x^2$ as follows,

$$P_{\lambda }\left(\right|x\left|\right)=P_{\lambda }\left({\left(x^2\right)}^{\frac{1}{2}}\right)\approx P_{\lambda }\left(\right|x_0\left|\right)+\frac{P_{\lambda }^{{}^{\prime }}\left(\right|x_0\left|\right)}{2|x_0|}(x^2-x_0^2).$$

(8)

Specifically, let ${\mathit{\beta }}^{(k-1)}$ denote the estimate of $\mathit{\beta }$ obtained after the $(k-1)$th iteration. At the kth iteration, we locally approximate $\rho (·)$, $P_{\lambda }(·)$, and $P_{\gamma }(·)$ around ${\mathit{\beta }}^{(k-1)}$, which yields

$$\begin{array}{cc}\hfill & Q^{\left(k\right)}(\mathit{\beta };\gamma ,\lambda )\hfill \\ & =\sum _{i=1}^N\sum _{t=1}^T\frac{\varphi \left(\right|y_{it}-{\mathit{z}}_{it}^T{\mathit{\beta }}_{it}^{(k-1)}\left|\right)}{2|y_{it}-{\mathit{z}}_{it}^T{\mathit{\beta }}_{it}^{(k-1)}|}{(y_{it}-{\mathit{z}}_{it}^T{\mathit{\beta }}_{it})}^2\hfill \\ & +\sum _{t=1}^T\sum _{i<j}\frac{P_{\lambda }^{{}^{\prime }}\left(\right||{\mathit{\beta }}_{it}^{(k-1)}-{\mathit{\beta }}_{jt}^{(k-1)}\left|\right|)}{2\left|\right|{\mathit{\beta }}_{it}^{(k-1)}-{\mathit{\beta }}_{jt}^{(k-1)}\left|\right|}\left|\right|{\mathit{\beta }}_{it}-{\mathit{\beta }}_{jt}{\left|\right|}^2\hfill \\ & +\sum _{i=1}^N\sum _{t<t^{{}^{\prime }}}\frac{P_{\gamma }^{{}^{\prime }}\left(\right||{\mathit{\beta }}_{it}^{(k-1)}-{\mathit{\beta }}_{i{t}^{{}^{\prime }}}^{(k-1)}\left|\right|)}{2\left|\right|{\mathit{\beta }}_{it}^{(k-1)}-{\mathit{\beta }}_{i{t}^{{}^{\prime }}}^{(k-1)}\left|\right|}\left|\right|{\mathit{\beta }}_{it}-{\mathit{\beta }}_{i{t}^{{}^{\prime }}}{\left|\right|}^2\hfill \\ & +C,\hfill \end{array}$$

(9)

where $\varphi (·)$, $P_{\lambda }^{{}^{\prime }}(·)$, and $P_{\gamma }^{{}^{\prime }}(·)$ are the derivatives of $\rho (·)$, $P_{\lambda }(·)$, and $P_{\gamma }(·)$, respectively. C depends on ${\mathit{\beta }}^{(k-1)}$ and can be treated as a constant when solving for the kth estimator. By minimizing $Q^{\left(k\right)}(\mathit{\beta };\gamma ,\lambda )$, we obtain ${\mathit{\beta }}^{\left(k\right)}$.

Equation (9) has an explicit solution. To simplify Equation (9), we first define some symbols as follows,

$$\mathit{Y}={(y_{11},\cdots ,y_{1T},\cdots ,y_{N1},\cdots ,y_{NT})}^{\top },$$

$${\mathit{Z}}_{\mathit{i}}=\mathrm{diag}({\mathit{z}}_{i1}^{\top },\cdots ,{\mathit{z}}_{iT}^{\top }),\mathit{Z}=\mathrm{diag}({\mathit{Z}}_1,\cdots ,{\mathit{Z}}_N),$$

$${\Delta }_1=\mathrm{diag}\left\{\sqrt{\varphi \left(\right|\mathit{Y}-\mathit{Z}{\mathit{\beta }}^{(k-1)}\left|\right)/|\mathit{Y}-\mathit{Z}{\mathit{\beta }}^{(k-1)}|}\right\},$$

where the square root symbol $\sqrt{·}$, the function $\varphi (·)$, the division symbol $·/·$, and the absolute value function $|·|$ represent the corresponding operations performed on each element of the vector when they act on vectors.

Let ${\mathit{e}}_i^{\left(c\right)}$ be an N-dimensional vector with 1 in the i-th dimension and 0 in the other dimensions, and let ${\mathit{e}}_t^{\left(r\right)}$ be a T-dimensional vector with 1 in the tth dimension and 0 in the other dimensions. We define

$${\delta }_{i,j}^{\left(c\right)}={\mathrm{I}}_{T\times T}\otimes \left[{({\mathit{e}}_i^{\left(c\right)}-{\mathit{e}}_j^{\left(c\right)})}^{\top }\otimes {\mathrm{I}}_{P\times P}\right],{\delta }_{t,t^{{}^{\prime }}}^{\left(r\right)}={\mathrm{I}}_{N\times N}\otimes \left[{({\mathit{e}}_t^{\left(r\right)}-{\mathit{e}}_{t^{{}^{\prime }}}^{\left(r\right)})}^{\top }\otimes {\mathrm{I}}_{P\times P}\right],$$

where ${\mathrm{I}}_{T\times T}$, ${\mathrm{I}}_{P\times P}$, and ${\mathrm{I}}_{N\times N}$ are identity matrices, and ⊗ represents the Kronecker product. We concatenate ${\delta }_{i,j}^{\left(c\right)}$ for $i<j$ and ${\delta }_{t,t^{{}^{\prime }}}^{\left(r\right)}$ for $t<t^{{}^{\prime }}$ to obtain

$${\delta }_c={({{\delta }_{1,2}^{\left(c\right)}}^{\top },\cdots ,{{\delta }_{N-1,N}^{\left(c\right)}}^{\top })}^{\top },{\delta }_r={({{\delta }_{1,2}^{\left(r\right)}}^{\top },\cdots ,{{\delta }_{T-1,T}^{\left(r\right)}}^{\top })}^{\top }.$$

Let $\mathit{U}={\delta }_c{\mathit{\beta }}^{(k-1)}$ and $\mathit{V}={\delta }_r{\mathit{\beta }}^{(k-1)}$. $\mathit{U}$ and $\mathit{V}$ are both NTP-dimensional vectors that can be expressed as $\mathit{U}={({\mathit{u}}_{11}^{\top },\cdots ,{\mathit{u}}_{NT}^{\top })}^{\top }$ and $\mathit{V}={({\mathit{v}}_{11}^{\top },\cdots ,{\mathit{v}}_{NT}^{\top })}^{\top }$, respectively, where ${\mathit{u}}_{it}$ and ${\mathit{v}}_{it}$ are P-dimensional vectors. Let ${\overline{u}}_{it}$ and ${\overline{v}}_{it}$ be the $L_2$ norms of ${\mathit{u}}_{it}$ and ${\mathit{v}}_{it}$, respectively. Let $\overline{\mathit{U}}={({\overline{u}}_{11},\cdots ,{\overline{u}}_{NT})}^{\top }$, $\overline{\mathit{V}}={({\overline{v}}_{11},\cdots ,{\overline{v}}_{NT})}^{\top }.$

Thus, Equation (9) can be written as

$$Q^{\left(k\right)}(\mathit{\beta };\gamma ,\lambda )=\frac{1}{2}{(\mathit{Y}-\mathit{Z}\mathit{\beta })}^{\top }{\Delta }_{\mathbf{1}}^{\top }{\Delta }_{\mathbf{1}}(\mathit{Y}-\mathit{Z}\mathit{\beta })+\frac{1}{2}{\mathit{\beta }}^{\top }{\Delta }_{\mathbf{2}}^{\top }{\Delta }_{\mathbf{2}}\mathit{\beta }+\frac{1}{2}{\mathit{\beta }}^{\top }{\Delta }_{\mathbf{3}}^{\top }{\Delta }_{\mathbf{3}}\mathit{\beta }+C,$$

(10)

where ${\Delta }_2=\left[{\mathrm{I}}_{P\times P}\otimes \sqrt{P_{\lambda }^{{}^{\prime }}\left(\overline{\mathit{U}}\right)/\overline{\mathit{U}}}\right]{\delta }_c,{\Delta }_3=\left[{\mathrm{I}}_{P\times P}\otimes \sqrt{P_{\gamma }^{{}^{\prime }}\left(\overline{\mathit{V}}\right)/\overline{\mathit{V}}}\right]{\delta }_r$.

By minimizing the above equation, we obtain the iteration formula for the kth step,

$${\mathit{\beta }}^{\left(k\right)}={({\mathit{Z}}^{\top }{\Delta }_{\mathbf{1}}^{\top }{\Delta }_{\mathbf{1}}\mathit{Z}+{\Delta }_{\mathbf{2}}^{\top }{\Delta }_{\mathbf{2}}+{\Delta }_{\mathbf{3}}^{\top }{\Delta }_{\mathbf{3}})}^{-1}{\mathit{Z}}^{\top }{\Delta }_{\mathbf{1}}^{\top }{\Delta }_{\mathbf{1}}\mathit{Y}.$$

(11)

We repeat this iteration process until the norm of the difference between ${\mathit{\beta }}^{\left(k\right)}$ and ${\mathit{\beta }}^{(k-1)}$ is smaller than a given threshold $\delta$ (set to 1e-5 in our experiments), at which point the algorithm terminates. As noted by Hunter and Li [19], this algorithm belongs to the class of MM algorithms, and its convergence is guaranteed.

To perform the iterative process, it is necessary to specify the initial value of the regression coefficients. An appropriate initial value can reduce the number of iterations and computation time. Following the approach of Wang et al. [18], we use ridge regression to obtain the initial values. The specific formula is as follows,

$$\begin{array}{cc}\hfill {\mathit{\beta }}^{\left(0\right)}& =\underset{\mathit{\beta }\in {\mathbb{R}}^{NTP}}{argmin}\{\sum _{i=1}^N\sum _{t=1}^{\top }{(y_{it}-{\mathit{z}}_{it}^{\top }{\mathit{\beta }}_{it})}^2+{\lambda }^{\ast }\sum _{t=1}^{\top }\sum _{i<j}\left|\right|{\mathit{\beta }}_{it}-{\mathit{\beta }}_{jt}{\left|\right|}^2\hfill \\ & +{\gamma }^{\ast }\sum _{i=1}^N\sum _{t<t^{{}^{\prime }}}\left|\right|{\mathit{\beta }}_{it}-{\mathit{\beta }}_{i{t}^{{}^{\prime }}}{\left|\right|}^2\}\hfill \\ \hfill & =\underset{\mathit{\beta }\in {\mathbb{R}}^{NTP}}{argmin}\left\{\left|\right|\mathit{Y}-{\mathit{Z}\mathit{\beta }\left|\right|}^2+{\lambda }^{\ast }\left|\right|{\delta }_{\mathit{c}}{\mathit{\beta }\left|\right|}^2+{\gamma }^{\ast }\left|\right|{\delta }_{\mathit{r}}\mathit{\beta }{\left|\right|}^2\right\}\hfill \\ \hfill & ={({\mathit{Z}}^{\top }\mathit{Z}+{\lambda }^{\ast }{\delta }_{\mathit{c}}^{\top }{\delta }_{\mathit{c}}+{\gamma }^{\ast }{\delta }_{\mathit{r}}^{\top }{\delta }_{\mathit{r}})}^{-1}{\mathit{X}}^{\top }\mathit{Y}.\hfill \end{array}$$

(12)

Here, ${\lambda }^{}$ and ${\gamma }^{}$ are tuning parameters, which are set to 1e-3 in all subsequent experiments.

To select the optimal tuning parameters in the objective function, we use the modified Bayesian information criterion (mBIC) [20], which has been widely utilized for hyperparameter selection in the field of heterogeneous structure recovery [8,10,21,22]. Notably, Cheng et al. [10] have demonstrate the selection consistency of mBIC within the context of subgroup identification tasks under the framework of M-estimation. In this paper, we denote the mBIC as follows,

$$\mathrm{mBIC}(\lambda ,\gamma )=log\left(\frac{1}{NT}\sum _{i=1}^N\sum _{t=1}^T\rho (y_{it}-{\mathit{z}}_{\mathit{it}}^{\top }{\widehat{\mathit{\beta }}}_{\mathit{i}\mathit{t}})\right)+c\frac{loglog\left(NT\right)}{NT}log\left(NTP\right)\widehat{L(\lambda ,\gamma )}P,$$

(13)

where $\widehat{L(\lambda ,\gamma )}$ is an estimate of the number of sub-blocks, and c is a constant. In this paper, when $\rho$ is the $L_2$ loss, we follow the setting of Ma and Huang [17] and set $c=10$; when $\rho$ is the $L_1$ loss, we follow the setting of Zhang et al. [8] and set $c=5$; when $\rho$ is Huber, we also set $c=5$. To search for the optimal values of the parameters $\lambda$, $\gamma$, and the controlling parameter a in the penalty functions, we use grid search to traverse the ranges of $[{\lambda }_{min},{\lambda }_{max}]$, $[{\gamma }_{min},{\gamma }_{max}]$, and $[a_{min},a_{max}]$, respectively, with a given step size. We calculate the mBIC value for each combination of $\lambda$, $\gamma$, and a. The combination that results in the minimum mBIC is selected as the optimal tuning parameters, which are then used to obtain the final estimation result.

2.4. Asymptotic Properties

We first investigate the property of oracle estimator. If the underlying block structure $\mathcal{B}=\{{\mathcal{B}}_l:l=1,...,L^0\}$ is known, the oracle estimator is defined by

$$\tilde{\mathit{\alpha }}=\underset{\mathit{\alpha }\in {\mathbb{R}}^{P{L}^0}}{argmin}\left\{\sum _{l=1}^L\sum _{(i,t)\in {\mathcal{B}}_l}\rho (y_{it}-z_{it}^T{\alpha }_l)\right\},$$

(14)

where $\tilde{\mathit{\alpha }}={({\tilde{\alpha }}_1^T,...,{\tilde{\alpha }}_L^T)}^T$. The oracle estimator is unavailable in practice because it assumes the knowledge of the real block structure, but it plays a significant role in theoretical analysis.

First, we define some notations. Let $z_{it,p}$ denote the pth element of ${\mathit{z}}_{it}$. ${\lambda }_{min}(·)$ and ${\lambda }_{max}(·)$ denote the minimum and maximum eigenvalues of a matrix, respectively. Let $\varphi$ denote the derivative of $\rho$, ${\varphi }^{{}^{\prime }}$ and ${\varphi }^{{}^{\prime }{}^{\prime }}$ denote the first and second derivatives of $\varphi$, respectively, and $f^{{}^{\prime }}$ denotes the first derivative of the distribution function f of ${ϵ}_{it}$. ${\mathrm{S}}_P=\{d\in {\mathcal{R}}^P{:\left|\right|d\left|\right|}^2=1\}$ denotes the unit sphere in ${\mathcal{R}}^P$.

Since $\rho$ may have nondifferentiable points, its derivative $\varphi$ may have discontinuities. Therefore, we need to classify and discuss $\varphi$ according to its properties. Following the method of He and Shao [23], we classify $\varphi$ into two categories: smooth function and jump function. When $\varphi$ is Lipschitz continuous on its domain, we call it a smooth function; when $\varphi$ has a finite number of jump points but is Lipschitz continuous on the intervals between two adjacent jump points, we call it a jump function. It is clear that $L_2$ loss and Huber loss are smooth functions, while $L_1$ loss is a jump function.

We introduce the following assumptions.

(A1). There exists a constant $M_1$ such that

$$|x_{it,p}|\le M_1,\forall 1\le i\le N,1\le t\le T,1\le p\le P,$$

and there exist two positive constants $C_1$ and $C_2$ such that

$$C_1\le {\lambda }_{min}\left(\frac{1}{NT}{\mathit{Z}}^{\top }\mathit{Z}\right)\le {\lambda }_{max}\left(\frac{1}{NT}{\mathit{Z}}^{\top }\mathit{Z}\right)\le C_2.$$

(A2). $L^{0}P=O\left({\left(NT\right)}^{c_1}\right)$, for some $0<c_1<\frac{1}{3}$

(A3). When the loss function is a smooth function, ${\varphi }^{{}^{\prime }}$ and ${\varphi }^{″}$ are bounded by $c_0=\mathrm{E}{\varphi }^{{}^{\prime }}\left({ϵ}_{it}\right)\in (0,\infty )$; when the loss function is a jump function, $\varphi$, f, and $f^{{}^{\prime }}$ are bounded by $c_0=-{\int }_{-\infty }^{\infty }\varphi \left(r\right)f^{{}^{\prime }}\left(r\right)dr\in (0,\infty )$.

(A4). ${sup}_{{\mathit{d}}_1,{\mathit{d}}_2\in {\mathrm{S}}_p}{\displaystyle \sum _{i=1}^N\sum _{t=1}^{\top }}|{\mathit{z}}_{it}^{\top }{\mathit{d}}_1{|}^2{\left|{\mathit{z}}_{it}^{\top }{\mathit{d}}_2\right|}^2=O\left(NT\right).$

Remark 1.

Assumption (A1) is a regularization assumption on the design matrix, where the minimum and maximum eigenvalues of ${\left(NT\right)}^{-1}{\mathit{Z}}^{\top }\mathit{Z}$ are bounded by constants, which is a common assumption in heterogeneity panel data analysis based on concave fused penalties; see Ma and Huang [17], Ma et al. [22], Wang and Zhu [3], etc. Assumption (A2) allows the real coefficients dimension $L^{0}P$ to increase with the sample size $NT$ but at a slower rate. Assumption (A3) provides bounds on the loss function and error term distribution for different types of ϕ. This assumption is used by He and Shao [23] to prove the asymptotic normality of the M-estimator in linear regression models. For commonly used loss functions in the M-estimation field (such as $L_1$, $L_2$, and Huber) and commonly used error term distributions (such as normal and t-distributions), it is easy to prove that assumption (A3) is satisfied. Assumption (A4) further imposes restrictions on the design matrix, where if $z_{it}$ is a random sample from a P-variate distribution and for any $d\in {\mathrm{S}}_P$, $E\left(\right|d^{\top }{\mathit{z}}_{it}{|}^4)$ that is uniformly bounded, then assumption (A4) holds, obviously.

Under these assumptions, we can obtain the consistency properties of the oracle estimator.

Theorem 1.

Under assumptions (A1)–(A4), we have

$$\left|\right|\tilde{\mathit{\alpha }}-{\mathit{\alpha }}^0\left|\right|=O_p\left(\sqrt{\frac{L^{0}P}{NT}}\right),\left|\right|\tilde{\mathit{\beta }}-{\mathit{\beta }}^0\left|\right|=O_p\left(\sqrt{\frac{L^{0}P\left|{\mathcal{B}}_{max}\right|}{NT}}\right),$$

$$\underset{i,t}{sup}\left|\right|{\tilde{\mathit{\beta }}}_{it}-{\mathit{\beta }}_{it}^0\left|\right|=O_p\left(\sqrt{\frac{L^{0}P}{NT}}\right).$$

We can also provide the asymptotic normal theory for the oracle estimator (Proof of Theorem 1 in Appendix A.1).

Theorem 2.

Under assumptions (A1)–(A4), we have

$$NT{\mathit{d}}^T(\tilde{\mathit{\alpha }}-{\mathit{\alpha }}^0)/\sigma \left(\mathit{d}\right)\to N(0,1),$$

where ${\sigma }^2\left(\mathit{d}\right)={\left(c_{0}E{\varphi }^2\left({ϵ}_{it}\right)\right)}^{-1}{\mathit{d}}^{\top }\left({\mathit{Z}}^{\top }\mathit{Z}\right)\mathit{d}$, and d is a $PL\times 1$ vector such that $\left|\right|\mathit{d}\left|\right|=1$ (Proof of Theorem 2 in Appendix A.2).

Let b denote the minimum difference between coefficients of any two sub-blocks, i.e., $b=\underset{l\ne l^{{}^{\prime }}}{min}\left|\right|{\mathit{\alpha }}_l^0-{\mathit{\alpha }}_{l^{{}^{\prime }}}^0\left|\right|$. Let $|{\mathcal{B}}_{min}|$ denote the sample size of the smallest sub-block. Let $p_{\lambda }\left(s\right)={\lambda }^{-1}{P}_{\lambda }\left(s\right)$ and $p_{\gamma }\left(s\right)={\gamma }^{-1}{P}_{\gamma }\left(s\right)$ denote the standardized penalty functions, where $p_{\lambda }^{{}^{\prime }}\left(s\right)$ and $p_{\gamma }^{{}^{\prime }}\left(s\right)$ are their derivatives. To derive the asymptotic properties of our proposed estimator, additional assumptions are required.

(A5). For any $c_1<c_2\le 1$, there exists ${\mathrm{M}}_2>0$ such that

$${\left(NT\right)}^{(1-c_2)/2}b\ge M_2,$$

where $c_1$ is defined in Assumption (A2).

(A6). There exist two positive constants $c_3$ and $c_4$ such that for any ${ϵ}_{it}$ and $c\in [-c_3,c_3]$, we have

$$\mathbb{P}\left(\right|\varphi ({ϵ}_{it}+c)|>x)\le 2exp(-c_4{x}^2).$$

(A7). The normalized penalty functions $p_{\lambda }\left(s\right)$ and $p_{\gamma }\left(s\right)$ are symmetric non-decreasing functions that are convex on $[0,\infty )$. We have $p_{\lambda }\left(0\right)=p_{\gamma }\left(0\right)=0$. There exist positive numbers $a>0$ and $a^{{}^{\prime }}>0$ such that $p_{\lambda }\left(s\right)$ and $p_{\gamma }\left(s^{{}^{\prime }}\right)$ are constant when $s\ge a\lambda$ and $s^{{}^{\prime }}\ge a^{{}^{\prime }}\gamma$, respectively. The derivatives $p_{\lambda }^{{}^{\prime }}\left(s\right)$ and $p_{\gamma }^{{}^{\prime }}\left(s\right)$ are continuous except at a finite number of points, and $p_{\lambda }^{{}^{\prime }}(0+)=p_{\gamma }^{{}^{\prime }}(0+)=1.$

Remark 2.

Assumption (A5) provides the minimum difference in regression coefficients between different sub-blocks, which is essential for the separability of the coefficients. Assumption (A6) further restricts the error term, which is relatively mild for M-estimators. Specifically, when ρ is the $L_2$ loss, $\varphi \left({ϵ}_{it}\right)=2{ϵ}_{it}$, and assumption (A6) is equivalent to requiring that the error term ${ϵ}_{it}$ has sub-Gaussian tails, which is a common assumption in the field of high-dimensional statistics. When ρ is the $L_1$ or Huber loss, assumption (A6) obviously holds because ϕ is bounded by a constant. Assumption (A7) restricts concave penalty functions, which can be easily verified to be satisfied by SCAD and MCP, where positive a and $a^{\prime }$ control the concavity of the penalty function. It should be noted that when $s\ge a\lambda$, $p_{\lambda }^{{}^{\prime }}\left(s\right)$ is constant. This means that when $(i,t)$ and $(j,t^{\prime })$ belong to different sub-blocks, the fused penalty term $p_{\lambda }\left(\right||{\mathit{\beta }}_{it}-{\mathit{\beta }}_{j{t}^{\prime }}\left|\right|)$ tends to be constant; i.e., it does not compress the coefficient differences of different sub-blocks.

Theorem 3.

Under assumptions (A1)–(A7) and $max(\lambda ,\gamma )=o\left({\left(NT\right)}^{-(1-c_2)/2}\right)$, $\frac{\sqrt{P}\sqrt{log\left(NT\right)}}{min(\lambda ,\gamma \left)\right|{\mathcal{B}}_{min}|}=o\left(1\right)$, the oracle estimator is a local minimizer of the objective function with probability tending to one, i.e., as both N and T $\to \infty$, we have

$$\underset{N,T\to \infty }{lim}\mathbb{P}(\widehat{\mathit{\beta }}=\tilde{\mathit{\beta }})\to 1.$$

Under the conditions of Theorems 2 and 3, we can obtain the following corollary (Proof of Theorem 3 in Appendix A.3).

Corollary 1.

$$NT{\mathit{d}}^T(\widehat{\mathit{\alpha }}-{\mathit{\alpha }}^0)/\sigma \left(\mathit{d}\right)\to N(0,1),$$

where ${\sigma }^2\left(\mathit{d}\right)={\left(c_{0}E{\varphi }^2\left({ϵ}_{it}\right)\right)}^{-1}{\mathit{d}}^{\top }\left({\mathit{Z}}^{\top }\mathit{Z}\right)\mathit{d}$, and d is a $PL\times 1$ vector such that $\left|\right|\mathit{d}\left|\right|=1$.

In practice, the distribution of ${ϵ}_{it}$ is unknown, and the estimate of $\mathrm{E}{\varphi }^2\left({ϵ}_{it}\right)$ can be taken as

$$\widehat{\mathrm{E}{\varphi }^2\left({ϵ}_{it}\right)}={(NT-\widehat{L}P)}^{-1}\sum _{i=1}^N\sum _{t=1}^{\top }{\left[\varphi (y_{it}-{\mathit{z}}_{it}^{\top }{\widehat{\mathit{\beta }}}_{it})\right]}^2.$$

When $\varphi (·)$ is a smooth function, the estimate of $c_0$ is denoted as

$${\widehat{c}}_0={\left(NT\right)}^{-1}\sum _{i=1}^N\sum _{t=1}^{\top }{\varphi }^{{}^{\prime }}(y_{it}-{\mathit{z}}_{it}^{\top }{\widehat{\mathit{\beta }}}_{it}).$$

3. Simulation

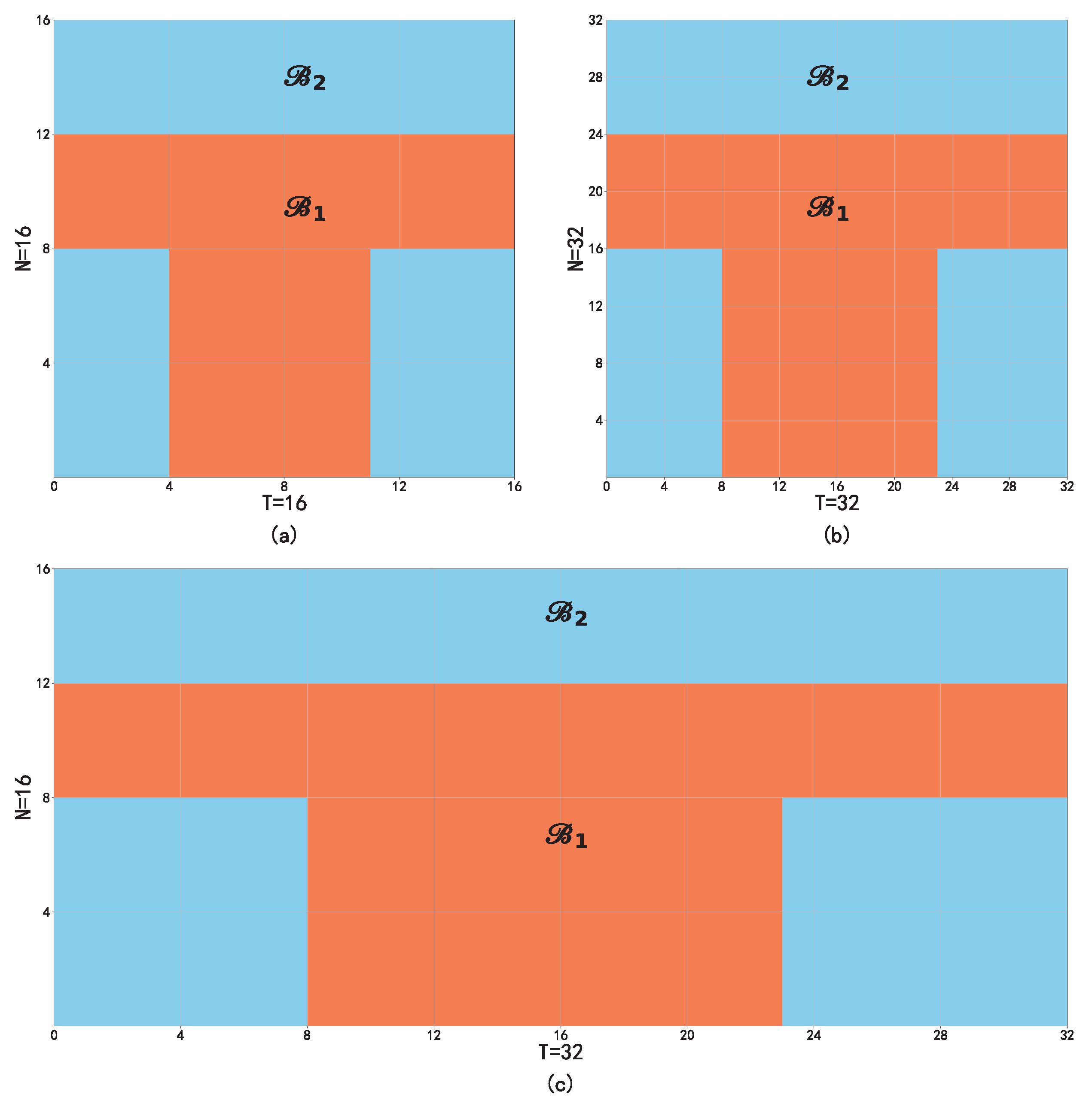
3.1. Simulation Setting

This section presents two artificially constructed examples to investigate the finite-sample performance of the proposed estimator. The simulated data are independently generated from the following model,

$$y_{it}={\mu }_{it}+{\mathit{x}}_{it}^T{\mathit{\eta }}_{it}+{ϵ}_{it},i=1,...,N;t=1,...,T,$$

We consider different combinations of the number of individuals N, the time range T, and the dimension of the regression coefficients P. For each combination of $(N,T)$, we change the distribution of ${ϵ}_{it}$ from normal to heavy-tailed and compared the estimation results under different loss functions, including L1, Huber, and L2 loss.

We use the MCP penalty function in the experiment, as SCAD yields similar results and is therefore not presented. The maximum number of iterations is set to 50, and the threshold $\delta$ is set to ${10}^{-5}$. The algorithm terminates when the number of iterations exceeds 50 or the update range of coefficients is less than ${10}^{-5}$. Each group of experiments is repeated $\mathcal{R}=100$ times. In each experiment, we perform a grid search to select the optimal tuning parameters $\lambda$, $\gamma$, and a by comparing the mBIC values. The range of $\lambda$ and $\gamma$ is $[0.1,1.5]$ with a step size of 0.2, and the range of a is $[2,10]$ with a step size of 2. We utilize the following metrics to assess the systematic error of the regression coefficient estimation and the precision of the block structure recovery.

• RMSE: root mean square error between the estimated parameter $\widehat{\mathit{\beta }}$ and the real parameter ${\mathit{\beta }}^0$.

  $$\frac{1}{\mathcal{R}}\sum _{r=1}^{\mathcal{R}}\sqrt{\frac{1}{NTP}\left|\right|{\widehat{\mathit{\beta }}}^r-{\mathit{\beta }}^0{\left|\right|}^2}$$
• Bias: bias between the estimated parameter $\widehat{\mathit{\beta }}$ and the real parameter ${\mathit{\beta }}^0$.

  $$\frac{1}{\mathcal{R}}\sum _{r=1}^{\mathcal{R}}\left[\frac{1}{NTP}\sum _{i=1}^N\sum _{t=1}^T\sum _{p=1}^P|{\widehat{\mathit{\beta }}}_{it,p}^r-{\mathit{\beta }}_{it,p}^0|\right]$$
• Per: the percentage that the estimated number of blocks and the real number of blocks are equal.

  $$\frac{1}{\mathcal{R}}\sum _{r=1}^{\mathcal{R}}\mathrm{I}({\widehat{L}}^r=L^0)$$
• ERI: The Rand Index (RI) is used to evaluate the accuracy of clustering, which ranges between 0 and 1, with higher values indicating better performance. Motivated by the formation of $RI$, we can calculate individual or period-specific $RI$s, denoted as $R{I}_t$ or $R{I}_i$, respectively. We define $ERI$ as the averages over all periods and individuals, as follows,

  $$ERI=\frac{1}{2}\left[\frac{1}{T}\sum _{t=1}^{T}R{I}_t+\frac{1}{N}\sum _{i=1}^{N}R{I}_i\right]$$

3.2. Simulation Examples

Example 1.

In this example, we generate simulated data from the following model,

$$y_{it}={\mu }_{it}+x_{it}{\eta }_{it}+{ϵ}_{it},i=1,\cdots ,N;t=1,\cdots ,T,$$

where $x_{it}=2\times e_{it}$ and $e_{it}$ are independent and identically distributed standard normal random variables. The intercept term ${\mu }_{it}$ and slope coefficients ${\eta }_{it}$ have dimension 1 and exhibit the same block structure. As shown in Figure 1, we construct three sets of panel data by varying the combinations of N and T. Each set of data can be partitioned into two sub-blocks ${\mathcal{B}}_1$ and ${\mathcal{B}}_2$, corresponding to coefficients ${\mathit{\beta }}_1=(2,3)$ and ${\mathit{\beta }}_2=(2,5)$, respectively.

Figure 1. Block structures corresponding to different combinations of N and T in Example 1. The orange regions correspond to block 1, and the blue regions correspond to block 2. (a) shows the block structure for $N=T=16$. (b) shows the block structure for $N=T=32$. (c) shows the block structure for $N=16$ and $T=32$.

To verify the robustness of the proposed method, we consider three scenarios for generating ${ϵ}_{it}$. Scenario 1 (normal distribution): ${ϵ}_{it}\sim \mathcal{N}(0,1)$. Scenario 2 (heavy-tailed distribution): ${ϵ}_{it}\sim 0.5\times t\left(3\right)$, where $t\left(3\right)$ denotes the Student’s t-distribution with 3 degrees of freedom. Scenario 3 (mixture distribution): ${ϵ}_{it}\sim 0.3\times \mathcal{N}(0,0.5^2)+0.2\times \mathcal{N}(0,5^2)$.

We obtain nine groups of panel data by varying the combinations of $(N,T)$ and the distribution of ${ϵ}_{it}$. For each group of data, we compare the performance of the oracle estimator, the $L_1$-loss-based estimator, the $L_2$-loss-based estimator, and the Huber-loss-based estimator. The oracle estimator is the estimator when the block structure is known, and for convenience, we use the $L_2$ loss as its loss function, so the oracle estimator has an explicit solution. The estimators under an unknown block structure are influenced by the tuning parameters $\lambda$, $\gamma$, and a. We use a grid search method to obtain the optimal hyperparameter combination following the setting in Section 2.3. Additionally, there is an extra parameter $\delta$ in the Huber loss function to control the shape of the loss function, and we use the default value of 1.345.

Example 2.

In this example, we adopt the block partitioning method under different combinations of $(N,T)$ as in Example 1 with the difference being an increase in the dimension of the regression coefficients from 2 to 4. The model is specified as follows,

$$y_{it}={\mu }_{it}+x_{i1}{\eta }_{it,1}+x_{i2}{\eta }_{it,2}+x_{i3}{\eta }_{it,3}+{ϵ}_{it},i=1,\cdots ,N;t=1,\cdots ,T,$$

where the real coefficients of the first block are ${\mathit{\beta }}_1=(2,3,-2,1)$, and those of the second block are ${\mathit{\beta }}_2=(-2,1,3,-1)$. The explanatory variables $(x_{i1},x_{i2},x_{i3})$ are generated from a multivariate normal distribution with mean $(0,0,0)$ and covariance matrix

$$\left(\begin{array}{ccc}1& 0.5& 0.25\\ 0.5& 1& 0.5\\ 0.25& 0.5& 1\end{array}\right)$$

The error term ${ϵ}_{it}$ is generated according to the same mixture distribution as in Example 1. We obtain three sets of panel data for different combinations of N and T.

For each set of data, we compute the oracle estimator and the estimator for the unknown block structure following the same procedure as in Example 1. Then, we analyze various result indicators to investigate the performance of the proposed method as the dimension of the regression coefficients increases.

Example 3.

To evaluate the effectiveness of a dual-penalty in handling two-dimensional heterogeneous panel data, we conduct an ablation experiment by removing either the individual dimension penalty or the time dimension penalty from the objective function (4) and comparing the results with the full objective function that includes both penalties.

We use a set of simulated data from Example 1, where the data have a dimension of $N=T=32$, the error term follows a standard normal distribution, and the loss term in the objective function is the $L_2$ loss.

3.3. Simulation Results

Table 1, Table 2 and Table 3 display the simulation results for Example 1, corresponding to three different distributions of the error term. In each table, we consider three combinations of $(N,T)$, reporting the results of the oracle estimator when the block structure is known, and the results based on three different loss functions when the block structure is unknown. The objective function for obtaining the oracle estimator is set to use the $L_2$ loss. Since obtaining the oracle estimator is difficult in practice, we use it only for comparison. We report the mean and standard deviation of 100 repeated experiments, with the standard deviation displayed in parentheses.

Table 1. Experimental Indicators of Each Combination When the Error Term is Normally Distributed in Example 1.

(N, T)	Model	Rmse	Bias	Per	ERI
(16, 16)	Oracle	0.034 (0.025)	0.056 (0.021)
	$L_1$	0.040 (0.031)	0.087 (0.041)	0.99	0.998 (0.002)
	$L_2$	0.039 (0.026)	0.073 (0.030)	1	0.999 (0.001)
	Huber	0.039 (0.026)	0.075 (0.031)	1	0.998 (0.001)
(16, 32)	Oracle	0.020 (0.015)	0.039 (0.014)
	$L_1$	0.024 (0.020)	0.068 (0.034)	1	0.999 (0.001)
	$L_2$	0.021 (0.016)	0.040 (0.020)	1	0.999 (0.001)
	Huber	0.022 (0.016)	0.041 (0.018)	1	0.998 (0.001)
(32, 32)	Oracle	0.015 (0.012)	0.028 (0.011)
	$L_1$	0.016 (0.014)	0.035 (0.021)	1	0.998 (0.001)
	$L_2$	0.016 (0.011)	0.028 (0.012)	1	0.999 (0.001)
	Huber	0.016 (0.010)	0.028 (0.012)	1	0.999 (0.001)

Table 2. Experimental Indicators of Each Combination When the Error Term is t-Distributed in Example 1.

(N, T)	Model	Rmse	Bias	Per	ERI
(16, 16)	Oracle	0.024 (0.020)	0.046 (0.022)
	$L_1$	0.023 (0.018)	0.058 (0.032)	0.98	0.998 (0.001)
	$L_2$	0.026 (0.021)	0.063 (0.039)	0.89	0.983 (0.011)
	Huber	0.024 (0.019)	0.060 (0.035)	0.99	0.998 (0.001)
(16, 32)	Oracle	0.016 (0.013)	0.030 (0.011)
	$L_1$	0.017 (0.013)	0.041 (0.019)	1	0.999 (0.001)
	$L_2$	0.023 (0.018)	0.054 (0.033)	0.91	0.987 (0.006)
	Huber	0.018 (0.014)	0.043 (0.028)	1	0.998 (0.002)
(32, 32)	Oracle	0.012 (0.009)	0.021 (0.009)
	$L_1$	0.012 (0.009)	0.032 (0.012)	1	0.999 (0.001)
	$L_2$	0.015 (0.012)	0.037 (0.023)	0.94	0.993 (0.004)
	Huber	0.012 (0.010)	0.033 (0.022)	1	0.999 (0.001)

Table 3. Experimental Indicators of Each Combination When the Error Term Follows a Mixture Distribution in Example 1.

(N, T)	Model	Rmse	Bias	Per	ERI
(16, 16)	Oracle	0.044 (0.037)	0.084 (0.038)
	$L_1$	0.054 (0.038)	0.122 (0.056)	0.79	0.986 (0.012)
	$L_2$	0.081 (0.066)	0.162 (0.098)	0.42	0.943 (0.037)
	Huber	0.057 (0.065)	0.151 (0.117)	0.74	0.980 (0.011)
(16, 32)	Oracle	0.034 (0.025)	0.062 (0.025)
	$L_1$	0.049 (0.034)	0.112 (0.530)	0.81	0.986 (0.010)
	$L_2$	0.088 (0.075)	0.207 (0.129)	0.49	0.953 (0.028)
	Huber	0.051 (0.040)	0.118 (0.073)	0.76	0.984 (0.010)
(32, 32)	Oracle	0.023 (0.017)	0.044 (0.017)
	$L_1$	0.032 (0.024)	0.086 (0.066)	0.89	0.989 (0.005)
	$L_2$	0.061 (0.073)	0.149 (0.106)	0.62	0.971 (0.021)
	Huber	0.044 (0.046)	0.093 (0.068)	0.83	0.987 (0.007)

In Table 1, the error terms follow the standard normal distribution. Simulations based on $L_1$ loss and Huber loss perform similarly to those based on $L_2$ loss. In terms of coefficient estimation, when $N=T=16$, the $L_2$ loss slightly outperforms $L_1$ and Huber losses, but as N and T increase, the differences among the three simulation results diminish, and they all approach the oracle estimator. In terms of structural recovery, the Per metric equals 1 in the second and third combinations of $(N,T)$, indicating that the estimated number of blocks equals the actual number of blocks. The ERI metric approaches 1, indicating that the method accurately classifies the samples into the correct sub-blocks.

In Table 2, the error terms follow a heavy-tailed t distribution. It is evident that the results based on $L_1$ loss and Huber loss outperform those based on $L_2$ loss. When $N=T=16$, we even observe that the RMSE metric based on $L_1$ loss is slightly lower than the oracle estimator based on $L_2$ loss. This is because the heavy-tailed distribution increases the probability of outliers in the simulated data, and $L_2$ loss is more sensitive to outliers than $L_1$ loss. As N and T increase, the results based on $L_1$ and Huber losses approach the oracle estimator, and the RMSE and Bias metrics for coefficient estimation become increasingly closer to those of the oracle estimator. The Per and ERI metrics reach or approach 1, indicating that the method accurately recovers the block structure.

In Table 3, the error terms follow a mixture of normal distributions with a stronger heavy-tailed effect. The simulation results are worse than those of the previous two cases, but those based on $L_1$ loss and Huber loss are still better than those based on $L_2$ loss. As N and T increase, the Per and ERI metrics gradually approach 1. This simulation experiment also confirms the robustness and block structure recovery ability of the proposed estimator.

Below, we analyze the performance of the proposed estimator as the dimension of the coefficient P increases. In Table 4, the error term follows a heavy-tailed mixture normal distribution. Increasing P makes coefficient estimation and block structure recovery more challenging, but the performance metrics corresponding to $L_1$ loss and Huber loss remain superior to those of $L_2$ loss. As N and T increase, all performance metrics of the estimator improve significantly, and the $Per$ metric corresponding to $L_1$ loss approaches 0.9 when $N=T=32$.

Table 4. Experimental Indicators of Each Combination When the Error Term Follows a Mixture Distribution and P = 4 in Example 2.

(N, T)	Model	Rmse	Bias	Per	ERI
(16, 16)	Oracle	0.044 (0.037)	0.084 (0.038)
	L1	0.054 (0.038)	0.122 (0.056)	0.79	0.986 (0.012)
	L2	0.073 (0.062)	0.157 (0.093)	0.42	0.943 (0.037)
	Huber	0.057 (0.045)	0.151 (0.087)	0.74	0.980 (0.011)
(16, 32)	Oracle	0.034 (0.025)	0.062 (0.025)
	L1	0.049 (0.034)	0.112 (0.053)	0.81	0.986 (0.010)
	L2	0.070 (0.063)	0.154 (0.091)	0.49	0.953 (0.028)
	Huber	0.051 (0.040)	0.118 (0.073)	0.76	0.984 (0.010)
(32, 32)	Oracle	0.023 (0.017)	0.044 (0.017)
	L1	0.032 (0.024)	0.086 (0.066)	0.89	0.989 (0.005)
	L2	0.061 (0.073)	0.149 (0.106)	0.62	0.971 (0.002)
	Huber	0.044 (0.036)	0.093 (0.068)	0.83	0.987 (0.007)

Finally, we present the results of the ablation experiment with fused penalty terms. Since the simulated data have a block structure, setting penalty terms only in one dimension cannot effectively compress the coefficient differences in the other dimension and thus cannot recover the block structure. Hence, we report only the results of the RMSE and Bias metrics in Table 5. The performance of the double-penalty method exceed those of any single-dimensional penalty method by a large margin, indicating the necessity of biclustering analysis for block panel data. The double-penalty method not only recovers unknown structures but also greatly reduces the estimation error of the coefficients.

Table 5. Ablation Experiment of Penalty Terms in Example 3.

Model	RMSE	Bias
Oracle	0.015 (0.012)	0.028 (0.011)
Double Penalties	0.016 (0.011)	0.028 (0.012)
Individual Penalty Only	0.155 (0.119)	0.799 (0.342)
Temporal Penalty Only	0.226 (0.130)	0.440 (0.154)

4. Discussion

Panel data models with heterogeneous coefficients have gained a lot of attention in various fields due to their ability to capture complex data patterns. In this paper, we extend the existing literature by proposing a more general block structure that captures heterogeneity in individual and time dimensions in a flexible manner. Our proposed model exhibits both an individual-group structure that can change at change points and temporal–structural breaks that can vary across different groups. A robust biclustering method based on M-estimation and double concave fused penalties is developed to estimate the coefficients, which can handle heavy-tailed data and outliers. Under certain regularity conditions, we established the asymptotic normality of the oracle estimator and the proposed estimator. Numerical simulations have validated the excellent finite-sample performance of our proposed method by evaluating the recovery of unknown structures as well as the estimated bias of regression coefficients. Furthermore, in our numerical simulations, we specifically investigate the performance of our proposed model in the presence of heavy-tailed distributions, which highlights the superior performance of our proposed method in handling outliers. We believe that our method has potential applications in various fields where data exhibit complex heterogeneity.

Despite the progress made, there are still some limitations and further research topics that warrant further exploration. First among these is the lack of convergence proof for the Bayesian information criterion. To achieve this, more regularization assumptions would be required for the distribution of covariates and error terms. For relevant work in this area, researchers can consider the methodology proposed by Cheng et al. [10] for clustering individual group structures. A second challenge arises from the high-dimensional matrix calculations involved in the algorithm for solving the objective function. The computational requirements increase exponentially with N and T. To address this issue, the divide-and-conquer method can be used for parallel computation to improve the algorithm’s efficiency. Finally, variable selection through L1 penalty on covariates is another promising area for further research, particularly in situations with high-dimensional covariate dimensions P. These areas of investigation will be the topic of future studies.

Appendix A.1. Proof of Theorem 1

Here, we present the proof of Theorem 1. The first conclusion of Theorem 1 follows directly from Example 1 in He and Shao [23].

Since $\left|\right|\tilde{\mathit{\alpha }}-{\mathit{\alpha }}^0\left|\right|=O_p\left(\sqrt{\frac{L^{0}P}{NT}}\right)$, there exists a positive constant C such that $\left|\right|\tilde{\mathit{\alpha }}-{\mathit{\alpha }}^{\mathbf{0}}\left|\right|\le C\sqrt{\frac{L^{0}P}{NT}}$. Using the relationship between $\tilde{\mathit{\alpha }}$ and $\tilde{\mathit{\beta }}$, we have

$$\begin{array}{cc}\hfill \left|\right|\tilde{\mathit{\beta }}-{\mathit{\beta }}^0{\left|\right|}^2& =\sum _{l=1}^{L^0}\sum _{(i,t)\in {\mathcal{B}}_l}\left|\right|{\tilde{\mathit{\alpha }}}_l-{\mathit{\alpha }}_{l^0}{\left|\right|}^2\hfill \\ \hfill & \le |{\mathcal{B}}_{max}|\sum _{l=1}^{L^0}\left|\right|{\tilde{\mathit{\alpha }}}_l-{\mathit{\alpha }}_{l^0}{\left|\right|}^2\hfill \\ \hfill & =|{\mathcal{B}}_{max}\left|\right||\tilde{\mathit{\alpha }}-{\mathit{\alpha }}^0{\left|\right|}^2\hfill \\ \hfill & \le \frac{C^2{L}^{0}P\left|{\mathcal{B}}_{max}\right|}{NT}.\hfill \end{array}$$

(A1)

Thus, $\left|\right|\tilde{\mathit{\beta }}-{\mathit{\beta }}^{\mathbf{0}}\left|\right|\le C\sqrt{\frac{L^{0}P\left|{\mathcal{B}}_{max}\right|}{NT}}$.

Finally, applying a simple inequality yields

$$\begin{array}{c}\hfill \underset{i,t}{sup}\left|\right|{\tilde{\mathit{\beta }}}_{it}-{\mathit{\beta }}_{it}^0\left|\right|=\underset{l}{sup}\left|\right|{\tilde{\mathit{\alpha }}}_l-{\mathit{\alpha }}_l^0\left|\right|\le \left|\right|\tilde{\mathit{\alpha }}-{\mathit{\alpha }}^0\left|\right|\le C\sqrt{\frac{L^{0}P}{NT}}.\end{array}$$

(A2)

This completes the proof of Theorem 1.

Appendix A.2. Proof of Theorem 2

By assumption (A2), there exists $0<c_1<\frac{1}{3}$ such that $L^{0}P=O\left({\left(NT\right)}^{c_1}\right)$. Clearly,

$${\left(L^{0}P\right)}^3{(log\left(L^{0}P\right))}^2=o\left(NT\right).$$

(A3)

Therefore, by Example 1 in He and Shao [23], the result of Theorem 2 follows directly.

Appendix A.3. Proof of Theorem 3

We partition the block structure of regression coefficients as follows: we first divide the samples into C groups according to the group structure in the dimension of individuals; then, we partition them into K time periods according to the structural breaks in the time dimension (if there exist structural breaks for any individuals at given time period, we perform segmentation on all individuals instead of splitting individuals under given groups). In this way, we obtain $KC$ sub-blocks, which obviously exceeds the number of true sub-blocks. Let ${\mathcal{B}}_{lc}$ be the set of sample indexes that belong to both the cth individual group and the l-th true sub-block, and let ${\mathcal{B}}_{lk}$ be the set of sample indexes that belong to both the kth time group and the lth true sub-block. Denote

$$L\left(\beta \right)=\sum _{i=1}^N\sum _{t=1}^T\rho (y_{it}-{\mathit{z}}_{it}^T{\mathit{\beta }}_{it}),$$

(A4)

$$P\left(\beta \right)=\sum _{t=1}^T\sum _{i<j}{P}_{\lambda }\left(\right||{\mathit{\beta }}_{it}-{\mathit{\beta }}_{jt}\left|\right|)+\sum _{i=1}^N\sum _{t<t^{{}^{\prime }}}{P}_{\gamma }\left(\right||{\mathit{\beta }}_{it}-{\mathit{\beta }}_{i{t}^{{}^{\prime }}}\left|\right|),$$

(A5)

$$L^{\mathcal{B}}\left(\alpha \right)=\sum _{l=1}^L\sum _{(i,t)\in {\mathcal{B}}_l}\rho (y_{it}-{\mathit{z}}_{it}^{\top }{\mathit{\alpha }}_l),$$

(A6)

$$\begin{array}{cc}\hfill P^{\mathcal{B}}\left(\mathit{\alpha }\right)& =\lambda \sum _{l<l^{{}^{\prime }}}\sum _{c=1}^C\left(\right|{\mathcal{B}}_{lc}\left|\right|{\mathcal{B}}_{l^{{}^{\prime }}c}\left|\right){\rho }_{\lambda }\left(\right||{\mathit{\alpha }}_l-{\mathit{\alpha }}_{l^{{}^{\prime }}}\left|\right|)\hfill \\ & +\gamma \sum _{l<l^{{}^{\prime }}}\sum _{k=1}^K\left(\right|{\mathcal{B}}_{lk}\left|\right|{\mathcal{B}}_{l^{{}^{\prime }}k}\left|\right)){\rho }_{\gamma }\left(\right||{\mathit{\alpha }}_l-{\mathit{\alpha }}_{l^{{}^{\prime }}}\left|\right|),\hfill \end{array}$$

(A7)

where the variable $|{\mathcal{B}}_{lc}|$ denotes the number of samples belonging to both the cth individual group and the lth true sub-block, while $|{\mathcal{B}}_{lk}|$ represents the number of samples belonging to both the kth time group and the lth true sub-block. To simplify the notation without creating confusion, we use $\mathit{Q}\left(\mathit{\beta }\right)$ to refer to the objective function in Equation (4), which is defined as

$$Q\left(\mathit{\beta }\right)=L\left(\mathit{\beta }\right)+P\left(\mathit{\beta }\right),$$

(A8)

and let

$$Q^{\mathcal{B}}\left(\mathit{\alpha }\right)=L^{\mathcal{B}}\left(\mathit{\alpha }\right)+P^{\mathcal{B}}\left(\mathit{\alpha }\right).$$

(A9)

Let ${\mathcal{M}}_{\mathcal{B}}$ denote the set of ${\mathbb{R}}^{NTP}$ coefficients with a block structure. We define a mapping $T:{\mathcal{M}}_{\mathcal{B}}\to {\mathbb{R}}^{LP}$, which maps a block-structured $NTP$-dimensional vector $\beta$ to an $LP$-dimensional vector $\alpha$. Here, $\mathit{\alpha }={({\mathit{\alpha }}_1^{\top },\cdots ,{\mathit{\alpha }}_L^{\top })}^{\top }$ is the concatenation of L P-dimensional vectors, with the lth vector ${\mathit{\alpha }}_l$ representing the coefficients for the lth sub-block. Additionally, we define a mapping $T^{\mathcal{B}}:{\mathbb{R}}^{NTP}\to {\mathbb{R}}^{LP}$, which maps any $NTP$-dimensional vector $\mathit{\beta }$ to an $LP$-dimensional vector $\mathit{\alpha }$ based on the block structure of $\mathcal{B}$ as follows. For any $\mathit{\beta }=\{{\mathit{\beta }}_{11}^{\top },\cdots ,{\mathit{\beta }}_{1T}^{\top },\cdots {\mathit{\beta }}_{N1}^{\top },\cdots ,{\mathit{\beta }}_{NT}^{\top }\}$ and $\mathcal{B}=\{{\mathcal{B}}_1,\cdots {\mathcal{B}}_L\}$, the mapping process is given by

$$T^{\mathcal{B}}\left(\mathit{\beta }\right)=\left\{|{\mathcal{B}}_1{|}^{-1}\sum _{(i,t)\in {\mathcal{B}}_1}{\mathit{\beta }}_{it}^{\top },\cdots ,{\left|{\mathcal{B}}_L\right|}^{-1}\sum _{(i,t)\in {\mathcal{B}}_L}{\mathit{\beta }}_{it}^{\top }\right\}.$$

(A10)

From the properties of the mappings T and $T^{\mathcal{B}}$, it follows that for any $\mathit{\beta }\in {\mathcal{M}}_{\mathcal{B}}$, we have $T\left(\mathit{\beta }\right)=T^{\mathcal{B}}\left(\mathit{\beta }\right)$, $P\left(\mathit{\beta }\right)=P^{\mathcal{B}}\left(T\left(\mathit{\beta }\right)\right)$. Let $\mathit{\alpha }=T\left(\mathit{\beta }\right)$, then $P\left(T^{-1}\left(\mathit{\alpha }\right)\right)=P^{\mathcal{B}}\left(\mathit{\alpha }\right)$. Therefore, we conclude that,

$$Q\left(\mathit{\beta }\right)=Q^{\mathcal{B}}\left(T\left(\mathit{\beta }\right)\right),Q^{\mathcal{B}}\left(\mathit{\alpha }\right)=Q\left(T^{-1}\left(\mathit{\alpha }\right)\right).$$

(A11)

We denote the true regression coefficients as ${\mathit{\beta }}^0$ and ${\mathit{\alpha }}^0$, and the oracle estimators as $\tilde{\mathit{\beta }}$ and $\tilde{\mathit{\alpha }}$. Then, we define the set

$${\Theta }_1=\left\{\mathit{\beta }\in {\mathbb{R}}^{NTP}:\underset{it}{sup}\left|\right|{\mathit{\beta }}_{it}-{\mathit{\beta }}_{it}^0\left|\right|\le \sqrt{\frac{L^{0}P}{NT}}\right\}.$$

(A12)

We now prove Theorem 2 in two steps.

(i) Let $\mathit{\beta }\in {\Theta }_1$, and denote ${\mathit{\beta }}^{\ast }=T^{-1}\left(T^{\mathcal{B}}\left(\mathit{\beta }\right)\right)$. For all ${\mathit{\beta }}^{\ast }\ne \tilde{\mathit{\beta }}$, we have $Q\left({\mathit{\beta }}^{\ast }\right)>Q\left(\tilde{\mathit{\beta }}\right)$ with a probability tending to 1.

(ii) Define the set ${\Theta }_2=\{{\mathit{\beta }}_{it}:\underset{it}{sup}\left|\right|{\mathit{\beta }}_{it}-{\widehat{\mathit{\beta }}}_{it}\left|\right|\le s\}$, where s is a positive sequence. When s is small enough, we have $Q\left(\mathit{\beta }\right)\ge Q\left({\mathit{\beta }}^{\ast }\right)$ with a probability tending to 1 for all $\mathit{\beta }\in {\Theta }_1\cap {\Theta }_2$.

Clearly, if (i) and (ii) are proved, then for any $\mathit{\beta }\in {\Theta }_1\cap {\Theta }_2$, we have $Q\left(\mathit{\beta }\right)>Q\left(\tilde{\mathit{\beta }}\right)$, which means that the oracle estimator $\tilde{\mathit{\beta }}$ is a local minimum of $Q\left(\mathit{\beta }\right)$, and this conclusion holds with probability tending to 1.

The proof for (i) is as follows. Let $\mathit{\alpha }=T^{\mathcal{B}}\left(\mathit{\beta }\right)$; then,

$$\begin{array}{cc}\hfill \underset{l}{sup}{∥{\mathit{\alpha }}_l-{\mathit{\alpha }}_l^0∥}^2& =\underset{l}{sup}{∥{\left|{\mathcal{B}}_l\right|}^{-1}\sum _{(i,t)\in {\mathcal{B}}_l}{\mathit{\beta }}_{it}-{\mathit{\alpha }}_l^0∥}^2\hfill \\ & =\underset{l}{sup}{∥{\left|{\mathcal{B}}_l\right|}^{-1}\sum _{(i,t)\in {\mathcal{B}}_l}\left({\mathit{\beta }}_{it}-{\mathit{\beta }}_{it}^0\right)∥}^2\hfill \\ \hfill & \le \underset{l}{sup}{\left|{\mathcal{B}}_l\right|}^{-1}\sum _{(i,t)\in {\mathcal{B}}_l}{∥{\mathit{\beta }}_{it}-{\mathit{\beta }}_{it}^0∥}^2\hfill \\ \hfill & \le \underset{i,t}{sup}{∥{\mathit{\beta }}_{it}-{\mathit{\beta }}_{it}^0∥}^2\hfill \\ & \le \frac{L^{0}P}{NT},\hfill \end{array}$$

(A13)

therefore, all l and $l^{{}^{\prime }}$, the following inequation holds,

$$\left|\right|{\mathit{\alpha }}_l-{\mathit{\alpha }}_{l^{{}^{\prime }}}\left|\right|\ge \left|\right|{\mathit{\alpha }}_l^0-{\mathit{\alpha }}_{l^{{}^{\prime }}}^0\left|\right|-2\underset{l}{sup}\left|\right|{\mathit{\alpha }}_l-{\mathit{\alpha }}_l^0\left|\right|\ge b-2\sqrt{\frac{L^{0}P}{NT}}.$$

(A14)

Using the inequality from assumption (A5), ${\left(NT\right)}^{(1-c_2)/2}b\ge M_2$, and the condition $max(\lambda ,\gamma )=o\left({\left(NT\right)}^{-(1-c_2)/2}\right)$, we can obtain

$$b-2\sqrt{\frac{L^{0}P}{NT}}>max(a\lambda ,a^{{}^{\prime }}\gamma ),$$

(A15)

Therefore, assumption (A7) implies $P^{\mathcal{B}}\left(\mathit{\alpha }\right)=C$, where C is a constant, and $Q^{\mathcal{B}}\left(\mathit{\alpha }\right)=L^{\mathcal{B}}\left(\mathit{\alpha }\right)+C$. Since $\tilde{\mathit{\alpha }}$ is the global minimum of $L^{\mathcal{B}}\left(\mathit{\alpha }\right)$, it follows that $Q^{\mathcal{B}}\left(\mathit{\alpha }\right)>Q^{\mathcal{B}}\left(\tilde{\mathit{\alpha }}\right)$ for any $\mathit{\alpha }\ne \tilde{\mathit{\alpha }}$. Finally, using (A11), we have $Q^{\mathcal{B}}\left(\alpha \right)=Q\left(T^{-1}\left(\mathit{\alpha }\right)\right)=Q\left({\mathit{\beta }}^{}\right)$ and $Q^{\mathcal{B}}\left(\tilde{\mathit{\alpha }}\right)=Q\left(\tilde{\mathit{\beta }}\right)$, so $Q\left({\mathit{\beta }}^{\ast }\right)>Q\left(\tilde{\mathit{\beta }}\right)$ for any ${\mathit{\beta }}^{}\ne \tilde{\mathit{\beta }}$. This completes the proof of conclusion (i).

Continuing with the proof for result (ii), we define two functions

$$P_1\left(\mathit{\beta }\right)=\sum _{t=1}^{\top }\sum _{i<j}{P}_{\lambda }\left(\right||{\mathit{\beta }}_{it}-{\mathit{\beta }}_{jt}\left|\right|),P_2\left(\mathit{\beta }\right)=\sum _{i=1}^N\sum _{t<t^{{}^{\prime }}}{P}_{\gamma }\left(\right||{\mathit{\beta }}_{it}-{\mathit{\beta }}_{i{t}^{{}^{\prime }}}\left|\right|).$$

(A16)

By Taylor expanding around ${\mathit{\beta }}_{it}$, we can decompose the difference of the objective function into three parts,

$$Q\left(\mathit{\beta }\right)-Q\left({\mathit{\beta }}^{\ast }\right)={\mathsf{\Gamma }}_1+{\mathsf{\Gamma }}_2+{\mathsf{\Gamma }}_3$$

(A17)

where each part takes the following form:

$${\mathsf{\Gamma }}_1=L\left(\mathit{\beta }\right)-L\left({\mathit{\beta }}^{\ast }\right),$$

(A18)

$${\mathsf{\Gamma }}_2=\sum _{t=1}^{\top }\sum _{i=1}^N\frac{\partial P_1\left({\mathit{\beta }}^m\right)}{\partial {\mathit{\beta }}_{it}}({\mathit{\beta }}_{it}-{\mathit{\beta }}_{it}^{\ast }),$$

(A19)

$${\mathsf{\Gamma }}_3=\sum _{i=1}^N\sum _{t=1}^{\top }\frac{\partial P_2\left({\mathit{\beta }}^m\right)}{\partial {\mathit{\beta }}_{it}}({\mathit{\beta }}_{it}-{\mathit{\beta }}_{it}^{\ast }).$$

(A20)

Here, ${\mathit{\beta }}^m=\theta \mathit{\beta }+(1-\theta ){\mathit{\beta }}^{\ast }$, where $\theta$ is a scalar between 0 and 1.

First, let us handle the first part,

$$\begin{array}{cc}\hfill {\mathsf{\Gamma }}_1& =\sum _{i=1}^N\sum _{t=1}^{\top }(\rho (y_{it}-{\mathit{z}}_{it}^{\top }{\mathit{\beta }}_{it})-\rho (y_{it}-{\mathit{z}}_{it}^{\top }{\mathit{\beta }}_{it}^{\ast }))\hfill \\ & =-\sum _{i=1}^N\sum _{t=1}^{\top }\varphi (y_{it}-{\mathit{z}}_{it}^{\top }{\mathit{\beta }}_{it}^m){\mathit{z}}_{it}^{\top }({\mathit{\beta }}_{it}-{\mathit{\beta }}_{it}^{\ast })\hfill \\ & =-\sum _{i=1}^N\sum _{t=1}^{\top }\varphi ({ϵ}_{it}+{\mathit{z}}_{it}^{\top }({\mathit{\beta }}_{it}^0-{\mathit{\beta }}_{it}^m)){\mathit{z}}_{it}^{\top }({\mathit{\beta }}_{it}-{\mathit{\beta }}_{it}^{\ast }).\hfill \end{array}$$

(A21)

By Assumption (A6) and ${\mathit{z}}_{it}^{\top }({\mathit{\beta }}_{it}^0-{\mathit{\beta }}_{it}^m)=o_p\left(1\right)$, we can deduce that,

$$P(\varphi ({ϵ}_{it}+{\mathit{z}}_{it}^{\top }({\mathit{\beta }}_{it}^0-{\mathit{\beta }}_{it}^m))>\sqrt{log\left(NT\right)})\le 2{\left(NT\right)}^{-c_4},$$

(A22)

which implies that as N and T approach infinity, $\varphi ({ϵ}_{it}+{\mathit{z}}_{it}^{\top }({\mathit{\beta }}_{it}^0-{\mathit{\beta }}_{it}^m))\le \sqrt{log\left(NT\right)}$ holds with probability tending to one. Thus, we can bound ${\mathsf{\Gamma }}_1$ as follows,

$$\begin{array}{cc}\hfill {\mathsf{\Gamma }}_1& \ge -\sum _{i=1}^N\sum _{t=1}^{\top }\sqrt{c_4^{-1}}\sqrt{log\left(NT\right)}{\mathit{z}}_{it}^{\top }({\mathit{\beta }}_{it}-{\mathit{\beta }}_{it}^{\ast })\hfill \\ & =-\sum _{l=1}^L\sum _{(i,t)\in {\mathcal{B}}_l}\sqrt{c_4^{-1}}\sqrt{log\left(NT\right)}{\mathit{z}}_{it}^{\top }({\mathit{\beta }}_{it}-{\left|{\mathcal{B}}_l\right|}^{-1}\sum _{(j,t^{{}^{\prime }})\in {\mathcal{B}}_l}{\mathit{\beta }}_{j{t}^{{}^{\prime }}})\hfill \\ & =-\sum _{l=1}^L\sum _{(i,t),(j,t^{{}^{\prime }})\in {\mathcal{B}}_l}\sqrt{c_4^{-1}}\sqrt{log\left(NT\right)}{\left|{\mathcal{B}}_l\right|}^{-1}{\mathit{z}}_{it}^{\top }({\mathit{\beta }}_{it}-{\mathit{\beta }}_{j{t}^{{}^{\prime }}})\hfill \\ & \ge -\sum _{l=1}^L\sum _{(i,t),(j,t^{{}^{\prime }})\in {\mathcal{B}}_l}\sqrt{c_4^{-1}}\sqrt{log\left(NT\right)}{\left|{\mathcal{B}}_{min}\right|}^{-1}\sqrt{P}{M}_1\left|\right|{\mathit{\beta }}_{it}-{\mathit{\beta }}_{j{t}^{{}^{\prime }}}\left|\right|.\hfill \end{array}$$

(A23)

For ${\mathsf{\Gamma }}_2$ and ${\mathsf{\Gamma }}_3$, using the results from Wang et al. [18] and Fang et al. [24], we have

$$\begin{array}{cc}\hfill & {\mathsf{\Gamma }}_2\ge \lambda \sum _{t=1}^{\top }\sum _{l=1}^L\sum _{(i,t),(j,t)\in {\mathcal{B}}_l,i<j}{\rho }^{{}^{\prime }}\left(4s\right)\left|\right|{\mathit{\beta }}_{it}-{\mathit{\beta }}_{jt}\left|\right|,\hfill \\ \hfill & {\mathsf{\Gamma }}_3\ge \gamma \sum _{i=1}^N\sum _{l=1}^L\sum _{(i,t),(i,t^{{}^{\prime }})\in {\mathcal{B}}_l,t<t^{{}^{\prime }}}{\rho }^{{}^{\prime }}\left(4s\right)\left|\right|{\mathit{\beta }}_{it}-{\mathit{\beta }}_{i{t}^{{}^{\prime }}}\left|\right|.\hfill \end{array}$$

(A24)

Finally, by combining the above results, we can obtain

$$\begin{array}{cc}\hfill Q\left(\mathit{\beta }\right)-Q\left({\mathit{\beta }}^{\ast }\right)& \ge -4\sum _{l=1}^L\sum _{(i,t),(j,t^{{}^{\prime }})\in {\mathcal{B}}_l,i<j,t<t^{{}^{\prime }}}\sqrt{c_4^{-1}}\sqrt{log\left(NT\right)}{\left|{\mathcal{B}}_{min}\right|}^{-1}\sqrt{P}{M}_1\left|\right|{\mathit{\beta }}_{it}-{\mathit{\beta }}_{j{t}^{{}^{\prime }}}\left|\right|\hfill \\ & +\sum _{l=1}^L[\sum _{t=1}^{\top }\sum _{(i,t),(j,t)\in {\mathcal{B}}_l,i<j}\lambda {\rho }^{{}^{\prime }}\left(4s\right)+\sum _{i=1}^N\sum _{(i,t),(i,t^{{}^{\prime }})\in {\mathcal{B}}_l,t<t^{{}^{\prime }}}\gamma {\rho }^{{}^{\prime }}\left(4s\right)]\left|\right|{\mathit{\beta }}_{it}-{\mathit{\beta }}_{j{t}^{{}^{\prime }}}\left|\right|\hfill \\ & \ge -4\sum _{l=1}^L\sum _{(i,t),(j,t^{{}^{\prime }})\in {\mathcal{B}}_l,i<j,t<t^{{}^{\prime }}}\sqrt{c_4^{-1}}\sqrt{log\left(NT\right)}{\left|{\mathcal{B}}_{min}\right|}^{-1}\sqrt{P}{M}_1\left|\right|{\mathit{\beta }}_{it}-{\mathit{\beta }}_{j{t}^{{}^{\prime }}}\left|\right|\hfill \\ & +\sum _{l=1}^L\sum _{(i,t),(j,t^{{}^{\prime }})\in {\mathcal{B}}_l,i<j,t<t^{{}^{\prime }}}min(\lambda ,\gamma ){\rho }^{{}^{\prime }}\left(4s\right)\left|\right|{\mathit{\beta }}_{it}-{\mathit{\beta }}_{j{t}^{{}^{\prime }}}\left|\right|.\hfill \end{array}$$

(A25)

As $s\to 0$, ${\rho }^{{}^{\prime }}\left(4s\right)\to 1$. Moreover, since $\frac{\sqrt{P}\sqrt{log\left(NT\right)}}{min(\lambda ,\gamma \left)\right|{\mathcal{B}}_{min}|}=o\left(1\right)$, we have $Q\left(\mathit{\beta }\right)-Q\left({\mathit{\beta }}^{\ast }\right)\ge 0$.

This completes the proof.