Synchronization Analysis of Linearly Coupled Systems with Signal-Dependent Noises

Abstract

In this paper, we propose methods for analyzing the synchronization stability of stochastic linearly coupled differential equation systems, with signal-dependent noise perturbation. We consider signal-dependent noise, which is common in many fields, to discuss the stability of the synchronization manifold of multiagent systems and linearly coupled nonlinear dynamical systems under sufficient conditions. Numerical simulations are performed in the paper, and the results show the effectiveness of our theorems.

1. Introduction

Complex networks refer to networks with complex topological structures and dynamic behaviors, which are described by graphs, with a large number of nodes connected by edges, such as highways, the World Wide Web, the Internet, electrical power grids, and food webs. In such a graph, every node represents an individual element of the system, and the edges represent relations between nodes. For decades, complex networks have been used in many disciplines, such as graph theory, statistical physics, computer science, management, economics, and sociology.

The word synchronization in science and technology has the meaning of “the time coherence of different processes”. In theoretical fields of complex networks, there are different types of synchronization, such as phase synchronization, cluster synchronization, lag synchronization, imperfect synchronization, etc. In the field of synchronization of differential equations, a coupled system is usually considered, and in this paper, we consider the concept of complete synchronization, which is defined as follows: if a coupled system is composed of $m$ systems, formulated as $d{x}_i(t)/dt=f_i(x_1(t),x_2(t),...,x_m(t),t)$ for $i=1,2,...,m$ and satisfies the fact that ${\lim }_{t\to \infty }\Vert x_i(t)-x_j(t)\Vert \to 0$ for all $i,j=1,2,...,m$, then we say that the system is synchronized. In the system above, $x_i\in R^n$ is an n-dimensional vector describing state of the i-th vector, and $f_i$ are continuous maps that can be nonlinear. Specifically, this kind of system can be limited to linearly coupled ordinary differential equations (LCODEs) [1,2,3,4,5,6,7], which is also a large class of dynamical systems with continuous time and state for describing coupled oscillators. In general, the LCODEs can be described as the following:

$$\frac{d{x}_i(t)}{dt}=f(x_i(t),t)+c{\displaystyle \sum _{j=1}^m{a}_{ij}\mathsf{\Gamma }[}{x}_j(t)-x_i(t)]$$

(1)

where $A={(a_{ij})}_{m\times m}$ is the matrix related to a graph, $\mathsf{\Gamma }=diag\{{\gamma }_1,{\gamma }_2,...,{\gamma }_n\}$ is a diagonal matrix with ${\gamma }_i\ge 0$, $f$ is a continuous map and can be nonlinear, and $c$ is a positive constant. The second term on the right side of the equation above can be considered as the control, so the problem is also called a synchronization control problem. There are a large number of studies concerning the synchronization control problem of the linearly coupled system. Studies such as [1,2,3,4,5,6,7,8,9,10,11,12] discuss the local and global synchronization of LCODE under certain conditions. In [1], the authors use a transverse space method to discuss the local and global exponential synchronization of LCODEs, and the synchronization of linearly coupled recurrent neural networks. In [2], the authors propose methods of synchronization analysis of LCODEs, with a coupling delay. In [3,4,5], the authors give sufficient condition ensuring consensus of directed time-varying graph on LCODEs. In [6,7], the authors investigate a cluster synchronization problem on LCODEs, and transfer the cluster synchronization problem into a pinning control problem on sufficient conditions. In [8], the authors give the results of cluster synchronization with identical and non-identical nodes, and adaptive feedback control algorithms. In [9], the authors design a centralized event-triggered control algorithm for cluster synchronization problems. In [10,11], the authors discuss the synchronization of state feedback control and pinning control, considering linearly coupled singular systems. In [12], the authors give the results of coupled systems and exponential synchronization without QUAD or weak-QUAD conditions, and also apply the theorems to a linearly coupled Hopfield neural network. The linearly coupled system can be simplified into a linear multiagent system if we set $f=0$ and $n=1$. Prior literature such as [13,14,15,16,17] shows the synchronization and consensus of a leaderless consensus case of multiagent system and its stability.

The synchronization of linearly coupled systems has applications in many fields. Previous literature such as [18,19] discusses the synchronization in stability of power grid networks. Some other studies, such as [20,21,22], apply the discussion of synchronization to neuroscience and show that synchronization relates to neural information processing and brain activity. Studies such as [23,24,25] show the application of the synchronization of LCODEs to the field of image processing and recognition.

Synchronization techniques are also widely used in investigating chaotic systems [26,27,28,29,30,31,32,33,34,35,36,37,38,39], especially while combining the linearly coupled systems with stochastic differential equations; synchronization of noisy systems and noisy couplings are investigated by state-of-the-art literature. In [26], the authors discuss the synchronization of unidirectionally coupled Chua’s circuits with stochastic perturbation. In [27], the author investigates the complete synchronization of two chaotic oscillators and proves that synchronization could be achieved with probability one merely via white-noise-based coupling. In [28], the authors study chaotic delayed neural networks with noise perturbation using feedback control techniques. In [29,30], the authors investigate nonlinear adaptive synchronization between two different noise-perturbed chaotic systems. In [31,32,33], the authors discuss coupled systems with noise perturbation and time delay. In [34], the author gives both complete synchronization and generalized synchronization criteria for a class of chaotic systems dissatisfying a globally Lipschitz condition with noise perturbation. In [35,36,37], the authors investigate certain chaotic systems and prove that noise-perturbed systems can be synchronized with sliding mode control. In [38], the authors design an adaptive-feedback controller to synchronize a class of noise comprising two bi-directionally coupled chaotic systems with time-delay and an unknown parametric mismatch with noise perturbation. In [39], the authors discuss the global synchronization of complex networks perturbed by Poisson noise. Also, literatures as [40,41,42,43,44] demonstrated the practical application synchronization in chaotic systems.

A special type of noise is the so-called signal-dependent noise, which exists in many fields. In the field of neuroscience, the authors of [45] establish a Granger causal model with signal-dependent noise, to show that signal-dependent noise exists in the fMRI blood-oxygen level dependent time series, and the variance of the noise increases approximately linearly with the square of the signal. In [46], the Granger causal model with signal-dependent noise is used to investigate a bargaining game, and shows that, in social cognition, strategies are supported by distinct patterns of directional connectivity among key brain regions. The signal-dependent noise can also be found in mechanical motor planning. In [47], the authors prove that a trajectory is selected to minimize the variance of the eye or arm position to reach the target within the presence of signal-dependent noise. In [48,49,50], the authors deal with adaptive dynamical control with signal-dependent noise and discuss the stability of close-looped control systems.

This paper is organized as follows: in Section 2, some necessary definitions, lemmas, and hypotheses are given; in Section 3, the synchronization of linear multiagent systems with noise perturbation is discussed; criteria for the synchronization of coupled nonlinear dynamical systems are obtained in Section 4; some numerical simulations for verifying the theoretical results are given in Section 5; and the paper is concluded in Section 6.

2. Preliminaries

Firstly, we give the model formulation in this paper and research objectives. The traditional continuous-time control system is written as

$$\frac{d{x}_i(t)}{dt}=f(x_i(t),t)+u_i(t)$$

(2)

where $i=1,2,...,m$, $x_i(t)\in R^n$ is the state variable, $t\in [0,+\infty )$ is continuous time, $f:R^n\times [0,+\infty )\to R^n$ is a continuous map and can be nonlinear, and $u_i(t)$ serves as the control signal. In this paper, we corrupt the control signal by signal-dependent noise, defined as the following:

Definition 1 .

The control signal is defined as $u_i(t)={\lambda }_i(t)+{\zeta }_i(t)$, where ${\lambda }_i(t)$ is the expectation of the control signal $u_i(t)$ and ${\zeta }_i(t)$ is the noise, which satisfies that $E({\zeta }_i(t))=0$ and $E({\zeta }_i(t){\zeta }_j(t^{\prime }))={\sigma }_i(t){\sigma }_j(t^{\prime })\delta (t-t^{\prime }){\delta }_{ij}$ (multiply by elements), in which $E(\cdot )$ denotes the expectation, $\delta (\cdot )$ denotes the Dirac delta function, ${\delta }_{ij}$ is the Kronecker delta, and ${\sigma }_i(t)$ denotes the variance of ${\zeta }_i(t)$. We call the signal-dependent noise ${\zeta }_i(t)$, which we define as ${\zeta }_i(t)dt=k\phi ({\lambda }_i(t))d{W}_i$, where $k$ is a positive constant, $\phi (\cdot ):R^n\to R^{+}$ is a differentiable function, and $W_i$ is a vector of independent normal Wiener processes.

According to Definition 1, system (2) becomes a stochastic differential equation. In this paper, we investigate the linear coupled system, in which we define as

$${\lambda }_i(t)=c{\displaystyle \sum _{j=1}^m{a}_{ij}\mathsf{\Gamma }[x_j(t)-x_i(t)]}$$

(3)

where $a_{ij}\ge 0$ if $i\ne j$, and $a_{ii}=-{\displaystyle {\sum }_{j=1,j\ne i}^m{a}_{ij}}$, $\mathsf{\Gamma }=diag\{{\gamma }_1,{\gamma }_2,...,{\gamma }_n\}$ is a diagonal matrix with ${\gamma }_i\ge 0$, and $c$ is a positive constant. According to Definition 1, ${\lambda }_i(t)$ is the expectation of the control signal; thus we can rewrite system (2) as

$$\frac{d{x}_i(t)}{dt}=f(x_i(t),t)+{\lambda }_i(t)+k\phi ({\lambda }_i(t))\frac{d{W}_i}{dt}$$

(4)

Specifically, system (2) or (4) can be degenerated into a linear multiagent system if $f=0$ and $n=1$.

From the signal-dependent noise defined in Definition 1, we know that all elements of the variance ${\sigma }_i(t)$ of the noise ${\zeta }_i(t)$ equal $k\phi ({\lambda }_i(t))$. Here, we give the definition of Poisson, sub-Poisson and supra-Poisson signal-dependent noises, as the following:

Definition 2 .

Suppose $\lambda (t)$ is the expectation of the control signal, and the signal-dependent function $\phi (\cdot )$ is defined as $\phi (\lambda (t))={\left|\lambda (t)\right|}^{\alpha }$, where $k$ is a positive constant, then if $\alpha <1/2$, the noise is called sub-Poisson; if $\alpha =1/2$, it is called Poisson; if $\alpha >1/2$, it is called supra-Poisson.

In this section, we also present some definitions, notations, and lemmas that are required throughout the paper.

We consider a directed weighted diagram $G$ with $m$ nodes, and we denote the diagram as $(V,E,B)$, in which $V$ denotes the node set $\{v_1,v_2,...,v_m\}$. E denotes the edge set, where $e_{ij}\in E$ if an edge from $v_i$ to $v_j$ exists. $B$ denotes a non-negative $m\times m$ weight matrix, where $b_{ij}$ are the weights between nodes, i.e., $b_{ij}>0$ if and only if an edge $e_{ij}\in E$ exists, and also $b_{ii}=0 (i=1,2,...,m)$. In this paper, we consider only simple diagrams without self-connection and multiple edges. The degree of a single node $v_j$ is defined as the sum of weights connected to the node:

$$d_i={\displaystyle \sum _{j=1}^m{b}_{ij}}$$

(5)

and the degree matrix is defined as a diagonal matrix $D\triangleq diag\{d_1,d_2,...,d_m\}$. The Laplace matrix of the diagram is defined as $L=D-B$. It is obvious that 0 is the eigenvalue of the matrix $L$. Using the Gerschgorin theorem [51], we have the following:

Lemma 1 .

If $L$ is a symmetric matrix, then all eigenvalues of $L$ are non-negative and real.

The diagram $G$ has a spanning tree if a node $v_r$ exists, which satisfies that for any other node $v_i$, a directed path exists from $v_r$ to $v_i$, and $v_r$ is called the root node of the spanning tree. We call the diagram $G$ a strongly connected diagram if and only if each node of the spanning tree is a root node. Using the Perron–Frobenius theorem in [52], we have the following:

Lemma 2 .

The diagram $G$ has a spanning tree if and only if the algebraic multiplicity and geometric multiplicity of the eigenvalue 0 of its Laplace matrix $L$ are both 1. If the diagram $G$ is a strongly connected diagram, then the left and right eigenvectors corresponding to eigenvalue 0 have all positive components; if the diagram $G$ is a strongly connected diagram with a non-symmetric Laplace matrix $L$, and its left eigenvector corresponding to eigenvalue 0 is denoted as $({\xi }_1,{\xi }_2,...,{\xi }_m)$, then for $\mathsf{\Lambda }=diag\{{\xi }_1,{\xi }_2,...,{\xi }_m\}$, $\mathsf{\Lambda }L+L^T\mathsf{\Lambda }$ is a real symmetric matrix, and all eigenvalues of $\mathsf{\Lambda }L+L^T\mathsf{\Lambda }$ are non-negative and real.

Obviously, ${(1,1,...,1)}^T$ is a right eigenvector of $L$ corresponding to its eigenvalue 0.

The objective of this paper is to discuss synchronization; the system is said to be synchronized if ${\lim }_{t\to \infty }\Vert x_i(t)-x_j(t)\Vert \to 0$ for all $i,j=1,2,...,m$, where $\Vert \cdot \Vert$ denotes the Euclidean norm. According to the definition of synchronization, we define the synchronization subspace, also called the synchronization manifold on system (4), as the following:

Definition 3 .

We define the full space as $R^{nm}=\{x=\left(x_1^T(t),x_2^T(t),...,x_m^T(t)\right)|x_i(t)\in R^n\}$, and the synchronization manifold $𝒮$ is defined as $\{(x_{\xi }^T(t),x_{\xi }^T(t),...,x_{\xi }^T(t))|x_{\xi }^T(t)\in R^n\}$, in which all nodes reach the same state.

Accordingly, we define another subspace of $R^{nm}$ as the following:

Definition 4 .

The subspace $ℒ$ of $R^{nm}$ is defined as

$$ℒ=\{\left(x_1^T(t),x_2^T(t),...,x_m^T(t)\right)|x_i(t)\in R^n,\exists \xi =({\xi }_1,{\xi }_2,...,{\xi }_m)\in R^m,{\xi }_i>0,{\displaystyle \sum _{k=1}^m{\xi }_k=1, }s.t.{\displaystyle \sum _{k=1}^m{\xi }_k{x}_k(t)=0}\}.$$

According to Definition 3 and Definition 4, it is easy to see that $R^{nm}=𝒮\oplus ℒ$, which means that any state in $R^{nm}$ can be expressed uniquely as a sum of a vector in $𝒮$ and a vector in $ℒ$. In Section 4, we will consider a class of function that satisfies the QUAD condition [1,2,3,4,5,12,53], which is defined as the following:

Definition 5 (QUAD condition).

Let $P$ be a positive semidefinite diagonal matrix. The function $f(x,t)$ in system (4) satisfies the QUAD condition, if $\delta >0$, $\beta \in R$, exists, such that ${(x-y)}^{T}P[f(x,t)-f(y,t)-\beta \mathsf{\Gamma }(x-y)]\le -\delta {(x-y)}^T(x-y)$ is satisfied for all $x,y\in R^n$ and $t>0$, and $\mathsf{\Gamma }=\{{\gamma }_1,{\gamma }_2,...,{\gamma }_n\}$ is a diagonal positive semidefinite matrix.

In Definition 5, we denote $f(x,t)\in QUAD(\mathsf{\Gamma },P)$, because the QUAD condition is related to matrix $\mathsf{\Gamma }$ and $P$.

Definition 6 (Local and global stochastic stability).

The synchronization manifold $𝒮$ is said to be locally stochastically stable if for every pair of $\epsilon \in (0,1)$ and $r>0$, a $\delta >0$ exists, such that for any $\Vert x_i(0)-x_j(0)\Vert <\delta$, $i,j=1,2,...,m$, $T>0$ exists, such that $P(\Vert x_i(t)-x_j(t)\Vert <r)\ge 1-\epsilon$ holds for all $t>T$; and the synchronization manifold $𝒮$ is said to be globally stochastically stable if for every pair of $\epsilon \in (0,1)$ and $r>0$, $T>0$ exists, such that $P(\Vert x_i(t)-x_j(t)\Vert <r)\ge 1-\epsilon$ holds for all $t>T$, $i,j=1,2,...,m$.

We shall use the term “stability” instead of “stochastic stability” without ambiguity. From system (4) and the condition of signal-dependent noise, we shall investigate the system in the following form:

$$dx(t)=F(x,t)dt+H(x,t)d{W}_t$$

(6)

where $x(t)={(x_1(t),x_2(t),...,x_m(t))}^T$. We first show the existence and uniqueness of the system.

Lemma 3 .

Suppose the stochastic differential Equation (3) satisfies the Lipschitz condition:

$${\Vert F(x_1,t)-F(x_2,t)\Vert }^2\vee {\Vert H(x_1,t)-H(x_2,t)\Vert }^2\le k{\Vert x_1-x_2\Vert }^2$$

(7)

then the stochastic differential Equation (3) has a unique solution.

The normally used method for discussing stability is the Lyapunov direct method. Suppose $V(x)$ is a legal differentiable Lyapunov function based on (4), we can calculate from the Ito formula that

$$dV(x)=LVdt+V_{x}H(x,t)d{W}_t$$

(8)

where $LV=V_{x}F+1/2Tr(H^T{V}_{xx}H)$. Now we show the result of stability in the following Lemma from [54]:

Lemma 4 .

If $V(x)$ is a Lyapunov function on system (8), then the stability of the system is only dependent on the term  $LV$, i.e., the following holds:

• If  $V(x)<0$  near  $x$, the system is locally stable near  $x$;
• If  $V(x)\to \infty$  as   $\Vert x\Vert \to \infty$, and  $V(x)<0$  for all  $x$, then system is globally stable;
• If $V(x)>0$ near $x$, the system is locally unstable near  $x$.

For simplicity, we denote $dV(x)/dt:=LV$, calling it the derivative of Lyapunov function. In synchronization problems, local and global stability are also called local and global synchronization. We denote here the synchronization manifold $𝒮$ as $\{{\overline{x}}_{\xi }=(x_{\xi }^T(t),x_{\xi }^T(t),...,x_{\xi }^T(t))|x_{\xi }^T(t)\in R^n\}$. Similarly, if a legal Lyapunov function $V(x)$ on $ℒ$ with $V(x)\to \infty$ as $\Vert x\Vert \to \infty$ holds that $dV(x)/dt<0$ near ${\overline{x}}_{\xi }$, the system manifold $𝒮$ is locally stable; if a negative constant $C_1$ exists, such that $dV(x)/dt<C_1{(x-{\overline{x}}_{\xi })}^T(x-{\overline{x}}_{\xi })$ is satisfied, then the synchronization manifold $𝒮$ is globally stable; if $dV(x)/dt>0$ near ${\overline{x}}_{\xi }$, then the synchronization manifold $𝒮$ is locally unstable.

3. Synchronization of Linear Multiagent Systems

In this section, we consider linear multiagent systems, and discuss the local and global synchronization of the system. In system (4), we set $n=1$ and $f=0$. We define the local neighborhood tracking error according to [55] as

$${\eta }_i={\displaystyle \sum _{j\in N_i}{e}_{ij}(x_i-x_j)}$$

(9)

and the overall local neighborhood tracking error $e=({\eta }_1,{\eta }_2,...,{\eta }_m)$. We denote $x={(x_1(t),x_2(t),...,x_m(t))}^T$. It is obvious that a Laplace matrix $L$ exists with rank $m-1$, such that $e=Lx$. Noticing that the control signal is a random variable, according to the control principle, a naive control function with global synchronization can be defined as $u:E(u)=-Lx$, where $u=(u_1,u_2,...,u_m)$ is corrupted by signal-dependent noise according to Definition 1, $u_i(t)dt={\lambda }_i(t)dt+k\phi ({\lambda }_i(t))d{W}_i$, $i=1,2,...,m$. Using Lemma 3, the Lipschitz condition is satisfied. According to Lemma 2, we define the left eigenvector which corresponds to the eigenvalue 0 of matrix $L$ as $\xi =({\xi }_1,{\xi }_2,...,{\xi }_m)$, which satisfies (1) ${\xi }_i>0, i=1,2,...m$, and (2) ${\displaystyle {\sum }_{i=1}^m{\xi }_i=1}$. In addition, we denote $\mathsf{\Lambda }=diag\{{\xi }_1,{\xi }_2,...,{\xi }_m\}$, $\lambda =({\lambda }_1,{\lambda }_2,...,{\lambda }_m)$, $L^{\prime }=-L$, $x_{\xi }(t)={\displaystyle {\sum }_{i=1}^m{\xi }_i{x}_i(t)}$, and the $m$ dimensional vector ${\overline{x}}_{\xi }=(x_{\xi }(t),...,x_{\xi }(t))$. According to Definition 3 and Definition 4, ${\overline{x}}_{\xi }\in 𝒮$, so $x-{\overline{x}}_{\xi }\in ℒ$. Using Lemma 2 again on the multiagent system, we have

$$\begin{array}{l}d(x-{\overline{x}}_{\xi })\\ =\frac{d(x-{\overline{x}}_{\xi })}{dt}dt\\ =[\frac{dx}{dt}-({\displaystyle \sum _{i=1}^m{\xi }_i}\frac{d{x}_i}{dt})1]dt\\ =[-Lx+(\xi Lx)1]dt+(k\phi ({\lambda }_i)d{W}_i-{\displaystyle \sum _{j}k{\xi }_j\phi ({\lambda }_j)d{W}_j}){}^T\\ =L^{\prime }(x-{\overline{x}}_{\xi })dt+(k\phi ({\lambda }_i)d{W}_i-{\displaystyle \sum _{j}k{\xi }_j\phi ({\lambda }_j)d{W}_j}){}^T\end{array}$$

(10)

where ${(k\phi ({\lambda }_i)d{W}_i-{\displaystyle \sum _{j}k{\xi }_j\phi ({\lambda }_j)d{W}_j})}^T:={(k\phi ({\lambda }_1)d{W}_1-{\displaystyle \sum _{j}k{\xi }_j\phi ({\lambda }_j)d{W}_j},...,k\phi ({\lambda }_m)d{W}_m-{\displaystyle \sum _{j}k{\xi }_j\phi ({\lambda }_j)d{W}_j})}^T$ and $1={(1,1,...,1)}^T$. From (10), system (4) can be transferred into the following for $i=1,2,...,m$:

$$d(x_i-x_{\xi })={[L^{\prime }(x-{\overline{x}}_{\xi })dt]}_i+(k\phi ({\lambda }_i)d{W}_i-{\displaystyle {\sum }_{j}k{\xi }_j\phi ({\lambda }_j)d{W}_j})$$

(11)

where ${[\cdot ]}_i$ denotes the i-th component. Investigating system (11), we have the following theorem:

Theorem 1 .

(1) If a positive constant $C$ exists, for which the signal-dependent function satisfies $\left|\phi (\lambda )\right|\le C{\left|\lambda \right|}^{\alpha }$, then if $\alpha >1/2$, the synchronization manifold $𝒮$ is locally stable (the case of supra-Poisson noise); if $\alpha =1/2$ and $k$ is small enough, the synchronization manifold $𝒮$ is globally stable (the case of Poisson noise); (2) If a positive constant $C$ exists, for which the signal-dependent function satisfies $\left|\phi (\lambda )\right|\ge C{\left|\lambda \right|}^{\alpha }$, then if $\alpha <1/2$, the manifold $𝒮$ is locally unstable (the case of sub-Poisson noise).

Proof. 

Define the function $V(x)$ on $ℒ$: $V(x)={(x-{\overline{x}}_{\xi })}^T\mathsf{\Lambda }(x-{\overline{x}}_{\xi })$. It is obvious that $V(x)$ is a Lyapunov function of (11); differentiating it using the Ito formula, we have

$$dV(x)=2{(x-{\overline{x}}_{\xi })}^T\mathsf{\Lambda }d(x-{\overline{x}}_{\xi })+d{(x-{\overline{x}}_{\xi })}^T\mathsf{\Lambda }d(x-{\overline{x}}_{\xi })$$

(12)

Using Lemma 4, we shall calculate $LV$ or $dV(x)/dt$, according to the definition. Calculating the first term of (12), and neglecting the terms of $d{W}_i$, we have

$$\begin{array}{l}2(x-{\overline{x}}_{\xi }){}^T\mathsf{\Lambda }d(x-{\overline{x}}_{\xi })\\ =2(x-{\overline{x}}_{\xi }){}^T\mathsf{\Lambda }{L}^{\prime }(x-{\overline{x}}_{\xi })dt\\ =(x-{\overline{x}}_{\xi }){}^T(\mathsf{\Lambda }{L}^{\prime }+{L^{\prime }}^T\mathsf{\Lambda })(x-{\overline{x}}_{\xi })dt\end{array}$$

(13)

According to Lemma 2, we know that all the eigenvalues of $(\mathsf{\Lambda }{L}^{\prime }+{L^{\prime }}^T\mathsf{\Lambda })$ are less than equal to zero; thus we denote ${\lambda }_1^{\prime }=\max \{{\lambda }_i^{\prime }\ne 0,{\lambda }_i^{\prime }\in \sigma (\mathsf{\Lambda }{L}^{\prime }+{L^{\prime }}^T\mathsf{\Lambda })\}$ as its maximum nonzero eigenvalue, and ${\lambda }_n^{\prime }=\min \{{\lambda }_i^{\prime }\ne 0,{\lambda }_i^{\prime }\in \sigma (\mathsf{\Lambda }{L}^{\prime }+{L^{\prime }}^T\mathsf{\Lambda })\}$ as its minimum non-zero eigenvalue. Then ${\lambda }_n^{\prime }\le {\lambda }_1^{\prime }<0$, and

$${\lambda }_n^{\prime }{(x-{\overline{x}}_{\xi })}^T(x-{\overline{x}}_{\xi })\le {(x-{\overline{x}}_{\xi })}^T(\mathsf{\Lambda }{L}^{\prime }+{L^{\prime }}^T\mathsf{\Lambda })(x-{\overline{x}}_{\xi })\le {\lambda }_1^{\prime }{(x-{\overline{x}}_{\xi })}^T(x-{\overline{x}}_{\xi })$$

(14)

Calculating the second term in (12), we have

$$\begin{array}{l}d(x-{\overline{x}}_{\xi }){}^T\mathsf{\Lambda }d(x-{\overline{x}}_{\xi })\\ ={\displaystyle \sum _i\left(k\phi ({\lambda }_i)d{W}_i-{\displaystyle \sum _{j}k{\xi }_j\phi ({\lambda }_j)d{W}_j}\right)}{\xi }_i\left(k\phi ({\lambda }_i)d{W}_i-{\displaystyle \sum _{k}k{\xi }_k\phi ({\lambda }_k)d{W}_k}\right)\\ ={\displaystyle \sum _i(k^2{\xi }_i{\phi }^2({\lambda }_i)}dt-k^2{\xi }_i^2{\phi }^2({\lambda }_i)dt)\\ ={\displaystyle \sum _i{k}^2({\xi }_i-{\xi }_i^2){\phi }^2({\lambda }_i)}dt\end{array}$$

(15)

Noticing that $0<{\xi }_i<1$, a positive constant $M$ exists, such that $d{(x-{\overline{x}}_{\xi })}^T\mathsf{\Lambda }d(x-{\overline{x}}_{\xi })\le M{k}^2{\displaystyle {\sum }_i{\phi }^2({\lambda }_i)}dt$. Now we are able to discuss the different preconditions in Theorem 1.

(1)

A constant $C$ exists, such that $\left|\phi (\lambda )\right|\le C{\left|\lambda \right|}^{\alpha }$; noticing that $\lambda =-Lx=-L(x-{\overline{x}}_{\xi })$, then the condition is equal to the existence of another constant $C_1$, such that ${\left|\phi (\lambda )\right|}^2\le C_1{[{(x-{\overline{x}}_{\xi })}^T(x-{\overline{x}}_{\xi })]}^{2\alpha }$. Using Formulas (12)~(15), a constant $C_1^{\prime }$ exists, such that

$$dV(x)/dt\le {\lambda }_1^{\prime }{(x-{\overline{x}}_{\xi })}^T(x-{\overline{x}}_{\xi })+C_1^{\prime }{k}^2{[{(x-{\overline{x}}_{\xi })}^T(x-{\overline{x}}_{\xi })]}^{2\alpha }$$

(16)

where $C_1^{\prime }>0$. We can see that if $\alpha >1/2$, the relation $dV(x)/dt<0$ is satisfied near the synchronization manifold $𝒮$; thus the synchronization manifold $𝒮$ is locally stable. If $\alpha =1/2$ and $k<\sqrt{-{\lambda }_1^{\prime }/C_1^{\prime }}$, then a $C_1^{″}<0$ exists, such that $dV(x)/dt<C_1^{″}{(x-{\overline{x}}_{\xi })}^T(x-{\overline{x}}_{\xi })$, which means that the synchronization manifold $𝒮$ is globally stable.

(2)

A constant $C$ exists, such that $\left|\phi (\lambda )\right|\ge C{\left|\lambda \right|}^{\alpha }$. Similarly, this condition is equal to the existence of another constant $C_2$, such that ${\left|\phi (\lambda )\right|}^2\ge C_2{[{(x-{\overline{x}}_{\xi })}^T(x-{\overline{x}}_{\xi })]}^{2\alpha }$. Using Formulas (12)~(15), we have

$$dV(x)/dt\ge {\lambda }_n^{\prime }{(x-{\overline{x}}_{\xi })}^T(x-{\overline{x}}_{\xi })+C_2^{\prime }{k}^2{[{(x-{\overline{x}}_{\xi })}^T(x-{\overline{x}}_{\xi })]}^{2\alpha }$$

(17)

where $C_2^{\prime }>0$. Then it is obvious that if $\alpha <1/2$, a $C_2^{″}>0$ exists which satisfies the relation $dV(x)/dt>0$. As a result, the synchronization manifold $𝒮$ is locally unstable. □

4. Synchronization of Linearly Coupled Nonlinear Dynamical Systems

In this section, we investigate the original linearly coupled nonlinear dynamical system of (4). We still consider a strongly connected diagram $G$ and its Laplace matrix $L$, and we rewrite system (4) as

$$d{x}_i(t)=f(x_i(t),t)dt+{\lambda }_i(t)dt+k\phi ({\lambda }_i(t))d{W}_i$$

(18)

where the control signal $u_i(t)$ satisfies $u_i(t)dt={\lambda }_i(t)dt+k\phi ({\lambda }_i(t))d{W}_i$, $i=1,2,...,m$. ${\lambda }_i(t)=c{\displaystyle {\sum }_{j=1}^m{a}_{ij}\mathsf{\Gamma }{x}_j(t)}$, and $A={(a_{ij})}_{i,j=1}^m$ satisfies that $A=-L$. Obviously, if $n=1$, $f=0$, and $\mathsf{\Gamma }=I_n$, it is the linear multiagent system discussed in Section 3.

In this case, we denote $x={(x_1{(t)}^T,...,x_m{(t)}^T)}^T\in R^{nm}$, $\overline{f}(x,t)={(f{(x_1,t)}^T,...,f{(x_m,t)}^T)}^T$. Similarly, we define $\xi =({\xi }_1,{\xi }_2,...,{\xi }_m)$ as the left eigenvector corresponding to the eigenvalue 0 of matrix $A$, which has all positive components, and also ${\displaystyle {\sum }_{i=1}^m{\xi }_i}=1$. In addition, we define $x_{\xi }(t)={\displaystyle {\sum }_{i=1}^m{\xi }_i{x}_i(t)}$, $f_{\xi }(x,t)={\displaystyle {\sum }_{i=1}^m{\xi }_{i}f(x_i,t)}$, and the $nm$ dimensional vector ${\overline{x}}_{\xi }={(x_{\xi }{(t)}^T,...,x_{\xi }{(t)}^T)}^T\in 𝒮$, the $nm$ dimensional vector ${\overline{f}}_{\xi }(x,t)={(f_{\xi }{(x,t)}^T,...,f_{\xi }{(x,t)}^T)}^T$.

According to the definitions above, $x-{\overline{x}}_{\xi }\in ℒ$, we have (on the subspace $ℒ$)

$$\begin{array}{l}d(x-{\overline{x}}_{\xi })\\ =[\frac{dx}{dt}-({\displaystyle \sum _{i=1}^m{\xi }_i}\frac{d{x}_i}{dt},{\displaystyle \sum _{i=1}^m{\xi }_i}\frac{d{x}_i}{dt},...,{\displaystyle \sum _{i=1}^m{\xi }_i}\frac{d{x}_i}{dt}{)}^T]dt\\ =[\overline{f}(x,t)+cA\otimes \mathsf{\Gamma }x-{\overline{f}}_{\xi }(x,t)-c((\xi A\otimes \mathsf{\Gamma })x,(\xi A\otimes \mathsf{\Gamma })x,...,(\xi A\otimes \mathsf{\Gamma })x{)}^T]dt\\ +(k\phi ({\lambda }_i)d{W}_i-{\displaystyle \sum _{j}k{\xi }_j\phi ({\lambda }_j)d{W}_j}{)}^T\\ =[\overline{f}(x,t)-{\overline{f}}_{\xi }(x,t)+cA\otimes \mathsf{\Gamma }x]dt+(k\phi ({\lambda }_i)d{W}_i-{\displaystyle \sum _{j}k{\xi }_j\phi ({\lambda }_j)d{W}_j}{)}^T\\ =[\overline{f}(x,t)-{\overline{f}}_{\xi }(x,t)+cA\otimes \mathsf{\Gamma }(x-{\overline{x}}_{\xi })]dt+(k\phi ({\lambda }_i)d{W}_i-{\displaystyle \sum _{j}k{\xi }_j\phi ({\lambda }_j)d{W}_j}{)}^T\end{array}$$

(19)

where $\otimes$ is the Kronecker product, ${\lambda }_i={({\lambda }_{i1},...,{\lambda }_{in})}^T$, $W_i={(W_{i1},...,W_{in})}^T$. As a result, system (18) can be expressed as the following on the subspace $ℒ$:

$$d(x_i-{\overline{x}}_{\xi })={[f(x_i,t)-{\overline{f}}_{\xi }(x,t)+cA\otimes \mathsf{\Gamma }(x-{\overline{x}}_{\xi })]}_{i}dt+(k\phi ({\lambda }_i)d{W}_i-{\displaystyle \sum _{j}k{\xi }_j\phi ({\lambda }_j)d{W}_j})$$

(20)

For system (20), we have the following theorem:

Theorem 2 .

Suppose the function $f(x,t)$ satisfies the QUAD condition, and the signal-dependent function $\phi (\lambda )$ satisfies that $\left|\phi (\lambda )\right|\le C{\left|\lambda \right|}^{\alpha }$. Then, if $\alpha >1/2$, and $c$ is large enough, the synchronization manifold $𝒮$ is locally stable (the case of supra-Poisson noise); if $\alpha =1/2$, $c$ is large enough and $k$ is small enough, the synchronization manifold $𝒮$ is globally stable (the case of Poisson noise).

Proof. 

Define the Lyapunov function $V(x)$ on $ℒ$: $V(x)={(x-{\overline{x}}_{\xi })}^T(\mathsf{\Lambda }\otimes P)(x-{\overline{x}}_{\xi })$, where $\mathsf{\Lambda }=diag\{{\xi }_1,{\xi }_2,...,{\xi }_m\}$, and the matrix $P$ is defined using the QUAD condition in Definition 5.

Differentiating the Lyapunov function using the Ito formula, we have

$$dV(x)=2{(x-{\overline{x}}_{\xi })}^T(\mathsf{\Lambda }\otimes P)d(x-{\overline{x}}_{\xi })+d{(x-{\overline{x}}_{\xi })}^T(\mathsf{\Lambda }\otimes P)d(x-{\overline{x}}_{\xi })$$

(21)

Calculating the first term on the right side of (21), neglecting the terms of $d{W}_i$, we have

$$\begin{array}{l}2(x-{\overline{x}}_{\xi }{)}^T(\mathsf{\Lambda }\otimes P)d(x-{\overline{x}}_{\xi })\\ =2(x-{\overline{x}}_{\xi }{)}^T(\mathsf{\Lambda }\otimes P)(\overline{f}(x,t)-{\overline{f}}_{\xi }(x,t)+cA\otimes \mathsf{\Gamma }(x-{\overline{x}}_{\xi }))dt\\ =2(x-{\overline{x}}_{\xi }{)}^T(\mathsf{\Lambda }\otimes P)(\overline{f}(x,t)-\overline{f}({\overline{x}}_{\xi },t)+\overline{f}({\overline{x}}_{\xi },t)-{\overline{f}}_{\xi }(x,t)+cA\otimes \mathsf{\Gamma }(x-{\overline{x}}_{\xi }))dt\end{array}$$

(22)

where $\overline{f}({\overline{x}}_{\xi },t)={(f{({\overline{x}}_{\xi },t)}^T,...,f{({\overline{x}}_{\xi },t)}^T)}^T$.

Because all of the $n$ dimensional components of the $nm$ dimensional vectors $\overline{f}({\overline{x}}_{\xi },t)$ and ${\overline{f}}_{\xi }(x,t)$ are the same, it is obvious that

$$2{(x-{\overline{x}}_{\xi })}^T(\mathsf{\Lambda }\otimes P)(\overline{f}({\overline{x}}_{\xi },t)-{\overline{f}}_{\xi }(x,t))=0$$

(23)

Using the QUAD condition, and considering each $n$ dimensional component of the $nm$ dimensional vectors, we have

$$\begin{array}{l}2(x-{\overline{x}}_{\xi }{)}^T(\mathsf{\Lambda }\otimes P)d(x-{\overline{x}}_{\xi })\\ =2(x-{\overline{x}}_{\xi }{)}^T(\mathsf{\Lambda }\otimes P)(\overline{f}(x,t)-\overline{f}({\overline{x}}_{\xi },t)+cA\otimes \mathsf{\Gamma }(x-{\overline{x}}_{\xi }))dt\\ =2(x-{\overline{x}}_{\xi }{)}^T(\mathsf{\Lambda }\otimes P)[\overline{f}(x,t)-\overline{f}({\overline{x}}_{\xi },t)-\beta (I\otimes \mathsf{\Gamma })(x-{\overline{x}}_{\xi })+(cA+\beta I)\otimes \mathsf{\Gamma }(x-{\overline{x}}_{\xi })]dt\\ \le -2\delta (x-{\overline{x}}_{\xi })(\mathsf{\Lambda }\otimes I)(x-{\overline{x}}_{\xi })dt+2(x-{\overline{x}}_{\xi }{)}^T\{[\mathsf{\Lambda }(cA+\beta I)]{}^S\otimes (P\mathsf{\Gamma }){}^S\}(x-{\overline{x}}_{\xi })dt\end{array}$$

(24)

where $I$ is the m-order unit matrix, and $M^S=(M+M^{\prime })/2$.

Using Lemma 2, all eigenvalues of the matrix ${[\mathsf{\Lambda }(cA+\beta I)]}^S$ are less than equal to zero if $c$ is large enough. Let ${\lambda }_n^{\prime }<0$ be the maximum eigenvalue. Noticing that $P\mathsf{\Gamma }$ is a positive semidefinite matrix, if $c\ge -\beta /{\lambda }_n^{\prime }$, a constant $C_1>0$ will exist, in which the relation $2{(x-{\overline{x}}_{\xi })}^T(\mathsf{\Lambda }\otimes P)d(x-{\overline{x}}_{\xi })<-C_1{(x-{\overline{x}}_{\xi })}^T(x-{\overline{x}}_{\xi })dt$ is satisfied.

We denote ${\lambda }_P$ as the maximum eigenvalue of $P$; calculating the second term on the right side of (21), we have

$$\begin{array}{l}d(x-{\overline{x}}_{\xi }){}^T(\mathsf{\Lambda }\otimes P)d(x-{\overline{x}}_{\xi })\\ ={\displaystyle \sum _{i=1}^m\left(k\phi ({\lambda }_i)d{W}_i-{\displaystyle \sum _{j}k{\xi }_j\phi ({\lambda }_j)d{W}_j}\right){\xi }_{i}P\left(k\phi ({\lambda }_i)d{W}_i-{\displaystyle \sum _{k}k{\xi }_k\phi ({\lambda }_k)d{W}_k}\right)}\\ \le {\displaystyle \sum _{i=1}^m(n{k}^2}{\xi }_i{\lambda }_P{\phi }^2({\lambda }_i)dt-n{k}^2{\xi }_i^2{\lambda }_P{\phi }^2({\lambda }_i)dt)\\ ={\displaystyle \sum _{i=1}^m(n{k}^2}({\xi }_i-{\xi }_i^2){\lambda }_P{\phi }^2({\lambda }_i)dt)\end{array}$$

(25)

Noticing that $0<{\xi }_i<1$, a positive constant $M$ exists, such that $d{(x-{\overline{x}}_{\xi })}^T(\mathsf{\Lambda }\otimes P)$$d(x-{\overline{x}}_{\xi })\le M{k}^2{\displaystyle {\sum }_i{\phi }^2({\lambda }_i)}dt$. Therefore, if $\left|\phi (\lambda )\right|\le C{\left|\lambda \right|}^{\alpha }$, using Formulas (22)~(25), another positive constant $C_1^{\prime }>0$ exists, such that

$$dV(x)/dt\le -C_1{(x-{\overline{x}}_{\xi })}^T(x-{\overline{x}}_{\xi })+C_1^{\prime }{k}^2{[{(x-{\overline{x}}_{\xi })}^T(x-{\overline{x}}_{\xi })]}^{2\alpha }$$

As a result, if $\alpha >1/2$, $dV(x)/dt<0$ is satisfied near the synchronization manifold $𝒮$, so the synchronization manifold $𝒮$ is locally stable; if $\alpha =1/2$ and $k<\sqrt{-C_1/C_1^{\prime }}$, a negative constant $C_1^{″}<0$ exists, such that $dV(x)/dt<C_1^{″}{(x-{\overline{x}}_{\xi })}^T(x-{\overline{x}}_{\xi })$ is satisfied, so the synchronization manifold $𝒮$ is globally stable. □

5. Numerical Experiments

In this section, we give several simulations to verify the theoretical results mentioned in the sections above. We give experiments on whether a multiagent system or a linearly coupled nonlinear dynamical system with strongly connected diagram can be synchronized under certain conditions.

In the experiments below, we use a diagram with three nodes; the illustration of the diagram is shown in Figure 1. The weights of the edges are labeled on the figure, and according to the definition of the Laplace matrix, we have

$$B=\left(\begin{array}{ccc}0& 1& 2\\ 1& 0& 2\\ 3& 1& 0\end{array}\right), D=\left(\begin{array}{ccc}3& 0& 0\\ 0& 3& 0\\ 0& 0& 4\end{array}\right) \mathrm{and} L=\left(\begin{array}{ccc}3& -1& -2\\ -1& 3& -2\\ -3& -1& 4\end{array}\right)$$

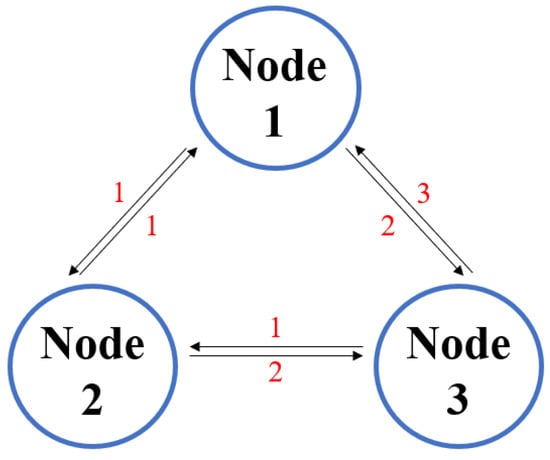
Figure 1. Illustration of the diagram used in the experiments.

The matrix $L$ has three left eigenvalues ${\lambda }_1^{\prime }=0$, ${\lambda }_2^{\prime }=4$ and ${\lambda }_3^{\prime }=6$, and the left eigenvector corresponding to the eigenvalue 0 is $\xi ={({\xi }_1,{\xi }_2,...,{\xi }_m)}^T={(0.4167,0.2500,0.3333)}^T$ (${\displaystyle {\sum }_{i=1}^m{\xi }_i=1}$).

In each simulation, the time step is set as 0.001 s, and the total time duration is 10 s. We use the following quantity to measure synchronization:

$$E=\frac{⟨error(t)⟩}{error(0)}$$

(26)

where

$$error(t)={\displaystyle \sum _{i=1}^m{\xi }_i}\Vert x_i(t)-{\overline{x}}_{\xi }(t)\Vert$$

(27)

and $⟨\cdot ⟩$ denotes average over time. Each experiment is conducted independently 50 times and the quantity $E$ is averaged. If $E$ is small enough, we can say that the system is synchronized.

5.1. Simulation of Synchronization on the Multiagent System

The multiagent system is the case mentioned in Section 3. In this case, $dx=udt$, where $x={(x_1,x_2,x_3)}^T$. The control signal $u$ is corrupted by a signal-dependent noise, so that the system formed as $d{x}_i={\lambda }_{i}dt+k\phi ({\lambda }_i)d{W}_i$, $i=1,2,3$, with $\lambda =-Lx$. The function $\phi$ is formulated as $\phi ({\lambda }_i)={\left|{\lambda }_i\right|}^{\alpha }$. The initial state in this experiment is $(x_1,x_2,x_3)=(0.010,$$0.015,0.020)$.

Using Formula (16), we can calculate in this case that if $k<0.506$, $dV(x)/dt<C_1^{″}{(x-{\overline{x}}_{\xi })}^T(x-{\overline{x}}_{\xi })$ is satisfied if $\alpha =1/2$, where $C_1^{″}<0$.

The relationship between $\alpha$ and $E$ is shown in Figure 2, establishing that $k=0.1$, and the relationship between $k$ and $E$ is shown in Figure 3, establishing that $\alpha =0.5$. From Figure 3, we can see that the condition “small $k$” is needed for synchronization.

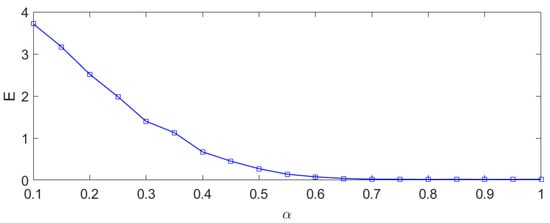
Figure 2. Dependences of $E$ on $\alpha$ in the multiagent system.

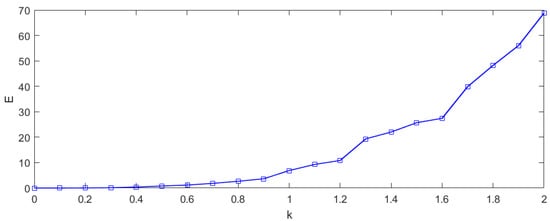
Figure 3. Dependences of $E$ on $k$ in the multiagent system.

The results of single experiments are shown in Figure 4 and Figure 5. In the experiment for Figure 4, we set $\alpha =0.7$ and $k=0.1$. In Figure 5, we set $\alpha =0.1$ and $k=0.1$. It is clear that the system in Figure 4 is eventually synchronized, while synchronization is not found in the Figure 5 experiment.

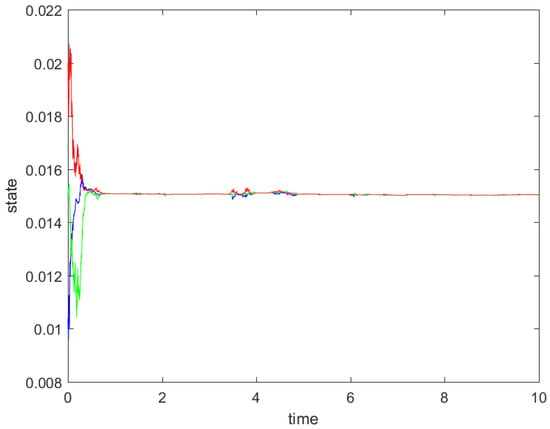
Figure 4. Single experiments in the multiagent system with $\alpha =0.7$ and $k=0.1$.

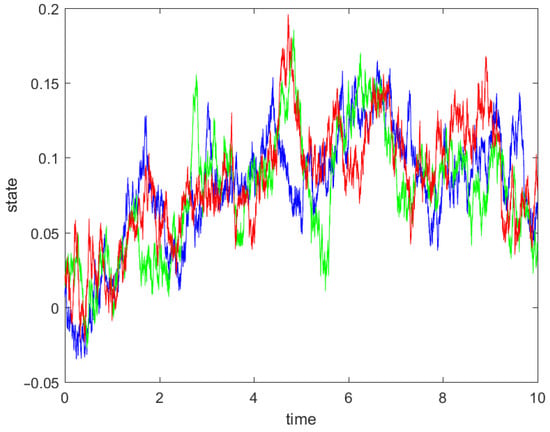
Figure 5. Single experiments in the multiagent system with $\alpha =0.1$ and $k=0.1$.

5.2. Simulation of Synchronization on the Linearly Coupled Nonlinear Dynamical Systems

In this part of the simulation, we use the system proposed by [1] for a chaotic generator. The original system in [1] is described as

$$\frac{d{x}_i}{dt}=(-D{x}_i+Tg(x_i)+c{\displaystyle \sum _{j=1}^m{a}_{ij}\mathsf{\Gamma }{x}_j})$$

(28)

where $i=1,2,...,m$ and $x_i={(x_i^1,x_i^2,x_i^3)}^T$ is a three-dimension vector state. In addition, $A={(a_{ij})}_{i,j=1}^m$ satisfies $A=-L$, $D=I_3$, $\mathsf{\Gamma }=I_3$, and $g(x_i)={(g(x_i^1),g(x_i^2),g(x_i^3))}^T$, where $g(s)=\frac{\left|s+1\right|-\left|s-1\right|}{2}$, and the matrix $T=\left(\begin{array}{ccc}1.250& -3.200& -3.200\\ -3.200& 1.100& -4.400\\ -3.200& 4.400& 1.000\end{array}\right)$.

Here, we corrupt the control signal with signal-dependent noise, where the system can be described in (29) as

$$d{x}_i=(-D{x}_i+Tg(x_i)+{\lambda }_i)dt+k\phi ({\lambda }_i)d{W}_t$$

(29)

where ${\lambda }_i=c{\displaystyle {\sum }_{j=1}^m{a}_{ij}\mathsf{\Gamma }{x}_j}$ and $\phi ({\lambda }_i)={\left|{\lambda }_i\right|}^{\alpha }$. In the following experiment, we set $m=3$.

It is obvious that the QUAD condition is satisfied. We set the initial states as $x_1=(1\times {10}^{-5},1\times {10}^{-5},1\times {10}^{-5})$, $x_2=(1.5\times {10}^{-5},1.5\times {10}^{-5},1.5\times {10}^{-5})$ and $x_3=(2\times {10}^{-5},2\times {10}^{-5}$$,2\times {10}^{-5})$, and $k=0.1$. Using Formula (24), we can calculate that $c\ge 1/6$ is needed for synchronization if $\alpha =0.5$. The relationship between $\alpha$ and $E$ is shown in Figure 6, establishing that $c=1$, and the relationship between $c$ and $E$ is shown in Figure 7, establishing that $\alpha =0.5$.

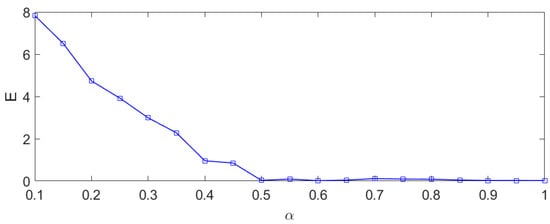
Figure 6. Dependences of E on $\alpha$ of linearly coupled nonlinear dynamical system.

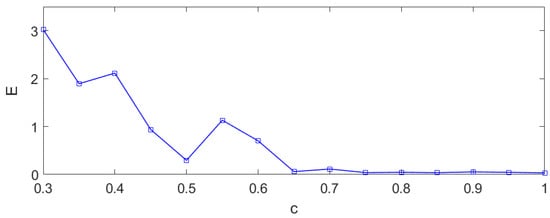
Figure 7. Dependences of E on $c$ of linearly coupled nonlinear dynamical system.

Figure 8 shows a single experiment with $c=1$ and $\alpha =0.5$, in which the system becomes synchronized. Figure 9 shows the error over time with $c=0.1$ and $c=0.5$, and the system is synchronized only at the bottom of Figure 9.

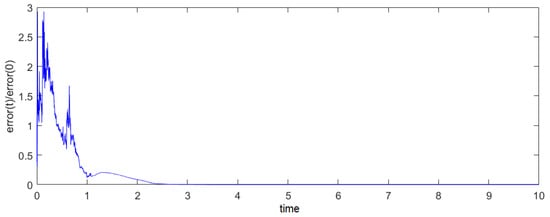
Figure 8. Single experiments on the linearly coupled nonlinear dynamical system with $\alpha =0.5$, $c=1$, and $k=0.1$.

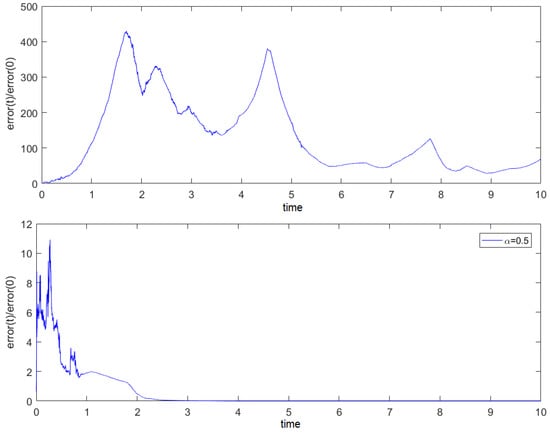
Figure 9. Single experiments on the linearly coupled nonlinear dynamical system with $\alpha =0.5$, $k=0.1$. (Top) Results with $c=0.1$. (Bottom) Results with $c=0.5$.

6. Conclusions

In this paper, we propose a theoretical framework for synchronization analysis, based on the control system of stochastic differential equations, with the control perturbed by signal-dependent noise. We investigate a multiagent system and a linearly coupled nonlinear dynamical system with the QUAD condition. With the theorems proved, we provide a discussion of the stability of the synchronization manifold with specific conditions for the signal-dependent function. The experiments all show the effectiveness of our theorems. This paper offers a new approach to the synchronization problem in stochastic differential equations with control perturbed by signal-dependent noise, which may be useful in many certain applications.