Dual Variational Formulations for a Large Class of Non-Convex Models in the Calculus of Variations

Abstract

This article develops dual variational formulations for a large class of models in variational optimization. The results are established through basic tools of functional analysis, convex analysis and duality theory. The main duality principle is developed as an application to a Ginzburg–Landau-type system in superconductivity in the absence of a magnetic field. In the first section, we develop new general dual convex variational formulations, more specifically, dual formulations with a large region of convexity around the critical points, which are suitable for the non-convex optimization for a large class of models in physics and engineering. Finally, in the last section, we present some numerical results concerning the generalized method of lines applied to a Ginzburg–Landau-type equation.

1. Introduction

In this section, we establish a dual formulation for a large class of models in non-convex optimization.

The main duality principle is applied to the Ginzburg–Landau system in superconductivity in the absence of a magnetic field.

Such results are based on the works of J.J. Telega and W.R. Bielski [1,2,3,4] and on a D.C. optimization approach developed in Toland [5].

About the other references, details on the Sobolev spaces involved are found in [6]. Related results on convex analysis and duality theory are addressed in [7,8,9,10]. Finally, similar models on the superconductivity physics may be found in [11,12].

Remark 1. 

It is worth highlighting that we may generically denote

$${\int }_{\Omega }\left[{(-\gamma {\nabla }^2+K{I}_d)}^{-1}{v}^{*}\right]v^{*}dx$$

simply by

$${\int }_{\Omega }\frac{{\left(v^{*}\right)}^2}{-\gamma {\nabla }^2+K}dx,$$

where $I_d$ denotes a concerning identity operator.

Other similar notations may be used along this text as their indicated meaning are sufficiently clear.

Additionally, ${\nabla }^2$ denotes the Laplace operator, and for real constants $K_2>0$ and $K_1>0$, the notation $K_2\gg K_1$ means that $K_2>0$ is much larger than $K_1>0.$

Finally, we adopt the standard Einstein convention of summing up repeated indices, unless otherwise indicated.

In order to clarify the notation, here, we introduce the definition of topological dual space.

Definition 1 

(Topological dual spaces). Let U be a Banach space. We define its dual topological space as the set of all linear continuous functionals defined on U. We suppose that such a dual space of U may be represented by another Banach space $U^{*}$, through a bilinear form ${\langle ·,·\rangle }_U:U\times U^{*}\to \mathbb{R}$ (here, we are referring to standard representations of dual spaces of Sobolev and Lebesgue spaces). Thus, given $f:U\to \mathbb{R}$ linear and continuous, we assume the existence of a unique $u^{*}\in U^{*}$ such that

$$\begin{array}{c}f\left(u\right)={\langle u,u^{*}\rangle }_U,\forall u\in U.\end{array}$$

(1)

The norm of f, denoted by ${\parallel f\parallel }_{U^{*}}$, is defined as

$$\begin{array}{c}{\parallel f\parallel }_{U^{*}}=\underset{u\in U}{sup}\left\{\right|{\langle u,u^{*}\rangle }_U{|:\parallel u\parallel }_U\le 1\}\equiv \parallel u^{*}{\parallel }_{U^{*}}.\end{array}$$

(2)

At this point, we start to describe the primal and dual variational formulations.

Let $\Omega \subset {\mathbb{R}}^3$ be an open, bounded, connected set with a regular (Lipschitzian) boundary denoted by $\partial \Omega .$

First, we emphasize that, for the Banach space $Y=Y^{*}=L^2(\Omega )$, we have

$${\langle v,v^{*}\rangle }_{L^2}={\int }_{\Omega }v{v}^{*}dx,\forall v,v^{*}\in L^2(\Omega ).$$

For the primal formulation, we consider the functional $J:U\to \mathbb{R}$, where

$$\begin{array}{ccc}J\left(u\right)\hfill & =\hfill & \frac{\gamma }{2}{\int }_{\Omega }\nabla u·\nabla udx\hfill \\ & \hfill & +\frac{\alpha }{2}{\int }_{\Omega }{(u^2-\beta )}^{2}dx-{\langle u,f\rangle }_{L^2}.\hfill \end{array}$$

(3)

Here, we assume $\alpha >0,\beta >0,\gamma >0$, $U=W_0^{1,2}(\Omega )$, $f\in L^2(\Omega )$. Moreover, we denote

$$Y=Y^{*}=L^2(\Omega ).$$

Define also $G_1:U\to \mathbb{R}$ by

$$G_1\left(u\right)=\frac{\gamma }{2}{\int }_{\Omega }\nabla u·\nabla udx,$$

$G_2:U\times Y\to \mathbb{R}$ by

$$G_2(u,v)=\frac{\alpha }{2}{\int }_{\Omega }{(u^2-\beta +v)}^{2}dx+\frac{K}{2}{\int }_{\Omega }{u}^{2}dx,$$

and $F:U\to \mathbb{R}$ by

$$F\left(u\right)=\frac{K}{2}{\int }_{\Omega }{u}^{2}dx,$$

where $K\gg \gamma .$

It is worth highlighting that in such a case,

$$J\left(u\right)=G_1\left(u\right)+G_2(u,0)-F\left(u\right)-{\langle u,f\rangle }_{L^2},\forall u\in U.$$

Furthermore, define the following specific polar functionals specified, namely, $G_1^{*}:{\left[Y^{*}\right]}^2\to \mathbb{R}$ by

$$\begin{array}{ccc}{G}_1^{*}(v_1^{*}+z^{*})\hfill & =\hfill & \underset{u\in U}{sup}\left\{{\langle u,v_1^{*}+z^{*}\rangle }_{L^2}-G_1\left(u\right)\right\}\hfill \\ & =\hfill & \frac{1}{2}{\int }_{\Omega }\left[{(-\gamma {\nabla }^2)}^{-1}(v_1^{*}+z^{*})\right](v_1^{*}+z^{*})dx,\hfill \end{array}$$

(4)

$G_2^{*}:{\left[Y^{*}\right]}^2\to \mathbb{R}$ by

$$\begin{array}{ccc}{G}_2^{*}(v_2^{*},v_0^{*})\hfill & =\hfill & \underset{(u,v)\in U\times Y}{sup}\left\{{\langle u,v_2^{*}\rangle }_{L^2}+{\langle v,v_0^{*}\rangle }_{L^2}-G_2(u,v)\right\}\hfill \\ & =\hfill & \frac{1}{2}{\int }_{\Omega }\frac{{\left(v_2^{*}\right)}^2}{2v_0^{*}+K}dx\hfill \\ & \hfill & +\frac{1}{2\alpha }{\int }_{\Omega }{\left(v_0^{*}\right)}^{2}dx+\beta {\int }_{\Omega }{v}_0^{*}dx,\hfill \end{array}$$

(5)

if $v_0^{*}\in B^{*}$, where

$$B^{*}=\{v_0^{*}\in Y^{*}:2v_0^{*}+K>K/2\mathrm{in}\Omega \}.$$

At this point, we give more details about this calculation.

Observe that

$$\begin{array}{ccc}{G}_2^{*}(v_2^{*},v_0^{*})\hfill & =\hfill & \underset{(u,v)\in U\times Y}{sup}\left\{{\langle u,v_2^{*}\rangle }_{L^2}+{\langle v,v_0^{*}\rangle }_{L^2}-G_2(u,v)\right\}\hfill \\ & =\hfill & \underset{(u,v)\in U\times Y}{sup}\left\{{\langle u,v_2^{*}\rangle }_{L^2}+{\langle v,v_0^{*}\rangle }_{L^2}-\frac{\alpha }{2}{\int }_{\Omega }{(u^2-\beta +v)}^{2}dx-\frac{K}{2}{\int }_{\Omega }{u}^{2}dx\right\}.\hfill \end{array}$$

(6)

Defining $w=u^2-\beta +v,$ we have $v=w-u^2+\beta ,$ so that

$$\begin{array}{ccc}\hfill & \hfill & G_2^{*}(v_2^{*},v_0^{*})\hfill \\ & =\hfill & \underset{(u,v)\in U\times Y}{sup}\left\{{\langle u,v_2^{*}\rangle }_{L^2}+{\langle v,v_0^{*}\rangle }_{L^2}-\frac{\alpha }{2}{\int }_{\Omega }{(u^2-\beta +v)}^{2}dx-\frac{K}{2}{\int }_{\Omega }{u}^{2}dx\right\}\hfill \\ & =\hfill & \underset{(u,w)\in U\times Y}{sup}\left\{{\langle u,v_2^{*}\rangle }_{L^2}+{\langle w-u^2+\beta ,v_0^{*}\rangle }_{L^2}-\frac{\alpha }{2}{\int }_{\Omega }{\left(w\right)}^{2}dx-\frac{K}{2}{\int }_{\Omega }{u}^{2}dx\right\}\hfill \\ & =\hfill & {\langle \tilde{u},v_2^{*}\rangle }_{L^2}+{\langle \tilde{w}-{\tilde{u}}^2+\beta ,v_0^{*}\rangle }_{L^2}-\frac{\alpha }{2}{\int }_{\Omega }{\left(\tilde{w}\right)}^{2}dx-\frac{K}{2}{\int }_{\Omega }{\tilde{u}}^{2}dx,\hfill \end{array}$$

(7)

where $(\tilde{u},\tilde{w})$ are solution of equations (optimality conditions for such a quadratic optimization problem)

$$v_0^{*}-\alpha \tilde{w}=0,$$

and

$$v_2^{*}-(2v_0^{*}+K)\tilde{u}=0,$$

and therefore,

$$\tilde{w}=\frac{v_0^{*}}{\alpha },$$

and

$$\tilde{u}=\frac{v_2^{*}}{2v_0^{*}+K}.$$

Substituting such results into (7), we obtain

$$\begin{array}{ccc}{G}^{*}(v_1^{*},v_0^{*})\hfill & =\hfill & \frac{1}{2}{\int }_{\Omega }\frac{{\left(v_2^{*}\right)}^2}{2v_0^{*}+K}dx\hfill \\ & \hfill & +\frac{1}{2\alpha }{\int }_{\Omega }{\left(v_0^{*}\right)}^{2}dx+\beta {\int }_{\Omega }{v}_0^{*}dx,\hfill \end{array}$$

(8)

if $v_0^{*}\in B^{*}.$

Finally, $F^{*}:Y^{*}\to \mathbb{R}$ is defined by

$$\begin{array}{ccc}{F}^{*}\left(z^{*}\right)\hfill & =\hfill & \underset{u\in U}{sup}\left\{{\langle u,z^{*}\rangle }_{L^2}-F\left(u\right)\right\}\hfill \\ & =\hfill & \frac{1}{2K}{\int }_{\Omega }{\left(z^{*}\right)}^{2}dx.\hfill \end{array}$$

(9)

Define also

$$A^{*}=\{v^{*}=(v_1^{*},v_2^{*},v_0^{*})\in {\left[Y^{*}\right]}^2\times B^{*}:v_1^{*}+v_2^{*}-f=0,\mathrm{in}\Omega \},$$

$J^{*}:{\left[Y^{*}\right]}^4\to \mathbb{R}$ by

$$J^{*}(v^{*},z^{*})=-G_1^{*}(v_1^{*}+z^{*})-G_2^{*}(v_2^{*},v_0^{*})+F^{*}\left(z^{*}\right)$$

and $J_1^{*}:{\left[Y^{*}\right]}^4\times U\to \mathbb{R}$ by

$$J_1^{*}(v^{*},z^{*},u)=J^{*}(v^{*},z^{*})+{\langle u,v_1^{*}+v_2^{*}-f\rangle }_{L^2}.$$

2. The Main Duality Principle, a Convex Dual Formulation, and the Concerning Proximal Primal Functional

Our main result is summarized by the following theorem.

Theorem 1. 

Considering the definitions and statements in the last section, suppose also that $({\widehat{v}}^{*},{\widehat{z}}^{*},u_0)\in {\left[Y^{*}\right]}^2\times B^{*}\times Y^{*}\times U$ is such that

$$\delta J_1^{*}({\widehat{v}}^{*},{\widehat{z}}^{*},u_0)=\mathbf{0}.$$

Under such hypotheses, we have

$$\delta J\left(u_0\right)=\mathbf{0},$$

$${\widehat{v}}^{*}\in A^{*}$$

and

$$\begin{array}{ccc}J\left(u_0\right)\hfill & =\hfill & \underset{u\in U}{inf}\left\{J\left(u\right)+\frac{K}{2}{\int }_{\Omega }{|u-u_0|}^{2}dx\right\}\hfill \\ & =\hfill & J^{*}({\widehat{v}}^{*},{\widehat{z}}^{*})\hfill \\ & =\hfill & \underset{v^{*}\in A^{*}}{sup}\left\{J^{*}(v^{*},{\widehat{z}}^{*})\right\}.\hfill \end{array}$$

(10)

Proof. 

Since

$$\delta J_1^{*}({\widehat{v}}^{*},{\widehat{z}}^{*},u_0)=\mathbf{0},$$

from the variation in $v_1^{*}$, we obtain

$$-\frac{({\widehat{v}}_1^{*}+{\widehat{z}}^{*})}{-\gamma {\nabla }^2}+u_0=0\mathrm{in}\Omega ,$$

so that

$${\widehat{v}}_1^{*}+{\widehat{z}}^{*}=-\gamma {\nabla }^2{u}_0.$$

From the variation in $v_2^{*}$, we obtain

$$-\frac{{\widehat{v}}_2^{*}}{2{\widehat{v}}_0^{*}+K}+u_0=0,\mathrm{in}\Omega .$$

From the variation in $v_0^{*}$, we also obtain

$$\frac{{\left({\widehat{v}}_2^{*}\right)}^2}{{(2{\widehat{v}}_0^{*}+K)}^2}-\frac{{\widehat{v}}_0^{*}}{\alpha }-\beta =0,$$

and therefore,

$${\widehat{v}}_0^{*}=\alpha (u_0^2-\beta ).$$

From the variation in u, we have

$${\widehat{v}}_1^{*}+{\widehat{v}}_2^{*}-f=0,\mathrm{in}\Omega$$

and, thus,

$${\widehat{v}}^{*}\in A^{*}.$$

Finally, from the variation in $z^{*}$, we obtain

$$-\frac{({\widehat{v}}_1^{*}+{\widehat{z}}^{*})}{-\gamma {\nabla }^2}+\frac{{\widehat{z}}^{*}}{K}=0,\mathrm{in}\Omega .$$

so that

$$-u_0+\frac{{\widehat{z}}^{*}}{K}=0,$$

that is,

$${\widehat{z}}^{*}=K{u}_0\mathrm{in}\Omega .$$

From such results and ${\widehat{v}}^{*}\in A^{*}$, we have

$$\begin{array}{ccc}0\hfill & =\hfill & {\widehat{v}}_1^{*}+{\widehat{v}}_2^{*}-f\hfill \\ & =\hfill & -\gamma {\nabla }^2{u}_0-{\widehat{z}}^{*}+2\left(v_0^{*}\right)u_0+K{u}_0-f\hfill \\ & =\hfill & -\gamma {\nabla }^2{u}_0+2\alpha (u_0^2-\beta )u_0-f,\hfill \end{array}$$

(11)

so that

$$\delta J\left(u_0\right)=\mathbf{0}.$$

Additionally, from this and from the Legendre transform proprieties, we have

$$G_1^{*}({\widehat{v}}_1^{*}+{\widehat{z}}^{*})={〈u_0,{\widehat{v}}_1^{*}+{\widehat{z}}^{*}〉}_{L^2}-G_1\left(u_0\right),$$

$$G_2^{*}({\widehat{v}}_2^{*},{\widehat{v}}_0^{*})={\langle u_0,{\widehat{v}}_2^{*}\rangle }_{L^2}+{\langle 0,v_0^{*}\rangle }_{L^2}-G_2(u_0,0),$$

$$F^{*}\left({\widehat{z}}^{*}\right)={\langle u_0,{\widehat{z}}^{*}\rangle }_{L^2}-F\left(u_0\right),$$

and thus, we obtain

$$\begin{array}{ccc}{J}^{*}({\widehat{v}}^{*},{\widehat{z}}^{*})\hfill & =\hfill & -G_1^{*}({\widehat{v}}_1^{*}+{\widehat{z}}^{*})-G_2^{*}({\widehat{v}}_2^{*},{\widehat{v}}_0^{*})+F^{*}\left({\widehat{z}}^{*}\right)\hfill \\ & =\hfill & -\langle u_0,{\widehat{v}}_1^{*}+{\widehat{v}}_2^{*}\rangle +G_1\left(u_0\right)+G_2(u_0,0)-F\left(u_0\right)\hfill \\ & =\hfill & -{\langle u_0,f\rangle }_{L^2}+G_1\left(u_0\right)+G_2(u_0,0)-F\left(u_0\right)\hfill \\ & =\hfill & J\left(u_0\right).\hfill \end{array}$$

(12)

Summarizing, we have

$$J^{*}({\widehat{v}}^{*},{\widehat{z}}^{*})=J\left(u_0\right).$$

(13)

On the other hand,

$$\begin{array}{ccc}{J}^{*}({\widehat{v}}^{*},{\widehat{z}}^{*})\hfill & =\hfill & -G_1^{*}({\widehat{v}}_1^{*}+{\widehat{z}}^{*})-G_2^{*}({\widehat{v}}_2^{*},{\widehat{v}}_0^{*})+F^{*}\left({\widehat{z}}^{*}\right)\hfill \\ & \le \hfill & -{\langle u,{\widehat{v}}_1^{*}+{\widehat{z}}^{*}\rangle }_{L^2}-{\langle u,{\widehat{v}}_2^{*}\rangle }_{L^2}-{\langle 0,v_0^{*}\rangle }_{L^2}+G_1\left(u\right)+G_2(u,0)+F^{*}\left({\widehat{z}}^{*}\right)\hfill \\ & =\hfill & -{\langle u,f\rangle }_{L^2}+G_1\left(u\right)+G_2(u,0)-{\langle u,{\widehat{z}}^{*}\rangle }_{L^2}+F^{*}\left({\widehat{z}}^{*}\right)\hfill \\ & =\hfill & -{\langle u,f\rangle }_{L^2}+G_1\left(u\right)+G_2(u,0)-F\left(u\right)+F\left(u\right)-{\langle u,{\widehat{z}}^{*}\rangle }_{L^2}+F^{*}\left({\widehat{z}}^{*}\right)\hfill \\ & =\hfill & J\left(u\right)+\frac{K}{2}{\int }_{\Omega }{u}^{2}dx-{\langle u,{\widehat{z}}^{*}\rangle }_{L^2}+F^{*}\left({\widehat{z}}^{*}\right)\hfill \\ & =\hfill & J\left(u\right)+\frac{K}{2}{\int }_{\Omega }{u}^{2}dx-K{\langle u,u_0\rangle }_{L^2}+\frac{K}{2}{\int }_{\Omega }{u}_0^{2}dx\hfill \\ & =\hfill & J\left(u\right)+\frac{K}{2}{\int }_{\Omega }{|u-u_0|}^{2}dx,\forall u\in U.\hfill \end{array}$$

(14)

Finally, by a simple computation, we may obtain the Hessian

$$\left\{\frac{{\partial }^2{J}^{*}(v^{*},z^{*})}{\partial {\left(v^{*}\right)}^2}\right\}<\mathbf{0}$$

in ${\left[Y^{*}\right]}^2\times B^{*}\times Y^{*}$, so that we may infer that $J^{*}$ is concave in $v^{*}$ in ${\left[Y^{*}\right]}^2\times B^{*}\times Y^{*}$.

Therefore, from this, (13) and (14), we have

$$\begin{array}{ccc}J\left(u_0\right)\hfill & =\hfill & \underset{u\in U}{inf}\left\{J\left(u\right)+\frac{K}{2}{\int }_{\Omega }{|u-u_0|}^{2}dx\right\}\hfill \\ & =\hfill & J^{*}({\widehat{v}}^{*},{\widehat{z}}^{*})\hfill \\ & =\hfill & \underset{v^{*}\in A^{*}}{sup}\left\{J^{*}(v^{*},{\widehat{z}}^{*})\right\}.\hfill \end{array}$$

(15)

The proof is complete. □

3. A Primal Dual Variational Formulation

In this section, we develop a more general primal dual variational formulation suitable for a large class of models in non-convex optimization.

Consider again $U=W_0^{1,2}(\Omega )$, and let $G:U\to \mathbb{R}$ and $F:U\to \mathbb{R}$ be three times Fréchet differentiable functionals. Let $J:U\to \mathbb{R}$ be defined by

$$J\left(u\right)=G\left(u\right)-F\left(u\right),\forall u\in U.$$

Assume that $u_0\in U$ is such that

$$\delta J\left(u_0\right)=\mathbf{0}$$

and

$${\delta }^{2}J\left(u_0\right)>\mathbf{0}.$$

Denote $v^{*}=(v_1^{*},v_2^{*})$, define $J^{*}:U\times Y^{*}\times Y^{*}\to \mathbb{R}$ by

$$J^{*}(u,v^{*})=\frac{1}{2}\parallel v_1^{*}-G^{\prime }\left(u\right){\parallel }_2^2+\frac{1}{2}\parallel v_2^{*}-F^{\prime }\left(u\right){\parallel }_2^2+\frac{1}{2}{\parallel v_1^{*}-v_2^{*}\parallel }_2^2$$

(16)

Denoting $L_1^{*}(u,v^{*})=v_1^{*}-G^{\prime }\left(u\right)$ and $L_2^{*}(u,v^{*})=v_2^{*}-F^{\prime }\left(u\right)$, define also

$$C^{*}=\left\{(u,v^{*})\in U\times Y^{*}\times Y^{*}:\parallel L_1^{*}(u,v_1^{*}){\parallel }_{\infty }\le \frac{1}{K}\mathrm{and}{\parallel L_2^{*}(u,v_1^{*})\parallel }_{\infty }\le \frac{1}{K}\right\},$$

for an appropriate $K>0$ to be specified.

Observe that in $C^{*}$, the Hessian of $J^{*}$ is given by

$$\left\{{\delta }^2{J}^{*}(u,v^{*})\right\}=\left\{\begin{array}{ccc}{G}^{″}{\left(u\right)}^2+F^{″}{\left(u\right)}^2+\mathcal{O}(1/K)\hfill & \hfill -G^{″}\left(u\right)& \hfill -F^{″}\left(u\right)\\ -G^{″}\left(u\right)\hfill & \hfill 2& \hfill -1\\ -F^{″}\left(u\right)\hfill & \hfill -1& \hfill 2\end{array}\right\},$$

(17)

Observe also that

$$det\left\{\frac{{\partial }^2{J}^{*}(u,v^{*})}{\partial v_1^{*}\partial v_2^{*}}\right\}=3,$$

and

$$det\left\{{\delta }^2{J}^{*}(u,v^{*})\right\}={(G^{″}\left(u\right)-F^{″}\left(u\right))}^2+\mathcal{O}(1/K)={\left({\delta }^{2}J\left(u\right)\right)}^2+\mathcal{O}(1/K).$$

Define now

$${\widehat{v}}_1^{*}=G^{\prime }\left(u_0\right),$$

$${\widehat{v}}_2^{*}=F^{\prime }\left(u_0\right),$$

so that

$${\widehat{v}}_1^{*}-{\widehat{v}}_2^{*}=\mathbf{0}.$$

From this, we may infer that $(u_0,{\widehat{v}}_1^{*},{\widehat{v}}_2^{*})\in C^{*}$ and

$$J^{*}(u_0,{\widehat{v}}^{*})=0=\underset{(u,v^{*})\in C^{*}}{min}{J}^{*}(u,v^{*}).$$

Moreover, for $K>0$ sufficiently big, $J^{*}$ is convex in a neighborhood of $(u_0,{\widehat{v}}^{*})$.

Therefore, in the last lines, we have proven the following theorem.

Theorem 2. 

Under the statements and definitions of the last lines, there exist $r_0>0$ and $r_1>0$ such that

$$J\left(u_0\right)=\underset{u\in B_{r_0}\left(u_0\right)}{min}J\left(u\right)$$

and $(u_0,{\widehat{v}}_1^{*},{\widehat{v}}_2^{*})\in C^{*}$ is such that

$$J^{*}(u_0,{\widehat{v}}^{*})=0=\underset{(u,v^{*})\in U\times {\left[Y^{*}\right]}^2}{min}{J}^{*}(u,v^{*}).$$

Moreover, $J^{*}$ is convex in

$$B_{r_1}(u_0,{\widehat{v}}^{*}).$$

4. One More Duality Principle and a Concerning Primal Dual Variational Formulation

In this section, we establish a new duality principle and a related primal dual formulation.

The results are based on the approach of Toland [5].

4.1. Introduction

Let $\Omega \subset {\mathbb{R}}^3$ be an open, bounded, connected set with a regular (Lipschitzian) boundary denoted by $\partial \Omega .$

Let $J:V\to \mathbb{R}$ be a functional such that

$$J\left(u\right)=G\left(u\right)-F\left(u\right),\forall u\in V,$$

where $V=W_0^{1,2}(\Omega )$.

Suppose $G,F$ are both three times Fréchet differentiable convex functionals such that

$$\frac{{\partial }^{2}G\left(u\right)}{\partial u^2}>0$$

and

$$\frac{{\partial }^{2}F\left(u\right)}{\partial u^2}>0$$

$\forall u\in V.$

Assume also that there exists ${\alpha }_1\in \mathbb{R}$ such that

$${\alpha }_1=\underset{u\in V}{inf}J\left(u\right).$$

Moreover, suppose that if $\left\{u_n\right\}\subset V$ is such that

$$\parallel u_n{\parallel }_V\to \infty ,$$

then

$$J\left(u_n\right)\to +\infty ,\mathrm{as}n\to \infty .$$

At this point, we define $J^{**}:V\to \mathbb{R}$ by

$$J^{**}\left(u\right)=\underset{(v^{*},\alpha )\in H^{*}}{sup}\{\langle u,v^{*}\rangle +\alpha \},$$

where

$$H^{*}=\{(v^{*},\alpha )\in V^{*}\times \mathbb{R}:{\langle v,v^{*}\rangle }_V+\alpha \le F\left(v\right),\forall v\in V\}.$$

Observe that $(0,{\alpha }_1)\in H^{*},$ so that

$$J^{**}\left(u\right)\ge {\alpha }_1=\underset{u\in V}{inf}J\left(u\right).$$

On the other hand, clearly, we have

$$J^{**}\left(u\right)\le J\left(u\right),\forall u\in V,$$

so that we have

$${\alpha }_1=\underset{u\in V}{inf}J\left(u\right)=\underset{u\in V}{inf}{J}^{**}\left(u\right).$$

Let $u\in V$.

Since J is strongly continuous, there exist $\delta >0$ and $A>0$ such that

$${\alpha }_1\le J^{**}\left(v\right)\le J\left(v\right)\le A,\forall v\in B_{\delta }\left(u\right).$$

From this, considering that $J^{**}$ is convex on V, we may infer that $J^{**}$ is continuous at u, $\forall u\in V.$

Hence, $J^{**}$ is strongly lower semi-continuous on V, and since $J^{**}$ is convex, we may infer that $J^{**}$ is weakly lower semi-continuous on V.

Let $\left\{u_n\right\}\subset V$ be a sequence such that

$${\alpha }_1\le J\left(u_n\right)<{\alpha }_1+\frac{1}{n},\forall n\in \mathbb{N}.$$

Hence,

$${\alpha }_1=\underset{n\to \infty }{lim}J\left(u_n\right)=\underset{u\in V}{inf}J\left(u\right)=\underset{u\in V}{inf}{J}^{**}\left(u\right).$$

Suppose that there exists a subsequence $\left\{u_{n_k}\right\}$ of $\left\{u_n\right\}$ such that

$$\parallel u_{n_k}{\parallel }_V\to \infty ,\mathrm{as}k\to \infty .$$

From the hypothesis, we have

$$J\left(u_{n_k}\right)\to +\infty ,\mathrm{as}k\to \infty ,$$

which contradicts

$${\alpha }_1\in \mathbb{R}.$$

Therefore, there exists $K>0$ such that

$$\parallel u_n{\parallel }_V\le K,\forall u\in V.$$

Since V is reflexive, from this and the Katutani Theorem, there exists a subsequence $\left\{u_{n_k}\right\}$ of $\left\{u_n\right\}$ and $u_0\in V$ such that

$$u_{n_k}\rightharpoonup u_0,\mathrm{weakly}\mathrm{in}V.$$

Consequently, from this and considering that $J^{**}$ is weakly lower semi-continuous, we have

$${\alpha }_1=\underset{k\to \infty }{lim\; inf}{J}^{**}\left(u_{n_k}\right)\ge J^{**}\left(u_0\right),$$

so that

$$J^{**}\left(u_0\right)=\underset{u\in V}{min}{J}^{**}\left(u\right).$$

Define $G^{*},F^{*}:V^{*}\to \mathbb{R}$ by

$$G^{*}\left(v^{*}\right)=\underset{u\in V}{sup}\{{\langle u,v^{*}\rangle }_V-G\left(u\right)\},$$

and

$$F^{*}\left(v^{*}\right)=\underset{u\in V}{sup}\{{\langle u,v^{*}\rangle }_V-F\left(u\right)\}.$$

Defining also $J^{*}:V\to \mathbb{R}$ by

$$J^{*}\left(v^{*}\right)=F^{*}\left(v^{*}\right)-G^{*}\left(v^{*}\right),$$

from the results in [5], we may obtain

$$\underset{u\in V}{inf}J\left(u\right)=\underset{v^{*}\in V^{*}}{inf}{J}^{*}\left(v^{*}\right),$$

so that

$$\begin{array}{ccc}{J}^{**}\left(u_0\right)\hfill & =\hfill & \underset{u\in V}{inf}{J}^{**}\left(u\right)\hfill \\ & =\hfill & \underset{u\in V}{inf}J\left(u\right)=\underset{v^{*}\in V^{*}}{inf}{J}^{*}\left(v^{*}\right).\hfill \end{array}$$

(18)

Suppose now that there exists $\widehat{u}\in V$ such that

$$J\left(\widehat{u}\right)=\underset{u\in V}{inf}J\left(u\right).$$

From the standard necessary conditions, we have

$$\delta J\left(\widehat{u}\right)=\mathbf{0},$$

so that

$$\frac{\partial G\left(\widehat{u}\right)}{\partial u}-\frac{\partial F\left(\widehat{u}\right)}{\partial u}=\mathbf{0}.$$

Define now

$$v_0^{*}=\frac{\partial F\left(\widehat{u}\right)}{\partial u}.$$

From these last two equations, we obtain

$$v_0^{*}=\frac{\partial G\left(\widehat{u}\right)}{\partial u}.$$

From such results and the Legendre transform properties, we have

$$\widehat{u}=\frac{\partial F^{*}\left(v_0^{*}\right)}{\partial v^{*}},$$

$$\widehat{u}=\frac{\partial G^{*}\left(v_0^{*}\right)}{\partial v^{*}},$$

so that

$$\delta J^{*}\left(v_0^{*}\right)=\frac{\partial F^{*}\left(v_0^{*}\right)}{\partial v^{*}}-\frac{\partial G^{*}\left(v_0^{*}\right)}{\partial v^{*}}=\widehat{u}-\widehat{u}=\mathbf{0},$$

$$G^{*}\left(v_0^{*}\right)={\langle \widehat{u},v_0^{*}\rangle }_V-G\left(\widehat{u}\right)$$

and

$$F^{*}\left(v_0^{*}\right)={\langle \widehat{u},v_0^{*}\rangle }_V-F\left(\widehat{u}\right)$$

so that

$$\begin{array}{ccc}\underset{u\in V}{inf}J\left(u\right)\hfill & =\hfill & J\left(\widehat{u}\right)\hfill \\ & =\hfill & G\left(\widehat{u}\right)-F\left(\widehat{u}\right)\hfill \\ & =\hfill & \underset{v^{*}\in V^{*}}{inf}{J}^{*}\left(v^{*}\right)\hfill \\ & =\hfill & F^{*}\left(v_0^{*}\right)-G^{*}\left(v_0^{*}\right)\hfill \\ & =\hfill & J^{*}\left(v_0^{*}\right).\hfill \end{array}$$

(19)

4.2. The Main Duality Principle and a Related Primal Dual Variational Formulation

Considering these last statements and results, we may prove the following theorem.

Theorem 3. 

Let $\Omega \subset {\mathbb{R}}^3$ be an open, bounded, connected set with a regular (Lipschitzian) boundary denoted by $\partial \Omega .$

Let $J:V\to \mathbb{R}$ be a functional such that

$$J\left(u\right)=G\left(u\right)-F\left(u\right),\forall u\in V,$$

where $V=W_0^{1,2}(\Omega )$.

Suppose $G,F$ are both three times Fréchet differentiable functionals such that there exists $K>0$ such that

$$\frac{{\partial }^{2}G\left(u\right)}{\partial u^2}+K>0$$

and

$$\frac{{\partial }^{2}F\left(u\right)}{\partial u^2}+K>0$$

$\forall u\in V.$

Assume also that there exists $u_0\in V$ and ${\alpha }_1\in \mathbb{R}$ such that

$${\alpha }_1=\underset{u\in V}{inf}J\left(u\right)=J\left(u_0\right).$$

Assume that $K_3>0$ is such that

$$\parallel u_0{\parallel }_{\infty }<K_3.$$

Define

$$\tilde{V}={\{u\in V:\parallel u\parallel }_{\infty }\le K_3\}.$$

Assume that $K_1>0$ is such that if $u\in \tilde{V}$, then

$$max\left\{\parallel F^{\prime }{\left(u\right)\parallel }_{\infty },\parallel G^{\prime }{\left(u\right)\parallel }_{\infty },\parallel F^{″}{\left(u\right)\parallel }_{\infty },\parallel F^{‴}{\left(u\right)\parallel }_{\infty },\parallel G^{″}{\left(u\right)\parallel }_{\infty },{\parallel G^{‴}\left(u\right)\parallel }_{\infty }\right\}\le K_1.$$

Suppose also

$$K\gg max\{K_1,K_3\}.$$

Define $F_K,G_K:V\to \mathbb{R}$ by

$$F_K\left(u\right)=F\left(u\right)+\frac{K}{2}{\int }_{\Omega }{u}^{2}dx,$$

and

$$G_K\left(u\right)=G\left(u\right)+\frac{K}{2}{\int }_{\Omega }{u}^{2}dx,$$

$\forall u\in V.$

Define also $G_K^{*},F_K^{*}:V^{*}\to \mathbb{R}$ by

$$G_K^{*}\left(v^{*}\right)=\underset{u\in V}{sup}\{{\langle u,v^{*}\rangle }_V-G_K\left(u\right)\},$$

and

$$F_K^{*}\left(v^{*}\right)=\underset{u\in V}{sup}\{{\langle u,v^{*}\rangle }_V-F_K\left(u\right)\}.$$

Observe that since $u_0\in V$ is such that

$$J\left(u_0\right)=\underset{u\in V}{inf}J\left(u\right),$$

we have

$$\delta J\left(u_0\right)=\mathbf{0}.$$

Let $\epsilon >0$ be a small constant.

Define

$$v_0^{*}=\frac{\partial F_K\left(u_0\right)}{\partial u}\in V^{*}.$$

Under such hypotheses, defining $J_1^{*}:V\times V^{*}\to \mathbb{R}$ by

$$\begin{array}{ccc}{J}_1^{*}(u,v^{*})\hfill & =\hfill & F_K^{*}\left(v^{*}\right)-G_K^{*}\left(v^{*}\right)\hfill \\ & \hfill & +\frac{1}{2\epsilon }{∥\frac{\partial G_K^{*}\left(v^{*}\right)}{\partial v^{*}}-u∥}_2^2+\frac{1}{2\epsilon }{∥\frac{\partial F_K^{*}\left(v^{*}\right)}{\partial v^{*}}-u∥}_2^2\hfill \\ & \hfill & +\frac{1}{2\epsilon }{∥\frac{\partial G_K^{*}\left(v^{*}\right)}{\partial v^{*}}-\frac{\partial F_K^{*}\left(v^{*}\right)}{\partial v^{*}}∥}_2^2,\hfill \end{array}$$

(20)

we have

$$\begin{array}{ccc}J\left(u_0\right)\hfill & =\hfill & \underset{u\in V}{inf}J\left(u\right)\hfill \\ \hfill & =\hfill & \underset{(u,v^{*})\in V\times V^{*}}{inf}{J}_1^{*}(u,v^{*})\hfill \\ & =\hfill & J_1^{*}(u_0,v_0^{*}).\hfill \end{array}$$

(21)

Proof. 

Observe that from the hypotheses, and the results and statements of the last subsection,

$$J\left(u_0\right)=\underset{u\in V}{inf}J\left(u\right)=\underset{v^{*}\in Y^{*}}{inf}{J}_K^{*}\left(v^{*}\right)=J_K^{*}\left(v_0^{*}\right),$$

where

$$J_K^{*}\left(v^{*}\right)=F_K^{*}\left(v^{*}\right)-G_K^{*}\left(v^{*}\right),\forall v^{*}\in V^{*}.$$

Moreover, we have

$$J_1^{*}(u,v^{*})\ge J_K^{*}\left(v^{*}\right),\forall u\in V,v^{*}\in V^{*}.$$

Additionally, from hypotheses and the results in the last subsection,

$$u_0=\frac{\partial F_K^{*}\left(v_0^{*}\right)}{\partial v^{*}}=\frac{\partial G_K^{*}\left(v_0^{*}\right)}{\partial v^{*}},$$

so that clearly, we have

$$J_1^{*}(u_0,v_0^{*})=J_K^{*}\left(v_0^{*}\right).$$

From these results, we may infer that

$$\begin{array}{ccc}J\left(u_0\right)\hfill & =\hfill & \underset{u\in V}{inf}J\left(u\right)\hfill \\ & =\hfill & \underset{v^{*}\in V^{*}}{inf}{J}_K^{*}\left(v^{*}\right)\hfill \\ & =\hfill & J_K^{*}\left(v_0^{*}\right)\hfill \\ & =\hfill & \underset{(u,v^{*})\in V\times V^{*}}{inf}{J}_1^{*}(u,v^{*})\hfill \\ & =\hfill & J_1^{*}(u_0,v_0^{*}).\hfill \end{array}$$

(22)

The proof is complete. □

Remark 2. 

At this point, we highlight that $J_1^{*}$ has a large region of convexity around the optimal point $(u_0,v_0^{*})$, for $K>0$ sufficiently large and corresponding $\epsilon >0$ sufficiently small.

Indeed, observe that for $v^{*}\in V^{*}$,

$$G_K^{*}\left(v^{*}\right)=\underset{u\in V}{sup}\{{\langle u,v^{*}\rangle }_V-G_K\left(u\right)\}={\langle \widehat{u},v^{*}\rangle }_V-G_K\left(\widehat{u}\right),$$

where $\widehat{u}\in V$ is such that

$$v^{*}=\frac{\partial G_K\left(\widehat{u}\right)}{\partial u}=G^{\prime }\left(\widehat{u}\right)+K\widehat{u}.$$

Taking the variation in $v^{*}$ in this last equation, we obtain

$$1=G^{″}\left(u\right)\frac{\partial \widehat{u}}{\partial v^{*}}+K\frac{\partial \widehat{u}}{\partial v^{*}},$$

so that

$$\frac{\partial \widehat{u}}{\partial v^{*}}=\frac{1}{G^{″}\left(u\right)+K}=\mathcal{O}\left(\frac{1}{K}\right).$$

From this, we have

$$\begin{array}{ccc}\frac{{\partial }^2\widehat{u}}{\partial {\left(v^{*}\right)}^2}\hfill & =\hfill & -\frac{1}{{(G^{″}\left(u\right)+K)}^2}{G}^{‴}\left(u\right)\frac{\partial \widehat{u}}{\partial v^{*}}\hfill \\ & =\hfill & -\frac{1}{{(G^{″}\left(u\right)+K)}^3}{G}^{‴}\left(u\right)\hfill \\ & =\hfill & \mathcal{O}\left(\frac{1}{K^3}\right).\hfill \end{array}$$

(23)

On the other hand, from the implicit function theorem,

$$\frac{\partial G_K^{*}\left(v^{*}\right)}{\partial v^{*}}=u+[v^{*}-G_K^{\prime }\left(\widehat{u}\right)]\frac{\partial \widehat{u}}{\partial v^{*}}=u,$$

so that

$$\frac{{\partial }^2{G}_K^{*}\left(v^{*}\right)}{\partial {\left(v^{*}\right)}^2}=\frac{\partial \widehat{u}}{\partial v^{*}}=\mathcal{O}\left(\frac{1}{K}\right)$$

and

$$\frac{{\partial }^3{G}_K^{*}\left(v^{*}\right)}{\partial {\left(v^{*}\right)}^3}=\frac{{\partial }^2\widehat{u}}{\partial {\left(v^{*}\right)}^2}=\mathcal{O}\left(\frac{1}{K^3}\right).$$

Similarly, we may obtain

$$\frac{{\partial }^2{F}_K^{*}\left(v^{*}\right)}{\partial {\left(v^{*}\right)}^2}=\mathcal{O}\left(\frac{1}{K}\right)$$

and

$$\frac{{\partial }^3{F}_K^{*}\left(v^{*}\right)}{\partial {\left(v^{*}\right)}^3}=\mathcal{O}\left(\frac{1}{K^3}\right).$$

Denoting

$$A=\frac{{\partial }^2{F}_K^{*}\left(v_0^{*}\right)}{\partial {\left(v^{*}\right)}^2}$$

and

$$B=\frac{{\partial }^2{G}_K^{*}\left(v_0^{*}\right)}{\partial {\left(v^{*}\right)}^2},$$

we have

$$\frac{{\partial }^2{J}_1^{*}(u_0,v_0^{*})}{\partial {\left(v^{*}\right)}^2}=A-B+\frac{1}{\epsilon }\left(2A^2+2B^2-2AB\right),$$

$$\frac{{\partial }^2{J}_1^{*}(u_0,v_0^{*})}{\partial u^2}=\frac{2}{\epsilon },$$

and

$$\frac{{\partial }^2{J}_1^{*}(u_0,v_0^{*})}{\partial \left(v^{*}\right)\partial u}=-\frac{1}{\epsilon }(A+B).$$

From this, we have

$$\begin{array}{ccc}det\left({\delta }^2{J}^{*}(v_0^{*},u_0)\right)\hfill & =\hfill & \frac{{\partial }^2{J}_1^{*}(u_0,v_0^{*})}{\partial {\left(v^{*}\right)}^2}\frac{{\partial }^2{J}_1^{*}(u_0,v_0^{*})}{\partial u^2}-{\left[\frac{{\partial }^2{J}_1^{*}(u_0,v_0^{*})}{\partial \left(v^{*}\right)\partial u}\right]}^2\hfill \\ & =\hfill & 2\frac{A-B}{\epsilon }+2\frac{{(A-B)}^2}{{\epsilon }^2}\hfill \\ & =\hfill & \mathcal{O}\left(\frac{1}{{\epsilon }^2}\right)\hfill \\ & \gg \hfill & \mathbf{0}\hfill \end{array}$$

(24)

about the optimal point $(u_0,v_0^{*}).$

5. A Convex Dual Variational Formulation

In this section, again for $\Omega \subset {\mathbb{R}}^3$, an open, bounded, connected set with a regular (Lipschitzian) boundary $\partial \Omega$, $\gamma >0,$$\alpha >0,$$\beta >0$ and $f\in L^2(\Omega )$, we denote $F_1:V\times Y\to \mathbb{R}$, $F_2:V\to \mathbb{R}$ and $G:V\times Y\to \mathbb{R}$ by

$$\begin{array}{ccc}{F}_1(u,v_0^{*})\hfill & =\hfill & \frac{\gamma }{2}{\int }_{\Omega }\nabla u·\nabla udx-\frac{K}{2}{\int }_{\Omega }{u}^{2}dx\hfill \\ & \hfill & +\frac{K_1}{2}{\int }_{\Omega }{(-\gamma {\nabla }^{2}u+2v_0^{*}u-f)}^{2}dx+\frac{K_2}{2}{\int }_{\Omega }{u}^{2}dx,\hfill \end{array}$$

(25)

$$F_2\left(u\right)=\frac{K_2}{2}{\int }_{\Omega }{u}^{2}dx+{\langle u,f\rangle }_{L^2},$$

and

$$G(u,v)=\frac{\alpha }{2}{\int }_{\Omega }{(u^2-\beta +v)}^{2}dx+\frac{K}{2}{\int }_{\Omega }{u}^{2}dx.$$

We define also

$$J_1(u,v_0^{*})=F_1(u,v_0^{*})-F_2\left(u\right)+G(u,0),$$

$$J\left(u\right)=\frac{\gamma }{2}{\int }_{\Omega }\nabla u·\nabla udx+\frac{\alpha }{2}{\int }_{\Omega }{(u^2-\beta )}^{2}dx-{\langle u,f\rangle }_{L^2},$$

and $F_1^{*}:{\left[Y^{*}\right]}^3\to \mathbb{R},$$F_2^{*}:Y^{*}\to \mathbb{R},$ and $G^{*}:{\left[Y^{*}\right]}^2\to \mathbb{R},$ by

$$\begin{array}{ccc}\hfill & \hfill & F_1^{*}(v_2^{*},v_1^{*},v_0^{*})\hfill \\ & =\hfill & \underset{u\in V}{sup}\{{\langle u,v_1^{*}+v_2^{*}\rangle }_{L^2}-F_1(u,v_0^{*})\}\hfill \\ & =\hfill & \frac{1}{2}{\int }_{\Omega }\frac{{\left(v_1^{*}+v_2^{*}+K_1(-\gamma {\nabla }^2+2v_0^{*})f\right)}^2}{(-\gamma {\nabla }^2-K+K_2+K_1{(-\gamma {\nabla }^2+2v_0^{*})}^2)}dx\hfill \\ & \hfill & -\frac{K_1}{2}{\int }_{\Omega }{f}^{2}dx,\hfill \end{array}$$

(26)

$$\begin{array}{ccc}{F}_2^{*}\left(v_2^{*}\right)\hfill & =\hfill & \underset{u\in V}{sup}\{{\langle u,v_2^{*}\rangle }_{L^2}-F_2\left(u\right)\}\hfill \\ & =\hfill & \frac{1}{2K_2}{\int }_{\Omega }{\left(v_2^{*}\right)}^{2}dx,\hfill \end{array}$$

(27)

and

$$\begin{array}{ccc}{G}^{*}(v_1^{*},v_0^{*})\hfill & =\hfill & \underset{(u,v)\in V\times Y}{sup}\{{\langle u,v_1^{*}\rangle }_{L^2}-{\langle v,v_0^{*}\rangle }_{L^2}-G(u,v)\}\hfill \\ & =\hfill & \frac{1}{2}{\int }_{\Omega }\frac{{\left(v_1^{*}\right)}^2}{2v_0^{*}+K}dx+\frac{1}{2\alpha }{\int }_{\Omega }{\left(v_0^{*}\right)}^{2}dx\hfill \\ & \hfill & +\beta {\int }_{\Omega }{v}_0^{*}dx\hfill \end{array}$$

(28)

if $v_0^{*}\in B^{*}$, where

$$B^{*}=\{v_0^{*}\in Y^{*}:\parallel v_0^{*}{\parallel }_{\infty }\le K/2\mathrm{and}-\gamma {\nabla }^2+2v_0^{*}<-\epsilon I_d\},$$

for some small real parameter $\epsilon >0$ and where $I_d$ denotes a concerning identity operator.

Finally, we also define $J_1^{*}:{\left[Y^{*}\right]}^2\times B^{*}\to \mathbb{R},$

$$J_1^{*}(v_2^{*},v_1^{*},v_0^{*})=-F_1^{*}(v_2^{*},v_1^{*},v_0^{*})+F_2^{*}\left(v_2^{*}\right)-G^{*}(v_1^{*},v_0^{*}).$$

Assuming

$$K_2\gg K_1\gg K\gg max\{1/\left({\epsilon }^2\right),1,\gamma ,\alpha \}$$

by directly computing ${\delta }^2{J}_1^{*}(v_2^{*},v_1^{*},v_0^{*})$, we may obtain that for such specified real constants, $J_1^{*}$ is convex in $v_2^{*}$ and it is concave in $(v_1^{*},v_0^{*})$ on $Y^{*}\times Y^{*}\times B^{*}.$

Considering such statements and definitions, we may prove the following theorem.

Theorem 4. 

Let $({\widehat{v}}_2^{*},{\widehat{v}}_1^{*},{\widehat{v}}_0^{*})\in Y^{*}\times Y^{*}\times B^{*}$ be such that

$$\delta J_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_1^{*},{\widehat{v}}_0^{*})=\mathbf{0}$$

and $u_0\in V$ be such that

$$u_0=\frac{{\widehat{v}}_1^{*}+{\widehat{v}}_2^{*}+K_1(-\gamma {\nabla }^2+2v_0^{*})f}{K_2-K-\gamma {\nabla }^2+K_1{(-\gamma {\nabla }^2+2{\widehat{v}}_0^{*})}^2}.$$

Under such hypotheses, we have

$$\delta J\left(u_0\right)=\mathbf{0},$$

so that

$$\begin{array}{ccc}J\left(u_0\right)\hfill & =\hfill & \underset{u\in V}{inf}\left\{J\left(u\right)+\frac{K_1}{2}{\int }_{\Omega }{(-\gamma {\nabla }^{2}u+2{\widehat{v}}_0^{*}u-f)}^{2}dx\right\}\hfill \\ & =\hfill & \underset{v_2^{*}\in Y^{*}}{inf}\left\{\underset{(v_1^{*},v_0^{*})\in Y^{*}\times B^{*}}{sup}{J}_1^{*}(v_2^{*},v_1^{*},v_0^{*})\right\}\hfill \\ & =\hfill & J_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_1^{*},{\widehat{v}}_0^{*}).\hfill \end{array}$$

(29)

Proof. 

Observe that $\delta J_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_1^{*},{\widehat{v}}_0^{*})=\mathbf{0}$ so that, since $J_1^{*}$ is convex in $v_2^{*}$ and concave in $(v_1^{*},v_0^{*})$ on $Y^{*}\times Y^{*}\times B^{*}$, we obtain

$$J_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_1^{*},{\widehat{v}}_0^{*})=\underset{v_2^{*}\in Y^{*}}{inf}\left\{\underset{(v_1^{*},v_0^{*})\in Y^{*}\times B^{*}}{sup}{J}_1^{*}(v_2^{*},v_1^{*},v_0^{*})\right\}.$$

Now, we show that

$$\delta J\left(u_0\right)=\mathbf{0}.$$

From

$$\frac{\partial J_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_1^{*},{\widehat{v}}_0^{*})}{\partial v_2^{*}}=\mathbf{0},$$

we have

$$-u_0+\frac{{\widehat{v}}_2^{*}}{K_2}=0,$$

and thus,

$${\widehat{v}}_2^{*}=K_2{u}_0.$$

From

$$\frac{\partial J_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_1^{*},{\widehat{v}}_0^{*})}{\partial v_1^{*}}=\mathbf{0},$$

we obtain

$$-u_0-\frac{{\widehat{v}}_1^{*}-f}{2{\widehat{v}}_0^{*}+K}=0,$$

and thus,

$${\widehat{v}}_1^{*}=-2{\widehat{v}}_0^{*}{u}_0-K{u}_0+f.$$

Finally, denoting

$$D=-\gamma {\nabla }^2{u}_0+2{\widehat{v}}_0^{*}{u}_0-f,$$

from

$$\frac{\partial J_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_1^{*},{\widehat{v}}_0^{*})}{\partial v_0^{*}}=\mathbf{0},$$

we have

$$-2D{u}_0+u_0^2-\frac{{\widehat{v}}_0^{*}}{\alpha }-\beta =0,$$

so that

$${\widehat{v}}_0^{*}=\alpha (u_0^2-\beta -2D{u}_0).$$

(30)

Observe now that

$${\widehat{v}}_1^{*}+{\widehat{v}}_2^{*}+K_1(-\gamma {\nabla }^2+2{\widehat{v}}_0^{*})f=(K_2-K-\gamma {\nabla }^2+K_1{(-\gamma {\nabla }^2+2{\widehat{v}}_0^{*})}^2)u_0$$

so that

$$\begin{array}{ccc}\hfill & & K_2{u}_0-2{\widehat{v}}_0{u}_0-K{u}_0+f\hfill \\ & =& K_2{u}_0-K{u}_0-\gamma {\nabla }^2{u}_0+K_1(-\gamma {\nabla }^2+2{\widehat{v}}_0^{*})(-\gamma {\nabla }^2{u}_0+2{\widehat{v}}_0^{*}{u}_0-f).\hfill \end{array}$$

(31)

The solution for this last system of Equations (30) and (31) is obtained through the relations

$${\widehat{v}}_0^{*}=\alpha (u_0^2-\beta )$$

and

$$-\gamma {\nabla }^2{u}_0+2{\widehat{v}}_0^{*}{u}_0-f=D=0,$$

so that

$$\delta J\left(u_0\right)=-\gamma {\nabla }^2{u}_0+2\alpha (u_0^2-\beta )u_0-f=0$$

and

$$\delta \left\{J\left(u_0\right)+\frac{K_1}{2}{\int }_{\Omega }{(-\gamma {\nabla }^2{u}_0+2{\widehat{v}}_0^{*}{u}_0-f)}^{2}dx\right\}=0,$$

and hence, from the concerning convexity in u on V,

$$J\left(u_0\right)=\underset{u\in V}{min}\left\{J\left(u\right)+\frac{K_1}{2}{\int }_{\Omega }{(-\gamma {\nabla }^{2}u+2{\widehat{v}}_0^{*}u-f)}^{2}dx\right\}.$$

Moreover, from the Legendre transform properties

$$F_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_1^{*},{\widehat{v}}_0^{*})={\langle u_0,{\widehat{v}}_2^{*}+{\widehat{v}}_1^{*}\rangle }_{L^2}-F_1(u_0,{\widehat{v}}_0^{*}),$$

$$F_2^{*}\left({\widehat{v}}_2^{*}\right)={\langle u_0,{\widehat{v}}_2^{*}\rangle }_{L^2}-F_2\left(u_0\right),$$

$$G^{*}({\widehat{v}}_1^{*},{\widehat{v}}_0^{*})=-{\langle u_0,{\widehat{v}}_1^{*}\rangle }_{L^2}-{\langle 0,{\widehat{v}}_0^{*}\rangle }_{L^2}-G(u_0,0),$$

so that

$$\begin{array}{ccc}{J}_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_1^{*},{\widehat{v}}_0^{*})\hfill & =\hfill & -F_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_1^{*},{\widehat{v}}_0^{*})+F_2^{*}\left({\widehat{v}}_2^{*}\right)-G^{*}({\widehat{v}}_1^{*},{\widehat{v}}_0^{*})\hfill \\ & =\hfill & F_1(u_0,{\widehat{v}}_0^{*})-F_2\left(u_0\right)+G(u_0,0)\hfill \\ & =\hfill & J\left(u_0\right).\hfill \end{array}$$

(32)

Joining the pieces, we have

$$\begin{array}{ccc}J\left(u_0\right)\hfill & =\hfill & \underset{u\in V}{inf}\left\{J\left(u\right)+\frac{K_1}{2}{\int }_{\Omega }{(-\gamma {\nabla }^{2}u+2{\widehat{v}}_0^{*}u-f)}^{2}dx\right\}\hfill \\ & =\hfill & \underset{v_2^{*}\in Y^{*}}{inf}\left\{\underset{(v_1^{*},v_0^{*})\in Y^{*}\times B^{*}}{sup}{J}_1^{*}(v_2^{*},v_1^{*},v_0^{*})\right\}\hfill \\ & =\hfill & J_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_1^{*},{\widehat{v}}_0^{*}).\hfill \end{array}$$

(33)

The proof is complete. □

Remark 3. 

We could have also defined

$$B^{*}=\{v_0^{*}\in Y^{*}:\parallel v_0^{*}{\parallel }_{\infty }\le K/2\mathit{and}-\gamma {\nabla }^2+2v_0^{*}>\epsilon I_d\},$$

for some small real parameter $\epsilon >0$. In this case, $-\gamma {\nabla }^2+2v_0^{*}$ is positive definite, whereas in the previous case, $-\gamma {\nabla }^2+2v_0^{*}$ is negative definite.

6. Another Convex Dual Variational Formulation

In this section, again for $\Omega \subset {\mathbb{R}}^3$, an open, bounded, connected set with a regular (Lipschitzian) boundary $\partial \Omega$, $\gamma >0,$$\alpha >0,$$\beta >0$ and $f\in L^2(\Omega )$, we denote $F_1:V\times Y\to \mathbb{R}$, $F_2:V\to \mathbb{R}$ and $G:Y\to \mathbb{R}$ by

$$\begin{array}{ccc}{F}_1(u,v_0^{*})\hfill & =\hfill & \frac{\gamma }{2}{\int }_{\Omega }\nabla u·\nabla udx+{\langle u^2,v_0^{*}\rangle }_{L^2}\hfill \\ & \hfill & +\frac{K_1}{2}{\int }_{\Omega }{(-\gamma {\nabla }^{2}u+2v_0^{*}u-f)}^{2}dx+\frac{K_2}{2}{\int }_{\Omega }{u}^{2}dx,\hfill \end{array}$$

(34)

$$F_2\left(u\right)=\frac{K_2}{2}{\int }_{\Omega }{u}^{2}dx+{\langle u,f\rangle }_{L^2},$$

and

$$G\left(u^2\right)=\frac{\alpha }{2}{\int }_{\Omega }{(u^2-\beta )}^{2}dx.$$

We define also

$$J_1(u,v_0^{*})=F_1(u,v_0^{*})-F_2\left(u\right)-{\langle u^2,v_0^{*}\rangle }_{L^2}+G\left(u^2\right),$$

$$J\left(u\right)=\frac{\gamma }{2}{\int }_{\Omega }\nabla u·\nabla udx+\frac{\alpha }{2}{\int }_{\Omega }{(u^2-\beta )}^{2}dx-{\langle u,f\rangle }_{L^2},$$

$$A^{+}=\{u\in V:uf>0,\mathrm{a}.\mathrm{e}.\mathrm{in}\Omega \},$$

$$V_2={\{u\in V:\parallel u\parallel }_{\infty }\le K_3\},$$

$$V_1=A^{+}\cap V_1,$$

and $F_1^{*}:{\left[Y^{*}\right]}^2\to \mathbb{R},$$F_2^{*}:Y^{*}\to \mathbb{R},$ and $G^{*}:Y^{*}\to \mathbb{R},$ by

$$\begin{array}{ccc}\hfill & \hfill & F_1^{*}(v_2^{*},v_0^{*})\hfill \\ & =\hfill & \underset{u\in V}{sup}\{{\langle u,v_2^{*}\rangle }_{L^2}-F_1(u,v_0^{*})\}\hfill \\ & =\hfill & \frac{1}{2}{\int }_{\Omega }\frac{{\left(v_2^{*}+K_1(-\gamma {\nabla }^2+2v_0^{*})f\right)}^2}{(-\gamma {\nabla }^2+2v_0^{*}+K_2+K_1{(-\gamma {\nabla }^2+2v_0^{*})}^2)}dx\hfill \\ & \hfill & -\frac{K_1}{2}{\int }_{\Omega }{f}^{2}dx,\hfill \end{array}$$

(35)

$$\begin{array}{ccc}{F}_2^{*}\left(v_2^{*}\right)\hfill & =\hfill & \underset{u\in V}{sup}\{{\langle u,v_2^{*}\rangle }_{L^2}-F_2\left(u\right)\}\hfill \\ & =\hfill & \frac{1}{2K_2}{\int }_{\Omega }{(v_2^{*}+f)}^{2}dx,\hfill \end{array}$$

(36)

and

$$\begin{array}{ccc}{G}^{*}\left(v_0^{*}\right)\hfill & =\hfill & \underset{v\in Y}{sup}\{{\langle v,v_0^{*}\rangle }_{L^2}-G\left(v\right)\}\hfill \\ & =\hfill & \frac{1}{2\alpha }{\int }_{\Omega }{\left(v_0^{*}\right)}^{2}dx+\beta {\int }_{\Omega }{v}_0^{*}dx\hfill \end{array}$$

(37)

At this point, we define

$$B_1^{*}=\{v_0^{*}\in Y^{*}:\parallel v_0^{*}{\parallel }_{\infty }\le K/2\},$$

$$B_2^{*}=\{v_0^{*}\in Y^{*}:-\gamma {\nabla }^2+2v_0^{*}+K_1{(-\gamma {\nabla }^2+2v_0^{*})}^2>\mathbf{0}\},$$

$$B_3^{*}=\{v_0^{*}\in Y^{*}:-1/\alpha +4K_1\left[u{(v_2^{*},v_0^{*})}^2\right]+100/K_2\le \mathbf{0},\forall v_2^{*}\in E_1^{*}\},$$

where

$$u(v_2^{*},v_0^{*})=\frac{{\phi }_1}{\phi },$$

$${\phi }_1=(v_2^{*}+K_1(-\gamma {\nabla }^2+2v_0^{*})f)$$

and

$$\phi =(-\gamma {\nabla }^2+2v_0^{*}+K_1{(-\gamma {\nabla }^2+2v_0^{*})}^2+K_2),$$

Finally, we also define

$$E_1^{*}=\{v_2^{*}\in Y^{*}:\parallel v_2^{*}{\parallel }_{\infty }\le (5/4)K_2\}.$$

$$E_2^{*}=\{v_2^{*}\in Y^{*}:f{v}_2^{*}>0,\mathrm{a}.\mathrm{e}.\mathrm{in}\Omega \},$$

$$E^{*}=E_1^{*}\cap E_2^{*},$$

$$B^{*}=B_1^{*}\cap B_3^{*},$$

and $J_1^{*}:E^{*}\times B^{*}\to \mathbb{R},$ by

$$J_1^{*}(v_2^{*},v_0^{*})=-F_1^{*}(v_2^{*},v_0^{*})+F_2^{*}\left(v_2^{*}\right)-G^{*}\left(v_0^{*}\right).$$

Moreover, assume

$$K_2\gg K_1\gg K\gg K_3\gg max\{1,\gamma ,\alpha \}.$$

By directly computing ${\delta }^2{J}_1^{*}(v_2^{*},v_0^{*})$, we may obtain that for such specified real constants, $J_1^{*}$ is concave in $v_0^{*}$ on $E^{*}\times B^{*}.$

Indeed, recalling that

$$\phi =(-\gamma {\nabla }^2+2v_0^{*}+K_1{(-\gamma {\nabla }^2+2v_0^{*})}^2+K_2),$$

$${\phi }_1=(v_2^{*}+K_1(-\gamma {\nabla }^2+2v_0^{*})f),$$

and

$$u=\frac{{\phi }_1}{\phi },$$

we obtain

$$\frac{{\partial }^2{J}_1^{*}(v_2^{*},v_0^{*})}{\partial {\left(v_2^{*}\right)}^2}=1/K_2-1/\phi >\mathbf{0},$$

in $E^{*}\times B_3^{*}$ and

$$\frac{{\partial }^2{J}_1^{*}(v_2^{*},v_0^{*})}{\partial {\left(v_0^{*}\right)}^2}=4u^2{K}_1-1/\alpha +\mathcal{O}(1/K_2)<\mathbf{0},$$

in $E^{*}\times B^{*}$.

Considering such statements and definitions, we may prove the following theorem.

Theorem 5. 

Let $({\widehat{v}}_2^{*},{\widehat{v}}_0^{*})\in E^{*}\times (B^{*}\cap B_2^{*})$ be such that

$$\delta J_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_0^{*})=\mathbf{0}$$

and $u_0\in V_1$ be such that

$$u_0=\frac{{\widehat{v}}_2^{*}+K_1(-\gamma {\nabla }^2+2{\widehat{v}}_0^{*})f}{K_2+2{\widehat{v}}_0^{*}-\gamma {\nabla }^2+K_1{(-\gamma {\nabla }^2+2{\widehat{v}}_0^{*})}^2}.$$

Under such hypotheses, we have

$$\delta J\left(u_0\right)=\mathbf{0},$$

so that

$$\begin{array}{ccc}J\left(u_0\right)\hfill & =\hfill & \underset{u\in V_1}{inf}\left\{J\left(u\right)+\frac{K_1}{2}{\int }_{\Omega }{(-\gamma {\nabla }^{2}u+2{\widehat{v}}_0^{*}u-f)}^{2}dx\right\}\hfill \\ & =\hfill & \underset{v_2^{*}\in E^{*}}{inf}\left\{\underset{v_0^{*}\in B^{*}}{sup}{J}_1^{*}(v_2^{*},v_0^{*})\right\}\hfill \\ & =\hfill & J_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_0^{*}).\hfill \end{array}$$

(38)

Proof. 

Observe that $\delta J_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_0^{*})=\mathbf{0}$ so that, since $J_1^{*}$ is concave in $v_0^{*}$ on $E^{*}\times B^{*}$, $v_0^{*}\in B_2^{*}$ and $J_1^{*}$ is quadratic in $v_2^{*}$, we have

$$\underset{v_0^{*}\in B^{*}}{sup}{J}_1^{*}({\widehat{v}}_2^{*},v_0^{*})=J_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_0^{*})=\underset{v_2^{*}\in E^{*}}{inf}{J}_1^{*}(v_2^{*},{\widehat{v}}_0^{*}).$$

Consequently, from this and the Min–Max Theorem, we obtain

$$J_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_0^{*})=\underset{v_2^{*}\in E^{*}}{inf}\left\{\underset{v_0^{*}\in B^{*}}{sup}{J}_1^{*}(v_2^{*},v_0^{*})\right\}=\underset{v_0^{*}\in B^{*}}{sup}\left\{\underset{v_2^{*}\in E^{*}}{inf}{J}_1^{*}(v_2^{*},v_0^{*})\right\}.$$

Now, we show that

$$\delta J\left(u_0\right)=\mathbf{0}.$$

From

$$\frac{\partial J_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_0^{*})}{\partial v_2^{*}}=\mathbf{0},$$

we have

$$-u_0+\frac{{\widehat{v}}_2^{*}}{K_2}=0,$$

and thus

$${\widehat{v}}_2^{*}=K_2{u}_0.$$

Finally, denoting

$$D=-\gamma {\nabla }^2{u}_0+2{\widehat{v}}_0^{*}{u}_0-f,$$

from

$$\frac{\partial J_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_0^{*})}{\partial v_0^{*}}=\mathbf{0},$$

we have

$$-2D{u}_0+u_0^2-\frac{{\widehat{v}}_0^{*}}{\alpha }-\beta =0,$$

so that

$${\widehat{v}}_0^{*}=\alpha (u_0^2-\beta -2D{u}_0).$$

(39)

Observe now that

$${\widehat{v}}_2^{*}+K_1(-\gamma {\nabla }^2+2{\widehat{v}}_0^{*})f=(K_2-\gamma {\nabla }^2+2{\widehat{v}}_0^{*}+K_1{(-\gamma {\nabla }^2+2{\widehat{v}}_0^{*})}^2)u_0$$

so that

$$\begin{array}{ccc}\hfill & \hfill & K_2{u}_0-2{\widehat{v}}_0{u}_0-K{u}_0+f\hfill \\ & =\hfill & K_2{u}_0-K{u}_0-\gamma {\nabla }^2{u}_0+K_1(-\gamma {\nabla }^2+2{\widehat{v}}_0^{*})(-\gamma {\nabla }^2{u}_0+2{\widehat{v}}_0^{*}{u}_0-f).\hfill \end{array}$$

(40)

The solution for this last equation is obtained through the relation

$$-\gamma {\nabla }^2{u}_0+2{\widehat{v}}_0^{*}{u}_0-f=D=0,$$

so that from this and (39), we have

$${\widehat{v}}_0^{*}=\alpha (u_0^2-\beta ).$$

Thus,

$$\delta J\left(u_0\right)=-\gamma {\nabla }^2{u}_0+2\alpha (u_0^2-\beta )u_0-f=0$$

and

$$\delta \left\{J\left(u_0\right)+\frac{K_1}{2}{\int }_{\Omega }{(-\gamma {\nabla }^2{u}_0+2{\widehat{v}}_0^{*}{u}_0-f)}^{2}dx\right\}=0,$$

and hence, from the concerning convexity in u on V,

$$J\left(u_0\right)=\underset{u\in V}{min}\left\{J\left(u\right)+\frac{K_1}{2}{\int }_{\Omega }{(-\gamma {\nabla }^{2}u+2{\widehat{v}}_0^{*}u-f)}^{2}dx\right\}.$$

Moreover, from the Legendre transform properties

$$F_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_0^{*})={\langle u_0,{\widehat{v}}_2^{*}\rangle }_{L^2}-F_1(u_0,{\widehat{v}}_0^{*}),$$

$$F_2^{*}\left({\widehat{v}}_2^{*}\right)={\langle u_0,{\widehat{v}}_2^{*}\rangle }_{L^2}-F_2\left(u_0\right),$$

$$G^{*}\left({\widehat{v}}_0^{*}\right)={\langle u_0^2,{\widehat{v}}_0^{*}\rangle }_{L^2}-G\left(u_0^2\right),$$

so that

$$\begin{array}{ccc}{J}_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_0^{*})\hfill & =\hfill & -F_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_0^{*})+F_2^{*}\left({\widehat{v}}_2^{*}\right)-G^{*}\left({\widehat{v}}_0^{*}\right)\hfill \\ & =\hfill & F_1(u_0,{\widehat{v}}_0^{*})-F_2\left(u_0\right)-{\langle u_0^2,{\widehat{v}}_0^{*}\rangle }_{L^2}+G\left(u_0^2\right)\hfill \\ & =\hfill & J\left(u_0\right).\hfill \end{array}$$

(41)

Joining the pieces, we have

$$\begin{array}{ccc}J\left(u_0\right)\hfill & =\hfill & \underset{u\in V_1}{inf}\left\{J\left(u\right)+\frac{K_1}{2}{\int }_{\Omega }{(-\gamma {\nabla }^{2}u+2{\widehat{v}}_0^{*}u-f)}^{2}dx\right\}\hfill \\ & =\hfill & \underset{v_2^{*}\in E^{*}}{inf}\left\{\underset{v_0^{*}\in B^{*}}{sup}{J}_1^{*}(v_2^{*},v_0^{*})\right\}\hfill \\ & =\hfill & J_1^{*}({\widehat{v}}_2^{*},{\widehat{v}}_0^{*}).\hfill \end{array}$$

(42)

The proof is complete. □

7. A Related Numerical Computation through the Generalized Method of Lines

In the next few lines, we present some improvements concerning the initial conception of the generalized method of lines, originally published in the book entitled “Topics on Functional Analysis, Calculus of Variations and Duality” [9], 2011.

Concerning such a method, other important results may be found in articles and books such as [7,9,13].

Specifically about the improvement previously mentioned, we have changed the way we truncate the series solution obtained through an application of the Banach fixed point theorem to find the relation between two adjacent lines. The results obtained are very good even as a typical parameter $\epsilon >0$ is very small.

In the next few lines and sections, we develop in details such a numerical procedure.

7.1. About a Concerning Improvement to the Generalized Method of Lines

Let $\Omega \subset {\mathbb{R}}^2$, where

$$\Omega =\{(r,\theta )\in {\mathbb{R}}^2:1\le r\le 2,0\le \theta \le 2\pi \}.$$

Consider the problem of solving the partial differential equation

$$\left\{\begin{array}{cc}-\epsilon \left(\frac{{\partial }^{2}u}{\partial r^2}+\frac{1}{r}\frac{\partial u}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}u}{\partial {\theta }^2}\right)+\alpha u^3-\beta u=f,\hfill & \mathrm{in}\Omega ,\hfill \\ u=u_0\left(\theta \right),\hfill & \mathrm{on}\partial {\Omega }_1,\hfill \\ u=u_f\left(\theta \right),\hfill & \mathrm{on}\partial {\Omega }_2.\hfill \end{array}\right.$$

(43)

Here,

$$\Omega =\{(r,\theta )\in {\mathbb{R}}^2:1\le r\le 2,0\le \theta \le 2\pi \},$$

$$\partial {\Omega }_1=\{(1,\theta )\in {\mathbb{R}}^2:0\le \theta \le 2\pi \},$$

$$\partial {\Omega }_2=\{(2,\theta )\in {\mathbb{R}}^2:0\le \theta \le 2\pi \},$$

$\epsilon >0,\alpha >0,\beta >0$, and $f\equiv 1,\mathrm{on}\Omega .$

In a partial finite differences scheme (about the standard finite differences method, please see [14]), such a system stands for

$$-\epsilon \left(\frac{u_{n+1}-2u_n+u_{n-1}}{d^2}+\frac{1}{t_n}\frac{u_n-u_{n-1}}{d}+\frac{1}{t_n^2}\frac{{\partial }^2{u}_n}{\partial {\theta }^2}\right)+\alpha u_n^3-\beta u_n=f_n,$$

$\forall n\in \{1,\cdots ,N-1\},$ with the boundary conditions

$$u_0=0,$$

and

$$u_N=0.$$

Here, N is the number of lines and $d=1/N.$

In particular, for $n=1$, we have

$$-\epsilon \left(\frac{u_2-2u_1+u_0}{d^2}+\frac{1}{t_1}\frac{(u_1-u_0)}{d}+\frac{1}{t_1^2}\frac{{\partial }^2{u}_1}{\partial {\theta }^2}\right)+\alpha u_1^3-\beta u_1=f_1,$$

so that

$$u_1=\left(u_2+u_1+u_0+\frac{1}{t_1}(u_1-u_0)d+\frac{1}{t_1^2}\frac{{\partial }^2{u}_1}{\partial {\theta }^2}{d}^2+(-\alpha u_1^3+\beta u_1-f_1)\frac{d^2}{\epsilon }\right)/3.0,$$

We solve this last equation through the Banach fixed point theorem, obtaining $u_1$ as a function of $u_2.$

Indeed, we may set

$$u_1^0=u_2$$

and

$$\begin{array}{ccc}{u}_1^{k+1}\hfill & =\hfill & \left(u_2+u_1^k+u_0+\frac{1}{t_1}(u_1^k-u_0)d+\frac{1}{t_1^2}\frac{{\partial }^2{u}_1^k}{\partial {\theta }^2}{d}^2\right.\hfill \\ & \hfill & \left.+(-\alpha {\left(u_1^k\right)}^3+\beta u_1^k-f_1)\frac{d^2}{\epsilon }\right)/3.0,\hfill \end{array}$$

(44)

$\forall k\in \mathbb{N}.$

Thus, we may obtain

$$u_1=\underset{k\to \infty }{lim}{u}_1^k\equiv H_1(u_2,u_0).$$

Similarly, for $n=2$, we have

$$\begin{array}{ccc}{u}_2\hfill & =\hfill & \left(u_3+u_2+H_1(u_2,u_0)+\frac{1}{t_1}(u_2-H_1(u_2,u_0))d+\frac{1}{t_1^2}\frac{{\partial }^2{u}_2}{\partial {\theta }^2}{d}^2\right.\hfill \\ & \hfill & \left.+(-\alpha u_2^3+\beta u_2-f_2)\frac{d^2}{\epsilon }\right)/3.0,\hfill \end{array}$$

(45)

We solve this last equation through the Banach fixed point theorem, obtaining $u_2$ as a function of $u_3$ and $u_0.$

Indeed, we may set

$$u_2^0=u_3$$

and

$$\begin{array}{ccc}{u}_2^{k+1}\hfill & =\hfill & \left(u_3+u_2^k+H_1(u_2^k,u_0)+\frac{1}{t_2}(u_2^k-H_1(u_2^k,u_0))d+\frac{1}{t_2^2}\frac{{\partial }^2{u}_2^k}{\partial {\theta }^2}{d}^2\right.\hfill \\ & \hfill & \left.+(-\alpha {\left(u_2^k\right)}^3+\beta u_2^k-f_2)\frac{d^2}{\epsilon }\right)/3.0,\hfill \end{array}$$

(46)

$\forall k\in \mathbb{N}.$

Thus, we may obtain

$$u_2=\underset{k\to \infty }{lim}{u}_2^k\equiv H_2(u_3,u_0).$$

Now reasoning inductively, having

$$u_{n-1}=H_{n-1}(u_n,u_0),$$

we may obtain

$$\begin{array}{ccc}{u}_n\hfill & =\hfill & \left(u_{n+1}+u_n+H_{n-1}(u_n,u_0)+\frac{1}{t_n}(u_n-H_{n-1}(u_n,u_0))d+\frac{1}{t_n^2}\frac{{\partial }^2{u}_n}{\partial {\theta }^2}{d}^2\right.\hfill \\ & \hfill & \left.+(-\alpha u_n^3+\beta u_n-f_n)\frac{d^2}{\epsilon }\right)/3.0,\hfill \end{array}$$

(47)

We solve this last equation through the Banach fixed point theorem, obtaining $u_n$ as a function of $u_{n+1}$ and $u_0.$

Indeed, we may set

$$u_n^0=u_{n+1}$$

and

$$\begin{array}{ccc}{u}_n^{k+1}\hfill & =\hfill & \left(u_{n+1}+u_n^k+H_{n-1}(u_n^k,u_0)+\frac{1}{t_n}(u_n^k-H_{n-1}(u_n^k,u_0))d+\frac{1}{t_n^2}\frac{{\partial }^2{u}_n^k}{\partial {\theta }^2}{d}^2\right.\hfill \\ & \hfill & \left.+(-\alpha {\left(u_n^k\right)}^3+\beta u_n^k-f_n)\frac{d^2}{\epsilon }\right)/3.0,\hfill \end{array}$$

(48)

$\forall k\in \mathbb{N}.$

Thus, we may obtain

$$u_n=\underset{k\to \infty }{lim}{u}_n^k\equiv H_n(u_{n+1},u_0).$$

We have obtained $u_n=H_n(u_{n+1},u_0)$, $\forall n\in \{1,\cdots ,N-1\}.$

In particular, $u_N=u_f\left(\theta \right),$ so that we may obtain

$$u_{N-1}=H_{N-1}(u_N,u_0)=H_{N-1}\left(0\right)\equiv F_{N-1}(u_N,u_0)=F_{N-1}(u_f\left(\theta \right),u_0\left(\theta \right)).$$

Similarly,

$$u_{N-2}=H_{N-2}(u_{N-1},u_0)=H_{N-2}\left(H_{N-1}(u_N,u_0)\right)=F_{N-2}(u_N,u_0)=F_{N-1}(u_f\left(\theta \right),u_0\left(\theta \right)),$$

an so on, until the following is obtained:

$$u_1=H_1\left(u_2\right)\equiv F_1(u_N,u_0)=F_1(u_f\left(\theta \right),u_0\left(\theta \right)).$$

The problem is then approximately solved.

7.2. Software in Mathematica for Solving Such an Equation

We recall that the equation to be solved is a Ginzburg–Landau-type one, where

$$\left\{\begin{array}{cc}-\epsilon \left(\frac{{\partial }^{2}u}{\partial r^2}+\frac{1}{r}\frac{\partial u}{\partial r}+\frac{1}{r^2}\frac{{\partial }^{2}u}{\partial {\theta }^2}\right)+\alpha u^3-\beta u=f,\hfill & \mathrm{in}\Omega ,\hfill \\ u=0,\hfill & \mathrm{on}\partial {\Omega }_1,\hfill \\ u=u_f\left(\theta \right),\hfill & \mathrm{on}\partial {\Omega }_2.\hfill \end{array}\right.$$

(49)

Here,

$$\Omega =\{(r,\theta )\in {\mathbb{R}}^2:1\le r\le 2,0\le \theta \le 2\pi \},$$

$$\partial {\Omega }_1=\{(1,\theta )\in {\mathbb{R}}^2:0\le \theta \le 2\pi \},$$

$$\partial {\Omega }_2=\{(2,\theta )\in {\mathbb{R}}^2:0\le \theta \le 2\pi \},$$

$\epsilon >0,\alpha >0,\beta >0$, and $f\equiv 1,\mathrm{on}\Omega .$ In a partial finite differences scheme, such a system stands for

$$-\epsilon \left(\frac{u_{n+1}-2u_n+u_{n-1}}{d^2}+\frac{1}{t_n}\frac{u_n-u_{n-1}}{d}+\frac{1}{t_n^2}\frac{{\partial }^2{u}_n}{\partial {\theta }^2}\right)+\alpha u_n^3-\beta u_n=f_n,$$

$\forall n\in \{1,\cdots ,N-1\},$ with the boundary conditions

$$u_0=0,$$

and

$$u_N=u_f\left[x\right].$$

Here, N is the number of lines and $d=1/N.$

At this point, we present the concerning software for an approximate solution.

Such a software is for $N=10$ (10 lines) and $u_0\left[x\right]=0$.

*************************************

• $m_8=10$;  $(N=10lines)$
• $d=1/m8$;
• $e_1=0.1$; ($\epsilon =0.1)$
• $A=1.0$;
• $B=1.0$;
• $For[i=1,i<m8,i++,f[i]=1.0];$  $(f\equiv 1,\mathrm{on}\Omega )$
• $a=0.0$;
• $For[i=1,i<m8,i++,$
  $Clear[b,u];$
  $t\left[i\right]=1+i\ast d;$
  $b\left[x_{-}\right]=u[i+1]\left[x\right];$
• $For[k=1,k<30,k++,$  $(\mathrm{we}\mathrm{have}\mathrm{fixed}\mathrm{the}\mathrm{number}\mathrm{of}\mathrm{iterations})$
  $$\begin{gathered} z=\left(u[i+1]\left[x\right]+b\left[x\right]+a+\frac{1}{t\left[i\right]}(b\left[x\right]-a)\ast d\right.\left. \\ +\frac{1}{t{\left[i\right]}^2}D[b\left[x\right],\{x,2\}]\ast d^2+(-A\ast b{\left[x\right]}^3+B\ast u\left[x\right]+f\left[i\right])\ast \frac{d^2}{e_1}\right)/3.0; \end{gathered}$$
  $$\begin{gathered} z= \\ Series[z,\{u[i+1]\left[x\right],0,3\},\{u{[i+1]}^{\prime }\left[x\right],0,1\},\{u{[i+1]}^{″}\left[x\right],0,1\}, \\ \{u{[i+1]}^{‴}\left[x\right],0,0\},\{u{[i+1]}^{⁗}\left[x\right],0,0\}]; \end{gathered}$$
  $z=Normal\left[z\right],$
  $z=Expand\left[z\right];$
  $b\left[x_{-}\right]=z];$
• $a_1\left[i\right]=z;$
• $Clear\left[b\right];$
• $u[i+1]\left[x_{-}\right]=b\left[x\right]$;
• $a=a_1\left[i\right]$];
• $b\left[x_{-}\right]=u_f\left[x\right];$
• $For[i=1,i<m8,i++,$
  $A_1=a_1[m8-i];$
  $A_1=Series[A_1,\{u_f\left[x\right],0,3\},\{u_f^{\prime }\left[x\right],0,1\},\{u_f^{″}\left[x\right],0,1\},\{u_f^{‴}\left[x\right],0,0\},\{u_f^{⁗}\left[x\right],0,0\}];$
  $A_1=Normal\left[A_1\right];$
  $A_1=Expand\left[A_1\right];$
  $u[m8-i]\left[x_{-}\right]=A_1;$
  $b\left[x_{-}\right]=A_1];$
  $Print\left[u\right[m8/2\left]\right[x\left]\right];$

*************************************

The numerical expressions for the solutions of the concerning $N=10$ lines are given by

$$\begin{array}{ccc}u\left[1\right]\left[x\right]\hfill & =\hfill & 0.47352+0.00691u_f\left[x\right]-0.00459u_f{\left[x\right]}^2+0.00265u_f{\left[x\right]}^3+0.00039\left(u_f^{″}\right)\left[x\right]\hfill \\ & \hfill & -0.00058u_f\left[x\right]\left(u_f^{″}\right)\left[x\right]+0.00050u_f{\left[x\right]}^2\left(u_f^{″}\right)\left[x\right]-0.000181213u_f{\left[x\right]}^3\left(u_f^{″}\right)\left[x\right]\hfill \end{array}$$

(50)

$$\begin{array}{ccc}u\left[2\right]\left[x\right]\hfill & =\hfill & 0.76763+0.01301u_f\left[x\right]-0.00863u_f{\left[x\right]}^2+0.00497u_f{\left[x\right]}^3+0.00068\left(u_f^{″}\right)\left[x\right]\hfill \\ & \hfill & -0.00103u_f\left[x\right]\left(u_f^{″}\right)\left[x\right]+0.00088u_f{\left[x\right]}^2\left(u_f^{″}\right)\left[x\right]-0.00034u_f{\left[x\right]}^3\left(u_f^{″}\right)\left[x\right]\hfill \end{array}$$

(51)

$$\begin{array}{ccc}u\left[3\right]\left[x\right]\hfill & =\hfill & 0.91329+0.02034u_f\left[x\right]-0.01342u_f{\left[x\right]}^2+0.00768u_f{\left[x\right]}^3+0.00095\left(u_f^{″}\right)\left[x\right]\hfill \\ & \hfill & -0.00144u_f\left[x\right]\left(u_f^{″}\right)\left[x\right]+0.00122u_f{\left[x\right]}^2\left(u_f^{″}\right)\left[x\right]-0.00051u_f{\left[x\right]}^3\left(u_f^{″}\right)\left[x\right]\hfill \end{array}$$

(52)

$$\begin{array}{ccc}u\left[4\right]\left[x\right]\hfill & =\hfill & 0.97125+0.03623u_f\left[x\right]-0.02328u_f{\left[x\right]}^2+0.01289u_f{\left[x\right]}^3+0.00147331\left(u_f^{″}\right)\left[x\right]\hfill \\ & \hfill & -0.00223u_f\left[x\right]\left(u_f^{″}\right)\left[x\right]+0.00182uf{\left[x\right]}^2\left(u_f^{″}\right)\left[x\right]-0.00074u_f{\left[x\right]}^3\left(u_f^{″}\right)\left[x\right]\hfill \end{array}$$

(53)

$$\begin{array}{ccc}u\left[5\right]\left[x\right]\hfill & =\hfill & 1.01736+0.09242u_f\left[x\right]-0.05110u_f{\left[x\right]}^2+0.02387u_f{\left[x\right]}^3+0.00211\left(u_f^{″}\right)\left[x\right]\hfill \\ & \hfill & -0.00378u_f\left[x\right]\left(u_f^{″}\right)\left[x\right]+0.00292u_f{\left[x\right]}^2\left(u_f^{″}\right)\left[x\right]-0.00132u_f{\left[x\right]}^3\left(u_f^{″}\right)\left[x\right]\hfill \end{array}$$

(54)

$$\begin{array}{ccc}u\left[6\right]\left[x\right]\hfill & =\hfill & 1.02549+0.21039u_f\left[x\right]-0.09374u_f{\left[x\right]}^2+0.03422u_f{\left[x\right]}^3+0.00147\left(u_f^{″}\right)\left[x\right]\hfill \\ & \hfill & -0.00634u_f\left[x\right]\left(u_f^{″}\right)\left[x\right]+0.00467u_f{\left[x\right]}^2\left(u_f^{″}\right)\left[x\right]-0.00200u_f{\left[x\right]}^3\left(u_f^{″}\right)\left[x\right]\hfill \end{array}$$

(55)

$$\begin{array}{ccc}u\left[7\right]\left[x\right]\hfill & =\hfill & 0.93854+0.36459u_f\left[x\right]-0.14232u_f{\left[x\right]}^2+0.04058u_f{\left[x\right]}^3+0.00259\left(u_f^{″}\right)\left[x\right]\hfill \\ & \hfill & -0.00747373u_f\left[x\right]\left(u_f^{″}\right)\left[x\right]+0.0047969u_f{\left[x\right]}^2\left(u_f^{″}\right)\left[x\right]-0.00194u_f{\left[x\right]}^3\left(u_f^{″}\right)\left[x\right]\hfill \end{array}$$

(56)

$$\begin{array}{ccc}u\left[8\right]\left[x\right]\hfill & =\hfill & 0.74649+0.57201u_f\left[x\right]-0.17293u_f{\left[x\right]}^2+0.02791u_f{\left[x\right]}^3+0.00353\left(u_f^{″}\right)\left[x\right]\hfill \\ & \hfill & -0.00658u_f\left[x\right]\left(u_f^{″}\right)\left[x\right]+0.00407u_f{\left[x\right]}^2\left(u_f^{″}\right)\left[x\right]-0.00172u_f{\left[x\right]}^3\left(u_f^{″}\right)\left[x\right]\hfill \end{array}$$

(57)

$$\begin{array}{ccc}u\left[9\right]\left[x\right]\hfill & =\hfill & 0.43257+0.81004u_f\left[x\right]-0.13080u_f{\left[x\right]}^2+0.00042u_f{\left[x\right]}^3+0.00294\left(u_f^{″}\right)\left[x\right]\hfill \\ & \hfill & -0.00398u_f\left[x\right]\left(u_f^{″}\right)\left[x\right]+0.00222u_f{\left[x\right]}^2\left(u_f^{″}\right)\left[x\right]-0.00066u_f{\left[x\right]}^3\left(u_f^{″}\right)\left[x\right]\hfill \end{array}$$

(58)

7.3. Some Plots Concerning the Numerical Results

In this section, we present the lines $2,4,6,8$ related to results obtained in the last section.

Indeed, we present such mentioned lines, in a first step, for the previous results obtained through the generalized of lines and, in a second step, through a numerical method, which is combination of the Newton one and the generalized method of lines. In a third step, we also present the graphs by considering the expression of the lines as those also obtained through the generalized method of lines, up to the numerical coefficients for each function term, which are obtained by the numerical optimization of the functional J, specified below. We consider the case in which $u_0\left(x\right)=0$ and $u_f\left(x\right)=sin\left(x\right)$.

For the procedure mentioned above as the third step, recalling that $N=10$ lines, considering that $u_f^{″}\left(x\right)=-u_f\left(x\right)$, we may approximately assume the following general line expressions:

$$u_n\left(x\right)=a(1,n)+a(2,n)u_f\left(x\right)+a(3,n)u_f{\left(x\right)}^2+a(4,n)u_f{\left(x\right)}^3,\forall n\in \{1,\cdots N-1\}.$$

Defining

$$W_n=-e_1\frac{(u_{n+1}\left(x\right)-2u_n\left(x\right)+u_{n-1}\left(x\right))}{d^2}-\frac{e_1}{t_n}\frac{(u_n\left(x\right)-u_{n-1}\left(x\right))}{d}-\frac{e_1}{t_n^2}{u}_n^{″}\left(x\right)+u_n{\left(x\right)}^3-u_n\left(x\right)-1,$$

and

$$J\left(\left\{a(j,n)\right\}\right)=\sum _{n=1}^{N-1}{\int }_0^{2\pi }{\left(W_n\right)}^{2}dx$$

we obtain $\left\{a\right(j,n\left)\right\}$ by numerically minimizing J.

Hence, we have obtained the following lines for these cases. For such graphs, we have considered 300 nodes in x, with $2\pi /300$ as units in $x\in [0,2\pi ].$

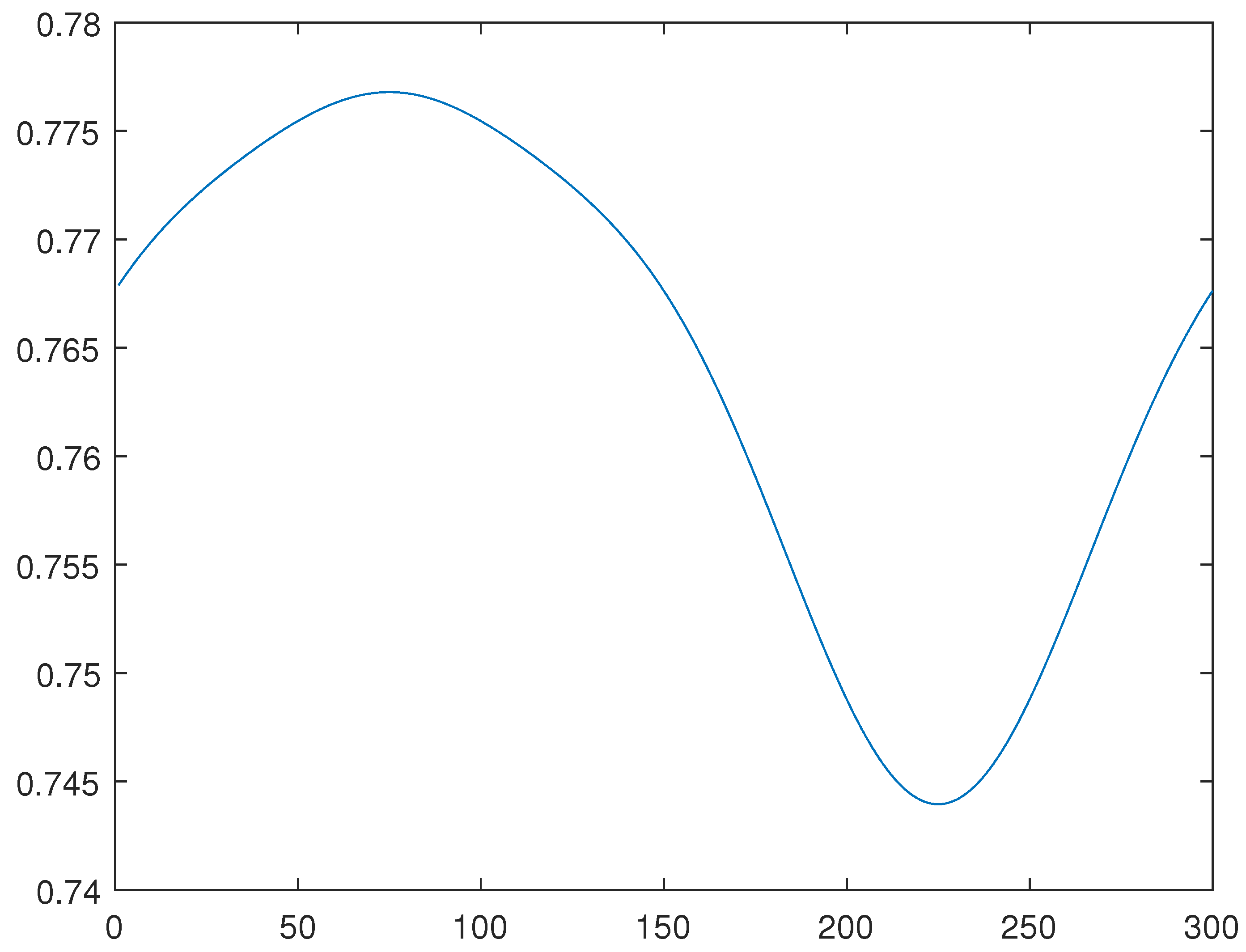
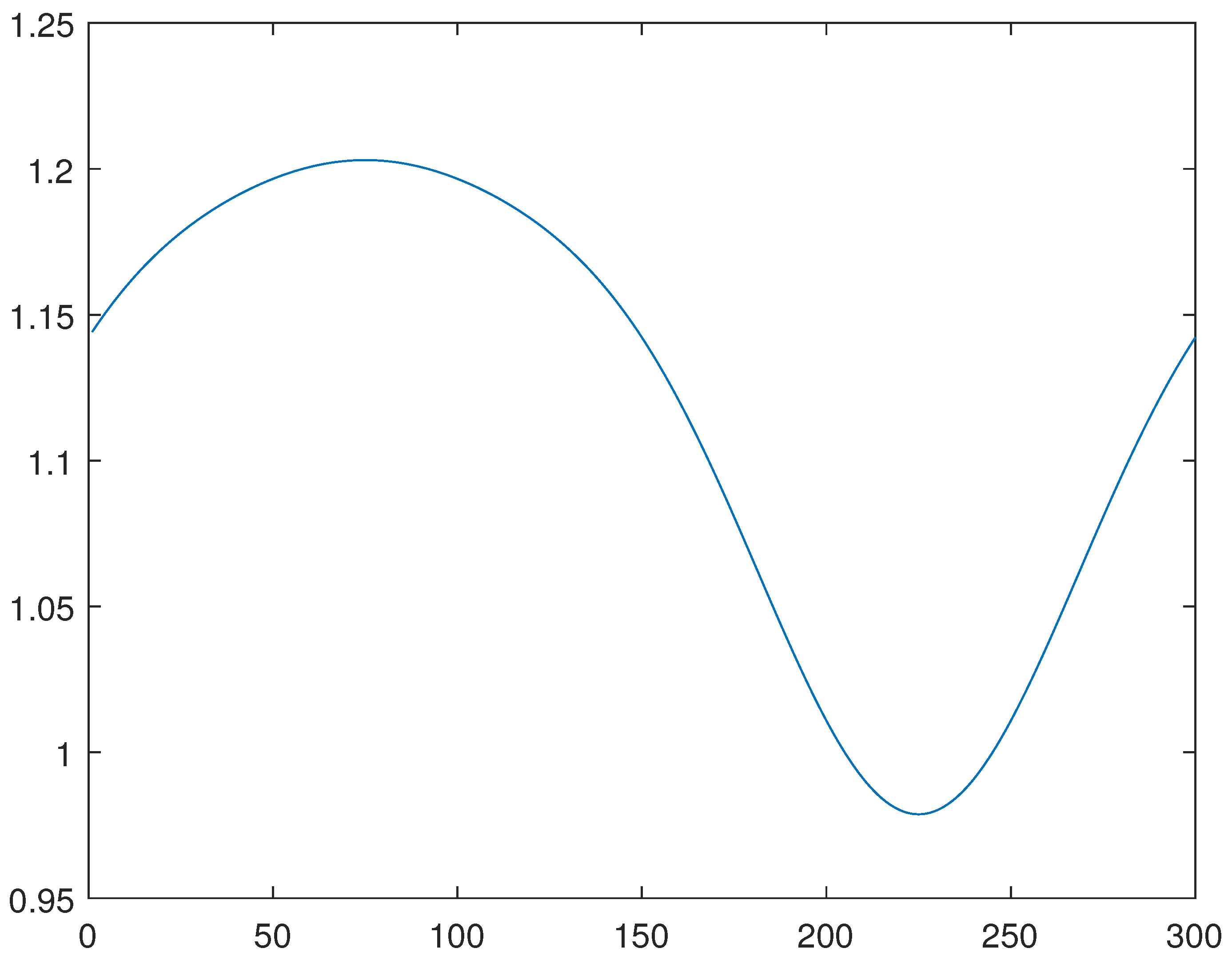
For the line 2, please see Figure 1, Figure 2 and Figure 3, obtained through the generalized method of lines, through a combination of the Newton and generalized methods of lines, and through the minimization of the functional J, respectively.

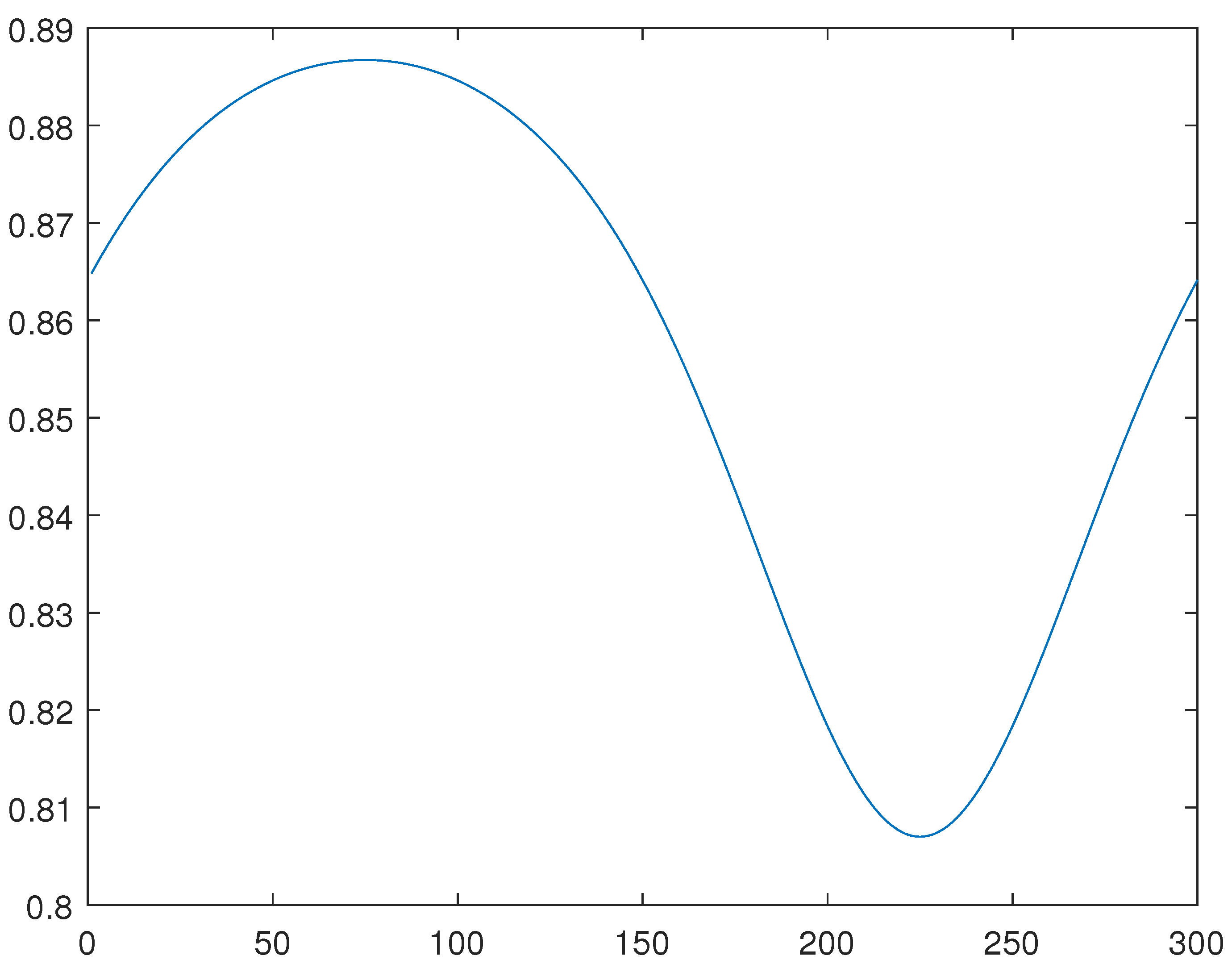
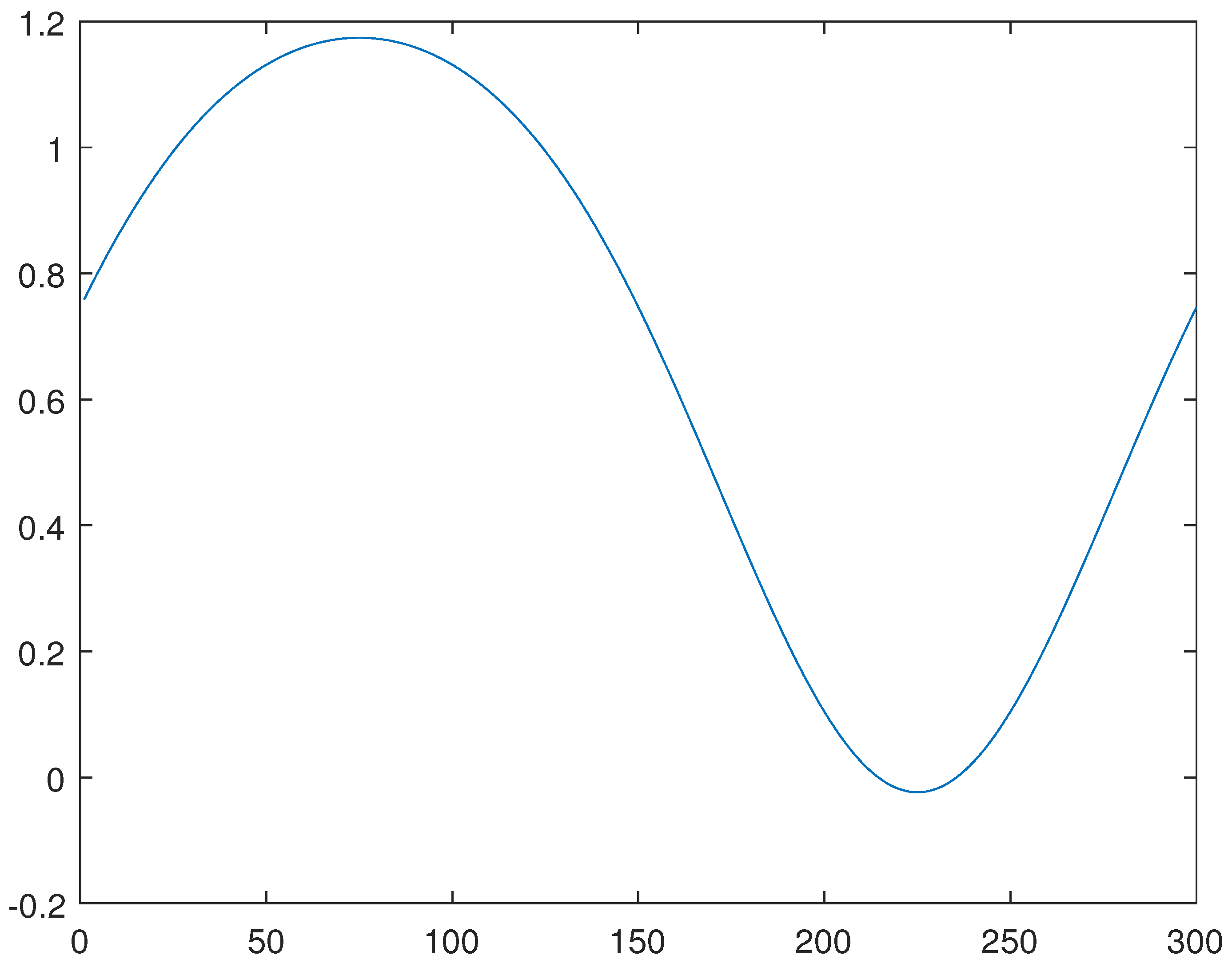
For the line 4, please see Figure 4, Figure 5 and Figure 6, obtained through the generalized method of lines, through a combination of the Newton and generalized methods of lines, and through the minimization of the functional J, respectively.

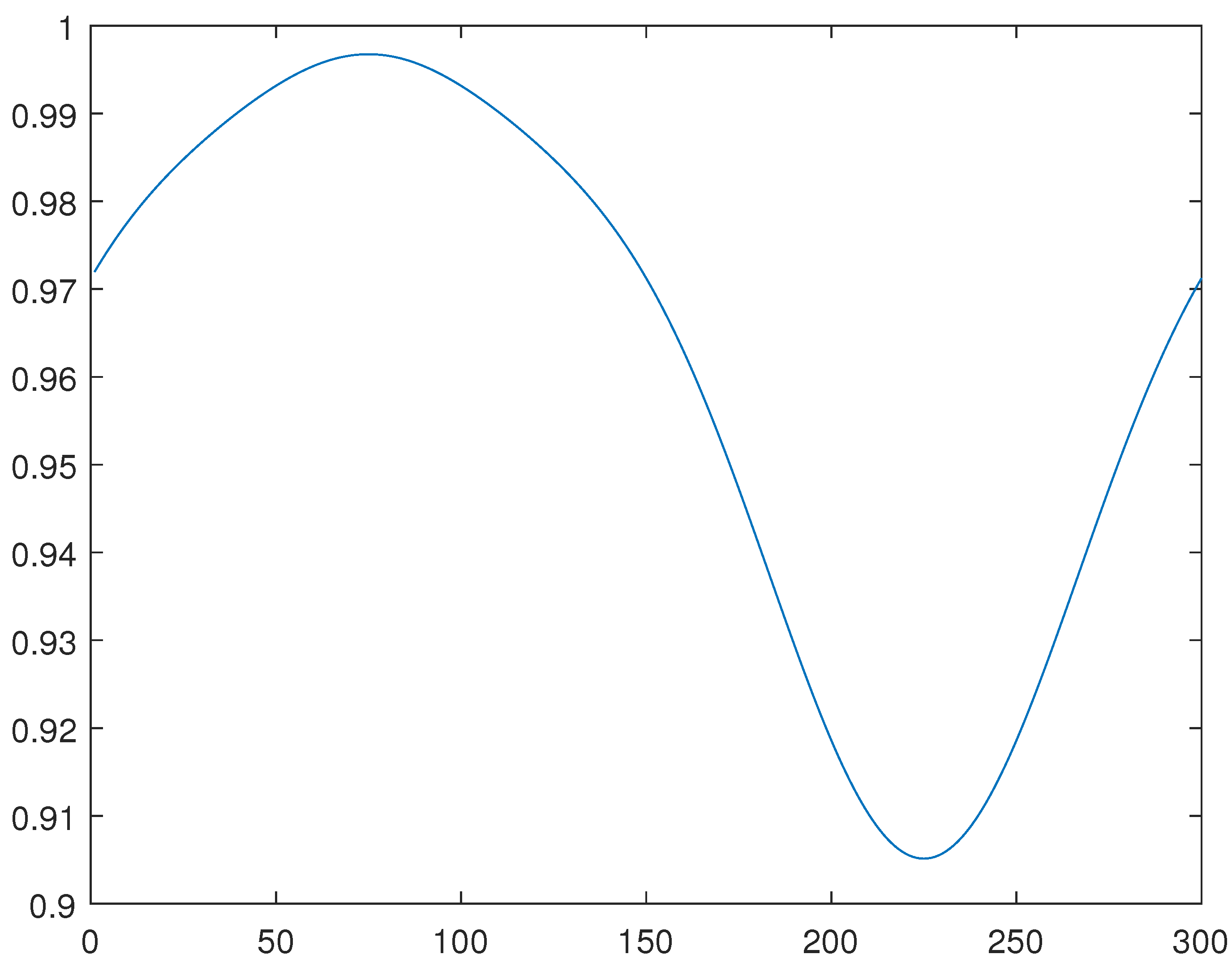
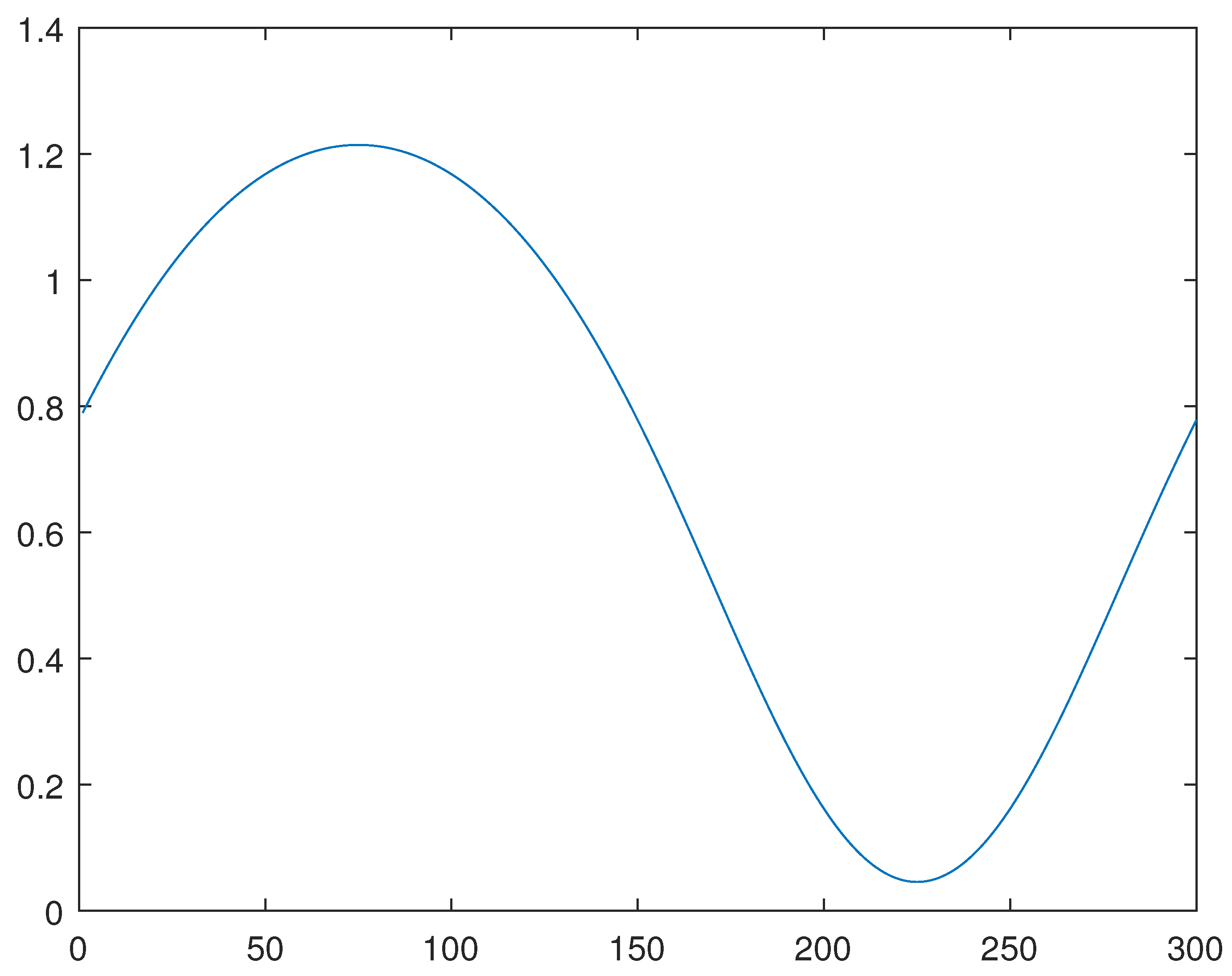
For the line 6, please see Figure 7, Figure 8 and Figure 9, obtained through the generalized method of lines, through a combination of the Newton and generalized methods of lines, and through the minimization of the functional J, respectively.

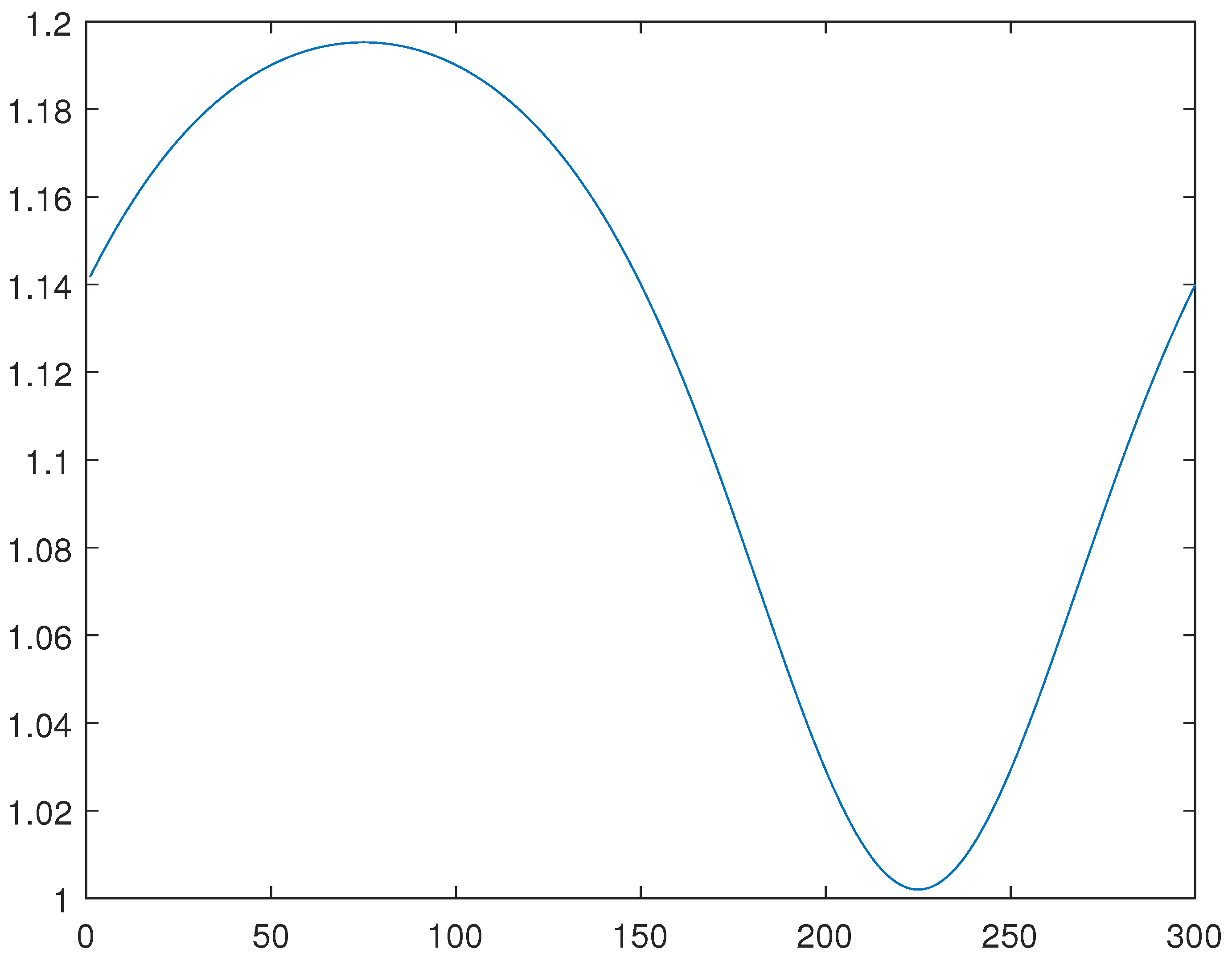
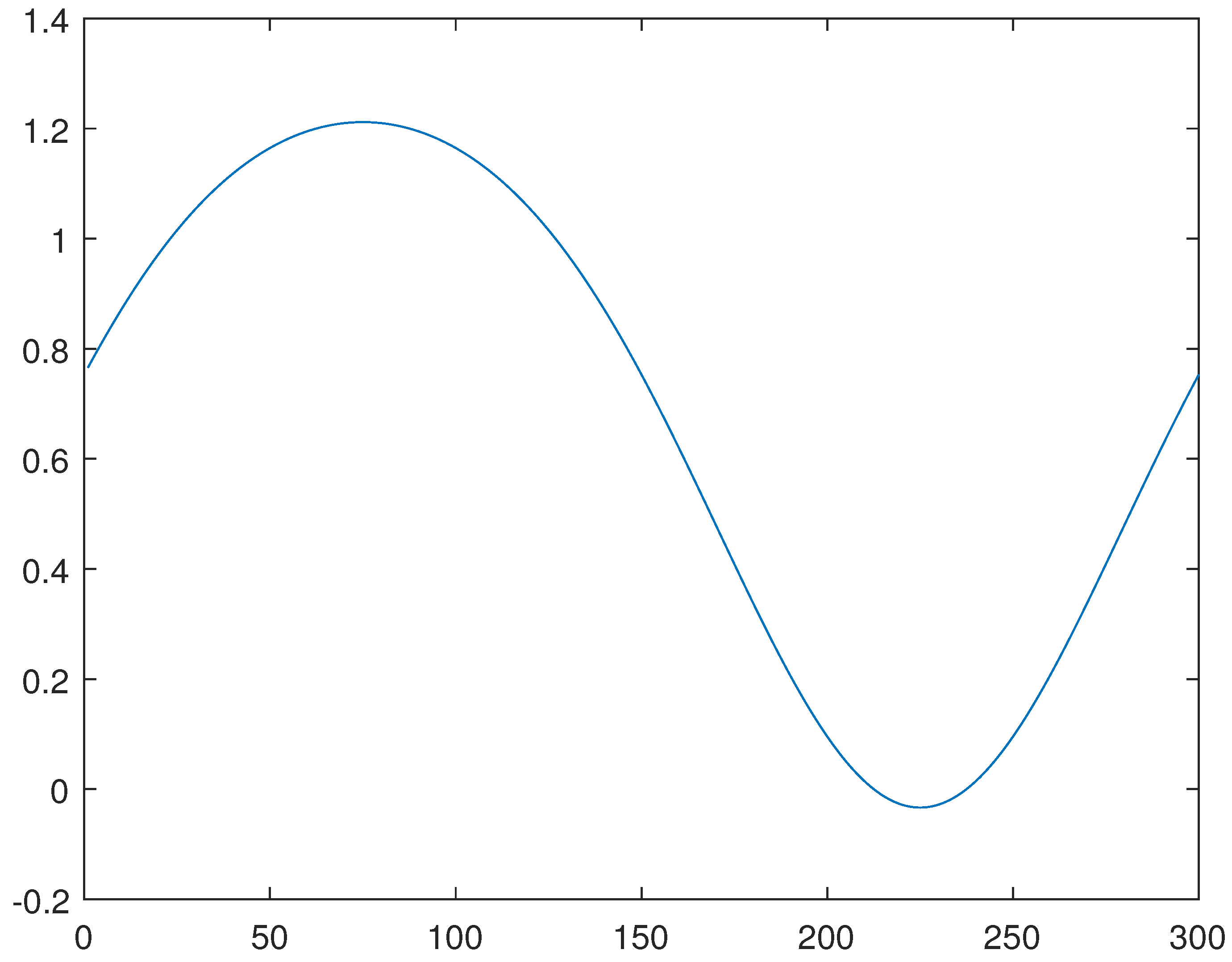
For the line 8, please see Figure 10, Figure 11 and Figure 12, obtained through the generalized method of lines, through a combination of the Newton and generalized methods of lines, and through the minimization of the functional J, respectively.

8. Conclusions

In the first part of this article, we developed duality principles for non-convex variational optimization. In the following sections, we proposed dual convex formulations suitable for a large class of models in physics and engineering. In the previous section, we presented an advance concerning the computation of a solution for a partial differential equation through the generalized method of lines. In particular, in its previous versions, we used to truncate the series in $d^2$; however, we have realized that the results are much better when taking line solutions in series for $u_f\left[x\right]$ and its derivatives, as is indicated in the present software.

This is a small difference from the previous procedure but results in great improvements as the parameter $\epsilon >0$ is small.

Indeed, with a sufficiently large N (number of lines), we may obtain very good qualitative results even as $\epsilon >0$ is very small.