New Explicit Oscillation Criteria for First-Order Differential Equations with Several Non-Monotone Delays
Abstract
1. Introduction
2. Main Results
- (1)
- It should be noted that
- (2)
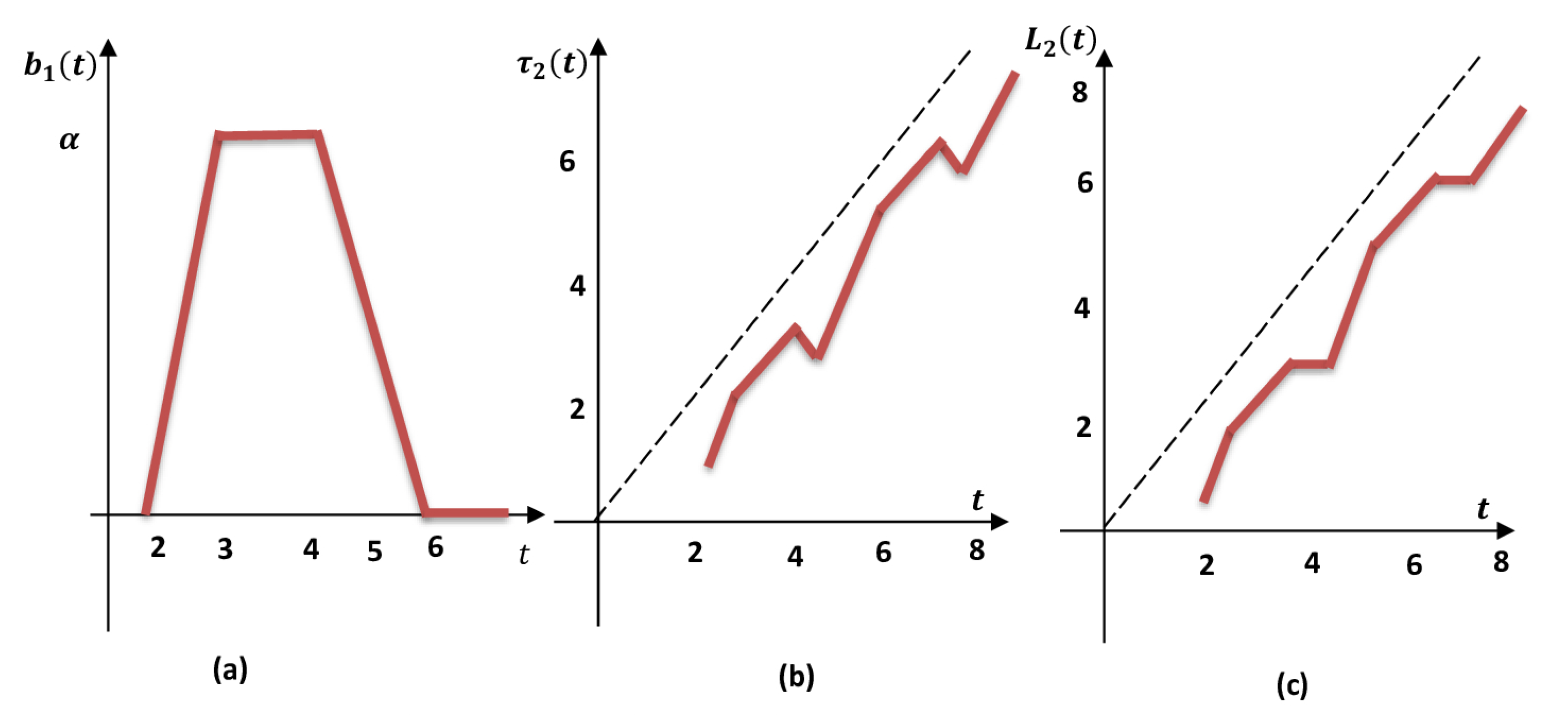
3. Numerical Examples
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gyori, I.; Ladas, G. Oscillation Theory of Delay Differential Equations with Applications; Clarendon Press: Oxford, UK, 1991. [Google Scholar]
- Agarwal, R.P.; Berezansky, L.; Braverman, E.; Domoshnitsky, A. Non-Oscillation Theory of Functional Differential Equations with Applications; Springer: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Grace, S.R.; ÓRegan, D. Oscillation Theory for Difference and Functional Differential Equations; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Akca, H.; Chatzarakis, G.E.; Stavroulakis, I.P. An oscillation criterion for delay differential equations with several non-monotone arguments. Appl. Math. Lett. 2016, 59, 101–108. [Google Scholar] [CrossRef]
- Attia, E.R.; Benekas, V.; El-Morshedy, H.A.; Stavroulakis, I.P. Oscillation of first order linear differential equations with several non-monotone delays. Open Math. 2018, 16, 83–94. [Google Scholar] [CrossRef]
- Attia, E.R.; El-Morshedy, H.A. Improved oscillation criteria for first order differential equations with several non-monotone delays. Mediterr. J. Math. 2021, 156, 11–16. [Google Scholar] [CrossRef]
- Attia, E.R.; El-Morshedy, H.A.; Stavroulakis, I.P. Oscillation criteria for first order differential equations with non-monotone delays. Symmetry 2020, 12, 718. [Google Scholar] [CrossRef]
- Attia, E.R.; El-Morshedy, H.A. New oscillation criteria for first order linear differential equations with non-monotone delays. J. Appl. Anal. Comput. 2022, 12, 1579–1594. [Google Scholar] [CrossRef]
- Bereketoglu, H.; Karakoc, F.; Oztepe, G.S.; Stavroulakis, I.P. Oscillation of first order differential equations with several non-monotone retarded arguments. Georgian Math. J. 2019, 27, 1–10. [Google Scholar] [CrossRef]
- Braverman, E.; Chatzarakis, G.E.; Stavroulakis, I.P. Iterative oscillation tests for differential equations with several non-monotone arguments. Adv. Differ. Equ. 2016, 2016, 87. [Google Scholar] [CrossRef][Green Version]
- Braverman, E.; Karpuz, B. On oscillation of differential and difference equations with non-monotone delays. Appl. Math. Comput. 2011, 218, 3880–3887. [Google Scholar] [CrossRef]
- Chatzarakis, G.E.; Péics, H. Differential equations with several non-monotone arguments: An oscillation result. Appl. Math. Lett. 2017, 68, 20–26. [Google Scholar] [CrossRef]
- Chatzarakis, G.E.; Jadlovská, I. Explicit criteria for the oscillation of differential equations with several arguments. Dyn. Syst. Appl. 2019, 28, 217–242. [Google Scholar] [CrossRef]
- Chatzarakis, G.E.; Purnaras, I.K.; Stavroulakis, I.P. Oscillations of deviating difference equations with non- monotone arguments. J. Differ. Equ. Appl. 2017, 23, 1354–1377. [Google Scholar] [CrossRef]
- Elbert, Á.; Stavroulakis, I.P. Oscillations of first order differential equations with deviating arguments. In Recent Trends in Differential Equations; World Scientific Publishing Co.: Singapore, 1992; pp. 163–178. [Google Scholar]
- El-Morshedy, H.A.; Attia, E.R. New oscillation criterion for delay differential equations with non-monotone arguments. Appl. Math. Lett. 2016, 54, 54–59. [Google Scholar] [CrossRef]
- Erbe, L.H.; Kong, Q.K.; Zhang, B.G. Oscillation Theory for Functional Differential Equations; Mareel Dekker: New York, NY, USA, 1995. [Google Scholar] [CrossRef]
- Garab, Á. A sharp oscillation criterion for a linear differential equation with variable delay. Symmetry 2019, 11, 1332. [Google Scholar] [CrossRef]
- Garab, Á.; Pituk, M.; Stavroulakis, I.P. A sharp oscillation criterion for a linear delay differential equation. Appl. Math. Lett. 2019, 93, 58–65. [Google Scholar] [CrossRef]
- Garab, Á.; Stavroulakis, I.P. Oscillation criteria for first order linear delay differential equations with several variable delays. Appl. Math. Lett. 2020, 106, 106366. [Google Scholar] [CrossRef]
- Gopalsamy, K. Stability and Oscillations in Delay Differential Equations of Population Dynamics; Kluwer Academic Publishers: Norwell, MA, USA, 1992. [Google Scholar]
- Hunt, B.R.; Yorke, J.A. When all solutions of x′(t)=−Σql(t)x(t−Tl(t)) oscillate. J. Differ. Equ. 1984, 53, 139–145. [Google Scholar] [CrossRef]
- Infante, G.; Koplatadze, R.G.; Stavroulakis, I.P. Oscillation criteria for differential equations with several retarded arguments. Funkcial. Ekvac. 2015, 58, 347–364. [Google Scholar] [CrossRef]
- Jaroš, J.; Stavroulakis, I.P. Oscillation tests for delay equations. Rocky Mt. J. Math. 1999, 29, 197–207. [Google Scholar] [CrossRef]
- Kolmanovskii, V.; Myshkis, A. Applied Theory of Functional Differential Equations; Kluwer: Boston, MA, USA, 1992. [Google Scholar]
- Koplatadze, R.G. Specific properties of solutions of first order differential equations with several delay arguments. J. Contemp. Math. Anal. 2015, 50, 229–235. [Google Scholar] [CrossRef]
- Koplatadze, R.G.; Chanturiya, T.A. Oscillating and monotonic solutions of first order differential equations with deviating arguments. Differ. Uravn. 1982, 18, 1463–1465. Available online: http://mi.mathnet.ru/de4645 (accessed on 20 November 2022). (In Russian).
- Kuang, Y. Delay Differential Equations with Applications in Population Dynamics; Academic Press: Boston, MA, USA, 1993. [Google Scholar]
- Kwong, M.K. Oscillation of first order delay equations. J. Math. Anal. Appl. 1991, 156, 274–286. [Google Scholar] [CrossRef]
- Ladas, G. Sharp conditions for oscillations caused by delays. Appl. Anal. 1979, 9, 93–98. [Google Scholar] [CrossRef]
- Ladas, G.; Lakshmikantham, V.; Papadakis, J.S. Oscillations of higher-order retarded differential equations generated by the retarded argument. In Delay and Functional Differential Equations and Their Applications; Academic Press: New York, NY, USA, 1972; pp. 219–231. [Google Scholar] [CrossRef]
- Ladde, G.S. Oscillations caused by retarded perturbations of first order linear ordinary differential equations. Atti Acad. Naz. Lincei Rendi. 1977, 63, 351–359. Available online: http://pascal-francis.inist.fr/vibad/index.php?action=getRecordDetail&idt=PASCAL7930393343 (accessed on 20 November 2022).
- Myshkis, A.D. Linear homogeneous differential equations of first order with deviating arguments. Uspekhi Mat. Nauk 1950, 5, 160–162. (In Russian) [Google Scholar]
- Pituk, M. Oscillation of a linear delay differential equation with slowly varying coefficient. Appl. Math. Lett. 2017, 73, 29–36. [Google Scholar] [CrossRef]
- Sficas, Y.G.; Stavroulakis, I.P. Oscillation criteria for first-order delay equations. Bull. Lond. Math. Soc. 2003, 35, 239–246. [Google Scholar] [CrossRef]
- Stavroulakis, I.P. Oscillation criteria for delay and difference equations with non-monotone arguments. Appl. Math. Comput. 2014, 226, 661–672. [Google Scholar] [CrossRef]
- Yu, J.S.; Wang, Z.C.; Zhang, B.G.; Qian, X.Z. Oscillations of differential equations with deviating arguments. Panamer. Math. J. 1992, 2, 59–78. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Attia, E.; El-Matary, B. New Explicit Oscillation Criteria for First-Order Differential Equations with Several Non-Monotone Delays. Mathematics 2023, 11, 64. https://doi.org/10.3390/math11010064
Attia E, El-Matary B. New Explicit Oscillation Criteria for First-Order Differential Equations with Several Non-Monotone Delays. Mathematics. 2023; 11(1):64. https://doi.org/10.3390/math11010064
Chicago/Turabian StyleAttia, Emad, and Bassant El-Matary. 2023. "New Explicit Oscillation Criteria for First-Order Differential Equations with Several Non-Monotone Delays" Mathematics 11, no. 1: 64. https://doi.org/10.3390/math11010064
APA StyleAttia, E., & El-Matary, B. (2023). New Explicit Oscillation Criteria for First-Order Differential Equations with Several Non-Monotone Delays. Mathematics, 11(1), 64. https://doi.org/10.3390/math11010064






