An Information-Reserved and Deviation-Controllable Binary Neural Network for Object Detection

Abstract

Object detection is a fundamental task in computer vision, which is usually based on convolutional neural networks (CNNs). While it is difficult to be deployed in embedded devices due to the huge storage and computing consumptions, binary neural networks (BNNs) can execute object detection with limited resources. However, the extreme quantification in BNN causes diversity of feature representation loss, which eventually influences the object detection performance. In this paper, we propose a method balancing Information Retention and Deviation Control to achieve effective object detection, named IR-DC Net. On the one hand, we introduce the KL-Divergence to compose multiple entropy for maximizing the available information. On the other hand, we design a lightweight convolutional module to generate scale factors dynamically for minimizing the deviation between binary and real convolution. The experiments on PASCAL VOC, COCO2014, KITTI, and VisDrone datasets show that our method improved the accuracy in comparison with previous binary neural networks.

1. Introduction

Convolutional-neural-network-based object detection [1] plays an important role in a wide variety of computer vision applications such as face recognition [2,3], auto-driving [4,5], and public security monitoring [6]. However, the traditional CNN-based object detection method [7] contains massive parameters with huge storage and computational consumption. Therefore, it cannot be transferred into portable devices because of the limited resources. With mobile devices growing rapidly more popular, it is essential to design a lightweight object detection model without large computing power.

The deep neural network can be compressed by quantification [8,9], efficient structure design [10,11,12], and pruning [13,14] to obtain lightweight models. Binary convolutional neural network (BNN) is the most extreme network quantification method, which not only reduces the memory footprint, but also greatly accelerates the network computing speed [15,16]. However, the efficiency and lightness of BNN comes at the cost of performance loss, which makes it hard to accomplish complex object detection tasks.

Limited expression ability and inadequate training are the main reasons for the performance loss of binary convolutional neural networks. To improve the network expression ability, XNOR-Net [17] can greatly reduce the performance loss caused by direct quantization and enhance the feature representation ability by introducing the scale factor of the weight part. However, because the weight scale factor is independent of the input, it is not flexible for mapping different input features, which greatly reduces the feature representation ability of the binary network. Constructing an excellent loss function can improve the training potentiality without increasing the cost. Therefore, a lot of research work [18,19,20,21] is focused on the loss function in network training, so that the loss function can still accurately guide the learning process of network parameters even in extremely binarization. In general, the previous binarization schemes only focus on the global loss but often ignore retaining critical information in training.

To solve the above problems and inspired by the perspectives of information flow and data drive, we propose a method balancing information retention and deviation control to achieve effective object detection. More specifically, we reduce the quantitative information loss by maximizing the information entropy of the binary object detection network and introduce KL divergence as a metric to constrain the distribution difference between the binary network and the full-precision network. We construct a loss function to retain more effective information through maximizing the information entropy and minimizing the quantization error as well as the distribution difference of the networks. Moreover, we introduce a lightweight convolutional module to automatically generate dynamic scaling factors to obtain better feature approximation ability and minimize the gap between real valued convolution and binary convolution. The experiments on the PASCAL VOC [22], COCO [23], KITTI [24], and VisDrone [25] datasets demonstrate that our IR-DC Net method outperforms other binary networks by a sizeable margin.

Our main contributions in this paper are summarized as follow:

• We propose a method with multiple entropy constraints to improve the performance of information retention networks, including information entropy and relative entropy.
• We propose a dynamic scaling factor to control the deviation between the binary network and the full-precision network, so that the performance of the binary network is closer to the full-precision network.
• We simultaneously optimize the binary network from both the perspectives of information retention and deviation control for effective object detection.
• We evaluate the IR-DC Net method on PASCAL VOC, COCO, KITTI, and VisDrone datasets to enable a comprehensive comparison with the state-of-the-art binary networks in object detection.

This paper is organized as follows: In Section 2, we describe the previous research work of binary neural network and object detection. In Section 3, we explain the basic description and operation process of the binary convolutional network. In Section 4, we illustrate the model structure of IR-DC Net and the implementation principle. In Section 5, we show the experimental datasets, implementation details and ablation study. In Section 6, we compare the performance of different methods in several datasets and display some visualization results;. In Section 7, we summarize our research work and make a conclusion.

2. Related work

2.1. Binary Convolutional Neural Network

In recent years, binary networks have been widely discussed due to their high efficiency in computing and storage. The naive binary calculation directly quantifies the weight and activation as +1 and −1 [26]. This extreme method causes serious damage to the rich information contained in the full-precision features and weights and greatly reduces the expression ability of the quantified network. On the basis of binary weight and activation, XNOR-Net [17] introduces a scale factor $\alpha$ to reduce the error between binary parameters and full-precision parameters, which greatly reduces the performance loss caused by direct quantization. However, the stationary scale factor cannot be flexibly adjusted according to different feature map inputs. Bi-Real Net [27] is improved on the basis of X-NOR Net. It provides a user-defined ApproxSign function to replace the sign function for gradient operation in backpropagation. IR-Net [28] minimizes the information loss in forward propagation from the perspective of maximizing information entropy, which makes the training of binary networks more robust through a simple regularization operation. ReActNet [29] improved the sign and PReLU functions and added the learnable coefficient to automatically learn the offset value and scaling value of each convolutional layer so that the binary network can learn the distribution similar to the full-precision network, and enhance the network expression ability. The binary detector BiDet [30] extends the information bottleneck principle to the field of object detection, which eliminates redundancy and improves detection accuracy by reducing false positives. BTM [31] explored a binary training mechanism based on feature distribution, which can enable binary networks to achieve excellent performance without a BatchNorm layer. It also proposes a new binary network structure and a multi-stage knowledge distillation strategy, which further improve the network expression ability. GroupNet [32] divides the network into multiple groups and proposes binary parallel convolution, which can embed rich multi-scale information into BNN, and significantly improve performance while maintaining complexity. CABNN [33] introduces the RPReLU self-adjusting activation distribution with learnable coefficients and uses the channel focus module to assign different weights to each channel to focus on key features and suppress unimportant features. The details of each method are shown in Table 1. The abovementioned binary network optimization methods only consider improving the expression ability or tapping the training potential. Although the extremely high compression ratio greatly reduces the complexity of the model, it also inevitably loses a lot of information, which limits the expression ability of a binary network. Coupled with inadequate training, binary networks perform poorly in difficult tasks, such as object detection, so there is always a large gap between the performance of binary networks and full-precision networks.

Table 1. Previous work of binary neural network [17,26,27,28,30,31,32,33].

Year	Method	Main Idea	Authors
2016	BNN	It quantifies the activation function and weight as +1 and −1.	COURBARIAUX M et al.
2016	XNOR-Net	On the basis of binary weight and activation, it introduces scale factor a to reduce the error.	RASTEGARI M et al.
2018	Bi-Real Net	It provides a user-defined ApprovSign function to replace the sign function for gradient operation in backpropagation.	Z. C. LIU et al.
2020	IR-Net	It keeps the information in the network from both the forward propagation and the back propagation.	H. T. QIN et al.
2020	ReActNet	It improves the sign and PReLU functions and increases the learnable coefficients to reduce the distribution error.	Z. C. LIU et al.
2020	BiDet	It introduces the information bottleneck principle to reduce false positives by eliminating redundancy.	Z. W. WANG et al.
2021	BTM	It proposes a binary training mechanism based on feature distribution and a multi-stage knowledge distillation strategy.	X. R. JIANG et al.
2022	GroupNet	It divides the network into several groups and proposes binary parallel convolution, which can embed multi-scale information into BNN.	B. H. ZHUANG et al.
2022	CABNN	It introduces a self-adjusting activation distribution of RPReLU with learnable coefficients for feature screening.	W. P. JING et al.

2.2. Object Detection

Object detection is a basic task in computer vision, which has earned wide attention with the rapid development of deep learning. The CNN-based object detection framework is divided into two-stage detection and one-stage detection based on whether or not there are proposed preprocessing steps. For the two-stage detector, R-CNN [34] applied convolutional neural networks to bottom-up candidate regions to locate and segment objects. However, the repetition of feature inputs make extra calculations which slow down the running speed. Fast R-CNN [35] proposed the RoI Pooling layer to unify the features, which can train the detector and the bounding box regressor simultaneously. It greatly improves the detection speed. The Faster R-CNN [36] is the first near-real-time and end-to-end deep learning detector, which uses Region Proposal Network instead of Selective Search, making the object detection break through the speed bottleneck. The FPN [37] developed a top-down architecture with lateral connections for difficult object-locating problems, and it is used for building high-level semantics. It has made great progress in detecting objects at various scales. Yolo [38] is the first single-stage detector in the era of deep learning. It applies a single neural network to the whole image and transforms the object detection problem into a regression problem. Compared to the two-stage detector, the detection speed is greatly improved, while it reduces the positioning accuracy, especially for small objects. SSD [39] introduced multi-reference and multi-resolution technology to improve the detection accuracy, including small objects. Retinanet [40] solved the imbalance between foreground and background levels by reconstructing the standard cross entropy loss, so that the one-stage detector can achieve the same accuracy as the two-stage detector while maintaining the detection speed. The details of each method are shown in Table 2. However, due to the huge amount of computation and storage requirements, the object detector based on the full-precision network is still difficult to deploy on the equipment with limited cost, and its application and promotion are still constrained. Therefore, our IR-DC Net can realize real-time object detection on mobile portable devices with minimal loss of accuracy.

Table 2. Previous work of classical object detection methods [23,35,36,37,38,39,40].

Year	Method	Main Idea	Authors
2014	R-CNN	It applies CNN to bottom-up candidate regions to locate and segment objects.	Ross Girshick et al.
2015	Fast R-CNN	It proposes RoI Pooling layer to unify features, which can train detectors and bounding box regressors simultaneously.	Ross Girshick
2015	Faster R-CNN	It uses Region Proposal Network instead of Selective Search, and it is the first near real-time and end-to-end deep learning detector.	S. H. REN et al.
2016	YOLO	It applies a single neural network to the whole image and transforms the object detection problem into a regression problem. It is the first single stage detector.	Joseph Redmon et al.
2016	SSD	It introduces multi-reference and multi-resolution technology to improve the detection accuracy, including small objects.	W. LIU et al.
2017	FPN	It develops a top-down architecture with lateral connections for difficult object-locating problems.	Tsung-Yi Lin et al.
2017	RetinaNet	It solves the imbalance between foreground and background levels by reconstructing the standard cross entropy loss.	Tsung-Yi Lin et al.

3. Preliminaries

In the full-precision convolutional neural network, the basic operations can be described as:

$$\mathbf{z}=\mathbf{w}\ast \mathbf{a},$$

(1)

where $\mathbf{w}$ represents weight, $\mathbf{a}$ represents activation value, and ∗ represents convolution operation. Binary network usually refers to a deep neural network with binary weight and binary activation. We usually use a sign function to binarize the weight and activation of floating-point representation in the full-precision network, from which we can obtain:

$$B_{\mathbf{x}}=Sign\left(\mathbf{x}\right)=\left\{\begin{array}{c}-1,\mathrm{if}\mathbf{x}<0\hfill \\ +1,\mathrm{otherwise}\hfill \end{array}\right.$$

(2)

where $\mathbf{x}$ represents the floating-point parameters in the neural network, including the weight $\mathbf{w}$ and the activation value $\mathbf{a}$. Therefore, the full-precision parameter quantization function in the depth neural network can be expressed as:

$$\mathrm{Q}\left(\mathbf{x}\right)=\alpha {\mathit{B}}_{\mathbf{x}},$$

(3)

where ${\mathit{B}}_{\mathbf{x}}$ represents the quantized binary parameter, and $\alpha$ represents the scale factor of the binary parameter. Thus, the operation of a binary neural network can be expressed as:

$$\widehat{z}=Q\left(\mathbf{w}\right)\mathrm{Q}\left(\mathbf{a}\right)=\alpha \left({\mathit{B}}_{\mathit{w}}\odot {\mathit{B}}_{\mathbf{a}}\right),$$

(4)

where ${\mathit{B}}_{\mathit{w}}$ and ${\mathit{B}}_{\mathbf{a}}$ is the binary value corresponding to the real value weight and the activation value, respectively, and ⊙ represents the inner product of vectors with bit operations and bit counts. The quantization process of the network is shown in Figure 1. The quantization error between the full-precision network and its corresponding binary network can be expressed as:

$$J\left({\mathit{B}}_{\mathrm{x}},\alpha \right)={∥\mathbf{x}-\alpha {\mathit{B}}_{\mathbf{x}}∥}^2.$$

(5)

Figure 1. The quantization process from full-precision convolutional neural network to binary convolutional neural network.

General quantized convolutional neural networks often obtain the best quantizer by minimizing the quantization error.

4. Proposed Method

In this section, we propose our Information Retention and Deviation Control Network, named IR-DC Net. As shown in Figure 2. Firstly, we extend the information entropy principle in information theory to object detection and maximize the information in the training process by constructing the loss function. Secondly, we introduce a lightweight convolutional module to automatically generate dynamic scaling factors to reduce the error caused by the quantization process, to obtain a high-precision binary model.

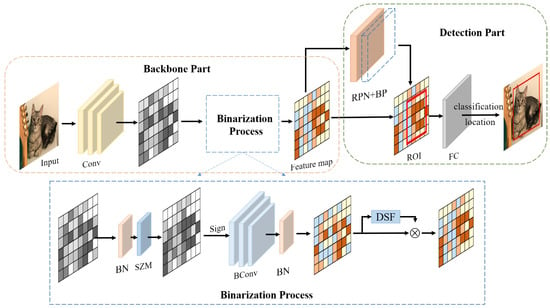
Figure 2. The object detector based on IR-DC net is composed of a backbone part and a detection part. We binarize the backbone part and the Region Proposal Networks (RPN) of the detection part. The Standard Zero Mean (SZM) maximizes the information entropy of the network, and the Dynamic Scale Factor (DSF) reduces the error between the binary parameter and the real parameter.

4.1. Information Retention with Multi-Entropy

In the forward propagation of neural networks, quantization operation will lead to the loss of network information. General quantized convolutional neural networks often obtain the best quantizer by minimizing quantization error, as follows:

$$minJ\left({\mathit{B}}_{\mathrm{x}},\alpha \right)={∥\mathbf{x}-\alpha {\mathit{B}}_{\mathbf{x}}∥}^2,$$

(6)

where $J\left({\mathit{B}}_{\mathrm{x}},\alpha \right)$ is the quantization error between the full-precision parameter and its corresponding binary parameter. When the full-precision parameters are quantized to a very low bit width, the mode of the quantization model does not fully follow the mode of the full-precision model, and the solution space of the binary network is also very different from that of the full-precision network. Therefore, it is difficult to obtain a binary network with good performance only by minimizing the quantization error.

We improve the IR-Net [28] with information entropy and relative entropy (Kullback–Leibler divergence), which maximizes the amount of information in the binary network and reduces the distribution difference between the binary network and the full-precision network as much as possible. We introduce the information entropy theory in information theory to measure the amount of information: the more information, the greater the entropy. Since all parameters in the binary network are quantized as +1 and −1, each parameter ${\mathit{B}}_{\mathbf{x}}$ in the binary network can be regarded as a random variable $b\in \{-1,+1\}$, which obeys the Bernoulli distribution, and its probability density function is:

$$f\left(b\right)=\left\{\begin{array}{cc}p,\hfill & \mathrm{if}b=+1\hfill \\ 1-p,\hfill & \mathrm{if}b=-1\hfill \end{array}\right.,$$

(7)

where p represents the probability that the binary parameter is +1, $p\in (0,1)$. For binary sources with only +1 and −1 elements, the entropy of the binarization parameter ${\mathit{B}}_{\mathbf{x}}$ can be estimated as:

$$\mathcal{H}\left({\mathit{B}}_{\mathbf{x}}\right)=-pln\left(p\right)-(1-p)ln(1-p).$$

(8)

Under the assumption of the Bernoulli distribution, when p = 0.5, the overall information entropy of the binarized parameters reaches the maximum, which means that the full-precision parameters should be uniformly distributed centered on 0. Therefore, we first zero-mean the full-precision weight, and then the probability that the quantized binary weight is +1 or −1 is almost equal, both close to 0.5. Meanwhile, the information entropy of the binary weight is maximized. After zero-mean, the full-precision weights are obviously concentrated around 0, and the range of data values is tiny. Moreover, a large number of symbols of full-precision weights are easy to flip in the back propagation, which directly leads to errors in the quantization process and instability of binary network training. In order to make the full-precision weight involved in the binarization process more dispersed, we further standardize the weight after zero-mean. The operation of standard zero-mean weight ${\widehat{\mathbf{w}}}_{\mathrm{szm}}$ is as follows:

$${\widehat{\mathbf{w}}}_{\mathrm{szm}}=\frac{\widehat{\mathbf{w}}}{\sigma \left(\widehat{\mathbf{w}}\right)},\widehat{\mathbf{w}}=\mathrm{w}-\overline{\mathbf{w}},$$

(9)

where $\overline{\mathbf{w}}$ is the average value of full-precision weight, and $\sigma (·)$ represents the standard deviation. Figure 3 shows that the use of the standard zero-mean method can make the full-precision weight update stably and make the binary weight $\mathrm{Q}\left({\widehat{\mathbf{w}}}_{\mathrm{szm}}\right)$ more stable during training.

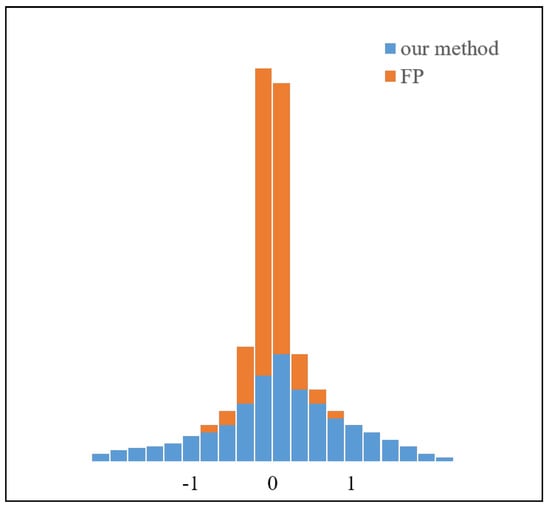
Figure 3. The full-precision weights in neural networks are always distributed around 0, and the data range is tiny enough. Their symbols are easily changed in the process of back propagation. Our method balances and normalizes the weights before binarization to make them more stable in the training process.

The value of the binary weight $\mathrm{Q}\left({\widehat{\mathbf{w}}}_{\mathrm{szm}}\right)$ depends on the sign of the ${\widehat{\mathbf{w}}}_{\mathrm{szm}}$, and the distribution of the full-precision weight ${\widehat{\mathbf{w}}}_{\mathrm{szm}}$ is almost symmetric centered around 0. Thus, the standard zero-mean operation can maximize the information entropy of the binary weight $\mathrm{Q}\left({\widehat{\mathbf{w}}}_{\mathrm{szm}}\right)$ overall, which means the information in the network can be retained to the maximum extent.

In addition, the network information can be preserved by minimizing the distribution gap between the full-precision network and the binary network. In this method, we use KL divergence as a metric to measure the information loss when the full-precision distribution is quantized into a binary distribution. The information loss function is defined as follows:

$${\mathcal{L}}_{\mathrm{Distribution}}=-\frac{1}{n}\sum _c\sum _{i=1}^n{p}_c\left(x_i\right)log\left(\frac{p_c\left(B_{x_i}\right)}{p_c\left(x_i\right)}\right),$$

(10)

where $p_c\left(x_i\right)$ and $p_c\left(B_{x_i}\right)$, respectively, represent the output probability of the category detection part of the full-precision and binary object detection network, c represents the category, n represents the batch size, and the value of ${\mathcal{L}}_{\mathrm{Distribution}}$ is proportional to the information loss. In conclusion, Our method proposes a new objective function, which is composed of network quantization error, binary network information entropy, and the distribution difference between the two networks. It is defined as:

$$minJ\left({\mathit{B}}_{\mathbf{x}},\alpha \right)-\mathcal{H}\left({\mathit{B}}_{\mathbf{x}}\right)+{\mathcal{L}}_{\mathrm{Distribution}}.$$

(11)

On the basis of minimizing the quantization error of the network, we try our best to retain the rich information in the network for improving the recognition accuracy and performance of the object detection network.

4.2. Deviation Control with Dynamic Scale Factor

In our proposed IR-DC Net, the quantization error mainly comes from the error between the full-precision weight and its corresponding binary weight. The weight quantization error can usually be expressed as:

$$J\left({\mathit{B}}_{\mathit{w}},\alpha \right)={∥\mathbf{w}-\alpha {\mathit{B}}_{\mathit{w}}∥}^2,$$

(12)

where $\mathbf{w}$ represents the weight of the full-precision network, and ${\mathit{B}}_{\mathit{w}}$ represents the corresponding binary weight. For the convenience of formula derivation, we transform the weight matrix $\mathbf{w}$ and ${\mathit{B}}_{\mathit{w}}$ into $1\times \mathrm{n}$-dimensional vector, $\mathrm{n}=\mathrm{c}\times \mathrm{w}\times \mathrm{h}$. The expanded Equation (12) can be obtained:

$$J\left({\mathit{B}}_w,\alpha \right)={\alpha }^2{\mathit{B}}_{\mathit{w}}^{\top }{\mathit{B}}_w-2\alpha {\mathbf{w}}^{\top }{\mathit{B}}_w+{\mathbf{w}}^{\top }\mathbf{w},$$

(13)

because ${\mathbf{w}}^{\top }\mathbf{w}$ and ${\mathit{B}}_{\mathit{w}}^{\top }{\mathit{B}}_w$ are constants, let $\mathrm{c}={\mathbf{w}}^{\top }\mathbf{w},\mathrm{n}={\mathit{B}}_{{\mathit{w}}^{\top }}{\mathit{B}}_{\mathit{w}}$. We can obtain:

$$J\left({\mathit{B}}_{\mathit{w}},\alpha \right)={\alpha }^{2}n-2\alpha {\mathbf{w}}^{\top }{\mathit{B}}_{\mathit{w}}+\mathrm{c},$$

(14)

thus, the optimal solution of $\alpha$ can be obtained:

$$\alpha =\frac{{\mathbf{w}}^{\top }sign\left(\mathbf{w}\right)}{n}=\frac{\sum \left|{\mathbf{w}}_i\right|}{n}=\frac{1}{n}{\parallel \mathbf{w}\parallel }_{\ell 1},$$

(15)

according to Equation (15). The scale factor is only related to the weight and is not related to the input. So, there is a big error between convolution layer output of binary networks $\widehat{z}$ and convolution layer output of full-precision network $\mathrm{z}$. To solve this problem, we construct scale factor $\alpha$ as a function of input a to increase the correlation between the scale factor and input a, so that the scale factor can adjust dynamically with the change of input and enhance the representation ability. The specific operations are as follows:

$${\widehat{z}}^{\prime }=\left({\mathit{B}}_{\mathit{w}}\odot {\mathit{B}}_{\mathbf{a}}\right)\alpha \left({\mathit{B}}_{\mathit{w}}\odot {\mathit{B}}_{\mathbf{a}}\right)$$

(16)

where $\alpha (·)$ represents the scale factor function related to the input. In order not to increase the computational burden of the network, we introduce a new lightweight module named dynamic scale factor(DSF) to solve it. Inspired by Equation (15), the design of this module will start from the two dimensions of channel and space.

In order to calculate the scale factor of the channel dimension, we consider the feature map from two perspectives: intra-channel and inter-channel. First, we introduce global average pooling to reduce the spatial dimension and the number of parameters, which integrates global spatial information while extracting features. Secondly, considering the interaction between channels, we use one-dimensional convolution to fuse the information of each channel with that of its adjacent channels ($C\times 1\times 1$). For the scale factor of the spatial dimension, we use a two-dimensional convolutional kernel to extract the feature of spatial dimension ($1\times H\times W$). Finally, we decompose the one-dimensional channel eigenvector into c $1\times 1$ convolutional kernels and convolute the extracted $1\times W\times H$-dimensional spatial scale matrix to obtain the solution matrix of the scale factor ($C\times H\times W$). Furthermore, since the full-precision convolutional parameter is usually close to zero, the result of binary convolution is usually much larger than that of real-value convolution. In order to control the size of the scale factor and ensure that the scale factor does not change the convolutional symbol, a sigmoid function is introduced. This process can be expressed as:

$$\alpha \left({\mathit{B}}_{\mathit{w}}\odot {\mathit{B}}_{\mathbf{a}}\right)=\sigma \left(\left(k_c\ast GAP\left({\mathit{B}}_w\odot {\mathit{B}}_{\mathbf{a}}\right)\right)\odot \left(k_s\ast \left({\mathit{B}}_w\odot {\mathit{B}}_{\mathbf{a}}\right)\right)\right),$$

(17)

where $\sigma$ is the sigmoid function, $k_c$ is the one-dimensional convolutional kernel, GAP is the global average pooling, and $k_s$ is the two-dimensional convolutional kernel. The position and function of the DSF module in the binary object detection network is shown in Figure 4.

Figure 4. The calculation process of dynamic scale factor. We combine the calculation of two different dimensions of channel and space to obtain the dynamic scale factor.

5. Experiments

In this section, we conduct a comprehensive experiment on the PASCAL VOC, COCO, KITTI, and VisDrone datasets to evaluate our proposed IR-DC Net. We first describe the details of the implementation of IR-DC Net and then verify the validity of the information retention with multi-entropy network and DSF in the binary object detector by ablation experiments. Finally, we compare our proposed method with the existing binary object detection methods to verify the effectiveness of IR-DC Net.

5.1. Datasets

The PASCAL VOC dataset includes 20 different categories of images and is divided into train, validation (trainval), and test according to their purpose. VOC 2007 and VOC 2012 datasets are currently commonly used by researchers because all of their data are mutually exclusive. Since only the test set of VOC 2007 is public, we use the train set of VOC 2007 and VOC 2012 (about 16K pictures) to train the model and the test set of VOC 2007 (about 5K pictures) to evaluate the effect of the model. According to the literature [22], we use the mean accuracy (mAP) as the evaluation criterion.

The COCO dataset includes 80 different types of images. We select the COCO 2014 dataset for this experiment. We use around 83k pictures from the training set to train our model and evaluate the effect on 40K pictures from validation set. According to the evaluation method of COCO, we adopt AP@0.5 as the evaluation standard. The AP is tested once every 0.05 change in IOU from 0.5 to 0.95, and the average value of the 10 measurement results is taken as the final AP.

The KITTI 2D Object Detection Evaluation 2012 Dataset includes 7.5k training sets and 7.5k testing sets. We follow most of the previous work to divide the training data into a train set with 3.7k samples and a validation set with 3.8k samples.

The VisDrone2019 dataset consists of 261,908 video frames and 10,209 static images, captured by various drone-mounted cameras, taken from 14 different cities in China. The objects include pedestrians, cars, bicycles, and tricycles. As a popular small object detection dataset, there are on average 146 people clustering in an image with 1920 × 1080 pixels. We separate the 26k images into 16k train set, 9k validation set, and remaining 1k test set. The details of each dataset are shown in Table 3.

Table 3. The details of experimental datasets.

Dataset	Types	Training Set	Validation Set	Evaluation Standard
PASCAL VOC	20	16k	5k	mAP
COCO	80	83k	40k	AP@0.5
KITTI	3	3.7k	3.8k	mAP
VisDrone	4	16k	9k	mAP

5.2. Implementation Details

We pre-train VGG16 [41] and ResNet20 [42] through ImageNet as our backbone network. The IR-DC Net is trained by several datasets corresponding to SSD and Faster R-CNN frameworks. The development environment is Pytorch1.3.0+CUDA11.3. The CPU is Intel Xeon Sliver 4210 and the GPU is 4*Nvida RTX 2080ti. To train an IR-DC Net, we jointly fine-tune the backbone and train the detection header. The batch size is specified as 32. On the PASCAL VOC dataset, the learning rate is initially set to 0.001, for a total of 80 epochs training. The learning rate decays to 0.0001 at the 30th epoch, and the learning rate attenuates to 0.00001 at the 60th epoch. On the COCO2014 dataset, the initial learning rate remains 0.001, training a total of 16 epochs, attenuating to 0.0001 at the 8th epoch, and attenuating to 0.00001 at the 14th epoch. At KITTI 2D on the Object Detection dataset, we use the ADAM optimizer with an initial learning rate of 0.001 and train a total of 60 epochs, attenuating to 0.0001 at the 30th epoch and 0.00001 at the 50th epoch. The hyperparameter $\alpha$ of IR-DC Net is initially set to 0.25, and the loss weight $\mu$ is 0.01. For binary object detection methods, we take the comparison from Table 4, Table 5 and Table 6, since the authors never supported the results of the KITTI dataset in their paper. We rebuild their method and fine-tune to obtain results on the KITTI dataset. For the VisDrone dataset, our network is optimized by the SGD, we set the learning rate to 0.005 and the batch size to 2. We train 12 epochs with weight decay of 0.0001 and momentum of 0.9.

Table 4. Results of car class in KITTI.

Methods	Type	Car (IoU = 0.5)			Car (IoU = 0.7)
		Easy	Moderate	Hard	Easy	Moderate	Hard
SE-SSD	FP	96.69	95.6	90.53	96.65	93.27	88.14
SE-SSD*	1/1	56.69	46.87	44.68	53.07	43.43	41.34
BNN	1/1	63.3	50.73	32.23	58.27	43.24	27.67
XNOR-Net	1/1	65.01	51.26	35.73	59.07	47.06	32.61
BiDet	1/1	64.1	56.36	40.56	59.76	44.06	29.07
AutoBiDet	1/1	65.57	57.88	41.16	61.38	46.63	32.2
IR-DC	1/1	69.8	59.09	49.45	61.66	48.63	41.69

Table 5. Results of cyclist class in KITTI.

Methods	Type	Cyclist (IoU = 0.5)
		Easy	Moderate	Hard
SE-SSD	FP	88.99	78.71	72.03
SE-SSD*	1/1	61.42	45.41	38.26
BNN	1/1	49.98	28.46	22.41
Xnor-Net	1/1	59.09	35.22	26.54
BiDet	1/1	52.47	42.86	34.97
AutoBiDet	1/1	62.44	47.15	40.87
IR-DC	1/1	61.53	48.4	39.43

Table 6. Results of pedestrian class in KITTI.

Methods	Type	Pedestrain (IoU = 0.3)
		Easy	Moderate	Hard
SE-SSD	FP	72.33	60.51	56.28
SE-SSD*	1/1	46.69	35.87	31.68
BNN	1/1	34.35	23.92	20.43
Xnor-Net	1/1	46.38	30.39	26.17
BiDet	1/1	41.38	31.97	30.15
AutoBiDet	1/1	49.55	33.5	27.12
IR-DC	1/1	51.58	35.79	31.14

5.3. Ablation Study

To analyze the effects of Information Retention, KL-Divergency Loss and Dynamic Scale Factor, we conduct an ablation study on the KITTI 2D Object Detection Evaluation 2012 Datasets. We use eight-fold cross validation and calculate the evaluation results on the validation set. We select Car as our object with IoU set to 0.5/0.7 and record the ablation study results in Table 7. Our full model is IR-DC Net with whole components.

Table 7. Ablation study for IR-DC Net (The ✓ indicates that the corresponding component is included in the experiment).

IR	KL-D	DSF	Car
			IoU = 0.5			IoU = 0.7
			Easy	Moderate	Hard	Easy	Moderate	Hard
✓			53.17	35.81	33.01	35.8	24.05	19.97
	✓		53.19	33.49	30.73	34.82	25.31	18.32
		✓	53.22	41.38	33.65	36.14	25.75	19.73
✓	✓		63.2	53.7	40.68	45.77	33.29	27.7
✓		✓	63.07	54.15	41.17	45.15	35.57	28.59
	✓	✓	60.13	51.15	43.01	47.5	36.64	31.81
✓	✓	✓	69.8	59.09	49.45	61.66	48.63	41.69

5.3.1. Effect of Information Retention

We evaluate our Information Retention module with the first and sixth rows in Table 7. We remove the Information Retention module and information entropy loss (sixth row) to compare with the whole IR-DC Net (seventh row). We find the accuracy is decreased by 5.13% (Easy), 2.82% (Moderate), and 4.06% (Hard).

5.3.2. Effect of KL-Divergency Loss

We evaluate our KL-Divergency loss with the second and fifth rows in Table 7. To compare with the whole IR-DC Net (seventh row), we remove the KL-Divergency loss. We find the accuracy is decreased by 8.55% (Easy), 4.05% (Moderate), and 4.28% (Hard).

5.3.3. Effect of Dynamic Scale Factor

To investigate the effect of Dynamic Scale Factor, we compare the accuracy results by removing or reserving the factor. As shown in the third and fourth rows of Table 7, the accuracy is decreased by 7.28% (Easy), 2.69% (Moderate), and 1.21% (Hard) when we remove the Dynamic Scale Factor (4th rows and 7th rows). However, if we raise the Dynamic Scale Factor to justify the imputed features, the results are increased by 17.15% (Easy), 22% (Moderate), and 23.2% (Hard). The dynamic scale factor achieves higher accuracy than other components.

In summary, in the basic binarized neural network, increasing the dynamic scale factor of the fitted input images can maximize the final target detection accuracy; in our proposed IR-DC Net, the KL scatter constraint has a greater impact on the overall experiment than the information entropy loss and the dynamic scale factor.

6. Discussion

6.1. The Results on PASCAL VOC

As shown in Table 8, we evaluate the kernel bit width, parameter size, and average precision to compare the performance of several object detection methods on the PASCAL VOC dataset. We apply VGG16 and ResNet20 as the backbone networks to correspond to two different frameworks (SSD and Faster R-CNN). Meanwhile, we compare the quantitative methods with BNN (binary), BiDet (binary), AutoBiDet (binary) [43], Xnor-Net (binary), and IR-DC Net (binary). We can notice the improvement of IR-DC net from Figure 5 intuitively.

Table 8. Results of PASCAL VOC.

Baseline		Bit-Width	Params	mAP
VGG16	BNN	1/1	22.06	42
	XNOR-Net	1/1	22.16	50.2
	BiDet	1/1	22.06	52.4
	AutoBiDet	1/1	22.06	53.5
	IR-DC	1/1	22.16	55.3
	MobileNet	32/32	100.28	72.4
ResNet20	BNN	1/1	2.38	35.6
	XNOR-Net	1/1	2.48	48.4
	BiDet	1/1	2.38	50
	AutoBiDet	1/1	2.38	50.7
	IR-DC	1/1	2.48	51.2
	IR-DC	4/1	2.68	58.1

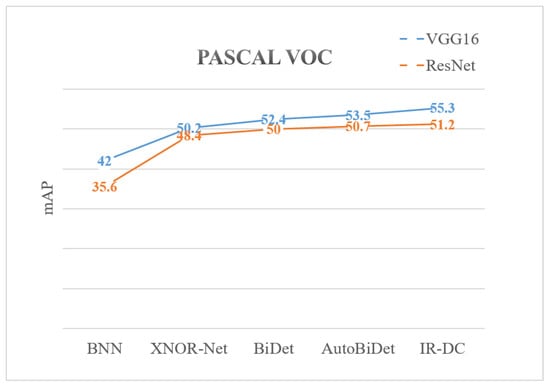
Figure 5. The results of different quantitative method in PASCAL VOC.

We can see that our approach outperforms competitors by a small improvement; the value in VGG16 framework is 1.8% (rows 2 and 5) and in ResNet20 is 0.5% (rows 8 and 11). However, our method still has a large margin with full-precision network because of the limitation on parameter size (rows five and six). If we replace the convolutional kernel bit width with 4 (rows 11 and 12), the result will be improved significantly.

6.2. The Results on COCO2014

Table 9 shows the comparison results on COCO2014. We provide various variations for average precision such as small object (S), medium object (M), and large object (L), and the IoU is set as 0.3, 0.5, respectively. Following the PASCAL VOC experiment, we choose BNN, BiDet, AutoBiDet, Xnor-Net, and our proposed IR-DC Net with two different backbone networks, VGG16 and ResNet20. As shown in Figure 6, we also provide a line chart to make our results more contrastive.

Table 9. Results of COCO2014.

Methods		AP
		S	M	L	IoU = 0.3	IoU = 0.5
VGG16	BNN	2.4	10	9.9	28.1	15.9
	XNOR-Net	2.6	8.3	13.3	33.4	19.5
	BiDet	5.1	14.3	20.5	46.1	28.3
	AutoBiDet	5.6	16.1	21.9	48.4	30.3
	IR-DC	6.2	17.6	22	49.7	32
ResNet20	BNN	2	8.5	9.3	26	14.3
	XNOR-Net	2.7	11.8	15.9	34.4	21.6
	BiDet	4.9	16.7	25.4	47.6	31
	AutoBiDet	5	17.2	25.9	48.4	31.5
	IR-DC	5.3	17.3	25.1	49.9	32

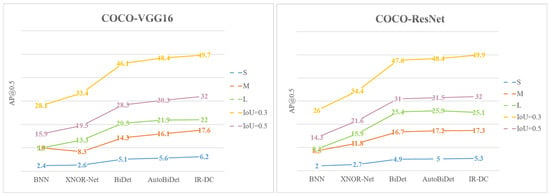
Figure 6. The results of different quantitative method in the COCO dataset.

The results show that our model performs better than others on most tasks except large object in the ResNet20 backbone. Our method outperforms the state-of-the-art by 0.6% (small), 1.5% (medium), 0.1% (large), 1.3% (IoU = 0.3), and 1.7% (IoU = 0.5) on the VGG16-based framework. In the ResNet20-based framework, we obtain a small improvement of 0.4% (small), 0.1% (medium), 1.5% (IoU = 0.3), and 1% (IoU = 0.5) but 0.8% less in large object detection.

6.3. The Results on KITTI

Table 4, Table 5 and Table 6 show the performance comparison of multiple object detection methods on the KITTI 2D Object Detection Evaluation 2012 dataset, and the evaluation metric is the average accuracy. We choose the SE-SSD [44] network as the full-accuracy model control group, while removing the 3D object detector and considering only the 2D experimental results, while changing its convolutional kernel to binarize to form SE-SSD* and fine-tuning it. Like the previous experiments, we select BNN, Xnor-Net, BiDet, and AutoBiDet with IR-DC Net for comparison and validation. Figure 7 shows the line chart of our experimental results for those methods above.

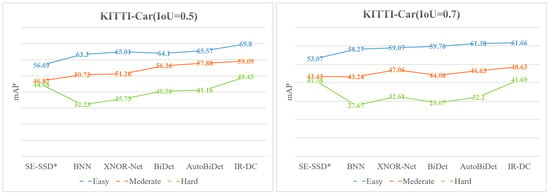
Figure 7. The results of different quantitative methods in the KITTI dataset (Car).

Table 4 shows the accuracy for the Car category with the Intersection over Union (IoU) set to 0.7, 0.5, with no occlusion and truncation (Easy), slight occlusion or truncation (Moderate), and large occlusion or truncation (Hard). By comparing the results of the binarized target detection group (third and seventh rows), we can see that accuracy of our proposed IR-DC Net outperforms the previous method in all aspects of truncated occlusion for both IoU values. When the intersection ratio is 0.5, the IR-DC Net improves over the other methods in the Easy, Moderate, and Hard by 4.23%, 1.21%, and 8.29%. When the intersection ratio is 0.7, the accuracy improvement is 0.28%, 1.57%, and 9.08%. The comparison with the full-precision object detection network shows (rows 1, 2, and 7) that the accuracy of the binary object detection network is much lower than the full-precision object detection network. It is inevitable because of fewer parameters.

Table 5 shows the accuracy data for the Cyclist with the IoU set to 0.5 in three kinds of occlusion truncation (Easy, Medium, Hard). By comparing the results of the binary target detection groups (rows 3–7), the accuracy of our proposed IR-DC Net for detecting a cyclist in medium occlusion improves by 1.25%. The results of Cyclist and Pedestrian in different methods are shown in Figure 8.

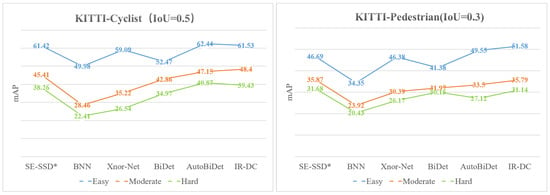
Figure 8. The results of a different quantitative method in the KITTI dataset (Cyclist and Pedestrian).

Table 6 shows the accuracy data for the Pedestrian category with IoU set to 0.3. We can see (rows 3–7) that IR-DC Net outperforms other binary object detection networks in all truncation or occlusion cases. More specifically, the results of IR-DC are 4.89% higher than SE-SSD* in Easy label. In conclusion, our proposed IR-DC Net shows better results than most binary object detection methods, even close to some full-precision networks.

6.4. The Results on VisDrone2019

Table 10 shows the average precision results for the several classes with the IoU set in the VisDrone2019 dataset. We list Pedestrian, Bicycle, Car, Van, Tricycle, Bus, and Motor results, respectively, in the table. Our IR-DC net obtains a good performance in some traditional classes such as pedestrian, car, and bus but miss detecting the tiny objects such as bicycle and motor.

Table 10. Results of VisDrone.

Method	Pedestrian	Bicycle	Car	Van	Tricycle	Bus	Motor	mAP
BNN	12.08	9.84	48.08	34.65	15.47	42.95	13.1	20.05
XNOR-Net	13.7	8.66	51.71	34.75	13.11	44.94	15.98	20.25
BiDet	15.46	10.02	52.33	34.63	14.83	50.78	20.69	22.05
AutoBiDet	18.17	14.73	57.38	34.81	18.64	50.22	19.67	26.23
IR-DC	19.18	14.29	59.19	34.37	15.62	52.29	20.03	26.2

6.5. Visualization Results

In order to more intuitively view the performance of IR-DC Net on object detection tasks, we show its visualization results on the COCO2014, KITTI, and VisDrone datasets. As can be seen from Figure 9, Figure 10 and Figure 11, the objects of different classes in the picture are marked by two-dimensional rectangular boxes of different sizes, and the categories of these objects are displayed at the same time. The great accuracy of visualization results proves the effectiveness of IR-DC Net in object detection tasks.

Figure 9. Visualization results on COCO2014.

Figure 10. Visualization results on KITTI.

Figure 11. Visualization results on VisDrone.

7. Conclusions

In this paper, we have proposed a binarized neural network learning method, called IR-DC Net, that balances information retention and deviation control for effective object detection. The presented IR-DC Net maximizes the available information via multiple entropy to improve the training potential and performance of the network. In addition, IR-DC Net introduces a dynamic scaling factor for minimizing the deviation between the binary network and a full-precision network. Extensive experiments prove that the IR-DC Net improves the accuracy in object detection compared with previous binary neural networks.