Abstract
A Ganymede-synchronous frozen orbit around Europa provides a stable spatial geometry between a Europa probe and a Ganymede lander, which facilitates the observation of Ganymede and data transmission between probes. However, the third-body gravitation perturbation of Ganymede continues to accumulate and affect the long-term evolution of the Europa probe. In this paper, the relative orbit of Ganymede with respect to Europa is considered to accurately capture the perturbation potential. The orbital evolution behaviors of the Europa probe under the non-spherical gravitation of Europa and the third-body gravitation of Jupiter and Ganymede are studied based on a double-averaging framework. Then, the initial orbital conditions of the Ganymede-synchronous frozen orbit are developed. A station-keeping maneuver was performed to maintain the orbital elements to achieve the Ganymede-synchronous and frozen behaviors. A numerical simulation showed that the consumption for orbital maintenance is acceptable.
MSC:
85-10; 70F15
1. Introduction
One of the scientific objectives for a practical Jovian system mission is exploring the Galilean moons such as Europa and Ganymede. NASA is carrying out the Europa Clipper mission to tour the Galilean moons by multiple fly-bys [1]. The Europa Clipper probe requires a wide-breadth imaging system to achieve global coverage with about 50 fly-bys, which constricts the imaging resolutions. The original design of the Europa Clipper mission includes a surface lander to improve the exploration efficiency [1]. However, this lander was canceled later due to budget issues. The ESA’s Jupiter Icy Moons Explorer (JUICE) will employ a high inclination that orbits around one of the Galilean moons to achieve global observing capacity [2,3]. Meanwhile, the imaging resolution of JUICE is improved with frequent revisits compared to that of the Europa Clipper mission. Theoretically, the exploration efficiency can be further enhanced if the JUICE probe carries a surface lander to investigate the surface of another Galilean moon, such as Ganymede. However, a probe orbiting around a Galilean moon suffers from multiple perturbations, resulting in a complicated evolution of the orbit. Meanwhile, to manage the data relay, the geometry of the Europa probe and the Ganymede lander should keep a stable transmission condition, which is also determined by the long-term orbital behavior of the Europa probe.
In order to study the long-term evolution behavior of the Galilean moon probe, researchers applied the mean element theory to eliminate the short-period variations in the orbital elements [4,5]. It was first employed to construct the secular evolution model with respect to classic orbital elements under the non-spherical gravitation perturbation of the central body such as the zonal terms J2 and J3 [6], the harmonic term C22 [7], and irregular celestial body shapes [8,9]. Later, the third-body gravitation perturbation of the planet was taken into account, and the secular evolution behavior was studied in the planetary system exploration mission [5,10,11,12]. Scheeres et al. [11] and Broucke [13] derived the secular Lagrange equations of a Europa probe under Europa’s non-spherical gravitation and Jovian third-body gravitation perturbations. They both employed a double-averaging method to eliminate the periodic terms of the motions of the probe around Europa and of Europa around Jupiter. The orbits around Europa are summarized as the stable orbits with low inclinations and the unstable orbits with high inclinations. More recently, further studies were performed to search for frozen orbits around Europa by considering more complex dynamic models [14,15,16,17]. The studies focus on the behaviors of the frozen orbits in aspect of the eccentricity, inclination, and argument of periapsis, which denote the motion with respect to the central moon. The evolution of the longitude of the ascending node, which represents the orbital behavior with respect to another Galilean moon, is always neglected. However, in order to achieve a stable condition for transmission, for instance, a moon-synchronous behavior, the evolution of the longitude of the ascending node should also be taken into account.
In previous studies, the methods of designing a series of synchronous orbits were proposed, such as the sun-synchronous orbit in the Sun–Earth system [18,19], around a comet [20], and the lunar synchronous orbit in the Earth–Moon system [21]. These synchronous orbits are generated by drifting the longitude of the ascending node in specific periods considering non-spherical gravitation perturbation [18] and solar radiation pressure [20]. A Galilean-moon-synchronous orbit, taking the Ganymede-synchronous orbit around Europa as an example, experiences a periodic behavior with respect to Ganymede. When Europa and Ganymede are synodic, the angle between the Europa–Ganymede vector and the normal vector of the orbital plane is a constant. Consequently, the orbit possesses a fixed spatial geometry with respect to Ganymede, which provides a periodic observing chance of Ganymede and a constant data transmission configuration between the Europa probe and the Ganymede lander. However, although the perturbation on the Europa probe from Ganymede gravity is small [22,23,24], this perturbation continues to accumulate due to the fixed space geometry. This brings about a long-term effect on the orbital evolution of the Europa probe. However, the corresponding evolution behavior has not been analyzed yet. Meanwhile, due to the fact that the orbital conditions of the synchronous are strict, an orbital maneuver is employed to loosen the constraint of the orbital condition and to generate the artificial synchronous orbits. Macdonald et al. generated an artificial sun-synchronous orbit by maintaining the right ascension of the ascending node [18]. This orbit can be of arbitrary inclination and semi-major axis. Wang et al. developed control strategies to eliminate the drift of the argument of periapsis and generated artificial sun-synchronous frozen orbits [25]. Wu et al. proposed a design method for an artificial sun-synchronous frozen orbit around Mars [26]. These research examples illustrate that an orbital maneuver can be executed to maintain the orbital elements to satisfy specific orbital constraints and generate artificial orbits.
This paper addresses the problem of the orbit evolution behavior of a Europa probe under Ganymede’s gravitation perturbation and generates a Ganymede-synchronous frozen orbit around Europa. The main contributions are summarized as follows: (1) Long-term Lagrange planetary equations for a Europa probe considering multiple gravitation perturbations are derived. Due to a transient impact on the probe when Ganymede is close to Europa, Ganymede’s gravitation is considered using an averaging method and a numerically double averaging framework [27]. Then, the Lagrange equations of the Europa probe in terms of classical orbital elements are obtained. (2) The long-term evolution behavior for a high-inclination near-circular orbit is analyzed. Since the perturbation of Ganymede’s gravitation accumulates, the analysis was conducted by numerical simulations to estimate the major influence on the orbit. The orbital conditions of the Ganymede-synchronous frozen orbit are summarized on the basis of these behaviors. (3) A design method for a Ganymede-synchronous frozen orbit is developed. In order to maintain a fixed perturbing effect of Ganymede’s gravitation, the design method is searching for an orbit with a synchronous behavior with respect to the longitude of the ascending node, and frozen behavior with respect to the inclination and argument of periapsis. Inspired by [28], the impulsive consumption of orbit maintenance is evaluated. The rest of the paper is organized as follows: In Section 2, a dynamic model of a Europa probe considering Jovian and Europa’s non-spherical gravitations is introduced. Long-term perturbation potential and corresponding Lagrange’s equations are derived based on the double-averaging method in Section 3. Then, the analyses of the orbital behaviors are performed in Section 4. Finally, the conclusion of the paper is presented in Section 5.
2. Dynamic Model
For the Jupiter–Europa–Ganymede–probe system where Europa and Ganymede are orbiting around Jupiter and the probe is orbiting around Europa, the coordinate systems and the equations of motion are established in this section. Then, a Legendre expansion is performed to simplify the perturbing potential.
2.1. Dynamical Model of Europa Probe
When Ganymede’s gravitation is considered, the perturbation effects on a Europa probe include Europa’s non-spherical gravitation and Jovian and Ganymede’s third-body gravitations. In this case, the perturbing potential from Europa’s non-spherical gravitation is calculated in the Europa-centric coordinate system, while the perturbing potentials from Jovian and Ganymede’s gravities and their positions are generally obtained in the Jovian-centric coordinate system. These coordinate systems and corresponding parameters are shown in Figure 1. In this figure, the Jovian-centric Jovian equator inertial (JCI) coordinate system [XJ, YJ, ZJ] and Jovian equator are shown in black. The XJ-axis points to the Jupiter equinox, the ZJ-axis is aligned with the Jupiter rotation axis, and the YJ-axis completes the right-handed frame. The Europa-centric inertial (ECI) coordinate system [XE, YE, ZE] and Ganymede-centric inertial coordinate system [XG, YG, ZG], which also represent the revolutions of Europa and Ganymede around Jupiter, are illustrated in red and blue, respectively. The XE-axis is in the intersection line between the Jovian equator and Europa’s revolution plane, the ZE-axis is normal to Europa’s revolution plane, and the YE-axis satisfies the positively oriented frame. In this case, the angle between XJ and XE is defined as the longitude of the ascending node ΩE of Europa’s revolution orbit with respect to Jupiter, and the angle between the fundamental planes of these two systems is the inclination iE of Europa’s revolution orbit. It should be noted that Europa’s equator and Europa’s revolution plane around Jupiter are assumed as coplanar since the axial tilt between these two planes around Jupiter is 0.0965°. Similarly, the XG-axis coincides with the intersection between the Jovian equator and Ganymede’s revolution plane, the ZG-axis is normal to Ganymede’s revolution plane, and the YG-axis completes the right-hand frame. The angle between XJ and XG defines the longitude of the ascending node ΩG of Ganymede’s revolution orbit around Jupiter. Additionally, the angle between the fundamental planes of these two systems is the inclination iG of Ganymede’s revolution plane.
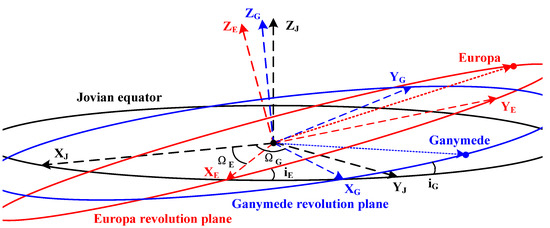
Figure 1.
The definition of coordinate systems for a Europa probe.
Depending on the definition of the Europa probe, the motion of the probe is described in the Europa-centric inertial coordinate system and suffers from the perturbations from Europa’s non-spherical gravitation, Jovian third-body gravitation, and Ganymede’s third-body gravitation. According to the research of Cinelli [17], as the mass of the probe is much smaller than those of Europa, Jupiter, and Ganymede, the equation of motion of the Europa probe can be expressed as:
where represents the acceleration vector of the probe; μE, μJ, μG are the gravitational parameters of Europa, Jupiter, and Ganymede, respectively; r represents the position vector of the probe in an Europa-centric inertial coordinate system, r = ||r||; rJP and rEJ are the vectors from Jupiter to the probe and from Europa to Jupiter, rJP = ||rJP||, rEJ = ||rEJ||, respectively; rGP and rEG are the vectors from Ganymede to the probe and from Europa to Ganymede, rGP = ||rGP||, rEG = ||rEG||, respectively.
Based on the above equation of motion, the perturbing potential on the probe due to Europa’s non-spherical gravitation is given by [17]
where J2 represents the coefficient of Europa’s J2 non-spherical gravitation; RE represents Europa’s radius; φ is the latitude of the probe regarding to the Europa.
Moreover, the perturbing potential on the probe due to Jovian gravitation is given as follows [17]:
The perturbing potential on the probe due to Ganymede’s gravity is given as follows:
Moreover, the relative positions between Jupiter, Europa, Ganymede, and the probe are illustrated in Figure 2. The angle α is the angle between the distances r (the distance between the probe and Europa) and rEG (the distance between Europa and Ganymede). Meanwhile, angle β defines the angle between the distances rEJ (the distance between Europa and Jupiter) and rJG (the distance between Jupiter and Ganymede). Consequently, distance rGP, from Ganymede to the probe, is determined by distances r, rJE, and rJG, as well as the angles α and β, which can be calculated in a simple trigonometric way as follows:
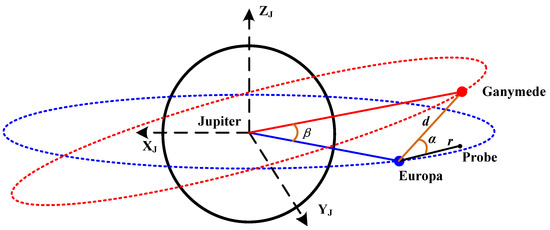
Figure 2.
Positions of the planet, moons, and the probe.
The intersection angles α and β can be calculated as follows:
where a, e, I, Ω, ω, and f are semi-major axis, eccentricity, inclination, longitude of the ascending node, argument of periapsis, and true anomaly, respectively, which constitutes the set of orbital elements oe, oe = [a, e, i, Ω, ω, f]. The symbol u is defined as the argument of latitude, u = ω + f. Particularly, the orbital elements without subscript denote the orbit of the probe in the ECI coordinate system. The subscripts “E” and “G” represents the orbital elements of Europa and Ganymede in the JCI coordinate system. is the difference of longitude of the ascending node between Ganymede’s and Europa’s revolution orbits, . The detailed expressions of variables K1 and K2 are given in Equations (35)–(39) of Appendix A.
Meanwhile, because Europa’s and Ganymede’s revolution orbits around Jupiter are near-circular, this study also considered the simplified conditions that the eccentricities of Europa’s and Ganymede’s revolution orbits are 0, and the inclinations of both Galilean moons are 0°. In these situations, both longitudes of the ascending nodes and arguments of periapsis of these two moons are 0°, respectively. These conditions are summarized as follows
Therefore, the distance between Europa and Ganymede is simplified as below:
and angle β in Equation (10) is given as β = fG − fE. The position vectors in Equations (5)–(8) are derived as follows:
It should be emphasized that since Europa and Ganymede are Galilean moons orbiting around Jupiter, the Europa–Ganymede distance rEG oscillates significantly, which makes the mean relative motion of Ganymede around Europa significantly different from that in other cases due to the apparent motion of Jupiter around Europa. The long-term orbit evolution behaviors of the Europa probe under the proposed accurate model and simplified model are investigated in the next section.
2.2. Legendre Expansion
Since previous studies have already discussed the long-term effect of Europa’s non-spherical gravitation perturbation and Jovian gravitation perturbation, the influence of Ganymede’s third-body gravitation perturbation is the main focus here. In order to simplify the derivation, the perturbing potential in Equation (4) is split into individual terms as follows:
According to Equations (5), (6), and (12), the perturbing effect from Ganymede’s gravitation on the probe depends on the relative motion between Ganymede and Europa, especially the relative distance rEG in Equation (6).
Based on the classic Legendre expansion method in Appendix A, the perturbing potential RG,a is given in Equation (16). Considering the magnitudes of distances r and rEG, the expansion is truncated to zero order, first order, and second order, respectively.
From Equation (13), the zero-order term of the Ganymede gravitation potential is irrelevant to the orbital elements of the probe. Therefore, this term is neglected in the following analysis. Furthermore, the first-order term compensates the potential RG,b in Equation (12). Therefore, the potential term RG,a,2 dominates the Ganymede gravitation perturbation on the long-term evolution of Europa probe.
Furthermore, according to Equation (12), the variable that denotes the relative motion of Ganymede to Europa is the Europa–Ganymede distance rEG. From the definition in Equation (6), the distance rEG is determined by the motions of Europa and Ganymede, whose orbits are not exactly circular and coplanar. In this situation, it is difficult to analytically expand the distance rEG to high order. Consequently, only the mean motion of the Europa probe is considered rather than the accurate model. Then, applying the simplified model in Equations (10) and (11), both the mean motion of the Europa probe and the mean relative motion of Ganymede around Europa are considered. The Legendre expansion is employed again towards the Europa–Ganymede distance rEG. Since the magnitudes of Europa’s and Ganymede’s semi-major axes are approximated, the expression of the distance rEG is truncated up to the fifth order (about 0.1 of order of magnitude) to guarantee the accuracy.
3. Long-Term Evolution and Analysis
In order to develop a Ganymede-synchronous frozen orbit around Europa, this section first derives the mean motion of the Europa probe. Then, the control strategy for generating a Ganymede-synchronous frozen orbit is provided.
3.1. Double-Averaging Method
In the Europa probe case, the magnitude of the orbital period for 1RE-3RE of semi-major axis is 104, while the revolution periods of Jovian and Ganymede’s apparent motions around Europa are about 3 × 105 s and 6 × 105 s, respectively. Therefore, the motion of the probe can be considered as a fast variable. Consequently, the secular effect of Ganymede gravitation can be obtained by eliminating the short-period term oscillations with a double-averaging method. The first averaging is performed regarding the mean motion of the probe to obtain the mean variations of the orbital elements in one orbital period:
where represents the orbital period of the probe and is its related mean motion, while .
Then, the second averaging is performed with respect to Ganymede’s apparent motion around Europa to obtain the mean variations in one revolution period. This second averaging is given as follows:
where TA represents the periods of Jovian and Ganymede’s apparent motions around Europa. The Jovian apparent motion period TA equals the revolution period of Europa around Jupiter. The period of Ganymede’s apparent motion TA,G is the synodic period of the relative motion of Ganymede to Europa as shown in Equation (15), where and . It should be noted that the orbit of Ganymede’s apparent motion around Europa is not a conic curve, and hence the right part of Equation (15) is invalid for Ganymede’s mean motion.
Using the double-averaging method, the mean motion of the probe under Europa’s non-spherical gravitation, Jovian third-body gravitation and Ganymede’s third-body gravitation is obtained.
3.2. Mean Motion of the Probe around Europa
Based on the perturbing potential RG,a,2, an accurate Europa–Ganymede distance rEG is first derived with the averaging method in Equation (14). The average potential of the probe under Ganymede’s gravitation in one orbit period is given as follows:
where the definitions of K1 and K2 are provided in Appendix A.
Since Ganymede’s apparent motion around Europa is non-elliptical, the Europa–Ganymede distance rEG is time-varying significantly, which makes it difficult to derive Ganymede’s mean apparent motion analytically using the double-averaging method in Equation (18). In this situation, the average potential for the Europa probe under Europa’s non-spherical gravitation and Jovian and Ganymede’s third-body gravitation is given as:
It should be emphasized that since the orbit of the probe and that of Jovian apparent motion around Europa are both near-circular, the double-averaging method is employed to eliminate the short-period terms of the probe and Jovian motions in research [11].
By substituting the potential term with the accurate average potential in the Lagrange planetary equations (seeing Appendix B), the equations of motion of the orbital elements are obtained analytically. The long-term evolution model for the Europa probe is given as follows:
It can be seen from the Lagrange equations that the semi-major axis keeps constant during the evolution, which means that Ganymede’s gravitation has no secular influence on the orbital energy of the probe. The variables in these Lagrange equations are provided in Equation (6) and in Equations (32)–(36) of Appendix A. Furthermore, although the analytical form of the mean potential of Ganymede’s gravity is difficult to obtain, the long-term evolution behavior of the probe can be studied following the accurate and simplified model using numerical propagation. Based on the double-averaging method in Equation (15), the average Lagrange equations of the probe’s orbital elements are computed as follows:
where φ represents the orbital element of the probe.
To validate the long-term evolution behavior based on the double-averaging method, a large-eccentricity, high-inclination orbit is taken as an example to simulate the orbital behavior under the accurate average model. The adopted values of the gravitational parameters of Jupiter, Europa, and Ganymede are given in Table 1. The initial orbital conditions of the probe are set to for a = 1.2 RE, i = 93°, Ω = 0°, and ω = 0°, unless otherwise specified in the following simulations. Eccentricity e = 0.1 is selected, and the evolution duration is set as 150 days. The orbital evolutions of the eccentricity, inclination, longitude of the ascending node and argument of periapsis are given in Figure 3. Blue and red curves represent the oscillating and mean orbits, respectively. Note that the semi-major axis remains constant and is not propagated.

Table 1.
Dynamical parameters of the Jovian system [23,24].
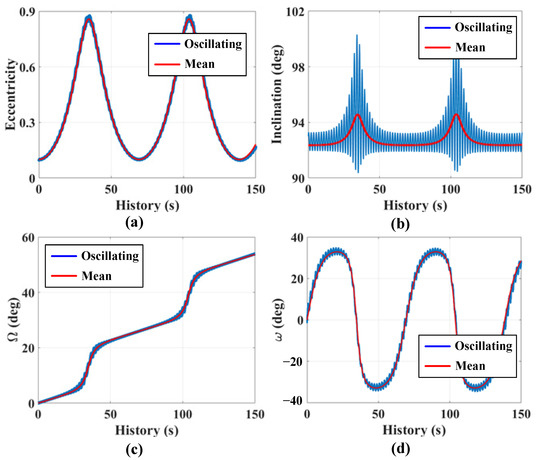
Figure 3.
Evolution behavior of a probe around Europa, for a = 1.2 RE, e = 0.1, i = 93°, Ω = 0°, and ω = 0°. Subplots (a–d) are the behaviors of the eccentricity, inclination, longitude of the ascending node and argument of periapsis, respectively.
As shown in Figure 3, the long-term evolution tendencies of the mean orbital elements and the oscillating orbital elements are consistent with each other. By removing the short-period oscillation, the evolution of the mean elements are smoother than that of the oscillating elements, which makes the mean orbit more applicable for the analysis of long-term evolution. Moreover, the orbital elements also suffer from long-period oscillations, which is similar to the research by Scheeres et al. [11]. This behavior suggests that Europa’s non-spherical gravitation and Jovian third-body gravitation are the major perturbations, while Ganymede’s gravitation is the weak perturbation. In the next section, the perturbing effect of Ganymede’s gravitation on the secular motion of the Europa probe is further analyzed, and a Ganymede-synchronous frozen orbit is generated.
3.3. Sensitivity Analysis
Based on the long-term models in Equations (21)–(25), the effects of Ganymede’s gravitation on the orbital elements with respect to the initial phase angle are studied. This initial phase angle is the difference between the initial longitude of the ascending node and the argument of latitude of Europa, i.e., Ω − uE. The average rates of change of the eccentricity and inclination are shown in Figure 4. The initial conditions of a near-circular orbit are considered by setting e = 0.001, ω = 35°. The average rates of change are propagated using the numerical integration method. From Figure 4a, it can be seen that the oscillation amplitude was four orders of magnitude smaller than the value of the rate of change, which suggests that Ganymede’s gravitation perturbation on the eccentricity is weaker compared to those of Europa’s non-spherical gravitation and Jovian gravitation. According to the literature [11,13], the eccentricity evolution mainly depends on the inclination and argument of periapsis.
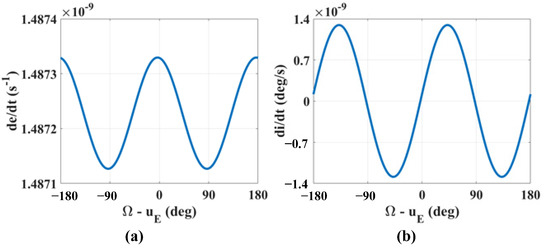
Figure 4.
Rates of change of the eccentricity (a) and inclination (b), for a = 1.2 RE, e = 0.001, i = 93°, and ω = 35°.
According to the average rate of change of the inclination in Figure 4b, the rate of change of the inclination oscillates significantly, which is different from that of the eccentricity. This suggests that for a near-circular orbit, the perturbing effects due to Europa’s non-spherical gravitation and Jovian gravitation are small, while Ganymede’s gravitation dominates the evolution of the inclination. Moreover, the initial phase angle Ω − uE determinates the value of the average rate of change. For a Ganymede-synchronous orbit, the initial phase angle is fixed with respect to both Europa and Ganymede for each Ganymede-apparent revolution period. In this situation, the average rate of change of the inclination is constant, which drifts the inclination continuously. Four zero-rate change conditions are obtained when the initial phase angle Ω − uE approximates −92.5°, −3°, 87.5°, and 177°. These conditions keep the inclination constant under Ganymede’s gravitation with a Ganymede-synchronous orbit.
Moreover, the average rates of change of the longitude of the ascending node and argument of periapsis with respect to the initial phase angle Ω − uE are studied. The initial orbital conditions of the probe are e = 0.001 and ω = 35°. The calculation results are shown in Figure 5. Similarly, the average rates of change are propagated using the numerical integral method. According to Figure 5a, for the average rate of change of the longitude of the ascending node, the oscillation amplitude is eight orders of magnitude smaller than the value of the average rate of change. This means that Ganymede’s gravitation has little effect on the longitude of the ascending node. Meanwhile, the literature [11,13] shows that the semi-major axis and inclination determine the rate of change of the longitude of the ascending node when considering Europa’s non-spherical gravitation and Jovian gravitation perturbations. Therefore, to generate the Ganymede-synchronous frozen orbit, it can be assumed that the evolution of the longitude of the ascending node is decoupled with the initial phase angle Ω − uE to simplify the design of the initial orbital conditions.
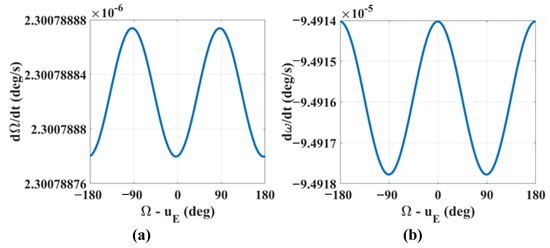
Figure 5.
Rates of change of the longitude of the ascending node (a) and the argument of periapsis (b), for a = 1.2 RE, e = 0.001, i = 93°, and ω = 35°.
Furthermore, from Figure 5b it can be seen that the oscillation amplitude of the argument of periapsis is four orders of magnitude smaller than the value of the average rate of change. Therefore, Ganymede’s gravitation perturbation on the argument of periapsis is a small disturbance. In order to generate a Ganymede-synchronous frozen orbit whose argument of periapsis is fixed, a station-keeping (SK) maneuver is employed to cancel out the slight drift caused by Ganymede’s gravity.
Next, the rate of change of the inclination with respect to the eccentricity and inclination are studied. The results are shown in Figure 6 for i = 93° (a) and e = 0.001 (b). Note that the distributions of the rate of change in other conditions are similar and not given here. The rate of change of the inclination with respect to the eccentricity is provided in Figure 6a. According to the distribution of the rate of change of the inclination di/dt, the orbits are divided into an elliptic case (for an elliptic orbit with eccentricity larger than 0.1) and a near-circular case (with eccentricity smaller than 0.1). For an elliptic orbit, the eccentricity has an influence on the rate of change of the inclination. However, for a near-circular orbit, the rate of change of the inclination is nearly constant with respect to the eccentricity. Therefore, small eccentricity is considered for the initial condition of the Ganymede-synchronous frozen orbit. Nevertheless, the effect of the eccentricity on the rate of change of the inclination is neglected.
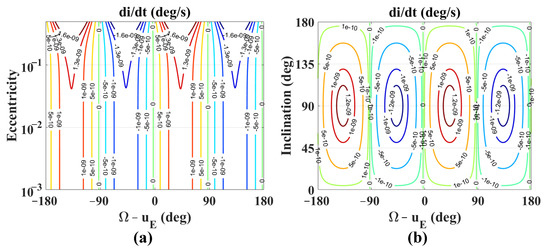
Figure 6.
Rates of change of the inclination with respect to the eccentricity in subplot (a) and inclination (b) in subplot (a), for a = 1.2 RE.
Then, the rate of change with respect to the inclination is shown in Figure 6b. According to Figure 6b, the rate of change of the inclination is divided into positive regions where the initial phase angle Ω − uE is (−180°, −90°) and (0°, 90°) and negative regions where the initial phase angle Ω − uE is (−90°, 0°) and (90°, 180°). Between these regions, the contour line of di/dt = 0 deg/sec is obtained (define this line as DIZL). Due to the fact that for the synchronous frozen orbit the initial phase angle Ω − uE and inclination keep constant, the rate of change of the inclination is fixed. Therefore, the initial condition should locate on the DIZL to achieve the frozen behavior.
Finally, the rate of change of the inclination with respect to the argument of periapsis is analyzed. A series of eccentricities 0.1, 0.05, 0.01, and 0.001 are taken as examples to study the evolution of di/dt. The results are contoured in Figure 7 for e = 0.1 (a), e = 0.05 (b), e = 0.01 (c), and e = 0.001 (d). According to Figure 7a for eccentricity e = 0.1, the argument of periapsis dominates the rate of change of the inclination for an elliptic orbit. The DIZLs are discovered when the argument of periapsis is about −180°, −90°, 0°, and 90°. Figure 7b,c show the transition of di/dt between the elliptic orbit and the near-circular orbit. With the eccentricity descending, the effect of the argument of periapsis decreases. Furthermore, for a near-circular orbit in Figure 7d, this rate of change mainly depends on the initial phase angle Ω − uE. The initial phase angles Ω − uE of the DIZL are about −91°, −1°, 89°, and 179°. Therefore, when a near-circular Ganymede-synchronous orbit is considered, the initial argument of periapsis can be chosen arbitrarily.
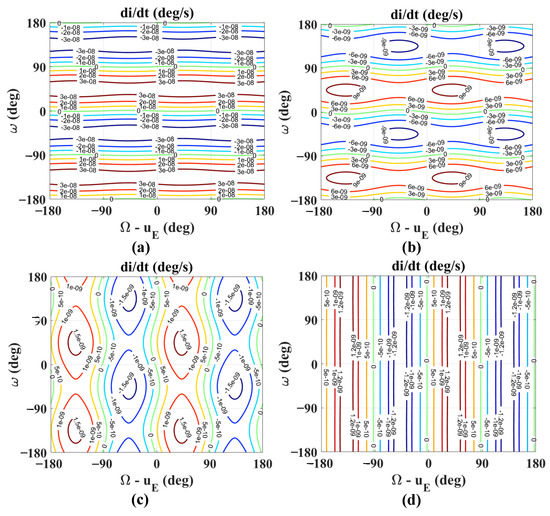
Figure 7.
Rates of change of the inclination with respect to the argument of periapsis for e = 0.1 (a), e = 0.05 (b), e = 0.01 (c), and e = 0.001 (d).
4. Design of a Ganymede-Synchronous Frozen Orbit
4.1. Conditions of Synchronous Frozen Orbit
A Ganymede-synchronous frozen orbit around Europa constitutes synchronous behavior with respect to Ganymede and frozen behavior in terms of the orbital elements. For Ganymede-synchronous behavior, when the Europa–Ganymede distance rEG approaches the minimum, the intersection angle of the orbital plane and the Europa–Ganymede vector should be a constant. Consequently, the geometry between the orbit and Ganymede is fixed. This Ganymede-synchronous condition can be described as in Equation (27). The rate of change of the longitude of the ascending node should be equal to the drift rate of the elongation in the inertial coordinate system to achieve Ganymede-synchronous behavior.
According to the synodic motion between Europa and Ganymede, the drift rate of the elongation is given as follows:
In addition, the literature [17] shows that a large velocity increment () is needed to freeze the eccentricity because of the drift of the argument of periapsis. A more cost-efficient way is to freeze the inclination and argument of periapsis. Meanwhile, the value of the argument of periapsis should be in the regions of (−90°, 0°) and (90°, 180°), where the eccentricity continuously decreases. In this situation, the orbit keeps circularizing and achieves a long lifetime. These frozen conditions are summarized as follows:
4.2. Preliminary Design of a Ganymede-Synchronous Frozen Orbit
Based on the dynamical evolution of the orbital elements and the conditions of the synchronous frozen orbit, the design method for a Ganymede-synchronous frozen orbit was developed. Since the accurate model is time-varying, it is difficult to analytically design a Ganymede-synchronous frozen orbit. Therefore, a preliminary design method based on the simplified model was developed and is given in Algorithm 1.
| Algorithm 1 Design Method for a Ganymede-Synchronous Frozen Orbit |
| Input: Semi-major axis a, eccentricity e; Output: Inclination i, initial phase angle Ω − uE, argument of periapsis 1: Assign as the initial conditions; 2: Assign as the expected rate of change of the longitude of ascending node; 3. Main |
| 4: Inclination ; 5: DIZL and DWZL ; 6: Initial phase angle and argument of periapsis ; 7: end |
Firstly, a semi-major axis is chosen according to the mission requirement. In this study, the initial eccentricity is set as e = 0.001. Then, according to literatures [11,14], the rate of change of the longitude of the ascending node is determined by the inclination. The inclination of the orbit is solved based on the synchronous condition in Equation (30). The rate of change of the longitude of the ascending node and the corresponding Ganymede-synchronous condition are shown in Figure 8. The purple dotted line represents the synchronous condition with respect to Ganymede. From Figure 8, because the drift rate of the elongation is negative, the inclination of the Ganymede-synchronous orbit ranges from 78.8° to 81.8° which is equivalent to about 98.96% and 98.98% of global coverage. For the semi-major axis a = 1.2 RE, the obtained inclination is given as i = 78.842°.
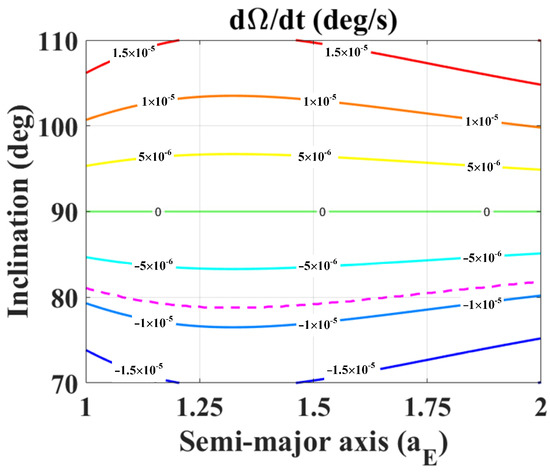
Figure 8.
Rate of change of the longitude of the ascending node for a = 1.2 RE and e = 0.001.
After obtaining the inclination, the longitude of the ascending node and argument of periapsis are designed. The contour lines of the inclination di/dt = 0 deg/sec (denoted as DIZL) and argument of periapsis dω/dt = 0 deg/sec (denoted as DWZL) with respect to the eccentricity are calculated. For the inclination i = 78.842°, the intersection of DIZL and DWZL is shown in Figure 9. Blue and red points represent DIZL and DWZL, respectively. From Figure 9, it is seen that the argument of periapsis of the intersection of the DIZL and DWZL was about –133.1°, −46.9°, 46.9°, and 133.1°. In order to keep the eccentricity decreasing, the argument of periapsis ω = 133.1° was chosen as the initial condition. The intersection line with respect to eccentricity is given in Figure 10, in which the initial phase angle Ω − uE is nearly constant when the eccentricity is small. In this situation, initial phase angle Ω − uE = 87.46° was chosen in the preliminary design phase. This orbit was considered as an expected orbit. The method of maintaining this orbit with the accurate model is discussed in the following section.
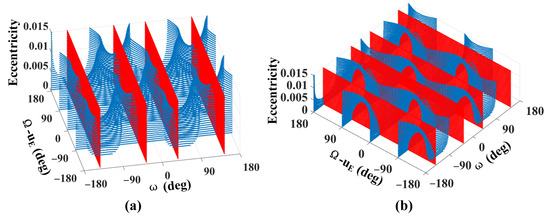
Figure 9.
Distributions of DIZL and DWZL. Subplots (a) and (b) are two different viewpoints.
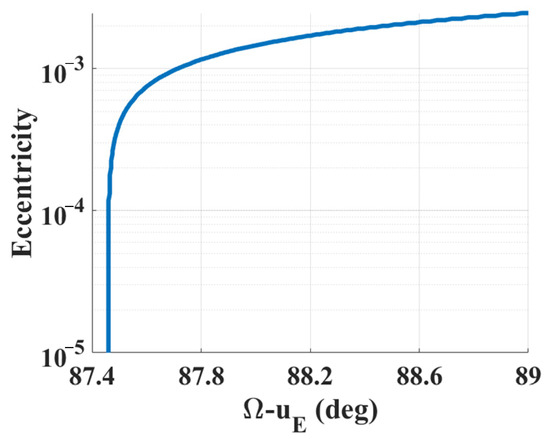
Figure 10.
Distribution of DIZL.
4.3. Orbit Maintenance with Accurate Model
Since the expected orbit was designed based on the simplified model in the preliminary phase, the actual orbit under an accurate dynamical model naturally drifts and deviates from the expected orbit. Therefore, in this section, the SK maneuver is designed to maintain the inclination, longitude of the ascending node, and argument of periapsis at their expected values. The ΔV consumptions for the inclination, longitude of the ascending node, and argument of periapsis are evaluated by taking the impulse propulsion as follows:
Using this SK strategy, the Ganymede-synchronous frozen orbit was validated by a numerical simulation. Except the perturbations of Europa’s J2 non-spherical gravitation, Jovian and Ganymede’s third body gravitations, the perturbations of Jovian J2 non-spherical gravitation and solar gravitation were both considered to guarantee the accuracy. The initial conditions were a = 1.2 RE, e = 0.001, i = 78.842°, Ω = 120.7575°, and ω = 133.07°. In order to achieve a collinear behavior of , the initial date MJD was selected as . The SK period was set as one synodic period of the Europa–Ganymede revolution TA,G. Fifteen numbers of SK maneuvers were performed to evaluate ∆V consumption. The evolution of the orbit is shown in Figure 11, and ΔV consumptions of the inclination (blue line), longitude of the ascending node (black line), and argument of periapsis (red line) are given in Figure 12.
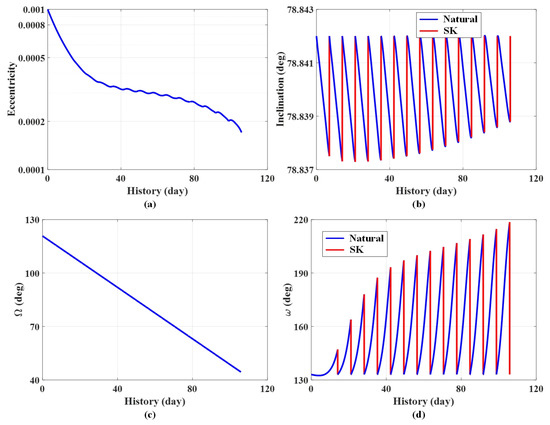
Figure 11.
Evolutions of orbital elements, for a = 1.2 RE, e = 0.001, i = 78.842°, Ω = 120.7575°, and ω = 133.07°. Subplots (a–d) show the evolutions of the eccentricity, inclination, longitude of the ascending node and argument of periapsis, respectively.
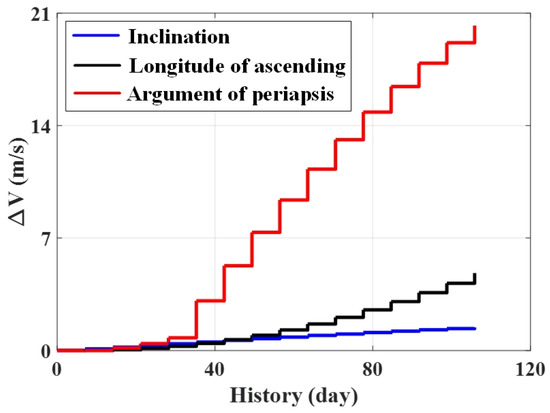
Figure 12.
Consumption of the Ganymede-synchronous frozen orbit.
In Figure 11, the blue and red curves represent the evolution of natural drift and SK maneuver, respectively. According to Figure 11, the eccentricity kept decreasing, which circularized the orbit. Due to the difference between the simplified dynamical model and accurate model, the inclination oscillated in a small amplitude, while the argument of periapsis oscillated heavily. The SK maneuver was employed to directly maintain these two elements at the expected values. Meanwhile, the longitude of the ascending node kept decreasing. According to the numerical calculation, the evolution period of the longitude was about 500 days, which equaled the synodic period of Europa and Ganymede. In this situation, the orbit demonstrated Ganymede-synchronous behavior.
Furthermore, according to Figure 12, for about 105 days of evolution, the maintaining ∆V for the inclination, longitude of the ascending node, and argument of periapsis were 1.36 m/s, 4.8 m/s, and 20 m/s. The total ∆V consumption was about 26.16 m/s, which was 0.25 m/s per day. This is an acceptable ∆V for a practical mission. Most of the ∆V is consumed to maintain the argument of periapsis, while maintaining the inclination cost the least ∆V. This suggests that the effect of an accurate dynamic model has little influence on the evolution of the inclination.
5. Conclusions
This paper focuses on the long-term evolution behavior of a probe around Europa. The non-spherical gravitation perturbation of Europa and the third-body gravitation perturbations of Ganymede and Jupiter were considered to derive the Lagrange equation based on the double-averaging framework. Then, a design method of a Ganymede-synchronous frozen orbit was proposed using the simplified model. The angle between the normal vector of this orbit and the Europa–Ganymede vector is constant when Europa and Ganymede come synodic. In this situation, the Europa probe has the stable capacity to observe Ganymede and to transmit data with the Ganymede lander.
The numerical simulation showed that Ganymede’s gravity has a small but continuously accumulated effect on the inclination. The rate of change of the inclination mainly depends on the argument of periapsis for an elliptic orbit, while it is determined by the phase angle between the longitude of the ascending node and the Europa–Ganymede vector. Moreover, due to the difference between the accurate model and the simplified model, the obtained orbit drifts slightly. A station-keeping maneuver was employed to maintain the longitude of the ascending node and argument of periapsis. With the proposed maintenance method, the eccentricity of the Ganymede-synchronous frozen orbit kept decreasing, while the inclination and argument of periapsis maintained the expected values. The evolution period of the longitude of the ascending node was 500 days, which achieved Ganymede-synchronous behavior. The total maintenance ∆V consumption was 26.16 m/s for 105 days of evolution, or 0.25 m/s per day, which is acceptable for practical mission application.
Author Contributions
Conceptualization, X.H. and B.Y.; methodology, X.H.; software, B.Y.; validation, X.H. and B.Y.; formal analysis, X.H.; investigation, B.Y.; resources, X.H.; data curation, X.H. and J.F.; writing—original draft preparation, B.Y. and J.F.; writing—review and editing, J.F. and J.J.M.; visualization, X.H.; supervision, S.L. and J.J.M.; project administration, S.L. and J.J.M.; funding acquisition, S.L. and J.J.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The work described in this paper was supported by the Postgraduate Research & Practice Innovation Program of Jiangsu Province (Grant No. KYCX20_0220) and the Chinese Scholarship Council (Grant No. 202006830124), funded by the Science and Technology on Space Intelligent Control Laboratory (Grant No. HTKJ2020KL502019, 6142208200203 and 2021–JCJQ–LB–010–04). The authors fully appreciate their financial support.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In this paper, Jovian and Ganymede’s apparent motions orbiting around Europa are considered. The distance from the Europa-to-Ganymede intersection is determined by the angle α. Angle α is expressed using Equation (7), whose variables are given as follows:
where .
The classical Legendre polynomial expansion is applied to express the perturbing potential in Equation (12) into individual terms. This expansion is shown as follows:
Appendix B
In order to study the long-term evolution of orbital elements, the Lagrange planetary equations which derive the effect of perturbing potential on the orbital elements are given as follows:
Then, the long-term evolution of Europa probe’s orbital elements can be obtained.
References
- Campagnola, S.; Buffington, B.B.; Lam, T.; Petropoulos, A.E.; Pellegrini, E. Tour design techniques for the Europa Clipper mission. J. Guid. Control. Dyn. 2019, 42, 2615–2626. [Google Scholar] [CrossRef]
- Bayer, T.; Bittner, M.; Buffington, B.; Castet, J.F.; Dubos, G.; Jackson, M.; Lee, G.; Lewis, K.; Kastner, J.; Schimmels, K.; et al. Europa clipper mission update: Preliminary design with selected instruments. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018; pp. 1–19. [Google Scholar] [CrossRef]
- Dougherty, M.K.; Grasset, O.; Bunce, E.; Coustenis, A.; Titov, D.V.; Erd, C.; Blanc, M.; Coates, A.J.; Coradini, A.; Drossart, P.; et al. JUICE (JUpiter ICy moon Explorer): A European-led mission to the Jupiter system. EPSC-DPS Jt. Meet. 2011, 2011, 1343. [Google Scholar]
- Kozai, Y. The motion of a close earth satellite. Astron. J. 1959, 64, 367. [Google Scholar] [CrossRef]
- Ely, T.A. Mean element propagations using numerical averaging. J. Astronaut. Sci. 2014, 61, 275–304. [Google Scholar] [CrossRef]
- Scheeres, D.J.; Hu, W. Secular motion in a 2nd degree and order-gravity field with no rotation. Celest. Mech. Dyn. Astron. 2001, 79, 183–200. [Google Scholar] [CrossRef]
- de Almeida Prado, A.F.B. Third-body perturbation in orbits around natural satellites. J. Guid. Control Dyn. 2003, 26, 33–40. [Google Scholar] [CrossRef]
- Baresi, N.; Scheeres, D.J.; Schaub, H. Bounded relative orbits about asteroids for formation flying and applications. Acta Astronaut. 2016, 123, 364–375. [Google Scholar] [CrossRef]
- Fu, T.; Wang, Y. Orbital Stability Around the Primary of a Binary Asteroid System. J. Guid. Control Dyn. 2021, 44, 1607–1620. [Google Scholar] [CrossRef]
- Anderson, J.D.; Schubert, G.; Jacobson, R.A.; Lau, E.L.; Moore, W.B.; Sjogren, W.L. Europa’s differentiated internal structure: Inferences from four Galileo encounters. Science 1998, 281, 2019–2022. [Google Scholar] [CrossRef]
- Scheeres, D.J.; Guman, M.D.; Villac, B.F. Stability analysis of planetary satellite orbiters: Application to the Europa orbiter. J. Guid. Control Dyn. 2001, 24, 778–787. [Google Scholar] [CrossRef]
- Low, S.Y.W.; Moon, Y.; Tao, L.W.; Tan, C.W. Designing a reference trajectory for frozen repeat near-equatorial low earth orbits. J. Spacecr. Rocket. 2022, 59, 84–93. [Google Scholar] [CrossRef]
- Broucke, R.A. Long-term third-body effects via double averaging. J. Guid. Control Dyn. 2003, 26, 27–32. [Google Scholar] [CrossRef]
- Lara, M. Simplified equations for computing science orbits around planetary satellites. J. Guid. Control Dyn. 2008, 31, 172–181. [Google Scholar] [CrossRef]
- Hesar, S.G.; Scheeres, D.J.; McMahon, J.W. Sensitivity analysis of the OSIRIS-REx terminator orbits to maneuver errors. J. Guid. Control Dyn. 2017, 40, 81–95. [Google Scholar] [CrossRef]
- Abouelmagd, E.I. Periodic solution of the two–body problem by KB averaging method within frame of the modified newtonian potential. J. Astronaut. Sci. 2018, 65, 291–306. [Google Scholar] [CrossRef]
- Cinelli, M.; Ortore, E.; Circi, C. Long lifetime orbits for the observation of Europa. J. Guid. Control Dyn. 2019, 42, 123–135. [Google Scholar] [CrossRef]
- Macdonald, M.; McKay, R.; Vasile, M.; Frescheville, F.B.D. Extension of the sun-synchronous orbit. J. Guid. Control Dyn. 2010, 33, 1935–1940. [Google Scholar] [CrossRef]
- Byram, S.M.; Scheeres, D.J. Stability of sun-synchronous orbits in the vicinity of a comet. J. Guid. Control Dyn. 2009, 32, 1550–1559. [Google Scholar] [CrossRef][Green Version]
- Ugai, S.; Ichikawa, A. Lunar Synchronous Orbits in the Earth-Moon Circular-Restricted Three-Body Problem. J. Guid. Control Dyn. 2010, 33, 995–1000. [Google Scholar] [CrossRef]
- Jaworski, S.; Kindracki, J. Feasibility of Synchronized CubeSat Missions from Low Earth Orbit to Near-Earth Asteroids. J. Spacecr. Rocket. 2020, 57, 1232–1245. [Google Scholar] [CrossRef]
- Anderson, J.D.; Jacobson, R.A.; Lau, E.L.; Moore, W.B.; Schubert, G. Io’s gravity field and interior structure. J. Geophys. Res. Planets 2001, 106, 32963–32969. [Google Scholar] [CrossRef]
- Anderson, J.D.; Jacobson, R.A.; Lau, E.L.; Moore, W.B.; Olsen, O.; Schubert, G.; Thomas, P.C. Shape, mean radius, gravity field and interior structure of Ganymede. AAS/Div. Planet. Sci. Meet. Abstr. 2001, 33, 35–39. [Google Scholar]
- Anderson, J.D.; Jacobson, R.A.; McElrath, T.P.; Moore, W.B.; Schubert, G.; Thomas, P.C. Shape, mean radius, gravity field, and interior structure of Callisto. Icarus 2001, 153, 157–161. [Google Scholar] [CrossRef]
- Wang, G.B.; Meng, Y.H.; Zheng, W.; Tang, G.J. Artificial Sun synchronous frozen orbit control scheme design based on J 2 perturbation. Acta Mech. Sin. 2011, 27, 809–816. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, F.; Li, J. Artificial Martian frozen orbits and Sun-Synchronous orbits using continuous low-thrust control. Astrophys. Space Sci. 2014, 352, 503–514. [Google Scholar] [CrossRef]
- Ho, K.; Wang, H.; DeTrempe, P.A.; du Jonchay, T.S.; Tomita, K. Semi-Analytical Model for Design and Analysis of On-Orbit Servicing Architecture. J. Spacecr. Rocket. 2020, 57, 1129–1138. [Google Scholar] [CrossRef]
- Chujo, T.; Takao, Y. Synodic Resonant Halo Orbits of Solar Sails in Restricted Four-Body Problem. J. Spacecr. Rocket. 2022, 56, 2129–2147. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).