Deep Neural Network-Based Footprint Prediction and Attack Intention Inference of Hypersonic Glide Vehicles
Abstract
1. Introduction
2. Problem Formulation
2.1. Reentry Dynamics
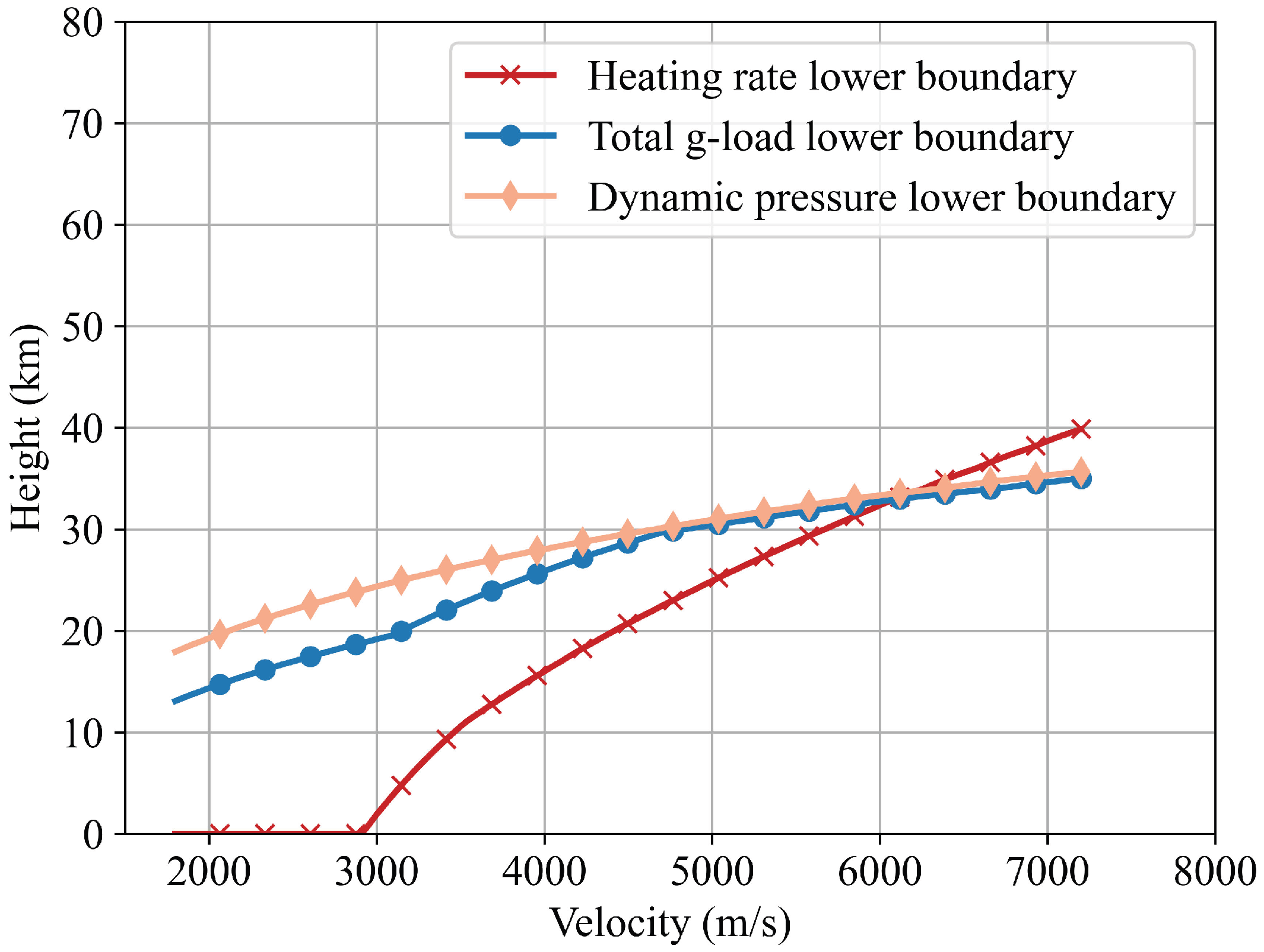
2.2. Reentry Constraints
2.3. Control Parameterization
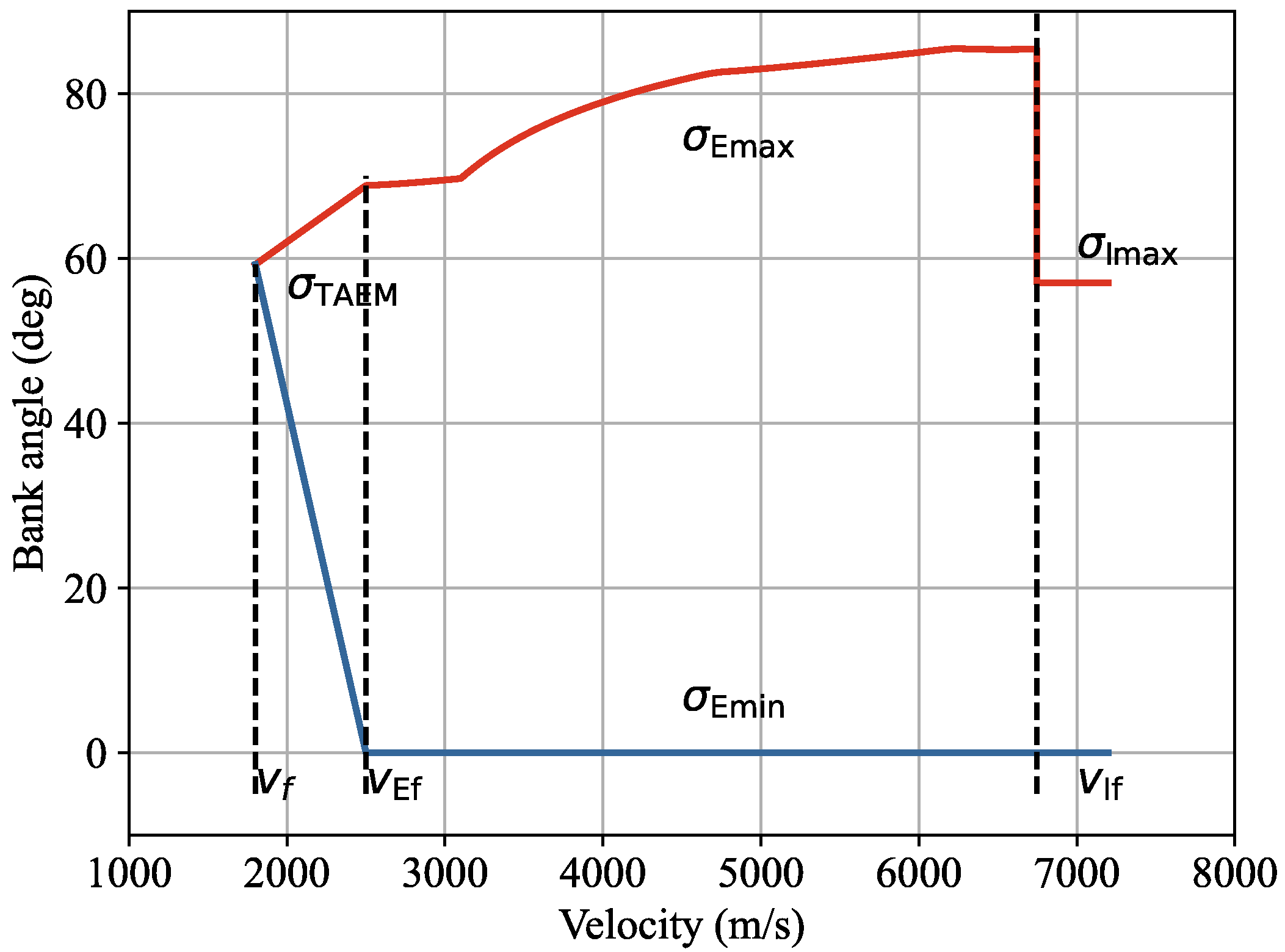
2.3.1. Bank Angle Corridor
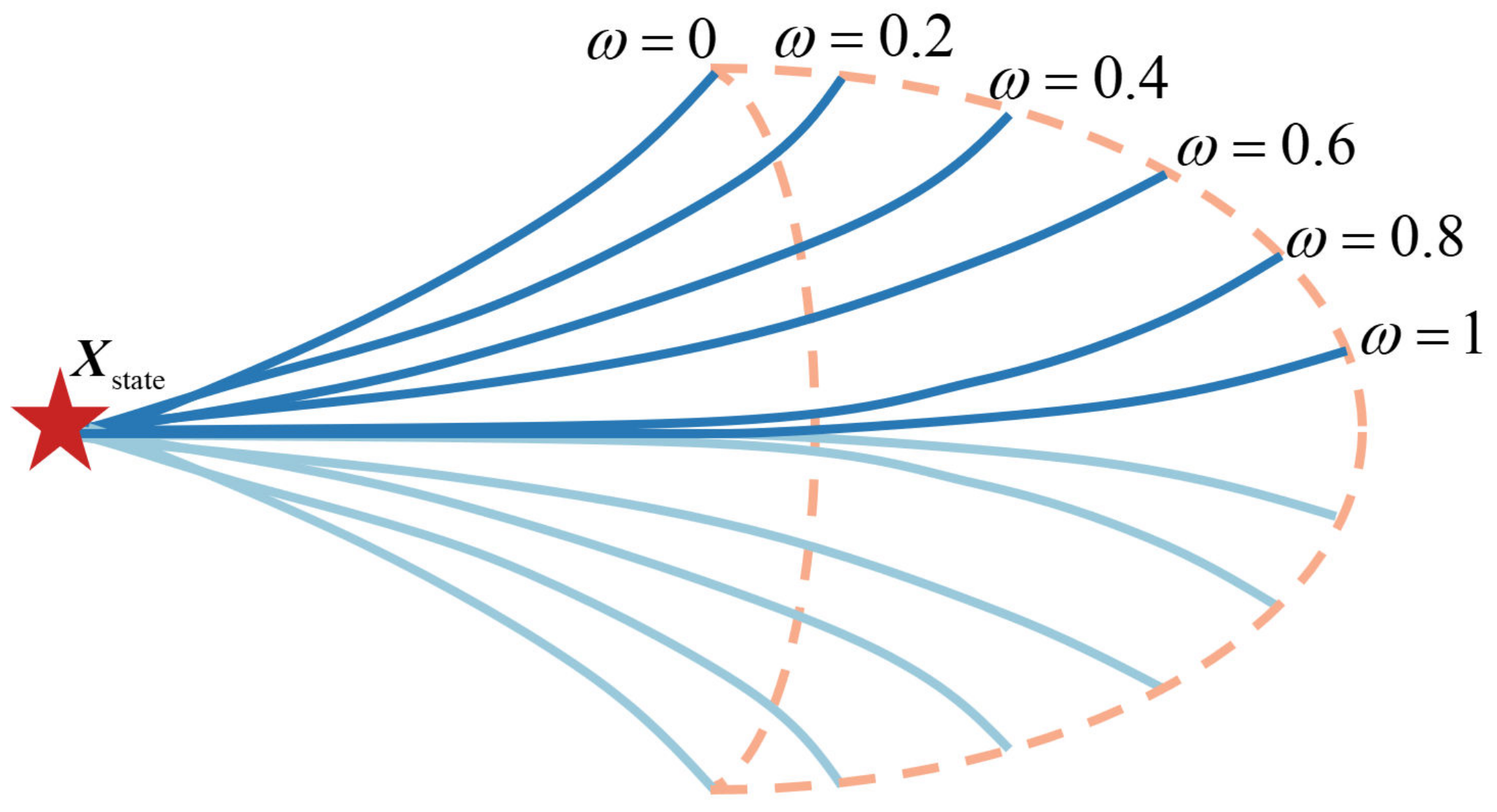
2.3.2. Control Parameterization
3. DNN-Based Footprint Prediction
3.1. DNN Development for Range Prediction
3.2. Accuracy and Rapidity Analysis
3.3. Real-Time Footprint Prediction
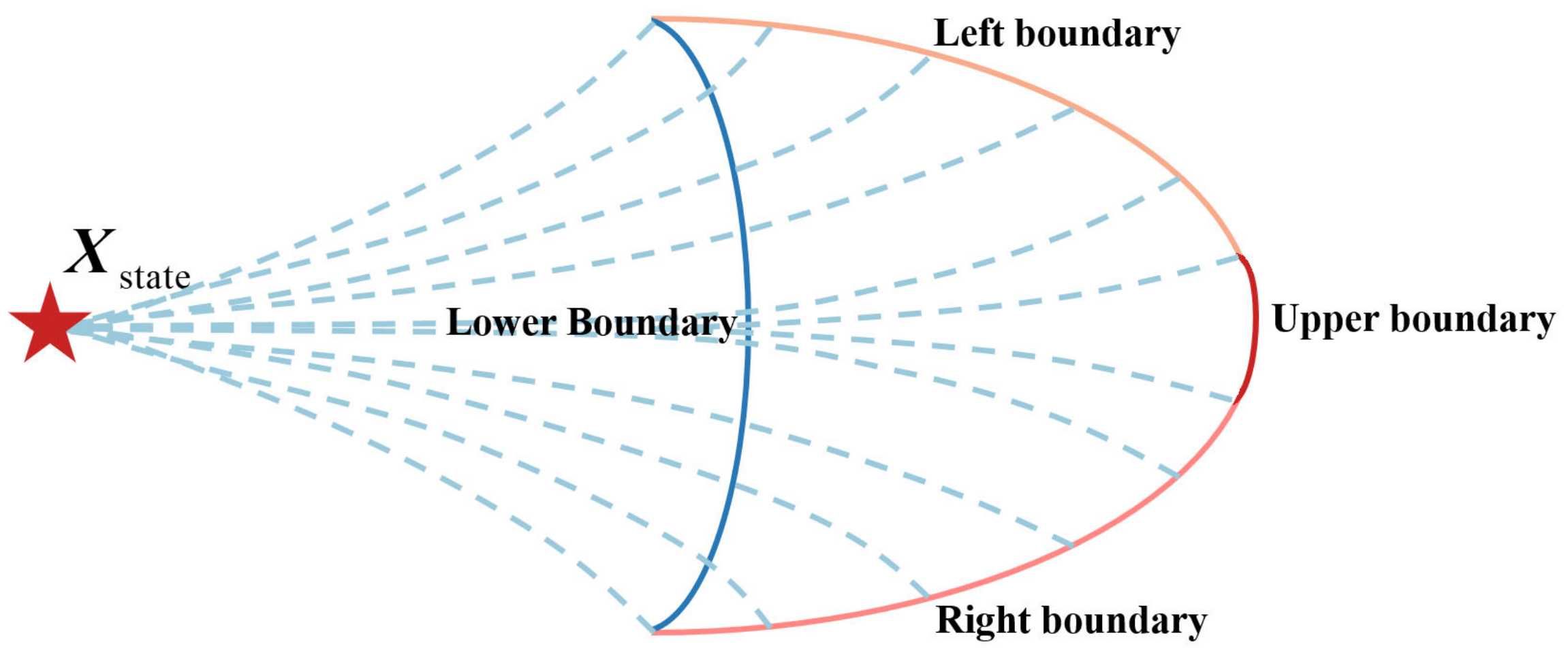
- Lower boundary: The downrange is , and the crossrange traverses. The downrange of this edge is the minimum downrange;
- Upper boundary: The downrange is , and the crossrange traverses. The downrange of this edge is the maximum downrange;
- Right boundary: When , the downrange is , and the crossrange is (Based on the heading direction of the enemy vehicle at the current moment, the lateral range of the left deviation is negative, and the right deviation is positive);
- Left boundary: When , the downrange is , and the crossrange is .
4. Attack Intention Inference
4.1. Intention Inference Criteria
4.1.1. Change Detection of the Control Strategy
- Step1: Set , . According to , and , and can be predicted by DNN. Then, calculate the distance between the current latitude and longitude of the HGV and the latitude and longitude of the jth landmark.
- Step2: Calculate . Then, set , .
- Step3: Calculate . The new downrange is obtained by DNN.
- Step4: If ( is the allowable deviation of the downrange), output . If , return to Step2.
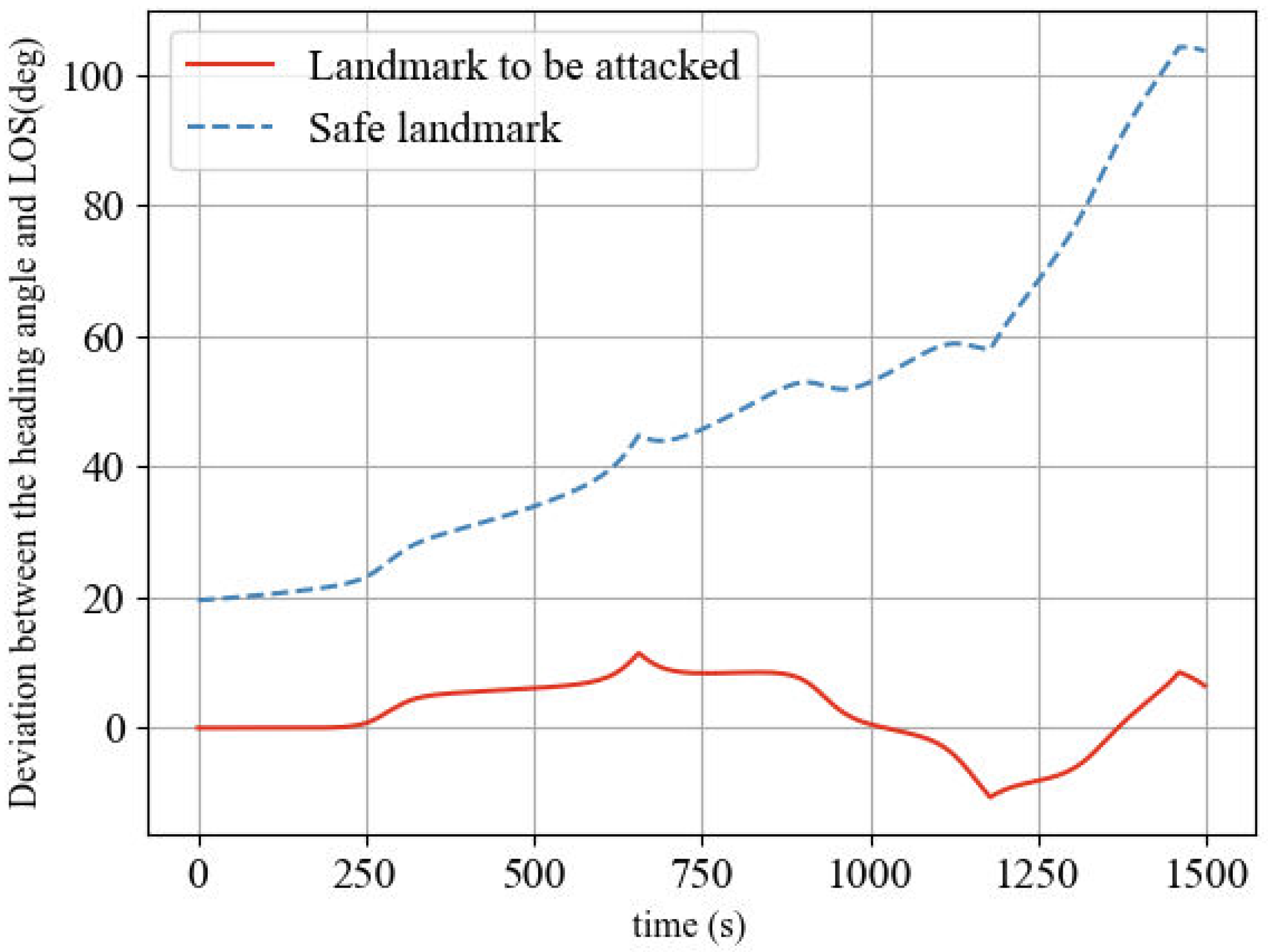
4.1.2. The Cumulative Deviation of and the LOS
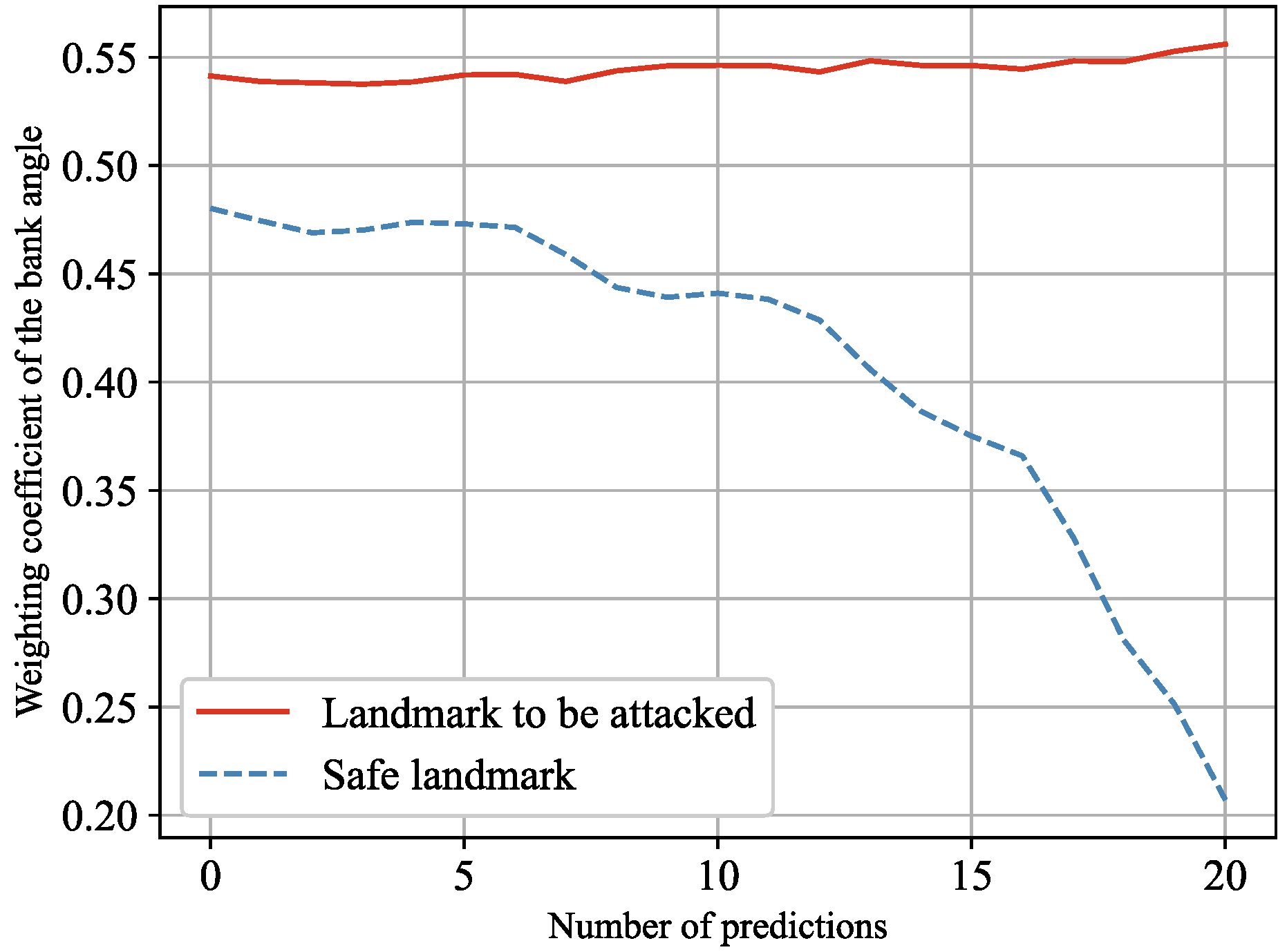
4.1.3. The Importance of Landmarks
4.2. Forgetting Mechanism
4.3. Attack Intention Inference System and Algorithm
| Algorithm 1 Attack Intention Inference Algorithm |
 |
- Ability to quickly and accurately predict the footprint: Since the DNN replaces the traditional integrator to approximate the ranges, the footprint prediction meets the real-time requirements while ensuring high accuracy;
- Ability to infer the intention of enemy HGVs: The underlying logic of the attack intention inference system in this study is that the defender infers from the perspective of the attacker. First, the control strategy of HGVs will not change sharply when the HGV aims at one specific target. Second, in order to achieve precise strikes, the HGVs’ heading angle should be maintained around the target direction. Third, attackers are more willing to attack important landmarks. It is precisely because these criteria are condensed from the rules discovered from the trajectory planning of the attacker side that the defending side can use these criteria to infer the enemy’s intention;
- Ability to identify enemy HGVs changing attack intention online and re-predict new targets: Mean and variance with forgetting properties makes the system more affected by the recent flight states. Therefore, the forgetting mechanism can gradually forget the early intention and predict new target based on the data of the recent period;
- Good real-time performance: Both the footprint prediction and the change detection of the control strategy avoid long-term trajectory integration, and DNN greatly improves the computational efficiency.
5. Simulations and Results
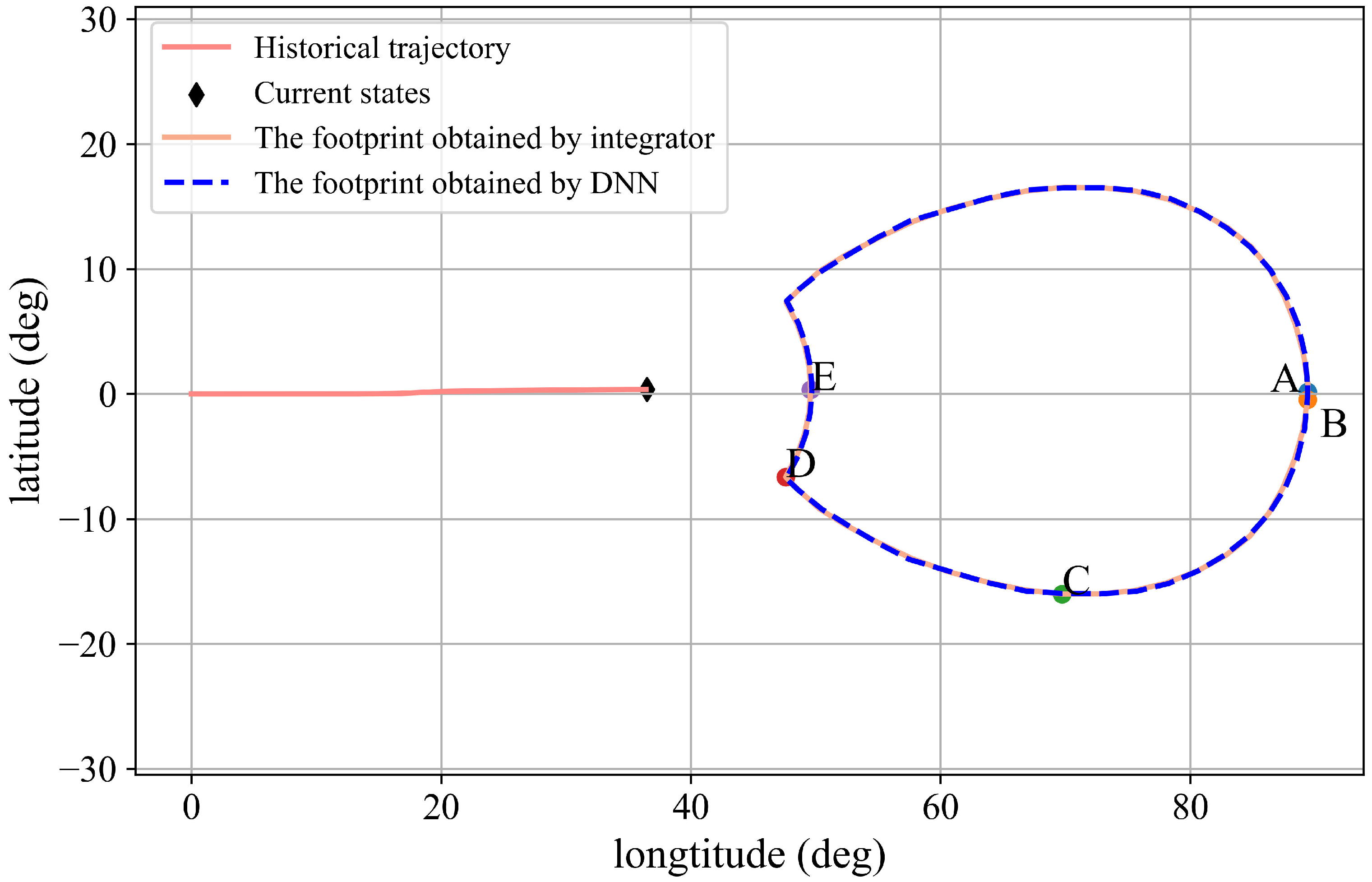
5.1. Evaluation of Footprint Prediction
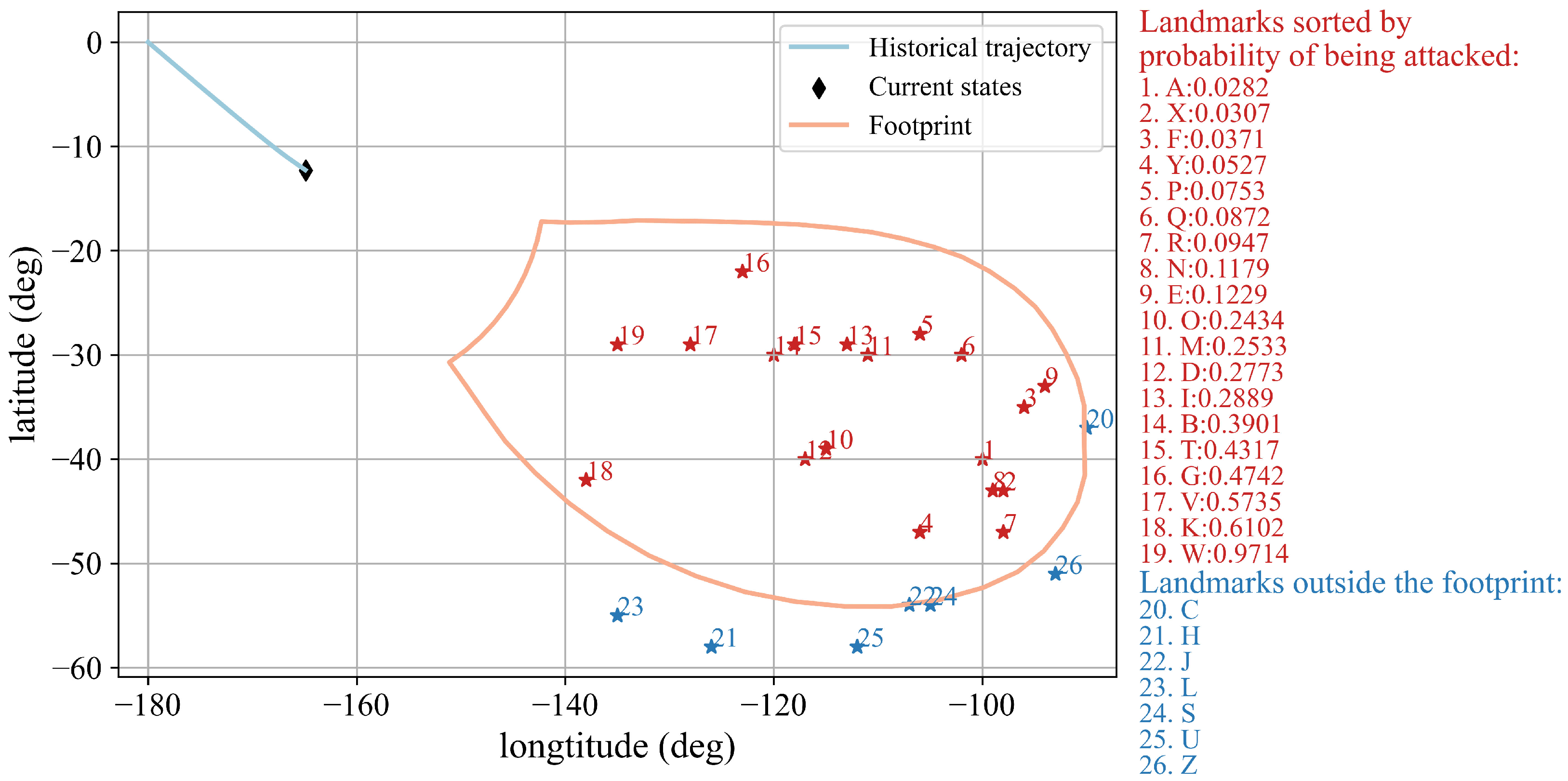
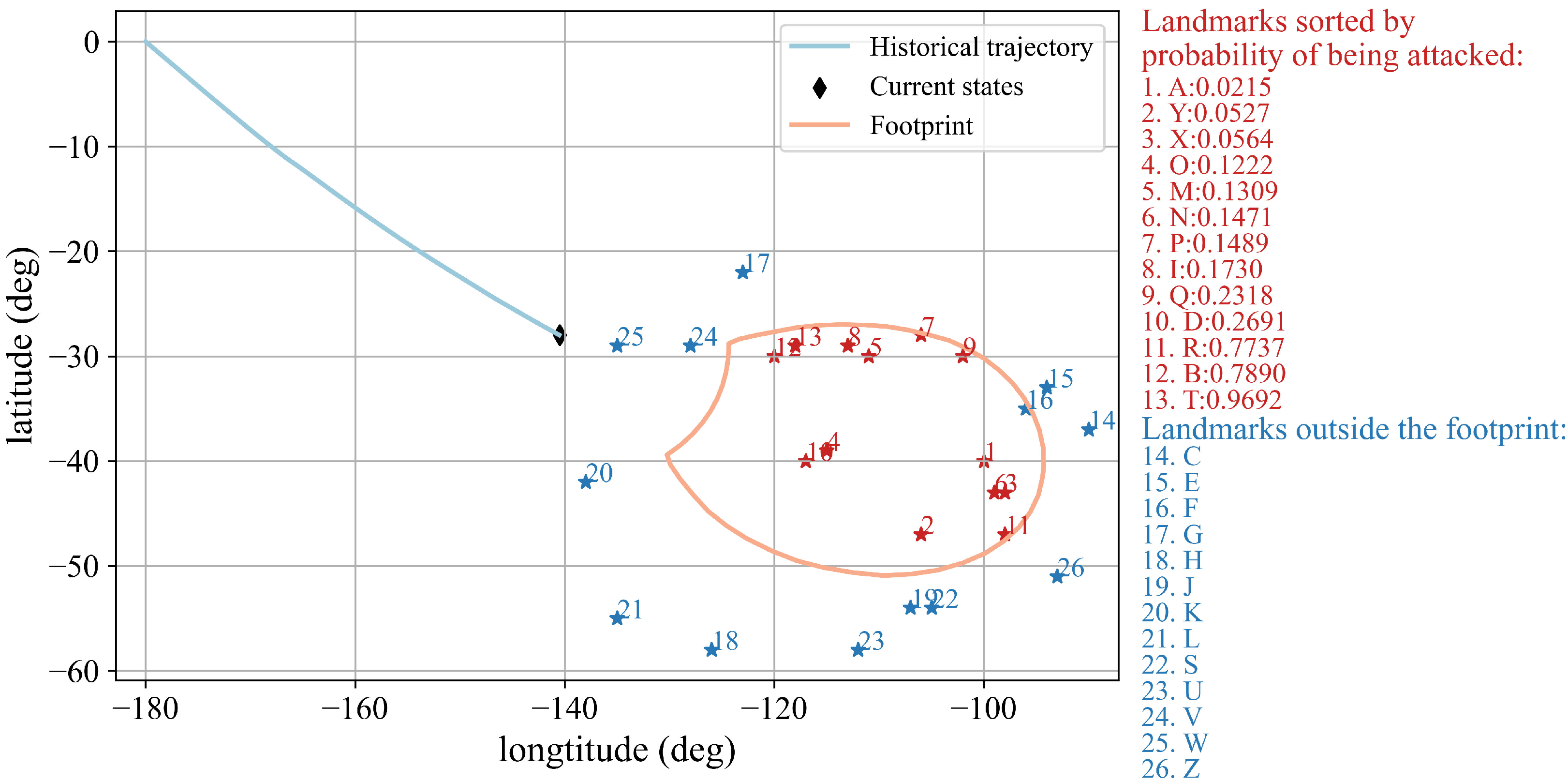
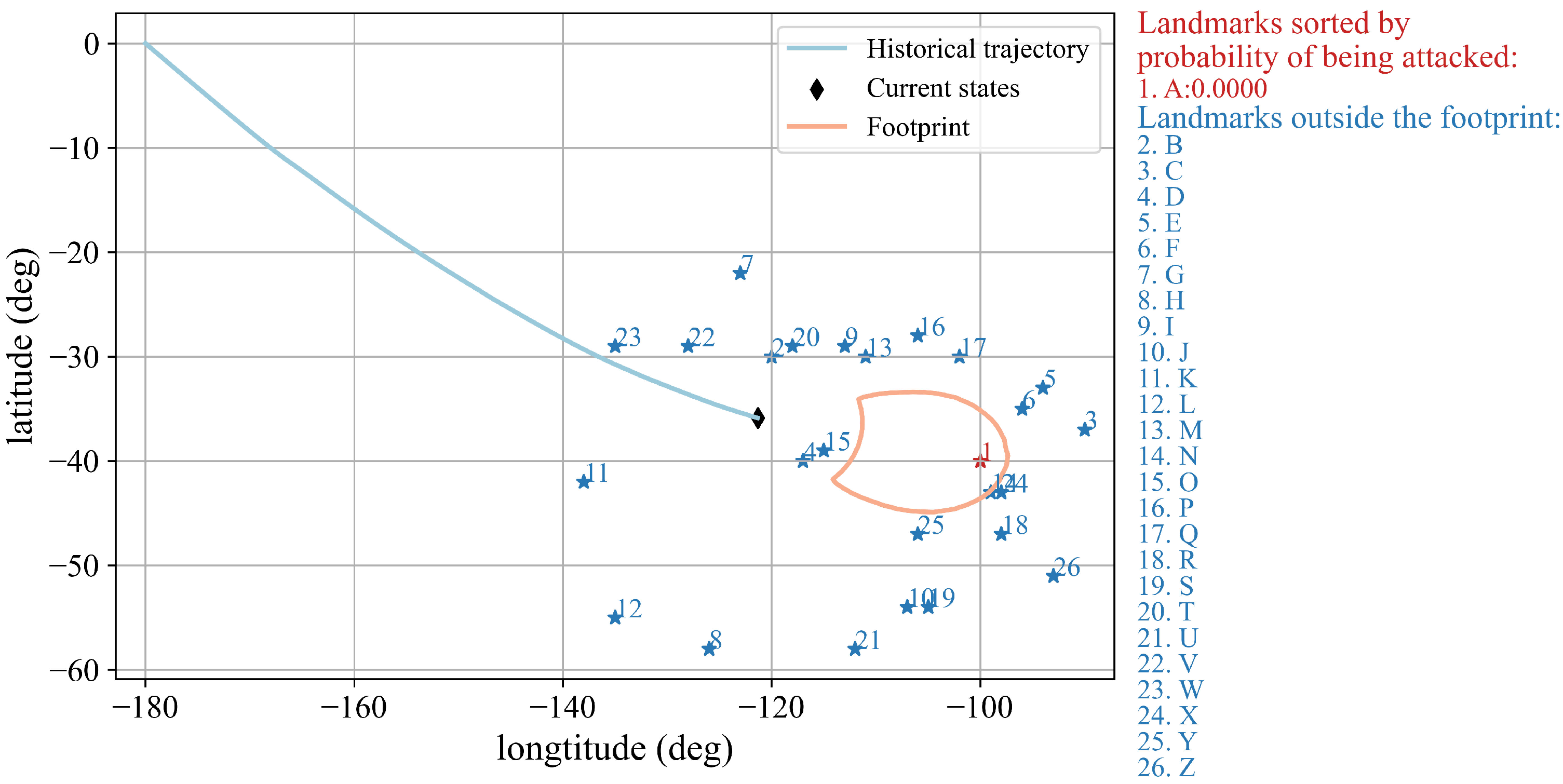
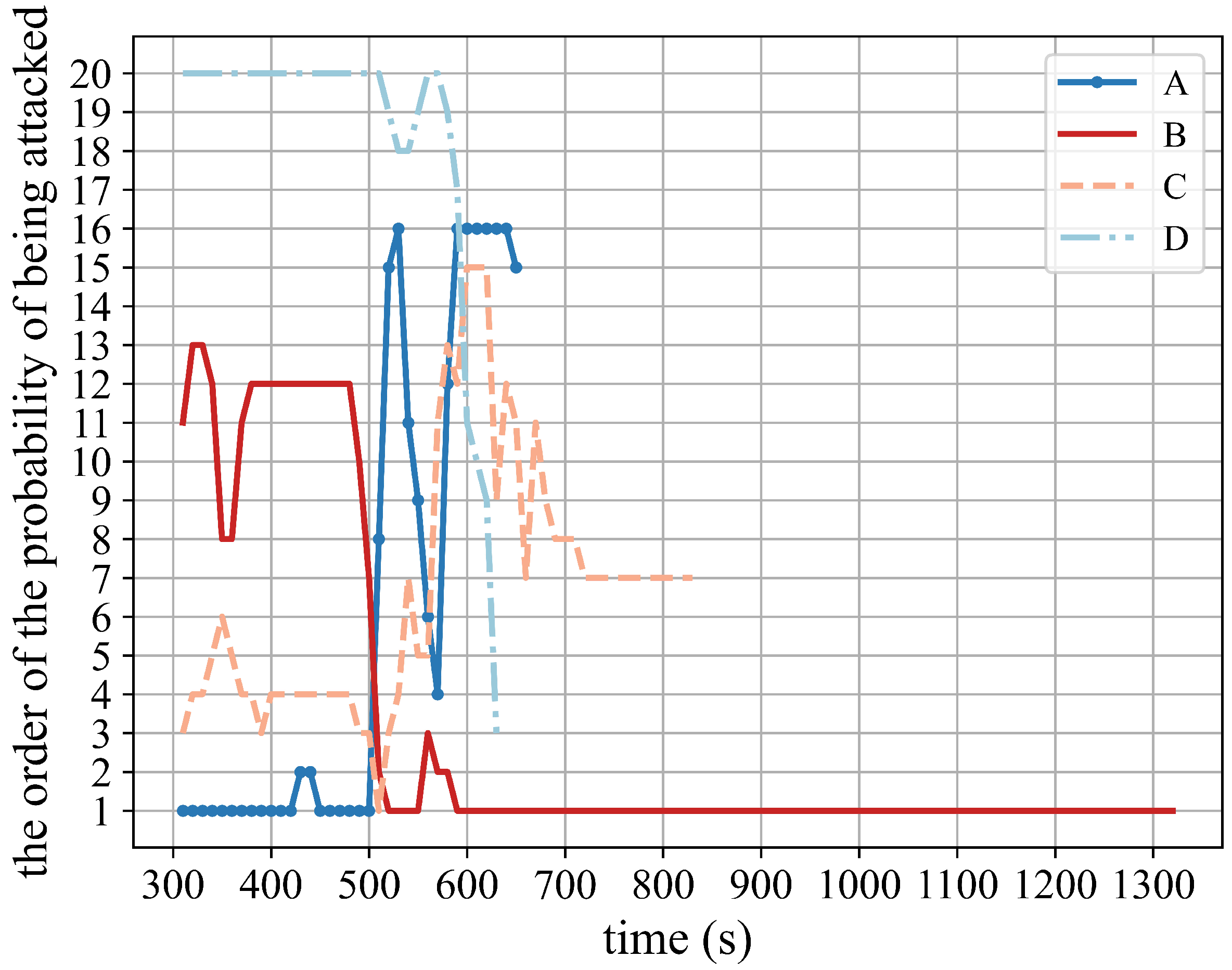
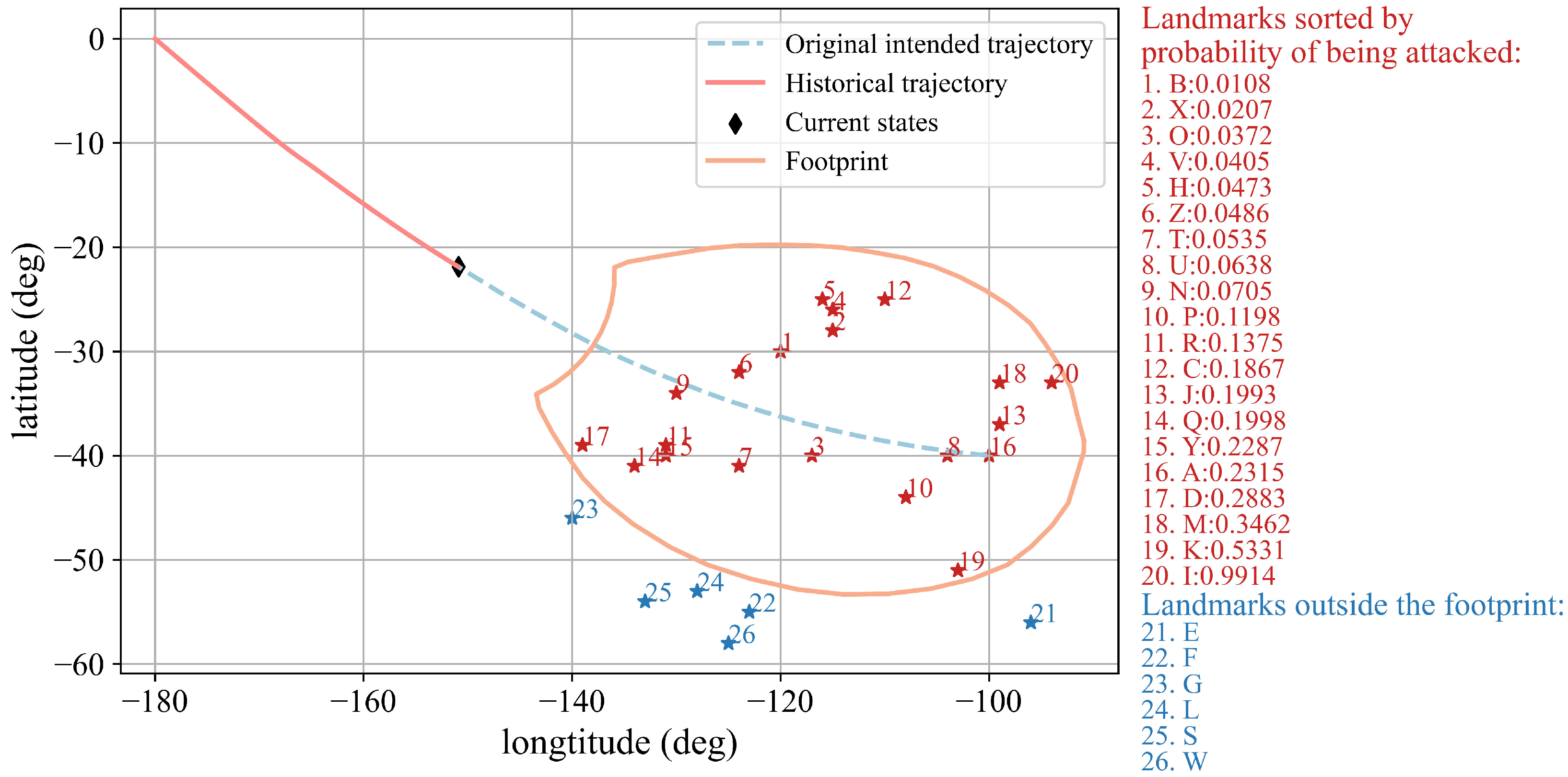
5.2. Typical Intention Inference Simulation
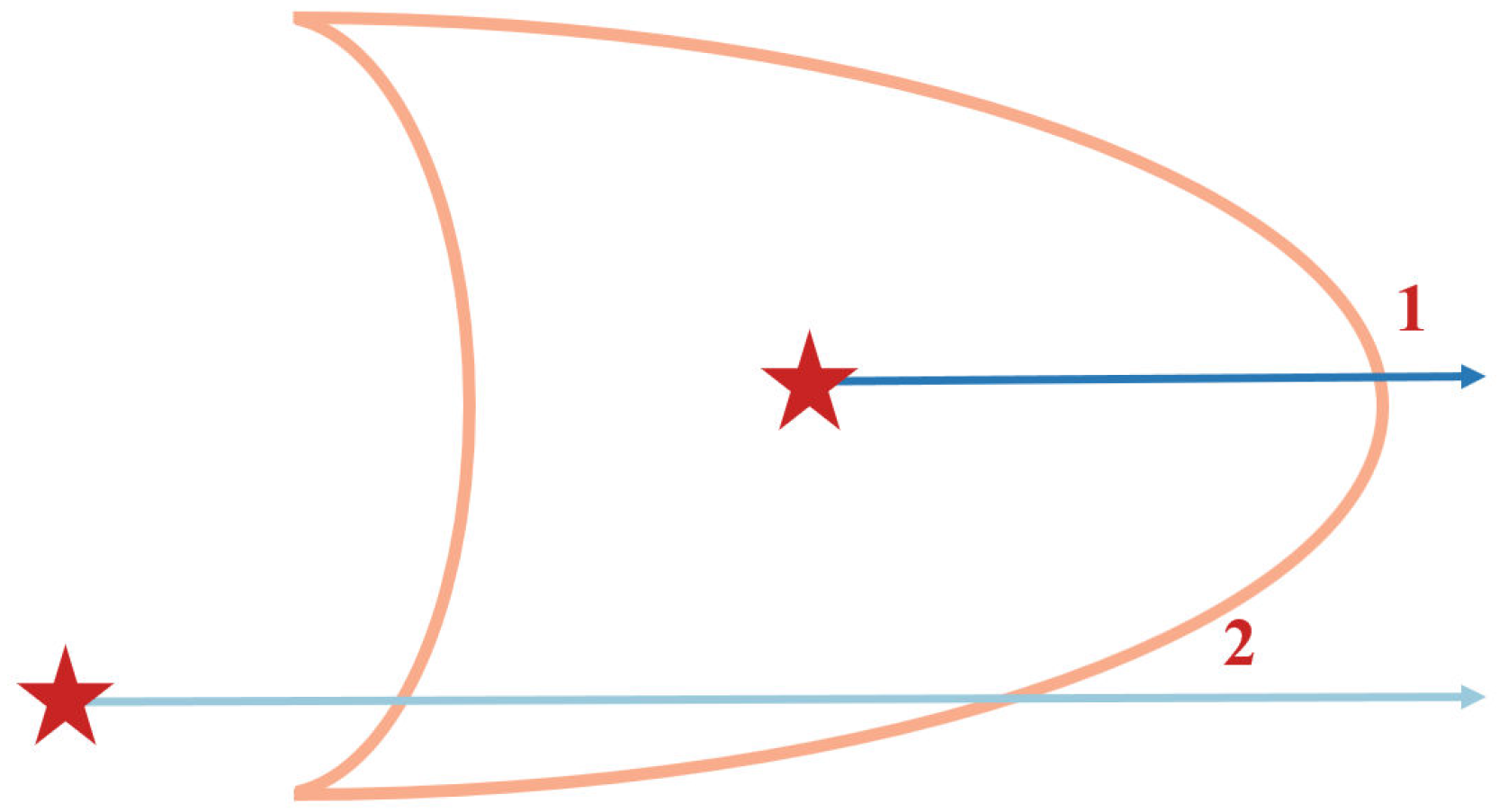
- Historical trajectory of the CAV;
- Footprint at the current state;
- Landmarks that may be attacked within the footprint;
- Temporarily safe landmarks outside the footprint;
- Landmarks within the footprint are ranked by probability of being attacked.
5.3. Evaluation of Forgetting Mechanism
5.4. Advantages and Disadvantages
- The system has good real-time performance.A maximum of 4.74 s is required for one footprint prediction and intention inference (predictions are made for 26 landmarks) due to the substitution of DNN for trajectory integration. Therefore, as long as each prediction period is more than 5 s, it can reconcile the requirements for real-time performance. Table 7 exhibits the comparison of the time consumption by trajectory integrator and DNN. We can see from the Table 7 that a high-precision trajectory integration is time-consuming due to the long flight time. For this reason, it is difficult to meet the demand of real-time performance for footprint prediction and intention inference. In contrast, the DNN shows obvious improvement of the real-time performance while ensuring an acceptable prediction accuracy.
- This system can infer the intention of HGVs that change attack target during flight.This system adopts EWMA and improves EWMV. Mean and variance with forgetting properties makes the system more affected by the recent flight states. Therefore, the forgetting mechanism can infer in a timely manner that the flying HGV has maneuvered and predict its new attack target.
- The system is forward-looking.The first few predictions after the initial descent segment can basically determine which landmark is most likely to be attacked. The flight time of a reentry is about 30 min, and the flight time of the initial descent segment is about five minutes. Forty seconds after the initial descent segment, the most likely landmark to be attacked can be predicted, leaving as much time as possible for the defender to intercept the enemy.In addition, when the HGV changes its attack target during its reentry, the system can also analyze that the HGV has changed its attack intention and predict the new target within 20 s.
- The DNN-based footprint prediction can not only provide decision-making reference for the defender, but also be utilized for the attacker to generate the current footprint of the own HGV.The current literature on footprint generation of HGVs is only from the perspective of the attacker. The footprint of HGVs provides critical information for trajectory planning, such as providing guidance for entering into the TAEM. It takes an average time of 13.42 s to generate a footprint in [13]. Compared with the footprint generation based on the Gaussian pseudospectral method, the calculation speed of [13] has been greatly improved, but it still has room for improvement. If the DNN is utilized to replace the traditional integrator to generate the footprint from the perspective of the attacker, the calculation time of each generation can be less than 1 s, which greatly improves the real-time performance of battlefield mission planning. In addition, since the model, aerodynamic parameters, guidance law, and constraints are completely known, the accuracy of generating the footprint of the friendly HGV will be greatly improved compared with the accuracy of predicting the footprint of the enemy in this study.
- This system can only infer the probability of attacking the set landmarks. If the set landmarks do not include the enemy’s real attack target, the system may only speculate that a set landmark close to the real target is most likely to be attacked.
- Because the research object of the intention inference in this study is non-cooperative vehicles, the overall design parameters and aerodynamic parameters of them are not completely known, and many of them are estimated based on reverse engineering estimation methods [33]. Therefore, the ranges approximated by DNN in this study are not accurate when the enemy model deviates greatly from the hypothetical model in this study, and the predicted footprint will also not be so accurate. In particular, landmarks near the boundary of the footprint are also likely to be attacked.In the future work, we will introduce parameter identification into the footprint prediction and intention inference system to improve the inaccuracy of range prediction and footprint prediction. One solution is to identify lift, drag, aircraft mass, reference area, and bank angle through aerodynamic parameter identification, as suggested in [15]. Another solution is to refer to the idea in [34], that is, to identify the disturbance of the standard aerodynamic data through Kalman filtering. In future work, the aerodynamic parameters will be identified according to the trajectory information of the flying HGVs in real time, and the aerodynamic model fitted by the existing public information or public literature will be continuously corrected. Using the revised aerodynamic model, DNNs can predict more accurate ranges, footprint, and intention in real time.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fahroo, F.; Doman, D.B.; Ngo, A.D. Footprint generation for reusable launch vehicles using a direct pseudospectral method. In Proceedings of the IEEE 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; Volume 3, pp. 2163–2168. [Google Scholar]
- Fahroo, F.; Doman, D. A direct method for approach and landing trajectory reshaping with failure effect estimation. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; p. 4772. [Google Scholar]
- Tian, B.; Fan, W.; Su, R.; Zong, Q. Real-time trajectory and attitude coordination control for reusable launch vehicle in reentry phase. IEEE Trans. Ind. Electron. 2014, 62, 1639–1650. [Google Scholar] [CrossRef]
- Benedikter, B.; Zavoli, A.; Colasurdo, G.; Pizzurro, S.; Cavallini, E. Convex optimization of launch vehicle ascent trajectory with heat-flux and splash-down constraints. J. Spacecr. Rocket. 2022, 59, 900–915. [Google Scholar] [CrossRef]
- Benedikter, B.; Zavoli, A.; Colasurdo, G.; Pizzurro, S.; Cavallini, E. Autonomous Upper Stage Guidance Using Convex Optimization and Model Predictive Control. In Proceedings of the AIAA ASCEND Forum, Online, 16–18 November 2020; p. 4268. [Google Scholar] [CrossRef]
- Benedikter, B.; Zavoli, A.; Colasurdo, G.; Pizzurro, S.; Cavallini, E. Autonomous Upper Stage Guidance with Robust Splash-Down Constraint. arXiv 2022, arXiv:2212.06518. [Google Scholar]
- Lu, P. Asymptotic analysis of quasi-equilibrium glide in lifting entry flight. J. Guid. Control Dyn. 2006, 29, 662–670. [Google Scholar] [CrossRef]
- Lu, P.; Xue, S. Rapid generation of accurate entry landing footprints. J. Guid. Control Dyn. 2010, 33, 756–767. [Google Scholar] [CrossRef]
- Li, H.; Zhang, R.; Zhaoying, L.; Zhang, R. Footprint problem with angle of attack optimization for high lifting reentry vehicle. Chin. J. Aeronaut. 2012, 25, 243–251. (In Chinese) [Google Scholar] [CrossRef]
- Liu, X.; Shen, Z.; Lu, P. Solving the maximum-crossrange problem via successive second-order cone programming with a line search. Aerosp. Sci. Technol. 2015, 47, 10–20. [Google Scholar] [CrossRef]
- Ngo, A.; Doman, D. Footprint determination for reusable launch vehicles experiencing control effector failures. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002; p. 4775. [Google Scholar]
- Saraf, A.; Leavitt, J.; Ferch, M.; Mease, K. Landing footprint computation for entry vehicles. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; p. 4774. [Google Scholar]
- Fu, S.; Lu, T.; Yin, J.; Xia, Q. Rapid algorithm for generating entry landing footprints satisfying the no-fly zone constraint. Int. J. Aerosp. Eng. 2021, 2021, 8827377. [Google Scholar] [CrossRef]
- Zhang, K.; Xiong, J.; Li, F.; Fu, T. Bayesian Trajectory Prediction for a Hypersonic Gliding Reentry Vehicle Based on Intent Inference. J. Astronaut. 2018, 39, 1258–1265. (In Chinese) [Google Scholar]
- Hu, Y.; Gao, C.; Li, J.; Jing, W.; Li, Z. Novel trajectory prediction algorithms for hypersonic gliding vehicles based on maneuver mode on-line identification and intent inference. Meas. Sci. Technol. 2021, 32, 115012. [Google Scholar] [CrossRef]
- Luo, Y.; Tan, X.; Wang, H.; Qu, Z. Method for predicting the attack intention of hypersonic vehicles. J. Xidian Univ. 2019, 46, 113–119. (In Chinese) [Google Scholar]
- Zhou, W.; Yao, P.Y.; Zhang, J.; Wang, X.; Wei, S. Combat Intention Recognition for Aerial Targets Based on Deep Neural Network. Acta Aeronaut. Et Astronaut. Sin. 2018, 39, 322468–322476. [Google Scholar]
- Izzo, D.; Märtens, M.; Pan, B. A survey on artificial intelligence trends in spacecraft guidance dynamics and control. Astrodynamics 2019, 3, 287–299. [Google Scholar] [CrossRef]
- Li, Z.; Sun, X.; Hu, C.; Liu, G.; He, B. Neural network based online predictive guidance for high lifting vehicles. Aerosp. Sci. Technol. 2018, 82, 149–160. [Google Scholar] [CrossRef]
- Horn, J.F.; Schmidt, E.M.; Geiger, B.R.; DeAngelo, M.P. Neural network-based trajectory optimization for unmanned aerial vehicles. J. Guid. Control Dyn. 2012, 35, 548–562. [Google Scholar] [CrossRef]
- Schierman, J.; Hull, J.; Ward, D. Adaptive guidance with trajectory reshaping for reusable launch vehicles. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002; p. 4458. [Google Scholar]
- Cheng, L.; Jiang, F.; Wang, Z.; Li, J. Multiconstrained real-time entry guidance using deep neural networks. IEEE Trans. Aerosp. Electron. Syst. 2020, 57, 325–340. [Google Scholar] [CrossRef]
- Lu, P. Entry guidance: A unified method. J. Guid. Control Dyn. 2014, 37, 713–728. [Google Scholar] [CrossRef]
- Wen, T.; Zeng, X.; Circi, C.; Gao, Y. Hop reachable domain on irregularly shaped asteroids. J. Guid. Control. Dyn. 2020, 43, 1269–1283. [Google Scholar] [CrossRef]
- Yang, H.; Li, S.; Bai, X. Fast homotopy method for asteroid landing trajectory optimization using approximate initial costates. J. Guid. Control. Dyn. 2019, 42, 585–597. [Google Scholar] [CrossRef]
- Cheng, L.; Wang, Z.; Song, Y.; Jiang, F. Real-time optimal control for irregular asteroid landings using deep neural networks. Acta Astronaut. 2020, 170, 66–79. [Google Scholar] [CrossRef]
- Shimrat, M. Algorithm 112: Position of point relative to polygon. Commun. ACM 1962, 5, 434. [Google Scholar] [CrossRef]
- Wang, X.; Guo, J.; Tang, S.; Qi, S.; Wang, Z. Entry trajectory planning with terminal full states constraints and multiple geographic constraints. Aerosp. Sci. Technol. 2019, 84, 620–631. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, L.; Wang, Y. On-line reentry guidance algorithm with both path and no-fly zone constraints. Acta Astronaut. 2015, 117, 243–253. [Google Scholar] [CrossRef]
- Li, Z.; Yang, X.; Sun, X.; Liu, G.; Hu, C. Improved artificial potential field based lateral entry guidance for waypoints passage and no-fly zones avoidance. Aerosp. Sci. Technol. 2019, 86, 119–131. [Google Scholar] [CrossRef]
- Finch, T. Incremental calculation of weighted mean and variance. Univ. Camb. 2009, 4, 41–42. [Google Scholar]
- Phillips, T.H. A common aero vehicle (CAV) model, description, and employment guide. Schafer Corp. AFRL AFSPC 2003, 27, 1–12. [Google Scholar]
- LI, H.; Jin, X.; LIN, P. Modeling and Analyzing of Common Aero Vehicle with Parametric Configuration. J. Astronantics 2011, 32, 2305–2311. [Google Scholar]
- Cui, N.; Lu, B.; Fu, Y.; Zhang, X. Aerodynamic Parameter Identification of a Reentry Vehicle Based on Kalman Filter Method. J. Chin. Inert. Technol. 2014, 6, 755–758. (In Chinese) [Google Scholar]
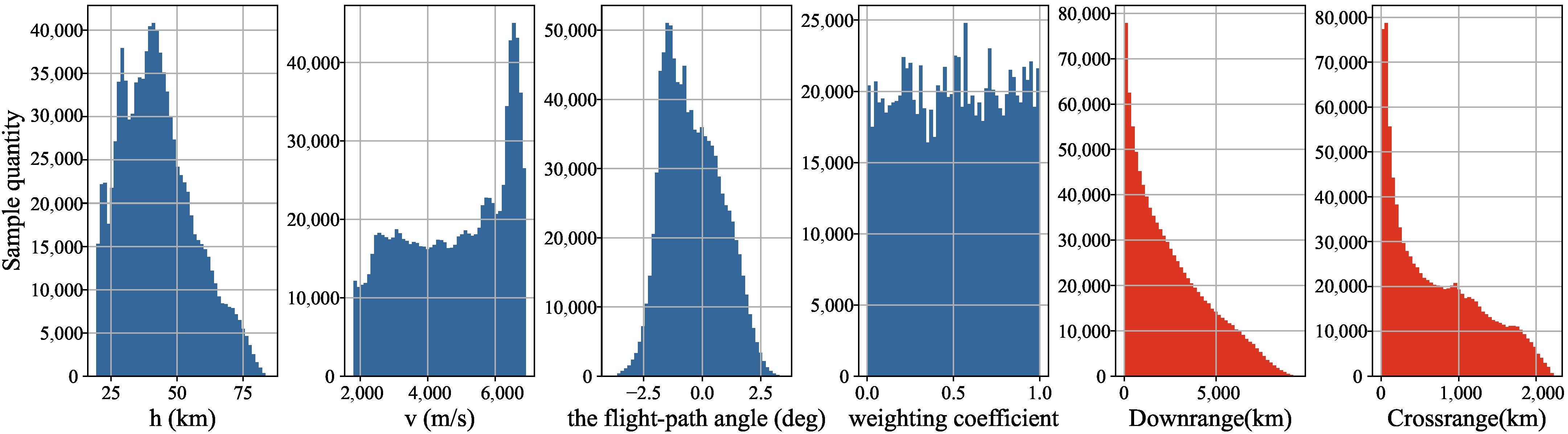



| State | Values | Distribution |
|---|---|---|
| Uniform | ||
| Uniform | ||
| Uniform | ||
| Uniform |
| Mean error | 0.508 km | 0.196 km |
| Mean square error | 0.458 km | 0.152 km |
| Maximum error | 17.01 km | 9.642 km |
| Correlation coefficient | 0.9999906 | 0.9999728 |
| Method | DNN | Integrator | |||
|---|---|---|---|---|---|
| The Number of Times of Range Prediction | 1 | 10 | 10,000 | 1 | 10 |
| Total Time Consumption | 0.041 s | 0.054 s | 0.29 s | 1.86 s | 13.07 s |
| Average Time Consumption | 0.041 s | 5.43 ms | 0.029 ms | 1.86 s | 1.31 s |
| Integrator | DNN | Deviation | |
|---|---|---|---|
| Coordinates of A (deg) | |||
| Coordinates of B (deg) | |||
| Coordinates of C (deg) | |||
| Coordinates of D (deg) | |||
| Coordinates of E (deg) |
| Initial Longitude | Initial Latitude | Longitude of the Target | Latitude of the Target | Guidance Law |
|---|---|---|---|---|
| 180 | 0 | 100 W | 40 S | NPCG |
| Initial Coordinates of the CAV | Coordinates of the Original Target | Time When the Target Is Changed | Coordinates of the Changed Target | Guidance Law |
|---|---|---|---|---|
| (180, 0) | (100 W, 40 S) | 500 s | (20 W, 30 S) | RTG |
| One Range Prediction | One Footprint Prediction | One Intention Inference | ||||
|---|---|---|---|---|---|---|
| Integrator | DNN | Integrator | DNN | Integrator | DNN | |
| Time consumption | 1.53 s | 0.6 ms | 52.71 s | 0.85 s | 189.95 s | 3.66 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Dong, C.; Cheng, L. Deep Neural Network-Based Footprint Prediction and Attack Intention Inference of Hypersonic Glide Vehicles. Mathematics 2023, 11, 185. https://doi.org/10.3390/math11010185
Xu J, Dong C, Cheng L. Deep Neural Network-Based Footprint Prediction and Attack Intention Inference of Hypersonic Glide Vehicles. Mathematics. 2023; 11(1):185. https://doi.org/10.3390/math11010185
Chicago/Turabian StyleXu, Jingjing, Changhong Dong, and Lin Cheng. 2023. "Deep Neural Network-Based Footprint Prediction and Attack Intention Inference of Hypersonic Glide Vehicles" Mathematics 11, no. 1: 185. https://doi.org/10.3390/math11010185
APA StyleXu, J., Dong, C., & Cheng, L. (2023). Deep Neural Network-Based Footprint Prediction and Attack Intention Inference of Hypersonic Glide Vehicles. Mathematics, 11(1), 185. https://doi.org/10.3390/math11010185





