A New Projection Method for a System of Fractional Cauchy Integro-Differential Equations via Vieta–Lucas Polynomials
Abstract
1. Introduction
2. Preliminaries
3. System of Fractional Cauchy Integro-Differential Equations
4. Vieta–Lucas Polynomials
5. Convergence Analysis
6. Numerical Example
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, C.; ur Rahman, M.; Baleanu, D. On fractional-order symmetric oscillator with offset-boosting control. Nonlinear Anal. Model. Control. 2022, 27, 994–1008. [Google Scholar] [CrossRef]
- Eskandari, Z.; Avazzadeh, Z.; Khoshsiar Ghaziani, R.; Li, B. Dynamics and bifurcations of a discrete-time Lotka–Volterra model using nonstandard finite difference discretization method. Math Meth. Appl. Sci. 2022. [Google Scholar] [CrossRef]
- Qu, H.D.; Liu, X.; Lu, X.; ur Rahman, M.; She, Z.H. Neural network method for solving nonlinear fractional advection-diffusion equation with spatiotemporal variable-order. Chaos Solitons Fractals 2022, 156, 111856. [Google Scholar] [CrossRef]
- Li, B.; Liang, H.; He, Q. Multiple and generic bifurcation analysis of a discrete Hindmarsh-Rose model. Chaos Solitons Fractals 2021, 146, 110856. [Google Scholar] [CrossRef]
- Li, B.; Liang, H.; Shi, L.; He, Q. Complex dynamics of Kopel model with nonsymmetric response between oligopolists. Chaos Solitons Fractals 2022, 156, 111860. [Google Scholar] [CrossRef]
- Mennouni, A. Two projection methods for skew-hermitian operator equations. Math. Comput. Model. 2012, 55, 1649–1654. [Google Scholar] [CrossRef]
- Araour, M.; Mennouni, A. A New Procedures for Solving Two Classes of Fuzzy Singular Integro-Differential Equations: Airfoil Collocation Methods. Int. J. Appl. Comput. Math. 2022, 8, 35. [Google Scholar] [CrossRef]
- Mennouni, A. A projection method for solving Cauchy singular integro-differential equations. Appl. Math. Lett. 2012, 25, 986–989. [Google Scholar] [CrossRef]
- Mennouni, A. Airfoil polynomials for solving integro-differential equations with logarithmic kernel. Appl. Math. Comput. 2012, 218, 11947–11951. [Google Scholar] [CrossRef]
- Tasci, D.; Yalcin, F. Vieta-Pell and Vieta-Pell-Lucas polynomials. Adv. Differ. Equ. 2013, 2013, 224. [Google Scholar] [CrossRef]
- Izadi, M.; Yüzbaşı, Ş.; Ansari, K.J. Application of Vieta–Lucas Series to Solve a Class of Multi-Pantograph Delay Differential Equations with Singularity. Symmetry 2021, 13, 2370. [Google Scholar] [CrossRef]
- Heydari, M.H.; Avazzadeh, Z.; Razzaghi, M. Vieta-Lucas polynomials for the coupled nonlinear variable-order fractional Ginzburg-Landau equations. Appl. Numer. Math. 2021, 165, 442–458. [Google Scholar] [CrossRef]
- Adel, M.; Assiri, T.A.; Khader, M.M.; Osman, M.S. Numerical simulation by using the spectral collocation optimization method associated with Vieta-Lucas polynomials for a fractional model of non-Newtonian fluid. Results Phys. 2022, 41, 105927. [Google Scholar] [CrossRef]
- Agarwal, P.; El-Sayed, A.A. Vieta–Lucas polynomials for solving a fractional-order mathematical physics model. Adv. Differ. Equ. 2020, 626, 2020. [Google Scholar] [CrossRef]
- Althubiti, S.; Mennouni, A. A Novel Projection Method for Cauchy-Type Systems of Singular Integro-Differential Equations. Mathematics 2022, 10, 2694. [Google Scholar] [CrossRef]
- Mennouni, A. A new efficient strategy for solving the system of Cauchy integral equations via two projection methods. Transylv. J. Math. Mech. 2022, 14, 63–71. [Google Scholar]
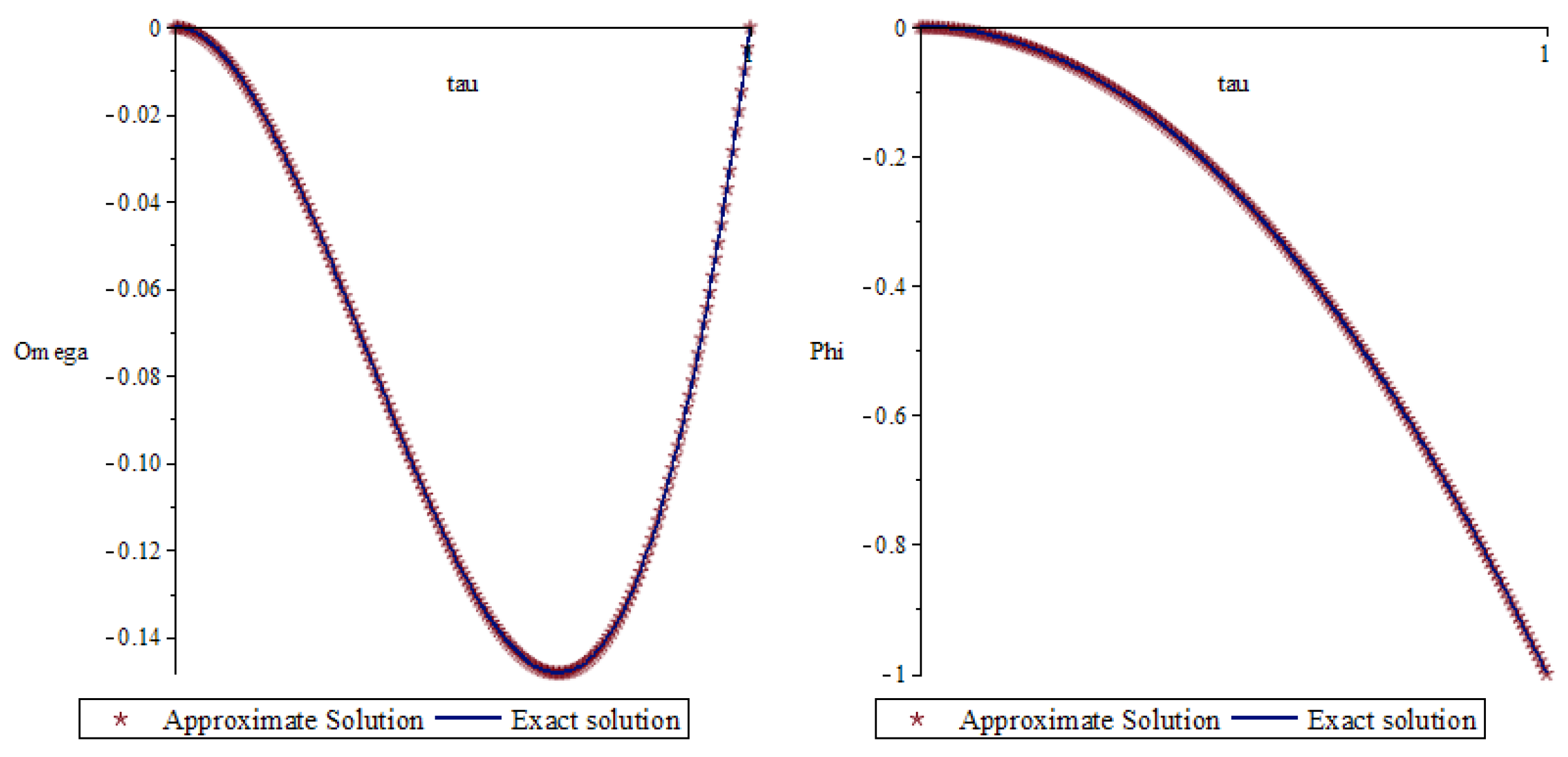
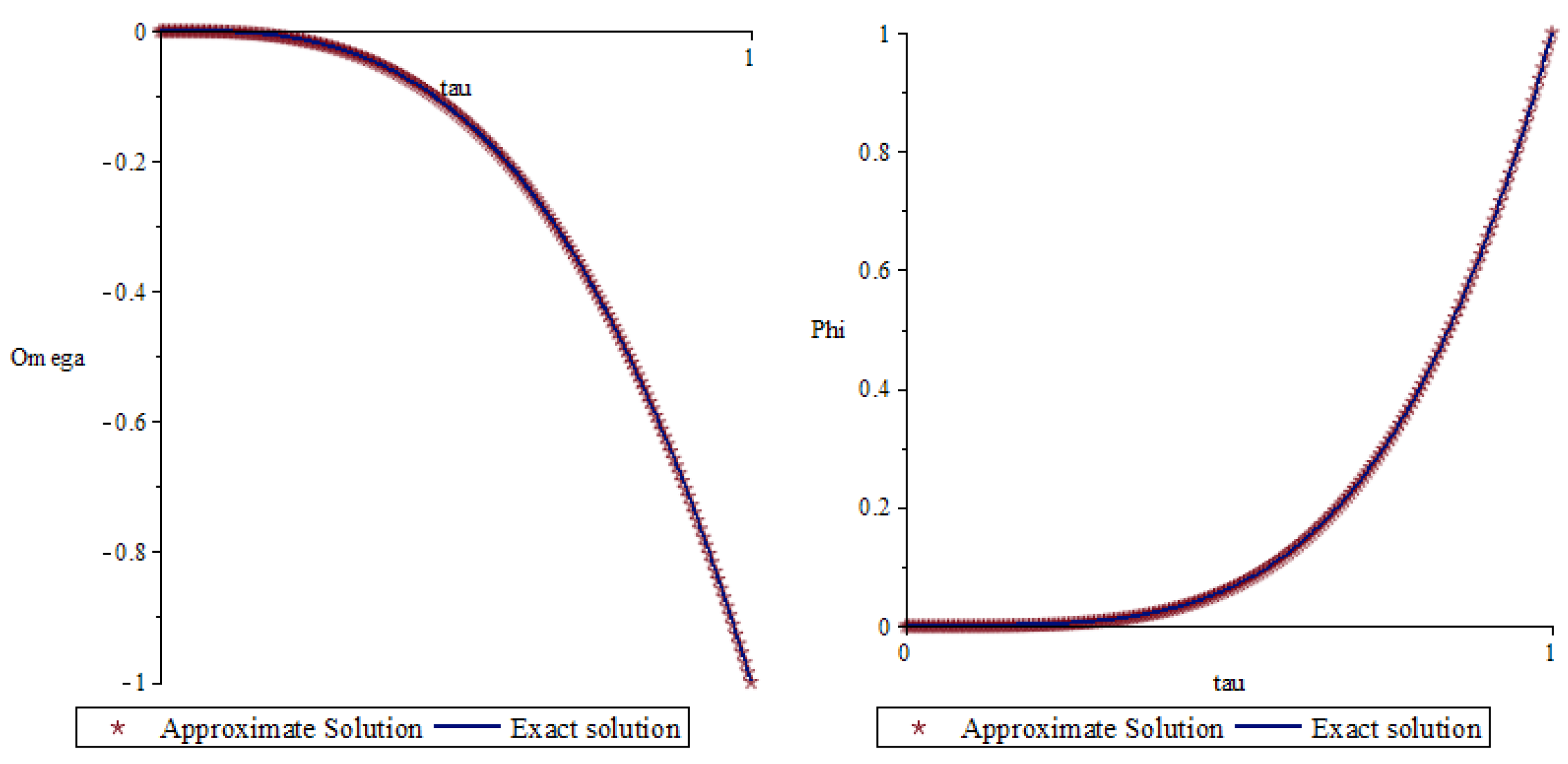
| n | ||
|---|---|---|
| 3 | 4.1428 × 10 | 1.5520 × 10 |
| 5 | 8.6994 × 10 | 3.5924 × 10 |
| 7 | 9.6542 × 10 | 8.2544 × 10 |
| 13 | 7.2543 × 10 | 7.2547 × 10 |
| 17 | 9.2541 × 10 | 3.8531 × 10 |
| 0.3 | 1.0548 × 10 | 3.1473 × 10 |
| 0.4 | 1.2668 × 10 | 1.0739 × 10 |
| 0.6 | 7.9977 × 10 | 3.2081 × 10 |
| 0.7 | 8.4737 × 10 | 4.7114 × 10 |
| 0.8 | 9.8905 × 10 | 9.2993 × 10 |
| 1.3 | 9.1313 | 9.7317 |
| 1.6 | 8.4393 × 10 | 2.3766 × 10 |
| 2.4 | 5.1952 × 10 | 7.0123 × 10 |
| 3.7 | 4.0924 × 10 | 1.4281 × 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moumen, A.; Mennouni, A. A New Projection Method for a System of Fractional Cauchy Integro-Differential Equations via Vieta–Lucas Polynomials. Mathematics 2023, 11, 32. https://doi.org/10.3390/math11010032
Moumen A, Mennouni A. A New Projection Method for a System of Fractional Cauchy Integro-Differential Equations via Vieta–Lucas Polynomials. Mathematics. 2023; 11(1):32. https://doi.org/10.3390/math11010032
Chicago/Turabian StyleMoumen, Abdelkader, and Abdelaziz Mennouni. 2023. "A New Projection Method for a System of Fractional Cauchy Integro-Differential Equations via Vieta–Lucas Polynomials" Mathematics 11, no. 1: 32. https://doi.org/10.3390/math11010032
APA StyleMoumen, A., & Mennouni, A. (2023). A New Projection Method for a System of Fractional Cauchy Integro-Differential Equations via Vieta–Lucas Polynomials. Mathematics, 11(1), 32. https://doi.org/10.3390/math11010032







